如皋市对口单招高三年级第二次联考数学试卷和答案
如皋高三数学考试卷子答案

一、选择题(本大题共10小题,每小题5分,共50分)1. 已知函数f(x) = x^2 - 4x + 3,其对称轴为()A. x = 2B. x = -2C. y = 2D. y = -2答案:A解析:函数f(x) = x^2 - 4x + 3是一个二次函数,其对称轴的公式为x = -b/2a。
代入a = 1,b = -4,得到对称轴为x = 2。
2. 若等差数列{an}的前n项和为Sn,且a1 = 1,d = 2,则S10等于()A. 90B. 100C. 110D. 120答案:B解析:等差数列的前n项和公式为Sn = n/2 (a1 + an)。
由a1 = 1,d = 2,得an = a1 + (n - 1)d = 1 + 2(n - 1)。
代入n = 10,得an = 19,所以S10 =10/2 (1 + 19) = 100。
3. 下列函数中,在其定义域内单调递增的是()A. y = x^2B. y = -x^2C. y = 2xD. y = -2x答案:C解析:单调递增函数的特点是随着自变量的增大,函数值也增大。
对于A和B,函数值在自变量增大时减小,所以排除。
对于C和D,C随着x增大而增大,D随着x 增大而减小,所以选C。
4. 若复数z满足|z - 1| = |z + 1|,则复数z在复平面上的对应点一定位于()A. 实轴B. 虚轴C. 第一象限D. 第二象限答案:A解析:由|z - 1| = |z + 1|,可知复数z到点1和点-1的距离相等,即z位于这两点的中垂线上。
中垂线与实轴重合,所以z位于实轴上。
5. 下列各对数式中,正确的是()A. log2(4) = 2B. log3(9) = 2C. log4(16) = 3D. log5(25) = 2答案:B解析:根据对数的定义,loga(b) = c当且仅当a^c = b。
所以log3(9) = 2,因为3^2 = 9。
6. 若直线y = kx + b与圆x^2 + y^2 = 4相切,则k^2 + b^2的取值范围是()A. (0, 4]B. [4, +∞)C. (0, 4)D. [0, 4]答案:A解析:圆心到直线的距离等于圆的半径,即|kx + b| / √(k^2 + 1) = 2。
江苏省如皋市2019—2020学年高三年级第二学期调研试题(二)数学(WORD版含解析)

江苏省如皋市2019—2020学年高三第二学期4月模拟卷(二)数学试题第I 卷(必做题,共160分)一、填空题(本大题共14小题,每小题5分,共70分,请将答案填写在答题卷相应的位置上.) 1.设全集U =Z ,集合A ={0,2,3},B ={}22x Z x x ∈-<,A I (U B ð)=. 2.若复数z 满足2ii iz ++=,其中i 为虚数单位,则z = . 3.某工厂为了了解一批产品的净重(单位:克)情况,从中随机抽测了100件产品的净重,所得数据均在区间[96,106]中, 其频率分布直方图如图所示,则在抽测的100件产品中,净重在区间[100,104)上的产品件数是 .4.某医院欲从积极扱名的甲、乙、丙、丁4名医生中选择2人去支援武汉抗击“新型冠状病毒”,若毎名医生被选择的机会均等,则甲、乙2人中至少有1人被选择的概率为 . 5.执行右边的伪代码后,输出的结果是 .6.在平面直角坐标系xOy 中,已知双曲线C :22221x y a b-=(a >0,b >0)的左,右焦点分别为F 1,F 2,设过右焦点F 2且与x 轴垂直的直线l 与双曲线C 的两条渐近线分别交于A ,B 两点,若△F 1AB 是正三角形,则双曲线C 的离心率为 . 7.已知函数()sin()f x x ωϕ=+(ω>0),将函数()y f x =的图象向右平移4π个单位长度后,所得图象与原函数图象重合,则ω的最小值等于 . 8.已知等比数列{}n a 的前n 项和为n S ,若121223a a a a =+,且34S ,43S ,52S 成等差数列,则满足不等式40392020n n S a >的n 的最小值为 .9.在三棱锥P —ABC 中,AB ⊥平面PAC ,PC =AB =2AC =2,PA接球O 的表面积为 .10.已知实数x ,y 满足条件05040x y x y y -≤⎧⎪+-≥⎨⎪-≤⎩,若不等式233128mx y x y ≤+恒成立,则实数m的最大值是 .11.如图,在四边形ABCD 中,对角线AC 与BD 相交于点O .已知AC =BC ,AC ⊥BC ,AD ⊥BD ,且O 是AC 的中点,若AD AB CD CB 2⋅-⋅=u u u r u u u r u u u r u u u r ,则AC BD ⋅u u u r u u u r的值为 .12.在平面直角坐标系xOy 中,已知MN 在圆C :22(2)4x y -+=上运动,且MN=若直线l :30kx y -+=上的任意一点P 都满足22PM PN +≥14,则实数k 的取值范围是 .13.已知函数2220()103x x ax a x f x e ex a x x⎧++≤⎪=⎨-+>⎪⎩,,,若存在实数k ,使得函数()y f x k =-有6个零点,则实数a 的取值范围为 .14.在△ABC 中,角A ,B ,C 所对的边分别是a ,b ,c ,若CD 是边AB 上的中线,且CD=CA ,则cos A cos Bb a +的最小值为 . 二、解答题(本大题共6小题,共计90分,请在答题纸指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.) 15.(本小题满分14分)在△ABC 中,角A ,B ,C 所对的边分别是a ,b ,c ,已知b sinA =a cos(B ﹣6π). (1)求角B 的大小;(2)若a =2,c =3,求cos(A ﹣B)的值.16.(本小题满分14分)在三棱柱ABC —A 1B 1C 1中,CA =CB ,AB =BB 1,且∠ABB 1=60°,D 为AC 的中点. (1)求证:B 1C ∥平面A 1BD ; (2)求证:AB ⊥B 1C .17.(本小题满分14分)现有一块废弃的半圆形钢板,其右下角一小部分因生锈无法使用,其形状如图所示,已知该钢板的圆心为O,线段AOB为其下沿,且OA=2m,OB m.现欲从中截取一个四边形AMPQ,其要求如下:点P,Q均在圆弧上,AP平分∠QAB,且PM⊥OB,垂足M 在边OB上.设∠QAB=θ,四边形AMPQ的面积为S(θ)m2.(1)求S(θ)关于θ的函数解析式,并写出其定义域;(2)当cosθ为何值时,四边形AMPQ的面积最大?18.(本小题满分16分)如图,在平面直角坐标系xOy中,已知椭圆C:22221x ya b+=(a>b>0)的焦距为2,且经过点(﹣1,2),过左焦点F且不与x轴重合的直线l与椭圆C交于点A,B两点.(1)求椭圆C的方程;(2)若直线OA,OB,AB的斜率之和为0,求直线l的方程;(3)设弦AB的垂直平分线分别与直线l,椭圆C的右准线m交于点M,N,求MN AB的最小值.19.(本小题满分16分)已知函数1()ln 1f x a x x=+-,其中a ∈R ,e 为自然对数的底数. (1)若a =l ,求函数()f x 在x =1处的切线方程;(2)若函数()f x 在定义域上恰有两个不同的零点,求实数a 的取值范围;(3)设函数1()()xg x e f x x=+-在区间(0,a e -)上存在极值,求证:11a a e a --+>+.20.(本小题满分16分)已知数列{}n a 的前n 项和为n S ,设2nn n a b =. (1)若4121n nS n a -=+,记数列{}n b 的前n 项和为n T .①求证:数列{}n a 为等差数列;②若不等式n nT a λ+≥3对任意的n N *∈都成立,求实数λ的最小值;(2)若n a >0,且112n n S a ++≥,是否存在正整数k ,使得无穷数列1k b +,2k b +,3k b +,…成公差不为0的等差数列?若存在,给出数列{}n a 的一个通项公式;若不存在,请说明理由.第II 卷(附加题,共40分)21.【选做题】本题包括A ,B 两小题,每小题10分共计20分,解答时应写出文字说明,证明过程或演算步骤. A .选修4—2:矩阵与变换已知矩阵A = 2 11 3⎡⎤⎢⎥⎣⎦,B =1 10 1⎡⎤⎢⎥-⎣⎦,求矩阵C ,使得AC =B .B .选修4—4:坐标系与参数方程在极坐标系中,求直线6πθ=(ρ∈R)被曲线4sin()6πρθ=+所截得的弦长.【必做题】第22题、第23题,每题10分,共计20分,解答时应写出文字说明,证明过程或演算步骤. 22.(本小题满分10分)在平面直角坐标系xOy 中,已知抛物线C :x 2=2py (p >0)上一点,m )到准线的距离与到原点O 的距离相等.(1)求抛物线的方程;(2)过不在y 轴上的点P 作抛物线C 的两条切线PA ,PB ,切点分别为A ,B ,若OP ⊥AB ,求证:直线AB 过定点. 23.(本小题满分10分)已知数列{}n a 的首项11a >,且211n n n a a a +=-,n N *∈.(1)求2a 的最小值; (2)求证:2115222nk k a n n =>+-∑.。
2020届高三年级如东-如皋联合调研数学参考答案及评分标准

2020届高三年级第二学期阶段联合调研数学参考答案及评分标准说明:1.本解答给出的解法供参考.如果考生的解法与本解答不同,可根据试题的主要考查内容比照评分标准制订相应的评分细则.2.对计算题,当考生的解答在某一步出现错误时,如果后续部分的解答未改变该题的内容和难度,可视影响的程度决定给分,但不得超过该部分正确解答应得分数的一半;如果后续部分的解答有较严重的错误,就不再给分.3.解答右端所注分数,表示考生正确做到这一步应得的累加分数.4.只给整数分数,填空题不给中间分数.一、填空题(本大题共14小题,每小题5分,计70分.不需写出解答过程,请把答案写在答题纸的指定位置上)1.{}|0x x>2.—23.534.65.3106.2337.348.19.2310.111212.[-34,+∞)13.[e2,4e]14.4333-二、解答题(本大题共6小题,计90分.解答应写出必要的文字说明,证明过程或演算步骤,请把答案写在答题纸的指定区域内)15.(本小题满分14分)(1)因为12 BD AD c-=,所以1cos cos2a Bb A c-=,………………2分由正弦定理,得1sin cos sin cos sin2A B B A C-=,所以sin2sin()C A B=-.………………6分(2)由(1)得,sin()2sin()A B A B+=-,所以sin cos cos sin2(sin cos cos sin)A B A B A B A B+=-,化简,得3cos sin sin cosA B A B=.………………8分又3cos5A=,所以4sin5A=,所以4tan3A=,4tan9B=,………………10分所以44tan tan4839tan tan()1tan tan4411139A BC A B A B++=-+=-=-=---⋅.………………14分16.(本小题满分14分)(1)如图,取BC的中点G,连结AG,FG.因为F为C1B的中点,所以FG=∥12C1C.………………2分在三棱柱ABC-A1B1C1中,A1A=∥C1C,且E为A1A的中点,所以FG=∥EA.所以四边形AEFG是平行四边形.所以EF∥AG.………………4分因为EF⊄平面ABC,AG⊂平面ABC,所以EF∥平面ABC.………………6分(2)因为在正三棱柱ABC-A1B1C1中,A1A⊥平面ABC,BD⊂平面ABC,所以A1A⊥BD.………………8分(第16题)ABC DEC1A1B1FG因为D 为AC 的中点,BA =BC ,所以BD ⊥AC .因为A 1A ∩AC =A ,A 1A ⊂平面A 1ACC 1,AC ⊂平面A 1ACC 1,所以BD ⊥平面A 1ACC 1.因为C 1E ⊂平面A 1ACC 1,所以BD ⊥C 1E .………………10分根据题意,可得EB =C 1E =62AB ,C 1B =3AB ,所以EB 2+C 1E 2=C 1B 2.从而∠C 1EB =90°,即C 1E ⊥EB .………………12分因为BD ∩EB =B ,BD ⊂平面BDE ,EB ⊂平面BDE ,所以C 1E ⊥平面BDE .………………14分17.(本小题满分14分)(1)由题意,得PQ =50-50cos θ.从而,当θ=2π3时,PQ =50-50cos 2π3=75.即点P 距地面的高度为75m .………………4分(2)方法一:由题意,得AQ =50sin θ,从而MQ =60-50sin θ,NQ =300-50sin θ.又PQ =50-50cos θ,所以tan ∠NPQ =NQ PQ =6-sin θ1-cos θ,tan ∠MPQ =MQ PQ =6-5sin θ5-5cos θ.从而tan ∠MPN =tan(∠NPQ -∠MPQ )=tan ∠NPQ -tan ∠MPQ1+tan ∠NPQ ⋅tan ∠MPQ =6-sin θ1-cos θ-6-5sin θ5-5cos θ1+6-sin θ1-cos θ×6-5sin θ5-5cos θ=12(1-cos θ)23-18sin θ-5cos θ.………………8分令g (θ)=12(1-cos θ)23-18sin θ-5cos θ,θ∈(0,π),则g '(θ)=12×18(sin θ+cos θ-1)(23-18sin θ-5cos θ)2,θ∈(0,π).………………10分由g '(θ)=0,得sin θ+cos θ-1=0,解得θ=π2.当θ∈(0,π2)时,g '(θ)>0,g (θ)为增函数;当θ∈(π2,π)时,g '(θ)<0,g (θ)为减函数,所以,当θ=π2时,g (θ)有极大值,也为最大值.………………12分因为0<∠MPQ <∠NPQ <π2,所以0<∠MPN <π2,从而当g (θ)=tan ∠MPN 取得最大值时,∠MPN 取得最大值.即当θ=π2时,∠MPN 取得最大值.………………14分方法二:以点A 为坐标原点,A M 为x 轴建立平面直角坐标系,则圆O 的方程为x 2+(y -50)2=502,即x 2+y 2-100y =0,点M (60,0),N (300,0).设点P 的坐标为(x 0,y 0),所以Q (x 0,0),且x 02+y 02-100y 0=0.从而tan ∠NPQ =NQ PQ =300-x 0y 0,tan ∠MPQ =MQ PQ =60-x 0y 0.从而tan ∠MPN =tan(∠NPQ -∠MPQ )=tan ∠NPQ -tan ∠MPQ1+tan ∠NPQ ⋅tan ∠MPQ =300-x 0y 0-60-x 0y 01+300-x 0y 0×60-x 0y 0=24y 010y 0-36x 0+1800.………………6分由题意知,x 0=50sin θ,y 0=50-50cos θ,所以tan ∠MPN ==12(1-cos θ)23-18sin θ-5cos θ.………………8分(下同方法一)18.(本小题满分16分)(1)由题意知:222222121321b a a b ⎧⎛⎫⎪-=⎪ ⎪⎪⎝⎭⎪⎨⎛⎫ ⎪⎝⎭+=⎩,解得2241a b ⎧=⎪⎨=⎪⎩,………………2分所以椭圆C 的方程为2214x y +=.………………4分(2)设直线PQ的方程为(2y x =-,与椭圆联立得2320x -+=,所以12433x x +=,1223x x =,则122PQ x =-==,又点A 到直线PQ 的距离为3233d +=,………………7分所以三角形APQ的面积为113322233PQ d ++⋅⋅=⋅⋅=………………9分(3)由题意知直线l 的斜率存在,设l 的方程为:()2y k x =+,联立方程组()42142x y y k x ⎧+=⎪⎨⎪=+⎩,消去y 整理得:()222214161640k x k x k +++-=,由22164214B k x k --=+,得222814B k x k -=+,………………12分将0x =代入()2y k x =+中,得到2C y k =,得2k =,解得218k =.………………14分所以直线l 的斜率为24±.………………16分19.(本小题满分16分)(1)令()ln 1g x x x =-+,所以()111xg x x x-'=-=.………………1分当()0,1x ∈时,()0g x '>,()g x 在()0,1上单调递增;当()1,x ∈+∞时,()0g x '<,()g x 在()1,+∞上单调递减;所以()()max 10g x g ==,所以()g x 的零点为1x =.………………3分(2)因为111222ln 1ln 1a x x x a x x x ⎧=+-⎪⎪⎨⎪=+-⎪⎩,所以211221ln ln 1x x a x x x x ⎛⎫-=⋅- ⎪-⎝⎭,………………5分要证121a x x x <-,即证211212121ln ln 1x x x x x x x x x ⎛⎫-⋅-<- ⎪-⎝⎭,即证2112ln 1x x x x ⎛⎫>-⎪⎝⎭,………………7分令211x t x =>,1ln 1t t>-,由(1)知ln 1x x ≤-,当且仅当1x =取等,所以11ln 1t t<-,即1ln 1t t>-,所以原不等式成立.………………9分(3)不等式()()221ln 1x x k x -≥-对一切正实数x 恒成立.因为()()()()22211ln 11ln 1k x x x k x x x x -⎡⎤---=--⎢⎥+⎣⎦.设()()1ln 1k x h x x x -=-+,则()()()()2222111211x k x k h x x x x x +-+'=-=++.………………10分记()()2211x x k x ϕ=+-+,()()241442k k k ∆=--=-,①当0∆≤,即02k <≤时,()0h x '≥恒成立,故()h x 单调递增.于是当01x <<时,()()10h x h <=,又210x -<,故()()221ln 1x x k x ->-,当1x >时,()()10h x h >=,又210x ->,故()()221ln 1x x k x ->-,又当1x =时,()()221ln 1x x k x -=-.因此当02k <≤时,不等式恒成立.………………13分②当0∆>,即2k >时,设()22110x k x +-+=的两个不等实数根分别为3x ,4x (34x x <).又()1420k ϕ=-<,于是3411x k x <<-<.故当()1,1x k ∈-时,()0h x '<,从而()h x 在()1,1k -在单调递减;当()1,1x k ∈-时,()()10h x h <=,此时210x ->,于是()()210x h x -<,即()()221ln 1x x k x -<-,舍去;………………15分综上,k 的取值范围是02k <≤.………………16分20.(本小题满分16分)(1)①因为3b 1,2b 2,b 3成等差数列,所以4b 2=3b 1+b 3,即4×3a +3d 2=3(2a +d )+4a +6d3,解得,a d =34.………………3分②由a n +1≤b n <a n +2,得a +nd ≤(n +1)a +(n +1)nd2n a +(n +1)d ,2-n -2ad ≤0,n 2+n -2a d>0,………………5分解得-1+1+8ad 2<n ≤1+1+8a d 2,由于1+1+8a d 2--1+1+8a d 2=1且-1+1+8a d 2>0.因此存在唯一的正整数n ,使得a n +1≤b n <a n +2.………………8分(2)因为b t b r =a 1(1-q t +1)t (1-q )a 1(1-q r +1)r (1-q )=t +2r +2,所以q t +1-1t (t +2)=q r +1-1r (r +2).………………9分设f (n )=q n +1-1n (n +2),n ≥2,n ∈N *.则f (n +1)-f (n )=q n +2-1(n +1)(n +3)-q n +1-1n (n +2)=q n +1[(q -1)n 2+2(q -2)n -3]+2n +3n (n +1)(n +2)(n +3),因为q >2,n ≥2,所以(q -1)n 2+2(q -2)n -3>n 2-3≥1>0,所以f (n +1)-f (n )>0,即f (n +1)>f (n ),即f (n )单调递增.………………12分所以当r ≧2时,t >r ≧2,则f (t )>f (r ),即q t +1-1t (t +2)>q r +1-1r (r +2),这与q t +1-1t (t +2)=q r +1-1r (r +2)互相矛盾.所以r =1,即q t +1-1t (t +2)=q 2-13.若t ≧3,则f (t )≥f (3)=q 4-115=q 2-13·q 2+15>q 2-13,即q t +1-1t (t +2)>q 2-13,与q t +1-1t (t +2)=q 2-13相矛盾.于是t =2,所以q 3-18=q 2-13,即3q 2-5q -5=0.又q >2,所以q =5+856.………………16分2020届高三年级第二学期阶段联合调研数学附加题参考答案及评分标准说明:1.本解答给出的解法供参考.如果考生的解法与本解答不同,可根据试题的主要考查内容比照评分标准制订相应的评分细则.2.对计算题,当考生的解答在某一步出现错误时,如果后续部分的解答未改变该题的内容和难度,可视影响的程度决定给分,但不得超过该部分正确解答应得分数的一半;如果后续部分的解答有较严重的错误,就不再给分.3.解答右端所注分数,表示考生正确做到这一步应得的累加分数.4.只给整数分数,填空题不给中间分数.21.【选做题】在A 、B 、C 三小题中只能选做2题,每小题10分,共计20分.请在答卷纸指定区域内作答.解答应写出文字说明、证明过程或演算步骤.A .选修4—2:矩阵与变换∵1101,20201A B ⎡⎤⎡⎤⎢⎥==⎢⎥⎢⎥⎣⎦⎣⎦,∴111011=22020102AB ⎡⎤⎡⎤⎡⎤⎢⎥⎢=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦.………………4分在直线l '上任取一点(,)P x y ,它是由l 上的点000(,)P x y 经矩阵AB 所对应的变换所得,∵点000(,)P x y 在直线:20l x y +-=上,∴0020x y +-=.①∴00x x AB y y ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦,即0011202x x y y ⎡⎤⎡⎤⎡⎤⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦,∴000122x y x y y ⎧+=⎪⎨⎪=⎩,即001412x x y y y ⎧=-⎪⎪⎨⎪=⎪⎩.②将②代入①得112042x y y -+-=,即480x y +-=,∴直线l '的方程为480x y +-=.………………10分B .选修4—4:坐标系与参数方程因为点M的极坐标为4π,所以点M 的直角坐标为(1,1),………………2分因为圆C的极坐标方程为04ρθπ++=,所以将cos x ρθ=,sin y ρθ=,222x y ρ=+代入上式,可得圆C 的直角坐标方程为22(1)(1)2x y +++=,………………4分当直线l 的斜率不存在时,直线l 与圆C 没有交点,………………6分当直线l 的斜率存在时,设直线l 的方程为1(1)y k x -=-,则圆心(1,1)C --到直线l的距离为d =因为直线l 被圆C 截得的弦长为2305,所以2230()25d +=,即245=,解得12k =或2k =,所以直线l 的方程为210x y -+=或210x y --=.………………10分【必做题】第22题、第23题,每题10分,共计20分.请在答卷卡指定区域内作答.解答应写出文字说明、证明过程或演算步骤.22.(本小题满分10分)(1)因为点A (1,a )(a >0)是抛物线C 上一点,且AF =2,所以p 2+1=2,所以p =2.………………2分(2)由(1)得抛物线方程为y 2=4x .(3)因为点A (1,a )(a >0)是抛物线C 上一点,所以a =2.………………4分设直线AM 方程为x -1=m (y -2)(m ≠0),M (x 1,y 1),N (x 2,y 2).-1=m (y -2),2=4x ,消去x ,得y 2-4m y +8m -4=0,………………6分即(y -2)(y -4m +2)=0,所以y 1=4m -2.因为AM ⊥AN ,所以-1m 代m ,得y 2=-4m-2,………………8分所以d 1d 2=|(y 1+2)(y 2+2)|=|4m ×(-4m)|=16.………………10分23.(本小题满分10分)(1)因为含元素1的子集有23C 个,同理含2,3,4的子集也各有23C 个,于是所求元素之和为23(1234)30C +++⨯=.………………2分(2)集合{}1,2,3,,M n = 的所有3个元素的子集中:以1为最小元素的子集有21n C -个,以n 为最大元素的子集有21n C -个;以2为最小元素的子集有22n C -个,以1n -为最大元素的子集有22n C -个;以2n -为最小元素的子集有22C 个,以3为最大元素的子集有22C 个.………………5分31n C i i m =∴∑312n C m m m =+++ 222122(1)()n n n C C C --=++++ 22231233(1)()n n n C C C C --=+++++ 22231244(1)()n n n C C C C --=+++++ 3(1)nn C ==+ 3131n C i i nm n C =∴=+∑………………8分32018132018201812019C i i m C =∴=+=∑………………10分。
江苏省南通市如皋市十四校联考2024-2025学年高三上学期教学质量调研(二) 数学试题

江苏省南通市如皋市十四校联考2024-2025学年高三上学期教学质量调研(二)数学试题一、单项选择题(本大题共8小题,每小题5分,共计40分.在每小题给出的四个选项中,只有一个是符合题目要求的,请把答案填涂在答题卡相应位置上)1.某运动员在一次训练中共射击6次,射击成绩(单位:环)如下:6,7,7,9,9,10.则下列说法正确的是()A 、成绩的极差为-4B .成绩的第50百分位数等于成绩的平均数C .成绩的中位数为7和9D .若增加一个成绩8,则成绩的方差不变2.已知集合{21,3,4},{},2R ,A B xx m x =-=-<∈‖∣,若R A B ⋂=∅ð,则实数m 取值范围为()A.4m > B.4m C.2m D.2m >3.抛掷质地均匀的骰子两次,得到的点数分别为m ,n .设平面向量(4,2),(,)a b m n == ,则向量,a b不能作为平面内的一组基底的概率为()A.112B.16 C.14D.134.若πtan 23α⎛⎫+= ⎪⎝⎭,则πcos 23α⎛⎫- ⎪⎝⎭的值为()A.45 B.45-C.35D.35-5.已知x ,y 为正实数,则可成为“x y <”的充要条件的是()A.11x y< B.ln ln x y y x +<+ C.sin sin x y < D.cos cos x y y x-<-6.位于如皋市定慧寺内的观音塔,是一座仿明清古塔建筑,具有七层、八角彩绘的外观.观音塔除去塔尖部分可近似视为一个正四棱台,现有一个除去塔尖的观音塔模型,塔底宽20cm ,塔顶宽10cm ,侧面面积为2,据此计算该观音塔模型体积为()3cm .A.31500B.30000C.10500D.100007.已知动点P 在拋物线24x y =上,定点(1,4)D .圆22:(1)3F x y +-=上两个动点A ,B 满足1||()2AB FM FA FB ==+,则||||PM PD + 的最小值为()A.7B.6C.5D.48.已知函数()f x 的定义域为(0,)+∞,对(0,)+∞内的任意两个不相等的数12,x x ,都有()()12120,()22(1)(2)f x f x f x f x x x x x ->+=-+≥-且(2)2f =.若实数m ,n 满足623m f n ⎛⎫<< ⎪⎝⎭,则n m -的最小值为()A.202B.192C.20D.19二、多项选择题(本大题共3小题,每小题6分,共计18分.在每小题给出的四个选项中,至少有两个是符合题目要求的,请把答案填涂在答题卡相应位置上)9.下列函数中,在区间ππ,42⎛⎫⎪⎝⎭上单调递减的函数是()A.πsin 4y x ⎛⎫=+⎪⎝⎭B.cos y x x =- C.|sin 2|y x = D.πcos 3y x ⎛⎫=-⎪⎝⎭10.随机事件A ,B 满足111(),(),()232P A P B P A B ===∣,则下列说法正确的是()A.事件AB 与AB 互斥B.事件A 与B 相互独立C.()()P A B P B += D.(()P B A P A =∣11.在平面直角坐标系xOy 中,椭圆22:143x y C +=的左、右焦点分别为12,F F ,经过点1F 的直线l 与椭圆C 交于A ,B 两点(其中点A 在x 轴上方),连接22,AF BF .现将平面12AF F 沿x 轴向上折叠,使得面12AF F ⊥面12F F B ,则下列说法正确的是()A.当直线l 的倾斜角为π3时,2AO BF ⊥B.当直线l 的倾斜角为π3时,三棱锥12A BF F -的外接球的表面积为884π75C.三棱锥12A BF F -的体积最大值为94D.当2ABF 折叠后的周长为152时,直线l 的斜率为33514±三、填空题(本大题共3小题,每小题5分,共计15分.请把答案填写在答题卡相应位置上)12.已知i 为虚数单位,复数z 满足42i i (1i)z z +=++,则||z =______.13.某工厂生产的A 产品的长度l (单位:cm )服从正态分布()25,3N ,按长度l 分为5级:10l为一级,810l < 为二级,68l < 为三级,46l < 为四级,4l <为废品.将一级与二级产品称为优品.对该工厂生产的A 产品进行随机抽查,每次抽取1个,则抽到优品的概率p =______(精确到0.1).若抽出的是优品,则抽查终止,否则继续抽查直到抽到优品,则抽查次数不超过两次的概率为______.附:()0.6827,(22)0.9545P Z P Z μσμσμσμσ-<+=-<+=,(33)0.9773P Z μσμσ-<+= 14.在平面直角坐标系xOy 中,椭圆2222:1(0)x y C a b a b+=>>的左、右焦点分别为12,F F ,点P 在椭圆C 上且121π,3F PF PF ∠=的平行线OQ 与12F PF ∠的角平分线交于,||Q OQ b =,则椭圆C 的离心率为______.四、解答题(本大题共5小题,共计77分.请在答题卡指定区域内作答.解答时应写出文字说明、证明过程或演算步骤)15.(本小题满分13分)在ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c ,点D 在边AC 上且||2||AD DC =,2sin sin cos sin sin cos 4sin B C A C A B A +=.(1)求证:2c a =;(2)若1a =,求||b BD ⋅的最大值.16.(本小题满分15分)为调查某地区学生在高中学习中错题订正整理情况与考试成绩的关系.首先对该地区所有高中学生错题订正整理情况进行分值评价,给出得分;再组织考试.从这些学生中随机抽取20名学生的错题订正整理情况得分x 和对应的考试成绩y 作为样本,得到样本数据(),(1,2,,20)i i x y i = ,其中i x 和i y 分别表示第i 个样本错题订正整理情况得分和对应的考试成绩,计算得20212080,ii xx =-=∑()20219000,ii yy =-=∑20120800i i i x y xy =-=∑.(1)求样本(),(1,2,,20)i i x y i = 的相关系数(精确到0.01),并推断考试成绩y 和错题订正整理情况得分x 的相关程度;(2)已知20个样本中有8个样本的考试成绩低于样本平均数y .利用频率估计概率,从该地区所有高中学生中随机抽取4个学生的错题订正整理情况得分和对应的考试成绩,记抽到考试成绩低于y 的个数为X ,求随机变量X 的分布列.附:相关系数()()1.414niix x y y r --=≈∑.17.(本小题满分15分)在三棱锥A BCD -中,ABD 是边长为2的正三角形,P ,M 分别为线段AD ,CD 的中点,,CDAD CD AD ⊥>,平面ABD ⊥平面BCD .(1)求证:BD CD ⊥;(2)若AC 与平面BCP 所成角的余弦值为26,求二面角P BM D --的余弦值.18.(本小题满分17分)已知函数()f x 的导函数为()f x ',且121()e(1)13x f x f x -'=++.(1)求函数()f x 在点(1,(1))f 处的切线方程;(2)若对于任意的[1,2],()x f x mx ∈-恒成立,求实数m 的取值范围.19.(本小题满分17分)已知双曲线2222:1(0,0)x y C a b a b-=>>过点(2,0)A -,其渐近线方程为20x y ±=.圆B 过点(3,0),(3,0)M N -,与y 轴交于E ,F .记直线EA 与双曲线C 的另一个交点为P ,直线FA 与双曲线C 的另一个交点为Q .(1)求双曲线C 的标准方程;(2)求证:直线AE 和直线AF 斜率之积为定值;(3)判断直线PQ 与圆B 的位置关系,并说明理由.2024-2025学年度高三年级第一学期教学质量调研(二)数学试题一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.【答案】B【解析】1064-=,极差为4 A ,错.第50百分位数7982+=,平均数1(6779910)86+++++=,B 对.2.【答案】A【解析】R A B ⋂=∅ð,则22},{B B xm x m ≠∅=-+<<+∣,{2B x x m =≤-R ∣ð或},2x m A B ≥+⋂=∅R ð,则22,424m m m -<-⎧∴>⎨+>⎩,选A.3.【答案】A【解析】,a b 不能作为基底,则42n m =,即,312361 2m n P ===,选A.4.【答案】C 【解析】π2ππcos 2cos 2πcos 2333ααα⎛⎫⎛⎫⎛⎫-=+-=-+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭222222πππcos sin 1tan 143333πππ145cos sin 1tan 333αααααα⎛⎫⎛⎫⎛⎫+-+-+ ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭=-=-=-=+⎛⎫⎛⎫⎛⎫+++++ ⎪ ⎪ ⎝⎭⎝⎭⎝⎭,选C.5.【答案】D 【解析】,110A x y x y<⇔>>错.ln ln ln ln x y y x x x y y x y +<+⇔-<-<¿,В错.sin sin x y x y <<¿,C 错,选D.6.【答案】C【解析】每个侧面面积,侧面的高1h,则111(2010)2h h +=∴=侧棱长=,正四棱台的高45h ==,1(400100200)4515003,0V =++⨯=选C.7.【答案】D【解析】1()2FM FA FB =+,则M 为AB 中点,22AB =,则1FM =1114PM PD PF PD PP PD DP ''+≥-+=+-≥-=(其中PP '为P 到准线1y =-的距离),选D.8.【答案】B【解析】(2)22(1)2(1)1f f f +=+⇒=,令()2[(1)(1)]f x ax b f x a x b ++=-+-+()2(1)2f x f x ax a b ⇒=-+-+和原式比较1,()2[(1)1]0a f x x f x x b =⎧⇒∴+=-+-⎨=⎩19196262556255622233333333f ff f ⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫∴+=+⇒=+- ⎪ ⎪ ⎪⎢⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦⎣⎦1212,0,x x x x ∀>≠ 都有()()12120,()f x f x f x x x ->∴-在(0,)+∞上单调递增191958626211621(1)(2)222333333f f f f ⎛⎫⎛⎫∴=<<=⇒⋅-<<⋅-⎪ ⎪⎝⎭⎝⎭19191919min 118222,()233n m n m ∴-≥⋅-⋅=-=,选:B.二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.9.【答案】AC 【解析】ππππ3ππ,,()sin 422444x x f x x ⎛⎫<<<+<=+ ⎪⎝⎭在ππ,42⎛⎫ ⎪⎝⎭单调递减,A 对.π2sin 6y x ⎛⎫=- ⎪⎝⎭在ππ,42⎛⎫ ⎪⎝⎭单调递增,B 错.|sin 2|sin 2y x x ==在ππ,42⎛⎫⎪⎝⎭单调递减,C 对.πcos 3y x ⎛⎫=- ⎪⎝⎭在ππ,43⎛⎫ ⎪⎝⎭单调递增,ππ,32⎛⎫⎪⎝⎭单调递减,D 错,选AC.10.【答案】ABC【解析】AB 与AB 一定互斥,A 对()()111()()()(),,1()2233P AB P AB P A B P AB P A P B A B P B ===∴=⨯=∴∣独立,B 对.11121()()()()1(23633P A B P A P B P AB P B +=+-=+-==-=对.(()()()(1())1(()(),D ()1()1()3P BA P B P AB P B P A P B A P B P A P A P A P A --=====≠--∣错11.【答案】ABD【解析】方法一:对于A ,当l 倾斜角为π3时,l方程为221)1)34,12y x y x x y ⎧=+⎪=+⎨+=⎪⎩221833580,,(1,0),(1,0)55,x x A B F F ⎛⎫⇒+=∴--- ⎪ ⎪⎝⎭此时A 位于椭圆短轴的一个端点,1212,AF AF AO F F ∴=∴⊥,又 平面12AF F ⊥平面12,F F B AO ∴⊥平面122,,A F F B AO BF ∴⊥正确.(图中绿色为平面12AF F 折叠后的面)对于B ,当1倾斜角为π3时,12AF F 为等边三角形,边长为2,121233535313tan ,sin ,11114BF BF BF BF k k k k θθ-===+⋅12AF F ∴外接圆半径11222sin 603,r BF F ︒==外接圆半径25314r ==∴三棱锥12A BF F -外接球半径为R =,2 2218844π4ππ,7575S R ∴==⨯=表B 正确.对于C ,设直线AB 方程为()()1122121,,, 00, ,,x my A x y B x y y y =-><()()()2222222134690,36363414413412x my m y my m m m x y =-⎧⇒+--=∆=++=+⎨+=⎩ 平面12AF F ⊥面()12122112211133,2323344A BF F F FB V y y y y m -∴=⋅⨯-⋅=-=≤+()12max 9,C 4A BF F V -∴=错.对于D ,如图建系,翻折前原先AB =,翻折后,()()1122,,0,,0,,A x y B x y A B ''''-∴=由2222 1518,, 22AB AF BF A B AF BF AB A B ''''++=++=∴-=1 2⇒=①12⇒124y y ⇒+=-②,联立①②21222111828||243443445AB y y m m m ⇒=-⇒=+⇒=++,D 14m k ∴===±正确,选ABD.方法二:当l 的倾斜角为π3时,835, 55A B ⎛⎫-- ⎪ ⎪⎝⎭,此时12AO F F ⊥,又 面12AF F ⊥面12, BF F AO ∴⊥面122, ,A BF F AO BF ∴⊥对.12AF F 外接圆圆心M 到12F F 距离123614,,35 5BF BF ==,1236196411532525cos sin ,6141414255 B B BF F +-===⨯⨯ 外接圆半径1r,1283143211515r rl ==∴=,圆心N 到12F F距离25外接球半径2236314221884,4ππ,625347575R S R =++===B 对.令12AF F α∠=,则1213133sin ,2sin 2cos 22cos 2cos BF F BF S ααααα==⋅⋅=+++ 13,2cos AF A α=-到12F F 距离2sin 2cos αα-12222213sin 2sin 3sin 3sin 332cos 2cos 4cos 3sin 4A BF F V αααααααα-=⋅⋅==≤+--+,C 错.对于D ,同法一三、填空题:本题共3小题,每小题5分,共15分.12.【解析】242i 2i i (2i)i 2i 4 , ,||,1i z z z z z z --+=+∴-=--∴==-.13.【答案】0.2;0.36【解析】优品满足8,(8)(53)()l P l P l P l μσ≥≥=≥+=≥+10.68270.158650.222=-=≈(第一空)0.20.80.20.36P =+⨯=(第二空)14.【答案】277【解析】延长OQ 与2PF 交于N ,则N 为2PF 中点,112QN ON OQ PF b =-=-而QPN 为等腰三角形,2111,22PN QN PF PF b ∴=∴=-,即122PF PF b -=又12122,,,PF PF a PF a b PF a b +=∴=+=- ()222222221212124,2242PF PF PF PF c a b a b c ∴+-⋅⋅=∴+--=()22222734,.7c a a c c a ∴+-=∴=四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.15.【解析】方法一:sin sin cos sin sin cos B C A C A B+2sin (sin cos cos sin )sin sin()sin C B A B A C A B C=+=⋅+=2sin sin cos sin sin cos 4sin B C A C A B A += 22sin 4sin C A∴=由正弦定理:sin sin a c A C=得224c a =2c a =.(2)2, 2c a BA BC =∴= ,又 2,BA ADAD DC BC DC=∴= 所以BD 为ABC ∠的角平分线,设, CBD BD xθ∠==则111sin sin sin 2222BC BD BD BA BC BA θθθ⨯⨯⨯+⨯⨯⨯=⨯⨯⨯3sin 2sin 2sin 2,3sin 4sin cos ,cos 4x x x xθθθθθθθ∴+=∴=∴=又在BCD 中,由余弦定理得22121cos 9b x x θ+-=⨯⨯⨯,2222223112,1,1949292b b b x x x x x +-=⨯-=∴+=≥即:322bx ≤,当且仅当132b ==时“=”号成立,max 32()2b BD ∴⋅=.方法二:(1)2sin sin cos sin sin cos 4sin B C A C A B A+= 2222222422b c a a c b bc ac a bc ac+-+-∴+=即22,2 4c a c a =∴=.(2)设 ,BD x BDA α=∠=,在ABD 中,22422cos 493x b x b α+-⋅=①,在BCD 中,22112cos(π)193x b x b α+-⋅-=②,由①②得,222363x b +=,下同法一方法三:(2)122,33AD DC BD BA BC =∴=+,两边同时平方得222944BD BA BA BC BC=+⋅+ 即294421cos 4x ABC =+⨯⨯⨯∠+,所以2241988221b x +-=+⨯⨯⨯,所以229182x b =-,下同法一.16.【解析】(1)()()202020iii ix x y y x y xyr ---=∑∑0.943===≈,r 接近1,∴考试成绩y 和错题订正整理情况得分x 高度相关.(2)考试成绩低于样本平均数y 的概率记为p ,则822,~4,205 5p x B ⎛⎫==∴ ⎪⎝⎭43014438123216(0)C ,(1)C 562555625p x p x ⎛⎫⎛⎫⎛⎫=====⨯= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭2232344232162396(2)C ,(3)C 5562555625p x p x ⎛⎫⎛⎫⎛⎫==⨯===⨯=⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭444216(4)C .5625p x ⎛⎫=== ⎪⎝⎭x 01234p 8625216625216625966251662517.【解析】(1)证明:取BD 中点Q ,连接AQABD 为正三角形,AB AD ∴=,Q 为BD 中点,AQ BD ∴⊥,,AQ BD AQ ⊥⊂面ABD ,面ABD ⊥面BCD ,面ABD ⋂面BCD BD =AQ ⇒上面BCD ,又CD ⊂ 面,BCD AQ CD ∴⊥,1, AQ CDAD CD CD AD AQ A AD AQ ABD ⊥⎫⎪⊥⎪⇒⊥⎬⋂=⎪⎪⊂⎭面面ABD又BD ⊂面,ABD CD BD∴⊥(2)方法一:由(1)可知CD ⊥面ABD ,建立空间直角坐标系如图,1(0,0,0),1,0),,,022D B A P ⎛⎫- ⎪ ⎪⎝⎭,设(0,0,)C t ,则(1,)AC t =- ,记平面BCP 的一个法向量为(,,)n x y z =30 33,,0,(),2222x y BP BC ty tz⎧⎛⎫-+=⎪=-=∴⎪⎨⎪⎝⎭⎪++=⎩令y t=,则,,,2)2xy t n tz⎧=⎪=∴=⎨⎪=⎩|cos,|AC n∴〈〉==AC与平面BCP 所成角余弦值为713,26∴正弦值为3926.423933712026t t=∴-+=()()22231120, 1t t t--=∴=或212t=又2,2,CD AD t t M>=∴>∴=∴.设面BPM的一个法向量为()1111,,n x y z=33,,0,1,22BP MB⎛⎫=-=-⎪⎪⎝⎭11111111113330222xx yy y nzy⎧=⎧⎪-+=⎪∴=⇒=∴=⎨⎨⎪=-=⎩取设面BMD的一个法向量为()2222,,n x y z=2221,0),(0,0,yDB DM-==-==取2222211(1,xx y nz=⎧⎪=⇒==⎨⎪=⎩1263cos,.424n n∴==⨯由图可知二面角的平面为锐角,∴二面角的余弦值为34.方法二:由(1)AQ⊥面BCD过Q 作//QN CD ,则QN BD ⊥,以{,,}QN QD QA为正交基底建立如图所示的空间直角坐标系,设130,,,(0,1,0),(,1,0)22,,CD a A P B C a ⎛⎫=- ⎪ ⎪⎝⎭所以33(,1,0,,,(,2,0)22AC a BP BC a ⎛⎫=== ⎪ ⎪⎝⎭,设平面BCP 的法向量为()111,,m x y z =11113302220y z ax y ⎧+=⎪⎨⎪+=⎩,令12x =得(2,)m a =- AC 与平面BCP所成角余弦值为26,AC ∴与平面BCP 所成角正弦值为3926.39|cos ,|26AC m ∴〈〉== 42337120a a ∴-+=,()()22231120,1a a a --=∴=或212a =又2,2,CD AD a a >=∴>∴= 因为平面BDM的法向量1(0,0,1),n BM ==设平面BMP 的法向量为()2222,,n x y z =2222302220y z y ⎧+=⎪+=,令22x =得2(2,n =123cos ,4n n ∴=,下同法一方法三:由(1)可知面ABD 得,CD BP AD BP ⊥⊥,所以BP ⊥面ACD ,面BCP ⊥面ACD ,AC ∴与平面BCP 所成角为ACP ∠,设CD a =,,CD AD AC ⊥= ,又P 为AD的中点,CP ∴=在ACP中,22cos ACP ∠==,21a ∴=或212a =,又22,,CD AD a a >=∴>∴= .过P 作PE BD ⊥交BD 于E ,过E 作EF BM ⊥于F ,连接PF,PFE ∠为二面角P BM D --的平面角.因为32,PE EF ==,所以3cos 4EF PF PFE PF =∠==.由图可知二面角的平面角为锐角,∴二面角的余弦值为34.18.【解析】方法一:(1)122()e(1)(1)1(1)(1)333x f x f x f f f '-''''=+⇒=+⇒=12()e 1x f x x -∴=++,切点(1,3),()f x ∴在(1,(1))f 处的切线方程为3(1)33y x x=-+=(2)12e1x x mx-++≥①当0x =时,左边110e=+>=右边,不等式显然成立.②当10x -≤<时,1max e 1x m x x x -⎛⎫≥++ ⎪⎝⎭令11122e 1e e 1(),()1x x x x g x x g x x x x x ---'⋅-=++=+-()11222e (1)(1)(1)1e 1x x x x x x x x x x---+--=+=++当10x -≤<时,1210e1e ,0()0(),,x x x g x g x --'-<++≥>∴<在[1,0)-上单调递减222max ()(1)e 11e 2,e 2.g x g m ---∴=-=---=--∴≥--③当02x <≤时,1min e 1x m x xx -⎛⎫⇒≤++ ⎪⎝⎭令()01g x x '=⇒=,当01x <<时,()0,()g x g x '<单调递减;当12x <≤时,()0,()g x g x '>单调递增.min ()(1)1113,3g x g m ∴==++=∴≤综上:m 的取值范围为2e 2,3-⎡⎤--⎣⎦.方法二:(1)12()e()3x f x f x '-'=+,令1x =,则2(1)1(,1)(1)33f f f '''=+∴=12()e 1,(1)1113,x f x x f -∴=++∴=++=:33(1)l y x ∴-=-,即:30x y -=.(2)令12()()e1x g x f x mx x mx-=-=++-11()e 2,()e 20x x g x x m g x '-''-∴=+-=+> 恒成立,()g x '∴在[1,2]-上递增.①若()e 40g z m '=+-≤,即e 4m ≥+对[1,2]()(0,2)x g x g ''∀∈-≤≤()g x ∴在[1,2]-单调递减,min e 5()(2)e 5202,g x g m m +∴==+-≥∴≤与e 4m ≥+矛盾,∴无解,舍去.②若2(1)e20g m '--=--≥,即212e m ≤-,[1,2],()(1)0,()x g x g g x ''∀∈-≥≥∴在[1,2]-上递增2min 21()(1)e 20,2e g x g m m -∴=-=++≥∴≥--故221122e e m --≤≤-.③若(1)0(2)0g g ''⎧-<⎨>⎩即:212e 4e m -<<+时,0(1,2)x ∃∈-使得()00g x '=,即:010e 2x x m-+=000111222min 00000()()e 10,e 1e 20x x x g x g x x mx x x x ---∴==++-≥++--≥即:()()()0011200001e10,1e 10x x x x x x ---+-≥-++≥0100001,e 10,10,11x x x x x -≥-∴++>∴-≥∴-≤≤ 01021e 22,3e x m x -⎡⎤∴=+∈-⎢⎥⎣⎦,故2123e m -≤≤综上2123em --≤≤.方法三:(2)①当0x =时,1e 10-+≥恒成立;②当(0,2]x ∈时,12e 1x x m x -++≤;③当[1,0)x ∈-时,12e 1x x m x -++≥,令()1122(1)e 1e 1(),()x x x x x g x g x x x --'-++++==所以()g x 在,[1,0)(0,1)-上单调递减,(0,2]上单调递增,所以2123em --≤≤.19.【解析】(1)由题意知22,112a ab b a =⎧=⎧⎪∴⎨⎨==⎩⎪⎩,双曲线C 的标准方程为2214x y -=.(2)方法一:设(0,)(0,)(,),0,B t E t r F t r ∴+-,其中229t r +=,而(2,0)A -2292244AE AFt r t r t r k k +--∴⋅=⋅==-方法二:设()()120,,0,F y E y ,则12121210,,222y y y y y y Q r y ++-⎛⎫=-= ⎪⎝⎭则()2212212:24y y y y Q x y -+⎛⎫+-= ⎪⎝⎭代入点(3,0)-得:()()22121212124999444,,y y y y y y y y +--+=∴=∴=-12129.2244AE AF y y y y k k ⋅=⋅==-(3)方法一:由(2)知94AP AQ k k =-⋅,将双曲线平移至22(2)14x y --=,即22440x y x --=,此时A 平移至(0,0)A '此时P ,Q 分别平移至()()1122,,P x y Q x y '',,设直线P Q ''方程为1mx my +=代入:双曲线222244()044(41)0x y x mx ny y nxy m x ⇒--+=⇒++-=244410y yn m x x⎛⎫⇒⋅+⋅+-=⎪⎝⎭12129419,2444AP AQ A P A Q y y m k k k k m x x ''''-∴⋅=⋅=⋅=-⇒=-∴=-∴直线P Q ''恒过定点1,0,2PQ ⎛⎫-∴ ⎪⎝⎭恒过定点5,02⎛⎫- ⎪⎝⎭,显然R 在圆B 内,PQ ∴恒与圆B 相交.方法二:1:2FA AF y l k =,()122211122(2):14440244FA y y x l y x y x y x y ⎧=+⎪⇒----=⎨⎪-=⎩2211221144222,11Q Q y y x x y y ++=∴=--2221111112221112222222212121Q y y y y y y y y y y ⎛⎫+++-=+⨯== ⎪---⎝⎭()2112211212,11y y Q y y ⎛⎫+ ⎪∴ ⎪--⎝⎭,同理:()2222222212,11y y P y y ⎛⎫+ ⎪ ⎪--⎝⎭()()()()()()()122222122112222221212122122221211121212121111PQ y y y y y y y y k y y y yy y y ------∴==+++-+----()()()()()121212221212122121444y y y y y y y y y y y y -++-===++-()2112211212124:11PQ y y l y x y y y y ⎛⎫+- ⎪∴-=- ⎪-+-⎝⎭12121241045 : 2x y x y y y y y y --⎛⎫=-=+ ⎪+++⎝⎭即PQ l ∴恒过点5,02T ⎛⎫- ⎪⎝⎭,由(2)圆2221212:24y y y y Q x y +-⎛⎫⎛⎫+-= ⎪ ⎪⎝⎭⎝⎭即:()221290x y y y y +-+-=,代入5,02⎛⎫-⎪⎝⎭得25904-<∴点T 在圆内,PQ l ∴与圆相交.。
江苏省如皋市2021届高三4月第二次适应性考试数学试卷(2.5模)及答案
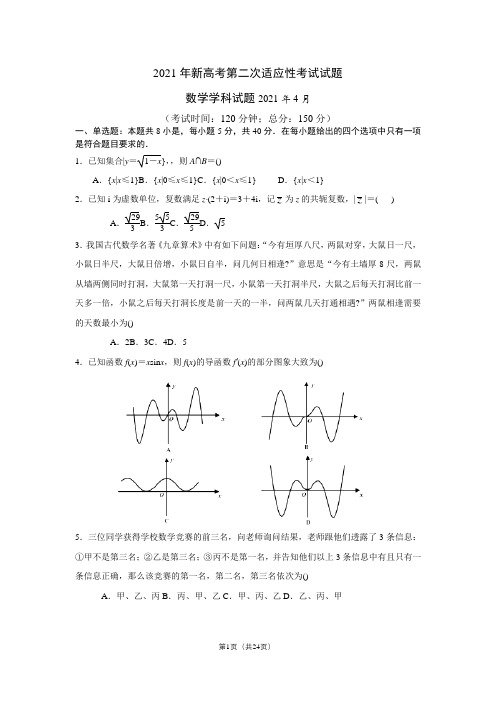
2021年新高考第二次适应性考试试题数学学科试题2021年4月(考试时间:120分钟;总分:150分)一、单选题:本题共8小是,每小题5分,共40分.在每小题给出的四个选项中只有一项是符合题目要求的.1.已知集合|y=1-x},,则A∩B=()A.{x|x≤1}B.{x|0≤x≤1}C.{x|0<x≤1} D.{x|x<1}2.已知i为虚数单位,复数满足z (2+i)=3+4i,记z为z的共轭复数,|z|=( )A.293B.553C.295D. 53.我国古代数学名著《九章算术》中有如下问题:“今有垣厚八尺,两鼠对穿,大鼠日一尺,小鼠日半尺,大鼠日倍增,小鼠日自半,问几何日相逢?”意思是“今有土墙厚8尺,两鼠从墙两侧同时打洞,大鼠第一天打洞一尺,小鼠第一天打洞半尺,大鼠之后每天打洞比前一天多一倍,小鼠之后每天打洞长度是前一天的一半,问两鼠几天打通相遇?”两鼠相逢需要的天数最小为()A.2B.3C.4D.54.已知函数f(x)=x sin x,则f(x)的导函数f′(x)的部分图象大致为()5.三位同学获得学校数学竞赛的前三名,向老师询问结果,老师跟他们透露了3条信息:①甲不是第三名;②乙是第三名;③丙不是第一名,并告知他们以上3条信息中有且只有一条信息正确,那么该竞赛的第一名,第二名,第三名依次为()A.甲、乙、丙B.丙、甲、乙C.甲、丙、乙D.乙、丙、甲6.已知α,β∈(0,π),cos α=-31010,若sin(2α+β)=12sin β,则α+β=( )A .54πB .23πC .76πD .74π7.在平面直角坐标系xOy 中,点分别是双曲线C :x 2a 2-y2b 2=1(a >0,b >0)的左,右焦点,过点且与直线l :垂直的直线交C 的右支于点M ,设直线l 上一点N (N 在第二象限)满足,且(→F 1N +→F 2M ) →MN =0,则双曲线C 的离心率的值为()A .5B .3C .2+1D .28.如图,在边长为2的正方形ABCD 中,点M 、N 分别是边CD 、BC 的中点,将△ADM 沿AM 翻折到△P AM ,在△ADM 翻折到△P AM 的过程中,tan ∠PND 的最大值为()A .54B .255C .55D .23二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.9.2020年突如其来的新冠肺炎疫情对房地市场造成明显的冲击,如图为某市2020年国庆节7天假期的楼房认购量与成交量的折线图,某同学根据折线图对这7天的认购量(单位: 套)与成交量(单位:套)作出如下判断,则下列判断正确的是()A .日成交量的中位数是16B .日成交量超过平均成交量的只有1天C .10月7日认购量的增长率大于10月7日成交量的增长率D .日认购量的方差大于日成交量的方差 10.已知a =log 3e ,b =log 23,c =ln3,则()A .a <b <cB .a <c <bC .a +c >bD .a +c <b11.如图,已知函数y =A sin(ωx +φ)(A >0,ω>0,|φ|<π2)的图象与x 轴交于点A ,B ,与y轴交于点C ,若|OB |=7|OA |,0<|AB |<52,且tan ∠ACB =98,则下列说法正确的是()A .f (x )的最小正周期为4B .将f (x )的图象向左平移π6个单位后的图象关于原点对称C .f (x )在区间(-1,1)上的值域为[-2,3)D .f (x )在区间(6,7)上单调递增12.在四面体ABCD 中,△ABC 是边长为2的正三角形.错误!未定义书签。
如皋高三联考试卷数学答案

一、选择题1. 答案:A解析:由题意可知,函数在区间(-∞,-2)上单调递减,在区间(-2,+∞)上单调递增,所以函数的对称轴为x=-2,故选A。
2. 答案:B解析:根据复数的乘法法则,有(1+i)^2 = 1 + 2i + i^2 = 1 + 2i - 1 = 2i,所以选B。
3. 答案:C解析:由等比数列的性质,有a1 a5 = a2 a4 = a3^2,代入a1 = 2,得到2a5 = 4 a4 = a3^2,所以a5 = 2a4 = 2 3^2 = 18,故选C。
4. 答案:D解析:由向量的数量积公式,有a·b = |a| |b| cosθ,其中θ为向量a和向量b的夹角。
由题意可知,|a| = 5,|b| = 3,且cosθ = -1/2,所以a·b = 5 3 (-1/2) = -15/2,故选D。
5. 答案:A解析:由不等式的性质,有-|a| ≤ -a ≤ |a|,所以-|x| ≤ -x ≤ |x|,当x < 0时,-x > 0,所以-|x| ≤ -x < 0,故选A。
二、填空题6. 答案:-1/2解析:由题意可知,|x-1| = 1/2,所以x-1 = ±1/2,解得x = 3/2 或 x = 1/2,又因为x < 0,所以x = 1/2不满足条件,故x = -1/2。
7. 答案:π解析:由圆的周长公式C = 2πr,代入C = 4π,解得r = 2,所以圆的面积S = πr^2 = π 2^2 = 4π。
8. 答案:x = 1解析:由题意可知,x^2 - 3x + 2 = 0,分解因式得(x - 1)(x - 2) = 0,解得x = 1 或 x = 2,又因为x < 1,所以x = 2不满足条件,故x = 1。
9. 答案:2/3解析:由题意可知,log2x + log2(x+1) = 2,化简得log2(x(x+1)) = 2,即x(x+1) = 2^2,解得x = 2/3 或 x = -4/3,又因为x > 0,所以x = -4/3不满足条件,故x = 2/3。
江苏高职对口招生考试数学模拟试题二(含答案)
数学试题一、填空题:本大题共14小题,每小题5分,共计70分.请把答案填写在答题卡相应位置.......上.. 1.若集合{}1,0,1A =-,{}21,B x x m m ==+∈R ,则B A = ▲ .2.设i 是虚数单位,复数1i3ia +-为纯虚数,则实数a 的值为 ▲ . 3.已知样本7,8,9,,x y 的平均数是8,且60xy =,则此样本的标准差是 ▲ .4.在集合{|,1,2,,10}6n M x x n π===中任取一个元素,所取元素恰好满足方程1cos 2x = 的概率是 ▲ . 5.已知双曲线与椭圆2212xy +=有相同的焦点,且它们的 离心率互为倒数,则该双曲线的方程为 ▲ . 6.已知某算法的伪代码如右,根据伪代码,若函数7.()()g x f x m =-在R 上有且只有两个零点,则实数m 的取值范围是 ▲ .7.已知32cos()23απ+=-,则cos2α= ▲ .8.有一个正四面体的棱长为3,现用一张圆形的包装纸将其完全包住(不能裁剪纸,但可以折叠),那么包装纸的最小半径为 ▲ .9.过点(1,1)P 的直线将圆224x y +=分成两段圆弧,要使这两段弧长之差最大,则该直线的方程为 ▲ .10.已知数列{}n a 的前n 项和21()2n S n kn k *=-+∈N ,且n S 的最大值为8,则=2a▲ .11.已知中心为O 的正方形ABCD 的边长为2,点,M N 分别为线段,BC CD 上的两个不同点,且1MN =,则OM ON 的取值范围是 ▲ .12.在数列{}n a 中,已知13a =,22a =,当2n ≥时,1n a +是1n n a a -⋅的个位数,则2013a = ▲ .13.已知2()log (1)f x x =-,若实数n m ,满足()()2f m f n +=,则mn 的最小值是▲ .Read xIf x ≤1- Thenf (x )←x +2Else If 1-<x ≤1 Then f (x )←x 2Elsef (x )←x -+2End If End IfPrint f (x )(第6题图)14.设曲线()1e x y ax =-在点()01,A x y 处的切线为1l ,曲线()1e x y x -=-在点()02,A x y 处的切线为2l .若存在030,2x ⎡⎤∈⎢⎥⎣⎦,使得12l l ⊥,则实数a 的取值范围是 ▲ .二、解答题: 本大题共6小题,共计90分.请在答题卡指定的区域........内作答,解答时应写出文字说明、求证过程或演算步骤. 15.(本小题满分14分)设ABC △的内角,,A B C 所对的边分别为,,a b c .已知1a =,2b =,12CA CB =. ⑴求边c 的长; ⑵求()C A -cos 的值.16.(本小题满分14分)如图,在四棱锥P ABCD -中,PA ⊥平面ABCD ,四边形ABCD 是平行四边形,且AC CD ⊥,PA AD =,M ,Q 分别是PD ,BC 的中点.(1)求证:MQ平面PAB ;(2)若AN PC ⊥,垂足为N ,求证:MN PD ⊥.17.(本小题满分14分)某人2002年底花100万元买了一套住房,其中首付30万元,70万元采用商业贷款.贷款的月利率为5‰,按复利计算,每月等额还贷一次,10年还清,并从贷款后的次月开始还贷.⑴这个人每月应还贷多少元?PABDCMNQ(第16题图)⑵为了抑制高房价,国家出台“国五条”,要求卖房时按照差额的20%缴税.如果这个人现在将住房150万元卖出,并且差额税由卖房人承担,问:卖房人将获利约多少元? (参考数据:120(10.005) 1.8≈+)18.(本小题满分16分)已知椭圆E :()222210x y a b a b =>>+的离心率为12,右焦点为F ,且椭圆E 上的点到点F 距离的最小值为2.⑴求椭圆E 的方程;⑵设椭圆E 的左、右顶点分别为,A B ,过点A 的直线l 与椭圆E 及直线8x =分别相交于点,M N .(ⅰ)当过,,A F N 三点的圆半径最小时,求这个圆的方程;(ⅱ)若cos AMB ∠=,求ABM △的面积.19.(本小题满分16分)已知数列{}n a ,其前n 项和为n S .⑴若对任意的n *∈N ,2-12+12,,n n n a a a 组成公差为4的等差数列,且1=1a ,220132nS n=,求n 的值; ⑵若数列{+}nnS a a 是公比为(1)q q ≠-的等比数列,a 为常数,求证:数列{}n a 为等比数列的充要条件为1=1+q a.20.(本小题满分16分)已知函数()ln a f x x x =+,21()222g x bx x =-+,,a b ∈R . ⑴求函数()f x 的单调区间;⑵记函数()()()h x f x g x =+,当0a =时,()h x 在(0,1)上有且只有一个极值点,求实数b 的取值范围;⑶记函数()()F x f x =,证明:存在一条过原点的直线l 与()y F x =的图象有两个切点.参考答案一、填空题:1.{1} 2.3 34.0.2 5.22221x y -= 6.(,0){1}-∞ 7.7981-8. 9.20x y +-= 10.5211.[2 12.6 13.9 14.31,2⎡⎤⎢⎥⎣⎦二、解答题: 15.⑴由12CA CB =,得1cos 2ab C =.………………………………………………2分 因为1a =,2b =,所以1cos 4C =,…………………………………………………4分所以2222cos 1414c a b ab C =-=-=++,所以2c =.…………………………………………………………………………… 7分⑵因为1cos 4C =,(0,)C π∈,所以sin C =,…………………………………9分所以sin 4sin 2a C A c ===,……………………………………………………11分 因为a c <,所以A C <,故A 为锐角,所以7cos 8A ,所以7111cos()cos cos sin sin 8416A C A C A C -==⨯=+. …………14分16.(1)取PA 的中点E ,连结ME ,BE ,因为M 是PD 的中点,所以ME AD ,12ME AD =,又因为Q 是BC 中点,所以12BQ BC =,因为四边形ABCD 是平行四边形;所以BC AD ∥,所以BQ ME ∥,所以四边形MQBE 是平行四边形,…………4分所以MQ BE .因为BE ⊂平面PAB , MQ ⊄平面PAB ,所以MQ 平面PAB .……………………6分 (2)因为PA ⊥平面ABCD ,CD ⊂平面ABCD , 所以PA CD ⊥,又因为AC CD ⊥,PA AC A =,PABDCM N QE (第16题图)PA ⊂平面PAC ,AC ⊂平面PAC ,所以CD ⊥平面PAC ,又AN ⊂平面PAC , 所以AN CD ⊥. ……………………………9分又AN PC ⊥,PC CD C =,PC ⊂平面PCD ,CD ⊂平面PCD ,所以AN ⊥平面PCD ,又PD ⊂平面PCD ,所以AN PD ⊥,……………………12分 又PA AD =,M 是PD 中点,所以AM PD ⊥,……………………………………13分 又AM AN A =,AM ⊂平面AMN ,AN ⊂平面AMN ,所以PD ⊥平面AMN ,又MN ⊂平面AMN ,所以MN PD ⊥.……………………………………………………14分17.⑴设每月应还贷x 元,共付款1210120⨯=次,则有2119120[1(10.005)(10.005)(10.005)]700000(10.005)x =++++++++,…………4分所以1201207000000.005(10.005)7875(10.005)1x ⨯⨯==-++(元).………………………………6分答:每月应还贷7875元.………………………………………………………………7分 ⑵卖房人共付给银行7875120945000⨯=元, 利息945000700000245000-=(元),………………………………………………10分 缴纳差额税(15000001000000)0.2100000-⨯=(元),………………………………12分500000(245000100000)155000-=+(元). 答:卖房人将获利约155000元.………………………………………………………14分18.⑴由已知,12c a =,且2a c -=,所以4a =,2c =,所以22212b a c =-=,所以椭圆E 的方程为2211612x y =+.………………………………………………………3分⑵(ⅰ)由⑴,(4,0)A -,(2,0)F ,设(8,)N t .设圆的方程为220x y dx ey f =++++,将点,,A F N 的坐标代入,得21640,420,6480,d f d f t d et f ⎧-=⎪=⎨⎪=⎩+++++++解得2,72,8,d e t t f =⎧⎪⎪=--⎨⎪=-⎪⎩……………………………………………6分 所以圆的方程为22722()80x y x t y t--=+++, 即222172172(1)[()]9()24x y t t t t-=+++++,因为2272()t t +≥,当且仅当72t t=±+故所求圆的方程为22280x y x ±-=++.………………………………………9分 (ⅱ)由对称性不妨设直线l 的方程为(4)(0)y k x k =>+.由22(4),1,1612y k x x y =⎧⎪⎨=⎪⎩++得222121624(,)3434k k M k k -++,……………………………………………11分所以222424(,)3434kMA k k --=++,2223224(,)3434k k MB k k -=++,所以cos 24MA MB AMB MA MB∠===, 化简,得42164090k k --=,…………………………………………………………14分解得214k =,或294k =,即12k =,或32k =, 此时总有3M y =,所以ABM △的面积为183122⨯⨯=.…………………………16分19.⑴因为21212,,n n n a a a -+成公差为4的等差数列,所以21212214,8)n n n n a a a a n *+---==+∈N (,……………………………………………2分 所以1352121,,,,,n n a a a a a -+是公差为4的等差数列,且2462135218n n a a a a a a a a n -++++=+++++, ……………………………4分又因为11a =,所以()21352128n n S a a a a n-=+++++2(1)2[4]8462(23)2n n n n n n n n -=⨯==++++,所以22320132n Sn n ==+,所以1005n =.……………………………………………6分⑵因为1(1)n n n Sa a q a -+=+,所以1(1)n n n n S a q a aa -=+-, ①所以111(1)n n n n S a q a aa +++=+-, ②②-①,得11(1)(1)[(1)]n n n n a q a a a q a -++-=-+, ③ ……………………………8分(ⅰ)充分性:因为11q a=+,所以0,1,1a q a aq ≠≠+=,代入③式,得 1(1)(1)n n n n q q a q a +-=-,因为1q ≠-,又1q ≠,所以11n n a a q+=,*n ∈N ,所以{}n a 为等比数列,……………………………………12分(ⅱ)必要性:设{}n a 的公比为0q ,则由③得10(1)(1)(1)n n a q q a a q -+-=-+,整理得()()00111()n a q a a q q q+-=+-,……………………………………………14分此式为关于n 的恒等式,若1q =,则左边0=,右边1=-,矛盾;1q ≠±若,当且仅当00(1,1(1(1)a q a a q a q+=⎧⎪⎨+=+⎪⎩))时成立,所以11q a =+.由(ⅰ)、(ⅱ)可知,数列{}n a 为等比数列的充要条件为1=1+q a.…………………16分20.(1)因为221()a x af x x x x-'=-+=,①若0a ≤,则()0f x '≥,()f x 在(0,)+∞上为增函数,…………………………2分 ②若0a >,令()0f x '=,得x a =,当0x a <<时,()0f x '<;当x a >时,()0f x '>.所以(0,)a 为单调减区间,(,)a +∞为单调增区间. 综上可得,当0a ≤时,(0,)+∞为单调增区间,当0a >时,(0,)a 为单调减区间, (,)a +∞为单调增区间. ……………4分(2)0a =时,21()()()22ln 2h x f x g x bx x x =+=-++,2121()2bx x h x bx x x-+'=-+=, ……………………………………………………5分 ()h x 在(0,1)上有且只有一个极值点,即()0h x '=在(0,1)上有且只有一个根且不为重根,由()0h x '=得2210bx x -+=, ………………………………………………………6分(i )0b =,12x =,满足题意;…………………………………………………………7分 (ii )0b >时,212110b ⋅-⋅+<,即01b <<;………………………………………8分 (iii )0b <时,212110b ⋅-⋅+<,得1b <,故0b <;综上得:()h x 在(0,1)上有且只有一个极值点时,1b <. ……………………………9分 注:本题也可分离变量求得. (3)证明:由(1)可知:(i )若0a ≤,则()0f x '≥,()f x 在(0,)+∞上为单调增函数,所以直线l 与()y F x = 的图象不可能有两个切点,不合题意.……………………10分 (ⅱ)若0a >,()f x 在x a =处取得极值()1ln f a a =+.若1ln 0a +≥,1ea ≥时,由图象知不可能有两个切点.…………………………11分故10ea <<,设()f x 图象与x 轴的两个交点的横坐标为,s t (不妨设s t <), 则直线l 与()y F x =的图象有两个切点即为直线l 与1ln ,(,)ay x x s t x=--∈和2ln ,(,)ay x x t x=+∈+∞的切点.1221a a x y x x x -'=-=,2221a x a y x x x-'=-+=, 设切点分别为1122(,),(,)A x y B x y ,则120x x <<,且 111122111ln a x y x a x x x x -==--,222222222ln x a y x a x x x x -==+,122212a x x ax x --=, 即1121ln ax x =-, ① 2221ln ax x =-, ② 12122212()x x x x a x x +=+,③①-②得:11212222ln ln ln x a ax x x x x -=-+=-,由③中的a 代入上式可得:121212212122()22()ln x x x x x x x x x x +-=-+, 即22121221222()ln x x x x x x -=+, ……………………………………………………………14分令12(01)x k k x =<<,则22(1)ln 22k k k +=-,令22()(1)ln 22(01)G k k k k k =+-+<<,因为213()10e e G =->,2414()0e eG =-<,故存在0(0,1)k ∈,使得()00G k =,即存在一条过原点的直线l 与()y F x =的图象有两个切点.………………16分。
2025届江苏省南通如皋市高三第二次模拟考试数学试卷含解析
2025届江苏省南通如皋市高三第二次模拟考试数学试卷注意事项:1.答题前,考生先将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形码区域内。
2.答题时请按要求用笔。
3.请按照题号顺序在答题卡各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试卷上答题无效。
4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑。
5.保持卡面清洁,不要折暴、不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知3log a =ln3b =,0.992c -=,则,,a b c 的大小关系为( ) A .b c a >>B .a b c >>C .c a b >>D .c b a >>2.已知函数()sin()(0,)2f x x πωϕωϕ=+><的最小正周期为(),f x π的图象向左平移6π个单位长度后关于y 轴对称,则()6f x π-的单调递增区间为( )A .5,36k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦B .,36k k k Z ππππ⎡⎤-++∈⎢⎥⎣⎦C .5,1212k k k Z ππππ⎡⎤-++∈⎢⎥⎣⎦D .,63k k k Z ππππ⎡⎤-++∈⎢⎥⎣⎦3.若x ,y 满足约束条件103020x y x y x +-≤⎧⎪-+≤⎨⎪+≥⎩,则22x y +的最大值是( )A .92B.2C .13D4.若集合{}|sin 21A x x ==,,42k B y y k Z ππ⎧⎫==+∈⎨⎬⎩⎭,则( ) A .A B A ⋃=B .R RC B C A ⊆C .AB =∅D .R R C A C B ⊆5.复数满足48i z z +=+,则复数z 在复平面内所对应的点在( ) A .第一象限B .第二象限C .第三象限D .第四象限6.设全集U =R ,集合{}221|{|}xM x x x N x =≤=,<,则UM N =( )A .[]0,1B .(]0,1C .[)0,1D .(],1-∞7.从集合{}3,2,1,1,2,3,4---中随机选取一个数记为m ,从集合{}2,1,2,3,4--中随机选取一个数记为n ,则在方程221x y m n +=表示双曲线的条件下,方程221x y m n+=表示焦点在y 轴上的双曲线的概率为( ) A .917B .817C .1735D .9358.下列函数中,值域为R 的偶函数是( ) A .21y x =+B .x x y e e -=-C .lg y x =D .2y x =9.已知函数()2sin()(0,0)3f x x A ωωπ=->>,将函数()f x 的图象向左平移3π个单位长度,得到函数()g x 的图象,若函数()g x 的图象的一条对称轴是6x π=,则ω的最小值为A .16B .23 C .53D .5610.如图,在四边形ABCD 中,1AB =,3BC =,120ABC ∠=︒,90ACD ∠=︒,60CDA ∠=︒,则BD 的长度为( )A .533B .3C .33D .3311.偶函数()f x 关于点()1,0对称,当10x -≤≤时,()21f x x =-+,求()2020f =( ) A .2B .0C .1-D .112.已知n S 是等差数列{}n a 的前n 项和,若201820202019S S S <<,设12n n n n b a a a ++=,则数列1n b ⎧⎫⎨⎬⎩⎭的前n 项和n T 取最大值时n 的值为( ) A .2020B .20l9C .2018D .2017二、填空题:本题共4小题,每小题5分,共20分。
江苏省南通市如皋市十四校联考2024-2025学年高三上学期教学质量调研(二)数学试题
江苏省南通市如皋市十四校联考2024-2025学年高三上学期教学质量调研(二)数学试题一、单选题1.某运动员在一次训练中共射击6次,射击成绩(单位:环)如下:6,7,7,9,9,10.则下列说法正确的是()A .成绩的极差为4-B .成绩的第50百分位数等于成绩的平均数C .成绩的中位数为7和9D .若增加一个成绩8,则成绩的方差不变2.已知集合{21,3,4},{},2R ,A B x x m x =-=-<∈‖∣,若R A B =∅ ð,则实数m 取值范围为()A .4m >B .4≥m C .2m ≤D .2m >3.抛掷质地均匀的骰子两次,得到的点数分别为m ,n .设平面向量(4,2),(,)a b m n ==,则向量,a b不能作为平面内的一组基底的概率为()A .112B .16C .14D .134.若πtan 23α⎛⎫+= ⎪⎝⎭,则πcos 23α⎛⎫- ⎪⎝⎭的值为()A .45B .45-C .35D .35-5.已知x ,y 为正实数,则可成为“x y <”的充要条件的是()A .11x y<B .ln ln x y y x +<+C .sin sin x y<D .cos cos x y y x-<-6.位于如皋市定慧寺内的观音塔,是一座仿明清古塔建筑,具有七层、八角彩绘的外观.观音塔除去塔尖部分可近似视为一个正四棱台,现有一个除去塔尖的观音塔模型,塔底宽20cm ,塔顶宽10cm ,侧面面积为2,据此计算该观音塔模型体积为()3cm .A .31500B .30000C .10500D .100007.已知动点P 在拋物线24x y =上,定点(1,4)D .圆22:(1)3F x y +-=上两个动点,A B 满足1||()2AB FM FA FB ==+ ,则||||PM PD +的最小值为()A .7B .6C .5D .48.已知函数()f x 的定义域为(0,)+∞,对(0,)+∞内的任意两个不相等的数12,x x ,都有()()12120,()22(1)(2)f x f x f x f x x x x x ->+=-+≥-且(2)2f =.若实数m ,n 满足623m f n ⎛⎫<< ⎪⎝⎭,则n m -的最小值为()A .202B .192C .20D .19二、多选题9.下列函数中,在区间ππ,42⎛⎫⎪⎝⎭上单调递减的函数是()A .πsin 4y x ⎛⎫=+ ⎪⎝⎭B .cos y x x=-C .sin2y x=D .πcos 3y x ⎛⎫=- ⎪⎝⎭10.随机事件A ,B 满足111(),(),()232P A P B P A B ===,则下列说法正确的是()A .事件AB 与AB 互斥B .事件A 与B 相互独立C .()()P A B P B +=D .()()P BA P A =∣11.在平面直角坐标系xOy 中,椭圆22:143x y C +=的左、右焦点分别为12,F F ,经过点1F 的直线l 与椭圆C 交于A ,B 两点(其中点A 在x 轴上方),连接22,AF BF .现将平面12AF F 沿x 轴向上折叠,使得面12AF F ⊥面12F F B ,则下列说法正确的是()A .当直线l 的倾斜角为π3时,2AO BF ⊥B .当直线l 的倾斜角为π3时,三棱锥12A BF F -的外接球的表面积为884π75C .三棱锥12A BF F -的体积最大值为94D .当2ABF △折叠后的周长为152时,直线l 的斜率为33514±三、填空题12.已知i 为虚数单位,复数z 满足42i i (1i)z z +=++,则||z =.13.某工厂生产的A 产品的长度l (单位:cm )服从正态分布()25,3N ,按长度l 分为5级:10l ≥为一级,810l ≤<为二级,68l ≤<为三级,46l ≤<为四级,4l <为废品.将一级与二级产品称为优品.对该工厂生产的A 产品进行随机抽查,每次抽取1个,则抽到优品的概率p =(精确到0.1).若抽出的是优品,则抽查终止,否则继续抽查直到抽到优品,则抽查次数不超过两次的概率为.附:()0.6827,(22)0.9545P Z P Z μσμσμσμσ-<≤+=-<≤+=,(33)0.9773P Z μσμσ-<≤+=14.在平面直角坐标系xOy 中,椭圆2222:1(0)x y C a b a b+=>>的左、右焦点分别为12,F F ,点P 在椭圆C 上且121π,3F PF PF ∠=的平行线OQ 与12F PF ∠的角平分线交于,Q OQ b =,则椭圆C 的离心率为.四、解答题15.在ABC V 中,内角A ,B ,C 所对的边分别为a ,b ,c ,点D 在边AC 上且2AD DC =,2sin sin cos sin sin cos 4sin B C A C A B A +=.(1)求证:2c a =;(2)若1a =,求b BD ⋅的最大值.16.为调查某地区学生在高中学习中错题订正整理情况与考试成绩的关系.首先对该地区所有高中学生错题订正整理情况进行分值评价,给出得分;再组织考试.从这些学生中随机抽取20名学生的错题订正整理情况得分x 和对应的考试成绩y 作为样本,得到样本数据(),(1,2,,20)i i x y i = ,其中i x 和i y 分别表示第i 个样本错题订正整理情况得分和对应的考试成绩,计算得202212080,ii x x =-=∑()20219000,ii yy =-=∑20120800i ii x y xy =-=∑.(1)求样本(),(1,2,,20)i i x y i = 的相关系数(精确到0.01),并推断考试成绩y 和错题订正整理情况得分x 的相关程度;(2)已知20个样本中有8个样本的考试成绩低于样本平均数y .利用频率估计概率,从该地区所有高中学生中随机抽取4个学生的错题订正整理情况得分和对应的考试成绩,记抽到考试成绩低于y 的个数为X ,求随机变量X 的分布列.附:相关系数()()1.414niix x y y r --=∑.17.在三棱锥A BCD -中,ABD △是边长为2的正三角形,P ,M 分别为线段A ,A 的中点,,CD AD CD AD ⊥>,平面ABD ⊥平面BCD .(1)求证:BD CD ⊥;(2)若AC 与平面BCP P BM D --的余弦值.18.已知函数()f x 的导函数为()f x ',且121()e (1)13x f x f x -'=++.(1)求函数()f x 在点(1,(1))f 处的切线方程;(2)若对于任意的[1,2],()x f x mx ∈- 恒成立,求实数m 的取值范围.19.已知双曲线()2222:10,0x y C a b a b-=>>过点()2,0A -,其渐近线方程为20x y ±=.圆B 过点()3,0M -、()3,0N ,与y 轴交于E 、F .记直线AE 与双曲线C 的另一个交点为P ,直线AF 与双曲线C 的另一个交点为Q .(1)求双曲线C 的标准方程;(2)求证:直线AE 和直线AF 的斜率之积为定值;(3)判断直线PQ 与圆B 的位置关系,并说明理由.。
江苏省对口单招2019年高三年级第二轮复习调研测试数学试卷带答案答题卡
中等职业学校对口单招2019届高三年级第二轮复习调研测试数学答案一、选择题(本大题共10小题,每小题4分,共40分.在下列每小题中,选出一个正确答案,请在答题卡上将所选的字母标号涂黑)题号12345678910答案C D B A D C C B B A二、填空题(本大题共5小题,每小题4分,共20分)11. 4 12. 4 13. 14. 15. 34-]1,43(]3,1[三、解答题(本大题共8小题,共90分)16.(本题满分8分)解(1)由题意得:不等式的解集为R.022>+-a ax x 即,0442<-=∆a a 所以. ……………………………4分10<<a (2)由题意得:,⎪⎩⎪⎨⎧+≤->+>-2210220122x x x x 所以,31≤<x所以不等式的解集为 ……………………………8分]3,1(17.(本题满分10分)解(1)由题意得:A (3,8),,0=b 所以,因为A (3,8)在上,x a x f =)()(x f 所以,2=a 所以. ……………………………5分x x f 2)(=(3),2=m 所以. ……………………………10分153162)9(log )4()213(4=-+=-+f g g 18.(本题满分12分)(1)由题意得:A=1,,126543ππ-=T 所以,W T ππ2==所以W=2,因为,),过点(1-65)2sin(πϕ+=x y 所以,所以. ……………………………6分6πϕ-=)62sin()(π-=x x f (2)因为,1)62sin()(=-=πA A f 因为为锐角,A 所以,3π=A因为,23sin 21==∆A bc S 所以,2=c 因为,3cos 2222=-+=A bc c b a 所以,3=a 所以 ……………………………12分2233sin sin sin ===++A a C B c b 19.(本题满分12分)解:(1)由题意知基本事件总数为12.表示双曲线的随机事件数为5.125)(=A P 所以方程表示双曲线的概率为. ……………………………6分122=+b y a x 125(2)满足条件的事件B 是所以.,1222≤+-n m n m 034≥-n m 165221431)(=⨯-=B P 直线与圆相交的概率是.……………………………12分0=-ny mx ()()12122=-+-y x 16520.(本题满分14分)解:(1)当时,解得1=n 12411=+a a 611=a 当时,,所以2≥n 12411=+--n n a S 0)1214()24(=-+--+n a n S n a n S 所以,即,所以01224=--+n a n a n a 126-=n a n a 311=-n a n a 所以为等比数列,所以=…………………………6分}{n a 11-=n q a n a n n 31(211)31(61⨯=-⨯(2)①因为,所以01211=+-+-+n a n a n b n a n b n a 211=-++n a n b n a n b 即,所以为等差数列,又21=-+n c n c }{n c 11=c 所以……………………………10分12-=n n c ②121121(21)12)(12(111+--=+-=+n n n n n c n c 所以……………………………14分12)1211215131311(21+=+--++-+-=n n n n n T21.(本题满分10分)(1)设该公司每天的最高产值为万 z 元。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2017-2018如皋市对口单招高三年级第二次联考数学试卷一、单项选择题(本大题共10小题,每小题4分,共40分。
在下列每小题中,选出一个正确答案,将答题卡上对应选项的方框涂满、涂黑)1.集合{}0652=--=x x x A 与{}022=+-=a x x x B 的并集有三个元素,则a 的 值为 ( ) A.3-=a B.243-=-=a a 或 C. 1=a D.1243=-=-=a a a 或或 2.数组)4,1,2,()1,1,3,2()3,2,1,2(-===x x x ,且4)(-=+,则 ( ) A.4=x B. 3-=x C.3=x D. 4-=x3.设z 的共轭复数为z ,若4=+z z ,8=⋅z z ,则zz等于 ( ) A.i B. i ± C.1± D. i -4.函数,1,1)31(1,13)(⎪⎩⎪⎨⎧≤+>-=x x x f xx =)4(log 3f ( ) A.3 B.-3 C.2 D.-25.书架上有7本书排成一排,其中有3本哲学书,大学物理、高等数学各一本,现要求3本哲学书排在一起,大学物理、高等数学不能排在一起,共有多少排法 ( ) A.72 B.144 C.288 D.4326.已知点1cos θ(,)到直线πsin cos 102x y θθθ+=<(≤)的距离为14,则θ等于 ( ) A .π6 B .π4 C .π3 D .π27.n 位二进制数最大可以表示的十进制数为 ( ) A .nB .n 2C .12+nD .12-n8.在正方体中,棱BC 与平面ABC 1D 1所成的角为 ( ) A .300B .450C .900D .609.在平面直角坐标系XOY 中,已知圆0442:221=-+-+y x y x C ,圆0222:222=--++y x y x C ,则两圆的公切线的条数是( )A .1条B .2条C .3条D .4条10.函数y =2221x x x +++ (x>-1)的图像最低点的坐标为( )A .(1,2)B .(1,-2)C .(0,2)D .(1,1) 二、填空题(本大题共5小题,每小题4分,共20分) 11.下表是活动房建设工作明细表:工程的总工期是 天 .12.在如下的程序框图中,若输出的结果是10,则判断框中应填a ≥ .13.若圆C的半径为1,圆心在第一象限,且与直线034=-yx和x轴都相切,则该圆的参数方程是 .14.在平面直角坐标系中,函数2)(1+=+x axf(0>a且1≠a)的图像恒过定点P,若角θ的终边过点P,则θθπ2cos)2sin(--= .15.已知函数f(x)满足下列关系:(1)(1)(1)f x f x+=-(2)当[]21,1,()x f x x∈-=.则方程f(x)=lgx解的个数为个.三、解答题(本大题共8小题,共90分)16.(8分)已知方程210,4x ax a a R-+=∈无实数根(1)求实数a的取值范围;(2)解不等式2log(2)log3a ax x->.17.(10分)定义在R上的奇函数()f x,当0x∈-∞(,)时,2()1f x x mx=-+-.(1)当0x∈+∞(,)时,求()f x的解析式;(2)若方程()0f x=有五个不相等的实根,求实数m的取值范围.18.(12分)已知函数()2cos sin)222x x xf x=-.(1)求函数的周期;(2)设ππ[]22θ∈-,,且()1fθ=,求cosθ的值;(3)在△ABC中,1AB=,()1f C=,且△ABC,求ba+的值.19.(12分)设O为坐标原点,点P的坐标为()yxx--,2(1)在一个盒子中,放有标号为3,2,1的三张卡片,现从此盒中有放回地先后抽到两张卡片的标号记为y x ,,求事件“OP 取到最大值”的概率;(2)在[]3,0内先后取两个数分别记为y x ,,求P 点在第一象限的概率.20.(12分)某工厂计划用甲、乙两台机器生产A 、B 两种产品,每种产品都要依次进行甲、乙机器的加工,已知生产一件A 产品在甲、乙机器上加工的时间分别为2 h 和3 h ,生产一件B 产品在甲、乙机器上加工的时间分别为4 h 和2 h ,甲、乙机器每周可分别工作180 h 和150 h ,若每件A 产品的利润是40元,每件B 产品的利润是60元,问此工厂应如何安排生产才能获得最大的利润(即如何确定一周内每种产品生产的数量)21.(12分)已知椭圆x 2a 2+y 2b 2=1(a >b >0)经过点(0,3),离心率为12,左右焦点分别为F 1(-c,0),F 2(c,0).(1)求椭圆的方程;(2)若直线l :y =-12x +m 与椭圆交于 A ,B 两点,与以F 1F 2 为直径的圆交于C ,D 两点,且满足|AB ||CD |=534,求直线l 的方程.22.(10分) 某单位有员工1000名,平均每人每年创造利润10万元.为了增加企业竞争力,决定优化产业结构,调整出,()x x N +∈名员工从事第三产业,调整出的员工他们平均每人每年创造利润为12万元,剩下的员工平均每人每年创造的利润可以提高0.2x%. (1)若要保证剩余员工创造的年总利润不低于原来1000名员工创造的年总利润,则最多调整出多少名员工从事第三产业?(2)在(1)的条件下,应分流出多少人才能使该市第二、三产业的总产值最多?最多为多少?23.(本题满分14分)已知等差数列{n a }的前n 项和为n S ,且a 6=-5,S 4=-62, (1)求数列{|n a |}的通项公式;(2)若数列{n b }满足:n a =13...131********++++++++n n b b bb ,求数列{n b }的通项公式及前n 项;(3)令Cn=,求数列{n c }的前2n 项和T 2n .2017-2018如皋市对口单招高三年级第二次联考数学试卷参考答案一、选择题1~5 DDBAD 6~10 ADBBC 二、填空题11.18 12.2 13. 为参数)(sin 1cos 2θθθ⎩⎨⎧+=+=y x 14.107- 15.9 三、解答题16. 解:(1)由题意知,0<∆ 即2140,4a a -⨯< 所以10<<a ; ……………2分 (2)因为10<<a ,所以原不等式等价于222023x x x x ⎧->⎪⎨-<⎪⎩,……………4分解得10x -<<或者23x <<所以原不等式的解集为(1,0)(2,3)-⋃ ……………………………8分 17.解:(1)若0>x ,则0-<x所以1)()()(2--+--=-x m x x f12---=mx x ……………………………………………2分又因为)(x f 是奇函数所以)()(x f x f -=- ……………………………………………3分所以1)(2---=-mx x x f则1)(2++=mx x x f ……………………………………………5分 (2)函数的解析式为:⎪⎩⎪⎨⎧<-+-=>++=0,10,00,1)(22x mx x x x mx x x f ……………………………………………6分 由题意,)0(012>=++x mx x 有两个不相等的正根所以⎩⎨⎧>-=+>-=∆004212m x x m解得2-<m ……………………………………………………9分m 的取值范围是2-<m ……………………………………………………10分18.解:(1)由题意得:3)3sin(2+-=x π…………………………………………………2分1=ωΘ πωπ22==∴T …………………………………………3分(2)13)(-=θf Θ21)3sin(-=-∴θπ………………………………………4分 ]65,6[3ππθπ-∈-∴ …………………………………… 5分 63πθπ-=-∴ 即 2πθ= ……………………………………6分 0cos =∴θ ……………………………………7分(3)13)(+=C f Θ63ππ=-∴C 即6π=C …………………………………………9分由正弦定理得23sin 21==∆C ab S ABC 解得32=ab ……………………………………………10分由余弦定理得232cos 222=-+=ab c b a C解得722=+b a32+=+∴b a …………………………………………12分19.解:(1)设事件=A {}取得最大值OP ,()()222y x x OP -+-=,列表如下:9)(=∴A P …………………………6分 (2)设事件B ={}在第一象限P 由P 点在第一象限,所以⎩⎨⎧∴⎩⎨⎧--y x x y x x φφφφ2002 如图:略()1853313221)(=⨯⨯+=B P …………………………12分20. 解:设每周生产A 产品x 件,B 产品y 件,可获利润z 元则 y x Maxz 6040+=,且⎪⎪⎩⎪⎪⎨⎧≥≥≤+≤+001502318042y x y x y x ,即⎪⎪⎩⎪⎪⎨⎧≥≥≤+≤+0015023902y x y x y x ……………………………4分 作如图所示可行域,如图所示点A 处目标函数达到最优解,……………………………8分解⎩⎨⎧=+=+15023902y x y x 得)30,30(A答:每周生产A 、B 产品各30件,才能获最大利润。
……………………………12分21.解:(1)由题设知⎩⎨⎧b =3,c a =12,b 2=a 2-c 2,解得a =2,b =3,c =1,∴椭圆的方程为x 24+y 23=1. ……………………………4分(2)由题设,以F 1F 2为直径的圆的方程为x 2+y 2=1,AxyO5090∴圆心到直线l 的距离d =2|m |5,由d <1得|m |<52.(*)∴|CD |=21-d 2=21-45m 2=255-4m 2. ……………………………6分 设A (x 1,y 1),B (x 2,y 2), 由⎩⎪⎨⎪⎧y =-12x +m ,x 24+y 23=1,得x 2-mx +m 2-3=0,由根与系数的关系可得x 1+x 2=m ,x 1x 2=m 2-3.∴|AB |=⎣⎢⎡⎦⎥⎤1+⎝ ⎛⎭⎪⎫-122[m 2-4?m 2-3?] =1524-m 2. ……………………………9分 由|AB ||CD |=534得 4-m 25-4m 2=1, 解得m =±33,满足(*). ……………………………11分 ∴直线l 的方程为y =-12x +33或y =-12x -33. ……………………12分22. 解:(1)由题意,得10(1000)(10.002)101000x x -+≥⨯,即25000x x -≤,又x N +∈所以0500,x x N +<≤∈,即最多调整500名员工从事第三产业. ……………………………4分 (2)设从事第二、三产业的员工创造的年总利润为y ,则 y=10(1000-x )(1+0.002x )+12x=-0.02x 2+22x+10000 ……………………6分 对称轴为x=550,因为0500,x x N +<≤∈ ……………………7分 所以当x=500时y 取得最大值为16000元 ……………………9分答:当分流出500人时能使第二三产业的年总利润最大为16000元。
