5.3正方形(2)(浙教版新教材课件)
八年级数学下册 5_3 正方形 第2课时 正方形的性质课件 (新版)浙教版
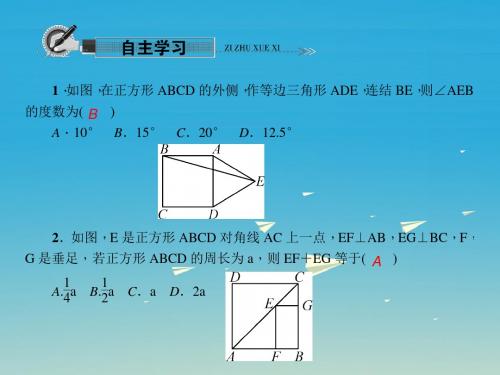
再证△GCE≌△GCF,∴GE=GF=GD+DF=GD+BE
15.如图①,已知正方形ABCD的对角线AC,BD相交于点O,E是AC上 一点,连结EB,过点A作AM⊥BE,垂足为M,AM交BD于点F. (1)求证:OE=OF; (2)如图②,若点E在AC的延长线上,AM⊥BE于点M,交DB的延长线于 点F,其它条件不变,则结论“OE=OF”还成立吗?如果成立,请给出证 明;如果不成立,请说明理由.
3.正方形ABCD在平面直角坐标系中的位置如图所示,已知点A的坐标 为(0,4),点B坐.(1,-4) D.(2,-4)
4.如图,在正方形ABCD中,G是BC上任意一点,连结AG,DE⊥AG于 点E,BF∥DE交AG于点F,探究线段AF,BF,EF三者之间的数量关系, 并说明理由.
5.如图,正方形ABCD中,对角线AC,BD相交于点O,则图中的等 腰三角形有( C )
A.4个 B.6个 C.8个 D.10个
6.正方形OGHK绕边长为10 cm的正方形ABCD的对角线的交点O旋转
到如图所示的位置,则阴影部分的面积为( D ) A.100 cm2 B.75 cm2
C.50 cm2 D.25 cm2
解:(1)∵四边形ABCD是正方形,∴∠BOE=∠AOF=90°,OB=OA.又
∵AM⊥BE,∴∠MEA+∠MAE=90°=∠AFO+∠MAE,∴∠MEA=
∠AFO,∴△BOE≌△AOF,∴OE=OF
(2)OE=OF成立,理由如下:∵四边形ABCD是正方形,∴∠BOE=
∠AOF=90°,OB=OA.又∵AM⊥BE,∴∠F+∠MBF=90°,∠E+ ∠OBE=90°.又∵∠MBF=∠OBE,∴∠F=∠E,∴△BOE≌△AOF,
1. 如图, 在正方形 ABCD 的外侧, 作等边三角形 ADE, 连结 BE, 则∠AEB 的度数为( B ) A.10° B.15° C.20° D.12.5°
浙教版八年级数学下册第五章《5.3正方形(2)》优质公开课课件

• 17、儿童是中心,教育的措施便围绕他们而组织起来。2021/7/302021/7/302021/7/302021/7/30
• 2、Our destiny offers not only the cup of despair, but the chalice of opportunity. (Richard Nixon, American President )命运给予我们的不是失望之酒,而是机会之杯。二〇二一年六月十七日2021年6月17日星期四 • 3、Patience is bitter, but its fruit is sweet. (Jean Jacques Rousseau , French thinker)忍耐是痛苦的,但它的果实是甜蜜的。10:516.17.202110:516.17.202110:5110:51:196.17.202110:516.17.2021 • 4、All that you do, do with your might; things done by halves are never done right. ----R.H. Stoddard, American poet做一切事都应尽力而为,半途而废永远不行6.17.20216.17.202110:5110:5110:51:1910:51:19 • 5、You have to believe in yourself. That's the secret of success. ----Charles Chaplin人必须相信自己,这是成功的秘诀。-Thursday, June 17, 2021June 21Thursday, June 17, 20216/17/2021
证明:如图,连结CG
在△AGD和△CGD中, ∠ADG=∠CDG(正方形的对角线平分一组对角) DG=DG, AD=CD(正方形的四条边相等)
正方形优质课件浙教版数学八年级下册

正方形优质课件浙教版数学八年级下册一、教学内容二、教学目标1. 理解并掌握正方形的定义,能够准确判断一个图形是否为正方形。
2. 掌握正方形的性质,能够运用性质解决相关问题。
3. 学会正方形的判定方法,能够运用判定方法解决实际问题。
三、教学难点与重点教学难点:正方形的判定方法。
教学重点:正方形的性质及其应用。
四、教具与学具准备1. 教具:正方形模型、直尺、圆规、三角板。
2. 学具:练习本、铅笔、直尺、圆规。
五、教学过程1. 实践情景引入:展示正方形在实际生活中的应用,如正方形瓷砖铺贴、正方形桌面等,引导学生思考正方形的特点。
2. 讲解正方形的定义,引导学生观察正方形模型,理解正方形的四条边相等且四个角都是直角。
3. 讲解正方形的性质,通过实例演示正方形的对角线互相垂直平分、对边平行且相等等性质。
4. 例题讲解:讲解如何利用正方形的性质解决实际问题,如计算正方形的面积、周长等。
(2)计算正方形的面积和周长。
7. 学生互相讨论,分享解题心得。
六、板书设计1. 正方形的定义2. 正方形的性质对角线互相垂直平分对边平行且相等四个角都是直角3. 正方形的判定方法4. 例题及解答5. 随堂练习七、作业设计1. 作业题目:(2)计算正方形的面积和周长。
2. 答案:(1)图形1是正方形,因为四条边相等且四个角都是直角。
(2)图形2不是正方形,因为对角线不互相垂直平分。
八、课后反思及拓展延伸1. 反思:本节课学生对正方形的性质和判定方法掌握情况,及时调整教学方法,提高教学效果。
2. 拓展延伸:引导学生探索正方形与其他图形的关系,如正方形与矩形、正方形与菱形等。
同时,鼓励学生将正方形性质应用于实际问题,提高解决问题的能力。
重点和难点解析1. 正方形的判定方法。
2. 正方形的性质在实际问题中的应用。
3. 教学过程中的实践情景引入和例题讲解。
4. 作业设计中的题目难度和答案解析。
一、正方形的判定方法1. 四条边相等。
2. 四个角都是直角。
浙教版八年级下册5.3正方形(2课时)教案设计

《正方形》教学设计【内容出处】浙江教育出版社八年级数学下册第5章第3课。
【素养指向】“直观想象”之“平行四边形边、角的特殊化”。
【教学目标】1.掌握正方形的概念。
2.经历探索正方形判别条件的过程,了解正方形与矩形、菱形的关系。
3.掌握正方形的判定。
4.掌握正方形的性质,进一步加深对特殊与一般的认识。
【时间预设】课内2课时加课前10分钟、课后15分钟。
第一课时【侧重目标】侧重目标1,2,3。
【内容段落】内容段落一,理解概念;内容段落二,判定探究。
【教学过程】一、先行学习用两个等腰直角三角形能拼成几个平行四边形,有特殊的平行四边形吗,特殊的平行四边形有什么特点?二、交互学习段落一 理解概念〖小组合学〗小组内讨论下列问题:正方形是否也可以说是平行四边形?矩形?菱形?与一般的平行四边形相比,它有何特殊性?与一般的矩形相比,它有何特殊性?与一般的菱形相比,它又有何特殊性?〖展示评析〗小组推荐代表展示交流,其他小组质疑与纠错,交流评析后得到:1.有一组邻边相等,并且有一个角是直角的平行四边形叫做正方形。
2.正方形既是特殊的矩形,又是特殊的菱形,故正方形具有矩形、菱形的性质.段落二 判定探究〖师生共学〗判定:一组邻边相等的矩形是正方形。
有一个角是直角的菱形是正方形。
〖检测评价〗独立完成下面题目,然后在小组内交流,进行互动评析。
已知,如图,在Rt △ABC 中,∠ACB=900,CD 是∠ACB 的平分线,DE ⊥BC ,DF ⊥AC ,垂足分别是E 、F求证:四边形CFDE 是正方形三、后续学习C AD BF E1.课本作业题第2,3,5题。
2.导学我达标第3,4题。
第二课时【侧重目标】侧重目标4。
【内容段落】内容段落三,综合运用。
【教学过程】一、交互学习段落三综合运用〖小组合学〗小组内讨论正方形还具有哪些性质,画出一个正方形,尽可能多的说出他的性质。
〖展示评析〗小组推荐代表展示交流,其他小组质疑与纠错,交流评析后得到:正方形性质:(1)边的性质:对边平行,四条边都相等.(2)角的性质:四个角都是直角.(3)对角线的性质:两条对角线互相垂直平分且相等,•每条对角线平分一组对角.(4)对称性:是轴对称图形,有四条对称轴.〖检测评价〗独立完成下面题目,然后在小组内交流,进行互动评析。
正方形 PPT课件 36 浙教版
•
63、彩虹风雨后,成功细节中。
•
64、有些事你是绕不过去的,你现在逃避,你以后就会话十倍的精力去面对。
•
65、只要有信心,就能在信念中行走。
•
66、每天告诉自己一次,我真的很不错。
•
67、心中有理想 再累也快乐
•
68、发光并非太阳的专利,你也可以发光。
•
69、任何山都可以移动,只要把沙土一卡车一卡车运走即可。
•
70、当你的希望一个个落空,你也要坚定,要沉着!
•
71、生命太过短暂,今天放弃了明天不一定能得到。
•
72、只要路是对的,就不怕路远。
•
73、如果一个人爱你、特别在乎你,有一个表现是他还是有点怕你。
•
74、先知三日,富贵十年。付诸行动,你就会得到力量。
•
75、爱的力量大到可以使人忘记一切,却又小到连一粒嫉妒的沙石也不能容纳。
的平行四边形叫做正方形。
定义法
有一个角是直角的菱形是正方形。 菱形法
有一组邻边相等的矩形是正方形。 矩形法
快速反应
判断题:
× ×
(1)正等方腰形 直的角一三条角对形角 (√线把正)方形分成两个全等的
(2)对角线互相垂直且相等的四边形是正方形( )
(3)对角线互相垂直,一个角是直角的四边形是正方形( ) (4)如果一个菱形的对角线相等,那么它一定
?
正方形的性质=
菱形性质
矩形性质
你觉得什么样的四边形是正 方形呢? ( 判断一个四边形是正方形 有哪些方法?)
常见说明方法
1、
一组邻边相等 平行四边形
一内角是直角
2、 菱形
一内角是直角
正方形 正方形
初二数学最新课件-正方形[下学期]浙教版1 精品
![初二数学最新课件-正方形[下学期]浙教版1 精品](https://img.taocdn.com/s3/m/7503c938700abb68a982fbc3.png)
一个角是直角且一组邻边相等
正
方
形
在你能收到的所有礼物中,它是最珍 贵的. 它是你送给自己的礼物,只有你自己 才能找到.
人生最珍贵的礼物就是:
当你全身心投入你正在做的事情, 你的心思就不会游离不定.你享受 生活,你也会更快乐更有效率.你 下决心只关注那一刻发生的事情, 那种集中和专注将带领你走向成 功.
上一点,CE⊥AF于E,交AD于M, 求证:∠MFD=45°
分析:
欲证∠MFD=45°,由于
△MDF是直角三角形,只须证 △MDF是等腰三角形,即只要证
_____=_____
要证MD=FD,大家只须证得哪两个三角形全等?
△CMD≌△ADF
试一形ABCD中,F为CD
D
BD相交于点O,且AC=6 2 cm,
面积S=___3_6____.则边长AB=__6____,
O
B
C
判定?
(可以平行四边形、菱形、矩形为基础)
有一组邻边相等且有一个角是直角的
平行四边形叫做正方形。
定义法
有一个角是直角的菱形是正方形。 有一组邻边相等的矩形是正方形。
菱形法 矩形法
下列说法对吗?
G
A
FD
B
C
E
(1)四个角都相等的四边形是正方形. 错误 (2)四条边都相等的四边形是正方形. 错误 (3)对角线相等的菱形是正方形. 正确 (4)对角线互相垂直的矩形是正方形.正确 (5)对角线垂直且相等的四边形是正方形. 错误 (6)四边相等,有一角是直角的四边形是正方形.正确
(7) 正方形的一条对角线把正方形分成两个全等的等腰直角三角
延长线上一点,CE⊥AF于E,交AD于M, 求证:∠MFD=45°
八年级数学下册《5.3 正方形(第2课时)》同步练习 浙教版(2021年整理)
浙江省绍兴市绍兴县杨汛桥镇八年级数学下册《5.3 正方形(第2课时)》同步练习(新版)浙教版编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(浙江省绍兴市绍兴县杨汛桥镇八年级数学下册《5.3 正方形(第2课时)》同步练习(新版)浙教版)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为浙江省绍兴市绍兴县杨汛桥镇八年级数学下册《5.3 正方形(第2课时)》同步练习(新版)浙教版的全部内容。
5.3 正方形(第2课时)课堂笔记正方形的个角都是直角,四条边;正方形的对角线 ,并且,每条对角线平分一组;正方形既是对称图形,又是对称图形,有条对称轴。
课时训练A组基础训练1. 如图,已知正方形ABCD,AC和BD交于点O,下列说法错误的是( )A。
AC=BD B。
OA≠OBC。
OA=OB,OC=OD D。
∠BAO=45°2. 如图,正方形ABCD中,∠DAF=25°,AF交对角线BD于点E,那么∠BEC等于(A. 45° B. 60° C. 70° D. 75°3。
如图,点P是正方形ABCD的对角线BD上一点,PE⊥BC于点E,PF⊥CD于点F,连结EF.给出下列五个结论:①AP=EF;②AP⊥EF;③△APD一定是等腰三角形;④∠PFE=∠BAP;⑤PD=2EC.其中正确结论的序号是( )A.①②③④ B.①②④⑤C.②③④⑤ D.①③④⑤4. 如图所示,正方形ABCD 的对角线相交于点O,点E 是DC 上任意一点,EG ⊥BD 于G,EF ⊥AC 于F ,若AC=10,则EG+EF 的值为( )A. 10B. 4C. 8D. 55。
5.3.1 正方形的判定 浙教版数学八年级下册同步课件
5.3.1 正方形的判定
情境导入
给你一张正方形的彩色纸,你能一剪刀剪出如图所示的正方 形孔吗?
获取新知
在第三步怎样剪才能剪一个正方形。
回顾并思考: 1.我们已经学习过哪些特殊的平行四边形? 2.是否存在一组邻边相等的特殊的矩形?若存在,它是什么图 形? 3.是否存在一个角是直角的菱形?若存在,它是什么图形?
我们可以得到一些正方形的判定定理 (1)直接用正方形的定义判定,即先判定一个四边形是平行四 边形,若这个平行四边形有一个角是直角,并且有一组邻边 相等,那么就可以判定这个平行四边形是正方形;
有一个角是直角,且有一组邻边ቤተ መጻሕፍቲ ባይዱ等的平行四边形是正方形;
(2)先判定一个四边形是矩形,再判定这个矩形是菱形,那 么这个四边形是正方形;
有一组邻边相等的矩形是正方形
(3)先判定四边形是菱形,再判定这个菱形是矩形,那么这个 四边形是正方形.
有一个角是直角的菱形是正方形.
做一做 (1)正方形的一条对角线把正方形分成两个全等的等腰直角三角 形(√ ) (2)对角线互相垂直且相等的四边形是正方形( × ) (3)如果一个菱形的对角线相等,那么它一定是正方形 ( √ ) (4)如果一个矩形的对角线互相垂直,那么它一定是正方形 (√) (5)四条边相等,且有一个角是直角的四边形是正方形( √ )
矩形在什么情况下成为正方形?
矩形
邻边相等
正方形
菱形在什么情况下成为正方形?
菱形
一个角是直角
正方形
∟
请在图中填上各种图形的名称和转化的条件
四边形
两组对 边平行
平行四边形
矩形 菱形
正方形
正方形定义: 有一组邻边相等并且有一个角是直角的平行四边形叫正方形.
正方形 PPT课件 27 浙教版
正方形
判断对错并说明理由(对的打√,错的打×)
正方形的一条对角线把正方形 分成两个全等的等腰直角三角形.( √ )
判断对错并说明理由(对的打√,错的打×)
如果一个矩形的对角线互相 垂直,那么它一定是正方形.(√ )
判断对错并说明理由(对的打√,错的打×)
如果一个菱形的对角线相 等,那么它一定是正方形.(√ )
方巾
七巧板
铜钱
5.3 正方 形
回顾
与 思考
特殊的平行四边形:矩形和菱形
. 矩形的定义:有一个角是直角 的平行四边形叫做矩形。 .菱形的定义:有一组邻边相等 的平行四边形叫做菱形。
正方形
矩形的定义:有一个角是直角的平行四边形叫做矩形。 菱形的定义:有一组邻边相等的平行四边形叫做菱形。
你觉得什么样的 平行四边形是正方形呢?
方 形
菱形
类 比 归 纳
回顾平行四边形,矩形,菱形的性质,完成表格前三列
性质 分类 图形
平行四 边形
对边平行 且相等 对角相等 对角线互 相平分
矩 形 (所特有)
菱形 (所特有)
四条边相等
正方形
对边平行且 四条边相等 四个角都 是直角
边 角
四个角都 是直角 对角线 相等
对角线
对角线相等且互 对角线互相 相垂直平分,每 垂直,每条 条对角线平分一 对角线平分 组对角 一组对角 既是中心对 称图形又是 轴对称图形
判断对错并说明理由(对的打√,错的打×)
四条边相等,且有一个角 是直角的四边形是 性质是( D ) A、四条边相等. B、对角线互相垂直平分. C、对角线平分一组对角. D、对角线相等.
选一选
正方形具有而矩形不一定具有的 性质是( B ) A、四条角相等. B、对角线互相垂直平分. C、对角互补. D、对角线相等.
原八级数学下册5.3正方形第2课时正方形的性质课件(新版)浙教版
7.如图,O为正方形ABCD的对角线AC与BD的交点,M,N两点分别在 BC与AB上,且OM⊥ON.
(1)求证:OM=ON; (2)试判断CN与DM的关系,并加以证明.
解:(1)证△AON≌△BOM (2)CN=DM,CN⊥DM.证△BCN≌△CDM
8.如图,正方形ABCD中,∠DAF=25°,AF交对角线BD于点E,那 么∠ BEC等于( C )
A.75° B.60° C.45° D.30°
13.如图,正方形 ABCD 中,AB=3,点 E 在边 CD 上,且 CD=3DE, 将△ADE 沿 AE 对折至△AFE,延长 EF 交边 BC 于点 G,连结 AG,CF.下列
结论:①点 G 是 BC 中点;②FG=FC;③S△FGC=190.其中正确的是( B ) A.①② B.①③ C.②③ D.①②③
14.如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且 DF=BE.
(1)求证:CE=CF; (2)若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?
解:(1)通过证△BCE≌△DCF,可得CE=CF (2)GE=BE+GD成立,理 由如下:由(1)知△BCE≌△DCF,∴∠BCE=∠DCF,∴∠GCF=∠GCD+ ∠DCF=∠GCD+∠BCE=∠BCD-∠ECG=45°=∠GCE,
1 A.4a
1 B.2a
C.a
D.2a
3.正方形ABCD在平面直角坐标系中的位置如图所示,已知点A的坐标 为(0,4),点B坐标为(-3,0),则点C的坐标为(B )
A.(1,3) B.(1,-3) C.(1,-4) D.(2,-4)
4.如图,在正方形ABCD中,G是BC上任意一点,连结AG,DE⊥AG于 点E,BF∥DE交AG于点F,探究线段AF,BF,EF三者之间的数量关系, 并说明理由.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
正方形是特殊的平行四边形, 也是特殊的矩形,也是特殊的菱形。
正方形会有哪些性质呢?
正方形的性质
请你从对称性、边、角、对角线四个方面进 行考虑,说说正方形有哪些性质吗? 从对称性看: 从边看: 从角看: 从对角线看: 正方形既是轴对称图形,又 是中心对称图形. 正方形的四边相等,对边平行; 正方形4个角都是直角;
H
D G
(2)
A M G
H
D F
N
G B
(1 )
E
F C
F
N
Байду номын сангаас
B
E
C
B
(3 )
E
C
课外拓展:
1. 如图,分别以△ABC的边AB,AC为一边向外 画正方形AEDB和正方形ACFG,连接CE,BG.求证: BG=CE.
证明:在正方形ABDE中, AE=AB,∠EAB=90°, 又在正方形ACFG中, AG=AC,∠GAC=90°, ∴∠EAB=∠GAC=90°. ∵∠EAC=∠EAB+∠BAC, ∠GAB=∠GAC+∠BAC, ∴∠EAC=∠GAB, ∴△EAC≌△GAB, ∴EC=GB.
A M E B C O F N
正方形是特殊的平行四边形,也是特殊的矩形, 也是特殊的菱形。
正方形的四个角是直角,四条边都相等。
正方形的对角线相等,并且互相垂直平分,每条 对角线平分一组对角。
正方形的性质=
证:∵四边形ABCD是正方形, 且AE⊥BF, ∴∠BAE+∠ABF=90°, ∠ABF+∠FBC=90°, ∴∠BAE=∠FBC. 又∵∠ABE=∠BCF=90°,AB=BC, ∴△ABE≌△BCF ∴AE=BF.
5.已知:如图(4)在正方形ABCD中,F为CD延长线
上一点,CE⊥AF于E,交AD于M,
正方形的两条对角线相等且互 相垂直平分;每一条对角线平 分一组对角
1. 正方形具有而矩形不一定具有的性质是( B) A、四个角相等. B、对角线互相垂直平分. C、对角互补. D、对角线相等. 2.正方形具有而菱形不一定具有的性质( D ) A、四条边相等. B、对角线互相垂直平分. C、对角线平分一组对角. D、对角线相等.
2、如图,在正方形ABCD中,M是正方形内一点, 且MC=MD=AD,求∠BAM的度数.
3.如图,在正方形ABCD中,E、F分别是AD、CD 上的点,且DE=DF,BM⊥EF于点M, 求证:ME=MF
4.已知:如图,在正方形ABCD中,E,F分别是BC,CD上的点, AE⊥BF. 求证:AE=BF.
求证:∠MFD=45°
2 3
分析:
欲证∠MFD=45°,由于
△MDF是直角三角形,只须证 △MDF是等腰三角形,即只要证
_____=_____
要证MD=FD,大家只须证得哪两个三角形全等?
△CMD≌△ADF
课内 作业
试一试
看能不能完成证明???
提高 小结
变式:如图,在矩形ABCD中,如图 (1)AE⊥BF,AE=BF,则四边形ABCD 是正方形吗?那么(2)和(3)呢? A D A
拓展2:如图,△BAC中,点O为AC边上一个动点,过点O 作直线MN∥BC,设MN交∠BCA的外角平分线CF于点F,交 ∠ACB的内角平分线CE于点E。 1)求证:EO=FO; 2)当点O运动到何处时,四边形AECF是矩形并说明理由。 3)在(2)的条件下,当∠ACB为多少度时,四边形 AECF是正方形,请说明理由。(改编)
例1 已知:如图,在正方形ABCD中,G是对角线 BD上的一点,GE⊥CD,GF⊥BC,E、F分别为 垂足,连结AG,EF 求证:AG=EF
例2:如图,正方形ABCD中,AC、BD相交于O,
∵四边形ABCD是正方形 证明: ∴OA=OB AB=BC ∠1=∠2=∠3=45° 又∵MN∥AB ∴∠OMN=∠1=∠3=∠ONM=45° ∴OM=ON ∴OA-OM=OB-ON 即:AM=BN ∴△ABM≌△BCN ∴BM=CN
复习回顾 矩形
正方形
平行四边形
菱形
几种特殊四边形的性质 边 角 对 角 线
对称性
平行 四边形
对边平行 且相等
对角相等, 邻角互补
对角线 互相平分 对角线相等 且互相平分
中心对 称图形 轴对称 图形、 中心对 称图形
矩 形
对边平行 且相等
四个角 都是直角
菱 形
对边平行 ,四边都 相等
对角线互相 轴对称 对角相等, 垂直平分, 图形、中 邻角互补 每条对角线 心对称图 平分一组对 形 角
MN∥AB且MN分别交OA、OB于M、N,求证:BM=CN。
1、正方形ABCD中,E是BC延长线上一点,且CE=AC, AE交DC于点F,试求∠E, ∠AFC的度数. 解: ∵四边形ABCD为正方形,
1 1 ACB BCD 900 450 2 2
A
D
j
F
B
C
∵CE=AC ∴∠E=∠CAE ∵∠ACB是⊿ACE的一个外角 ∴∠ACB=∠E+∠CAE=2∠E 1 1 E ACB 450 22.50 2 2 E ∵∠AFC是△CEF的一个外角 ∴∠AFC=∠E+∠FCE=22.5°+90°=112.5° ∴∠E=22.5°, ∠AFC=112.5°
