梅逊公式
合集下载
用梅逊公式求传递函数

C(s) R(s)
1
G1(s)G2 (s) G1(s)G2 (s)H (s)
Φr(s)为输入信号r(t)作用下系统的闭环传递函数。此时系统输出的 拉氏变换式为
C
(s)
r
(s)R(s)
1
G1(s)G2 (s) G1(s)G2 (s)H
(s)
R(s)
7
2). 扰动 n(t)作用下系统的闭环传递函数
在下图(a)所示的反馈系统中,为求取r(t)作用下系统的闭环传递 函数,可令n(t)=0。
R(s)
E(s)
- B(s)
G1(s)
N(s)
+
C(s)
G2(s)
H(s)
(a)
R(s)
- B(s)
G1(s)
C(s) G2(s)
H(s)
(b)
6
由图(b)求得输出C(t)和输入r(t)之间的传递函数为
r
(s)
用梅逊(S.J.Mason)公式求传递函数
梅逊公式一般形式为
n
Pk k
(s) k1
式中 (s)为待求的总传递函数。
称为特征式,且
其中
1 Li Li L j Li L j Lk Li ——所有不同回路传递函数之和。 Li L j ——所有两两互不接触回路的回路传递函数乘积之和。 Li L j Lk ——所有三个互不接触回路的回路传递函数乘积之和。
n
(s)
N
(s)
1
G1
G2 (s) (s)G2 (s)H
(s)
N
(s)
梅逊增益公式及应用

L1 G1G2H1 L2 G2G3H2 L3 G1G2G3
-H2
1
②
G1 G2
G3
1 C(s)
① -H1
-1 ③
3
1 Li 1 G1G2H1 G2G3H2 G1G2G3
i 1
1 1
T
C(s) R( s )
1
P11
1
G1G2 H1
G1G2G3 G2G3H2
G1G2G3
例:求系统的总增益。
G(s) C(s) P11
G1G2G3G4
R(s) 1 G2G3G6 G3G4G5 G1G2G3G4G7
R(s)+ +
H2(s)
—
G1(s) +
G2 ( s )
G3 ( s )
C(s)
——
H1(s)
R(s) 1
-H2
1
G1 G2
G3
1 C(s)
-H1
-1
R(s) 1
P1 G1G2G3
G1G2G3 G1G4 G2G3H2 G1G2G3
G1G4
G4H2
② E(s)/R(s) E(s)
1
R(s)
1 1 G1
-H1
④⑤
G4
G2
G3
① -H2 ②
前向通道: P1 1
-1 ③
L1 G1G2H1 L2 G2G3 H2
反馈回路: L3 G1G2G3
1 1 G1G2H1 G2G3H2 G4H2
梅逊增益公式及应用
信号流图上从输入节点(源节点)输出节点到(汇节点)的总增 益公式,即梅逊公式(Mason),表达式为:
T
G(s)
C(s) R( s )
-H2
1
②
G1 G2
G3
1 C(s)
① -H1
-1 ③
3
1 Li 1 G1G2H1 G2G3H2 G1G2G3
i 1
1 1
T
C(s) R( s )
1
P11
1
G1G2 H1
G1G2G3 G2G3H2
G1G2G3
例:求系统的总增益。
G(s) C(s) P11
G1G2G3G4
R(s) 1 G2G3G6 G3G4G5 G1G2G3G4G7
R(s)+ +
H2(s)
—
G1(s) +
G2 ( s )
G3 ( s )
C(s)
——
H1(s)
R(s) 1
-H2
1
G1 G2
G3
1 C(s)
-H1
-1
R(s) 1
P1 G1G2G3
G1G2G3 G1G4 G2G3H2 G1G2G3
G1G4
G4H2
② E(s)/R(s) E(s)
1
R(s)
1 1 G1
-H1
④⑤
G4
G2
G3
① -H2 ②
前向通道: P1 1
-1 ③
L1 G1G2H1 L2 G2G3 H2
反馈回路: L3 G1G2G3
1 1 G1G2H1 G2G3H2 G4H2
梅逊增益公式及应用
信号流图上从输入节点(源节点)输出节点到(汇节点)的总增 益公式,即梅逊公式(Mason),表达式为:
T
G(s)
C(s) R( s )
梅逊公式的应用

2.6
解: 前向通道(1条): 反馈回路(5个):每个均为
P1
系统信号流图及梅逊公式
1
R C s 1
RCs
3
3
3
1 1
则
a
La
5 RCs
两个互不接触回路(6个):①②、①③、③④、①⑤、②③、④⑤
每对传递函数之积为:
1 R C s
2 2 2
则
Lb Lc
6 R C s
3
2 2 2
系统信号流图及梅逊公式
②
-
1/G2(s) G2(s) H1(s)
①
H2(s) Y0 G4(s)
+
Xi(s)
+
G1(s)
+
X0(s)
-
-
-
G3(s)
③ ④
第二步、消去反馈回路①,另相加点(比较点)③前移
1/G2 H2
Xi(s)
+
G1
②
+
③
G3(1+G2H1)/G2G4
X0(s)
G2G4 /(1+G2 H1 )
2.6
系统信号流图及梅逊公式
二、梅逊公式的应用示例
例1:利用梅逊公式求如图所示系统的传递函数
R(s)
1/R 1/Cs
④
1/R 1/Cs
⑤
1/R 1/Cs
Y(s)
①
②
③
系统的信号流图为:
-1 -1
R(s) 1
④
1/R 1/Cs 1 1/R 1 1/Cs
⑤
1 1/R 1/Cs
Y(s)
①
-1
如何用梅逊公式求传递函数
• 通路传输(增益):通路中各支路传输的乘积称为通路传输或通 路增益。前向通路中各支路传输的乘积称为前向通路传输或前 向通路增益。
• 回路传输(增益):回路上各支路传输的乘积称为回路传输或回
路增益。
1/8/2024
如何用梅逊公式求传递函数
4
信号流图的等效变换
• 串联支路合并:
ab x1 x2 x3
8
例2: 已知结构图如下,可在结构图上标出节点,如上图所示。 然后画出信号流图如下图所示。
k
R(S) b
m
d
V1
l
g V3 e
V2
h
C(S)
f f
m
h
R1
Ⅰ
b
l
Ⅱ
V3
k
Ⅲ
Ⅳ
C
V1 d Ⅴ e V2 1
g
1/8/2024
如何用梅逊公式求传递函数
9
信号流图的绘制
例2: 按微分方程拉氏变换后
的代数方程所表示的变量间
信号流图的概念
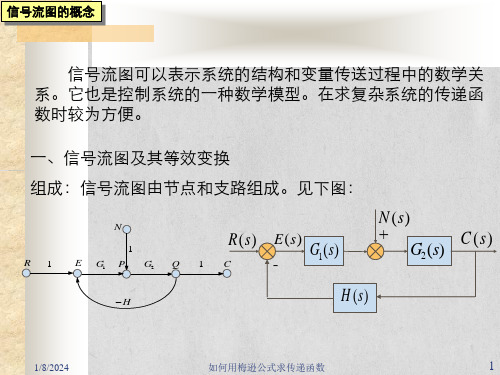
信号流图可以表示系统的结构和变量传送过程中的数学关 系。它也是控制系统的一种数学模型。在求复杂系统的传递函 数时较为方便。
一、信号流图及其等效变换
组成:信号流图由节点和支路组成。见下图:
R1
N
1
E G1 P
G2
Q
1
R(s)
C
E(s)
-
G1(s)
N (s)
+ G2(s) C (s)
H
H (s)
式中: La 流图中所有不同回路的回路传输之和;
LbLc 所有互不接触回路中,每次取其中两个回
路传输乘积之和;
LdLeLf 所有互不接触回路中,每次取其中三个
1梅逊增益公式

=1+ G1 +G2+G3 +2G1G2+G2G3 + G1 G3 + 2G1G2G3 6
G1 G1 R R 1 1 1 1
G2 G2 1 1
G3 G3
K K C C
1 1
前向通道:P1 = G1 G2G3 K P2 = G2G3 K P3 = G3 K P4 = G2 (1)G3 K
分别是:P1 = G1G2G3 ,1 = 1; P2 = G1G4 ,2= 1。
梅逊公式小结
梅逊公式同时适用于信号流图和结构图;
关键:数清楚前向通道数、单回环数、互不接触回环数; 注意:反馈环是正反馈还是负反馈;
bc
k , 在所有两两互不接触的 回环中,每次不重复取 其中的两个回环增益之 积之和; L PL — 第K条前向通路的传输;
其余的以此类推
3
例2-20 求图所示系统的信号流图输入x0至输出x8的总
传输P。 a
x0
b i
c
d j m
e
f
k
g
h x
8
解:
前向通道:1条, P1 = abcdefgh;
C(s)/R(s)=P=(P=1+1G G H 2 )/ +P2 +G G H 3、 特征式: 1
1 2 1 2 3
2、互不接触回环数: 0
2
+G1G2G3 + G4H2 + G1G4
=4、前向通道数:1G4 )/ (1+ G1G2H1 +G2G3H2 +G1G2G3 + G4H2 + G1G4 ) (G1G2G3 +G 2,
2.7 梅逊公式

△1= 1
∑Pk△k= P1△1= G1 G2 G3 G4G5 G6 将中△与第K条前向通道相接触 条前向通道相接触( △k:将中△与第 条前向通道相接触(有 重合部分)回路所在项去掉之后的余子式。 重合部分)回路所在项去掉之后的余子式。
例:试用梅逊公式求传函C(S)/R(S)。 试用梅逊公式求传函 。
一、梅逊公式
∑Pk△k C(s) : G(S)= R(s) = i G = G1 G3 2 △ 1、G(S):从输入通道到输出通道总的传递 、 : H1 H2 H3 函数(总增益)。 函数(总增益)。 2、△:称为系统主特征式 、 △=1- ∑La+ ∑LbLc-∑LdLeLf+…
所有单独回路增益 回路增益之和 ∑La — 所有单独回路增益之和 ∑LbLc—所有两两互不接触回路增益乘积之和 所有两两互不接触回路增益乘积之和 ∑LdLeLf—所有三个互不接触回路增益乘积之和 所有三个互不接触回路增益乘积之和
R G1 G2 1 H2 G3 H4 H1 4 G4 C
2 H3
G5
G6 3
解: 3、G(S) 、
△=1+G2G3H2 +G4G5H3 +G3G4H4 +G1G2G3G4G5G6H1+G2G3G4G5H2 H3
∑Pk△k= P1△1= G1 G2 G3 G4G5 G6 ∑Pk△k C(s) : G(S)= R(s) = i = △
= G1 G2 G3 G4G5 G6
n
△
应用梅逊公式, 应用梅逊公式,将大大简化结构 变换的计算。 变换的计算。但当系统结构较复 杂时,容易将前向通道、 杂时,容易将前向通道、回路数 及余子式判断错,需格外注意。 及余子式判断错,需格外注意。
例:试用梅逊公式求传函C(S)/R(S)。 试用梅逊公式求传函 。 G4 4 G3 2 H2
梅森公式-信号流图
L4 a23a34a45a52
x5 L5 a23a35a52
P
a12 a23a34 a45 (1 a44 )a12 a23a35
1 (a23a32 a23a34a42 a44 a23a34a52 a23a35a52 ) a23a32 a44 a23a35a52a44
G3(s)
梅逊公式求E(s)
R(s)
E(SG)GG3(33s(()ss))
RRR(s(()ss)) EEE(S((S)S))
P2= - G3G2H3
GGG1(11s(()ss))
△2= 1 P2△2=?
HHH1(11s(()ss))
G1(s)
NNN((s(ss)))
G2(s)
GGG2(22s(()ss))
CCC(s(()ss))
HHH2(22s(()ss)) H3(s)
HHH3(33s(()ss))
C(s)
R(s)
E(S) P1=H–P1G(s1)2=H13 △△1=11=+G1 2HH2 2(s)P1△1= ?
E(s)= R(s)[ (1+G2H2) +(- G3G2H3)] +(–G2H3)N(s)
1 G1H1 G2G7 H 2 G6G4G5 H 2 G2G3G4G5 H 2 G4G5G7 H1H 2
x1
x2
x3
x7 I(s) x4
x5
o在源节点上,只有信号输出 支路而没有信号输入的支路,
1/R1 1+R1C1s R2
它一般代表系统的输入变量。
-1
•阱节点(输出节点):
在阱节点上,只有信号输入的支路而没有信号输出的支路,它
梅逊公式及其应用
P2 kgi 2 1 cd
• 将以上结果代入式公式,可得总传输
P
P P
11
22
1L L L L L L
a
bc
de f
1
2
3
acegi kgi(1 cd )
1 (ab cd ef gh ij kfdb) (abef abgh abij cdgh cdij efij kfdbij) abefij
=每两个互不接触回路增益乘积之和
2
L LL de f
=每三个互不接触回路增益乘积之和
3
Δk=信号流图中除去与第k条前向通道Pk相接触的支路和节点后余下的信 号流图的特征式,称为Pk的余因式。
例2-4 将图所示的系统方块图化为信号流程图并
将其简化。求系统传递函数
C(s)
R(s)
H2
R
+- ++
G1
+-
x7 C(s) 图2-13 信号流程图
解:• 此系统有六个回环,即ab、cd、ef、ij和kfdb,因此 L ab cd ef gh ij kfdb
a 1
• 两个互不接触的回环有七种组合,即abef、abgh、 abij、cdgh、cdij、efij及kfdbij,所以
L L abef abgh abij cdgh cdij efij kfdbij bc 2
G2
C G3
H1
图2-11 多回路系统
解:• 首先将图2-11方块图化为图2-12的信号流程图
-H2
1 R( s)
1
Байду номын сангаасG1
G2
G3
H1 -1
1
C( s)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
回章首
回节首
10
3. 信号流图的绘制
可按线性代数方程组和结构图绘制。 1) 按线性代数方程组绘制信号流图 对线性微分方程组进行拉氏变换变为代数方程组后再进行绘制。 通常把输入节点放在左边,把输出节点放在右边。 举例说明。
回章首
回节首
11
T] 形电路如图所示,试绘制信号流图。 [加例1 解
i1 (U1 U 2 )
如果有多个源点和阱点,则可以多次应用梅逊公式,然后用叠加 原理算出各个输出信号。
回章首
回节首
17
梅逊总增益计算公式
1 n P i pi i 1
公式中, P—源点到阱点之间的总增益; n —源点到阱点的前向通路的总数; Pi—从输入到输出的第i条前向通路增益; —梅逊公式特征式; i—第i条前向通路的余子式。
把混合节点变为阱点时,此两节 点均采用同一符号来表示。如图中 x5 。 用这种方法,不能把混合节点变 为源点。
回章首
回节首
9
5) 对于给定的系统,信号流图不是 唯一的。 由于一个给定的系统,可以用 不同形式的微分方程组来进行描述。 而信号流图或结构图是按微分方程 组的拉氏变换式进行绘制的。
(2-123)
回章首
回节首
18
特征式
的计算公式为
1 La Lb Lc
a b,c
d ,e, f
L
d
Le L f ....
(2-124)
L —所有独立回路增益之和; —所有每两个互不接触回路增益乘积之和; L L —所有每三个互不接触回路增益乘积之和。 L L L
2-5-3 梅逊公式
根据结构图等效化简原则,将结构图化成简单方块,可以求得系统 的传递函数。但是化简步骤仍然需要一步一步地进行。 采用梅逊公式 (Mason)化简结构图求取系统的传递函数,只需要作 少量的计算,就可以将传递函数一次写出。所以是一种简捷方便的方 法。 梅逊公式是基于信号流图理论得出的计算公式,用于计算线图的总 传输。
+ G1(s) + H(s) F(s)
A(s)
G2(s)
Y(s)
1
R(s) E(s)
G1(s)
A(s)
1
G2(s)
Y(s)
1 Y(s)
-H(s)
回章首 回节首 14
R(s) -
-
H2 (s) G2(s) G3(s) Y(s)
+
G1(s)
+
+
H1 (s) -1
-H2 (s) R(s) 1 G1(s) G2(s) G3(s) Y(s) 1 Y(s)
回章首
回节首
5
前向通路传输:在前向通路中 , 各支路传输的乘积。 如图中abc和ade。 回路传输:回路中各支路传输的 乘积。 如图中的df和g。
回章首
回节首
6
2. 信号流图的基本性质
1) 信号在支路上只能沿箭头单向传 递,后一节点对前一节点没有负载 效应。 2) 支路表示了一个信号对另一信号 的关系,支路传输相应于比例系数, 信号经支路时,被乘以支路传输变 为另一信号。 如图中x2经支路b变换为x3=bx2 , 经支路d变换为x4=dx2 。
信号(或变量)变为节点;
相加点和分支点可视作为节点。
注意: 相加点视作为 “节点”是指相加点输出的信号。
在相减的情况下 (例负反馈 ),可将此“负”号加在传输前面,亦即 使正传输变为负传输。
回章首
回节首
13
R(s)
G(s)
Y(s)
R(s) F(s)
G(s)
Y(s)
R(s) + -
E(s)
1 R1 1 R3
U 2 (i1 i3 ) R2 i3 (U 2 U 3 ) U 3 i3 R4
U1为输入量,U3为输出量,i1, i3,U2 为中间变量。 按上述方程组绘制信号流图如图 所示。
混合节点 U3 通过增加一个单位传 输的支路变为阱点。
回章首
回节首
12
2) 按结构图绘制信号流图 方法: 将传递函数变为传输;Leabharlann 回章首回节首7
3) 节点可以把所有输入支路的信 号相加(注意:是相加而不是相减), 并把总的信号传递到所有输出支 路。 如图中节点 x2=ax1+fx4 如果此反馈为负反馈,则将“-” 号表示在传输 f 上,即信号流图上 f变为-f,此时x2=ax1+(-f)x4
回章首
回节首
8
4) 对混合节点通过增加一个单位传 输(即传输等于1)的支路,可以把它 变为阱点来处理。如图中x5 。 注意:
回章首
回节首
1
1. 信号流图和术语介绍
下图表示了一个信号流图,现介绍信号流图中的一些术语。
节点:用来表示变量或信号的 点,以小圆圈“o”表示。 如图中x1,x2,x3,x4,x5。
支路:是连接两个节点的定向 线段,以带箭头的方向线表示。 如图中的线段: x1x2 , x2 x3, x2 x4 , x3 x5 , x4 x5
回章首
回节首
2
传输:两个节点之间的增益, 它 也 是 支 路 传 输 。 图 中 a,b,c,d,e,f,1。 输入节点(源点):只有输出支路 的节点,它对应于输入量。如图 中 x1。 输出节点(阱点):只有输入支路 的节点,它对应于输出量。如图 中 x5。 混合节点:既有输入支路,又 有输出支路的节点。如图中x2,x3, x4 , x5 。
H1 (s)
回章首 回节首 15
从图中可以看到,支路、支路增益、回路等,两图一一对应。 信号流图 结构图 这样,在应用梅逊公式作结构图化简时,可以省去信号流图,直 接在结构图上完成。
回章首
回节首
16
4. 梅逊公式
梅逊公式可以直接计算出某一源点到某一阱点的总增益,而不需 对信号流图作任何变换。
回章首
回节首
3
通路:沿支路箭头方向而穿过相 连支路的途径。 如 图 中 x1x2x3x5 , x4x2x4 等。
前向通路:如果从源点到阱点的 通路上,通过任何节点不多于一次, 则该通路称为~。 如图中 x1x2x3x5x5,x1x2x4x5 x5 。
回章首
回节首
4
回路:通路的终点就是通路的起点, 并且与任何其它节点相交不多于一次 叫 ~。 如图中的x4x2x4 ,节点x5上的自回 路。 不接触回路:若一些回路没有任何 公共节点,叫~。 如图中的x4x2x4 ,节点x5上的自回 路。 自回路:回路的一种特殊情况,即 从某一节点出发只经一条支路而又终 止于同一节点所构成的回路。 如图中节点x5上的自回路。
