第九章压杆的稳定习题
压杆稳定习题

第九章压杆稳固姓名班级学号一、填空和选择1.理想平均直杆与轴向力 F=F cr 时处于直线均衡状态, 当其遇到一细小横向扰乱力后发生微 小曲折变形,若此时排除扰乱力,则压杆( ) A 曲折变形消逝,恢复直线形状; B 曲折变形减小,不可以恢复直线形状;C 微弯变形状态不变;D 曲折变形持续增大 2. 压杆的柔度集中地反应了压杆的( )对临界应力的影响A 长度、拘束条件、截面形状和尺寸;B 资料、长度和拘束条件;C 资料、拘束条件、截面形状和尺寸;D 资料、长度、截面形状和尺寸3.两头铰支圆截面修长压杆,在某一截面上开一个小孔,对于小孔对杆承载能力的影响, 以下阐述正确的选项是( )A 对强度和稳固承载能力都有较大消弱;B 对强度有较大消弱,对稳固承载能力消弱极微C 对强度无消弱,对稳固承载能力有较大消弱;D 对强度和稳固承载能力都不会消弱 4.修长杆在图示拘束状况下,其长度要素μ的大小在( )范围内。
(A) μ>2;(B) 2>μ >;(C) >μ >;(D) μ <。
题4图题5图5. 上端自由、下端固定的压杆,横截面为 80*80*5 号等边角钢,失稳时截面会绕轴弯曲。
(A) z 或 y 轴;(B)zc 或 yc 轴;(C) y0 轴; (D) z0 轴。
6. 图示为支撑状况不一样的圆截面修长杆,各杆的直径和资料同样, 的柔度最大, 数值为 ; 的柔度最小, 数值为 ; 的临界力最大,数值为 ; 的临界力最小,数值为 ;7. 两根修长压杆的长度、横截面面积、拘束状态以及资料均同样,若横截面形状分为正方 形和圆形, 则截面形状为 的柔度大, 截面形状为 的临界力大。
8. 以下对于压杆临界应力cr 的结论中,( )是正确的。
A 修长杆的cr 与杆的资料没关;B 中长杆的crC 中长杆的cr 与杆的资料没关; D 短粗杆的cr与杆的柔度没关与杆的柔度没关二、图示两头铰支压杆,用两根8 号槽钢( Q235 钢)按图示方式组合而成,试确立两根槽钢间距为多少时组合杆的临界力最大,并计算此临界力。
压杆稳定习题
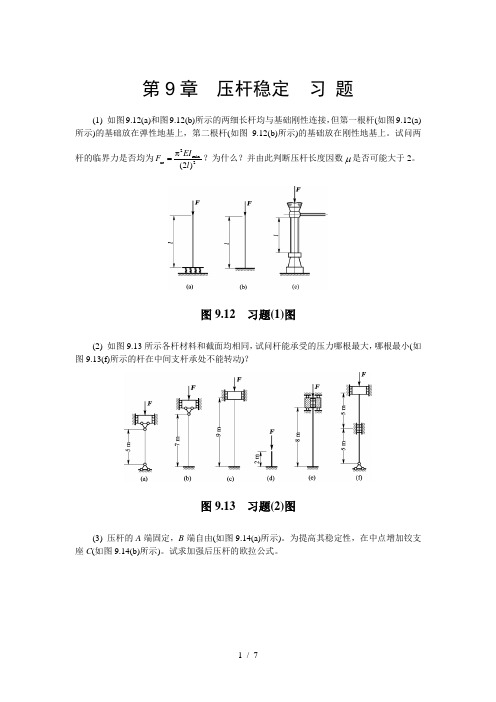
第9章压杆稳定习题(1) 如图9.12(a)和图9.12(b)所示的两细长杆均与基础刚性连接,但第一根杆(如图9.12(a)所示)的基础放在弹性地基上,第二根杆(如图9.12(b)所示)的基础放在刚性地基上。
试问两杆的临界力是否均为2mincr2(2)EIFlπ=?为什么?并由此判断压杆长度因数μ是否可能大于2。
图9.12 习题(1)图(2) 如图9.13所示各杆材料和截面均相同,试问杆能承受的压力哪根最大,哪根最小(如图9.13(f)所示的杆在中间支杆承处不能转动)?图9.13 习题(2)图(3) 压杆的A端固定,B端自由(如图9.14(a)所示)。
为提高其稳定性,在中点增加铰支座C(如图9.14(b)所示)。
试求加强后压杆的欧拉公式。
图9.14 习题(3)图(4) 如图9.15所示正方形桁架,5根相同直径的圆截面杆,已知杆直径d=50mm,杆长a=1m,材料为Q235钢,弹性模量E=200GPa。
试求桁架的临界力。
若将荷载F方向反向,桁架的临界力又为何值?图9.15 习题(4)图λ=100,(5) 如图9.16所示两端固定的空心圆柱形压杆,材料为Q235钢,E=200GPa,p外径与内径之比 1.2D d=。
试确定能用欧拉公式时,压杆长度与外径的最小比值,并计算这时压杆的临界力。
图9.16 习题(5)图(6) 如图9.17所示的结构ABCD,由3根直径均为d的圆截面钢杆组成,在B点铰支,而在A 点和C 点固定,D 为铰接点,10ld=π。
若此结构由于杆件在平面ABCD 内弹性失稳而丧失承受能力,试确定作用于节点D 处的荷载F 的临界力。
图9.17 习题(6)图(7) 如图9.18所示的铰接杆系ABC由两根具有相同材料的细长杆所组成。
若由于杆件在平面ABC 内失稳而引起毁坏,试确定荷载F 为最大时的θ角(假定02θπ<<)。
图9.18 习题(7)图(8) 下端固定、上端铰支、长l =4m 的压杆,由两根10号槽钢焊接而成,如图9.19所示,符合钢结构设计规范(GB50017—2003)中实腹式b 类截面中心受力压杆的要求。
第九章压杆稳定答案

i - . D 2 d 2 / 4 = 52 2 442 / 4mm = 0.017mm第九章压杆稳定1、图示铰接杆系ABC 由两根具有相同截面和同样材料的细长杆所组成。
若由于杆件在平面ABC 内失稳而引起破坏,试确定荷载 F 为最大时的二角(假设0 —岂㊁)。
解:由平衡条件二 Fy = 0, F NAB = F COSd二 F x - 0, F NBC - F sin T 使F 为最大值条件使杆AB 、BC 的内力同 时达到各自的临界荷载。
设 AC 间的距离为I , AB 、BC 杆的临界荷载分别为H 2EI 兀 2EI F NAB= 7T = 7S —5 F NBC 二 2EI 二 2EI由以上两式得2、一承受轴向压力的两端铰支的空心圆管,外径 D 二52mm ,内径 d 二 44mm ,I 二 950mm 。
材料的二 1600MPa ,二 p 二1200MPa ,E = 210GPa 。
试求此杆的临界压力和临界应力。
支承可视为两端铰支,故 J =1,BC (I cos 。
f二 41.6 解:2 9 ■: 210 10 \ 1200 106回转半径为44斜撑杆得柔度■ - l. i =1 0.95/0.017 =55.9因■ ■ !,为大柔度杆,故可用欧拉公式计算临界荷载,临界压力为F cr 和临界 应力二cr 分别为:29 : .•4 4 _.2 二2 210 109 0.0524 -0.0444F cr ' -3 64 2 N =402KN(H ) (1x0.95) ”-心 匹=666 MPaA3、蒸汽机车的连杆如图所示,截面为工字型,材料为 Q235钢,连 杆所受最大轴向压力为465kN 。
连杆在xy 平面内发生弯曲,两端可视 为铰支,在xz 平面内发生弯曲,两端可视为固定。
试确定工作安全系 数。
|3100解连杆横截面的几何特性:2 2 A =[ 14>9.6- (9.6-1.4) >8.5] cm =64.7cm4I y=407 cm *yLI z=1780 cm4i y = |厂A = ,407 64.7 = 2.51cmi z = l z A = .1780 64.7 = 5.24cmQ235钢的「f%2E 「200 109 200 10—99.3a —0's 304 —240■■■■2 57.1b 1.12 在xy 平面内弯曲时连杆的柔度在xz 平面内弯曲时连杆的柔度y =0.5 3.1/0.0251 =61.8「1所以在计算两个方向上产生弯曲时的临界荷载,都要用经验公式,并且只须计算在柔度较大 的方向上产生弯曲时的临界荷载 F c 「二 a-b y A -丨304-1.12 61.8106 64.7 10*N=1520kN工作安全系数 n = F cr / F = 1520/465 = 3.274、油缸柱塞如图所示。
2020年材料力学习题册答案-第9章 压杆稳定

作者:非成败作品编号:92032155GZ5702241547853215475102时间:2020.12.13第九章压杆稳定一、选择题1、一理想均匀直杆受轴向压力P=P Q时处于直线平衡状态。
在其受到一微小横向干扰力后发生微小弯曲变形,若此时解除干扰力,则压杆( A )。
A、弯曲变形消失,恢复直线形状;B、弯曲变形减少,不能恢复直线形状;C、微弯状态不变;D、弯曲变形继续增大。
2、一细长压杆当轴向力P=P Q时发生失稳而处于微弯平衡状态,此时若解除压力P,则压杆的微弯变形( C )A、完全消失B、有所缓和C、保持不变D、继续增大3、压杆属于细长杆,中长杆还是短粗杆,是根据压杆的( D )来判断的。
A、长度B、横截面尺寸C、临界应力D、柔度4、压杆的柔度集中地反映了压杆的( A )对临界应力的影响。
A、长度,约束条件,截面尺寸和形状;B、材料,长度和约束条件;C、材料,约束条件,截面尺寸和形状;D、材料,长度,截面尺寸和形状;5、图示四根压杆的材料与横截面均相同,试判断哪一根最容易失稳。
答案:( a )6、两端铰支的圆截面压杆,长1m,直径50mm。
其柔度为 ( C )A.60;B.66.7;C.80;D.507、在横截面积等其它条件均相同的条件下,压杆采用图( D )所示截面形状,其稳定性最好。
8、细长压杆的( A ),则其临界应力σ越大。
A 、弹性模量E 越大或柔度λ越小;B 、弹性模量E 越大或柔度λ越大;C 、弹性模量E 越小或柔度λ越大;D 、弹性模量E 越小或柔度λ越小; 9、欧拉公式适用的条件是,压杆的柔度( C )A 、λ≤、λ≤C 、λ≥π D、λ≥10、在材料相同的条件下,随着柔度的增大( C )A 、细长杆的临界应力是减小的,中长杆不是;B 、中长杆的临界应力是减小的,细长杆不是;C 、细长杆和中长杆的临界应力均是减小的;D 、细长杆和中长杆的临界应力均不是减小的; 11、两根材料和柔度都相同的压杆( A )A. 临界应力一定相等,临界压力不一定相等;B. 临界应力不一定相等,临界压力一定相等;C. 临界应力和临界压力一定相等;D. 临界应力和临界压力不一定相等;12、在下列有关压杆临界应力σe 的结论中,( D )是正确的。
压杆稳定习题

压杆稳定一、判断题1.临界力Fij只与压杆的长度及两端的支撑情况有关。
()2.对于细长压杆,临界应力σij的值不应大于比例极限σp。
()3.压杆的柔度与压杆的长度,横截面的形状和尺寸以及两端的支撑情况有关。
()4.压杆的杆端约束作用愈强,那么长度系数越小,临界压力越大。
()5.压杆的临界应力应该由欧拉公式计算。
()6.欧拉公式的适用条件是。
()7.细长压杆,若长度系数μ增大一倍,则临界力Fij增加一倍。
()图 18.两端铰支细长压杆,若在其中加一铰支座如图1所示,则欧拉临界力是原来的4倍。
()9.如果细长压杆有局部削弱,削弱部分对压杆的稳定性没有影响。
()10.在材料,长度,横截面形状和尺寸保持不变的情况下,杆端约束越强,则压杆的临界力越小。
11.压杆的临界荷载是压杆保持不稳定平衡所承受的最大轴向压力。
()二、选择题1.在压杆的材料、长度、横截面形状和尺寸保持不变的情况下,杆端约束越强,则压杆的临界力()。
A. 越大B.保持不变C.越小D.以上三种可能都有2.已知细长压杆两端球形铰支,若截面面积相等时,采用下列那种截面最稳定?()A B CD三、分析题1.在压杆稳定计算中,是一个与_______,________和______有关的参数,称为压杆的。
2.欧拉公式的适用范围是什么?3.图2两根杆件的截面形状、尺寸及材料均相同,试比较哪一根杆件稳定性好?为什么?图 24.两根细长压杆,材料相同,一根截面形状为正方形,一根截面为圆形。
假设两根杆截面面积相同,支承相同,试问:①横截面惯性矩各为多少?②哪根杆容易受压失稳?为什么?5.一压杆两端约束一定,在截面面积不变情况下,为了更有效地提高其临界力应采用()措施。
6.若两根细长压杆的回转半径()相等。
当相等时,它们的柔度()相等,若两杆的柔度相等,当_______相等时,它们的临界应力相等。
7.写出压杆稳定条件的计算公式。
8.图3所示两根直径均为d的圆截面压杆,材料相同,已知,d=20mm,试判断哪根压杆容易失稳图 3四、计算题1.二圆形截面受压杆的材料相同,尺寸如图4所示,已知二杆均为大柔度杆,试比较二杆的临界力和临界应力2.圆形截面受压杆,长L=1.5m,直径d=3cm,钢材的弹性模量,比例极限σp=200Mpa,试求压杆的临界力。
第九章压杆的稳定习题

第九章压杆的稳定习题第九章 压杆的稳定习题一、填空题1、对于大柔度杆,用 计算临界压力;对于中柔度杆,用 计算临界压力2、对于大柔度杆,用来计算临界压力的欧拉公式为 ;对于中柔度杆,用来计算临界压力的经验公式为 。
3、求临界应力的公式22cr Eλπσ=。
式中的λ称为压杆的 ,根据λ数值由大 到小, 把压杆具体分为 , 和 。
二、计算题1、如图有一截面为圆形的大柔度压杆,杆长2.5m ,截面直径为40mm 。
杆的一端固定,一端铰支,材料的弹性模量E =210G pa 。
试求杆的临界压力P cr 。
2、如图所示,某液压作动筒的活塞杆,长度l =1800mm ,直径d =60mm ,承受轴向载荷F =120kN,可认为两端铰支。
活塞杆材料的弹性模量E =210Gpa ,λp =100。
若规定稳定安全系数[n st ]=3,试对活塞杆的稳定性进行校核。
图图3、图示托架中杆AB的直径d=40mm,长度l=800mm,两端可视为铰支,材料是Q235钢。
材料的弹性模量E=210Gpa。
(1)试按杆AB的稳定条件求托架的临界压力F cr。
(2)若已知实际载荷F=70kN,稳定安全系数[n st]=2,问此托架是否安全。
(注:Q235钢,a=310Mpa b=1.14Mpa λp=100 λs=60)图4、如图一截面为12×20cm2的矩形木柱为大柔度杆,杆长L=4m,在最小刚度平面内弯曲时,长度系数μ=1,木材的弹性模量E=10Gpa,试求木柱的临界压力。
图5、如图一横截面为圆的大柔度杆,横截面直径d=16cm,杆长L=5m,材料的弹性模量E=210Gpa。
杆的两端铰支,长度系数μ=1。
试求杆的临界压力P cr。
图6、某型柴油机的挺杆为大柔度压杆,该挺杆长为l =257mm,圆形横截面的直径d =8mm 。
所用钢材的E =210 GPa 。
试求该挺杆的临界力。
(提示:挺杆的两端可简化为铰支座)7、某轧钢车间使用的螺旋推钢机的示意图如图所示。
压杆稳定习题及答案

压杆稳定习题及答案【篇一:材料力学习题册答案-第9章压杆稳定】xt>一、选择题1、一理想均匀直杆受轴向压力p=pq时处于直线平衡状态。
在其受到一微小横向干扰力后发生微小弯曲变形,若此时解除干扰力,则压杆( a )。
a、弯曲变形消失,恢复直线形状;b、弯曲变形减少,不能恢复直线形状; c、微弯状态不变; d、弯曲变形继续增大。
2、一细长压杆当轴向力p=pq时发生失稳而处于微弯平衡状态,此时若解除压力p,则压杆的微弯变形( c )a、完全消失b、有所缓和c、保持不变d、继续增大 3、压杆属于细长杆,中长杆还是短粗杆,是根据压杆的( d)来判断的。
a、长度b、横截面尺寸c、临界应力d、柔度 4、压杆的柔度集中地反映了压杆的( a)对临界应力的影响。
a、长度,约束条件,截面尺寸和形状;b、材料,长度和约束条件;c、材料,约束条件,截面尺寸和形状;d、材料,长度,截面尺寸和形状; 5、图示四根压杆的材料与横截面均相同,试判断哪一根最容易失稳。
答案:( a )6、两端铰支的圆截面压杆,长1m,直径50mm。
其柔度为 ( c )a.60;b.66.7;c.80;d.50 7、在横截面积等其它条件均相同的条件下,压杆采用图( d )所示截面形状,其稳定性最好。
≤?≥?- 1 -10、在材料相同的条件下,随着柔度的增大( c)a、细长杆的临界应力是减小的,中长杆不是;b、中长杆的临界应力是减小的,细长杆不是; c、细长杆和中长杆的临界应力均是减小的; d、细长杆和中长杆的临界应力均不是减小的; 11、两根材料和柔度都相同的压杆( a )a. 临界应力一定相等,临界压力不一定相等;b. 临界应力不一定相等,临界压力一定相等;c. 临界应力和临界压力一定相等;d. 临界应力和临界压力不一定相等;a、杆的材质b、杆的长度c、杆承受压力的大小d、杆的横截面形状和尺寸二、计算题1、有一长l=300 mm,截面宽b=6 mm、高h=10 mm的压杆。
《材料力学》第9章压杆稳定习题解[整理]
![《材料力学》第9章压杆稳定习题解[整理]](https://img.taocdn.com/s3/m/058fcb1b854769eae009581b6bd97f192279bf25.png)
第九章 压杆稳定 习题解[习题9-1] 在§9-2中已对两端球形铰支的等截面细长压杆,按图a 所示坐标系及挠度曲线形状,导出了临界应力公式。
试分析当分别取图b,c,d 所示坐标系及挠曲22l EIP cr π=线形状时,压杆在作用下的挠曲线微分方程是否与图a 情况下的相同,由此所得公cr F cr F 式又是否相同。
解: 挠曲线微分方程与坐标系的y 轴正向规定有关,与挠曲线的位置无关。
因为(b )图与(a )图具有相同的坐标系,所以它们的挠曲线微分方程相同,都是。
(c )、(d)的坐标系相同,它们具有相同的挠曲线微分方程:)("x M EIw -=,显然,这微分方程与(a )的微分方程不同。
)("x M EIw =临界力只与压杆的抗弯刚度、长度与两端的支承情况有关,与坐标系的选取、挠曲线的位置等因素无关。
因此,以上四种情形的临界力具有相同的公式,即:。
22l EIP cr π=[习题9-2] 图示各杆材料和截面均相同,试问杆能承受的压力哪根最大,哪根最小(图f 所示杆在中间支承处不能转动)?解:压杆能承受的临界压力为:。
由这公式可知,对于材料和截面相同的压22).(l EI P cr μπ=杆,它们能承受的压力与 原压相的相当长度的平方成反比,其中,为与约束情况有l μμ关的长度系数。
(a )ml 551=⨯=μ(b )ml 9.477.0=⨯=μ(c )ml 5.495.0=⨯=μ(d )ml 422=⨯=μ(e )ml 881=⨯=μ(f )(下段);(上段)m l 5.357.0=⨯=μm l 5.255.0=⨯=μ故图e 所示杆最小,图f 所示杆最大。
cr F cr F[习题9-3] 图a,b 所示的两细长杆均与基础刚性连接,但第一根杆(图a )的基础放在弹性地基上,第二根杆(图b )的基础放在刚性地基上。
试问两杆的临界力是否均为2min2).2(l EI P cr π=为什么并由此判断压杆长因数是否可能大于2。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第九章 压杆的稳定习题
一、填空题
1、对于大柔度杆,用 计算临界压力;对于中柔度杆,用 计算临界压力
2、对于大柔度杆,用来计算临界压力的欧拉公式为 ;对于中柔度杆,用来计算临界压力的经验公式为 。
3、求临界应力的公式22cr E λ
πσ=。
式中的λ称为压杆的 ,根据λ数值由大 到小, 把压杆具体分为 , 和 。
二、计算题
1、如图有一截面为圆形的大柔度压杆,杆长2.5m ,截面直径为40mm 。
杆的一端固定,一端铰支,材料的弹性模量E =210G pa 。
试求杆的临界压力P cr 。
2、如图所示,某液压作动筒的活塞杆,长度l =1800mm ,直径d =60mm ,承受轴向载荷F =120kN,可认为两端铰支。
活塞杆材料的弹性模量E =210Gpa ,λp =100。
若规定稳定安全系数[n st ]=3,试对活塞杆的稳定性进行校核。
图 9.2.1
图9.2.2
3、图示托架中杆AB的直径d=40mm,长度l=800mm,两端可视为铰支,材料是Q235钢。
材料的弹性模量E=210Gpa。
(1)试按杆AB的稳定条件求托架的临界压力F cr。
(2)若已知实际载荷F=70kN,稳定安全系数[n st]=2,
问此托架是否安全。
(注:Q235钢,a=310Mpa b=1.14Mpa λp=100 λs=60)
4、如图一截面为12×20cm2的矩形木柱为大柔度杆,杆长L=4m,在最小刚度平面弯曲时,长度系数μ=1,木材的弹性模量E=10Gpa,试求木柱的临界压力。
5、如图一横截面为圆的大柔度杆,横截面直径d=16cm,杆长L=5m,材料的弹性模量E=210Gpa。
杆的两端铰支,长度系数μ=1。
试求杆的临界压力P cr。
图9.2.3
图9.2.4
图9.2.5
6、某型柴油机的挺杆为大柔度压杆,该挺杆长为l =257mm,圆形横截面的直径d =8mm 。
所用钢材的E =210 GPa 。
试求该挺杆的临界力。
(提示:挺杆的两端可简化为铰支座)
7、某轧钢车间使用的螺旋推钢机的示意图如图所示。
推杆由丝杆通过螺母来带动。
已知推杆横截面的直径d =13cm ,材料为Q 235钢,E =210Gpa ,λp =93。
当推杆全部退出时,前段可能有微小的侧移,故简化为一端固定、一端自由的压杆。
这时推杆的伸出长度为最大值,l max =3m 。
取稳定安全因数[n st ] =4。
试校核压杆的稳定性。
8、无缝钢管厂的穿孔顶杆如图所示。
杆端承受压力。
杆长l =4.5m ,横截面直径d =15cm 。
材料为低合金钢,E =210Gpa ,λp =102。
两端可简化为铰支座,规定的安全因数为[n st ] =3.3。
试求顶杆的许可载荷。
第九章 压杆的稳定习题答案
一 、填空题
1、欧拉公式 经验公式
2、2cr cr 2EI P P (a b )A ()
p l mi ==- 3、柔度(或长细比) 大柔度杆 中柔度杆 小柔度杆
二、计算题
1、 解:μ=0.7
44
4
54d 0.1d I 0.0540 1.2810mm 642
p ===?? 2cr 2EI P l ()p m == 3.1421010 1.281086.5kN 0.7 2.51023532()
创创=创 2、μ
=1
4
54
0.10.0560 6.4810mm 64215mm 4
1180012010015
44
P d d I d i l i p m l l ===??===´===>= 22cr πEI F l ()m ==23523.1421010 6.4810420kN 11800()
创创=´ []420 3.53120
cr st st F n n F ===>= 故活塞杆的稳定性足够。
3、μ
=1
B B
C C
D P P sin l F l 0
d i 10mm 4
l 180080100i 10
a m l l ??===´===<=
cr 2cr cr cr cr a b 310 1.1480
218.8MPa 40P A
218.8274.8kN 4F P 121.2kN 6
s l p s =-=-?´=??== []274.8 1.732158.74
B cr st st 158.74P n <n 如果F=70kN,得P kN
P ===== 故此托架不安全。
4、P cr =22EI l πμ=()232292411210121020101014.3)
()(⨯⨯⨯⨯⨯⨯⨯⨯--(N ) =17747.3(N )
5、P cr = 22EI l πμ=()()()
429220.13.14210101610215-⨯⨯⨯⨯⨯⨯(N ) =2714(kN )
6、解:(1)挺杆的横截面为圆形,两端简化为铰支座,μ=1;
挺杆是大柔度杆,可使用欧拉公式计算临界力。
(2)计算临界压力
()() 6.31kN )(257.0164008.010*********cr =⨯⨯⨯⨯⨯==N l EI F ππμπ 7、解:一端固定、另一端自由的压杆的长度系数μ=2。
推杆的柔度 931854
13.0324=>=⨯===p d l
i l
λμμλ, 属于大柔度杆,故用欧拉公式计算临界载荷,即
()()()2942cr 22210100.1364(N)807kN 23EI P l πππμ⨯⨯⨯⨯===⨯
推杆的工作安全系数 n st =807/150=5.38>[n st ]=4
因推杆的工作安全因数大于规定的稳定安全因数,所以可以安全工作。
8、解:
解:由于顶杆两端可简化为铰支座,所以μ=1 。
顶杆的柔度
1021204
15.05.414=>=⨯===p d l
i l
λμμλ,
属于大柔度杆,故用欧拉公式计算临界载荷,即 ()()()2942cr 22210100.1564(N)2540kN 1 4.5EI F l πππμ⨯⨯⨯⨯===⨯ 顶杆的许可载荷[]()770kN kN 3.32540cr ===st n F F。
