运筹学应用实例
简单的运筹学实际应用案例
简单的运筹学实际应用案例运筹学（Operations Research）是一门研究如何有效利用有限资源进行决策的学科，它通过数学、统计学和经济学等方法，帮助管理者做出最佳决策。
下面将介绍几个简单的运筹学实际应用案例。
1.生产线优化假设一公司拥有多条生产线，每条生产线对应不同的产品。
公司希望通过优化生产线的调度，以达到最大的产出和利润。
运筹学可以通过数学模型和算法，对生产线进行优化调度。
例如，可以使用线性规划模型来确定每条生产线的产量和调度，以最大化总利润；也可以使用整数规划模型来考虑生产线的限制和约束条件。
2.物流网络设计一家物流公司需要设计其物流网络，以最小化成本并满足客户对快速物流的需求。
运筹学可以通过数学模型和算法，帮助物流公司优化物流网络的设计。
例如，可以使用网络流模型来确定货物在物流网络中的最佳路线和节点，以最小化总运输成本；也可以使用线性规划模型来决定在不同节点上的仓库和货物库存量，以满足客户的需求。
3.航班调度问题一家航空公司需要制定最佳航班调度计划，以最大化航班利润并排除延误风险。
运筹学可以通过数学模型和算法，帮助航空公司优化航班调度。
例如，可以使用线性规划模型来决定不同航班的起降时间和机型，以最大化航班利润；也可以使用排队论模型来评估航班的延误风险，并制定相应的调度策略。
4.人员调度问题一家超市需要制定最佳的员工调度计划，以最大化服务质量和节约人力成本。
运筹学可以通过数学模型和算法，帮助超市优化员工调度。
例如，可以使用整数规划模型来决定不同时间段需要多少员工，并考虑员工的技能匹配和工作时间的合理安排；也可以使用模拟仿真方法来评估不同调度策略的效果，并做出相应的决策。
以上是几个简单的运筹学实际应用案例，运筹学在实际生产和管理中有着广泛的应用。
通过数学模型和算法的应用，可以帮助企业优化资源配置、提高效率和决策质量，从而实现最佳的经济效益。
运筹学实例 含解析
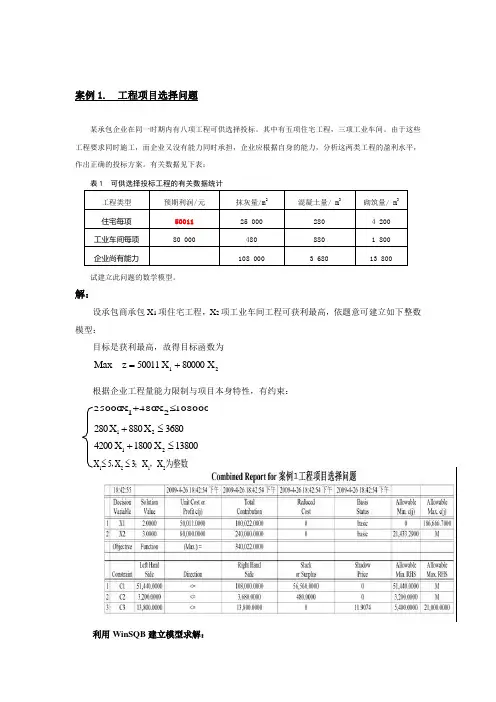
案例1. 工程项目选择问题某承包企业在同一时期内有八项工程可供选择投标。
其中有五项住宅工程，三项工业车间。
由于这些工程要求同时施工，而企业又没有能力同时承担，企业应根据自身的能力，分析这两类工程的盈利水平，作出正确的投标方案。
有关数据见下表：表1 可供选择投标工程的有关数据统计工程类型 预期利润/元 抹灰量/m 2混凝土量/ m 3砌筑量/ m 3住宅每项 50011 25 000 280 4 200 工业车间每项 80 000480 880 1 800 企业尚有能力108 0003 68013 800试建立此问题的数学模型。
解：设承包商承包X 1项住宅工程，X 2项工业车间工程可获利最高，依题意可建立如下整数模型：目标是获利最高，故得目标函数为21X 80000X 50011z Max +=根据企业工程量能力限制与项目本身特性，有约束：利用WinSQB 建立模型求解：1080002X 4801X 25000≤+3680X 880X 28021≤+13800X 1800X 420021≤+为整数，；，2121X X 3X 5X ≤≤综上，承包商对2项住宅工程，3项车间工程进行投标，可获利最大，目标函数Max z=340022 元。
案例2. 生产计划问题某厂生产四种产品。
每种产品要经过A，B两道工序加工。
设该厂有两种规格的设备能完成A工序，以A1 ，A2表示；有三种规格的设备能完成B工序，以B1 ，B2，B3 表示。
产品D可在A，B任何一种规格的设备上加工。
产品E可在任何规格的A设备上加工，但完成B工序时只能在B1设备上加工。
产品F可在A2及B2 ，B3上加工。
产品G可在任何一种规格的A设备上加工，但完成B工序时只能在B1 ，B2设备上加工。
已知生产单件产品的设备工时，原材料费，及产品单价，各种设备有效台时如下表，要求安排最优的生产计划，使该厂利润最大？设设产品设备有效台时1 2 3 4A1 A2 B1 B2 B357647109812111068108601110000400070004000原料费（元/件）单价（元/件）0.251.250.352.000.502.800.42.4解：设Xia(b)j为i产品在a(b)j设备上的加工数量,i=1,2,3,4;j=1,2,3，得变量列表设备产品设备有效台时Ta(b)j1 2 3 4A1 A2 B1 B2 B3X1a1X1a2X1b1X1b2X1b3X2a1X2a2X2b1X3b2X3b3X3a1X3a2X3b1X3b2X3b3X4a1X4a2X4b1X4b2X4b3601110000400070004000原料费Ci （元/件） 单价Pi （元/件） 0.25 1.25 0.352.00 0.50 2.80 0.4 2.4其中，令X 3a 1，X 3b 1，X 3b 2，X 3b 3，X 4b 3=0 可建立数学模型如下： 目标函数: ∑∑==-=4121)](*[Maxi j iaj Ci Pi X z=1.00*（X 1a 1+X 1a 2）+1.65*（X 2a 1+X 2a 2）+2.30* X 3a 2+2.00*（ X 4a 1+X 4a 2）约束条件：利用WinSQB 求解（X1~X4，X5~X8,X9~X12,X13~X17,X18~X20分别表示各行变量）：4,3,2,1X21j 31==∑∑==i X j ibjiaj2,1T X 41iaj=<=∑=j Taj i iaj 3,2,141=<=∑=j TbjT Xi ibj ibj2,1;4,3,2,10X iaj ==>=j i 且为整数32,1;4,3,2,10X ibj ，且为整数==>=j i 0X X X X X 4b33b33b23b13a1=====综上，最优生产计划如下：设备产品1 2 3 4A1 A2 B1 B2 B3774235004004008732875目标函数zMax=3495，即最大利润为3495案例3. 高校教职工聘任问题 （建摸）由校方确定的各级决策目标为：P 1 要求教师有一定的学术水平。
运筹学案例集
运筹学案例集常州宝菱重工机械有限公司孔念荣收集整理运筹学的一些典型性应用•合理利用材料问题：如何在保证生产的条件下，下料最少•配料问题：在原料供应量的限制下，如何获取最大收益•投资问题：从投资项目中选取最佳组合，使投资回报最大•产品生产计划：合理利用人力、物力、财力等，使获利最大•劳动力安排：用最少的劳动力来满足工作的需要•运输问题：如何制定最佳调运方案，使总运费最少一、生产计划问题案例1（2-4）、某工厂用A、B、C、D四种原料生产甲、乙两种产品，生产甲和乙所需各种原料的数量以及在一个计划期内各种原料的现有数量见下表所示。
又已知每单位产品甲、乙的售价分别为400元和600元，问应如何安排生产才能获得最大收益？已知生产单位产品所需的设备台时及A、B两种原材料的消耗、资源的限制，如下表：问题：工厂应分别生产多少单位Ⅰ、Ⅱ产品才能使工厂获利最多？案例3（2-25）、某公司面临一个是外包协作还是自行生产的问题。
该公司生产甲、乙、丙三种产品，都需要经过铸造、机加工和装配三个车间。
甲、乙两种产品的铸件可以外包协作，亦可以自行生产，但产品丙必须本厂铸造才能保证质量，数据如下表所示。
问题：公司为了获得最大利润，甲、乙、丙三种产品各生产多少件？甲、乙两种产品的铸造中，由本公司铸造和由外包协作各应多少件？案例4（2-28）、永久机械厂生产Ⅰ、Ⅱ、Ⅲ三种产品，均要经过A、B两道工序加工。
设有两种规格的设备A1、A2能完成A工序；有三种规格的设备B1、B2、B3能完成B 工序。
Ⅰ可在A、B的任何规格的设备上加工；Ⅱ可在任意规格的A设备上加工，但对B工序，只能在B1设备上加工；Ⅲ只能在A2与B2设备上加工，数据如下表所示。
问题：为使该厂获得最大利润，应如何制定产品加工方案？案例5、某造纸厂用原材料白坯纸生产原稿纸、笔记本和练习本三种产品。
该厂现有工人100人，每月白坯纸供应量为3万公斤。
已知工人的劳动生产率为：每人每月生产原稿纸30捆，或生产日记本30打，或练习本30箱。
运筹学应用案例
运筹学应用案例运筹学是一门应用数学，研究如何在资源有限的情况下，最优地组织和管理这些资源。
运筹学的应用范围非常广泛，涉及到各个领域。
以下是一个关于运筹学应用的实际案例。
某公司是一家制造业企业，主要生产产品A和产品B。
这家公司有两个生产车间和一个物流中心，每个车间配备了不同的生产设备。
公司的目标是最大化利润。
产品A在车间1中生产，车间1的生产设备可以在一小时内生产5个单位的产品A。
产品B在车间2中生产，车间2的生产设备可以在一小时内生产4个单位的产品B。
物流中心负责将产品A和产品B运送到市场，物流中心的运输能力为每小时20个单位。
同时，公司还面临一个资源的限制，即每天生产的产品A和产品B的总数不能超过400个单位。
另外，公司还有一个库存的限制，即每天生产的产品A和产品B的总数不能超过600个单位。
为了系统地解决这个问题，公司决定使用运筹学的方法进行决策。
首先，公司需要确定目标函数。
由于公司的目标是最大化利润，所以可以将目标函数定义为利润函数。
假设公司每个单位的产品A的利润为10美元，每个单位的产品B的利润为8美元。
那么公司的目标函数可以定义为：Z=10A+8B。
然后，公司需要确定约束条件。
根据资源的限制，可以得到以下约束条件：A≤5×小时数（车间1的生产能力）B≤4×小时数（车间2的生产能力）A+B≤400（每天生产的总数限制）A+B≤600（库存的限制）20A+20B≤600（物流中心的运输能力）接下来，公司需要确定变量的取值范围。
由于产量和库存数量为实数，所以可以将A和B的取值范围定义为非负实数。
最后，公司需要使用线性规划算法来求解最优解。
线性规划算法可以通过求解目标函数的最大值来找到最优解。
在这个案例中，可以使用单纯形法来求解最优解。
通过使用运筹学的方法，公司可以得到最优的生产和运输计划，以最大化利润。
对于公司而言，这个案例展示了如何在资源有限的情况下，通过合理的规划和管理，实现最优的生产和销售策略。
运筹学案例集
运筹学案例集常州宝菱重工机械有限公司孔念荣收集整理运筹学的一些典型性应用•合理利用材料问题：如何在保证生产的条件下，下料最少•配料问题：在原料供应量的限制下，如何获取最大收益•投资问题：从投资项目中选取最佳组合，使投资回报最大•产品生产计划：合理利用人力、物力、财力等，使获利最大•劳动力安排：用最少的劳动力来满足工作的需要•运输问题：如何制定最佳调运方案，使总运费最少一、生产计划问题案例1（2-4）、某工厂用A、B、C、D四种原料生产甲、乙两种产品，生产甲和乙所需各种原料的数量以及在一个计划期内各种原料的现有数量见下表所示。
又已知每单位产品甲、乙的售价分别为400元和600元，问应如何安排生产才能获得最大收益？已知生产单位产品所需的设备台时及A、B两种原材料的消耗、资源的限制，如下表：问题：工厂应分别生产多少单位Ⅰ、Ⅱ产品才能使工厂获利最多？案例3（2-25）、某公司面临一个是外包协作还是自行生产的问题。
该公司生产甲、乙、丙三种产品，都需要经过铸造、机加工和装配三个车间。
甲、乙两种产品的铸件可以外包协作，亦可以自行生产，但产品丙必须本厂铸造才能保证质量，数据如下表所示。
问题：公司为了获得最大利润，甲、乙、丙三种产品各生产多少件？甲、乙两种产品的铸造中，由本公司铸造和由外包协作各应多少件？案例4（2-28）、永久机械厂生产Ⅰ、Ⅱ、Ⅲ三种产品，均要经过A、B两道工序加工。
设有两种规格的设备A1、A2能完成A工序；有三种规格的设备B1、B2、B3能完成 B 工序。
Ⅰ可在A、B的任何规格的设备上加工；Ⅱ可在任意规格的A设备上加工，但对B工序，只能在B1设备上加工；Ⅲ只能在A2与B2设备上加工，数据如下表所示。
问题：为使该厂获得最大利润，应如何制定产品加工方案？案例5、某造纸厂用原材料白坯纸生产原稿纸、笔记本和练习本三种产品。
该厂现有工人100人，每月白坯纸供应量为3万公斤。
已知工人的劳动生产率为：每人每月生产原稿纸30捆，或生产日记本30打，或练习本30箱。
运筹学在工业领域的应用案例
运筹学在工业领域的应用案例运筹学是一门研究如何通过数学模型和优化方法来解决实际问题的学科。
它广泛应用于工业领域，帮助企业提高生产效率、优化资源利用以及优化决策。
本文将以一些实际案例来展示运筹学在工业领域的应用。
案例一：物流调度在现代物流中心，卡车调度是一个重要而复杂的问题。
一家物流企业面临着如何合理安排卡车的运输路线以及如何将货物分配给不同的卡车的问题。
运筹学通过建立数学模型和优化算法，可以帮助企业快速找到最佳的调度方案。
通过考虑货物的重量、体积、运输距离等因素，运筹学能够帮助企业节省时间和成本，提高物流效率。
案例二：生产计划在工业生产中，合理的生产计划对企业的运营至关重要。
运筹学可以通过建立生产计划的数学模型，考虑原材料、人力资源、设备利用率等因素，制定最优的生产计划。
这种方法可以帮助企业合理安排生产任务、减少生产成本，并确保产品按时交付。
案例三：库存管理有效的库存管理对于企业的正常运营非常重要。
过多的库存会增加企业的成本，而库存不足则会导致订单无法及时完成。
运筹学可以利用数学模型和优化算法，预测需求并制定合理的库存策略。
通过运筹学的方法，企业可以实时调整库存水平，减少库存成本，同时确保生产进度和客户需求之间的平衡。
案例四：供应链优化供应链优化是一个复杂的问题，涉及到多个环节和多个参与者之间的协调。
运筹学可以帮助企业建立供应链的数学模型，考虑供应商、生产商、分销商等各个环节的需求和约束，通过优化算法找到最佳的供应链配置方案。
通过运筹学的方法，企业可以提高供应链的响应速度和灵活性，降低整体成本，提供更好的服务。
案例五：设备维护与优化在工业领域，设备的维护和优化是保证生产连续性和降低成本的关键。
运筹学可以利用数据分析和模型建立，制定设备的维护计划和优化方案。
通过预测设备故障、制定维护策略和排班方案，运筹学可以帮助企业降低设备故障率，最大限度地提高设备利用率，进而提高生产效率和降低成本。
综上所述，运筹学在工业领域有着广泛的应用。
2.6-运筹学应用实例汇总
一、生产计划问题例：某工厂拥有A、B、C三种类型的设备，生产甲、乙、丙、丁四种产品。
每件产品在生产中需要占用的设备机时数，每件产品可以获得的利润以及三种设备每月可利用的时数如下表所示，求使总利润最大的月度生产计划。
建模思路■用线性规划制订使总利润最大的生产计划。
■设变量X1为第i种产品的生产件数(i=1, 2, 3, 4),目标函数z为相应的生产计划可以获得的总利润。
在加工时间以及利润与产品产量成线性关系的假设下，可以建立如下的线性规划模型：建模max z= 5.24X1 +7.30x2 +8.34x3 +4.18x4目标函数1.5Xj +1.0x2+2.4X3+1.0X4<2000LOX1 +5.0X2+1.0X3+3.5X4<8000 约束条件1・5X] +3.0X2+3.5X3+1.0X4<5000Xp X2, X3, X4 >0 变量非负约束练习：某公司面临一个是外包协作还是自行生产的问题。
该公司生产甲、乙、丙三种产品，都需要经过铸造、机加工和装配三个车间。
甲、乙两种产品的铸件可以外包协作，亦可以自行生产，但产品丙必须本厂铸造才能保证质量。
数据如下表。
问：公司为了获得最大利润，甲、乙、丙三种产品各生产多少件？甲、乙两种产品的铸造中，由本公司铸造和由外包协作各应多少件？甲 .乙丙资源限制铸造工时（小时/件）51078000机加工工时（小时/件）64812000装配工时（小时/件）32210000自产铸件成本（兀/件）354外协铸件成本（兀/件）56一机加工成本（元/件）213装配成本（元/件）322产品售价（元/件）231816解：设孙孙寺分别为三道工序都由本公司加工的甲、乙、丙三种产品的件数，同，幅分别为由外协铸造再由本公司加工和装配的甲、乙两种产品的件数。
求占的利润：利润二售价-各成本之和产品甲全部自制的利润产品甲铸造外协，其余自制的利润产品乙全部自制的利润产品乙铸造外协，其余自制的利润产品丙的利润可得到毛（i = 1,2, 3,4,5）的利润分别为15、10、7、13、9=23-（3+2+3）=15 =23-（5+2+3）=13 =18-（5+1+2）=10 =18-（6+1+2）=9 =16-（4+3+2）=7通过以上分析,可建立如下的数学模型：目标函数：Max 15百+ 10电+ 7两+ 13题+ 9不约束条件：5为+ 10西+ 7玛＜80006为+ 4出+ 8^ + 6々+ 4不3百+ 2X2 + 2均+ 3局+ 2不毛，演，传，演，与12000 10000二、混合配料问题例：某工厂要用四种合金T1, T2, T3和T4为原料，经熔炼成为一种新的不锈钢G。
运筹学经典案例
运筹学经典案例案例一：鲍德西（（B AWDSEY）雷达站的研究20世纪 30 年代，德国内部民族沙文主义及纳粹主义日渐抬头。
以希特勒为首的纳粹势力夺取了政权开始为以战争扩充版图，以武力称霸世界的构想作战争准备。
欧洲上空战云密布。
英国海军大臣丘吉尔反对主政者的“绥靖”政策，认为英德之战不可避免，而且已日益临近。
他在自己的权力范围内作着迎战德国的准备，其中最重要、最有成效之一者是英国本土防空准备。
1935 年，英国科学家沃森—瓦特（ R．Watson-Wart ）发明了雷达。
丘吉尔敏锐地认识到它的重要意义，并下令在英国东海岸的 Bawdsey 建立了一个秘密的雷达站。
当时，德国已拥有一支强大的空军，起飞 17 分钟即可到达英国。
在如此短的时间内，如何预警及做好拦截，甚至在本土之外或海上拦截德机，就成为一大难题。
雷达技术帮助了英国，即使在当时的演习中已经可以探测到160 公里之外的飞机，但空防中仍有许多漏洞，1939 年，由曼彻斯特大学物理学家、英国战斗机司令部科学顾问、战后获诺贝尔奖金的P.M.S.Blachett 为首，组织了一个小组，代号为“ Blachett 马戏团”，专门就改进空防系统进行研究。
这个小组包括三名心理学家、两名数学家、两名应用数学家、一名天文物理学家、一名普通物理学家、一名海军军官、一名陆军军官及一名测量人员。
研究的问题是：设计将雷达信息传送给指挥系统及武器系统的最佳方式；雷达与防空武器的最佳配置；对探测、信息传递、作战指挥、战斗机与防空火力的协调，作了系统的研究，并获得了成功，从而大大提高了英国本土防空能力，在以后不久对抗德国对英伦三岛的狂轰滥炸中，发挥了极大的作用。
二战史专家评论说，如果没有这项技术及研究，英国就不可能赢得这场战争，甚至在一开始就被击败。
“ Blackett 马戏团”是世界上第一个运筹学小组。
在他们就此项研究所写的秘密报告中，使用了“Operatio nal Research” 一词，意指作战研究”或"运用研究"。
运筹学经典案例
运筹学经典案例运筹学是一门研究在有限资源下进行有效决策的学科，它涉及到数学、经济学、管理学等多个领域。
在现实生活中，我们经常会遇到需要做出决策的情况，而运筹学正是帮助我们在复杂的情况下做出最优决策的学科。
下面，我们将介绍一些运筹学的经典案例，希望能够帮助大家更好地理解运筹学的应用。
1. 供应链优化。
供应链优化是运筹学中非常重要的一个领域，它涉及到如何在有限的资源下，实现最佳的供应链效率。
一个经典的案例是，某公司需要将产品从生产地运送到各个销售点，而在运输过程中需要考虑到运输成本、时间、货物损耗等多个因素。
通过运筹学的方法，可以帮助公司找到最佳的运输方案，从而降低成本、提高效率。
2. 生产排程优化。
在工厂生产过程中，如何合理地安排生产顺序和时间，是一个典型的运筹学问题。
通过对生产设备的利用率、生产时间、生产成本等因素进行综合考虑，可以利用运筹学的方法找到最优的生产排程，从而提高生产效率，降低生产成本。
3. 库存管理。
对于零售商来说，如何合理地管理库存是一个关键问题。
库存过多会增加成本，而库存过少又会导致无法满足客户需求。
通过运筹学的方法，可以帮助零售商找到最佳的库存管理策略，使得库存成本和客户满意度达到最优平衡。
4. 交通规划。
在城市交通规划中，如何合理地安排交通流量、制定最佳的交通信号灯配时方案等，都是典型的运筹学问题。
通过对交通流量、道路容量、交通需求等因素进行分析和优化，可以帮助城市交通管理部门制定出更加合理的交通规划方案，提高交通效率，减少拥堵。
5. 项目管理。
在企业项目管理中，如何合理地安排资源、时间和任务分配，是一个重要的问题。
通过运筹学的方法，可以帮助项目经理制定出最佳的项目计划，提高项目执行效率，降低项目成本，确保项目顺利完成。
总结。
运筹学在现实生活中有着广泛的应用，它帮助我们在复杂的决策情况下找到最佳解决方案，提高效率，降低成本。
通过对供应链优化、生产排程、库存管理、交通规划、项目管理等经典案例的分析，我们可以更好地理解运筹学的应用，希望大家能够在实际工作中运用运筹学的方法，解决复杂的决策问题，取得更好的效果。
运筹学案例
运筹学案例（第一部分）案例1 高压电器强电流试验计划的安排某高压电器研究所属行业归口所，是国家高压电器试验检测中心，每年都有大量的产品试验、中试、出口商检等任务.试验计划安排及实施的过程一般如下：·提前一个月接受委托试验申请·按申请的高压电器类别及台数编制下月计划·按计划调度,试验产品进入试验现场·试验检测，出检测报告·试验完成,撤出现场高压电器试验分强电流试验和高压电试验两部分，该研究所承担的强电流实验任务繁重,委托试验的电器量很大，因此科学地计划安排试验计划显得非常重要。
高压电器分十大类，委托试验的产品有一定随机性,但是试验量最多的产品(占85%以上)是以下八类：1．35KV断路器2．10KV等级断路器3．35KV开关柜4．10KV等级开关柜5．高压熔断器6．负荷开关7．隔离开关8．互感器这八类产品涉及全国近千个厂家，市场广阔，数量庞大。
当前的强电流产品试验收费标准见表1—1。
表1-1 强电流产品试验收费标准由于强电流试验用的短路发电机启动时，会给城市电网造成冲击,严重影响市网质量，故只能在中午1点用电低谷时启动，从而影响全月连续试验工时只有约108小时,任务紧张时只能靠加班调节。
正常情况下各种试验所需试验工时见表8—2。
表1—2 各类产品试验所需工时强电流试验特点是开机时耗电量大,而每次实验短路时,只持续几秒钟,虽然短路容量在“0”秒时达2500 MVA,但瞬时耗电量却很小.每天试验设备提供耗电量限制为5000千瓦,每月135千千瓦，那麽每种产品耗量如表8-3所示。
各类产品的冷却水由两个日处理能力为14吨的冷却塔供给.每月按27天计，冷却水月供给量为14×27=378吨.每月各类产品冷却水处理量见表8-3。
表1—3 各类产品试验耗电量与冷却水处理量根据以往的经验和统计报表显示第一类产品和第二类产品每月最多试验台数分别为6台和4台，第三类和第四类产品则每月至少需分别安排8台和10台。
运筹学在生活中的例子
运筹学在生活中的例子
运筹学是一门研究如何做出最佳决策的学科，它在各个领域都有着广泛的应用。
从日常生活中的时间管理到复杂的商业运营决策，都可以看到运筹学的身影。
下面我们就来看看运筹学在生活中的一些例子。
首先，让我们来看看日常生活中的时间管理。
每天我们都需要面对各种各样的
任务和活动，如工作、家务、社交等。
如何合理安排时间，让每一件事情都能得到充分的安排，就需要运用运筹学的方法。
比如，我们可以利用时间表来规划每天的活动，将重要的任务优先安排，避免时间的浪费和碎片化，从而提高工作效率。
另一个例子是在商业领域中的供应链管理。
在现代商业运营中，供应链管理是
非常重要的一环。
通过运筹学的方法，可以帮助企业优化供应链的运作，降低成本、提高效率。
比如，利用运筹学的方法可以帮助企业确定最佳的库存水平，避免过多或过少的库存，从而降低库存成本和避免缺货现象的发生。
此外，运筹学还可以应用在交通规划中。
比如，城市交通拥堵是一个普遍存在
的问题，如何合理规划交通路线，减少拥堵，提高交通效率，就需要运用运筹学的方法。
通过分析交通流量、优化信号灯控制、调整道路规划等方式，可以帮助城市降低交通拥堵，提高交通效率。
总的来说，运筹学在生活中有着广泛的应用，它可以帮助我们合理安排时间、
优化商业运营、改善交通状况等。
通过运用运筹学的方法，我们可以做出更加理性和科学的决策，从而提高效率，降低成本，改善生活质量。
因此，我们应该更加重视运筹学的学习和应用，让它成为我们生活中的得力助手。
运筹学应用范例与解法
运筹学应用范例与解法以运筹学应用范例与解法为题，我们将探讨一些实际问题，并介绍如何运用运筹学的方法来解决这些问题。
一、生产调度问题假设某工厂有多条生产线，每条生产线可以生产不同种类的产品。
每个产品的生产时间、成本和销售价格都不同。
我们需要确定每条生产线的生产计划，以最大化总利润。
解决方案：可以使用线性规划模型来解决这个问题。
首先，我们需要列出每条生产线的生产时间、成本和销售价格表。
然后，我们将每条生产线的生产计划表示为决策变量，并设置约束条件，如生产时间不能超过工作时间，每个产品的生产数量不能为负数等。
最后，我们通过求解线性规划模型，得到最佳的生产计划。
二、配送路线问题假设某物流公司需要将货物从若干个仓库送往多个客户，每个仓库和客户之间的距离和货物数量都不同。
我们需要确定最佳的配送路线，以最小化总运输成本。
解决方案：可以使用旅行商问题（TSP）模型来解决这个问题。
首先，我们需要计算每个仓库和客户之间的距离，并列出距离矩阵。
然后，我们将每个客户的配送路线表示为决策变量，并设置约束条件，如每个客户只能被访问一次，每个仓库的货物数量不能超过容量等。
最后，我们通过求解TSP模型，得到最佳的配送路线。
三、项目调度问题假设某公司有多个项目需要进行调度，每个项目都有不同的工期、资源需求和利润。
我们需要确定最佳的项目调度方案，以最大化总利润。
解决方案：可以使用动态规划模型来解决这个问题。
首先，我们需要列出每个项目的工期、资源需求和利润表。
然后，我们将每个项目的调度方案表示为决策变量，并设置约束条件，如资源不能超过容量，每个项目的工期不能延迟等。
最后，我们通过求解动态规划模型，得到最佳的项目调度方案。
四、库存管理问题假设某零售商需要决定每个产品的订货量，以满足客户需求并最小化库存成本。
每个产品的需求量、订货时间和库存成本都不同。
解决方案：可以使用库存模型来解决这个问题。
首先，我们需要列出每个产品的需求量、订货时间和库存成本表。
运筹学经典案例
运筹学经典案例
运筹学是一门研究如何有效地组织、管理和优化资源的学科，它在现代管理中
起着至关重要的作用。
在实际应用中，我们可以通过一些经典案例来了解运筹学的具体运用，下面就介绍几个经典案例。
第一个案例是关于生产调度的。
在一个工厂中，有多条生产线，每条生产线上
有不同的产品需要生产。
如何合理安排生产顺序，以最大程度地提高生产效率，是一个典型的运筹学问题。
通过运筹学的方法，可以建立数学模型，考虑到各种约束条件，最终得出一个最优的生产调度方案，从而实现生产效率的最大化。
第二个案例是关于物流配送的。
在物流配送中，如何合理规划配送路线，以最
大程度地降低成本，提高配送效率，也是一个典型的运筹学问题。
通过对各种因素的分析和考虑，可以利用运筹学方法建立配送优化模型，从而得出最优的配送路线和方案。
第三个案例是关于库存管理的。
在企业的库存管理中，如何合理控制库存水平，以最大程度地降低库存成本，同时又能够保证供应链的稳定性，也是一个典型的运筹学问题。
通过对需求的预测和供应链的优化，可以利用运筹学方法建立库存管理模型，从而实现库存水平的最优控制。
通过以上几个经典案例的介绍，我们可以看到，运筹学在实际应用中发挥着重
要作用。
通过建立数学模型，考虑各种约束条件，运用运筹学方法进行优化，可以帮助企业提高生产效率，降低成本，提高配送效率，优化供应链，从而实现经济效益的最大化。
总的来说，运筹学经典案例的研究和实践对于企业的管理和运营具有重要的指
导意义。
希望通过对运筹学经典案例的深入学习和研究，可以更好地应用运筹学理论，解决实际管理中的问题，实现企业的可持续发展。
生活中的运筹学案例
生活中的运筹学案例生活中的运筹学案例无处不在，它们展现了运筹学在实际生活中的应用和重要性。
运筹学是一门研究如何有效地组织和管理资源，以最大化效益的学科。
通过分析、建模和优化，运筹学可以帮助人们在生活中做出更加明智的决策，提高效率，节约资源，降低成本，提高生活质量。
下面我们将通过几个生活中的案例来看看运筹学是如何应用的。
首先，我们可以看看购物中的运筹学。
在购物过程中，我们需要考虑如何在有限的预算下购买最多的商品。
这就涉及到了“多重背包问题”，即在有限的背包容量下，如何选择商品来使得总价值最大化。
运筹学可以帮助我们建立数学模型，通过优化算法来解决这个问题，从而使我们在购物时可以更加理性地选择商品，最大化利益。
其次，生活中的旅行也是一个充满运筹学的场景。
在旅行中，我们需要考虑如何安排行程、选择交通工具和酒店，以及如何合理安排时间和预算。
这就涉及到了“旅行商问题”和“背包问题”。
运筹学可以帮助我们制定最佳的旅行计划，通过优化算法来确定最短的旅行路线和最合适的行程安排，使得旅行更加高效和愉快。
另外，生活中的排队问题也是一个典型的运筹学案例。
在超市、银行、医院等场所，我们经常需要排队等候。
如何合理安排队伍，减少等待时间，提高服务效率，是一个重要的问题。
运筹学可以帮助我们通过排队理论和优化算法来设计更加合理的排队系统，从而提高服务质量和顾客满意度。
最后，生活中的日常安排也离不开运筹学的帮助。
比如，如何合理安排工作和学习时间，如何有效规划饮食和锻炼计划，如何管理个人财务和投资等等，都可以通过运筹学的方法来进行优化和改进，使得生活更加有序和高效。
总之，生活中的运筹学案例无处不在，它们展现了运筹学在实际生活中的应用和重要性。
通过分析、建模和优化，运筹学可以帮助人们在生活中做出更加明智的决策，提高效率，节约资源，降低成本，提高生活质量。
希望大家能够在日常生活中更加关注和运用运筹学的方法，使得生活更加美好。
优秀的运筹学案例
优秀的运筹案例1. 孙武与《孙子兵法》孙武，字长卿，后人尊称其为孙武子、孙子，中国历史上著名军事家.公元前535年左右出生于齐国乐安（今山东惠民）. 后来到了吴国，因为献上兵法十三篇，被吴王阖闾重用，拜为大将，和伍子胥共事，辅佐吴王，领兵攻破楚国都城郢（今湖北江陵县纪南城）.孙武在春秋末期（公元前476年前后）所著《孙子兵法》，是世界上现存最古老的兵书.其中的《始计第一》论述怎样在开战之前和战争中实行谋划的问题，以及谋划在战争中的重要意义；《作战第二》论述速战速胜的重要性；《谋攻第三》论述用计谋征服敌人的问题；《军形第四》论述用兵作战要先为自己创造不被敌人战胜的条件，以等待敌人可以被我战胜的时机，使自己“立于不败之地”；《兵势第五》论述用兵作战要造成一种可以压倒敌人的迅猛之势，并要善于利用这种迅猛之势；《虚实第六》论述用兵作战须采用“避实而击虚”的方针；《军争第七》论述如何争夺制胜的有利条件，使自己掌握作战主动权的问题；《九变第八》论述将帅指挥作战应根据各种具体情况灵活机动地处置问题，不要机械死板而招致失败，并对将帅提出了要求；《行军第九》论述行军作战中怎样安置军队和判断敌情问题；《地形第十》论述用兵作战怎样利用地形的问题，并着重论述深入敌国作战的好处；《九地第十一》进一步论述用兵作战怎样利用地形及统兵之道的问题；《火攻第十二》论述在战争中使用火攻的办法、条件和原则等问题；《用间第十三》论述使用间谍侦察敌情在作战中的重要意义，以及间谍的种类和使用间谍的方法.《孙子兵法》是体现我国古代军事运筹思想的最早的典籍.它考察了战争中各种依存、制约关系，总结了战争的规律，并依此来研究如何筹划兵力以争取全局的胜利. 书中的语言叙述简洁，内容也很有哲理性，后来的很多将领用兵都受到了该书的影响.《孙子兵法》对中国的文化发展有深远的影响.2. 孙膑与齐王赛马孙膑（约公元前380－公元前432），孙武的后世子孙，战国中期的著名军事家. 少时孤苦，年长后从师鬼谷子（著名隐士，精通兵学和纵横学）学习《孙子兵法》十三篇等兵书战策. 庞涓妒孙膑之才而将其骗至魏,施以膑刑(割去膝盖骨).后来乘齐国使团来魏之机，孙膑被齐使秘密接到齐国,并被大将田忌所赏识，留在府中做幕僚，奉为上宾. 孙膑的“斗马术”是我国古代运筹思想中争取总体最优的脍炙人口的著名范例（记载于《史记·孙子吴起列传》），成为军事上一条重要的用兵规律，即要善于用局部的牺牲去换取全局的胜利，从而达到以弱胜强的目的. “斗马术”的基本思想是不强求一局的得失，而争取全盘的胜利. 这是一个典型的博弈问题.3. 围魏救赵公元前354年，魏将庞涓发兵8万，以突袭的办法将赵国的都城邯郸包围. 赵国抵挡不住，求救于齐. 齐王拜田忌为大将，孙膑为军师，发兵8万，前往救赵. 大军既出，田忌欲直奔邯郸，速解赵国之围. 孙膑提出应趁魏国国内兵力空虚之机，发兵直取魏都大梁（今河南开封），迫使魏军弃赵回救. 这一战略思想，将避免齐军长途奔袭的疲劳，而致魏军于奔波被动之中，立即为田忌采纳，率领齐军杀往魏国都城大梁. 庞涓得知大梁告急的消息，忙率大军驰援大梁. 齐军事先在魏军必经之路的桂陵（今河南长垣南），占据有利地形，以逸待劳，打败了魏军. 这就是历史上有名的“围魏救赵”之战.“围魏救赵”之妙，妙在善于调动敌人. 调动敌人的要诀，则在“攻其所必救”.4. 减灶之法公元前342年，魏将庞涓带领10万大军进攻韩国. 韩国向齐国求救. 齐王召集群臣商讨对策，齐国的成侯邹忌主张不救，田忌主张早救. 孙膑建议先答应韩国的请求，致使韩国必倾力抗敌. 等到韩、魏双方战到疲惫不堪时，再出兵救韩，可用力少而见功多，取胜易而受益大. 韩国仗恃有齐国相援，倾全力抗魏，五战皆败，只得于公元前341年再次向齐求助. 齐王才决定派兵救韩，仍以田忌为主将，孙膑为军师. 战役之初，按照孙膑的计策，齐军长驱直入把攻击的矛头指向魏国的都城大梁. 庞涓听到消息，立即回援，但齐军已经进入魏国境内. 孙膑对田忌说，魏国军队素来慓悍勇武而看不起齐国，善于作战的人只能因势利导. 兵法上说，行军百里与敌争利会损失上将军，行军五十里而与敌争利只有一半人能赶到. 为了让魏军以为齐军大量掉队，应使齐军进入魏国境内后先设10万个灶，过一天设5万个灶，再过一天设3万个灶. 庞涓行军三天，见到齐军所留灶迹，判断齐军士兵已经逃跑一大半，所以丢下步兵，只率轻车锐骑用加倍的速度追赶齐军. 孙膑计算魏军行程，日暮时必然赶到马陵（今河南范县西南）.马陵道路狭窄，两旁地形险阻.孙膑预先布置好伏兵，并集中优秀弩手夹道设伏. 庞涓日暮追至马陵，进入齐军伏击阵地. 齐军万弩齐发，魏军大乱，庞涓兵败自刎. 齐军乘胜全歼10万魏军.马陵之战，孙膑的因势利导、调动敌人、变劣势为优势、力争发挥突然性的作战指导主动，是颇有参考价值的. 其退军设伏的战法，也给了后人不少的启示.“围魏救赵”与“减灶之法”都充分体现了如何运用筹划兵力，选择最佳时间、地点，趋利避害，集中优势兵力以弱克强的运筹思想.5. 运筹帷幄中，决胜千里外在公元前3世纪楚汉相争中，汉高祖刘邦的著名谋士张良为推翻秦朝，打败项羽，统一全国立下了盖世奇功，刘邦赞誉他“夫运筹策帷帐之中，决胜于千里之外”. 这千古名句也可以说是对张良运筹思想的赞颂和褒奖. 《史记》在《留侯世家》及其他多处提及“夫运筹策帷帐之中，决胜于千里之外”. 这里的“运筹”，指张良在帷幄中制定作战谋略与决策的过程. 在西汉时代，“运筹”已被当作制定谋略与决策职能分工的代名词.20世纪30年代发展起来的运筹学，其基本宗旨是探讨事理，强调做一项工作之前要明确目的，制定效果，衡量指标体系作为估计不同方案所达到预定目标程度的依据，在此基础上选择最优方案和实施有效管理. 我国1955年开始研究运筹学时，从《史记》中摘取“运筹”一词作为“Operations Research”的意译，包含了运用筹划、以智取胜的深刻含义. 从《史记》对“运筹”的记述表明，我国运筹思想源远流长，至今对运筹学的发展仍有重要影响.6. 贾思勰与《齐民要术》贾思勰，北魏时期的科学家，益都(在山东寿光南)人，祖、父两代都善于经营，有着丰富的劳动经验，并都非常重视农业技术方面的学习和研究. 贾思勰从小在田园长大，对很多农作物都非常熟悉，他还跟着父亲身体力行参加各种农业劳动，学习掌握了大量农业科技. 他家里拥有大量藏书，这使他从小就有机会博览群书，从中汲取各方面的知识，也为他以后编撰《齐民要术》打下了基础. 大约在北魏永熙二年（533年）到东魏武定二年（554年）期间，他将自己积累的许多古书上的农业技术资料、询问老农获得的丰富经验以及他自己的亲身实践，加以分析、整理、总结，写成农业科学技术巨著《齐民要术》.《齐民要术》一书，不仅是我国古代农业科学一部杰出的学术著作，也是一部蕴含丰富运筹思想的宝贵文献,它记载了我国古代农民如何根据天时、地利和生产条件去合理筹划农事的经验. 其中所提出的不同作物的播种时间和各种作物茬口安排上的先后关系，可以说是现代运筹学中二阶段决策问题的雏型.7. 丁渭修皇宫[6]图1.1 丁渭修皇宫引水示意图[7]宋真宗大中祥符年间(1008—1017)，都城开封里的皇宫失火，需要重建. 右谏议大夫、权三司使丁渭受命负责限期重新营造皇宫. 建造皇宫需要很多土，丁渭考虑到从营建工地到城外取土的地方距离太远，费工费力，于是下令将城中街道挖开取土，节省了不少工时. 挖了不久，街道便成了大沟. 丁渭又命人挖开官堤，引汴河水进入大沟之中，然后调来各地的竹筏、木船经这条大沟运送建造皇宫所用的各种物材，十分便利（见图1. 1）. 等到皇宫营建完毕，丁渭命人将大沟中的水排尽，再将拆掉废旧皇宫以及营建新皇宫所丢弃的砖头瓦砾添入大沟中，大沟又变成了平地，重新成为街道. 这样，丁渭一举三得，挖土、运送物材、处理废弃瓦砾等三件工程一蹴而成，节省的工费数以亿万计.这是我国古代大规模工程施工组织方面运筹思想的典型例子.8. 沈括运粮[6]沈括(1031—1095), 北宋时期大科学家、军事家. 在率兵抗击西夏侵扰的征途中，曾经从行军中各类人员可以背负粮食的基本数据出发，分析计算了后勤人员与作战兵士在不同行军天数中的不同比例关系，同时也分析计算了用各种牲畜运粮与人力运粮之间的利弊，最后做出了从敌国就地征粮，保障前方供应的重要决策，从而减少了后勤人员的比例，增强了前方作战的兵力.当时沈括的分析计算过程译意如下：凡是行军作战，如何从敌方取得粮食，是最急迫的事情. 自己运粮不仅耗费大，而且沈括势必难以远行. 我曾经作过计算：假设一个民夫可以背六斗米，士兵自带五天的干粮.如果一个民夫供应一个士兵，单程只能进军十八天（六斗米，每人每天吃两升米，两人吃十八天*）. 若要计回程的话，只能进军九天.如果两个民夫供应一个士兵，单程可进军二十六天（两个民夫背一石二斗米，三个人每天要吃六升米. 八天以后，其中一个民夫背的米已经吃光，给他六天的口粮让他先返回，以后的十八天，两人每天吃四升米）.若要计回程的话，只能前进十三天的路程（前八天每天吃六升，后五天及回程每天吃四升米，能够进军十三天）.如果三个民夫供应一个士兵，单程可进军三十一天（三人背米一石八斗，前六天半四个人，每天吃八升米，遣返一个民夫，给他四天口粮. 中间的七天三个人同吃，每天吃六升米，再遣返一个民夫，给他九天口粮；最后的十八天两人吃，每天四升米）.如果要计回程的话，只可以前进十六天的路程（开始六天半每天吃八升米，中间七天，每天吃六升米，最后两天半以及十六天回程每天吃四升米）.三个民夫供应一个士兵，已经到极限了.如果要出动十万军队，辎重占去三分之一兵源，能够上阵打仗的士兵不足七万人.这就要用三十万民夫运粮，再要扩大规模很困难了.每人背六斗米的数量也是根据民夫的总数平均来说的. 因为其中的队长不背，伙夫减半，他们所减少的要摊在众人头上.*士兵干粮相当于十升米，连同民夫背的米共有七十升，每天吃四升米，实际上只能维持十七天半. 十八天是以整数来说的. 以下计算类同.更何况还会有患病和死亡的人，他们所背的米又要由众人分担.所以军队中不容许饮食无度，如果有一个人暴食，两三个人供应他还不够.如果用牲畜运输，骆驼可以驮三石，马或骡可以驮一石五斗，驴子可以驮一石.与人工相比，虽然能驮得多，花费也少，但如果不能及时放牧或喂食，牲口就会瘦弱而死.一头牲口死了，只能连它驮的粮食也一同丢弃.所以与人工相比，实际上是利害相当.这种军事后勤问题的分析计算是具有现代意义的运筹思想的范例.9. 高超治河[6]高超,宋朝人，河工. 宋仁宗庆历年间(1041—1048)黄河在北都（今太原）商胡地区决口，很长时间都没有堵上决口. 朝廷派三司度支副使（官职名）郭申锡亲自前往监督工程进行. 凡是堵决口将要合拢的时候，都要在决口中间压上一埽（用树枝、芦苇、石头等捆紧做成圆柱形），叫做“合龙门”，这是成败的关键. 当时好几次压埽都合不上. 那时合龙门用的埽长六十步（步，古代的长度计量单位）.有个叫做高超的水工献策说：埽身太长，人力压不住，埽到达不了水底，所以水流不断. 应当把六十步的埽身分为三节，每节长二十步，中间用绳索连起来. 先放下第一节，等它到了水底，再压第二节、第三节. 老河工和他争论，认为不可行，说：“二十步的埽不能阻断水流，白白使用三节埽，浪费好几倍成本，而决口依然堵不上”.高超对他说：“第一节河水确实没有被阻断，但是水势必然被削弱一半. 压第二节时只用一半的力气，水就算没有被阻断，也不过是很少往外漏出. 第三节就是在平地上施工，足以能够让人使出全部力气. 压完第三节以后，上两节自来就被浊泥淤积，不用再麻烦人力来加固它们了.” 郭申锡遵照从前的方法，不采纳高超的建议.当时魏公（爵位名）贾将军镇守北门（地名），只有他认为高超的话是对的，暗地派遣几千人在下游收集漂下来的埽. 而上游的埽压上以后，果然被水冲走了，黄河的决口更加大，郭申锡因此被贬官. 最后还是采用了高超的建议，才堵上了商胡地区的决口.这种分阶段作业优于一次作业的分析与论证，是运筹思想的典型范例.10、为何说一名数学家等于十个师？在第二次世界大战中，盟军为了和德国法西斯作战，大量军需物品要穿过大西洋运送到各个战场。
运筹学应用实例
A
B
C
D
E
F
陆地、河流及桥梁示意图
解：
将A，B，C，D，E，F分别用一种点表达，相互之间有桥相连 旳连一条弧；弧旳容量就是两点间旳桥梁数；设一种方向，得 到网络图如下：
A
例3.设备更新问题
某单位使用一台生产设备，在每年年底，单位领导都要决 策下年度是购置新设备还是继续使用旧设备。
若购置新设备，需要支付一笔购置费；假如继续使用旧旳， 则要支付一定旳维修费用。
一般说来，维修费随设备使用年限旳延长而增长。根据以 往旳统计资料，已经估算出设备在各年年初旳价格和不同 使用年限旳年维修费用，分别示于表1和表2。
相应旳开门方案如图所 示，共开10个门。
B C IJ
H
A
D GK
E
F
开门方案
例5：选址问题
有六个居民点v1，v2，v3，v4，v5，v6，拟定建一夜校，已知 各点参加学习旳人数为25、20、30、10、35、45人，其道路 如图所示，试拟定学校位于哪一种居民点，才干使学习者 所走旳总旅程至少？（图中边旁旳数字为路段长度）
用一条边把代表这两个项目
v2
旳顶点连接起来。这么得到
v3
下图
v1
为了处理这个问题，只需
找到一条包括全部顶点旳
v4
初等链。
v5
如：{v4，v1，v2，v3，v5}是一条初等链，相应旳比赛是： 100m自由泳，50m仰泳，50m蛙泳，100m碟泳，200m自由泳。
此问题旳方案不唯一。
例 2.线路铺设问题
0 50 150 175 200 275 40 0 80 100 120 180 180 120 0 30 60 150 D= 70 50 10 0 10 40 280 210 70 35 0 105 495 405 225 180 135 0
运筹学案例集
运筹学案例集常州宝菱重工机械有限公司孔念荣收集整理运筹学的一些典型性应用•合理利用材料问题：如何在保证生产的条件下，下料最少•配料问题:在原料供应量的限制下，如何获取最大收益•投资问题：从投资项目中选取最佳组合，使投资回报最大•产品生产计划:合理利用人力、物力、财力等，使获利最大•劳动力安排：用最少的劳动力来满足工作的需要•运输问题：如何制定最佳调运方案，使总运费最少一、生产计划问题案例1(2-4）、某工厂用A、B、C、D四种原料生产甲、乙两种产品,生产甲和乙所需各种原料的数量以及在一个计划期内各种原料的现有数量见下表所示.又已知每单位产品甲、乙的售价分别为400元和600元，问应如何安排生产才能获得最大收益？已知生产单位产品所需的设备台时及A、B两种原材料的消耗、资源的限制，如下表：问题：工厂应分别生产多少单位Ⅰ、Ⅱ产品才能使工厂获利最多？案例3（2—25）、某公司面临一个是外包协作还是自行生产的问题。
该公司生产甲、乙、丙三种产品，都需要经过铸造、机加工和装配三个车间.甲、乙两种产品的铸件可以外包协作，亦可以自行生产，但产品丙必须本厂铸造才能保证质量，数据如下表所示。
问题：公司为了获得最大利润，甲、乙、丙三种产品各生产多少件?甲、乙两种产品的铸造中，由本公司铸造和由外包协作各应多少件？案例4(2-28）、永久机械厂生产Ⅰ、Ⅱ、Ⅲ三种产品，均要经过A、B两道工序加工。
设有两种规格的设备A1、A2能完成A工序；有三种规格的设备B1、B2、B3能完成B 工序。
Ⅰ可在A、B的任何规格的设备上加工；Ⅱ可在任意规格的A设备上加工，但对B工序,只能在B1设备上加工;Ⅲ只能在A2与B2设备上加工，数据如下表所示。
问题:为使该厂获得最大利润,应如何制定产品加工方案？案例5、某造纸厂用原材料白坯纸生产原稿纸、笔记本和练习本三种产品。
该厂现有工人100人，每月白坯纸供应量为3万公斤。
已知工人的劳动生产率为：每人每月生产原稿纸30捆，或生产日记本30打,或练习本30箱。
四个运筹学案例
1、年度配矿计划优化——线性规划j（单位：万吨）2 约束条件：包括三部分1）供给（资源）约束：x1 ≤70 x2≤7 x3≤17 x4≤23 x5≤3 x6≤9.5 x7≤1 x8≤15.4 x9≤ 2.7 x10≤7.6 x11≤13.5 x12≤2.7 x13≤1.2 x14≤7.22）品位约束3）非负约束： x j ≥ 0 j = 1,2,3, … ,143 目标函数：此题目要求“效益最佳”有一定的模糊性，由于配矿后的混合矿石将作为后面 工序的原料而产生利润，故在初始阶段，可将目标函数选作配矿总量的极大化。
三、计算结果及分析1 计算结果利用单纯形法可得出该问题的最优解为：x1 = 31.121 x2 = 7 x3 = 17 x4 = 23 x5 = 3 x6 = 9.5 x7 = 1 x8 = 15.4 x9 = 2.7 x10 = 7.6 x11 = 13.5 x12 = 2.7 x13 = 1.2 x14 = 7.2 最优值：Z* = 141.921（万吨）2 分析与讨论1）计算结果是否可被该公司接受？——回答是否定因为：①在最优解中，除第1个采矿点有富裕外，其余13个采矿点的出矿量全部参与了配矿。
而矿点1在配矿以后尚有富余量 70 －31.12 ＝38.879 （万吨），但矿点1的矿石品位仅为37.16%，属贫矿。
②该公司花费了大量人力、物力、财力后，在矿点1生产的贫矿中却有近39万吨矿石被闲置，而且在大量积压的同时，还会对环境造成破坏，作为该公司的负责人或公司决策者是难以接受这样的生产方案的。
———原因何在？出路何在？2）解决问题的思路经过分析后可知：在矿石品位T Fe 及出矿量都不可变更的情况下，只能把注意力集中在 混合矿石的品位T Fe 要求上。
——不难看出，降低T Fe 的值，可以使更多的低品位矿石参与配矿。
问题：T Fe 的值有可能降低吗？在降低T Fe 的值，使更多的贫矿入选的同时，会产生什么影响？——以上问题就属于运筹学的灵敏度分析（优化后分析）3）经调查，以及与现场操作人员、工程技术人员、管理人员学习、咨询，拟定了三个T Fe 的新值：44％ 、43％ 、42％3 变动参数之后再计算，结果如下表所示：∑==+++++++++++++14114131211109875432145.0502.04073.05692.05271.04022.0408.04834.05141.064996.04200.04700.0400.05125.03716.0j jx x x x x x x x x x x x x x x ∑==141max j jx zFe境的破坏，故不予以考虑。
运筹学运输问题应用实例
运筹学运输问题应用实例运筹学是一门研究企业决策问题的学科，包括线性规划、整数规划、网络优化、排队论、决策理论等多个分支。
运筹学可以应用于许多领域，其中之一就是运输问题。
运输问题是指在给定的供应和需求条件下，如何合理地安排物资或者人员的调度和运输，使得运输成本最小、效率最高。
以下是几个运输问题的实例，展示了运筹学在现实生活中的应用：1.货物运输问题：某物流公司需要将若干货物从不同的供应地点运送到不同的需求地点，运输成本根据不同的供应-需求对有所差异。
如何设计最优的运输方案，使得总运输成本最小？解决方法：可以使用线性规划模型来描述这个问题。
将各个供需点之间的距离、运输成本等作为变量，建立一个目标函数和一系列约束条件，并通过求解线性规划问题来得到最优的运输方案。
2.配送车辆路径问题：某公司有若干辆配送车辆，需要将货物按照一定的规则分配到不同的配送点，并且保证每个配送点都能得到及时的配送。
如何合理地安排车辆的路径，使得配送成本最小、效率最高？解决方法：可以使用网络优化模型来描述这个问题。
将配送点、车辆、交通网络等抽象成一个图，其中每个节点表示一个配送点或者车辆，边表示两个节点之间的路径。
然后通过求解网络优化问题，找到最优的车辆路径。
3.乘客调度问题：某出租车公司需要根据乘客的叫车需求，合理地调度出租车，以提高乘客的满意度，并最大化车辆的利用率。
如何在不同的时间和地点调度出租车，使得乘客的等待时间最小、出租车的行驶里程最小？解决方法：可以使用排队论模型来描述这个问题。
根据乘客到达的服从分布，建立一个排队论模型，模拟乘客叫车的过程。
然后根据这个模型，确定最佳的出租车调度策略。
4.航班调度问题：某航空公司需要合理地调度飞机的起飞和降落时间，以提高航班的准点率和乘客的满意度。
如何在不同的起降时间和航线之间进行合理的安排，并考虑飞机的机场停靠时间和维修等因素？解决方法：可以使用决策理论和整数规划模型来描述这个问题。
运筹学经典案例
运筹学经典案例案例一：鲍德西（（B AWDSEY）雷达站的研究20世纪30年代，德国内部民族沙文主义及纳粹主义日渐抬头。
以希特勒为首的纳粹势力夺取了政权开始为以战争扩充版图，以武力称霸世界的构想作战争准备。
欧洲上空战云密布。
英国海军大臣丘吉尔反对主政者的“绥靖”政策，认为英德之战不可避免，而且已日益临近。
他在自己的权力范围内作着迎战德国的准备，其中最重要、最有成效之一者是英国本土防空准备。
1935年，英国科学家沃森—瓦特（R．Watson-Wart）发明了雷达。
丘吉尔敏锐地认识到它的重要意义，并下令在英国东海岸的Bawdsey建立了一个秘密的雷达站。
当时，德国已拥有一支强大的空军，起飞17分钟即可到达英国。
在如此短的时间内，如何预警及做好拦截，甚至在本土之外或海上拦截德机，就成为一大难题。
雷达技术帮助了英国，即使在当时的演习中已经可以探测到160公里之外的飞机，但空防中仍有许多漏洞，1939年，由曼彻斯特大学物理学家、英国战斗机司令部科学顾问、战后获诺贝尔奖金的P.M.S.Blachett为首，组织了一个小组，代号为“Blachett 马戏团”，专门就改进空防系统进行研究。
这个小组包括三名心理学家、两名数学家、两名应用数学家、一名天文物理学家、一名普通物理学家、一名海军军官、一名陆军军官及一名测量人员。
研究的问题是：设计将雷达信息传送给指挥系统及武器系统的最佳方式；雷达与防空武器的最佳配置；对探测、信息传递、作战指挥、战斗机与防空火力的协调，作了系统的研究，并获得了成功，从而大大提高了英国本土防空能力，在以后不久对抗德国对英伦三岛的狂轰滥炸中，发挥了极大的作用。
二战史专家评论说，如果没有这项技术及研究，英国就不可能赢得这场战争，甚至在一开始就被击败。
“Blackett马戏团”是世界上第一个运筹学小组。
在他们就此项研究所写的秘密报告中，使用了“Operational Research”一词，意指作战研究”或“运用研究”。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
Wij— 第 i 年年初购进的新设备一直使用到第 j 年年初
这段 期间的全部费用。
精品课件
v2
15
21
15 40 29
30
21
v1
29
40 55
v3
16 22
23
v4
17
v6
18
v5
求解得v1到v6得最短路径为： v1-v3-v6，最短路长为51。 设备更新的计划是：第一年初购置一台新设备，使用到第二年末， 第三年初购置一台新设备，使精用品到课件第五年末，总费用为51。
V5 V6
89 69 25 14 03 30
V V1 V2 V3 V4 V5 V6
1
V 11 2345
2
V
C6= 3
V
4
V
22 23 33 44
2345 3345 4445 4555
5 55 5566
V
6
考虑各点的学习人数，对矩阵D6的每一行乘以相应各点的 人数，得到：
精品课件
0 50 150 175 200 275 40 0 80 100 120 180 180 120 0 30 60 150 D= 70 50 10 0 10 40 280 210 70 35 0 105 495 405 225 180 135 0
2
V
C0= 3
V
22 2 33 3 44 4
222 333 444
4
V 8 3 1 0 3
4
V 55 5 5 5 5
5 6 3 0
5 66 6 6 6 6
V
V0和相应的中间点矩阵C0如下：
精品课件
V
1
V
2
V D6=3V
4
V
5
V
6
V1 V2 V3 V4
02 67 20 45 64 01 75 10 8 621 11 9 5 4
年份
1
购置费
10
使用年限 0 -1
维修费
5
2
3
10
11
1- 2 2- 3
6
8
精品课件
4
5
表1
12 13
3- 4 4- 5 表2 11 15
解：为解决好这一问题，建立下述网络模型，并用最短路
令法：求解vi。— 第 i 年年初购进一台新设备，i=1 , 2 , 3 ,
4,5,6 v6 指第五年年末。
（vi，vj）— 第 i年年初引进新设备一直使用到第 j 年
下图是一个城镇的地图，现在要在该城镇的各地点铺设 管道，已知各点相互之间的铺设费用（单位：千元）， 如何设计铺设线路，使各地互通的总铺设费用最少？
8
3
74
5
10
7
2
6
7 9
8 12
51
5
4
精品课件
解：求各边相通且总费用最少的方案，实际上求最小树， 保证了各点之间连通且费用最少。
3
4
7
5
2
1
4
5
其总费用为：31千元
精品课件
市场 仓库
A1 A2 A3
B1 B2 B3 B4
30 10 0 40 0 0 10 50 20 10 40 5
需 求 量 20 20 60 20
精品课件
例 6：网络运输容量问题
有三个仓库运送某种产品到四个市场上去，仓库的供应量 是20、20和100件，市场需求量是20、20、60和20件。仓库 与市场之间的线路上的容量如下表所示（容量零表示两点 之间无直接的线路可通）。确定现有线路容量是否能满足 市场的需求。若不能，应修改哪条线路的容量。
v2
6
2
1
v1
48
7
v3
3
v4 6
1
v6
3 v5
精品课件
解：首先计算各点对间的最短路，每个学习者为使所走的路 程最短，应走最短路。
V V1 V2 V3 V4 V5 V6
1
V V1 V2 V3 V4 V5
1
V6
V 0 2 7
V 11 1 1 1 1
2
V
D0= 3
V
2 04 6 8 74 0 1 3 6 1 0 1 6
用一条边把代表这两个项目
v2
的顶点连接起来。这样得到
v3
下图
v1
为了解决这个问题，只需
找到一条包含所有顶点的
v4
初等链。
v5
如：{v4，v1，v2，v3，v5}是一条初等链，对应的比赛是： 100m自由泳，50m仰泳，50m蛙泳，100m碟泳，200m自由泳。
此问题的方案不唯一。 精品课件
例 2.线路铺设问题
例4.房屋设计问题
下图是某建筑物的平面图，要求在建筑物的内部从每一房间 都能走到别的所有房间，问至少要在墙上开多少门？试给出 一个开门的方案。
C B
A
D
E
I J
H
K G
F
精品课件
解：
把每一房间看作一个顶点，如果两房间相邻（有共同的隔 墙），则用边把对应的两个顶点连起来，这样就得到一个 无向图，如图。
§4.7 应 用 举 例
例1：比赛安排问题 有五名运动员参加游泳比赛，下表给出了每位运动员参加的 比赛项目，问如何安排比赛，才能使每位运动员都不连续地 参加比赛？
运动员 50m仰泳 50m蛙泳 100m蝶泳 100m自由泳 200m自由泳
A
*
B
*
*
*
C
*
*
D
*
*
E
*
*
精品课件
解：
用顶点v1，v2，v3，v4，v5表示五项比赛项目 如果两项比赛没有同一名运动员参加，把这两项紧排在一起
I H
G F
对应的开门方案如图所 示，共开10个门。
J B C IJ
K A
H D GK
E
F
精品课件
开门方案
例5：选址问题
有六个居民点v1，v2，v3，v4，v5，v6，拟定建一夜校，已知 各点参加学习的人数为25、20、30、10、35、45人，其道路 如图所示，试确定学校位于哪一个居民点，才能使学习者所 走的总路程最少？（图中边旁的数字为路段长度）
从一个房间到另一房间相当于从这个顶点有一条链能到另一 个顶点。
C
I
B
J 图的任意一个连通
H
A
D
G
的生成子图，在它
的所有边对应的隔 K 墙上开门，即可达
到要求。
E
F 精品课件
令所有边的权为1，为了使开的门尽可能少，就要使这个连 通子图的生成子图的边尽可能少，即求图的最小生成树。
B
C
D A
E
最小生成树
D = [1065 835 535 520 525 750]
V1…….V4：V1- V2 - V3 V4
V2…….V4： V2 - V3 - V4 V3…….V4： V3 - V4 V5…….V4： V5 - V4 V6…….V4： V6- V5 - V4
最短路程为520，即夜校应设在v4点，由
C6得到相应路径。
精品课件
例3.设备更新问题
某单位使用一台生产设备，在每年年底，单位领导都要决 策下年度是购买新设备还是继续使用旧设备。
若购置新设备，需要支付一笔购置费；如果继续使用旧的， 则要支付一定的维修费用。
一般说来，维修费随设备使用年限的延长而增加。根据以 往的统计资料，已经估算出设备在各年年初的价格和不同 使用年限的年维修费用，分别示于表1和表2。