高中数学:第三章概率 小结 (28)
高中数学必修2《概率》知识点讲义

第三章 概率一.随机事件的概率1、基本概念:⎧⎧⎪⎨⎨⎩⎪⎩不可能事件确定事件事件必然事件随机事件(1)必然事件:在条件S 下,一定会发生的事件,叫相对于条件S 的必然事件;(2)不可能事件:在条件S 下,一定不会发生的事件,叫相对于条件S 的不可能事件;(3)确定事件:必然事件和不可能事件统称为相对于条件S 的确定事件;(4)随机事件:在条件S 下可能发生也可能不发生的事件,叫相对于条件S 的随机事件;(5)事件:确定事件和随机事件统称为事件,一般用大写字母A ,B ,C ……表示。
2、概率与频数、频率:在相同的条件S 下重复n 次试验,观察某一事件A 是否出现,称n 次试验中事件A 出现的次数n A 为事件A 出现的频数;称事件A 出现的比例f n (A)= A n n为事件A 出现的概率:对于给定的随机事件A ,如果随着试验次数的增加,事件A 发生的频率f n (A) 稳定在某个常数上,把这个常数记作P (A ),称为事件A 的概率。
频率与概率的区别与联系:随机事件的频率,指此事件发生的次数nA 与试验总次数n 的比值A n n ,它具有一定的稳定性,总在某个常数附近摆动,且随着试验次数的不断增多,这种摆动幅度越来越小。
我们把这个常数叫做随机事件的概率,概率从数量上反映了随机事件发生的可能性的大小。
频率在大量重复试验的前提下可以近似地作为这个事件的概率。
二.概率的基本性质1、各种事件的关系:(1)并(和)事件(2)交(积)事件(3)互斥事件(4)对立事件2、概率的基本性质:(1)必然事件概率为1,不可能事件概率为0,因此0≤P(A)≤1;(2)P(E)=1(E 为必然事件);(3)P(F)=0(F 为必然事件);(4)当事件A 与B 互斥时,满足加法公式:P(A ∪B)= P(A)+ P(B);(5)若事件A 与B 为对立事件,则A ∪B 为必然事件,所以P(A ∪B)= P(A)+ P(B)=1,于是有P(A)=1—P(B);三.古典概型(1)古典概型的使用条件:试验结果的有限性和所有结果的等可能性。
必修3第三章-概率-知识点总结和强化练习:

高中数学必修3 第三章 概率 知识点总结及强化训练一、 知识点总结3.1.1 —3.1.2随机事件的概率及概率的意义 1、基本概念:(1)必然事件:在条件S 下,一定会发生的事件,叫相对于条件S 的必然事件; (2)不可能事件:在条件S 下,一定不会发生的事件,叫相对于条件S 的不可能事件; (3)确定事件:必然事件和不可能事件统称为相对于条件S 的确定事件;(4)随机事件:在条件S 下可能发生也可能不发生的事件,叫相对于条件S 的随机事件;(5)频数与频率:在相同的条件S 下重复n 次试验,观察某一事件A 是否出现,称n 次试验中事件A出现的次数nA 为事件A 出现的频数;称事件A 出现的比例fn(A)=n n A为事件A 出现的概率:对于给定的随机事件A ,如果随着试验次数的增加,事件A 发生的频率fn(A)稳定在某个常数上,把这个常数记作P (A ),称为事件A 的概率。
(6)频率与概率的区别与联系:随机事件的频率,指此事件发生的次数nA 与试验总次数n 的比值n n A,它具有一定的稳定性,总在某个常数附近摆动,且随着试验次数的不断增多,这种摆动幅度越来越小。
我们把这个常数叫做随机事件的概率,概率从数量上反映了随机事件发生的可能性的大小。
频率在大量重复试验的前提下可以近似地作为这个事件的概率3.1.3 概率的基本性质 1、基本概念:(1)事件的包含、并事件、交事件、相等事件(2)若A ∩B 为不可能事件,即A ∩B=ф,那么称事件A 与事件B 互斥;(3)若A ∩B 为不可能事件,A ∪B 为必然事件,那么称事件A 与事件B 互为对立事件;(4)当事件A 与B 互斥时,满足加法公式:P(A ∪B)= P(A)+ P(B);若事件A 与B 为对立事件,则A ∪B 为必然事件,所以P(A ∪B)= P(A)+ P(B)=1,于是有P(A)=1—P(B)2、概率的基本性质:1)必然事件概率为1,不可能事件概率为0,因此0≤P(A)≤1; 2)当事件A 与B 互斥时,满足加法公式:P(A ∪B)= P(A)+ P(B);3)若事件A 与B 为对立事件,则A ∪B 为必然事件,所以P(A ∪B)= P(A)+ P(B)=1,于是有P(A)=1—P(B);4)互斥事件与对立事件的区别与联系,互斥事件是指事件A 与事件B 在一次试验中不会同时发生,其具体包括三种不同的情形:(1)事件A 发生且事件B 不发生;(2)事件A 不发生且事件B 发生;(3)事件A 与事件B 同时不发生,而对立事件是指事件A 与事件B 有且仅有一个发生,其包括两种情形;(1)事件A 发生B 不发生;(2)事件B 发生事件A 不发生,对立事件互斥事件的特殊情形。
高中数学(高一至高三)知识点汇总
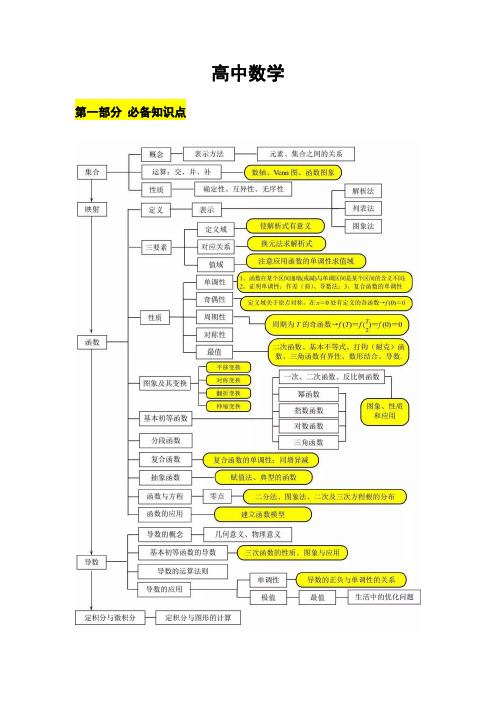
高中数学第一部分必备知识点第二部分学习难点必修1知识点重难点高考考点第一章:集合与函数1.1.1、集合1.1.2、集合间的基本关系1.1.3、集合间的基本运算1.2.1、函数的概念1.2.2、函数的表示法1.3.1、单调性与最大(小)值1.3.2、奇偶性重点:1、集合的交、并、补等运算。
2、函数定义域的求法3、函数性质难点:函数的性质1、集合的交、并、补等运算。
2、集合间的基本关系3、函数的概念、三要素及表示方法4、分段函数5、奇偶性、单调性和周期性第二章:基本初等函数(Ⅰ)2.1.1、指数与指数幂的运算2.1.2、指数函数及其性质2.2.1、对数与对数运算2..2.2、对数函数及其性质2.3、幂函数重点:1、指数函数的图像与性质2、对数函数的图像与性质3、特殊的幂函数的图像与性质4、指数、对数的运算难点:1、指数函数与对数函数相结合2、指数对数与不等式、导数、三角函数等结合1、指数函数的图像与性质2、对数函数的图像与性质3、特殊的幂函数的图像与性质4、指数、对数的运算5、数值大小的比较6、习惯与不等式、导数、三角函数等结合,难度较大第三章:函数的应用3.1.1、方程的根与函数的零点3.1.2、用二分法求方程的近似解3.2.1、几类不同增长的函数模型3.2.2、函数模型的应用举例重点:1、零点的概念2、二分法求方程近似解的方法难点:1、函数模型2、函数零点与导数,含有字母的参数相结合1、零点的概念2、二分法必修2知识点重难点高考考点第一章:空间几何体1、空间几何体的结构2、空间几何体的三视图和直观图3、空间几何体的表面积与体积重点:1、认识柱、锥、台、球及其简单组合体的结构特征2、几何体的三视图和直观图3、会利用公式求一些简单几何体的表面积和体积难点:空间想象能力1、几何体的三视图和直观图2、空间几何体的表面积与体积第二章:点、直线、平面之间的位置关系(重点)1、空间点、直线、平面之间的位置关系2、直线、平面平行的判定及其性质3、直线、平面垂直的判定及其性质重点:1、线面平行、面面平行的有关性质和判定定理2、证明线面垂直3、点到平面的距离难点:1、线面垂直2、点到平面的距离1、以选择填空的形式考查线与面、面与面的平行关系,考查线面位置的关系2、以解答的形式考查线与面、面与面的位置3、证明线面垂直4、点到平面的距离第三章:直线与方程1、直线的倾斜角与斜率2、直线方程3、直线的交点坐标与距离公式重点:1、初步建立代数方法解决几何问题的观念2、正确将几何条件与代数表示进行转化3、掌握直线方程并会用于定理地研究点与直线、直线与直线的位置关系。
高中数学知识点总结-

第一章初步算法(Basic Algorithm)1.1算法的逻辑结构:顺序结构、条件结构、循环结构(UNTIL/WHILE)1.3算法案例案例1:辗转相除法(欧几里得算法)更相减损术——《九章算术》案例2:秦九韶算法:nf(x)=∑a n x n=(⋯((a n x+a n−1)x+a n−2)x+⋯+a1)x+a0i=0案例3:进位制——几进制的基数就是几除k取余法第二章统计2.1.1简单随机抽样(simple random sampling):从N个个体中逐个不放回地抽取n个个体,每个个体被抽到的机会相等(总体个数较少时宜使用)。
(1) 抽签法(抓阄法)(2) 随机数法2.1.2 系统抽样(systematic sampling):按照固定的间隔从N 个个体中抽取n个个体(总体个数较多时宜使用)。
2.1.3 分层抽样(stratified sampling):将总体分成互不交叉的层,按照一定比例从各层中抽取个体(总体中差异明显时宜使用)。
2.2 用样本估计总体2.2.1 用样本频率分布估计总体分布频率分布(frequency distribution):(1)求极差(2)决定组距与组数(3)数据分组(4)列频率分布表(5)画频率分布直方图(频率(面积)=频率组距×组距)(6)频率分布直线图总体密度曲线:反映总体在各个范围内取值的百分比。
茎叶图(stem-and-leaf display)2.2.2 用样本的数字特征估计总体的数字特征众数——出现频率(次数)最多的数。
中位数——数据从小到大排列,处于最中间的一位或最中间的两位的平均数。
样品中50%的个体≤中位数,50%的个体≥中位数(在频率分布直方图中,中位数左边和右边的直方图面积应相等)平均数(约等于频率分布直方图中每个小矩形面积×小矩形底边中点横坐标之和)标准差(standard deviation):样本数据到平均数的一种平均距离(考察数据分散程度)S=|x1−x̅|+|x2−x̅|+⋯+|x n−x̅|ns=√1n[(x1−x̅)2+(x2−x̅)2+⋯+(x n−x̅)2]方差s2=1n[(x1−x̅)2+(x2−x̅)2+⋯+(x n−x̅)2]*正态分布(高斯分布):N(μ,σ2)其中μ为平均数,σ2为方差;区间(μ-λσ,μ+λσ),λ∈N*2.3 变量间的相关关系(1)散点图(scatterplot),正相关,反相关线性相关关系:回归直线(regression line)——通过样本点的中心(x̅,y̅)回归方程:最小二乘法(method of least square)对于一组具有线性相关关系的数据(x1,y1),(x2,y2),⋯,(x n,y n) Q=(y1−bx1−a)2+(y2−bx2−a)2+⋯+(y n−bx n−a)2{b̂=∑(x i−x̅)(y ini=1−y̅)∑(x i−x̅)2ni=1=∑x i y ini=1−nx̅y̅∑x i2ni=1−nx̅2â=y̅−b̂x̅其中x̅=1n∑x ini=1,y̅=1n∑y ini=1,回归方程:ŷ=b̂x+â相关系数r ——衡量两个变量之间线性关系的强弱r=∑(x i−x̅)(y ini=1−y̅)√∑(x i−x̅)2ni=1∑(y j−y̅)2nj=1如r∈[−1,−0.75],则负相关很强;如r∈[0.75,1],则正相关很强;如r∈(−0.75,−0.30]或r∈[0.30,0.75),则相关性一般;如r∈[−0.25, 0.25],则相关性较弱。
人教A版高中数学必修三课件:第三章章末小结

等于(
).
1
2
3
4
A.5 B.5 C.5 D.5
【方法指导】选出的两球只与颜色有关,与顺序无关,可把不
同颜色的小球分别进行编号,无序列举出基本事件,利用古典概
型计算.
【解析】把 1 个红球记为 a,2 个白球分别记为 b1,b2,3 个黑
满足两球颜色为一红一黑的基本事件有(a,c1),(a,c2),(a,c3),共
3 1
3 个,故所求事件的概率为15 =5,故选 A.
【答案】A
【小结】在进行摸球活动中,所求概率一般只与球的颜色有
关,而与先后顺序无关,列举时只需把摸出的球的编号列举出来
即可,无需再颠倒顺序.如果按照有序性列举基本事件,那么个数
两种,则甲、乙两同学各自所选的两种水果相同的概率
为
.
【解析】将四种水果每两种分为一组,有 6 种方法,则甲、乙
1
两位同学各自所选的两种水果相同的概率为6.
1
【答案】
6
3.(2015 年福建卷)如图,矩形 ABCD 中,点 A 在 x 轴上,点 B 的坐标
+ 1, ≥ 0,
为(1,0),且点 C 与点 D 在函数 f(x)= 1
函数.
(2)Excel 软件产生区间[0,1]上的均匀随机数的函数为
“rand()”.
题型一:概率与频率
某险种的基本保费为 a(单位:元),继续购买该险种的投保人
称为续保人,续保人本年度的保费与其上年度出险次数的关联如
下:
上年度
出险次 0 1 2 3 4 ≥5
数
1.2 1.5 1.7
0.8
高中数学 第三章 概率 概率的应用“分赌金”问题知识素材 北师大版必修3

概率的应用——“分赌金”问题17世纪中时,法国数学家巴斯卡写信给当时号称数坛"怪杰"的费尔马,信中提到赌徒德梅尔,向他提出的一个"分赌金"问题。
有一天,德梅尔和赌友保罗赌钱,他们事先每人拿出6枚金币作赌金,用扔硬币作赌博手段,一局中若掷出正面,则德梅尔胜,否则保罗胜。
约定谁先胜三局谁就能得到所有的12枚金币,已知他们在每局中取胜的可能性是相同的,比赛开始后,保罗胜了一局,德梅尔胜了两局,这时一件意外的事中断了他们的赌博,后来他们也不再想继续这场还没有结局的赌博,于是一起商量这12枚金币应如何分才公平合理。
保罗对德梅尔说:"你胜了两局,我只胜了一局,因此你的金币应是我的两倍,你得总数的2/3即8枚金币,我得总数的1/3即4枚金币"。
"这不公平"精通赌博的德梅尔对此提出异议:"我只要再胜一局就能得到全部金币,而你要得到全部金币还须再胜两局。
即使你接下来胜一局,我们两人也是平分秋色,何况就这次我还有一半的机会获胜呢!所以我应得到全部赌金的3/4,即9枚金币,而你只能得到1/4即3枚金币"。
到底谁的分法对呢?当时可使两位数学家费了不少脑筋,历史上古典概率正是由研究诸如此类的赌博游戏中的问题引起的。
现在我们一起来求解,显然,为确保能分出胜负,最多需要再赛两局,为简单计,用"+"表示"德梅尔胜",用"-"表示"保罗胜",于是这两局的所有可能结果为:其中使德梅尔获胜(即至少有一个"+"的情形)有3种,而使保罗获胜(至少有两个"-"的情形)有一种,故德梅尔获胜的概率为3/4,保罗胜的概率为1/4。
这样,德梅尔应得全部赌金的3/4,而保罗则应得1/4。
精美句子1、善思则能“从无字句处读书”。
读沙漠,读出了它坦荡豪放的胸怀;读太阳,读出了它普照万物的无私;读春雨,读出了它润物无声的柔情。
【红对勾】高中数学 第三章 函数的应用本章小结课件 新人教版必修1

20 km/h,巡逻艇不停地往返于A,B两港口巡逻(巡逻艇掉 头的时间忽略不计).
(3)有,x=0,它来源于2x-1=0;x=-1,它来源于 -x-1=0. (4)规定k的范围是{k|k≤-1}.
【例2】
已知f(x)=1-(x-a)(x-b)(a<b),m,n是f(x) )
的零点,且m<n,则实数a,b,m,n的大小关系是( A.m<a<b<n C.a<m<b<n B.a<m<n<b D.m<a<n<b
确定函数零点的个数有两个基本方法:一是利用图象 研究与x轴的交点个数或转化成两个函数图象的交点个数 定性判断.二是利用零点存在性定理判断,但还需结合函 数的图象和单调性,特别是二重根容易漏掉.
【例1】
x 2 ,x≥0, 设f(x)= -x,x<0.
(1)f(x)有零点吗? (2)设g(x)=f(x)+k,为了使方程g(x)=0有且只有一个 根,k应该怎样限制? (3)当k=-1时,g(x)有零点吗?如果有,把它求出 来,如果没有,请说明理由; (4)你给k规定一个范围,使得方程g(x)=0总有两个 根.
3.二分法的定义:对于在区间[a,b]上连续不断,且 f(a)f(b)<0的函数y=f(x),通过不断地把函数f(x)的零点所在 区间一分为二,使区间的两个端点逐步逼近零点,进而得 到零点近似值的方法叫做二分法.
4.几种不同增长的函数模型. (1)一次函数型模型:y=kx+b(k≠0); (2)二次函数型模型:y=ax2+bx+c(a≠0); (3)指数函数型模型:y=abx+c(a≠0); (4)对数函数型模型:y=mlogax+n(m≠0,且a>0, a≠1,x>0); (5)幂函数型模型:y=axn+b(a≠0).
高中数学第三章三角恒等变换第28课时倍角公式B版公开课课件省市一等奖完整版

解析:(1)①原式=11+-tatnanθθ-11+-tatnanθθ =1-2tatannθ2θ=tan2θ. ②原式= 2cos250°- 2sin250°= 2cos50°- 2sin50° =2(cos45°cos50°-sin45°sin50°)=2cos95°=-2sin5°.
(2)证明:①左边=11++22ssiinnθθccoossθθ+-21c-os22sθi-n2θ1 =22csoinsθθcsoinsθθ++csoinsθθ=csoinsθθ=tanθ=右边,所以原式成立. ②左边=2cos2θ2-sisninθc2θos+θ+2ssiinn2θθ+cosθ =csoinsθθ22ccoossθθ++11=tanθ=右边,所以原式成立.
讲拓展 二倍角公式的变形 (1)升幂公式:1+cos2α=2cos2α 1-cos2α=2sin2α (2)降幂公式:cos2α=1+c2os2α sin2α=1-c2os2α
(3)万能公式:sin2α=1+2tatannα2α cos2α=11- +ttaann22αα
2 说方法·分类探究 类型一 给角求值问题 【例 1】 求下列各式的值: (1)sin2π8-cos2π8;
点评 被化简的式子中有切函数和弦函数时,常首先切化弦,然后 分析角的内部关系,是否有互余或互补的,若有,应用诱导公式 转化,若没有,再分析角间是否存在线性关系,并利用两角和与 差的三角函数展开,经过这样处理后,一般就会化简完毕.
变式训练 3 (1)化简: ①1-1tanθ-1+1tanθ;
② 1+cos100°- 1-cos100°. (2)求证:①11+ +ssiinn22θθ- +ccooss22θθ=tanθ; ②2cos2sθin+22θs+ins2iθn+θ cosθ=tanθ.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
返回目录
考点五 互斥事件与对立事件的概率
(1) 当 A , B 互 斥 时 , 公 式 P(A∪B) = P(A) + P(B) 成 立 ; 当 A , B 互 为 对 立 事 件 时 , 公 式 P(A) = 1 - P(B) 成 立.
返回目录
【变式3】 判断下列每对事件是否为互斥事件,是 否为对立事件,并说明理由.
从40张扑克牌(红桃、黑桃、方块、梅花,点数从 1~10)中任取一张.
(1)“抽出红桃”与“抽出黑桃”; (2)“抽出红色牌”与“抽出黑色牌”; (3)“抽出的牌点数为5的倍数”与“抽出的牌点数大 于9”.
返回目录
返回目录
图示
定义
表示法
事
互斥 事件
若A∩B为_不_可__能__事__件, 则称事件A与事件B互 斥
若 _A_∩__B_=__∅_,
则A与B互斥
件
若A∩B为
的
__不_可__能__事__件__,A∪B 若A∩B=
运 对立 为_必__然_事__件__,那么称 ∅,A∪B=
算 事件 事件A与事件B互为对 U,则A与B
返回目录
由表格可知P(和大于7)=
5 12
,P(和小于或等于7)=
172, 即李红和张明得分的概率不相等,所以这个游戏对
双方不公平.对双方公平的游戏规则:点数之和大于7 时,李红得1分,点数之和小于7时,张明得1分.
返回目录
【变式1】 玲玲和倩倩是一对好朋友,她们都想去 观看周杰伦的演唱会,可手里只有一张票,怎么办呢? 玲玲对倩倩说:“我向空中抛2枚同样的一元硬币,如 果落地后一正一反,就我去;如果落地后两面一样,就 你去!”你认为这个游戏公平吗?为什么?
返回目录
考点三 事件关系的判断
事件关系的判断方法 (1)两个事件是互斥事件还是对立事件,要根据互斥 事件与对立事件的定义来判断,互斥事件是在任何一次 试验中不能同时发生的两个事件,对立事件除要求两个 事件互斥外,还要求在一次试验中必有一个事件发生. (2)对立事件是互斥事件,是互斥中的特殊情况,但 互斥事件不一定是对立事件.
返回目录
第二章
概 率(必修3)
返回目录
2.1 随机事件的概率 2.1.2 概率的意义
2.1.3 概率的基本性质
返回目录
课前 教材预案 课堂 深度拓展 课末 随堂演练 课后 限时作业
返回目录
课前教材预案
要点一 概率的正确理解 随 机 事 件 在 一 次 试 验 中 发 生 与 否 是 __随__机_的___ , 但 _随__机__性___中 含 有 _规__律__性___ , 认 识 了 这 种 __随__机_性___ 中 的 _规__律__性___,就能使我们比较准确地__预__测____随机事件发 生的可能性.
返回目录
(3)不是互斥事件,也不是对立事件.理由是:从40 张扑克牌中任意抽取1张,“抽出的牌点数为5的倍数” 与“抽出的牌点数大于9”这两个事件可能同时发生,如 抽出的牌点数为10,因此,二者不是互斥事件,当然不 可能是对立事件.
返回目录பைடு நூலகம்
考点四 事件的运算
(1)利用事件间运算的定义,列出同一条件下的试验 所有可能出现的结果,分析并利用这些结果进行事件间 的运算.
3.天气预报的“降水”是一个__随_机__事__件____,“降 水 概 率 为 90%” , 指 明 了 “ 降 水 ” 这 个 _随__机_事__件__发__生_的__概__率__,在一次试验中,概率为90%的事 件 也 __可__能__不_出__现________ , 因 此 , “ 昨 天 没 有 下 雨”_并__不__能__说_明____“昨天的降水概率为90%”的天气预报 是_____错__误_的.
由①②两式,得20n0=12500,解得n=1 500. 所以该自然保护区中天鹅的数量约为1 500只.
返回目录
【变式2】 某水产试验厂实行某种鱼的人工孵化, 10 000个鱼卵能孵化8 513尾鱼苗,根据概率的统计定义 解答下列问题.
(1)这种鱼卵的孵化率(即孵化概率)是多少? (2)30 000个鱼卵大约能孵化多少尾鱼苗? (3)要孵化5 000尾鱼苗,大概需要多少个鱼卵?(精 确到百位)
要点三 事件的关系与运算
事件 的运 算
定义
表示法
一般地,对于事件A
包 含 关 系
与事件B,如果事件 B⊇A A发生,则事件 ________( B_一__定__发_生__,这时称 或 事件B包含事件A(或 __A_⊆__B___) 称事件A包含于事件
B)
返回目录
图示
定义
表示法
若某事件发生当且
事件 并 仅当__事__件_A__发_生__或_ 的运 事 ___事__件__B_发__生_,则 算 件 称此事件为事件A
返回目录
思维导引:根据频率等于频数除以样本总数得频 率,再根据等可能性以频率估计概率,最后根据总数等 于频数除以概率得结果.
解析 设保护区中天鹅的数量约为n,假定每只天鹅 被捕到的可能性是相等的,从保护区中任捕一只,设事
件A={带有记号的天鹅},则P(A)=20n0.①
返回目录
第二次从保护区中捕出150只天鹅,其中有20只带 有记号,由概率的统计定义可知P(A)=12500,②
返回目录
要点二 游戏的公平性与天气预报的概率解释 1.裁判员用抽签器决定谁先发球,不管哪一名运 动员先猜,猜中并取得发球的_概__率__均__为__12_______,所以 这个规则是公平的. 2.在设计某种游戏规则时,一定要考虑这种规则 对每个人都是__公__平____的这一重要原则.
返回目录
返回目录
解析 公平.因为两枚硬币落地共有四种结果: 正,正;正,反;反,正;反,反.由此可见,她们两 人得到门票的概率都是12,所以公平.
返回目录
考点二 概率的实际应用
此类题型往往与随机抽样相结合.一般根据题中条 件可求出样本的数目以及在总体中的频率,用频率估计 概率,进而可估计总体的数目.
返回目录
个红球,1个白球或3个均为红球,所以A⊆C,故C∩A
=A.
返回目录
【变式4】 掷一枚骰子,下列事件: A={出现奇数点},B={出现偶数点},C={点数小 于3},D={点数大于2},E={点数是3的倍数}. 求:(1)A∩B,BC; (2)A∪B,B+C; (3) D ,AC, D + E .
返回目录
(2)利用Venn图,借助集合间运算的思想,分析同 一条件下的试验所有可能出现的结果,把这些结果在图 中列出,并进行运算.
返回目录
【例题4】 盒子里有6个红球,4个白球,现从中任 取3个球,设事件A={3个球中有1个红球2个白球},事 件B={3个球中有2个红球1个白球},事件C={3个球中 至 少 有 1 个 红 球 } , 事 件 D = {3 个 球 中 既 有 红 球 又 有 白 球}.
求:(1)事件D与A,B是什么样的运算关系? (2)事件C与A的交事件是什么事件?
返回目录
思维导引:确定事件C,D分别包含哪些基本事 件,然后结合事件A,B和交集、并集的知识即可得到 答案.
解析 (1)对于事件D,可能的结果为1个红球,2个
白球或2个红球,1个白球,故D=A∪B.
(2)对于事件C,可能的结果为1个红球,2个白球或2
思维导引:列出所有可能性来比较双方各自获胜可 能性的大小,然后得出比较的结论.
返回目录
解析 不公平.所有可能情况如表所示. 和123 4 5 6 1 234 5 6 7 2 345 6 7 8 3 456 7 8 9 4 5 6 7 8 9 10 5 6 7 8 9 10 11 6 7 8 9 10 11 12
解析 (1)是互斥事件,不是对立事件.理由是:从 40张扑克牌中任意抽取1张,“抽出红桃”和“抽出黑 桃”是不可能同时发生的,所以是互斥事件.同时,不 能保证其中必有一个发生,这是由于还可能抽出“方 块”或“梅花”,因此,二者不是对立事件.
(2)既是互斥事件,又是对立事件.理由是:从40张 扑克牌中,任意抽取1张,“抽出红色牌”与“抽出黑 色牌”两个事件不可能同时发生,但其中必有一个发 生,所以它们既是互斥事件,又是对立事件.
返回目录
解析 (1)这种鱼卵的孵化率为180501030=0.851 3.
(2)30 000个鱼卵大约能孵化 30 000×0.851 3=25
539(尾)鱼苗.
(3)设大概需要x个鱼卵,由题意知 5
000 x
=0.851
3,
解得x=05.8050103≈5 900,所以大概需要5 900个鱼卵.
判断游戏是否公平的思路 无论是怎样的游戏,游戏公平与否就是看参与游戏 的每个个体获胜的概率是否相同,相同则公平,不相同 则不公平.具体判断时,可以求出按所给规则双方的获 胜概率,再进行比较.
返回目录
【例题1】 李红和张明正在玩掷骰子游戏,两人各 掷一枚骰子.当两枚骰子的点数之和大于7时,李红得1 分,否则张明得1分.这个游戏公平吗?为什么?如果 不公平,请你提出一个对双方公平的游戏规则.
返回目录
(2)不是互斥事件,也不是对立事件. 理由是:“至少有1名男生”包括“1名男生、1名 女生”和“2名都是男生”两种结果. “至少有1名女生”包括“1名女生、1名男生”和 “2名都是女生”两种结果,它们可同时发生.
返回目录
(3)不是互斥事件,也不是对立事件. 理由是:“至少有1名男生”包括“1名男生、1名 女生”和“2名都是男生”,这与“全是男生”可同时 发生. (4)是互斥事件,也是对立事件. 理由是:“至少有1名男生”包括“1名男生、1名 女生”和“2名都是男生”两种结果,它与“全是女 生”不可能同时发生.其并事件是必然事件,所以是对 立事件.
