23_第23讲__最值问题一
第23讲梯形
第23讲 梯 形考点•方法•破译１. 掌握梯形的定义与特殊梯形的性质． ２. 掌握特殊梯形的判定方法．３. 掌握梯形中常见５种辅助线：①平移腰，②平移对角线，③作高，④延长两腰，⑤平移底．经典•考题•赏析【例１】（齐齐哈尔）梯形ABCD 中，AD ‖BC ，AD ＝1,BC ＝4,∠C ＝70°,∠B ＝40°,则AB 的长为（ ）A ．2B ．3C ． 4D ． 5【解法指导】过A 作AE ∥DC ,将梯形转化为一个平行四边形和一个 三角形，其中△ABE 中各内角可求出，易知AB ＝BE ,故选B . 【变式题组】 01．如图，四边形ABCD 中,AB ∥CD ,∠B ＝２∠D ,若AB ＝3,BC ＝5,则CD ＝______. 02．已知四边形ABCD中，AB ＝DC ,AC ＝BD ,AD ≠BC ,求证：四边形ABCD 是等腰梯形． 03．(荆州)如图,梯形ABCD 中,AD ∥BC ,∠C ＝90°中 AB ＝AD ,连接BD 过A 作BD 的垂线,交BC 于E ,如果EC ＝3㎝,CD ＝4㎝,那么梯形ABCD 的面积是_______cm 2.04．(宿迁)如图,在梯形ABCD 中, AD ∥BC ,AB ＝CD .∠B ＋∠C ＝90°,AD ＝1,BC ＝3,E .F分别是AD 、BC 的中点，则EF ＝________.【例２】（桂林）梯形ABCD 中，AD ∥BC ,AB ＝CD ,AC ⊥BD ,AD ＝6,BC ＝8,求梯形的高．【解法指导】由于条件与对角线有关，因而可考虑平移对角线，从而构造等腰直角三角形解决问题．解：过D 作DE ‖AC 交BC 的延长线于E ，过D 作DF ⊥BC ,∵AD ‖BC ,AB ＝AD ∴AC ＝BD ,∵AD ‖CE ,AC ‖DE ∴四边形ACED 是平行四边形，∴AC ＝DE ∴Rt △BDE 中,BD ＝DE ,∵DF ⊥BE ∴DF 是BE 边上的中线∴DF ＝()11722BE AD BC =+=【变式题组】01．（临沂）如图在等腰梯形ABCD 中，AD ‖BC ,对角线AC ⊥BD 于点O ,DF ⊥BC ,垂足分别为E 、F ,设AD ＝a ，BC ＝b ,则四边形AEFD 的周长是( )． A .3a ＋b B .2(a ＋ｂ) C .2b ＋a D .4a ＋b02．如图，在梯形ABCD 中，AD ‖BC ,对角线AC ⊥BD ,AC ＝8㎝,BD ＝6㎝.则梯形的高为__㎝.A BC D E第１题A BC DE 第３题图 B C 第２题图 A B CD E F第４题A BCD EF03．在数学活动课中，老师让同学们做一个对角线互相垂直的等腰梯形形状的风筝，其面积为４５０㎝２，则两对角线所用的竹条至少需要（ ）．A.㎝. B .30㎝. C .60㎝. D. ㎝04．(上海)已知梯形ABCD 中，AB ∥BC ,AB ＝AD (如图所示)，∠BAD 的平分线AE 交BC 于点E ,连接DE ．（１）求证：四边形ABED 是菱形；（２）∠ABC ＝60°EC ＝2BE ,求证：ED ⊥DC【例３】(乐山)在直角梯形ABCD 中，AD ‖BC .点E 是边CD 的中点，若AB ＝AD ＋BC ,52BE,求梯形的面积． 【解法指导】若梯形中已知条件与腰的中点有关，则可作另一腰中点构造梯形的中位线或连接AE 并延长交BC 的延长线天F 点，从而构造全等三角形，这样求出△ABF 的面积即为梯形的面积．解：连接AE 并延长交BC 延长线于F .∵AD ∥BF ,∠D ＝∠ECF , ∠DEA ＝∠CEF ,DE ＝CE ∴△ADE ≌△FCE∴AE ＝EF ,AD ＝CF ∵AB ＝AD ＋BC ∴AB ＝BF∴△ABF 为等腰直角三角形．∴BE ⊥AF ,2BE ＝AF ＝5 ∴S 梯形ABCD ＝ S △ABF ＝12×5×52＝254【变式题组】01．(浙江湖州)如图，已知在直角梯形AOBC 中，AC ∥OB ,CB ⊥OB ,OB ＝18,BC ＝12,AC＝9,对角线OC 、交天点D ,点E 、F 、G 分别是CD ,BD ,BC 的中点，以O 为原点，直线OB 为x 轴建立平面直角坐标系，则G 、E 、D 、F 四个点中与点A 在同一反比例函数图象上的是（ ）．A .点GB .点EC .点D D .点F 02．（东营）如图，点C 是线段AB 上的一个动点，△ACD 和△BCE 是在AB 同侧的两个等边三角形，DM 、EN 分别是△ACD 和△BCE 的高，点C 在线段AB 上沿着从点A 向点B 的方向移动（不与点A 、BT 重合），连接DE ,这个四边形的面积变化情况为（ ）． A .逐渐增大 B . .逐渐减小 C .始终不变 D .先增大后变小B E FA BC D第2题图 A BCDOE A BCDEF03．（桂林）如图：已知AB ＝10，点C 、D 在线段AB 上，且AC ＝DB ＝2;P 是线段CD 上的动点，分别以AP 、PB 为边在线段AB 的同侧作等边△AEP 和等边△PFB ,连接EF ，设EF 的中点为G ；当点P 从点C 运动到点D 时，则点G 移动的路径的长是_______. 04． (眉山)在直角梯形ABCD 中，AB ∥DC ,AB ⊥BC ,AB ＝2CD ,E 、F 分别为AB 、AD 的中点，连接EF 、BF 、CF .在不添加其他条件下，写出图中一对全等三角形，并证明．演练巩固 反馈提高.01．(荆门)等腰梯形ABCD 中,E 、F 、G ﹑H 分别是各边的中点,则四边形EFGH 的形状是( )A .平行四边形B .矩形C .菱形D .正方形 02．(威海)在梯形ABCD 中,AB ∥CD ,∠A ＝60°, ∠B ＝30°,AD ＝CD ＝6,则AB 的长度为( ). A .9 B .12 C .18 D .6＋3303．(淄博)如图,梯形ABCD 中, ∠ABC 和∠DCB 的平分线相交于梯形中位线EF 上的一点P ,若EF ＝3,则梯形ABCD 的周长为( )A .9B .10.5C .12D .1504．(鄂州)已知直角梯形ABCD 中,AD ∥BC ,AB ⊥BC ,AD ＝2BC ＝CD ＝5,点P 在BC 上移动,则当P A ＋PD 取最小值时,△APD 中边AP 上的高为( ). A .17172 B .17174 C . 17178D .3 05．(遂宁)如图,在梯形ABCD 中, ,AB ∥CD , ∠D ＝90°AD ＝DC ＝4,AB ＝1,F 为AD 的中点,则点 F 到BC 的距离是( ) A .2 B .4 C .8 D .106．(山西太原)在梯形ABCD 中,AD ∥BC ,AB ＝DC ＝3,沿对角线BD 翻折梯形ABCD ,若点A恰好落在下底BC 的中点E 处,则梯形的周长为________.07．如图(1), △ABC 是直角三角形,如果用四张与△ABC 全等的三角纸片恰好拼成一个等腰梯形,如图(2),那么在R t △ABC 中,ABBC的值是_______. A BCD E F P3题图•●A BCD P4题图●ABCD5题图AB C D E M N 2题图●● ●A CB D P E G F 3题图 A BCDE F 4题图08．(白银)如图(1)是一个等腰梯形,由6个这样的等腰梯形恰好可以拼出如图(2)所示的一个菱形,对于图(1)中的等腰梯形,请写出它的内角度数或腰与底边长度之间关系的一个正确结论____________.09．(陕西省)如图,梯形ABCD 中,AB ∥DC , ∠ADC ＋∠BCD ＝90°,且DC ＝2AB ,分别以DA ,AB ,BC 为 边向梯形外作正方形,其面积分别为要 S 1、S 2、S 3,则S 1、S 2、S 3之间的关系是__________.10．如图,在梯形ABCD 中, AD ∥BC , ∠B ＝90°,AB ＝4cm ,AD ＝18cm ,BC ＝21cm ,点P 从点A 出发,沿边AD 向点D 以2cm /s 的速度移动,点Q 从点C 出发沿边BC 向点B 以6cm /s 速度移动,P ﹑Q 同时出发,若有一点运动到端点时,另一点也随之停止,则经过____移后,PQ ＝CD .11．如图,直角梯形ABCD 中,AD ∥BC , AB ⊥BC ,AD ＝2,将腰CD 以D 为中心逆时针旋转90°至ED ,连接AE ,CE , △ADE 面积为3,则BC 的长为________.12．(威海)从边长为ɑ的大正方形纸板中间挖去一个边长为b 的小正方形后,将其截成四个相,同的等腰梯形(如图1),可以拼成一个平行四边形(如图2),已知∠A ＝45°,AB ＝6,AD ＝4,若将该纸片按图2方式截成四个相同的等腰梯形,然后按图1方式拼图,则得到的大正方形的面积为_______.13.(深圳)如图在梯形ABCD 中,AB ∥DC ,DB 平分∠ADC ,过点A 作AE ∥BD ,交CD 的延长于点E ,且∠C ＝2∠E .(1)求证:梯形ABCD 是等腰梯形; (2)若∠BDC ＝30°,AD ＝5,求CD 的长.ABC图(1) 图(2) 图3ɑ AB CDEABCD10题图11题 图ABCD图(1)图(2)7题图(1)(2)8题图S 1S 2S 39题图 A B CDC DEP A BCDEFA B CD EA B 14．(河南)如图,直线b x k y +=1与反比例函数xk y 2=的图象交于A (1,6),B (ɑ,3)两点. (1)求k 1,K 2的值;(2)直接写出k 1x ＋b －xk2＞0时x 的取值范围;(3)如图,等腰梯形OBCD 中,BC ∥OD ,OB ＝CD ,OD 过点C 作CE ⊥OD 于点E ,CE 和反比例函数的图象交于点P ,当梯形OBCD 的面积为12时,请判断PC 和PE 的大小关系,并说明理由.15.(河南)如图梯形ABCD 中.AD ∥BC ,E 是BC 的中点,AD ＝5,BC ＝12,CD ＝24,∠C ＝45°,点P 是BC 边上一动点,设PB 的长为x .(1)当x 的值为_____时,以点P 、A 、D 、E 、为顶点的四边形为直角梯形; (2)当x 的值 为____时,以点P 、A 、D 、E 为顶点的四边形为平行四边形;(3)点P 在BC 边上运动的过程中,以P 、A 、D 、为顶点的四边形能否构成菱形？时说明理由．16．（重庆）已知:如图,在梯形ABCD 中,AD ∥BC ,BC ＝DC ,CF 平分∠BCD ,DF ∥AB ,BF 的延长线交DC 于点E .求证:(1)△BFC ≌△DFC ;(2)AD ＝DE17.(泰安)如图所示,在直角梯形ABCD 中, ∠ABC ＝90°, AD ∥BC ,E 是AB 的中点,CE ⊥BD .(1)求证:BE ＝AD ;(2)求证:AC 是线段ED 的垂直平分线; (3) △DBC 是等腰三角形吗?并说明理由.C D EFPABMADE F 3题图A B CC 1题图 E BH 2题图 D 18.(重庆)已知:如图,在直角梯形ABCD 中, AD ∥BC , ∠ABC ＝90°, ,E 是DC 的中点,过点E 作DC 的垂线交AB 于点P ,交CB 的延长线于点M 上.且满足CF ＝AD ,MF ＝MA . (1)若∠MFC ＝120°,求证:AM ＝2MB ;(2)求证: ∠MPB ＝90°－21∠FCM .19.(绥化)如图,在平面直角坐标系中,函数y ＝2x ＋12的图象分别交x 轴,y 轴于A .B 两点,过点A 的直线交y 轴正半轴于点M ,且点M 为线段OB 的中点. (1)求直线AM 的解析式; (2)试在直线AM 上找一点P ,使得S △ABP ＝ S △AOB , 请直接写出点P 的坐标.(3)若点H 为直坐标平面内任意一点,在坐标平面内是否存在这样的点H ,使以点A 、B 、M 、H 为顶点的四边形是等腰梯形?若存在直接写出点H 的坐标,若不存在,请说明理由.培优升级 奥赛检测01.(武汉)在直角梯形ABCD 中, AD ∥BC , ∠ABC ＝90°,AB ＝BC ,E 为AB 边上一点,∠BCE ＝15°,且AE ＝AD .连接DE 交对角线AC 于H ,连接BH .下列结论:①△ACD ≌△ACE ②△CDE 为等边三角形;③2=BE EH ;④CHAHS S EHC EDC =∆∆,其中结论正确的是( )A . 只有①②B .只有①②④C .只有③④D . ①②③④02.(浙江竞赛)如图,在平面直角坐标系内放置一个直角梯形AOCD ,已知AD ＝3,AO ＝8,OC ＝5,若点P 在梯形内且PCD PAO PO C PAD S S S S ∆∆∆∆==,,那么点P 的坐标是＿＿＿.03．梯形ABCD 中,AD ∥BC ,F 是CD 的中点,AF ⊥AB ,E 是BC 上一点,且AE ＝BE ,若AB＝m ,则EF 的长为________.04.(齐齐哈尔)有一底角为60°的直角梯形,上底为10cm ,与底垂直的腰长为10cm ,以上AB CDE FA BCD A B C DE F P A BC D C 图(1) 图(2) EA BM N 图3pD FEF MN A E F P CGD 底或与底垂直的腰为一边作三角形,使三角形的另一边为15cm ,第三个顶点落在下底上.请计算所作三角形的面积为_____.05.如图,梯形ABCD 中,AB ∥DC ,AB ＝AC ,DA ＝DB , ∠ADB ＝90°,求∠BAC 的度数.06.(义乌)如图,直角梯形纸片ABCD ,AD ⊥AB ,AB ＝8,AD ＝CD ＝4,点E ,F 分别在线段AB 、AD 上将△AEF 沿EF 翻折,点A 的落点记为P . (1)当AE ＝5,P 落在线段CD 上时,求PD 的值;(2)当P 落在直角梯形ABCD 内部时,求PD 的最小值.07.(江西)如图在等腰梯形ABCD 中, AD ∥BC , E 为AB 的中点,过点E 作EF ∥BC 交CD 于点F ,AB ＝4,BC ＝6, ∠B ＝60° (1)求点E 到BC 的距离;(2)点P 为线段EF 上的一个动点,过P 作PM ⊥EF ,交BC 于点M ,过M 作MN ∥AB 交折线ADC 于点N ,连接PN ,设PN ＝x①当点N 线段AD 上时, △PMN 的形状是否发生改变?若不变,求出△PMN 的周长;若改变,请说 明理由.②当点N 在线段DC 上时,是否存在点P , △PMN 为等腰三角形?若存在,请求出所有满足要求的x 的值;若不存在请说明理由.08.(四川)如图,分别以△ABC 的边AC 和BC 为一边,向三角形外作正方形ACDE 和CBFG ,点P 是EF 的中点,PH ⊥AB ,垂足是H ,如果AB ＝310,求PH .09.(吉林)如图,在直角梯形ABCD 中, AD ∥BC , AE ⊥BC 于点E ,DF ⊥BC 于点F ,ADPB CD E FP ABCDEA FFQ备用图BC D P ABC D●图(1)A E M Q 备用图●M ＝2cm ,BC ＝6cm ,AE ＝4cm .点P ,Q 分别在线段AE 、DF 上,顺次连接B 、P 、Q 、C ,线段BP 、PQ 、QC 、CB 所围成封闭图形记为M ,若点P 在线段AE 上运动时,点Q 也随之在线段DF 上运动,使图形M 的形状发生改变,但面积始终为10cm 2,设EP ＝xcm ,FQ ＝ycm ,解答下列问题(1)直接写出当x ＝3时y 的值;(2)求y 与x 之间的函数 关系式,并写出自变量x 的取值范围. (3)当x 取何值时,图形M 成为等腰梯形?图形M 成为三角形? (4)直接写出线段PQ 在运动过程中所能扫过的区域面积.,10.(河北)如图,在直角梯形ABCD 中AD ∥BC ,∠B ＝90°,AD ＝6,BC ＝8,AB ＝33,点M 是BC 的中点,点P 从点M 出发沿MB 以1个单位长的速度向点B 匀速运动,到达点B 后立刻以原速度沿BM 返回;点Q 从点M 出发以每秒1个单位长的速度在射线MC 上匀速运动,在点P 、Q 的运动过程中，以PQ 为边作等边△EPQ ,使它与梯形ABCD 在射线BC 同侧.点P 、Q 同时 出发，当点P 返回到点M 时停止运动,点Q 也随之停止.设点P ﹑Q 运动的时间是t 秒(t ﹥0).(1)设PQ 的长为y ,在点P 从点M 向点B 运动的过程中,写出y 与t 之间的函数关系式(不必写t 的取值范围);(2)当BP ＝1时,求△EPQ 与梯形ABCD 重叠部分的面积.(3)随着时间t 的变化,线段AD 会有一部分被△EPQ 覆盖,被覆盖线段的长度在某个时刻会达到最大值,请回答:该最大值能否持续一个时段?若能,请直接写出t 的取值范围;若不能,请说明理由.11.(陕西)问题探究图(2) B C D ABC D图(1) A ●M BAC (1)请你在图1中作一条直线,使它将矩形ABCD 分成面积相等的两部分;(2)如图2,点M 是长矩形ABCD 内一点,请你在图2中过点M 作一条直线,使它将矩形ABCD 分成面积相等的两部分. 问题解决(3)如图3,在平面直角坐标系中,直角梯形OBCD 是某市将要筹建的高新技术开发区用地示意图,其中DC ∥OB ,OB ＝6,CD ＝4.开发区统合服务管理委员会(其占地面积不计)设在点P (4,2)处．为了方便驻区单位准备过点P 修一条笔直的道路（路宽不计），并且是这条路所在的直线l 将直角梯形OBCD 分成面积相等的两部分，你认为直线l 是否存在？若存在，请说明理由．12.（北京）问题：已知△ABC 中，∠BAC ＝2∠ACB ,点D 是△ABC 内的一点，且AD ＝CD ,BD ＝BA ,探究∠DBC 与∠ABC 度数的比值． 请你完成下列探究过程：先将图形特殊化，得出猜想，再对一般情况进行分析并加以证明． ⑴当∠BAC ＝90°时，依问题中的条件补全右图． 观察图形，AB 与AC 的量关系为____;当推出∠DAC ＝15°时，可进一步推出∠DBC 的度数为＿＿＿； 可得到∠DBC 与∠ABC 度数的比值为＿＿＿；⑵当∠BAC ≠90°时，请你画出图形，研究∠DBC 与∠ABC 度数的比值是否与⑴中的结论相同，写出你的猜想并加以证明．。
高考化学一轮复习：《第23讲 化学平衡状态的建立与移动》巩固训练(学生版)
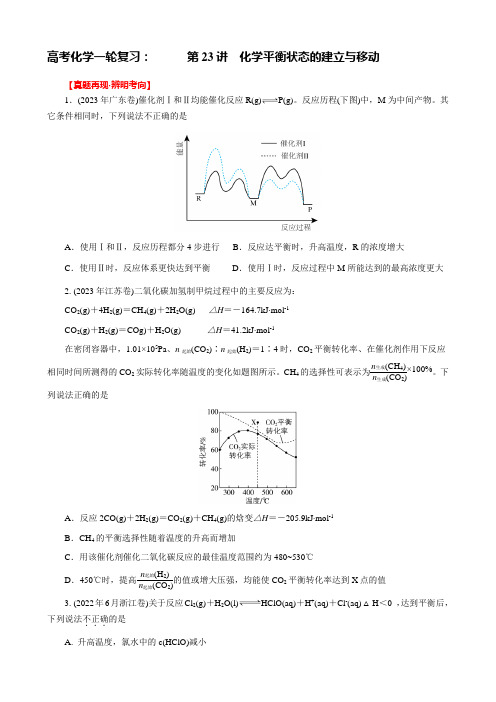
高考化学一轮复习：第23讲化学平衡状态的建立与移动【真题再现·辨明考向】1．(2023年广东卷)催化剂Ⅰ和Ⅱ均能催化反应R(g)P(g)。
反应历程(下图)中，M为中间产物。
其它条件相同时，下列说法不正确的是A．使用Ⅰ和Ⅱ，反应历程都分4步进行B．反应达平衡时，升高温度，R的浓度增大C．使用Ⅱ时，反应体系更快达到平衡D．使用Ⅰ时，反应过程中M所能达到的最高浓度更大2. (2023年江苏卷)二氧化碳加氢制甲烷过程中的主要反应为：CO2(g)＋4H2(g)＝CH4(g)＋2H2O(g) △H＝－164.7kJ∙mol-1CO2(g)＋H2(g)＝COg)＋H2O(g) △H＝41.2kJ∙mol-1在密闭容器中，1.01×105Pa、n起始(CO2)∶n起始(H2)＝1∶4时，CO2平衡转化率、在催化剂作用下反应相同时间所测得的CO2实际转化率随温度的变化如题图所示。
CH4的选择性可表示为n生成(CH4)n生成(CO2)×100%。
下列说法正确的是A．反应2CO(g)＋2H2(g)＝CO2(g)＋CH4(g)的焓变△H＝－205.9kJ∙mol-1 B．CH4的平衡选择性随着温度的升高而增加C．用该催化剂催化二氧化碳反应的最佳温度范围约为480~530℃D．450℃时，提高n起始(H2)n起始(CO2)的值或增大压强，均能使CO2平衡转化率达到X点的值3. (2022年6月浙江卷)关于反应Cl2(g)＋H2O(l)HClO(aq)＋H+(aq)＋Cl-(aq) △H＜0 ，达到平衡后，下列说法不正确．．．的是A. 升高温度，氯水中的c(HClO)减小B. 氯水中加入少量醋酸钠固体，上述平衡正向移动，c(HClO)增大C. 取氯水稀释，c(Cl－)c(HClO)增大D. 取两份氯水，分别滴加AgNO3溶液和淀粉KI溶液，若前者有白色沉淀，后者溶液变蓝色，可以证明上述反应存在限度4. (2022年北京卷)某MOFs的多孔材料刚好可将N2O4“固定”，实现了NO2与N2O4分离并制备HNO3，如图所示：己知：2NO2(g)N2O4(g) △H＜0下列说法不正确．．．的是A. 气体温度升高后，不利于N2O4的固定B. N2O4被固定后，平衡正移，有利于NO2的去除C. 制备HNO3的原理为：2N2O4＋O2＋2H2O＝4HNO3D. 每制备0.4molHNO3，转移电子数约为6.02×10225. (2022年广东卷)恒容密闭容器中，BaSO4(s)＋4H2(g)BaS(s)＋4H2O(g)在不同温度下达平衡时，各组分的物质的量(n)如图所示。
最值问题归纳
最值问题是初中数学的重要内容，是一类综合性较强的问题，它贯穿初中数学的始终，是中考的热点问题，无论是代数题还是几何题都有最值问题。
数形结合的思想贯穿始终。
一、代数中的最值问题1、代数求最值方法 ①利用一次函数的增减性一次函数(0)y kx b k =+≠的自变量x 的取值范围是全体实数，图象是一条直线，因而没有最大（小）值；实际问题中，当m x n ≤≤时，则一次函数的图象是一条线段，根据一次函数的增减性，就有最大（小）值。
1、某工程队要招聘甲、乙两种工种的工人150人，甲、乙两种工种的工人的月工资分别是600元和1000元，现要求乙种工种的人数不少于甲种工种人数的2倍，问甲、乙两种工种各招聘多少人时可使得每月所付的工资最少？②配方法，利用非负数的性质2、（1）求二次三项式223x x -+的最小值（2）设a 、b 为实数，那么222a ab b a b ++--的最小值为_______。
③判别式法3、（1）求2211x x x x -+++的最大值与最小值。
（2）,x y 为实数且x y m ++=5，xy ym mx ++=3，求实数m 最大值与最小值。
④零点区间讨论法4、求函数|1||4|5y x x =--+-的最大值。
⑤基本不等式性质222()020a b a ab b -≥∴-+≥即222a b ab +≥，仅当a b =时，等号成立由此可推出222a b ab +≤(0,0)2a ba b +≤≥≥⑥夹逼法通过转化、变形和估计，将有关的量限制在某一数值范围内，再通过解不等式获取问题的答案，这一方法称为夹逼法。
5、不等边三角形的两边上的高分别为4和12且第三边上的高h 为整数，那么此高h 的最大值可能为________。
⑦二次函数模型（中考第23题，应用题）该题基本来自课本3个探究例题不断的变化、加深：探究1：商品定价 探究2：磁盘计算（含圆） 探究3：拱桥问题 变化趋势：前几年武汉中考主要考查经济类问题，求最经济、最节约和最高效率等这种类型的考题（探究1的演变）；近2年变化为建立函数模型解决实际问题（探究2、3的演变），即利用二次函数的对称性及增减性，确定某范围内函数的最大或最小值。
专题23 圆锥曲线中的最值、范围问题 微点1 圆锥曲线中的最值问题试题及答案
例7．
7．已知点A(−2,0)，B(2,0)，动点M(x,y)满足直线AM与BM的斜率之积为− .记M的轨迹为曲线C.
（1）求C的方程，并说明C是什么曲线；
（2）过坐标原点的直线交C于P，Q两点，点P在第一象限，PE⊥x轴，垂足为E，连结QE并延长交C于点G.
（i）证明： 是直角三角形；
最值问题不仅解答题中分量较大，而且客观题中也时常出现．
一、常用方法
解决圆锥曲线中的最值问题，常见的方法有：
（1）函数法：一般需要找出所求几量的函数解析式，要注意自变量的取值范围．求函数的最值时，一般会用到配方法、均值不等式或者函数单调性．
（2）方程法：根据题目中的等量关系建立方程，根据方程的解的条件得出目标量的不等关系，再求出目标量的最值．
题型三、与向量有关的最值问题
例6．
6．如图，已知椭圆C1： ＋ ＝1(a>b>0)的右焦点为F，上顶点为A，P为椭圆C1上任一点，MN是圆C2：x2＋(y－3)2＝1的一条直径，在y轴上截距为3－ 的直线l与AF平行且与圆C2相切．
(1)求椭圆C1的离心率；
(2)若椭圆C1的短轴长为8，求 · 的最大值．
题型二、与角度有关的最值问题
例5．
5．在平面直角坐标系 中，椭圆 ： 的离心率为 ，焦距为 .
（Ⅰ）求椭圆 的方程；
（Ⅱ）如图，动直线 ： 交椭圆 于 两点， 是椭圆 上一点，直线 的斜率为 ，且 ， 是线段 延长线上一点，且 ， 的半径为 ， 是 的两条切线，切点分别为 .求 的最大值，并求取得最大值时直线 的斜率.
专题23 圆锥曲线中的最值、范围问题 微点1 圆锥曲线中的最值问题
专题23圆锥曲线中的最值、范围问题
中考物理讲义课件 第23课时 欧姆定律的理解及相关计算
图像的分析与计算(重点) ☞样题 3 如图所示是电阻甲和乙的 IU 图像，下列说法中不正确的是( C )
A．甲和乙均是定值电阻 B．当乙两端电压为 4V 时，通过它的电流为 0.2A C．将甲和乙串联，若电路中的电流为 0.4A，则它们两端的总电压为 10V D．将甲和乙并联，若电源电压为 4V，则干路中的电流为 0.6A
☞样题 6 如图所示，电源电压恒定不变。当开关 S1、S2 闭合，若甲、乙两 表均为电压表时，两表示数之比 U 甲∶U 乙＝4∶1；当开关 S1 闭合、S2 断开， 若甲、乙两表均为电流表时，两表的示数之比为( C )
A．4∶3 B．3∶2 C．3∶4 D．3∶1
动态电路计算(重点、难点) ☞样题 7 如图所示，电源电压恒为 12V，电阻 R1 的阻值为 10Ω。开关 S 闭合后，当滑动变阻器 R3 的滑片 P 位于最左端时，电压表的示数为 6V，则 电阻 R2 的阻值为 10 Ω。调节滑片 P，使电压表的示数从 3V 变为 1.5V， 则 R3 接入电路中的阻值变化了 40 Ω。
同一性：I、U、R对应同一导体或同一电路
I、U、R 一一对应同时性：I、U、R对应同一时刻的值 统一性：I、U、R单位要统一，分别是A、V、Ω
3.变形公式： U＝IR (求电压)； R＝UI (求电阻)。
公式 R＝UI 只能计算导体的电阻大小，不能说“导体的电阻跟导体两端的电 压成正比，跟通过导体的电流成反比”，因为导体的电阻与导体本身的材 料、长度、横截面积和温度有关。
重点难点素养 拓展
基本运算(重点) ☞样题 1 如图所示，电源电压恒为 9V，电阻 R1 阻值为 10Ω。闭合开关 S 后，电流表 A 示数为 1.2A。求： (1)电流表 A1 示数；
高斯小学奥数四年级上册含答案第23讲_最值问题一
第二十三讲最值问题一最值问题，即求最大值、最小值的问题．这类问题中，有时满足题目条件的情况并不多，这时我们就可以用枚举法将所有可能情况一一列出，再比较大小．例题1（1）在五位数12435的某一位数字后面插入一个同样的数字可以得到一个六位数（例如：在2的后面插入2可以得到122435）．请问：能得到的最大六位数是多少？（2）在七位数9876789的某一位数字后面再插入一个同样的数字．请问：能得到的最小八位数是多少？「分析」一共有多少种不同的插入数字的方法？你能将它们全部枚举出来吗？练习1在五位数41729的某一位数字前面插入一个同样的数字（例如：在7的前面插入7得到417729），能得到的最大六位数是多少？直接枚举的优点是不用过多思考，大家都能理直气壮地说，直接比较大小得到的答案一定是正确的．事实上，我们应该多想一想，为什么这个答案是最大或最小的，有没有什么道理，其中有没有什么规律．例题2有9个同学要进行象棋比赛．他们准备分成两组，不同组的任意两人之间都进行一场比赛，同组的人不比赛，那么一共最多有多少场比赛？「分析」把9个同学分成两组，有多少种情况呢？你能算出这些分法各自对应的比赛场数吗？练习2有7个同学要进行乒乓球单打比赛．他们准备分成两组，不同组的任意两人之间都进行一场比赛，同组的人不比赛，那么一共最多有多少场比赛？从例题2我们可以得出：两个数的和相等，当它们越接近时（也就是它们的差越小时），两数乘积越大，也可以简单记成“和同近积大”．“和同近积大”的应用非常广泛，接下来我们分析一下比较典型的“篱笆问题”．例题3墨爷爷要用长20米的篱笆围成一个长方形养鸡场，已知长和宽均为整数米，那么怎样围所得的养鸡场面积最大？（正方形是特殊的长方形）「分析」长方形面积是长、宽的乘积，要想长、宽乘积最大，可以不可以应用“和同近积大”的道理来解决呢？能找到“和同”吗？练习3墨爷爷要用长30米的篱笆围成一个长方形养鸡场，已知长和宽均为整数米，那么怎样围所得的养鸡场面积最大？例题4请将1、2、3、4、5、6这六个数填入下面的方格中，使得乘法算式的结果最大．⨯□□□□□□ 「分析」要使得乘积最大，百位应当填哪两个数？十位呢？个位呢？练习4请将1、2、3、4、5、6、7、8这八个数填入下面的方格中，使得乘法算式的结果最大．⨯□□□□□□□□例题5墨爷爷要用长20米的篱笆围成一个靠墙的直角三角形养鸡场，已知靠墙的恰好为三角形斜边，两条直角边长均为整数米，那么怎样围所得的养鸡场面积最大？「分析」长方形篱笆我们已经解决了，三角形的与长方形的有什么联系吗？养鸡场想一想要用篱笆围一个靠墙的三角形，那么锐角三角形、直角三角形、钝角三角形中的哪一种面积会最大呢？在很多问题中，我们都需要先进行整体的思考，再对局部进行一些调整．千万不能“丢了西瓜捡芝麻”！例题6各位数字互不相同的多位数中，数字之和为23的最小数是多少？最大数是多少？「分析」两个多位数比较大小，首先要比较它们的位数．如果位数相同，还要从高位到低位依次比较．课堂内外动物之最最大的动物：蓝鲸（平均长30米，重达160吨）最大的路上动物：非洲象（平均重达9吨）最高的路上动物：长颈鹿（平均高5米）嘴巴最大的陆生哺乳动物：河马最聪明的动物：海豚（人除外）最大的鸟类：鸵鸟（平均身高2.5米，最重可达155千克）翅膀最长的鸟类：信天翁（翅展2~3米）嘴巴最大的鸟：巨嘴鸟（最长24厘米，宽9厘米）形体最小的鸟：蜂鸟飞得最高的鸟：天鹅（最高能达17000米）最耐寒的鸟：企鹅路上奔跑速度最快的动物：猎豹（可高达时速130公里）速度最快的海洋动物：旗鱼（可高达时速190公里）飞行速度最快的动物：军舰鸟（可高达时速418公里）现存最古老的生物：舌形贝（有4.5亿年历史）牙齿最多的动物：蜗牛（共有25600颗牙齿）飞行能力最强的昆虫：蝗虫（每天能够连续飞行近10小时）力气最大的昆虫：屎壳郎（可以支撑或拖走相当于自己体重1141倍的物体）外形最奇特的鱼：海马最大的两栖动物：大鲵（即娃娃鱼）毒性最强的蛇：海蛇（其毒性为眼镜蛇的2倍）寿命最长的动物：海葵（已发现最年长的海葵有2000多岁了）冬眠时间最长的动物：睡鼠（冬眠时间5~6个月）作业1.在六位数129854的某一位数字前面再插入一个同样的数字（例如：可以在2的前面插入2得到1229854），能得到的最小七位数是多少？2.两个自然数之和等于10，那么它们的乘积最大是多少？3.用20根长1厘米的火柴棒围成一个长方形，这个长方形的面积最大是多少平方厘米？4.请将3，4，5，6，7，8这六个数分别填入算式□□□□□□的方格中，使这个乘法算式的结果最大．5.各位数字互不相同的多位数中，数字之和为32的最小数是多少，最大数是多少？第二十三讲 最值问题一1. 例题1答案：（1）124435；（2）98766789详解：（1）枚举：112435、122435、124435、124335、124355，最大的六位数是124435；（2）枚举：99876789、98876789、98776789、98766789、98767789、98767889、98767899，最小的八位数是98766789．2. 例题2答案：20场详解：如果是（1，8），那么共188⨯=场；如果是（2，7），那么共2714⨯=场；如果是（3，6），那么共3618⨯=场；如果是（4，5），那么共4520⨯=场；所以一共最多有20场比赛．3. 例题3答案：长、宽 都为5米时，面积最大为25平方米详解：长方形周长是20米，长、宽之和为10，是固定不变的；长方形面积为长、宽之积，根据“和同近积大”，可知长、宽越接近，面积越大； 当长、宽相等，即篱笆为正方形时，面积最大，最大面积为5525⨯=平方米．4. 例题4答案：631542⨯详解：要使得乘积最大，那么就要百位上的数字最大、个位上的数字最小；所以百位填5、6，十位填3、4，个位填1、2；在这个前提下，无论怎么填，最后两个三位数的和都固定等于5006003040121173+++++=，所以要想让它们的乘积最大，就要让这两个三位数差最小，尝试可得是631542⨯．5. 例题5答案：两条直角边都为10米时，面积最大为50平方米详解：设两条直角边分别为A 、B ，则20+=A B 米；直角三角形面积为“2⨯÷底高”，即面积大小是由“⨯A B ”决定的；A 、B 之和为20米，越接近则乘积越大，所以当10==A B 米时， “⨯A B ”有最大值； 所以，三角形面积最大为1010250⨯÷=平方米．6. 例题6答案：689；8543210详解：数的大小，首先是要考虑位数，再考虑各个数位上的数的大小．（1）最小：即要位数最少，那么就得要让每个数位上的数字都尽量的大，把23拆开：23986=++，所以最小数为689；（2）最大：即要位数最多，那么就得要让每个数位上的数字都尽量的小，把23拆开：230123458=++++++，所以最大数为8543210．7.练习1答案：441729详解：枚举：441729、411729、417729、417229、417299，最大的六位数为441729．8.练习2答案：12场详解：如果是（1，6），那么共166⨯=场；如果是（2，5），那么共2510⨯=场；如果是（3，4），那么共3412⨯=场；所以一共最多有12场比赛．9.练习3答案：长8米，宽7米时，面积最大为56平方米简答：长、宽和为15米，当长为8米、宽为7米时，长、宽最接近，长、宽乘积最大，最大面积为56平方米．10.练习4答案：76428531⨯简答：要使得乘积最大，那么就要千位上的数字最大、个位上的数字最小；所以千位填7、8，百位填5、6，十位填3、4，个位填1、2；在这个前提下，无论怎么填，最后两个四位数的和都固定等于+++++++=，所以要想让它们的乘积最大，就要让这两个四7000800050060030401216173位数差最小，尝试可得是76428531⨯．11.作业1答案：1129854简答：在原数某一位前面插入相同数一共可以得到1129854、1229854、1299854、1298854、1298554、1298544这些数，对比可知1129854最小．12.作业2答案：25简答：两个数的和为10，根据“和同近积大”的原则，当两个数都为5时乘积最大，为25．13.作业3答案：25平方厘米简答：长、宽的和是10厘米，根据“和同近积大”的原则，正方形的时候面积最大，此时边长为5厘米，面积为25平方厘米．14.作业4答案：853764⨯简答：最高位填8和7，十位填6和5，个位填4和3，相差越小乘积越大，所以应为853764⨯．15.作业5答案：26789；98543210简答：3298762=++++，所以最小为26789；3201234589=+++++++，所以最大为98543210．。
七年级数学第九章《不等式(组)-复习训练》知识梳理、考点精讲精练、课堂小测、课后作业第23讲(有答案)
第23讲 不等式（组）－复习训练⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎨⎧⎩⎨⎧⎪⎩⎪⎨⎧⎪⎪⎩⎪⎪⎨⎧与实际问题组一元一次不等式法一元一次不等式组的解不等式组一元一次不等式组性质性质性质不等式的性质一元一次不等式不等式的解集不等式的解不等式不等式相关概念不等式与不等式组)(3211、用“＜”或“＞”号表示大小关系的式子叫做不等式。
2、不等式的符号统称不等号，有“＞” “＜” “≠”. 其中“≤” “≥”,也是不等号.其中，“≤”表示，不大于、不超过，“≥”表示不小于、不低于。
3、使不等式成立的未知数的值叫做不等式的解。
4、一个含有未知数的不等式的所有的解，组成这个不等式的解集。
5、解与解集的关系：不等式的解集包括不等式全体的解；解集中的任何一个数都是不等式的解。
6、用数轴表示解集：在数轴上标出某一区间，其中的点对应的数值都是不等式的解。
①方向线向左表示小于，方向线向右表示大于；②空心圆圈表示不包括； ③实心圆圈表示包括。
7、用数轴表示解集的步骤：①画数轴；②找点；③定向；④画线。
8、求不等式的解集的过程叫做解不等式。
9、含有一个未知数，未知数的次数是1的不等式，叫做一元一次不等式。
1、不等式的性质1 不等式两边同时加（或减）同一个数（或式子），不等号的方向不变。
如果a ＞b ，那么a±c ＞b±c 。
不等式的性质2 不等式两边同乘（或除以）同一个正数，不等号的方向不变。
如果a ＞b,c ＞0,那么ac ＞bc （或c a ＞cb ）。
不等式的性质3 不等式两边同乘（或除以）同一个负数，不等号的方向改。
如果a＞b,c ＜0,那么ac ＜bc （或c a ＜cb ）。
2、解未知数为x 的不等式，就是要使不等式逐步化为x ＞a 或x ＜a 的形式。
3、解不等式时也可以“移项”，即把不等式一边的某项变号后移到另一边，而不改变不等号的方向。
4、解不等式时要注意未知数系数的正负，以决定是否改变不等号的方向。
--四年级第二十三讲-最值问题一教师版
第23讲最值问题一内容概述求最大值与最小值的问题，解题时宜首先考虑起主要作用的量，有时还需要局部调整或者枚举各种可能情形．和为定值的两数的乘积随着两数之差的增大而减小．典型问题兴趣篇1．3个连续奇数相乘，所得乘积的个位数字最小可能是多少? 答案：3分析：乘积的个位数字是由这三个奇数的个位数字决定的。
个位数字可能是：1、3、5、7、9。
通过试验个位是7、9、1的三个连续奇数相乘满足条件，7×9×1=63个位最小是3.2. 用1、2、4可以组成6个没有重复数字的三位数，这些三位数中相差最小的两个数之差是多少?答案：9分析：要使两个数差最小百位数字相同十位与个位数字相近。
满足条件的是412和421.差是421-412=9.3. 用24根长l厘米的火柴棒围成一个矩形，这个矩形的面积最大是多少?如果用22根火柴棒呢?答案：36平方厘米；30平方厘米。
分析：（1）矩形的周长是24厘米。
长和宽的和：24÷2=12（厘米）和为定值的两数的乘积随两数之差的增大而减少。
和是12的两数差为0是积最大。
这两个数相等都是6.即长和宽相等面积是6×6=36（平方厘米）。
（2）周长是22厘米。
长和宽的和是22÷2=11（厘米）和是11差是0时，这样的两个数不是整数。
差是1时两数分别为6和5.积是30.4．三个自然数的和是19，它们的乘积最大可能是多少?答案：252分析：和一定差越小积越大。
19÷3=6……1，6+6+6=18再加1得19，三个数分别是6、6、7时积最大。
最大是6×6×7=252. 5．(1)请将l、2、3、4填人算式“口口×口口”的方格中．要使得算式结果最大，应该怎么填?(2)请将1、2、3、4、5、6填人算式“口口口×口口口”的方格中．要求5、6分别填在百位，4、3分别填在十位，1、2分别填在个位，并使得算式结果最大．应该怎么填?答案：（1）41×32 （2）542×631分析：（1）要使积最大，两个数应尽量大所以4、3分别在十位，1、2在个位。
初中数学竞赛辅导讲义及习题解答 第23讲 圆与圆
第二十三讲圆与圆圆与圆的位置关系有外离、外切、相交、内切、内含五种情形，判定两圆的位置关系有文档设计者：设计时间：文档类型：文库精品文档，欢迎下载使用。
Word精品文档，可以编辑修改，放心下载如下三种方法：1．通过两圆交点的个数确定；2．通过两圆的半径与圆心距的大小量化确定；3．通过两圆的公切线的条数确定．为了沟通两圆，常常添加与两圆都有联系的一些线段，如公共弦、共切线、连心线，以及两圆公共部分相关的角和线段，这是解圆与圆位置关系问题的常用辅助线．熟悉以下基本图形、基本结论：【例题求解】【例1】如图，⊙O l与半径为4的⊙O2内切于点A，⊙O l经过圆心O2，作⊙O2的直径BC 交⊙O l于点D，EF为过点A的公切线，若O2D=22，那么∠BAF= 度．思路点拨直径、公切线、O2的特殊位置等，隐含丰富的信息，而连O2O l必过A点，先求出∠D O2A的度数．注：(1)两圆相切或相交时，公切线或公共弦是重要的类似于“桥梁”的辅助线，它可以使弦切角与圆周角、圆内接四边形的内角与外角得以沟通．同时，又是生成圆幂定理的重要因素．(2)涉及两圆位置关系的计算题，常作半径、连心线，结合切线性质等构造直角三角形，将分散的条件集中，通过解直角三角形求解．【例2】如图，⊙O l与⊙O2外切于点A，两圆的一条外公切线与⊙O1相切于点B，若AB 与两圆的另一条外公切线平行，则⊙O l 与⊙O2的半径之比为( )A．2：5 B．1：2 C．1：3 D．2：3思路点拨添加辅助线，要探求两半径之间的关系，必须求出∠CO l O2 (或∠DO2O l)的度数，为此需寻求∠CO1B、∠CO1A、∠BO1A的关系．【例3】如图，已知⊙O l与⊙O2相交于A、B两点，P是⊙O l上一点，PB的延长线交⊙O2于点C，PA交⊙O2于点D，CD的延长线交⊙O l于点N．(1)过点A作AE∥CN交⊙O l l于点E，求证：PA=PE；(2)连结PN，若PB=4，BC=2，求PN的长．思路点拨(1)连AB，充分运用与圆相关的角，证明∠PAE=∠PEA；(2)PB·PC=PD·PA，探寻PN、PD、PA对应三角形的联系．【例4】如图，两个同心圆的圆心是O，AB是大圆的直径，大圆的弦与小圆相切于点D，连结OD并延长交大圆于点E，连结BE交AC于点F，已知AC=24，大、小两圆半径差为2．(1)求大圆半径长；(2)求线段BF的长；(3)求证：EC与过B、F、C三点的圆相切．思路点拨(1)设大圆半径为R，则小圆半径为R-2，建立R的方程；(2)证明△EBC∽△ECF；(3)过B、F、C三点的圆的圆心O′，必在BF上，连OˊC，证明∠O′CE=90°．注：本例以同心圆为背景，综合了垂径定理、直径所对的圆周角为直角、切线的判定、勾股定理、相似三角形等丰富的知识．作出圆中基本辅助线、运用与圆相关的角是解本例的关键．【例5】 如图，AOB 是半径为1的单位圆的四分之一，半圆O 1的圆心O 1在OA 上，并与弧AB 内切于点A ，半圆O 2的圆心O 2在OB 上，并与弧AB 内切于点B ，半圆O 1与半圆O 2相切，设两半圆的半径之和为x ，面积之和为y ． (1)试建立以x 为自变量的函数y 的解析式； (2)求函数y 的最小值．思路点拨 设两圆半径分别为R 、r ，对于(1)，)(2122r R y +=π，通过变形把R 2+r 2用“x =R+r ”的代数式表示，作出基本辅助线；对于(2)，因x =R+r ，故是在约束条件下求y 的最小值，解题的关键是求出R+r 的取值范围．注：如图，半径分别为r 、R 的⊙O l 、⊙O 2外切于C ，AB ，CM 分别为两圆的公切线，O l O 2与AB 交于P 点，则： (1)AB=2r R ；(2) ∠ACB=∠O l M O 2=90°； (3)PC 2=PA ·PB ； (4)sinP=rR rR +-； (5)设C 到AB 的距离为d ，则dR r 211=+．学力训练1．已知：⊙O l 和⊙O 2交于A 、B 两点，且⊙O l 经过点O 2，若∠AO l B=90°，则∠A O 2B 的度数是 ．2．矩形ABCD 中，AB=5，BC=12，如果分别以A 、C 为圆心的两圆相切，点D 在圆C 内，点B 在圆C 外，那么圆A 的半径r 的取值范围 ． (2003年上海市中考题)3．如图；⊙O l 、⊙O 2相交于点A 、B ，现给出4个命题：(1)若AC 是⊙O 2的切线且交⊙O l 于点C ，AD 是⊙O l 的切线且交⊙O 2于点D ，则AB 2=BC ·BD ；(2)连结AB 、O l O 2，若O l A=15cm ，O 2A=20cm ，AB=24cm ，则O l O 2=25cm ；(3)若CA 是⊙O l 的直径，DA 是⊙O 2 的一条非直径的弦，且点D 、B 不重合，则C 、B 、D 三点不在同一条直线上，(4)若过点A 作⊙O l 的切线交⊙O 2于点D ，直线DB 交⊙O l 于点C ，直线CA 交⊙O 2于点E ，连结DE ，则DE 2=DB ·DC ，则正确命题的序号是 (写出所有正确命题的序号) ．4．如图，半圆O 的直径AB=4，与半圆O 内切的动圆O l 与AB 切于点M ，设⊙O l 的半径为y ，AM 的长为x ，则y 与x 的函数关系是 ，自变量x 的取值范围是 ．5．如图，施工工地的水平地面上，有三根外径都是1米的水泥管两两相切摞在一起，则其最高点到地面的距离是( )A ．2B ．221+C ．231+D ．231+ 6．如图，已知⊙O l 、⊙O 2相交于A 、B 两点，且点O l 在⊙O 2上，过A 作⊙O l l 的切线AC交B O l 的延长线于点P ，交⊙O 2于点C ，BP 交⊙O l 于点D ，若PD=1，PA=5，则AC 的长为( )A ．5B ．52C ．52+D ．537．如图，⊙O l 和⊙O 2外切于A ，PA 是内公切线，BC 是外公切线，B 、C 是切点①PB=AB ；②∠PBA=∠PAB ；③△PAB ∽△O l AB ；④PB ·PC=O l A ·O 2A ． 上述结论，正确结论的个数是( )A ．1B ．2C ．3D ．48．两圆的半径分别是和r (R>r)，圆心距为d ，若关于x 的方程0)(222=-+-d R rx x 有两个相等的实数根，则两圆的位置关系是( )A．一定内切B．一定外切C．相交D．内切或外切9．如图，⊙O l和⊙O2内切于点P，过点P的直线交⊙O l于点D，交⊙O2于点E，DA与⊙O2相切，切点为C．（1）求证：PC平分∠APD；(2)求证：PD·PA=PC2+AC·DC；(3)若PE=3，PA=6，求PC的长．10．如图，已知⊙O l和⊙O2外切于A，BC是⊙O l和⊙O2的公切线，切点为B、C，连结BA并延长交⊙O l于D，过D点作CB的平行线交⊙O2于E、F，求证：(1)CD是⊙O l的直径；(2)试判断线段BC、BE、BF的大小关系，并证明你的结论．11．如图，已知A是⊙O l、⊙O2的一个交点，点M是O l O2的中点，过点A的直线BC垂直于MA，分别交⊙O l、⊙O2于B、C．(1)求证：AB=AC；(2)若O l A切⊙O2于点A，弦AB、AC的弦心距分别为d l、d2，求证：d l+d2=O1O2；(3)在(2)的条件下，若d l d2=1，设⊙O l、⊙O2的半径分别为R、r，求证：R2+r2= R2r2．12．已知半径分别为1和2的两个圆外切于点P，则点P到两圆外公切线的距离为．13．如图，7根圆形筷子的横截面圆半径为r，则捆扎这7根筷子一周的绳子的长度为．14．如图，⊙O l和⊙O2内切于点P，⊙O2的弦AB经过⊙O l的圆心O l，交⊙O l于C、D，若AC：CD：DB=3：4：2，则⊙O l与⊙O2的直径之比为( )A．2：7 B．2：5 C．2：3 D．1：315．如图，⊙O l与⊙O2相交，P是⊙O l上的一点，过P点作两圆的切线，则切线的条数可能是( )A．1，2 B．1，3 C．1，2，3 D．1，2，3，416．如图，相等两圆交于A、B两点，过B任作一直线交两圆于M、N，过M、N各引所在圆的切线相交于C，则四边形AMCN有下面关系成立( )A．有内切圆无外接圆B有外接圆无内切圆C．既有内切圆，也有外接圆D．以上情况都不对17．已知：如图，⊙O与相交于A，B两点，点P在⊙O上，⊙O的弦AC切⊙P于点A，CP及其延长线交⊙P P于点D，E，过点E作EF⊥CE交CB的延长线于F．（1）求证：BC是⊙P的切线；(2)若CD=2，CB=22，求EF的长；(3)若k=PE：CE，是否存在实数k，使△PBD恰好是等边三角形?若存在，求出是的值；若不存在，请说明理由．18．如图，⊙A和⊙B是外离两圆，⊙A的半径长为2，⊙B的半径长为1，AB=4，P为连接两圆圆心的线段AB上的一点，PC切⊙A于点C，PD切⊙B于点D．(1)若PC=PD，求PB的长；(2)试问线段AB上是否存在一点P，使PC2+PD2=4？，如果存在，问这样的P点有几个?并求出PB的值；如果不存在，说明理由；(3)当点F在线段AB上运动到某处，使PC⊥PD时，就有△APC∽△PBD．请问：除上述情况外，当点P在线段AB上运动到何处(说明PB的长为多少，或PC、PD 具有何种关系)时，这两个三角形仍相似；并判断此时直线CP与OB的位置关系，证明你的结论．19．如图，D、E是△ABC边BC上的两点，F是BA延长线上一点，∠DAE=∠CAF．(1)判断△ABD的外接圆与△AEC的外接圆的位置关系，并证明你的结论；(2)若△ABD的外接圆半径是△AEC的外接圆半径的2倍，BC=6，AB=4，求BE的长．20．问题：要将一块直径为2cm的半圆形铁皮加工成一个圆柱的两个底面和一个圆锥的底面．操作：方案一：在图甲中，设计一个使圆锥底面最大，半圆形铁皮得以最充分利用的方案(要求，画示意图) ．方案二；在图乙中，设计一个使圆柱两个底面最大，半圆形铁皮得以最充分利用的方案(要求：画示意图)；，探究：(1)求方案一中圆锥底面的半径；(2)求方案二中圆锥底面及圆柱底面的半径；(3)设方案二中半圆圆心为O，圆柱两个底面的圆心为O1、O2，圆锥底面的圆心为O3，试判断以O1、O2、O3、O为顶点的四边形是什么样的特殊四边形，并加以证明．参考答案温馨提示After writing the test paper, you must remember to check Oh, I wish you all can achieve good results!可以编辑的试卷（可以删除）。
第23讲 三角不等式
第23讲 三角不等式竞赛热点含有未知数的三角函数的不等式叫做三角不等式。
在高中数学竞赛内容中，涉及三角不等式的问题有三类：一是三角不等式的证明，二是解三角不等式，三是应用三角不等式求最值。
处理三角不等式的问题一方面要有扎实的三角变形能力，另一方面还需要有三角函数的图象和性质的认识。
同时，对不等式的有关性质和证明方法要能灵活运用。
解题示范例1：已知N n ∈，2≥n ，求证：.321cos31cos21cos>n思路分析：本题从三角变形入手不易，不可考虑利用x x <sin 放缩，转化为代数不等式。
证明：因为.121311110<<<<-<< n n所以.11sin 0kk<<又.)1)(1(111sin 11cos2222k k k kkk+-=->-= 所以)11()3432)(2321()1cos31cos 21(cos2nn nn n +∙-∙∙>.)32(2121)1453423)(1433221(2>>+=+∙∙-∙∙=nn nn nn即.321cos31cos21cos>n点评：此题应用三角函数中重要的不等式：若)2,0(π∈x ，则.tan sin x x x <<此结论的应用，将三角不等式转化为代数不等式，叠乘即证得。
例2：当],0[,,321n ∈ααα时，求证：.3sin 3sin sin sin 321321αααααα++≤++思路分析；利用和差化积公式和变为乘积的形式，再放缩证明。
证明：因为3sinsin sin sin 321321αααααα+++++62cos64sin22cos2sin23213212121αααααααααα-++++-+=3sin462cos3sin 464sin22sin 232132132132121αααααααααααααα++≤-+++=++++≤所以.3sin3sin sin sin 321321αααααα++≤++引申：此证明中利用1cos ≤α进行放缩，从证明过程中可以看出，等号当且仅当321ααα==时成立。
最新小学五年级奥数全册讲义(1-30讲)(含详解)【值得拥有】
小学五年级奥数全册讲义第1讲数字迷(一)第2讲数字谜(二)第3讲定义新运算(一)第4讲定义新运算(二)第5讲数的整除性(一)第6讲数的整除性(二)第7讲奇偶性（一）第8讲奇偶性（二）第9讲奇偶性（三）第10讲质数与合数第11讲分解质因数第12讲最大公约数与最小公倍数（一）第13讲最大公约数与最小公倍数（二）第14讲余数问题第15讲孙子问题与逐步约束法第16讲巧算24第17讲位置原则第18讲最大最小第19讲图形的分割与拼接第20讲多边形的面积第21讲用等量代换求面积第22 用割补法求面积第23讲列方程解应用题第24讲行程问题（一）第25讲行程问题（二）第26讲行程问题（三）第27讲逻辑问题（一）第28讲逻辑问题（二）第29讲抽屉原理(一)第30讲抽屉原理(二)第1讲数字谜（一）数字谜的内容在三年级和四年级都讲过，同学们已经掌握了不少方法。
例如用猜想、拼凑、排除、枚举等方法解题。
数字谜涉及的知识多，思考性强，所以很能锻炼我们的思维。
这两讲除了复习巩固学过的知识外，还要讲述数字谜的代数解法及小数的除法竖式问题。
例1 把+，-，×，÷四个运算符号，分别填入下面等式的○内，使等式成立（每个运算符号只准使用一次）：（5○13○7）○（17○9）=12。
分析与解：因为运算结果是整数，在四则运算中只有除法运算可能出现分数，所以应首先确定“÷”的位置。
当“÷”在第一个○内时，因为除数是13，要想得到整数，只有第二个括号内是13的倍数，此时只有下面一种填法，不合题意。
（5÷13-7）×（17+9）。
当“÷”在第二或第四个○内时，运算结果不可能是整数。
当“÷”在第三个○内时，可得下面的填法：（5+13×7）÷（17-9）=12。
例2 将1～9这九个数字分别填入下式中的□中，使等式成立：□□□×□□=□□×□□=5568。
第23讲_最值问题一
第二十三讲最值问题一最值问题，即求最大值、最小值的问题．这类问题中，有时满足题目条件的情况并不多，这时我们就可以用枚举法将所有可能情况一一列出，再比较大小．例题1（1）在五位数12435的某一位数字后面插入一个同样的数字可以得到一个六位数（例如：在2的后面插入2可以得到122435）．请问：能得到的最大六位数是多少？（2）在七位数9876789的某一位数字后面再插入一个同样的数字．请问：能得到的最小八位数是多少？「分析」一共有多少种不同的插入数字的方法？你能将它们全部枚举出来吗？练习1在五位数41729的某一位数字前面插入一个同样的数字（例如：在7的前面插入7得到417729），能得到的最大六位数是多少？直接枚举的优点是不用过多思考，大家都能理直气壮地说，直接比较大小得到的答案一定是正确的．事实上，我们应该多想一想，为什么这个答案是最大或最小的，有没有什么道理，其中有没有什么规律．例题2.有9个同学要进行象棋比赛．他们准备分成两组，不同组的任意两人之间都进行一场比赛，同组的人不比赛，那么一共最多有多少场比赛？「分析」把9个同学分成两组，有多少种情况呢？你能算出这些分法各自对应的比赛场数吗？练习2有7个同学要进行乒乓球单打比赛．他们准备分成两组，不同组的任意两人之间都进行一场比赛，同组的人不比赛，那么一共最多有多少场比赛？从例题2我们可以得出：两个数的和相等，当它们越接近时（也就是它们的差越小时），．“和同近积大”的应用非常广泛，接下来我们分析一下比较典型的“篱笆问题”．例题3墨爷爷要用长20米的篱笆围成一个长方形养鸡场，已知长和宽均为整数米，那么怎样围所得的养鸡场面积最大？（正方形是特殊的长方形）「分析」长方形面积是长、宽的乘积，要想长、宽乘积最大，可以不可以应用“和同近积大”的道理来解决呢？能找到“和同”吗？练习3墨爷爷要用长30米的篱笆围成一个长方形养鸡场，已知长和宽均为整数米，那么怎样围所得的养鸡场面积最大？例题4请将1、2、3、4、5、6这六个数填入下面的方格中，使得乘法算式的结果最大．「分析」要使得乘积最大，百位应当填哪两个数？十位呢？个位呢？⨯□□□□□□练习4.请将1、2、3、4、5、6、7、8这八个数填入下面的方格中，使得乘法算式的结果最大．⨯□□□□□□□□例题5. 墨爷爷要用长20米的篱笆围成一个靠墙的直角三角形养鸡场，已知靠墙的恰好为三角形斜边，两条直角边长均为整数米，那么怎样围所得的养鸡场面积最大？「分析」长方形篱笆我们已经解决了，三角形的与长方形的有什么联系吗？养鸡场在很多问题中，我们都需要先进行整体的思考，再对局部进行一些调整．千万不能“丢了西瓜捡芝麻”！例题6各位数字互不相同的多位数中，数字之和为23的最小数是多少？最大数是多少？「分析」两个多位数比较大小，首先要比较它们的位数．如果位数相同，还要从高位到低位依次比较．动物之最最大的动物：蓝鲸（平均长30米，重达160吨）最大的路上动物：非洲象（平均重达9吨）最高的路上动物：长颈鹿（平均高5米）嘴巴最大的陆生哺乳动物：河马最聪明的动物：海豚（人除外）最大的鸟类：鸵鸟（平均身高2.5米，最重可达155千克）翅膀最长的鸟类：信天翁（翅展2~3米）嘴巴最大的鸟：巨嘴鸟（最长24厘米，宽9厘米）形体最小的鸟：蜂鸟飞得最高的鸟：天鹅（最高能达17000米）最耐寒的鸟：企鹅路上奔跑速度最快的动物：猎豹（可高达时速130公里）速度最快的海洋动物：旗鱼（可高达时速190公里）飞行速度最快的动物：军舰鸟（可高达时速418公里）现存最古老的生物：舌形贝（有4.5亿年历史）牙齿最多的动物：蜗牛（共有25600颗牙齿）飞行能力最强的昆虫：蝗虫（每天能够连续飞行近10小时）力气最大的昆虫：屎壳郎（可以支撑或拖走相当于自己体重1141倍的物体）外形最奇特的鱼：海马最大的两栖动物：大鲵（即娃娃鱼）毒性最强的蛇：海蛇（其毒性为眼镜蛇的2倍）寿命最长的动物：海葵（已发现最年长的海葵有2000多岁了）冬眠时间最长的动物：睡鼠（冬眠时间5~6个月）作业1.在六位数129854的某一位数字前面再插入一个同样的数字（例如：可以在2的前面插入2得到1229854），能得到的最小七位数是多少？2.两个自然数之和等于10，那么它们的乘积最大是多少？3.用20根长1厘米的火柴棒围成一个长方形，这个长方形的面积最大是多少平方厘米？4.请将3，4，5，6，7，8这六个数分别填入下面的算式中，使这个乘法算式的结果最大．□□□□□□5.各位数字互不相同的多位数中，数字之和为32的最小数是多少，最大数是多少？。
2025年湖南中考数学一轮复习考点研析 第五章 四边形第23讲 多边形
(－3)
n边形共有__________条对角线.
2
(4)稳定性:三角形具有稳定性,四边形不具有稳定性
类别
内容
(1)定义:在平面内,边相等、角也都相等的多边形叫作正多边形.
(－2)·180°
(2)内角:正n(n≥3)边形每个内角的度数为_____________.
正多边
360°
形 (3)外角:正n(n≥3)边形每个外角的度数为_______.
( C )
A.15°B.20°C.25°D.30°
变式2－2
如果梯形中位线的长为4,其中一条底边长为2,一条腰长为6,那
2＜x＜10
么另外一条腰长x的取值范围是________________.
答案
1.在学习完多边形后,小华同学将一个五边形沿如图所示的直线l剪掉一个
角后,得到一个多边形,下列说法正确的是( C )
形”.如果一个“余角梯形”的较短底边的长为5,两腰长分别是3和4,那么它的
15
2
中位线的长是____.
答案
2025年湖南中考数学一轮复习考点研析
第一部分 考点研析
第五章 四边形
第23讲 多边形
考点1
类别
多边形
内容
(n－2)·180°
(1)内角和:n(n≥3)边形的内角和等于_____________________.
(2)外角和:任意多边形的外角和等于____________.
360°
多边形
(3)对角线:过n边形的一个顶点可以引______________条对角线,
A.这个多边形是一个五边形
B.从这个多边形的顶点A出发,最多可以画4条对角线
C.从顶点A出发的所有对角线将这个多边形分成4个三角形
第6模块 解析几何 (第23讲)抛物线的性质及应用
第23节 抛物线焦点弦的性质及应用一、能力素养 (一)核心知识1．与焦点弦有关的性质（1）通径长为2p （最短的焦点弦）（2） 如图，AB 是抛物线y 2＝2px (p ＞0)过焦点F 的一条弦，设A (x 1，y 1)，B (x 2，y 2)． ①1212,,22p pAF x BF x AB x x p =+=+=++； ②221212,4p y y p x x =-=； ③12124OA OB y yk k x x ⋅==- ；④22,,1cos 1cos sin p p pAF BF AB θθθ===-+. (θ为AB 的倾斜角)． ⑤112AF BF p+=. ⑥焦点弦端点与顶点构成的三角形面积：S △AOB ＝p 22sin θ＝12|AB ||d |＝12|OF |·|y 1－y 2|.⑦以AB 为直径的圆与准线相切． ︒=∠⇒901B AM ⑧以AF 或BF 为直径的圆与y 轴相切．⑨过焦点弦的端点的切线互相垂直且交点在准线上．⑩过准线上任意一点向抛物线所作的两条切线互相垂直，且两切点连线必过焦点。
2．抛物线x 2＝2py (p >0)的切线方程和切点弦方程①过抛物线x 2＝2py (p >0)上一点（x 0,y 0）的切线方程: x 0x=p(y+ y 0) ②过抛物线x 2＝2py (p >0)外一点（x 0,y 0）的切点弦方程: x 0x=p(y+ y 0) （二）答题套路：(1)利用抛物线的定义解决问题，应灵活地进行抛物线上的点到焦点的距离与到准线距离的等价转化．即“看到准线想到焦点，看到焦点想到准线”．(2)直线与抛物线的位置关系和直线与椭圆、双曲线的位置关系类似，一般要用到根与系数的关系．(3)有关直线与抛物线的弦长问题，要注意直线是否过抛物线的焦点，若过抛物线的焦点，可直接使用公式|AB |＝|x 1|＋|x 2|＋p ，若不过焦点，则必须用一般弦长公式． （三）微点提醒：(1)注意灵活运用抛物线上一点P (x ，y )到焦点F 的距离|PF |＝|x |＋p 2或|PF |＝|y |＋p2.(2)涉及抛物线的弦长、中点、距离等相关问题时，一般利用根与系数的关系采用“设而不求”“整体代入”等解法．涉及弦的中点、斜率时，一般用“点差法”求解． (3)注意发现试题中隐藏的几何特征（平几应用，定义解题）。
第23讲最值问题-完整版
第23讲最值问题-完整版第23讲最值问题⼀内容概述求最⼤值与最⼩值的问题，解题时宜⾸先考虑起主要作⽤的量，有时还需要局部调整或者枚举各种可能情形。
和为定值的两数的乘积随着两数之差的增⼤⽽减少。
典型例题兴趣篇1． 3个连续奇数相乘，所得乘积的个位数字最⼩可能是多少？答案：3解析：3个连续奇数相乘，乘积的个位数字只有5种可能：①这3个奇数的个位数字分别为1、3、5时，乘积的个位数字为5．②这⼀3个奇数的个位数字分别为3、5、7时，乘积的个位数字为5．③这3个奇数的个位数字分别为5、7、9时，乘积的个位数字为5．④这3个奇数的个位数字分别为7、9、l时，乘积的个位数字为3．⑤这3个奇数的个位数字分别为9、1、3时，乘积的个位数字为7．因此，乘积的个位数字最⼩等于3．2．⽤1、2、4可以组成6个没有重复数字的三位数，这些三位数中相差最⼩的两个数之差是多少？答案：9解析：将这6个数按从⼤到⼩的顺序写出：421、412、241、214、11 2、1 2计算所有相邻两数的差：421-412=9,412-241=l7l, 241-214=27.214-142=72. 142-124=18.其中差最⼩的两个数是421与412，它们相差9．3．阿呆和阿⽠两⼈⼿⾥各拿着⼀张扑克牌，两⼈牌的点数之和刚好是10．请问两⼈牌的点数的乘积最⼤可能是多少？答案：25解析：两⼈牌的点数之和为10，那么两⼈牌的点数只能是1和9，2和8，3和7，4和6，5和5．它们乘积分别为9，16，21，24，25．所以两⼈牌的点教的乘积最⼤可能是25．4． 3个⾃然数的和是19，它们的乘积最⼤可能是多少？答案：252解析：3个数的乘积最⼤时．应该是它们每2个数的差都最⼩的时候．所以3个数的乘积最⼤⼨，每2个数的差都等于O或1．它们的和等于19，19÷3=6……l，则这3个数是6、6、7时其乘积最⼤．所以乘积最⼤等于6×6×7=252．5． (1)请将1～4这4个数分别填⼈算式“⼝⼝×⼝⼝”的⼝中，要使得算式结果最⼤，应该怎么填？(2)请将1～6这6个数分别填⼊算式“⼝⼝⼝×⼝⼝⼝”的[中，要求5、6分别填在百位，4、3分别填在⼗位，1、2分别填在个位，并使得算式结果最⼤．应该怎么填？答案：(1) 41×32 (2) 631×542解析：(1)要使乘积最⼤，⾸位应当尽可能⼤，4、3填在⼗位上，这样1、2就填在个位上，此时这两个数的和固定，要使乘积最⼤，只要差最⼩即可．因此，乘积最⼤时应该是41×32．(2)因百位的两个数固定了，那么百位之和就固定了．同样个位、⼗位的和也固定了，所以这两个三位数的和⼀定，此时要使它们的乘积最⼤，只需使它们的差最⼩，因此6的后两位数应该尽量⼩，5的后两位数应该尽量⼤．那么这两个数就应该是631和042，即乘积最⼤时是631×542．6．在图23-1的中间O内填⼀个数，计算每⼀条线段两端的数之差（⼤减⼩），然后把这3个差数相加．那么所得的和最⼩是多少？答案：7解析：⽅法⼀：在中间的○内填上0，则3个差数分别是3、7、10，因此差数之和等于3+7+10=20．将0换成1，则3个差数都减1，则差数之和减3，等于20-3=17.同理，将1换成2后，差数之和等于17-3=14．将2换成3．差数之和等于l4-3=ll.将3换成4时．此时其中2个仍然是减1．有⼀个差数却由0变成了l，是加1，因此差数之和减1，等于11—1=10.同理，从4到7之间变化时，中间填的数每次加1，差数之和就减1，因此中间填7时，差数之和⽐填1到6都要⼩．将7换成8时，2个差数都加1，⼀个差数减1，因⽐差数之和加1．同样，将8换成9，9换成10，差数之和都加l.将10换成11， 11换成12，我们可以发现，以后中间的数每次加1，差数之和都会增加3.综上所述，中间填的数由1变到7时，差数之和选来越⼩；中间填的数由7变⼤时，差数之和越来越⼤．因此中问填7时，差数之和取到最⼩值，等于(7-3)+(7-7)+(10-7)=7⽅法⼆：①如果中间填的数是1～3，则每⼀线段两端的两数作差，都是⽤给出的数减去这个填的数，因此填的数越⼤，这3个差越⼩．所以这种情况下填3差数之和最⼩．②如果中间填的数是4～7，则这3个差中，⼀个⼰⽤这个数减去3．⼀个是⽤1O减去这个数，这2个差加起来就是10-3=7．还剩下⼀个差是7减去这个数，显然这个数等于7时，剩下的差数取到最⼩值．因此差数之和最⼩等于l．③如果中间填的数是7～10，则这3个差中，仍然⼀个是⽤这个数减去3，⼀个是⽤10减去这个数，这2个差加起来还是7．还剩下⼀个差是7减去汶个数，因此仍然是这个数等于7时，差数之和最⼩．④如果中间填的数⼤于等于10，则这3个差分别是⽤填的数减去3、7、10．显然这个数越⼩越好，因此当填10时，差数之和最⼩．综上所述，中间填1～3时，填3差数之和最⼩；填3～10时，填7差数之和最⼩；填10或⽐它⼤的势时，填10差数之和最⼩．因此当O内填7时，差数之和取到最⼩值7．7．在所有包含3个相同数码的四位数中，与1389之差（⼤减⼩）最⼩的⼀个是多少？答案：1411解析：①⾸位显然取1或2，⼜1000与1389更接近所以⾸位等于1．②百位数字应该等于3或4．如果百位是3，由于有3个数字相同，则这个四位数只能是1311或1333，其中1333与1389更接近，刖时它们的差等于1389 -1333=56．如果百位是4，则这个四位数只能是1411或1444，其中1411与1389更接近，此时它们的差等余1411-1389=22．因此有3个数字相同的四位数中，与1389最拒近的四位数为1411.8．把1～6这6个数分别填⼊算式“⼝⼝⼝⼀⼝⼝⼝”的⼝中，要求前⼀个三位数⽐后⼀个三位数⼤. (l)这个减法算式的结果最⼤可能是多少？(2)最⼩可能是多少？答案：(1)最⼤531 (2)最⼩47解析：(1)要使算式的结果最⼤，只要让被减数最⼤，德数最⼩就⾏，所以算式的结果最⼤为654-123=531.(2)要使算式的结果最⼩，就要使被减数尽量⼩减数尽量⼤，但是被减数要⼤于减数，因此应该使在减数⽐减教的⾸位⼤1，还应该使被减数的⼗位和个位组成的两位数尽量⼩，使减数的⼗位和个位组成的两位数尽量⼤．由1、2、3、4、5、6组成的两位数最⼩是12，最⼤是65，我们希望被减数为12，减数为65，这样还剩下3、4，取4为被减数的⾸位，3为减数的⾸位，刚好使被减数⽐减数的⾸位⼤1，满⾜我们的要求．因此原来算式的结果最⼩是412-365=47.9．⼀个⾃然数是由数字8、9组成的，它的任意相邻两位都可以看成⼀个两位数，并且这些相邻数字组成的两位数都不相等．请问：满⾜条件的⾃然数最⼤是多少？答案：99 889解析：如果这个⾃然数超过5位，则⾄少有5个相邻数字组成的两位数，⽽8、9最多兵能组成4个不同的两位数88、89、98、99．由简单抽屉原理，⼀定有两个相邻数字组成的两位数相同，这与题⽬条件⽭盾，因此，这个⾃然数最多是五位数．从⾸位开始取，万位取9，千位取9，百位取8. -定要出现88，所以⼗位取8．个位取9．因此满⾜条件的最⼤⾃然数是99 889. 10.如果3个互不相同的⾃然数之和为20，那么其中最⼩的数最⼤可能是多少？最⼤的数最⼩可能是多少？答案：5 8解析：要使最⼩的数最⼤，最⼤的数最⼩，则3个数尽可能接近，20÷3=6……2，⼜3个数互不相同，发现最接近的是5、7、8和0、6、9，所以最⼩的数最⼤是5，最⼤的数最⼩是8．拓展篇1．3个连续⾃然数相乘，所得乘积的个位数字最⼤可能是多少？答案：6解析：如果3个连续⾃然数的个位数字中有⼀个是O，则其乘积个位等于O；如果3个连续⾃然数的个位数字中有⼀个是5，其中必然还有⼀个是4或6，这时，它们乘积的个位也等于0．除此之外，3个连续⾃然数的个位数字还有可能是1、2、3，2、3、4，6、7、8，7、8、9这四种情况．因为1×2×3=6,2×3×4=24,6×7×8=336,7×8×9= 504，所以，3个连续⾃然数的乘积个位数字最⼤是6．2． (1)在五位数12435的某⼀位数字后⾯再插⼊⼀个同样的数字（例如：可以在2的后⾯插⼊2得到122435），这样得到的六位数最⼤可能是多少？(2)在七位数9876789的某⼀位数字后⾯再插⼊⼀个同样的数字，这样得到的⼋位数最⼩是多少？答案：(1) 124435 (2) 98766789解析：(1) 12435按要求插⼊数字，可以分别插在1、2、4、3、5后⾯，得到5个数：112435, 122435. 124435, 124335. 124355.⽐较可知，124435是其中最⼤的数．(2) 9876789按要求插⼊数字，可以分别插在9、8、7、6、7、8、9后⾯，得到7个数：99876789, 98876789, 98776789. 98766789,98767789, 98767889, 98707899.此较可知，98766789是其中最⼩的数．3．⽤24根长1厘⽶的⽕柴棒围成⼀个矩形，(1)这个矩形的⾯积最⼤是多少？(2)如果⽤22根⽕柴棒呢？。
(完整版)高思导引四年级第二十三讲最值问题一教师版
第23讲最值问题一内容概述求最大值与最小值的问题，解题时宜首先考虑起主要作用的量，有时还需要局部调整或者枚举各种可能情形．和为定值的两数的乘积随着两数之差的增大而减小．典型问题兴趣篇1．3个连续奇数相乘，所得乘积的个位数字最小可能是多少? 答案：3分析：乘积的个位数字是由这三个奇数的个位数字决定的。
个位数字可能是：1、3、5、7、9。
通过试验个位是7、9、1的三个连续奇数相乘满足条件，7×9×1=63个位最小是3.2. 用1、2、4可以组成6个没有重复数字的三位数，这些三位数中相差最小的两个数之差是多少?答案：9分析：要使两个数差最小百位数字相同十位与个位数字相近。
满足条件的是412和421.差是421-412=9.3. 用24根长l厘米的火柴棒围成一个矩形，这个矩形的面积最大是多少?如果用22根火柴棒呢?答案：36平方厘米；30平方厘米。
分析：（1）矩形的周长是24厘米。
长和宽的和：24÷2=12（厘米）和为定值的两数的乘积随两数之差的增大而减少。
和是12的两数差为0是积最大。
这两个数相等都是6.即长和宽相等面积是6×6=36（平方厘米）。
（2）周长是22厘米。
长和宽的和是22÷2=11（厘米）和是11差是0时，这样的两个数不是整数。
差是1时两数分别为6和5.积是30.4．三个自然数的和是19，它们的乘积最大可能是多少?答案：252分析：和一定差越小积越大。
19÷3=6……1，6+6+6=18再加1得19，三个数分别是6、6、7时积最大。
最大是6×6×7=252. 5．(1)请将l、2、3、4填人算式“口口×口口”的方格中．要使得算式结果最大，应该怎么填?(2)请将1、2、3、4、5、6填人算式“口口口×口口口”的方格中．要求5、6分别填在百位，4、3分别填在十位，1、2分别填在个位，并使得算式结果最大．应该怎么填?答案：（1）41×32 （2）542×631分析：（1）要使积最大，两个数应尽量大所以4、3分别在十位，1、2在个位。
人教版四年级数学上册【详解】四年级上第23讲_最值问题一
第二十三讲 最值问题一1. 例题1答案：（1）124435；（2）98766789详解：（1）枚举：112435、122435、124435、124335、124355，最大的六位数是124435；（2）枚举：99876789、98876789、98776789、98766789、98767789、98767889、98767899，最小的八位数是98766789．2. 例题2答案：20场详解：如果是（1，8），那么共188⨯=场；如果是（2，7），那么共2714⨯=场；如果是（3，6），那么共3618⨯=场；如果是（4，5），那么共4520⨯=场；所以一共最多有20场比赛．3. 例题3答案：长、宽 都为5米时，面积最大为25平方米详解：长方形周长是20米，长、宽之和为10，是固定不变的；长方形面积为长、宽之积，根据“和同近积大”，可知长、宽越接近，面积越大； 当长、宽相等，即篱笆为正方形时，面积最大，最大面积为5525⨯=平方米．4. 例题4答案：631542⨯详解：要使得乘积最大，那么就要百位上的数字最大、个位上的数字最小；所以百位填5、6，十位填3、4，个位填1、2；在这个前提下，无论怎么填，最后两个三位数的和都固定等于5006003040121173+++++=，所以要想让它们的乘积最大，就要让这两个三位数差最小，尝试可得是631542⨯．5. 例题5答案：两条直角边都为10米时，面积最大为50平方米详解：设两条直角边分别为A 、B ，则20+=A B 米；直角三角形面积为“2⨯÷底高”，即面积大小是由“⨯A B ”决定的；A 、B 之和为20米，越接近则乘积越大，所以当10==A B 米时， “⨯A B ”有最大值； 所以，三角形面积最大为1010250⨯÷=平方米．6. 例题6答案：689；8543210详解：数的大小，首先是要考虑位数，再考虑各个数位上的数的大小．=++，（1）最小：即要位数最少，那么就得要让每个数位上的数字都尽量的大，把23拆开：23986所以最小数为689；（2）最大：即要位数最多，那么就得要让每个数位上的数字都尽量的小，把23拆开：230123458=++++++，所以最大数为8543210．7.练习1答案：441729详解：枚举：441729、411729、417729、417229、417299，最大的六位数为441729．8.练习2答案：12场详解：⨯=场；如果是（1，6），那么共166⨯=场；如果是（2，5），那么共2510⨯=场；如果是（3，4），那么共3412所以一共最多有12场比赛．9.练习3答案：长8米，宽7米时，面积最大为56平方米简答：长、宽和为15米，当长为8米、宽为7米时，长、宽最接近，长、宽乘积最大，最大面积为56平方米．10.练习4⨯答案：76428531简答：要使得乘积最大，那么就要千位上的数字最大、个位上的数字最小；所以千位填7、8，百位填5、6，十位填3、4，个位填1、2；在这个前提下，无论怎么填，最后两个四位数的和都固定等于+++++++=，所以要想让它们的乘积最大，就要让这两个四7000800050060030401216173⨯．位数差最小，尝试可得是7642853111.作业1答案：1129854简答：在原数某一位前面插入相同数一共可以得到1129854、1229854、1299854、1298854、1298554、1298544这些数，对比可知1129854最小．12.作业2答案：25简答：两个数的和为10，根据“和同近积大”的原则，当两个数都为5时乘积最大，为25．13.作业3答案：25平方厘米简答：长、宽的和是10厘米，根据“和同近积大”的原则，正方形的时候面积最大，此时边长为5厘米，面积为25平方厘米．14. 作业4答案：853764⨯简答：最高位填8和7，十位填6和5，个位填4和3，相差越小乘积越大，所以应为853764⨯．15. 作业5答案：26789；98543210简答：3298762=++++，所以最小为26789；3201234589=+++++++，所以最大为98543210．。
第二十三讲计数原理原卷版2023届高考数学二轮复习讲义
第二十三讲：计数原理【考点梳理】1.排列与组合的概念名称定义排列从n 个不同元素中取出m （m n ≤）个元素按照一定的顺序排成一列组合合成一组2.排列问题的解题策略（1）特殊元素优先安排的策略；（2）合理分类与准确分步的策略；（2）正难则反、等价转化的策略；（4）相邻问题捆绑处理的策略；（5）不相邻问题插空处理的策略；（6）定序问题除法处理的策略；3.二项式定理011222()n n n n k n k k n n n n n n n a b C a C a b C a b C a b C b ---+=++++++ ．4.二项展开式的通项公式二项展开式的通项：1r n r r r n T C a b -+=()0,1,2,3,,r n =⋯公式特点：①它表示二项展开式的第1r +项，该项的二项式系数是r n C ；②字母b 的次数和组合数的上标相同；③a 与b 的次数之和为n ．5.二项式系数的性质（1）对称性；（2）增减性与最大值；（3）二项式系数的和【典型题型讲解】考点一：排列、组合【典例例题】例1．（2022·广东中山·高三期末）3男3女六位同学站成一排，则3位女生中有且只有两位女生相邻的不同排法种数是（）A ．576B ．432C ．388D ．216例2．（2022·广东·铁一中学高三期末）高三一班周一上午有四节课，分别安排语文､数学､英语和体育.其中语文不安排在第一节，数学不安排在第二节，英语不安排在第三节，体育不安排在第四节，则不同的课表安排方法共有______种.【方法技巧与总结】排列、组合搞清楚区别【变式训练】1．（2022·广东清远·高三期末）为了做好新冠肺炎疫情常态化防控工作，推进疫苗接种进度，降低新冠肺炎感染风险，某医院准备将3名医生和6名护士分配到3所学校，设立疫苗接种点，免费给学校老师和学生接种新冠疫苗，若每所学校分配1名医生和2名护士，则不同的分配方法共有_______种．2．（2022·广东惠州·一模）现有3名学生报名参加校园文化活动的3个项目，每人须报1项且只报1项，则恰有2名学生报同一项目的报名方法有（）A．36种B．18种C．9种D．6种3．（2022·广东湛江·一模）为提高新农村的教育水平，某地选派4名优秀的教师到甲､乙､丙三地进行为期一年的支教活动，每人只能去一个地方，每地至少派一人，则不同的选派方案共有（）A．18种B．12种C．72种D．36种4．（2022·广东韶关·一模）在一次学校组织的研究性学习成果报告会上，有A B C D E F､､､､､共6项成果要汇报，如果B成果不能最先汇报，而A､C､D按先后顺序汇报（不一定相邻），那么不同的汇报安排种数为（）A．100B．120C．300D．6005．（2022·广东茂名·二模）某大学计算机学院的丁教授在2021年人工智能方向招收了6名研究生．丁教授拟从人工智能领域的语音识别、人脸识别、数据分析、机器学习、服务器开发共5个方向展开研究，每个方向均有研究生学习，每位研究生只参与一个方向的学习．其中小明同学因录取分数最高主动选择学习人脸识别，其余5名研究生均表示服从丁教授统一安排．则这6名研究生不同的分配方向共有（）A．480种B．360种C．240种D．120种6．（2022·广东·二模）某校安排高一年级（1）～（5）班共5个班去A，B，C，D四个劳动教育基地进行社会实践，每个班去一个基地，每个基地至少安排一个班，则高一（1）班被安排到A基地的排法总数为（）A．24B．36C．60D．2407.有甲、乙、丙、丁、戊5名同学站成一排参加文艺汇演，若甲不站在两端，丙和丁相邻，则不同排列方式共有（）A．12种B．24种C．36种D．48种8.将5名北京冬奥会志愿者分配到花样滑冰、短道速滑、冰球和冰壶4个项目进行培训，每名志愿者只分配到1个项目，每个项目至少分配1名志愿者，则不同的分配方案共有（）A．60种B．120种C．240种D．480种9.将4个1和2个0随机排成一行，则2个0不相邻的概率为（）A．13B．25C．23D．4510.已知有1、2、3、4四个数字组成无重复数字，则比2134大的四位数的个数为________考点二：二项式定理【典例例题】例1．（2022·广东汕尾·高三期末）已知22()n x x -的展开式中第2项和第6项的二项式系数相等，则22()n x x -的展开式中的常数项为（）A ．-240B ．240C ．-60D ．60例2．（2022·广东深圳·高三期末）()()3122x x -+的各项系数和为（）A ．27-B ．27C ．16D ．16-例3．（2022·广东揭阳·高三期末）（多选）已知二项式240121n n n n n n x a x a x a x a x x ---⎛⎫+=++++ ⎪⎝⎭ 的展开式中各项的系数和为64，则下列说法正确的是（）A ．展开式中的常数项为1B ．6n =C ．展开式中二项式系数最大的项是第四项D ．展开式中x 的指数均为偶数【方法技巧与总结】1.在形如()m n N ax bx +的展开式中求t x 的系数，关键是利用通项求r ，则Nm t r m n-=-．2.三项式()()n a b c n N ++∈的展开式：()[()]n n a b c a b c ++=++()n r r r n C a b c -=+++ ()r q n r q q r n n r C C a b c ---=++++ r q n r q q r n n r C C a b c ---=++ 若令n r q p --=，便得到三项式()()n a b c n N ++∈展开式通项公式：()r q p q r n n r C C a b c p q r N p q r n -∈++=，，，，其中!(r)!!!()!!()!!!!r q n n r n n n C C r n r q n r q p q r --==---叫三项式系数．3.二项展开式二项式系数和：2n ；奇数项与偶数项二项式系数和相等：12n -．系数和：赋值法，二项展开式的系数表示式：2012()...n n n ax b a a x a x a x +=++++（01...n a a a ，，，是系数），令1x =得系数和：01...()n n a a a a b +++=+．【变式训练】1．（2022·广东潮州·高三期末）261()x x+的展开式中常数项是_________．2．（2022·广东·一模）二项式62x-展开式中的常数项为__________.3．（2022·广东·珠海市第三中学二模）()512x -的展开式中，3x 的系数为（）A ．160-B ．80-C ．80D ．1604．（2022·广东汕头·二模）二项式24+展开式中，有理项共有（）项．A ．3B ．4C ．5D ．75．（2022·广东汕头·高三期末）8()()x y x y +-的展开式中27x y 的系数为________.(用数字填写答案)6．（2022·广东东莞·高三期末）234(1)(1)(1)x x x +++++的展开式中2x 项的系数是（）A ．9B ．10C ．11D ．127．（2022·广东佛山·高三期末）5(2)x y -+的展开式中，3x y 的系数为（）A ．80B ．40C ．80-D ．40-8.（2022·广东惠州·一模）若()202222022012202212x a a x a x a x -=+++⋅⋅⋅+，则122022a a a ++⋅⋅⋅+=（）A ．1-B ．0C ．1D ．29．（2022·广东广州·一模）6(3)(2)x y x y +-的展开式中52x y 的系数为（）A ．60B ．24C ．12-D ．48-10．（2022·广东深圳·二模）（多选）已知8280128(2)x a a x a x a x -=+++⋅⋅⋅+，则（）A ．802a =B ．1281a a a +++= C ．812383a a a a ++++= D ．12382388a a a a ++++=- 11．（2022·广东茂名·二模）已知2n x ⎛ ⎝的展开式共有13项，则下列说法中正确的有（）A ．所有奇数项的二项式系数和为122B ．所有项的系数和为123C ．二项式系数最大的项为第6项或第7项D ．有理项共5项12.（2022·广东湛江·二模）511813x x ⎛⎫⎛⎫+- ⎪⎪⎝⎭⎝⎭的展开式中常数项为___________.13.（2022·广东·普宁市华侨中学二模）(2+1x )(2＋x)5的展开式中x2的系数是____．(用数字作答）14．（2022·广东潮州·二模）设()4432432102x a x a x a x a x a -=++++，则0124a a a a +++=______．【巩固练习】一、单选题1．6名志愿者要到A ，B ，C 三个社区进行志愿服务，每个志愿者只去一个社区，每个社区至少安排1名志愿者，若要2名志愿者去A 社区，则不同的安排方法共有（）A ．105种B ．144种C ．150种D ．210种2．2022年3月中旬，新冠肺炎疫情突袭南昌，南昌市统一指挥，多方携手、众志成城，构筑起抗击疫情的坚固堡垒．某小区有小王、小张等5位中学生积极参加社区志愿者，他们被分派到测温和扫码两个小组，若小王和小张不同组，且他们所在的两个组都至少需要2名中学生志愿者，则不同的分配方案种数有（）A ．8B ．10C ．12D ．143．甲乙丙丁四个同学星期天选择到东湖公园，西湖茶经楼，历史博物馆和北湖公园其中一处去参观游玩，其中茶经楼必有人去，则不同的参观方式共有（）种.A ．24B ．96C ．174D ．1754．若分配甲、乙、丙、丁四个人到三个不同的社区做志愿者，每个社区至少分配一人，每人只能去一个社区．若甲分配的社区已经确定，则乙与甲分配到不同社区的概率是（）A ．14B ．56C ．13D ．5125．近日，各地有序开展新冠疫苗加强针接种工作，某社区疫苗接种点为了更好的服务市民，决定增派5名医务工作者参加登记､接种､留观3项工作，每人参加1项，接种工作至少需要2人参加，登记､留观至少1人参加，则不同的安排方式有（）A ．50B ．80C ．140D ．1806．甲､乙､丙等七人相约到电影院看电影《长津湖》，恰好买到了七张连号的电影票，若甲､乙两人必须相邻，且丙坐在七人的正中间，则不同的坐法的种数为（）A ．240B ．192C ．96D ．487．某校有5名大学生打算前往观看冰球，速滑，花滑三场比赛，每场比赛至少有1名学生且至多2名学生前往，则甲同学不去观看冰球比赛的方案种数有（）A ．48B ．54C ．60D ．728．()()8x y x y -+的展开式中36x y 的系数为（）A ．28B ．28-C ．56D ．56-9．在()522x x +-的展开式中，含4x 的项的系数为（）A ．-120B ．-40C ．-30D ．20010．101x ⎛⎫ ⎪⎝⎭的展开式中，2x 的系数等于（）A ．45-B ．10-C ．10D ．4511．若()526012612(12)x x a a x a x a x +-=++++ ，x ∈R ，则2a 的值为（）A ．20-B ．20C ．40D ．6012．已知()522x a x x ⎛⎫+- ⎪⎝⎭的展开式中各项系数的和为3-，则该展开式中x 的系数为（）A ．0B ．120-C ．120D ．160-二、多选题13．已知660(2)i i i x a x =+=∑，则（）A ．123456666a a a a a a +++++=B ．320a =C ．135246a a a a a a ++>++D ．1034562234a a a a a a +=+++14．在二项式6⎛ ⎝的展开式中，正确的说法是（）A ．常数项是第3项B ．各项的系数和是1C ．偶数项的二项式系数和为32D ．第4项的二项式系数最大15．已知函数()6260126()(12),0,1,2,3,,6i f x x a a x a x a x a i =-=+++⋅⋅⋅+∈=⋅⋅⋅R 的定义域为R ．（）A ．01261a a a a +++⋅⋅⋅+=-B ．135364a a a ++=-C ．123623612a a a a +++⋅⋅⋅+=D ．(5)f 被8整除余数为716．已知2012(12)n n n x a a x a x a x +=++++ ，下列结论正确的是（）A ．0123n n a a a a +++=+B ．当5,==n x ()(12),*+=+∈n x a a b N ，则a b =C ．当12n =时，012,,,,n a a a a 中最大的是7a D ．当12n =时，3124111223411121222222-+-++-= a a a a a a 17．已知()610ax a x ⎛⎫+> ⎪⎝⎭的展开式中含2x -的系数为60，则下列说法正确的是（）A ．61ax x ⎛⎫+ ⎪⎝⎭的展开式的各项系数之和为1B ．61ax x ⎛⎫+ ⎪⎝⎭的展开式中系数最大的项为2240x C ．61ax x ⎛⎫- ⎪⎝⎭的展开式中的常数项为160-D ．61ax x ⎛⎫- ⎪⎝⎭的展开式中所有二项式的系数和为32三、填空题18．甲、乙、丙三名志愿者需要完成A ，B ，C ，D ，E 五项不同的工作，每项工作由一人完成，每人至少完成一项，且E 工作只有乙能完成，则不同的安排方式有______种．19．志愿团安排去甲､乙､丙､丁四个精准扶贫点慰问的先后顺序，一位志愿者说：不能先去甲，甲的困难户最多；另一位志愿者说：不能最后去丁，丁离得最远．他们共有多少种不同的安排方法____20．将中国古代四大名著——《红楼梦》《西游记》《水浒传》《三国演义》，以及《诗经》等12本书按照如图所示的方式摆放，其中四大名著要求放在一起，且必须竖放，《诗经》《楚辞》《吕氏春秋》要求横放，若这12本书中7本竖放5本横放，则不同的摆放方法共有___________种.21.5位学生被分配到3个志愿点作志愿者，每个志愿点至少分配一位学生，其中甲乙不能分配到同一个志愿点，则共有___________种不同的分配方式（用数字作答）.22．有甲、乙、丙三项任务，甲、乙各需1人承担，丙需2人承担且至少1人是男生，现有2男2女共4名学生承担这三项任务，不同的安排方法种数是______．（用具体数字作答）23.已知()52345601234561(1)x x a a x a x a x a x a x a x +-=++++++，则03a a +的值为___________.24．已知51m x x x x ⎛⎫⎛⎫-+ ⎪⎪⎝⎭⎝⎭的展开式中常数项为20，则m =___________.。
高考数学二轮专名师讲义：第23讲-高考题中的应用题解法(含答案)
第23讲 高考题中的应用题解法江苏近几年高考数学试卷加大了对应用题的考查力度，新高考(08年开始)以来，每年除了在小题(填空)考查外，都还有一道大题，其中2008年、2010年、2011年、2012年都是放在试卷的第17题，2013年放在试卷的第18题，2009年放在试卷的第19题，考查的知识点都是B 级考点的综合应用，试题的难度属于中档题．所谓数学应用题就是利用数学知识解决一些非数学领域中的问题．由于数学的高度抽象性，这就决定了数学应用的广泛性，而应用题的非数学背景的多样性，也就导致了解应用题往往是要在陌生的背景中去理解、分析所给出的有关问题，舍去与数学无关的非本质因素，通过抽象转化为相应的数学问题．江苏高考数学试题中，对数学应用于解决实际问题的考查已经趋于成熟，它主要考查函数、方程、三角、解三角形、导数、数列、基本不等式等基础知识，考查数学建模能力、抽象概括能力、空间想象能力、数学阅读能力和解决实际问题的能力．解数学应用题的一般思路实际上就是(1) 读：理解文字(图形)表达的意图，分清条件和结论；(2) 建：进行语言转化(文字语言及图形语言转化为数学语言)，利用数学知识建立相应的数学模型；(3) 解：求解数学模型，得到数学结论；(4) 答：把用数学方法所得到的结论还原为实际问题，要符合实际意义．高考数学应用题常见模型：(1) 函数应用模型：涉及最值问题；(2) 三角应用模型：涉及测量问题；(3) 不等式(组)应用模型：涉及优化问题；(4) 方程(组)及坐标系应用模型：涉及等量问题；(5) 数列应用模型：涉及年代及预测问题；(6) 立体几何模型：涉及空间图形问题；(7) 概率、统计模型：涉及数据计算、预估等问题．1. 在长为12 cm 的线段AB 上任取一点C. 现作一矩形，邻边长分别等于线段AC 、CB的长，则该矩形面积大于20 cm 2的概率为________.答案：232. 已知某生产厂家的年利润y(万元)与年产量x(万件)的函数关系式为y ＝－13x 3＋81x －234，则使该生产厂家获得最大年利润的年产量为________万件．答案：93. 如图，一块曲线部分是抛物线形的钢板，其底边长为2，高为1，将此钢板切割成等腰梯形的形状，记CD ＝2x ，梯形面积为S ，则S 的最大值是________．答案：3227解析：建立坐标系，B 点坐标为(1，－1)，求出抛物线方程为x 2＝－y ，得D 点坐标(x ，－x 2)，等腰梯形的高为1－x 2，S ＝2x ＋22(1－x 2)，0＜x ＜1，求导可以得到x ＝13时S 取最大值3227. 4. 某人于2009年7月1日去银行存款a 元，存的是一年定期储蓄，2010年7月1日他将到期存款的本息一起取出，再加a 元后，还存一年的定期储蓄，此后每年7月1日他都按照同样的方法，在银行取款和存款．设银行一年定期储蓄利率r 不变，则到2014年7月1日，他将所有的存款和利息全部取出时，取出的钱数共有________元．答案：a （1＋r ）[（1＋r ）5－1]r题型一 通过建立坐标系，得到函数模型来解应用题例1 如图所示的镀锌铁皮材料ABCD ，上沿DC 为圆弧，其圆心为A ，圆半径为2 m ，AD ⊥AB ，BC ⊥AB ，且BC 长1 m ．现要用这块材料裁一个矩形PEAF(其中P 在圆弧DC 上，E 在线段AB 上，F 在线段AD 上)作圆柱的侧面，若以PE 为母线，问如何裁剪可使圆柱的体积最大？其最大值是多少？解：分别以AB 、AD 所在直线为x 轴、y 轴建立直角坐标系xOy ，则圆弧DC 的方程为x 2＋y 2＝4(0≤x≤3，y ＞0)，设P(x ，y)(0＜x≤3)，圆柱半径为r ，体积为V ，则PE ＝4－x 2，2πr ＝AE ＝x ，则r ＝x 2π，∴ V ＝πr 2l ＝π⎝⎛⎭⎫x 2π2·4－x 2＝14πx 24－x 2，即V 2＝116π2x 4(4－x 2)．设t ＝x 2∈(0，3]，则u ＝t 2(4－t)，u ′＝－3t 2＋8t ＝－3t ⎝⎛⎭⎫t －83， 令u′＝0，得t ＝83.当83＜t≤3时，u ′＜0，u 是减函数；当0＜t ＜83时，u ′＞0，u 是增函数，∴ 当t ＝83时，u 有极大值，也是最大值，∴ 当x ＝23 6 m 时，V 有最大值439πm 3，此时y ＝4－x 2＝233 m. 故裁一个矩形，两边长分别为23 6 m 和23 3 m ，能使圆柱的体积最大，其最大值为439πm 3.某汽车厂有一条价值为a 万元的汽车生产线，现要通过技术改造来提高该生产线的生产能力，提高产品的增加值．经过市场调查，产品的增加值y 万元与技术改造投入的x 万元之间满足：① y 与(a －x)和x 2的乘积成正比；② x ∈⎝⎛⎦⎤0，2am 2m ＋1，其中m 是常数．若x ＝a 2时，y＝a 3.(1) 求产品增加值y 关于x 的表达式；(2) 求产品增加值y 的最大值及相应的x 的值．解：(1) 设y ＝f(x)＝k(a －x)x 2，因为当x ＝a 2时，y ＝a 3，所以k ＝8，所以f(x)＝8(a －x)x 2 ，x ∈⎝⎛⎦⎤0，2am 2m ＋1. (2) 因为f′(x)＝－24x 2＋16ax ，令f′(x)＝0，则x ＝0(舍)，x ＝2a 3. ① 当2am 2m ＋1≥2a 3，即m≥1时， 当x ∈⎝⎛⎭⎫0，2a 3时，f ′(x)＞0，所以f(x)在⎝⎛⎭⎫0，2a 3上是增函数， 当x ∈⎝⎛⎭⎫2a 3，2am 2m ＋1时，f ′(x)＜0，所以f(x)在⎝⎛⎭⎫2a 3，2am 2m ＋1上是减函数， 所以y max ＝f ⎝⎛⎭⎫2a 3＝3227a 3；② 当2am 2m ＋1＜2a 3，即0＜m ＜1时， 当x ∈⎝⎛⎭⎫0，2am 2m ＋1时，f ′(x)＞0，所以f(x)在⎝⎛⎭⎫0，2am 2m ＋1上是增函数， 所以y max ＝f ⎝⎛⎭⎫2am 2m ＋1＝32m 2（2m ＋1）3a 3. 综上，当m≥1时，投入2a 3万元，最大增加值3227a 3；当0＜m ＜1时，投入2am 2m ＋1万元，最大增加值32m 2（2m ＋1）3a 3. 题型二 通过建立不等式模型来解应用题例2 某环线地铁按内、外环线同时运行，内、外环线的长均为30 km(忽略内、外环线长度差异)．(1) 当9列列车同时在内环线上运行时，要使内环线乘客最长候车时间为10 min ，求内环线列车的最小平均速度；(2) 新调整的方案要求内环线列车平均速度为25 km/h ，外环线列车平均速度为30 km/h.现内、外环线共有18列列车全部投入运行，要使内、外环线乘客的最长候车时间之差不超过1 min ，问：内、外环线应各投入几列列车运行？解：(1) 设内环线列车运行的平均速度为v km/h ，由题意可知309v×60≤10v ≥20.所以，要使内环线乘客最长候车时间为10 min ，列车的最小平均速度是20 km/h.(2) 设内环线投入x 列列车运行，则外环线投入(18－x)列列车运行，内、外环线乘客最长候车时间分别为t 1、t 2 min ，则t 1＝3025x ×60＝72x ，t 2＝3030（18－x ）×60＝6018－x.于是有|t 1－t 2|＝⎪⎪⎪⎪72x －6018－x ≤1⎩⎪⎨⎪⎧x 2－150x ＋1 296≤0x 2＋114x －1 296≤0150－17 3162≤x ≤－114＋18 1802. 又x ∈N *，所以x ＝10，所以当内环线投入10列，外环线投入8列列车运行时，内、外环线乘客最长候车时间之差不超过1 min.如图，摄影爱好者S 在某公园A 处，发现正前方B 处有一立柱，测得立柱顶端O 的仰角和立柱底部B 的俯角均为π6.设S 的眼睛距地面的距离为 3 m. (1) 求摄影者到立柱的水平距离和立柱的高度；(2) 立柱的顶端有一长2 m 的彩杆MN 绕其中点O 在S 与立柱所在的平面内旋转．摄影者有一视角范围为π3的镜头，在彩杆转动的任意时刻，摄影者是否都可以将彩杆全部摄入画面？说明理由．解：(1) 作SC 垂直OB 于C ，则∠CSB ＝30°，∠ASB ＝60°.又SA ＝3，故在Rt △SAB 中，可求得BA ＝3，即摄影者到立柱的水平距离为3 m. 由SC ＝3，∠CSO ＝30°，在Rt △SCO 中，可求得OC ＝ 3.因为BC ＝SA ＝3，故OB ＝23，即立柱高为2 3 m.(2) 连结SM 、SN ，设SN ＝a ，SM ＝b.在△SON 和△SOM 中， （23）2＋1－b 22·23·1＝－（23）2＋1－a 22·23·1，得a 2＋b 2＝26. cos ∠MSN ＝a 2＋b 2－222ab ＝11ab ≥22a 2＋b 2＝1113＞12. 又∠MSN ∈(0，π), 则∠MSN ＜π3. 故摄影者可以将彩杆全部摄入画面．题型三 通过建立三角模型来解应用题例3 在路边安装路灯，灯柱AB 与地面垂直，灯杆BC 和灯柱AB 所在平面与道路垂直，且∠ABC ＝120°，路灯C 采用锥形灯罩，射出的光线如图中阴影部分所示，已知∠ACD ＝60°，路宽AD ＝24 m ．设灯柱高AB ＝h(m)，∠ACB ＝θ(30°≤θ≤45°)．(1) 求灯柱的高h(用θ表示)；(2) 若灯杆BC 与灯柱AB 所用材料相同，记此用料长度和为S ，求S 关于θ的函数表达式，并求出S 的最小值．解：(1) ∵ ∠ABC ＝120°，∠ACB ＝θ，∴ ∠BAC ＝60°－θ.∵ ∠BAD ＝90°，∴ ∠CAD ＝30°＋θ.∵ ∠ACD ＝60°，∴ ∠ADC ＝90°－θ.在△ACD 中，∵ AD sin ∠ACD ＝AC sin ∠ADC， ∴ AC ＝24cos θsin60°＝163cos θ. 在△ABC 中，∵ AB sin ∠ACB ＝AC sinB， ∴ AB ＝ACsin θsin120°＝16sin2θ，即h ＝16sin2θ. (2) 在△ABC 中，∵ BC sin ∠BAC ＝AC sinB，∴ BC ＝ACsin （60°－θ）sin120°＝32cos θsin(60°－θ) ＝83＋83cos2θ－8sin2θ.则S ＝AB ＋BC ＝83＋83cos2θ＋8sin2θ＝83＋16sin(2θ＋60°)．∵ 30°≤θ≤45°，∴ 120°≤2θ＋60°≤150°.∴ 当θ＝45°时，S 取得最小值为(83＋8)m.如图所示，一吊灯的下圆环直径为4 m ，圆心为O ，通过细绳悬挂在天花板上，圆环呈水平状态，并且与天花板的距离(即OB)为2 m ，在圆环上设置三个等分点A 1、A 2、A 3.点C 为OB 上一点(不包含端点O 、B)，同时点C 与点A 1、A 2、A 3、B 均用细绳相连接，且细绳CA 1、CA 2、CA 3的长度相等．设细绳的总长为y.(1) 设∠CA 1O ＝θ(rad)，将y 表示成θ的函数关系式；(2) 请你设计θ，当角θ正弦值的大小是多少时，细绳总长y 最小，并指明此时 BC 应为多长．解：(1) 在Rt △COA 1中，CA 1＝2cos θ，CO ＝2tan θ，则y ＝3CA 1＋CB ＝3·2cos θ＋(2－2tan θ)＝2（3－sin θ）cos θ＋2⎝⎛⎭⎫0<θ<π4. (2) y′＝2⎣⎢⎡⎦⎥⎤－cos 2θ－（3－sin θ）（－sin θ）cos 2θ＝2⎝ ⎛⎭⎪⎫3sin θ－1cos 2θ. 令y′＝0，则sin θ＝13. 当sin θ>13时，y ′>0；当sin θ<13时，y ′<0. ∵ y ＝sin θ在⎣⎡⎦⎤0，π4上是增函数， ∴ 当角θ满足sin θ＝13时，y 最小，最小值为42＋2，此时BC ＝⎝⎛⎭⎫2－22 m. 题型四 通过建立方程来解决应用问题例4 将52名志愿者分成A 、B 两组参加义务植树活动，A 组种植150捆白杨树苗，B 组种植200捆沙棘树苗．假定A 、B 两组同时开始种植．(1) 根据历年统计，每名志愿者种植一捆白杨树苗用25 h ，种植一捆沙棘树苗用12h ．应如何分配A 、B 两组的人数，使植树活动持续时间最短；(2) 在按(1)分配的人数种植1 h 后发现，每名志愿者种植一捆白杨树苗用时仍为25h ，而每名志愿者种植一捆沙棘树苗实际用时23h ，于是从A 组抽调6名志愿者加入B 组继续种植，求植树活动所持续的时间.解：(1) 设A 组人数为x ，且0<x<52，x ∈N *， 则A 组活动所需时间f(x)＝150×25x ＝60x； B 组活动所需时间g(x)＝200×1252－x ＝10052－x .令f(x)＝g(x)，即60x ＝10052－x ，解得x ＝392. 所以两组同时开始的植树活动所需时间F(x)＝⎩⎨⎧60x ，x ≤19，x ∈N *，10052－x，x ≥20，x ∈N *， 而F(19)＝6019，F(20)＝258，故F(19)>F(20)． 所以当A 、B 两组人数分别为20、32时，植树活动持续时间最短．(2) A 组所需时间为1＋150×25－20×120－6＝367(h)， B 组所需时间为1＋200×23－32×132＋6＝323(h), 所以植树活动所持续的时间为367h.为了迎接青奥会，南京在主干道统一安装某种新型节能路灯，该路灯由灯柱和支架组成．在如图所示的直角坐标系中，支架ACB 是抛物线y 2＝2x 的一部分，灯柱CD 经过该抛物线的焦点F 且与路面垂直，其中C 在抛物线上，B 为抛物线的顶点，DH 表示道路路面，BF ∥DH ，A 为锥形灯罩的顶，灯罩轴线与抛物线在A 处的切线垂直．安装时要求锥形灯罩的顶到灯柱的距离是1.5 m ，灯罩的轴线正好通过道路路面的中线．(1) 求灯罩轴线所在的直线方程；(2) 若路宽为10 m ，求灯柱的高．解：(1) 由题意知，BF ＝12，则x A ＝1.5＋12＝2， 代入y 2＝2x 得y A ＝2，故A(2，2)．设点A 处的切线方程为y －2＝k(x －2)，代入抛物线方程y 2＝2x 消去x ，得ky 2－2y ＋4－4k ＝0.则Δ＝4－4k(4－4k)＝0，解得k ＝12. 故灯罩轴线的斜率为－2，其方程为y －2＝－2(x －2)，即y ＝－2x ＋6.(2) 由于路宽为10，则当x ＝112时，y ＝－5，从而FD ＝5. 又CF ＝1，则CD ＝6.答：灯柱的高为6 m.1. (2013·四川卷)如图，在平行四边形ABCD 中，对角线AC 与BD 交于点O ，AB →＋AD →＝λAO →，则λ＝________．答案：2解析：AB →＋AD →＝AC →＝2AO →，λ＝2.2. (2013·湖南卷)某工厂甲、乙、丙三个车间生产了同一种产品，数量分别为120件、80件、60件．为了解它们的产品质量是否存在显著差异，用分层抽样方法抽取了一个容量为n 的样本进行调查，其中从丙车间的产品中抽取了3件，则n ＝________．答案：13解析：n ＝3×120＋80＋6060＝13. 3. 设圆锥曲线r 的两个焦点分别为F 1、F 2，若曲线r 上存在点P 满足|PF 1|∶|F 1F 2|∶|PF 2|＝4∶3∶2，则曲线r 的离心率等于________．答案：12或32解析：∵ |PF 1|∶|F 1F 2|∶|PF 2|＝4∶3∶2，设|PF 1|＝4k ，|F 1F 2|＝3k ，|PF 2|＝2k ，k>0，若圆锥曲线为椭圆，则2a ＝|PF 1|＋|PF 2|＝6k ，2c ＝|F 1F 2|＝3k ，则离心率e ＝2c 2a ＝3k 6k ＝12；当圆锥曲线为双曲线时，则2a ＝|PF 1|－|PF 2|＝2k ，2c ＝|F 1F 2|＝3k ，离心率e ＝2c 2a ＝3k 2k ＝32. 4. (2014·江苏卷)设抽测的树木的底部周长均在区间[80，130]上，其频率分布直方图如图所示，则在抽测的60株树木中，有________株树木的底部周长小于100 cm.答案：24解析：由题意，在抽测的60株树木中，底面周长小于100 cm 的株数为(0.015＋0.025)×10×60＝24.5. (2013·江苏卷)如图，游客从某旅游景区的景点A 处下山至C 处有两种路径．一种是从A 沿直线步行到C ，另一种是先从A 沿索道乘缆车到B ，然后从B 沿直线步行到C.现有甲、乙两位游客从A 处下山，甲沿AC 匀速步行，速度为50 m/min.在甲出发2 min 后，乙从A 乘缆车到B ，在B 处停留1 min 后，再从B 匀速步行到C.假设缆车匀速直线运动的速度为130m/min ，山路AC 长为1 260 m ，经测量，cosA ＝1213，cosC ＝35. (1) 求索道AB 的长；(2) 问乙出发多少分钟后，乙在缆车上与甲的距离最短？(3) 为使两位游客在C 处互相等待的时间不超过3 min ，乙步行的速度应控制在什么范围内？解：(1) ∵ cosA ＝1213，cosC ＝35. ∴ A 、C ∈⎝⎛⎭⎫0，π2，∴ sinA ＝513，sinC ＝45. ∴ sinB ＝sin[π－(A ＋C)]＝sin(A ＋C)＝sinAcosC ＋cosAsinC ＝6365.根据AB sinC ＝AC sinB，得AB＝AC sinBsinC ＝1 040 m ， 所以索道AB 的长为1 040 m.(2) 设乙出发t min 后，甲、乙距离为d ，则d 2＝(130t)2＋(100＋50t)2－2×130t×(100＋50t)×1213＝200(37t 2－70t ＋50)．∵ 0≤t≤1 040130，即0≤t≤8， ∴ 当t ＝3537时，即乙出发3537min 后，乙在缆车上与甲的距离最短． (3) 由正弦定理BC sinA ＝AC sinB ，得BC ＝AC sinB sinA ＝1 2606365×513＝500(m)， 乙从B 出发时，甲已经走了50(2＋8＋1)＝550(m)，还需走710 m 才能到达C.设乙的步行速度为v m/min ，则⎪⎪⎪⎪500v －71050≤3.∴ －3≤500v －71050≤3，∴ 1 25043≤v ≤62514. ∴ 为使两位游客在C 处互相等待的时间不超过 3 min ，乙步行的速度应控制在⎣⎡⎦⎤1 25043，62514(m/min)范围内． 6. (2014·上海卷)如图，某公司要在A 、B 两地连线上的定点C 处建造广告牌CD ，其中D 为顶端，AC 长35 m ，CB 长80 m ，设A 、B 在同一水平面上，从A 和B 看D 的仰角分别为α和β.(1) 设计中CD 是铅垂方向，若要求α≥2β，问CD 的长至多为多少(结果精确到0.01 m)?(2) 施工完成后，CD 与铅垂方向有偏差，现在实测得α＝38.12°，β＝18.45°，求CD 的长(结果精确到0.01 m)．解：(1) 由题得，∵α≥2β，且0<2β≤α<π2， ∴ tan α≥tan2β，即|CD|35≥|CD|401－|CD|26 400，解得|CD|≤202， ∴ |CD|≈28.28 m.(2) 由题得，∠ADB ＝180°－38.12°－18.45°＝123.43°，∵ 35＋80sin123.43°＝|AD|sin18.45°，∴ |AD|≈43.61 m. ∵ |CD|2＝352＋|AD|2－2×35×|AD|×cos38.12°，∴ |CD|≈26.93m.(本题模拟高考评分标准，满分14分)第十八届省运会于2014年9月在徐州市举办．为营造优美的环境，举办方决定在某“葫芦”形花坛中建喷泉．如图，该花坛的边界是两个半径为10 m 的圆弧围成，两圆心O 1、O 2之间的距离为10 m.(1) 如图甲，在花坛中建矩形喷泉，四个顶点A 、B 、C 、D 均在圆弧上，O 1O 2⊥AB 于点M.设∠AO 2M ＝θ，求矩形的宽AB 为多少时，可使喷泉ABCD 的面积最大；(2) 如图乙，在花坛中间铺设一条宽为2 m 的观赏长廊以作休闲之用，则矩形喷泉变为两个全等的等腰三角形，其中NA ＝NB ，NO 2＝4 m ．若∠AO 2M ＝θ∈⎣⎡⎦⎤π6，π4，求喷泉面积的取值范围．解：(1) 在直角△AO 2M 中，AM ＝10sin θ，O 2M ＝10cos θ，则AD ＝20cos θ＋10，所以矩形ABCD 的面积S ＝20sin θ(20cos θ＋10)＝200(2sin θcos θ＋sin θ)，(4分)令f(θ)＝2sin θcos θ＋sin θ，0<θ≤π3， 则f′(θ)＝2cos2θ＋cos θ＝4cos 2θ＋cos θ－2，令f′(θ)＝0，得cos θ＝33－18.设cos θ0＝33－18，且0<θ0≤π3，列表如下： θ (0，θ0) θ0 ⎝⎛⎭⎫θ0，π3 f ′(θ) ＋ 0 －f (θ) Z 极大值] 所以当θ＝θ0，即AB ＝530＋2332时，矩形ABCD 的面积最大．(10分) (2) 由(1)易得，喷泉的面积S ＝20sin θ(10cos θ＋4)＝100sin2θ＋80sin θ，由θ∈⎣⎡⎦⎤π6，π4知，2θ∈⎣⎡⎦⎤π3，π2， 所以函数g(θ)＝100sin2θ＋80sin θ是单调增函数，所以S ∈[503＋40，100＋402]．(13分)答：(1) 矩形的宽AB ＝530＋2332m 时，可使喷泉ABCD 的面积最大；(2) 喷泉的面积的取值范围是[503＋40，100＋402](m 2)．(14分)1. 某公司为了加大产品的宣传力度，准备立一块广告牌，在其背面制作一个形如△ABC的支架，要求∠ACB ＝60°，BC 的长度大于1 m ，且AC 比AB 长0.5 m ．为节省材料，要求AC 的长度越短越好． (1) 设BC ＝x m ，AC ＝y m ，将y 写成关于x 的函数，并写出定义域；(2) 当BC 的长度为多少时，AC 最短，求出最短长度．解：(1) 由题设知BC ＝x m(x>1)，AC ＝y m ，则AB ＝y －12.在△ABC 中，由余弦定理，得⎝⎛⎭⎫y －122＝y 2＋x 2－2xycos60°.所以y ＝x 2－14x －1，定义域为{x|x>1}． (2) (解法1)y ＝x 2－14x －1＝(x －1)＋34（x －1）＋2≥2＋3，当且仅当x －1＝34（x －1），即x＝1＋32时，y 有最小值2＋ 3. (解法2)y′＝2x （x －1）－⎝⎛⎭⎫x 2－14（x －1）2＝x 2－2x ＋14（x －1）2. 由y′＝0，得x ＝1＋32.因为当1<x<1＋32时，y ′<0； 当x>1＋32时，y ′>0，所以当x ＝1＋32时，y 有最小值2＋ 3. 故AC 的最短长度为(2＋3) m ，此时BC 的长度为⎝⎛⎭⎫1＋32 m. 2. 某商店经销一种纪念品，每件产品的成本为30元，并且每卖出一件产品需向税务部门上交a 元(a 为常数，2≤a ≤5)的税收．设每件产品的售价为x 元(35≤x≤41)，根据市场调查，日销售量与e x (e 为自然对数的底数)成反比例．已知当每件产品的售价为40元时，日销售量为10件．(1) 求该商店的日利润L(x)元与每件产品的售价x 的函数关系式；(2) 当每件产品的日售价为多少元时，该商店的日利润L(x)最大，并求出L(x)的最大值． 解：(1) 设日销售量为k e x ，则k e 40＝10，∴ k ＝10e 40，则日销售量为10e 40ex 件，售价为x 元时，每件利润为(x －30－a)元，则日利润L(x)＝(x －30－a)10e 40e x ＝10e 40·x －30－a e x(35≤x ≤41)． (2) L′(x)＝10e 40·31＋a －x e 2x. ① 当2≤a≤4时，33≤31＋a≤35，而35≤x≤41，∴ L ′(x)≤0，L(x)在[35，41]上是单调递减函数，则当x ＝35时，L(x)取得最大值为10(5－a)e 5.② 当4<a≤5时，35<31＋a≤36，令L′(x)＝0，得x ＝a ＋31.当x ∈[35，a ＋31)时，L ′(x)>0，L(x)在[35，a ＋31)上是单调递增函数；当x ∈(a ＋31，41]时，L ′(x)<0，L(x)在(a ＋31，41]上是单调递减函数．∴ 当x ＝a ＋31时，L(x)取得最大值为10e 9－a .综上，当2≤a≤4时，L(x)max ＝10(5－a)e 5；当4<a≤5时，L(x)max ＝10e 9－a .。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
最值问题一
1.
2.
3.3个连续奇数相乘，所得乘积的个位数字最小可能是多少？
4.用1，2，4可以组成6个没有重复数字的三位数，这些三位数中相差最小的两个数之差是多少？
5.阿呆和阿瓜两人手里各拿着一张扑克牌，两人牌得的点数之和刚好是10. 请问两人牌的点数的成绩最大可能是多少？
6.三个自然数的和是19，它们的乘积最大可能是多少？
7.（1）请将1~4这4个数字填入算式“□□×□□”的□中，要使得算式结果最大，应该怎么填？
（2）请将1~6这6个数字填入算式“□□□×□□□”的□中，要求5、6分别填在百位，4、3分别填在十位，1、2分别填在个位，并使得算式结果最大，应该怎么填？
6. 在图的中间圆圈内填一个数，计算每一条线段两端的之差
（大减小），然后把这3个数相加，那么所得的和最小是多少？
7. 在所有包含3个相同数码的四位数中，与1389之差(大减小)最小的一个是多少？
8. 把1~6这6个数字填入算式“□□□—□□□”的□中，要求前一个三位数比后一个三位数大. 这个减法算式的结果最大可能是多少？最小可能是多少？
9. 一个自然数是由数字8、9组成的，它的任意相邻两位都可以看成一个两位数，并且这些相邻数字组成的两位数都不相等.请问：满足条件的自然数最大是多大？
10. 如果3个互不相同的自然数之和为20，那么其中最小的数最大可能是多少? 最大的数最小可能是多少？
拓展篇
1.3个连续自然数相乘，所得的乘积的个位数字最大可能是多少？
2.（1）在五位数12 435的某一位数字后面再插入一个同样的数字（例如：可以在2的后
面插入2得到12 2435，这样得到的六位数最大可能是多少？
（2）在七位数9 876 789的某一位数字后面再插入一个同样的数字，这样得到的八位数最小是多少？
3．用24根长1厘米的火柴棒围成一个矩形，这个矩形的面积最大是多少？如果用22根火柴棒呢？
4. 有9个同学要进行象棋比赛，他们准备分成两组，不同组的人之间只比赛一场，同组的人之间不比赛.他们一共最多能比赛多少场？
5. 3个互不相同的自然数之和是17，它们的乘积最大可能是多少？
6. 请将2，3，4，5，6，8这6个数填入算式“□□□×□□□”的□中，要使得算式结果最大，应该怎么填？
7. 请将6~9这4个数字填入算式“□×□﹢□□”的□中，要使得算式结果最大，应该怎么填？
8. 在图的中间空白○内填入一个数，计算每一条线段两端的数之差（大减小），然后把这五个差数相加.问：所得的和最小是多少？
9. 如果7个互不相同的自然数之和为100，那么其中最小的数最大可能是多少？最大的数最小可能是多少？
10. 一个多位数的各个数字互不相同，而且个位数字之和为23.这样的多位数最小可能是多少？最大可能是多少？
11. 有7个盘子排成一排，依次编号为1~7. 每个盘子里都放有若干个玻璃球，一共放了80个，其中1号盘子里放了18个玻璃球，并且任意编号相邻的3个盘子里放的玻璃球数之和都相等.请问：第6个盘子中最多放了多少个玻璃球？
12. 黑板上写着1~10这10个数字，小明每次擦去两个奇偶性相同的数，再写上他们的平均数.最后当黑板上只剩下一个自然数时，这个数最大可能是多少？
13. 如图，这是一个正方体的展开图.将它折成一个正方体后，相交于同一顶点的3个面上的
数之和最大是多少？
14. 如图，在一个正方体方块的下角A点处有一只蚂蚁，
它要沿着正方体的表面爬行至右上角的B点，去搬运一块
食物.为了使得这个蚂蚁所走的线路最短，它应该怎么爬
行？它可以选择的最短线路一共有几条？
超越篇
1.一个两位数除以它的各个数字之和，余数最大是多少？
2.4个小朋友，每个人的体重是整数千克，而且其中任意3人体重之和都大于99千克.这4个小朋友体重之和最小是多少？
3.将1~30依次写成12345^282930，形成一个对位数，从这个多位数中划掉45个数字，剩下的数最大是多少？如果要求剩下的数首位不能为零，这个数最小是多少？
4.用1，2，3，4，6，7，8，9这8个数字组成2个四位数，使这两个数的差最小（大减小），这个差最小是多少？
5.将2~8这7个自然数填入算式“□□×□□－□□÷□”的□中，如果算式的计算结果为整数，那么这个结果最大是多少？最小是多少？
6.如图，一只木箱的长、宽、高分别为5厘米、3厘米、4厘米.有一只甲虫从A点出发，沿棱爬行，每条棱只允许爬一次，甲虫最多能爬行多少厘米？如果要求甲虫最后回到A点，那么它最多能爬行多少厘米？
7.如图，黑板上写有一个三位数减三位数的算式，其中首位已经确定.接下来，甲每次报一个数字，乙就把它放入四个方框中的一个，甲要使得差尽量大，乙要使得差尽量小，如果两人都使用最佳的策略，那么最后的差是多少？
8.一栋大楼共33层，电梯停在第一层，有32个人分别要去第2层、第3层……第33层，他们可以选择坐电梯或者走楼梯.有一天电梯坏了，电梯只能在某一层停下，每个人可以选择走楼梯或乘电梯到这一层再走楼梯.每个人上一层楼梯会有3份不满意，下一层楼梯会有1份不满意.请问：电影停在哪一层，才能使得所有人不满意的总份数最小？。