倒立摆实验报告(PID控制)
一阶倒立摆双闭环PID控制实验报告

姓名:戴鹏指导老师:胡立坤成绩:学院:电气工程学院专业:自动化班级:自093------年------月-------日实验内容:基于双闭环PID控制的一阶倒立摆控制器的设计与验证实验其他组员:黄育尚【实验时间】 2013年1月18日星期五【实验地点】综合楼702【实验目的】1.理解一阶倒立摆的工作机理及其数学模型的建立及简化的方法;2.通过对一阶倒立摆的建模,掌握使用Matlab/Simulink软件对控制系统的建模方法;3.通过对一阶倒立摆控制系统的设计,理解和掌握双闭环PID控制系统的设计方法;4.掌握双闭环PID控制器参数整定的方法;5.掌握Simulink子系统的创建方法;6.理解和掌握控制系统设计中稳定性、快速性的权衡以及不断通过仿真实验优化控制系统的方法。
【实验原理】本实验的被控对象为固高公司的倒立摆实验系统,一阶倒立摆的结构原理图如图1所示,一阶倒立摆系统的组成框图如图2所示。
一阶倒立摆精确模型如图3所示。
一阶倒立摆系统包括计算机、运动控制卡、伺服机构、倒立摆本体和光电码盘几大部分,组成了一个闭环系统。
光电码盘1 将小车的位移、速度信号反馈给伺服驱动器和运动控制卡,摆杆的位置、速度信号由光电码盘反馈给控制卡。
计算机从运动控制卡中读取实时数据,确定控制决策(小车向哪个方向移动、移动速度、加速度等),并由运动控制卡来实现该控制决策,产生相应的控制量,使电机转动,通过皮带带动小车运动,保持摆杆平衡。
运运运运运运运运运运运运运运运运运运运运运运运运运运1运运运运运运运运运2图1 一阶倒立摆的结构原理图图2 一阶倒立摆系统的组成框图图3 一阶倒立摆精确模型2一阶倒立摆系统建模,系统在平衡点附近近似模型为:2222222222()()()()()()()()()I ml bm gl I ml uI M m Mml I M m Mml I M m Mml mlbmgl M m mluI M m Mml I M m Mml I M m Mml x x x φφφ••••••-++=++++++++-+=++++++++实际系统的模型参数如下: M 小车质量 1.096 Kg m 摆杆质量 0.109 Kgb 小车摩擦系数 0 .1N/m/secl 摆杆转动轴心到杆质心的长度 0.2 5m I 摆杆惯量 0.0034 kg*m*m把上述参数代入,可以得到系统的实际模型。
直线一级倒立摆PID控制实验报告
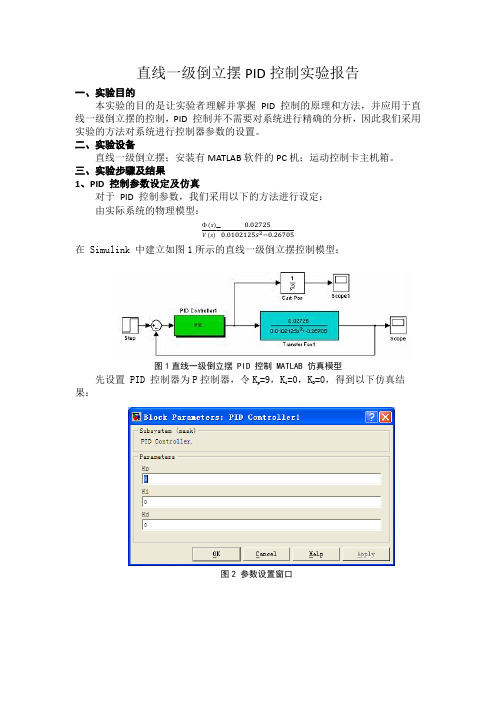
直线一级倒立摆PID 控制实验报告一、实验目的本实验的目的是让实验者理解并掌握 PID 控制的原理和方法,并应用于直线一级倒立摆的控制,PID 控制并不需要对系统进行精确的分析,因此我们采用实验的方法对系统进行控制器参数的设置。
二、实验设备直线一级倒立摆;安装有MATLAB 软件的PC 机;运动控制卡主机箱。
三、实验步骤及结果1、PID 控制参数设定及仿真对于 PID 控制参数,我们采用以下的方法进行设定:由实际系统的物理模型:(s)V (s)=0.027250.0102125s 2−0.26705 在 Simulink 中建立如图1所示的直线一级倒立摆控制模型:图1直线一级倒立摆 PID 控制 MATLAB 仿真模型先设置 PID 控制器为P 控制器,令K p =9,K i =0,K D =0,得到以下仿真结果:图2 参数设置窗口图3直线一级倒立摆P控制仿真结果图(K p=9)从图3中可以看出,控制曲线不收敛,因此增大控制量,令Kp =50,Ki=0,KD=0,得到以下仿真结果:图4直线一级倒立摆P控制仿真结果图(K p=50)从图4中可以看出,闭环控制系统持续振荡,周期约为 0.6s。
为消除系统的振荡,增加微分控制参数KD ,令 Kp=50, Ki=0, KD=16 ,得到仿真结果如下:图5直线一级倒立摆PD控制仿真结果图(K p=50,K D=16)从图5中可以看出,系统稳定时间过长,大约为7秒,因此再增加微分控制参数KD ,令:Kp=50, Ki=4, KD=16,仿真得到如下结果:图6直线一级倒立摆 PID 控制仿真结果图(K p=50,K i=4,K D=16)由于 PID 控制器为单输入单输出系统,所以只能控制摆杆的角度,并不能控制小车的位置,所以小车会往一个方向运动。
2、PID 控制实验1) 打开直线一级倒立摆 PID 控制界面入下图6所示:图6直线一级倒立摆 MATLAB 实时控制界面2) 双击"PID"模块进入 PID 参数设置,如下图7所示:图7 参数设置窗口把仿真得到的参数输入 PID 控制器,保存参数。
倒立摆实验报告

摘要系统采用msp430f5438a作为控制核心,实现了增大摆杆角度,令摆杆做圆周运动,在倒立状态下保持平衡,做圆周运动,并具有一定的稳定性,可自起摆。
硬件电路由单片机最小系统板,电机驱动模块,编码器测量转角模块,电源模块,测试表明各项指标均符合要求。
System USES msp430f5438a as control core, has realized the increase the Angle of swinging rod, the swinging rod do circular motion, upside down in a state of balance, to do circular motion, and has certain stability, but since the pendulum.Hardware circuit by the single chip microcomputer minimum system board, motor drive module, encoder measuring Angle module, power module, test showed that all the indexes meet the requirements.一.方案论证根据题目要求,系统要求通过旋转臂的运动来控制摆杆的姿态,系统由msp430系统控制模块,电机驱动模块,角度测量模块,机械部分,电源模块组成。
下面论证其中几个模块的选择。
1.控制器的论证与选择方案一:采用以ARM Cortex - M3为内核的STM32系列控制芯片,其主频很高,功能强大,可进行复杂的逻辑控制,但对于本题而言,其优势资源无法得以体现,且成本稍高。
方案二:采用MSP430f5438a作为控制芯片,其功耗低,成本低,片内外设资源丰富,主要是编程灵活,自由度大,尤其是定时器资源非常丰富。
一阶直线倒立摆双闭环PID控制仿真报告

目录摘要 (2)一、一阶倒立摆系统建模 (3)1、对象模型 (3)2、电动机、驱动器及机械传动装置的模型 (4)二、双闭环PID控制器设计 (5)1、仿真验证 (6)2、内环控制器的设计 (9)3、系统外环控制器设计 (12)三、仿真实验 (15)1、绘图子程序 (15)2、仿真结果 (16)四、结论 (18)摘要本报告旨在借助Matlab 仿真软件,设计基于双闭环PID 控制的一阶倒立摆控制系统。
在如图0.1所示的“一阶倒立摆控制系统”中,通过检测小车的位置与摆杆的摆动角,来适当控制驱动电动机拖动力的大小,控制器由一台工业控制计算机(IPC )完成。
图0.1 一阶倒立摆控制系统分析工作原理,可以得出一阶倒立摆系统原理方框图:图0.2 一阶倒立摆控制系统动态结构图本报告将借助于“Simulink 封装技术——子系统”,在模型验证的基础上,采用双闭环PID 控制方案,实现倒立摆位置伺服控制的数字仿真实验。
一、一阶倒立摆系统建模1、对象模型如图1.1所示,设小车的质量为m 0,倒立摆均匀杆的质量为m ,摆长为2l ,摆的偏角为θ,小车的位移为x ,作用在小车上的水平方向的力为F ,O 1为摆角质心。
θxyOFF xF x F yF yllxO 1图1.1 一阶倒立摆的物理模型根据刚体绕定轴转动的动力学微分方程,转动惯量与角加速度乘积等于作用于刚体主动力对该轴力矩的代数和,则 1)摆杆绕其中心的转动方程为θθθcos sin y l F l F J x-= (1-1) 2)摆杆重心的水平运动可描述为)sin (22x θl x dtd m F += (1-2)3)摆杆重心在垂直方向上的运动可描述为)cos (22y θl dtd m mg F =- (1-3)4)小车水平方向上的运动可描述为220dtxd m F F x =- (1-4)由式(1-2)和式(1-4)得F ml x m m =⋅-⋅++)sin (cos )(20θθθθ (1-5) 由式(1-1)、(式1-2)和式(1-3)得θθθsin g cos 2ml x ml ml J =⋅++ )( (1-6) 整理式(1-5)和式(1-6),得⎪⎪⎩⎪⎪⎨⎧++-+-⋅+⋅=-++-⋅+++=))((cos sin )(cos sin cos cos ))((cos sin sin )()(x 2022202222220222222m l J m m l m m l m m l m F m l l m m m m l J g l m m l J lm F m l J θθθθθθθθθθθθ(1-7) 以上式1-7为一阶倒立摆精确模型。
pid控制倒立摆

PID控制倒立摆前言直线一级倒立摆,是由沿直线导轨运动的小车以及一端固定于小车的匀质长杆组成的非线性的、不稳定的系统。
本文主要讲了采用机理建模的方法得到一阶倒立摆的数学模型,并采用PID 双闭环控制的方式来控制它,从而使其成为稳定的系统,并对整个过程进行了matlab仿真分析。
AbstractFirst-order linear inverted pendulum is composed of a trolley, moved along the linear guides, and a homogeneous pole, one end of which is fixed at the car. However, this system is non-linear and unstable.This article stresses the use of modeling approach to the mechanism of first-order mathematical model of the inverted pendulum, and the use of double-loop PID control to control it, making it a stable system, and the whole process simulation analysis with MATLAB.倒立摆系统是一个非线性自然不稳定系统,是进行控制理论教学及开展各种控制实验的理想实验平台.许多抽象的控制概念,如控制系统的稳定性、可控性、系统抗干扰能力等,都可以通过倒立摆系统直观地表现出来.除教学用途外,倒立摆系统的高阶次、不稳定、多变量、非性和强耦合等特性,使得许多现代控制理论的研究人员一直将它视为研究对象.他们不断从研究倒立摆控制方法中发掘出新的控制方法,并将其应用于航天科技和机器人学等高新科技领域.倒立摆系统是典型的机电一体化系统,其机械部分遵循牛顿的力学定律,其电气部分遵守电磁学的基本定理.因此,可以通过机理建模方法得到较为准确的系统数学模型,通过实际测量和实验来获取系统模型参数.无论哪种类型的倒立摆系统,都具有3个特性,即:不确定性、耦合性、开环不稳定性.直线型倒立摆系统,是由沿直线导轨运动的小车以及一端固定于小车上的匀质长杆组成的系统.小车可以通过传动装置由交流伺服电机驱动.小车导轨般有固定的行程,因而小车的运动范围是受到限制的.设计目的及意义1)、理论联系实际,加强对自动控制理论的理解。
倒立摆的PID控制

(3)
2 小车位置控制算法的仿真 去Kp=100,kd=1,kp=20,阶跃响应仿真曲线 如图所示。
有仿真结果能过看出,当摆杆角度处于很好 的闭环控制下时,小车位置处于失控状态, 会沿着某一方向运动下去。
PID控制器的传递函数为 KD(s)=Kds+Kp+ki/s=(Kd(s^2)+Kps+Ki)/s= numPID/denPID 只需要调节PID控制器的参数,就可以得到满 意的控制效果。 2.小车位置控制 小车位置输出时,系统框图如图1所示。
(1)位置控制图
其中,G1(s)是摆杆传递函数,G2(s)是小车传递函数。
(1)
(2)
改系统的输出为 y(s)=G(s)/(1+KD(s)G(s))*F(s)= (num/den)/(1+(numPID)*(num)/(denPID)*(den))*F(s) =num(denPID)/((denPID)*(den)+(numPID)*(num))*F(s) 式中,num表示被控对象传递函数的分子项;den表示 控对象传递函数的分母项; numPID表示PID控制器传递函数的分子项;denPID表示 PID控制器传递函数的分母项。 被控对象的传递函数是 Φ(s)/U(s)=m*l/q*(s^2)/(s^4+b*(l+m*(l^2)/q*(s^3)(M+m)*m*g*l/q*(s^2)-b*m*g*l/q*s)=num/den 式中,q=[(M+m)*(I+m*l^2)-(m*l)^2].
S= -2.3635+20.43961 -2.3635-20.43961 -0.0001 -0.0001 系统的脉冲响应曲线如图(2)所示:
倒立摆实验报告1

专业实验报告学生姓名学号指导老师实验名称倒立摆与自动控制原理实验实验时间一、实验内容(1)完成Matlab Simulink环境下电机控制实现;(2)完成.直线倒立摆建模、仿真与分析;(3)完成直线一级倒立摆PID控制实验:1)理解并掌握PID控制的原理和方法,并应用于直线一级倒立摆的控制;2)在Simulink中建立直线一级倒立摆模型,通过实验的方法调整PID参数并仿真波形;3)当仿真效果达到预期控制目标后,下载程序到控制机,进行物理实验并获得实际运行图形。
二、实验过程1. 实验原理(1)Matlab Simulink环境下电机控制实现实验对象为倒立摆系统上的交流伺服电机。
将运动控制器当前轴设定成速度控制模式,用户需要设定最大速度和加速度两个参数。
该模式下,开始运动时将以设定的加速度连读加速到设定的最大速度,运动方向由速度的符号确定。
(2)直线倒立摆建模方法对于倒立摆系统,由于其本身是自不稳定的系统,实验建模存在一定的困难,但忽略一些次要因素后,它是一个典型的刚体系统,可应用经典力学理论,建立系统的状态方程数学模型。
(3)直线一级倒立摆PID控制原理经典控制理论的研究对象主要是单输入单输出的系统,控制器设计时一般需要有关被控对象的较精确模型。
PID控制器因其结构简单,容易调节,且不需对系统建立精确的模型,在控制上应用较广。
比例(P作用)增大,系统响应快,对提高稳态精度有益,但过大易引起过度的振荡,降低相对稳定性。
微分(D作用)对改善动态性能和抑制超调有利,但过强,即校正装置的零点靠近原点或者使开环的截止频率增大,不仅不能改善动态性能,反而易引入噪声干扰。
积分(I作用)主要是消除或减弱稳态误差,但会延长调整时间,参数调整不当容易振荡。
2. 实验方法(1)Matlab Simulink环境下电机控制实现在MA TLAB Simulink仿真环境中,利用“Googol Education Products\GT-400-SV Block Library”建立模型,然后进行仿真并分析结果。
直线一级倒立摆实验报告

Gs KDs2 KPs KI
s
相当于给系统增加了一个位于原点的开环极点和两个位置可变的开环零点,因此 对于低阶已知数学模型的系统,根据期望的性能指标可以采用根轨迹法确定PID 参数。
2、频域法确定PID参数 对于已知频率特性曲线的系统,PID控制器相当于 给频率特性曲线增加了积分环节和一个二阶微分环节,通过调整PID参数,可以 改变PID控制器的频率特性,进而改变闭环系统的频率特性。
当摆杆被控时,小车的运动的位移也受到导轨实际长度的限制。因此,输出量除 了摆杆角度外,还有一个小车运动的位移。位移与输入量小车加速度之间的关系 为:
X (s) 1
Rs s2
控制系统结构图:
1
s2
Transfer Fcn1
Pos
3
In1 Out1
Step
s2+-29.4
Addห้องสมุดไป่ตู้
Transfer Fcn
Step 0.08
0.06
0.04
0.02
0
0
1
2
3
4
5
6
7
8
9
10
Pos.
0
-2
-4
0
1
2
3
4
5
6
7
8
9
10
Ang.
4
3
2
1
0
0
1
2
3
4
5
6
7
8
9
10
由曲线可以看出,系统角度超调量为33.6%,调整时间接近0.55秒,位移变化平 稳,角度输出稳定。故这组参数可以作为PID控制参数;
2、基于计算机MATLAB 平台进行现场倒立摆控制,绘制实验曲线; 直线一级倒立摆系统是小车在光滑的导轨上运动,小车上铰链了一根摆杆,
