电路分析第十三章
合集下载
第十三章 拉普拉斯变换

拉普拉斯反变换的计算较复杂,一般多采用部分分式展开的 方法间接求得。 设F(s)可以表示为如下的有理分式,m 和n 为正整数,且 n ≥m 。
N ( s ) a0 s m + a1s m −1 + L + am F ( s) = = D( s ) b0 s n + b1s n −1 + L + bn
∞
−
F (s) f (ξ )dξ ] = s
e-stdt,
利用∫ udv = uv − ∫ vdu
则: 0 [(
1 − st ∴ du = f (t )dv,v = − e s
− st ∞
∫ ∫
= (∫
t
t
0−
f (ξ )dξ )e − st dt ] = ( ∫
t
0−
0−
e f (ξ )dξ ) −s
16
例:13-7
s+3 求:F(s) = 2 的原函数f (t ) s + 2s + 5
17
3、D(s)=0 具有q阶重根p1 , 其余为单根p2、 p3、
K11 K2 则:F ( s ) = + +L+ +( + L) 2 q s − p1 ( s − p1 ) ( s − p1 ) s − p2
则 f(t)的拉氏变换F(s)总是存在。 本书涉及的f(t)均满足上述条件
1 c + j∞ 拉普拉斯反变换的定义: f (t ) = F ( s )e st ds 2πj ∫c − j∞
式中,M , c为正的有限常数
−1
用 [ ]表示对中括号中的时域函数作拉氏变换 用 [ ]表示对中括号中的复变函数作拉氏反变换 例如:F(s)= [f(t)]=
08版电路基础第13章一阶电路时域分析

第十三章 一阶电路时域分析
电路分析: 激励 线性定常电路
响应
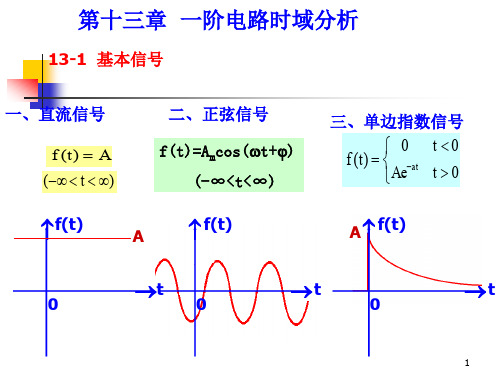
13-1 基本信号
一、直流信号 二、正弦信号 三、单边指数信号
f (t) A f(t)=Amcos(t+)
( t ) (-∞<t<∞)
0 t0
f
(t)
Aeat
t0
一、直流信号 二、正弦信号 三、单边指数信号
f (t) A f(t)=Amcos(t+)
电路初始值
独立初始值: uc (o+)、 iL(o+)
非独立初始值: 其余电量在t= o+时的值
非独立初始值的确定: o+等效电路法
步骤:
1、求出电路的初始状态: uc (o-)、 iL(o-) 2、求出独立初始值: uc (o+)、 iL(o+)
3、画出o+等效电路:
4、求得非独立初始值
电容用uc (o+)电压源替代 电感用iL (o+)电流源替代 电路其余结构不变
电荷守恒定律:
换路时刻,电容联 接处电荷守恒。即:
Ckuk (o ) Ckuk (o )
k 1
k 1
或: qk (o ) qk (o )
k 1
k 1
+ u1 - + u2 -
正负号:由电压的参考极性确定(与+极接时取+ ,否则取-)
电容电压u(t)突跳时:ic (t)
确定电容电压初始值:
t0
t0
(t
t0
)dt
1
推广1:
(t
t0
)
0
t t0 t t0
(t
t0
)dt
电路分析: 激励 线性定常电路
响应
13-1 基本信号
一、直流信号 二、正弦信号 三、单边指数信号
f (t) A f(t)=Amcos(t+)
( t ) (-∞<t<∞)
0 t0
f
(t)
Aeat
t0
一、直流信号 二、正弦信号 三、单边指数信号
f (t) A f(t)=Amcos(t+)
电路初始值
独立初始值: uc (o+)、 iL(o+)
非独立初始值: 其余电量在t= o+时的值
非独立初始值的确定: o+等效电路法
步骤:
1、求出电路的初始状态: uc (o-)、 iL(o-) 2、求出独立初始值: uc (o+)、 iL(o+)
3、画出o+等效电路:
4、求得非独立初始值
电容用uc (o+)电压源替代 电感用iL (o+)电流源替代 电路其余结构不变
电荷守恒定律:
换路时刻,电容联 接处电荷守恒。即:
Ckuk (o ) Ckuk (o )
k 1
k 1
或: qk (o ) qk (o )
k 1
k 1
+ u1 - + u2 -
正负号:由电压的参考极性确定(与+极接时取+ ,否则取-)
电容电压u(t)突跳时:ic (t)
确定电容电压初始值:
t0
t0
(t
t0
)dt
1
推广1:
(t
t0
)
0
t t0 t t0
(t
t0
)dt
第13章 拉普拉斯变换

k2 s2
k3 s5
0 .1 s
0 .5 s2
0 .6 s5
k 1 sF ( s )
s0
1 25
0 .1
k1
2s 1 3s 14s 10
2 s0
1 10
0 .1
k 2 ( s 2 ) F ( s ) s 2
2( 2) 1 2 ( 2 5)
I2(s) + sL2
+ i1
u1 –
u 1 L1
M
L1 L2
i2
+
u2 –
+ –
+ – + –
+
L2i2(0-)
U2(s)
–
Mi1(0-)
+
–
d i1 dt d i2 dt
M
d i2 dt
U 1 ( s ) sL 1 I 1 ( s ) L1 i 1 ( 0 ) sMI 2 ( s ) Mi 2 ( 0 ) U 2 ( s ) sL 2 I 2 ( s ) L 2 i 2 ( 0 ) sMI 1 ( s ) Mi 1 ( 0 )
本章重点:
1. 运算形式的电路定律和元件约束
2. 用运算法分析线性电路
§13-1 拉普拉斯变换的定义
一、定义
F 双边拉氏变换:( s ) F 单边拉氏变换:( s ) 1 f (t ) 拉氏反变换: 2 j
f (t ) e
0
c j
c j
把傅氏变换的 j s j F f ( t ) e dt 记作 ( s ) L [ f ( t )] 正变换 1 F ( s ) e ds 记作 f ( t ) L [ F ( s )] 反变换
电路分析基础课件第13章 二端口网络

•
I
•
2I
2
+
NN
•
U2
••
I 1I 1
•+
U1
••
II2 2
++
NN
••
UU2 2
Y12
I1 U 2
U1 0
Y22
I2 U 2
U1 0
转移导纳 输入导纳
Y → 短路导纳参数
例2-1 求图示二端口的Y 参数。
解
•
I I I •
•
1 11
Yb YbYb
•
I I I •
•
2
2
2
++
•
••
UU1
1U01
第13章 二端口网络
13-1 13-2 13-3 13-4 13-5 13-6
二端口网络 二端口的方程和参数 二端口的等效电路 二端口的转移函数 二端口的连接 回转器和负阻抗转换器
重点
1. 二端口的参数和方程 2. 二端口的等效电路 3. 二端口的转移函数
13-1 二端口网络
在工程实际中,研究信号及能量的传输和 信号变换时,经常碰到如下二端口电路。
•
I1
例2-8 求二端口T 参数。 +
•
U1
解
n 0
T
0
1
n
1
2
•
I2
+
2
•
U2
A U1 U2
I2 0 1.5
B
U1 I2
U2 0
4Ω
C I1 U2
I2 0 0.5 S
D I1 I2
U2 0
2
电路分析第十三章-拉普拉斯变换

⑵ 在t充分大时, f (t) 满足不等式
f (t) ≤ Me ct
其中M和c 都是实常数,即f(t)为指数级函数。
∫ 则 F (s) = ∞ f (t)e−st dt 0− 在σ > c 的范围内存在。
西南交通大学
证明条件⑵:
∫ 若 ∞ f (t)e−st dt 收敛, 则 L[ f (t)] 也收敛。 0−
)
−
Eε (t
−
t0
)
F (s)
=
L
[
f
(t)] =
E t0
⋅
1 s2
−
E t0
⋅
1 s2
e − st0
−
E
1 e−st0 s
=
E s 2t0
[1− (1+
st0 )e−st0 ]
西南交通大学
3、复频域位移 f (t) ↔ F (s)
f (t)e−αt ↔ F (s + α)
∫ 证明:L [ f (t)e−αt ] = ∞ f (t)e−αte−st dt 0− ∫= ∞ f (t)e−(s+α)t dt = F (s + α) 0−
同理
L[
cosω0t ⋅ε (t)
]=
s
s2 + ω02
5、幂函数tn ,n为正整数
L [ tn
]=
n! s n+1
L[
t
]=
1 s2
西南交通大学
4、幂指数信号 tn n为正整数
L ∫ [t n ] =
∞ 0−
t
en −st
dt
| ∫ =
− tn s
e − st
∞ 0−
f (t) ≤ Me ct
其中M和c 都是实常数,即f(t)为指数级函数。
∫ 则 F (s) = ∞ f (t)e−st dt 0− 在σ > c 的范围内存在。
西南交通大学
证明条件⑵:
∫ 若 ∞ f (t)e−st dt 收敛, 则 L[ f (t)] 也收敛。 0−
)
−
Eε (t
−
t0
)
F (s)
=
L
[
f
(t)] =
E t0
⋅
1 s2
−
E t0
⋅
1 s2
e − st0
−
E
1 e−st0 s
=
E s 2t0
[1− (1+
st0 )e−st0 ]
西南交通大学
3、复频域位移 f (t) ↔ F (s)
f (t)e−αt ↔ F (s + α)
∫ 证明:L [ f (t)e−αt ] = ∞ f (t)e−αte−st dt 0− ∫= ∞ f (t)e−(s+α)t dt = F (s + α) 0−
同理
L[
cosω0t ⋅ε (t)
]=
s
s2 + ω02
5、幂函数tn ,n为正整数
L [ tn
]=
n! s n+1
L[
t
]=
1 s2
西南交通大学
4、幂指数信号 tn n为正整数
L ∫ [t n ] =
∞ 0−
t
en −st
dt
| ∫ =
− tn s
e − st
∞ 0−
邱关源《电路》第十三章拉普拉斯变换2

I1(s)
s(s 200)2
BUCT
14
(4)反变换求原函数
I1(s)
5( s 2
700s 40000) s(s 200)2
F2(s) 0有3个根s1 0,s2 s3 200
BUCT
I1(s)
K5 1 s
s
K021 200
(s
1K52020 200)2
类似地:
u(t) U (s)
运算形式KCL、KVL
i(t) I(s) U(s) Z(s) I(s) 元件 运算阻抗、运算导纳
运算形式 电路模型
2
1.电路定律的运算形式
BUCT
KCL i 0 KVL u 0
I(s) 0 U(s) 0
2.电路元件的运算形式
25 3.75s (s 12.5)s
2 1.75 s s 12.5
5 3.75
i1
i2
2
0
i1(0 ) i1(0 )
i2(0 ) i2(0 )
t
18
I 1(S)
1.5 0.3s – +
+
2
UL1(s)
I(2 s)I1(s)
2 s
s
1.75 12.5
0.1s
1 sC
BUCT
uC (0 ) 0 iL(0 ) 0
时域电路
运算电路
1. 电压、电流用象函数形式
2. 元件用运算阻抗或运算导纳
3.电容电压和电感电流初始值用附加电源表示
9
I C (s)
uC(0 -) /s
电路第十三章 一阶电路时域分析
或 q (o+)= q (o-)
意义:
能量不能发生突变
6
2、引例2: 图示电路
t<0 ,K打开,有 iL (0 ) 0
t=0 ,K闭合,有
iL
(t)
1 L
t
uL
()d
若uL有限,则: iL (o+)=iL (o-)
1 L
0
uL ()d
ቤተ መጻሕፍቲ ባይዱ
1 L
t
uL ()d
0
t0
f
(t)
Aeat
cos(t
)
t0
五、单位阶跃信号
实现:开关电路
定义:
U
(t
)
0 1
t0 t0
U (t)
性质:切除性
0 t0
y(t)=f(t)U(t)
f
(t)
t0
推广:
0 U(t t0) 1
t t0 t t0
0 t 0
R 0
2
C2
du2 ]dt dt 2
若u1和u2有限值,则有 C1u1(o ) C1u1(o ) C2u2 (o ) C2u2 (o )
C1u1(o ) C2u2 (o ) C1u1(o ) C2u2 (o ) u1(o ) u2 (o ) Us
3、线性性 : 若 f 1(t) y1 (t) f 2(t) y2 (t)
则 Af 1(t) +B f 2(t) A y1 (t)+ By2 (t)
4、时不变性:若 f (t) y (t) 则 f (t - t0) y (t - t0)
意义:
能量不能发生突变
6
2、引例2: 图示电路
t<0 ,K打开,有 iL (0 ) 0
t=0 ,K闭合,有
iL
(t)
1 L
t
uL
()d
若uL有限,则: iL (o+)=iL (o-)
1 L
0
uL ()d
ቤተ መጻሕፍቲ ባይዱ
1 L
t
uL ()d
0
t0
f
(t)
Aeat
cos(t
)
t0
五、单位阶跃信号
实现:开关电路
定义:
U
(t
)
0 1
t0 t0
U (t)
性质:切除性
0 t0
y(t)=f(t)U(t)
f
(t)
t0
推广:
0 U(t t0) 1
t t0 t t0
0 t 0
R 0
2
C2
du2 ]dt dt 2
若u1和u2有限值,则有 C1u1(o ) C1u1(o ) C2u2 (o ) C2u2 (o )
C1u1(o ) C2u2 (o ) C1u1(o ) C2u2 (o ) u1(o ) u2 (o ) Us
3、线性性 : 若 f 1(t) y1 (t) f 2(t) y2 (t)
则 Af 1(t) +B f 2(t) A y1 (t)+ By2 (t)
4、时不变性:若 f (t) y (t) 则 f (t - t0) y (t - t0)
第十三章拉普拉斯变换

t f (ξ )dξ e − st dt 所以 ∫ ∫ 0− 0−
∞
t f (ξ )dξ e = ∫ 0− −s t f (ξ )dξ e = ∫ 0− −s
− st ∞
− ∫ f (t )e − st dt
0−
∞ ∞
其中,当t<t0时,f (t-t0)=0。令τ=t-t0
ℓ[ f (t − t 0 )] = ∫ f (t − t 0 )e dt = ∫ f (t − t 0 )e − st dt
0− ∞ t0 − st ∞
= ∫ f (τ )e
0−
− s (τ + t 0 )
dτ = e
− st 0
∫
0−
−t
( s − pi ) n 的因 3、如果D(s)=0具有重根,则应含 ( s − pi )3的因式,p1为 式。现设D(s)中含有
即
N (s) Ki = (i = 1、、 …、n) 2 3、 D′( s) s = pi
确定了各待定系数后,相应的原函数为
f (t ) = ℓ [ F ( s)] = ∑ K i e
−1 i =1 n pi t
N ( pi ) pit =∑ e i =1 D′( pi )
n
例13-6
解 因为
2s + 1 求 F ( s) = s 3 + 7 s 2 + 10s
ω = 2 s +ω2
(2)ℓ[ K (1 − e −αt )] = ℓ[ K ] − ℓ[ Ke −αt ] K K = − s s +α Kα = s( s + α )
由此可见,根据拉氏变换的线性性质, 求函数乘以常数的象函数以及求几个函数 相加减的结果的象函数时,可以先求各函 数的象函数再进行计算。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
26385-13A
图 13-7
一、非线性电阻的串联
26385-13A
图 13-8
二、非线性电阻的并联
26385-13A
图 13-9
一、非线性电阻的串联
26385-13A
图 13-10
三、非线性电阻的混联
26385-13A
图 13-11
三、非线性电阻的混联
26385-13A
图 13-12
四、仅含一个非线性电阻的电路
26385-13A
图 13-13
第四节 小信号分析法
26385-13A
图 13-14
第四节 小信号分析法
26385-13A
图 13-15
第五节 应 用 示 例
26385-13A
图 13-16
第五节 应 用 示 例
26385-13A
图 13-17
第五节 应 用 示 例
26385-13A
图 13-18
第五节 应 用 示 例
26385-13A
图 13-30
第五节 应 用 示 例
26385-13A
图 13-31
26385-13A
图 13-24
第五节 应 用 示 例
26385-13A
图 13-25
第五节 应 用 示 例
26385-13A
图 13-26
第五节 应 用 示 例
26385-13A
图 13-27
第五节 应 用 示 例
26385-13A
图 13-28
第五节 应 用 示 例
26385-13A
图 13-29
26385-13A
图 13-4
二、非线性电容元件
26385-13A
图 13-5
三、非线性电感元件
26385-13A
图 13-6
第三节 应用于非线性直流电路的图解 法
一、非线性电阻的串联 二、非线性电阻的并联 三、非线性电阻的混联 四、仅含一个非线性电阻的电路
26385-13A
一、非线性电阻的串联
第十三章 非线性电路
第一节 第二节 第三节 第四节 第五节
概述 非线性电阻、电感和电容 应用于非线性直流电路的图解法 小信号分析法 应用示例
26385-13A
第一节 概 述
以前各章讨论的内容均为线性电路,其中的电阻、电 感和电容等元件的参数都是常数。严格地说,实际电 路元件或多或少都具有非线性,只是当该元件所加电 压和电流局限在一定范围内时,按线性元件处理计算 误差可予忽略;但当超过此范围时,再按线性元件处 理时,会导致很大误差。此外,在电工技术中,还广 泛使用一类有别于上述可线性化处理的实质性的非线 性元件,用于产生整流、稳压、分频与振荡等功能。
第五节 应 用 示 例
26385-13A
图 13-19
第五节 应 用 示 例
26385-13A
图 13-20
第五节 应 用 示 例
2638 例
26385-13A
图 13-22
第五节 应 用 示 例
26385-13A
图 13-23
第五节 应 用 示 例
26385-13A
第二节 非线性电阻、电感和电容 一、非线性电阻元件 二、非线性电容元件 三、非线性电感元件
26385-13A
一、非线性电阻元件
图 13-1 26385-13A
一、非线性电阻元件
26385-13A
图 13-2
一、非线性电阻元件
26385-13A
图 13-3
一、非线性电阻元件
