圆柱、圆锥、圆台
合集下载
圆柱、圆锥、圆台

情境引入 一个形的世界,我处处离不开你
情境引入
情境引入
情境引入
圆柱、圆锥、圆台
圆柱、圆锥、 圆柱、圆锥、圆台
名称 圆柱 圆锥 圆台
图形
h h l
l
h
r
l
r
r
以直角三角形一直 角边所在直线为轴, 其余各边旋转而成 的曲面所围成的几 何体 轴截面是全等等腰 三角形
R
以直角梯形垂直于 底边的腰所在直线 为轴,其余各边旋 转而成的曲面所围 成的几何体 轴截面是全等等腰 梯形
定义
以矩形一边所在 直线为轴,其余 各边旋转而成的 曲面所围成的几 何体。 轴截面是全等的 矩形
轴截面
圆柱、圆锥、圆台之间的关系
底面 圆柱 圆锥 圆台 平行于底面 轴截面 的截面
有两个、平 与两底面全 矩形 行且相等 等 只有一个 与底面相似 等腰三角形
有两个平行 与两底面相 等腰梯形 且相似 似
1、下列命题正确的是(D ) ⑴、在圆柱的上下地面各取一点,则这两点的连线是圆柱的母线。 ⑵、圆锥顶点与底面圆周上任意一点的连线是圆锥的母线。 ⑶ 、在圆周上下底面圆上各取一点,则这两点的连线是圆台的母线。 ⑷、圆柱的任意两条母线所在的直线都是互相平行的。 A 、⑴ ⑵ B 、⑵ ⑶ C、⑴⑶ D、⑵⑷
o1 r
l
ቤተ መጻሕፍቲ ባይዱ
o R
Q R = r + a = 2r
∴r = a
∴ R = 2a
2、下列说法正确的是(C) A直角三角形绕一边旋转得到的旋转体是圆锥 B夹在圆柱两个平行截面间的几何体还是圆柱 C圆锥截去一个小圆锥后剩余部分是圆台 D通过圆台侧面上一点,有无数条母线 3、一个圆柱的母线长为5,底面圆半径为2,则圆柱的轴截面积为:(C ) A、10 B、15 C、20 D、40
情境引入
情境引入
情境引入
圆柱、圆锥、圆台
圆柱、圆锥、 圆柱、圆锥、圆台
名称 圆柱 圆锥 圆台
图形
h h l
l
h
r
l
r
r
以直角三角形一直 角边所在直线为轴, 其余各边旋转而成 的曲面所围成的几 何体 轴截面是全等等腰 三角形
R
以直角梯形垂直于 底边的腰所在直线 为轴,其余各边旋 转而成的曲面所围 成的几何体 轴截面是全等等腰 梯形
定义
以矩形一边所在 直线为轴,其余 各边旋转而成的 曲面所围成的几 何体。 轴截面是全等的 矩形
轴截面
圆柱、圆锥、圆台之间的关系
底面 圆柱 圆锥 圆台 平行于底面 轴截面 的截面
有两个、平 与两底面全 矩形 行且相等 等 只有一个 与底面相似 等腰三角形
有两个平行 与两底面相 等腰梯形 且相似 似
1、下列命题正确的是(D ) ⑴、在圆柱的上下地面各取一点,则这两点的连线是圆柱的母线。 ⑵、圆锥顶点与底面圆周上任意一点的连线是圆锥的母线。 ⑶ 、在圆周上下底面圆上各取一点,则这两点的连线是圆台的母线。 ⑷、圆柱的任意两条母线所在的直线都是互相平行的。 A 、⑴ ⑵ B 、⑵ ⑶ C、⑴⑶ D、⑵⑷
o1 r
l
ቤተ መጻሕፍቲ ባይዱ
o R
Q R = r + a = 2r
∴r = a
∴ R = 2a
2、下列说法正确的是(C) A直角三角形绕一边旋转得到的旋转体是圆锥 B夹在圆柱两个平行截面间的几何体还是圆柱 C圆锥截去一个小圆锥后剩余部分是圆台 D通过圆台侧面上一点,有无数条母线 3、一个圆柱的母线长为5,底面圆半径为2,则圆柱的轴截面积为:(C ) A、10 B、15 C、20 D、40
圆柱、圆锥、圆台和球

似三角形的性质得
3 r 3 l 4r
解得l=9.
所以,圆台的母线长为9cm.
例2. 我国首都北京靠近北纬40度。
求北纬40度纬线的长度约为多少千米 (地球半径约为6370千米)?
解:如图,设A是北纬40°圈上一点,AK 是它的半径,所以 OK⊥AK,
设c是北纬40°的纬线长, 因为∠OAK= ∠AOB = 40°,
3.表示方法:用表示它的轴的字母表示, 如圆柱OO’ .
4.有关性质: (1)用平行于底面的平面去截,截面都 是圆。 (2)圆柱、圆锥、圆台的轴截面分别是 全等的矩形、全等的等腰三角形、全等的 等腰梯形;
5.侧面展开图:
(1)圆柱的侧面展开图是矩形。 (2)圆锥的侧面展开图是扇形. (3)圆台的侧面展开图是扇环.
所以 c=2π·AK=2π·OA·cos∠OAK =2π·OA·cos40° ≈2×3.1416×6370×0.7660 ≈3.066×104(km),
即北纬40°的纬线长约为3.066×104km.
练习: 1、圆柱的轴截面是正方形,它的面
h
积为9 ,求圆柱的高与底面的周长。
(h=3, c=2πr=3π)
即O到截面圆心O1的距离;
(4)大圆与小圆:球面被经过球心的平面截 得的圆叫做球的大圆, 被不经过球心的平面截得的圆叫做球 的
小圆;
5.球面距离:在球面
上,两点之间的最短距
离就是经过这两点的大
A
圆在这两点间的一段劣
弧的长度。这个弧长叫 B
做两点的球面距离。
O
三.旋转体的概念
由一个平面图形绕着一条直线旋转产生的 曲面所围成的几何体叫做旋转体,这条直线 叫做旋转体的轴。比如常见的旋转体有圆柱、 圆锥、圆台和球.
圆柱圆锥圆台PPT课件

§2.4 圆柱、圆锥、圆台
一、素质教育目标
(一)知识教学点
1.圆柱、圆锥、圆台的概念和性质。
2.圆柱、圆锥、圆台的直观图的画法。
3.圆柱、圆锥、圆台的侧面积。
(二)能力训练点
1.理解圆柱、圆锥、圆台的概念,掌握它们的性质,能利用它们之间的内在联 系进行转化,不断提高学生分析问题的能力。
2.通过它们直观图画法的教学,使学生掌握正等测法的作图,进一步提高学生 作图及识图能力。
3.掌握它们侧面积的计算公式,能综合应用这些公式计算有关图形的面积, 提高学生综合应用知识的能力。
完整版课件
1
(三)德育渗透点
1.圆柱、圆锥、圆台的形成是通过平面图形的旋转而得到,即通过运动的 形式来给出定义.教学过程要结合实际注意培养学生掌握运用运动变化的观 点来分析问题.
2.圆柱、圆锥及圆台的共同属性是,都由平面多边形旋转而得到,因此平 面图形之间的关系决定了它们之间的关系.教学过程要注意培养学生抓住它 们的内在联系来把握它们的变化,帮助学生树立联系变化的辩证唯物主义观 点.
生:有,应该加上全等两个字.
(教师肯定学生的答案后,板书出两条性质.)
师:性质2.给出了圆柱、圆锥、圆台的本质特征.今后有关三个几何 体的计算问题只要在它们轴截面上作文章,甚至今后分析有关问题可直 接在其轴截面上进行而不必画出它们的实际图形.另外有了性质1.我们 可以认为圆台是一个圆锥截掉一个小圆锥后余下的部分,所以有关圆台 的问题就可以转化为圆锥的问题来解决.
性质2给出了圆柱圆锥圆台的本质特征今后有关三个几何体的计算问题只要在它们轴截面上作文章甚至今后分析有关问题可直接在其轴截面上进行而不必画出它们的实际图形另外有了性质1我们可以认为圆台是一个圆锥截掉一个小圆锥后余下的部分所以有关圆台的问题就可以转化为圆锥的问题来解决例1把一个圆锥截成圆台已知圆台的上下底面半径是14母线长是10cm求圆锥的母线长分析
一、素质教育目标
(一)知识教学点
1.圆柱、圆锥、圆台的概念和性质。
2.圆柱、圆锥、圆台的直观图的画法。
3.圆柱、圆锥、圆台的侧面积。
(二)能力训练点
1.理解圆柱、圆锥、圆台的概念,掌握它们的性质,能利用它们之间的内在联 系进行转化,不断提高学生分析问题的能力。
2.通过它们直观图画法的教学,使学生掌握正等测法的作图,进一步提高学生 作图及识图能力。
3.掌握它们侧面积的计算公式,能综合应用这些公式计算有关图形的面积, 提高学生综合应用知识的能力。
完整版课件
1
(三)德育渗透点
1.圆柱、圆锥、圆台的形成是通过平面图形的旋转而得到,即通过运动的 形式来给出定义.教学过程要结合实际注意培养学生掌握运用运动变化的观 点来分析问题.
2.圆柱、圆锥及圆台的共同属性是,都由平面多边形旋转而得到,因此平 面图形之间的关系决定了它们之间的关系.教学过程要注意培养学生抓住它 们的内在联系来把握它们的变化,帮助学生树立联系变化的辩证唯物主义观 点.
生:有,应该加上全等两个字.
(教师肯定学生的答案后,板书出两条性质.)
师:性质2.给出了圆柱、圆锥、圆台的本质特征.今后有关三个几何 体的计算问题只要在它们轴截面上作文章,甚至今后分析有关问题可直 接在其轴截面上进行而不必画出它们的实际图形.另外有了性质1.我们 可以认为圆台是一个圆锥截掉一个小圆锥后余下的部分,所以有关圆台 的问题就可以转化为圆锥的问题来解决.
性质2给出了圆柱圆锥圆台的本质特征今后有关三个几何体的计算问题只要在它们轴截面上作文章甚至今后分析有关问题可直接在其轴截面上进行而不必画出它们的实际图形另外有了性质1我们可以认为圆台是一个圆锥截掉一个小圆锥后余下的部分所以有关圆台的问题就可以转化为圆锥的问题来解决例1把一个圆锥截成圆台已知圆台的上下底面半径是14母线长是10cm求圆锥的母线长分析
高中数学 必修2(人教版)8.3.2圆柱、圆锥、圆台、球的表面积和体积

圆 台
上底半径为r,下底半径为R,高为h,V=
1 3
π(r2+rR+R2)h
球
V=43πR3
状元随笔 (1)求旋转体的表面积时,要清楚常见旋转体的侧 面展开图是什么,关键是求其母线长与上、下底面的半径.
(2)柱体、锥体、台体体积之间的关系 柱体、锥体、台体的关系如下:
(3)两个结论 ①两个球的体积之比等于这两个球的半径之比的立方. ②两个球的表面积之比等于这两个球的半径之比的平方.
易错警示
易错原因
纠错心得
球心所在的截面位置判断错误, 对多面体及外接球的几何特点理
解模糊,基本量之间的关系不 清.
解决此类问题要确定球心的位置 及其所在的截面,在截面中寻找 球半径与多面体基本量的关系.
×2×1×r×2+
ห้องสมุดไป่ตู้
1 3
×
1 2
×1×1×r+
1 3
×12× 2× 答案:4π
5-12×r,解得r=14. 故内切球的表面积为4πr2=π4.
方法归纳
对于正四面体,有以下结论:
(1)正四面体的外接球与内切球的球心重合;
(2)棱长为a的正四面体的高为
6 3
a,其外接球的半径为
6 4
a,
内切球的半径为
解析:设球的半径为R,则圆柱的底面半径为R,高为2R. ∵V球=43πR3,V圆柱=πR2·2R=2πR3, ∴V球:V圆柱=43πR3:2πR3=23. 答案:2:3
易错辨析 对球的“切、接”的结构特点认识模糊致错 例5 设三棱柱的侧棱垂直于底面,所有棱长都为a,顶点在 一个球面上,则该球的表面积为( ) A.πa2 B.73πa2 C.74πa2 D.5πa2
解析:在三棱锥P - ABC中,PA,PB,PC两两垂直,则以 PA,PB,PC为邻边作一长方体,所以三棱锥P - ABC的外接球即
圆柱、圆锥、圆台的概念和性质

3.掌握它们侧面积的计算公式,能综合应用这些公式计算有关图形的面积, 提高学生综合应用知识的能力。
完整版ppt
1
(三)德育渗透点
1.圆柱、圆锥、圆台的形成是通过平面图形的旋转而得到,即通过运动的 形式来给出定义.教学过程要结合实际注意培养学生掌握运用运动变化的观 点来分析问题.
2.圆柱、圆锥及圆台的共同属性是,都由平面多边形旋转而得到,因此平 面图形之间的关系决定了它们之间的关系.教学过程要注意培养学生抓住它 们的内在联系来把握它们的变化,帮助学生树立联系变化的辩证唯物主义观 点.
二、教学重点、难点、疑点及解决办法
1.教学重点:圆柱、圆锥、圆台的概念、性质及侧面积公式.
2.教学难点:圆柱、圆锥、圆台的直观图的画法.
3.教学疑点:直观图为什么用正等测法,而不用斜二测法,通过比较让学 生明白用正等测法的便利.
三、课时安排
2课时.
完整版ppt
2
四、教与学的过程设计
第一课时 圆柱、圆锥、圆台的概念、性质及直观图的画法
完整版ppt
6
例1 把一个圆锥截成圆台,已知圆台的上、下底面半径是1∶4,母线长 是10cm,求圆锥的母线长.
分析:如图2-28,△O'OA是圆锥轴截面的一半,则直角梯形COAB是圆台 轴截面的一半,由BC∥AO易得O'B∶O'A=BC∶AO=1∶4
(具体解答请同学们阅读课本)
师:(小结).注意“还台于锥”以及利用平行式相似来解决问题.
的任意一对相垂直的直径变为椭圆的一对直径(它们称为椭圆的共扼直
径).既然圆的直观图是椭圆,为方便起见,今后我们可以直接用椭圆模板或
椭圆的近似画法来画.
完整版ppt
8
例3 一个圆锥的底面半径是1.6cm,在它的内部有一个底面半径为0.7cm, 高为1.5cm的内接圆柱,画出它们的直观图.
完整版ppt
1
(三)德育渗透点
1.圆柱、圆锥、圆台的形成是通过平面图形的旋转而得到,即通过运动的 形式来给出定义.教学过程要结合实际注意培养学生掌握运用运动变化的观 点来分析问题.
2.圆柱、圆锥及圆台的共同属性是,都由平面多边形旋转而得到,因此平 面图形之间的关系决定了它们之间的关系.教学过程要注意培养学生抓住它 们的内在联系来把握它们的变化,帮助学生树立联系变化的辩证唯物主义观 点.
二、教学重点、难点、疑点及解决办法
1.教学重点:圆柱、圆锥、圆台的概念、性质及侧面积公式.
2.教学难点:圆柱、圆锥、圆台的直观图的画法.
3.教学疑点:直观图为什么用正等测法,而不用斜二测法,通过比较让学 生明白用正等测法的便利.
三、课时安排
2课时.
完整版ppt
2
四、教与学的过程设计
第一课时 圆柱、圆锥、圆台的概念、性质及直观图的画法
完整版ppt
6
例1 把一个圆锥截成圆台,已知圆台的上、下底面半径是1∶4,母线长 是10cm,求圆锥的母线长.
分析:如图2-28,△O'OA是圆锥轴截面的一半,则直角梯形COAB是圆台 轴截面的一半,由BC∥AO易得O'B∶O'A=BC∶AO=1∶4
(具体解答请同学们阅读课本)
师:(小结).注意“还台于锥”以及利用平行式相似来解决问题.
的任意一对相垂直的直径变为椭圆的一对直径(它们称为椭圆的共扼直
径).既然圆的直观图是椭圆,为方便起见,今后我们可以直接用椭圆模板或
椭圆的近似画法来画.
完整版ppt
8
例3 一个圆锥的底面半径是1.6cm,在它的内部有一个底面半径为0.7cm, 高为1.5cm的内接圆柱,画出它们的直观图.
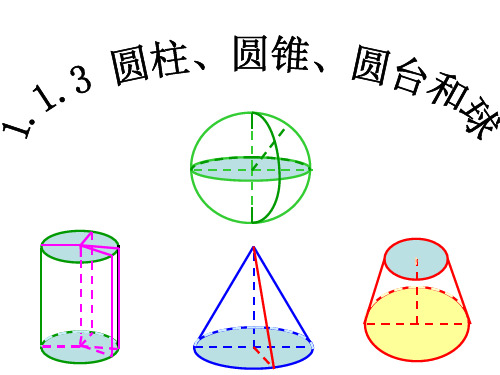
1.1.3 圆柱、圆锥、圆台和球
组合体
简单组合体
日常生活中我们常用到的日用品,比如:消毒液、 暖瓶、洗洁精等的主要几何结构特征是什么? 由柱、锥、台、球组成了一些简单的组合体.认 识它们的结构特征要注意整体与部分的关系.
圆柱
圆台
圆柱
简单组合体
走在街上会看到一些物体,它们的主要几何结构特 征是什么?
简单组合体
一些螺母、带盖螺母又是有什么主要的几何结构特 征呢?
90° 60° 66.5°北极圈
40°
20° 30° 0° 20° 40° 60° 90° 60° 90° 120° 150° 赤道 23.5° 南回归线 23.5° 北回归线
南极圈 66.5°
P地的纬度就是经过 P点的球半径和赤道 平面所成的线面角 ∠POA的度数
北极
G
r R
P
O
A
南极
球面离
简单组合体
蒙古大草原上遍布蒙古包,那么蒙古包的主要几 何结构特征是什么?
简单组合体
居民的住宅又有什么主要几何结构特征?
简单组合体
下图是著名的中央电视塔和天坛,你能说说它们的 主要几何结构特征吗?
你能从旋转体的概念说说它们是由什么图形旋转而 成的吗?
旋转体
你能想象这条曲线绕轴旋转而成的几何图形吗?
O S
O
2、表示:如圆锥SO。
圆台
O1 O
用一个平行于圆锥底面的平面去截 圆锥,底面与截面之间的部分是圆台.
思考:圆柱、圆锥和圆台都是旋转体,当 底面发生变化时,它们能否互相转化?
上底扩大 上底缩小
思考:圆柱、圆锥、圆台过轴的截面分 别是什么图形?
例1. 用一个平行圆锥底面的平面截这个 圆 锥,截得圆台上下底面半径的比是1:4,截 去的圆锥的母线长是3cm,求圆台的母线长。
圆柱、圆锥、圆台和球

12345
课堂小结
KE TANG XIAO JIE
1.知识清单: (1)圆柱、圆锥、圆台的结构特征. (2)球的结构特征. (3)复杂空间图形的结构特征. 2.方法归纳:分类讨论、转化与化归. 3.常见误区:同一平面图形以不同的轴旋转形成的旋转体一般是不 同的.
4 课时对点练
PART FOUR
基础巩固
√B.圆锥的顶点、底面圆的圆心与圆锥底面圆周上任意一点这三点的连线都
可以构成直角三角形 C.在圆台的上、下两底面圆周上各取一点,则这两点的连线是圆台的母线
√D.圆柱的任意两条母线所在的直线是互相平行的
解析 由圆柱、圆锥、圆台的定义及母线的性质可知BD正确,AC错误.
二、复杂的空间图形的结构特征
例2 请描述如图所示的空间图形是如何形成的.
知识点二 球
球
定义
相关概念
图形及表示
半圆绕着它的直径所在 的直线旋转一周所形成 球心:半圆的 圆心, 球 的曲面叫作球面,球面 半径:半圆的 半径, 围成的空间图形叫作球 直径:半圆的_直__径__
如图可记作:球O 体,简称球
知识点三 旋转面与旋转体
一条平面曲线绕它所在平面内的 一条定直线 旋转所形成的曲面叫作旋 转面,封闭的旋转面围成的空间图形称为 旋转体 .圆柱、圆锥、圆台和 球都是特殊的旋转体.
反思 感悟
(1)判断简单旋转体结构特征的方法 ①明确由哪个平面图形旋转而成; ②明确旋转轴是哪条直线. (2)简单旋转体的轴截面及其应用 ①简单旋转体的轴截面中有底面半径、母线、高等体现简单旋 转体结构特征的关键量; ②在轴截面中解决简单旋转体问题体现了化空间图形为平面图 形的转化思想.
跟踪训练1 (多选)下列说法,正确的是 A.圆柱的母线与它的轴可以不平行
课堂小结
KE TANG XIAO JIE
1.知识清单: (1)圆柱、圆锥、圆台的结构特征. (2)球的结构特征. (3)复杂空间图形的结构特征. 2.方法归纳:分类讨论、转化与化归. 3.常见误区:同一平面图形以不同的轴旋转形成的旋转体一般是不 同的.
4 课时对点练
PART FOUR
基础巩固
√B.圆锥的顶点、底面圆的圆心与圆锥底面圆周上任意一点这三点的连线都
可以构成直角三角形 C.在圆台的上、下两底面圆周上各取一点,则这两点的连线是圆台的母线
√D.圆柱的任意两条母线所在的直线是互相平行的
解析 由圆柱、圆锥、圆台的定义及母线的性质可知BD正确,AC错误.
二、复杂的空间图形的结构特征
例2 请描述如图所示的空间图形是如何形成的.
知识点二 球
球
定义
相关概念
图形及表示
半圆绕着它的直径所在 的直线旋转一周所形成 球心:半圆的 圆心, 球 的曲面叫作球面,球面 半径:半圆的 半径, 围成的空间图形叫作球 直径:半圆的_直__径__
如图可记作:球O 体,简称球
知识点三 旋转面与旋转体
一条平面曲线绕它所在平面内的 一条定直线 旋转所形成的曲面叫作旋 转面,封闭的旋转面围成的空间图形称为 旋转体 .圆柱、圆锥、圆台和 球都是特殊的旋转体.
反思 感悟
(1)判断简单旋转体结构特征的方法 ①明确由哪个平面图形旋转而成; ②明确旋转轴是哪条直线. (2)简单旋转体的轴截面及其应用 ①简单旋转体的轴截面中有底面半径、母线、高等体现简单旋 转体结构特征的关键量; ②在轴截面中解决简单旋转体问题体现了化空间图形为平面图 形的转化思想.
跟踪训练1 (多选)下列说法,正确的是 A.圆柱的母线与它的轴可以不平行
9.13 圆柱圆锥与圆台
二、圆柱、圆锥与圆台的性质 名称
平行于底面的截面
圆 全等的矩形 等腰三角形 等腰梯形
轴截面
侧面积
S圆柱侧=cl 2rl
1 S 侧 cl r l 2
1 1 V圆锥= Sh r 2 h 3 3
1 S 侧 (c c' )l (r r ' ) l 2
全面积
体积
画法:第一步:以点o作为原点,按正等轴侧画法画出x轴、y轴、 z轴. z
o x y
第二步:画底面.以原点o作为圆心,在原来的圆上画上一些与直径 平行的弦,相应地画一些与y轴平行的线段,其长度等于对应的弦长,而 且使x轴平分这些弦.然后把这些弦的端点用一条光滑曲线联结起来,便 得到圆锥的底面的直观图.
9.13 圆柱、圆锥与圆台
一、概念:
1.圆柱的概念
• 圆柱:以矩形的一边所在的直线为轴,其余三边绕 这根轴旋转一周形成的曲面所围成的几何体叫圆柱.
2.圆锥的概念
圆锥:以直角三角形的一条直角边所在的直线为轴,其 余两边绕这根轴旋转一周形成的曲面所围成的几何体叫圆 锥.
3.圆台的概念
圆台:直角梯形垂直于底边的腰所在直线为轴,其余三 边绕这根轴旋转一周形成的曲面所围成的几何体叫圆台.
第三步:在z轴上取一点S使 so 2.5cm
第四步:从点S作圆锥侧面的左右现两条对称的母线,如图.
z
s
s
o
o
x y
第五步:把看得见的线用实线,被遮档的线挡的线改为虚线,把x轴、y 轴、z轴在圆锥外面的部分擦掉.
课堂练习:
课堂小结:
P178 1、2
1. 旋转体的概念 2. 旋转体的主要性质 3. 用正等轴测画法画旋转体的 直观图.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A
得求圆圆台台上的、母下线底长面. 的面积之比为1:16,原来圆B锥的母线长O 是16cm,A
六、应用举例
2、轴截面问题
• 1、一个圆柱的母线长为5,底面半径为2,求圆柱的轴截面 的面积.
• 2、一个圆锥的母线长20cm,母线与轴的夹角为 300 ,求圆 锥的高.
• 3、一个圆台的母线长为5,上底面和下底面直径分别为2和 8,求圆台的高.
2020年6月17日
一、复习引入
前面我们学习了几个常见的多面体,棱柱、棱 锥和棱台。明确了它们的定义及相关概念。
棱柱、棱锥和棱台的特征,三者之间有什么联系?
一、复习引入
1.棱柱的面至少有___5__个. 2.棱柱的侧面是 平行四边 形,棱锥的侧面
是 三角 形,棱台的侧面是__ 梯 _形。
二、提
用图展示出来
五、拓展延伸
平行于底面的截面是什么样的图形?
平行于底面的截面都是圆
圆柱、圆锥、圆台.gsp
五、拓展延伸
过轴的截面——轴截面
圆柱的轴截面是 全等的 矩形 圆锥的轴截面是 全等的等腰三角形 圆台的轴截面是 全等的等腰梯形
观看演示轴截面.gsp
请欣赏下面几幅图片
二、提出问题
请欣赏下面几幅图片
圆柱
圆锥
圆台
二、提出问题
问题1.下面的几何体与多面体不同,仔细观察这些 几何体,它们有什么共同特点或生成规律?
它们可以由一个平面图形通过旋转而生成
观看演示
三、概念形成
圆柱、圆锥、圆台的生成过程
分别以矩形一边、直角三角形的直角边、 直角梯形垂直于底边的腰所在的直线为旋转轴, 其余各边旋转而成的曲面所围成的几何体, 分 别叫做圆柱,圆锥,圆台。
圆柱
圆锥
圆台
概念检测
1、判断下列几何体是否是圆柱、圆锥、圆台
×
(1)
×
(2)
×
(3)
概念检测
2、有以下命题:
(1)以直角三角形一边为旋转轴,旋转所得的旋
转体是圆锥;(2)以直角梯形的一条腰所在直线
为旋转轴,旋转所得的几何体是圆台;(3)圆柱、
圆锥、圆台的底面都是圆;(4)分别以矩形两条
不同的边所在直线为旋转轴,将矩形旋转,所得
决的转化思想 • (4)运动变化、类比联想的观点
课外作业
1.请同学们课后找一找生活中具有圆柱、圆锥、 圆台几何结构特征的实物. 2.观察生活中的一些组合体可以分割成我们学 习过的哪些简单的几何体 .
课后思考
将下列平面图形绕直线AB旋转一周,所
的连线是圆柱的母线。
()
(2)通过圆台侧面上一点,有无数条母线.( )
(3)圆台所有的轴截面是全等的等腰梯形. ( ) (4)与圆锥的轴平行的截面是等腰三角形(. )
深化检测
2、下列命题中,正确命题的个数是____4_ __.
①圆柱的轴经过上、下底面的圆心,并且垂直于底 面; ②圆柱的母线长都相等,并且都等于圆柱的高; ③平行于圆柱底面的平面截圆柱所得的截面是和底 面全等的圆; ④经过圆柱轴的平面截圆柱所得的截面是矩形,这 个矩形的一组对边是母线,另一组对边是底面圆的 直径.
么样的平面图形?
点击这里进行演示
圆柱、圆锥、圆台的侧面展开图
沿着任意一条母线剪开
r O
l 2r
O
2r
l
r
O
r' O
’
r
O
六、应用举例
1、平行截面问题
例1.用一个平行于圆锥底面的平面截这个圆锥,
截得圆台的上下底面半径的比是1:4,截去的圆
锥母线长为10cm,求圆台的母线长。
S
S
O' A'
O' A'
O
七 1.下列图形中是圆柱体的是( )
、
当
堂 检 测
A
B
2.圆锥的侧面展开图是(
A 三角形
B 长方形
C )
C圆
D D 扇形
3.将直角三角形绕它的一边旋转一周,形成的几何体一定是( )
A 圆锥
B 圆柱
C 圆台
D 以上均不正确
4.用一张6×8的矩形纸卷成一个圆柱,其轴截面的面积是( )
5.把图形与对应的图形名称用线连结起来
五、拓展延伸 表示方法:
s
o
o
o'
圆柱oo'
o'
圆锥so'
o'
圆台oo'
五、拓展延伸
对圆柱、圆锥、圆台思考以下问题
重点讨论:
1、平行于底面的截面是什么样的图形?
合
用图展示出来
作 2、过轴的截面分别是什么样的图形?
探 究
用图展示出来
3、圆柱、圆锥、圆台之间的关系?
4、圆柱、圆锥、圆台分别去掉底面,沿着任
A
B
C
D
E
三棱柱
圆锥
三棱锥
圆柱
长方体
6.圆台的上下底面的直径分别是2cm, 10cm, 高为3cm,
求圆台的母线长。
7. 一个圆锥的高是2,母线与轴的夹角为30°,求圆锥的母线长以及圆
锥的轴截面的面积。
回顾小结
• (1)圆柱、圆锥、圆台的概念 • (2)圆柱、圆锥、圆台的结构特征 • (3)立体几何问题转化为平面问题解
• 4、圆锥的轴截面是正三角形,它的面积是 3 ,则圆锥的高
与母线的长分别为?
方法感悟
(1)研究圆柱、圆锥、圆台等问题的主要方法是 研究它们的轴截面,这是因为在轴截面中,集 中反映了旋转体的各主要元素之间的位置、数 量关系. (2)将圆柱、圆锥、圆台的侧面展开是把立体几 何问题转化为平面几何问题处理的重要方法之 一. (3)圆(棱)台问题有时需要将圆(棱)台还原为 圆(棱)锥来解决.
的两个圆柱可能是两个不同的圆柱.
其中正确的个数是( A )
A.1
B.2
C.3
D.4
四、概念延伸
轴 底面
母线
圆柱
圆锥
圆台
轴: 旋转前不动的一边所在的直线.
底面: 垂直于轴的边旋转所成的圆面.
侧面: 不垂直于轴的边旋转所成的曲面.
母线: 不垂直于轴的边.
深化检测
1、判断题:
(1)在圆柱的上下底面上各取一点,这两点
五、拓展延伸 想 一 如何把圆柱变成圆锥? 想 ?
将圆柱的一个底面向中心收缩成一点
五、拓展延伸
想
如何从圆锥变成圆台?
一
想
?
O′ O
五、拓展延伸
圆柱、圆锥、圆台的关系
圆 柱
上底面变小 上底面扩大到
圆 台
上底面缩小到一个点 圆
上底面扩大
锥
与下底面相等
五、拓展延伸
思考:圆柱、圆锥、圆台的侧面展开图是什
A
O
A
例1.用一个平行于圆锥底面的平面截这个圆锥,
截得圆台的上下底面半径的比是1:4,截去的圆
锥母线长为10cm,求圆台的母线长。
S
解:
设圆锥的母线长为 y ,则有
D
O A
10 = 1 y4
B
O
A
y 40(cm)
圆锥的母线长为40cm.
S
10cm
答:圆台的母线长为 30cm
O
跟踪训练:用一个平行于圆锥底面的平面截这个圆D 锥,截
