初二数学 反比例函数
八年级数学反比例函数知识点
反比例函数1、反比例函数的定义：一般地，xky =（k 为常数，k ≠0）叫做反比例函数，即y 是x 的反比例函数。
x 为自变量，y 为因变量，其中x 不能为零 2、反比例函数的等价形式：①y 是x 的反比例函数 ←→ )0(≠=k x ky （定义式） 1.u 与t 成反比，且当u ＝6时，81=t ，这个函数解析式为 ；2.矩形的面积为6cm 2，那么它的长y cm 与宽x cm 之间的函数关系用图象表示大致（ ）ABCD3.如图，为反比例函数的图象，则它的解析式为_________.4.反比例函数x k y =的图像经过（－23，5）点、（a ，－3）及（10，b ）点， 则k ＝ ，a ＝ ，b ＝ ；②)0(≠=k k xy 判断一个函数是否为反比例函数，判定两点是否在同一反比例函数上 4、已知反比例函数的图像经过点（a ，b ），则它的图像一定也经过（ ） A 、 (－a ,－b ) B 、 (a ,－b ) C 、(－a ，b ) D 、（0，0） 5、函数x k y =的图象经过点（－4，6），则下列各点中不在xky =图象上的是（ ） A 、（3，8） B 、（3，－8） C 、（－8，－3） D 、（－4，－6） 6、已知变量y 与x 成反比例，当x =3时，y =―6；那么当y =3时，x 的值是（ ） A 、6 B 、―6 C 、9 D 、―9 7.已知y 与 2x 成反比例，且当x=3时，y=61，那么当x =2时，y =_________，当y =2时，x =_________. ③)0(1≠=-k kx y 系数待定问题： 1. 已知函数22(1)m y m x -=-，当m=_____时，它的图象是双曲线．2.已知函数2(1)k y k x -=+ (k 为整数)，当k 为_________时，y 是x 的反比例函数.3、()22105m y m x-=-是y 关于x 的反比例函数，且图象在第二、四象限，则m 的值为 ；3.反比例函数性质：①当k>0时，双曲线的两支分别位于一、三象限；在每个象限内，y 随x 的增大而减小； ②当k<0时，双曲线的两支分别位于二、四象限；在每个象限内，y 随x 的增大而增大；oyy o y o y o③双曲线的两支会无限接近坐标轴（x 轴和y 轴），但不会与坐标轴相交。
初二数学：反比例函数知识点
初二数学：反比例函数知识点初二数学：反比例函数知识点反比例函数知识放送：形如函数y=k/x(k为常数且k≠0)叫做反比例函数，其中k叫做比例系数，x是自变量，y是自变量x的函数，x的取值范畴是不等于0的一切实数。
反比例函数表达式x是自变量，y是x的函数y=k/x=k·1/xxy=ky=k·x^(-1) (即：y等于x的负一次方，此处x必须为一次方)y=k/x(k为常数且k≠0，x≠0)若y=k/nx现在比例系数为：k/n自变量的取值范畴①在一样的情形下, 自变量x 的取值范畴能够是不等于0的任意实数;②函数y 的取值范畴也是任意非零实数。
解析式y=k/x 其中x是自变量，y是x的函数，其定义域是不等于0的一切实数,即{x|x≠0,x∈R}。
下面是一些常见的形式：y=k/x=k·1/xxy=ky=k·x^(-1)y=kx(k为常数(k≠0)，x不等于0)单靠“死”记还不行,还得“活”用,姑且称之为“先死后活”吧。
让学生把一周看到或听到的新奇事记下来,摒弃那些假话套话空话,写出自己的真情实感,篇幅可长可短,并要求运用积存的成语、名言警句等,定期检查点评,选择优秀篇目在班里朗读或展出。
如此,即巩固了所学的材料,又锤炼了学生的写作能力,同时还培养了学生的观看能力、思维能力等等,达到“一石多鸟”的成效。
反比例函数图象要练说，先练胆。
说话胆小是幼儿语言进展的障碍。
许多幼儿当众说话时显得可怕：有的结巴重复，面红耳赤；有的声音极低，自讲自听；有的低头不语，扯衣服，扭身子。
总之，说话时外部表现不自然。
我抓住练胆那个关键，面向全体，偏向差生。
一是和幼儿建立和谐的语言交流关系。
每当和幼儿讲话时，我总是笑脸相迎，声音亲切，动作亲昵，排除幼儿恐惧心理，让他能主动的、自由自在地和我交谈。
二是注重培养幼儿敢于当众说话的适应。
或在课堂教学中，改变过去老师讲学生听的传统的教学模式，取消了先举手后发言的约束，多采取自由讨论和谈话的形式，给每个幼儿较多的当众说话的机会，培养幼儿爱说话敢说话的爱好，对一些说话有困难的幼儿，我总是认真地耐心地听，热情地关心和鼓舞他把话说完、说好，增强其说话的勇气和把话说好的信心。
八年级数学反比例函数知识点归纳和典型例题
八年级数学反比例函数知识点归纳和典型例题反比例函数是数学中的一个重要概念，也是学生在八年级学习数学的一部分。
本文将对八年级数学中的反比例函数知识点进行归纳和解析，并给出一些典型例题进行讲解。
一、反比例函数的定义和性质反比例函数，也称为倒数函数，是指在定义域内，变量的值和函数的值成反比关系，即一个变量的增大导致函数值的减小，而变量的减小导致函数值的增大。
反比例函数的一般形式可以表示为 y = k/x ，其中 k 是非零常数。
反比例函数的性质如下：1. 函数图像：反比例函数的图像通常是一个经过原点的开口向上的函数。
2. 定义域和值域：反比例函数的定义域是除去 x = 0 的所有实数，值域是除去 y = 0 的所有实数。
3. 单调性：反比例函数在其定义域内是单调递减的。
4. 零点：当x ≠ 0 且 y = 0 时，我们可以得到反比例函数的一个零点。
二、反比例函数的典型例题下面我们将通过一些典型例题来帮助理解反比例函数的性质和应用。
例题1：已知函数 y = 3/x ，求当 x = 2 时，函数的值 y 是多少？解析：根据反比例函数的定义，当 x = 2 时，y = 3/2。
所以函数在 x = 2 时的值为 3/2。
例题2：若反比例函数 y = k/x 的图线经过点 (2, 6)，求常数 k 的值。
解析：将点 (2, 6) 代入反比例函数的表达式，得到 6 = k/2。
解方程可以得到 k = 12，因此常数 k 的值为 12。
例题3：已知 y 和 x 成反比例关系，且 y = 15 当 x = 3，求 y = 2 时x 的值。
解析：由反比例函数的性质可知，在反比例关系中，y 和 x 是互相倒数的关系，即 y = 1/x。
根据已知条件可得 15 = 1/3，所以当 y = 2 时，x =1/2，即反比例函数的值。
例题4：若反比例函数 y = 4/x 经过点 (3, 2)，求函数的值域。
解析：将点 (3, 2) 代入反比例函数的表达式，得到 2 = 4/3x。
初二下数学(反比例函数)纯原版
二．反比例函数
k的函数叫做反比例函数。
1.概念：形如y=)0
k
(
x
2.性质：A. k>0时，在1,3象限之内，y随x的增大而缩小。
K<0时，在2,4象限之内，y随x的增大而增大。
B．k值相等的反比例函数重合，k值不相等的反比例函数永不相交。
）|k|越大（注意，这里是k的绝对值），
反比例函数的图象离坐标轴的距离越远。
C．k>0时，函数在x<0上同为减函数、在x>0上同为减函数；k<0时，函数在x<0上为增函数、在x>0上同
为增函数。
定义域为x≠0；值域为y≠0.
E．反比例函数的图象既是轴对称图形，又是中心对称图形，它有两条对称轴y=x和y=-x（即第一三，二四
象限角平分线），对称中心是坐标原点
3.在反比例函数的习题中，有几个窍门：
a．给出了一点坐标，想快速求出k的值，只需把x与y相乘即可。
即k=xy，此式也可由原式导出。
b．在反比例函数图像中，在函数上取一点，向x轴与y轴做垂线，那么得到的长方形的面积就是k。
若是单向一轴做
垂线，并且与原点连线，得到的直角三角形的面积就是二
分之一k。
c．做函数图像选择题时，我们一般用排除法做，有时幸运，前2个就会碰到。
d. 在一个反比例函数图象上任取两点P，Q，过点P，Q分别作
x轴，y轴的平行线，与坐标轴围成的矩形面积为S1，S2，则S1=S2=|K。
八年级反比例函数知识点
八年级反比例函数知识点反比例函数是初中数学中比较难理解的重点之一，也是必修内容。
下面我们将为大家详细介绍八年级反比例函数的相关知识点。
一、什么是反比例函数反比例函数是指形式为y=k/x的函数，其中k为常数，x≠0，y≠0 。
反比例函数的图像是一个“开口朝下”的双曲线。
二、反比例函数的性质1.值域反比例函数的值域是由x取值的范围决定的，当x趋近于正无穷时，y趋近于0，当x趋近于0时，y趋近于正无穷。
2.特殊函数值当x=1/k时，y=k/(1/k)=k²，即x=1/k时，反比例函数的函数值为k²。
3.增减性反比例函数在定义域上是单调递减函数。
4.对称性反比例函数的图像在y轴上具有对称性。
5.渐近线反比例函数的图像有两条渐近线，即x轴和y轴。
当x趋近于0或正无穷时，y趋近于0，此时y轴成为反比例函数的一个渐近线；当y趋近于0或正无穷时，x趋近于0，此时x轴成为反比例函数的一个渐近线。
三、反比例函数的图像及基本形状反比例函数的图像是一条双曲线，其基本形状为“开口朝下”的形式。
四、如何求反比例函数的解析式当已知反比例函数的函数图像时，我们可以通过图像上的两个点来求解析式。
对于y=k/x来说，只需给出两组x和y的值即可确定k的取值。
如已知函数图像经过点(1,3)和(2,1.5)，则可列出方程组：3=k/11.5=k/2通过方程组求解k的值，即可得到反比例函数的解析式为y=k/x，其中k=4.5。
另外，还有一种方法，即设已知反比例函数的解析式为y=k/x，将待求的常数k表示成y和x的函数，即k=xy，代入原方程中，可得yx=k或xy=k，这样就求出了反比例函数的解析式。
综上所述，反比例函数是初中数学中重点难点之一，希望同学们能够认真掌握，熟练应用。
八年级反比例函数
八年级反比例函数第一章概述1.1 定义八年级反比例函数（Inverse Proportion Function）是指函数y=1/x，其中x和y变量的变化符合反比例关系。
1.2 特征八年级反比例函数的主要特征有以下几点：（1）八年级反比例函数的图形是一条抛物线，其中x和y分别表示横坐标与纵坐标，与正比例函数的图形相反。
（2）八年级反比例函数的图象中，x轴上的点处于y轴上，因此函数的定义域是正数区间，而它的值域是所有实数。
（3）八年级反比例函数的斜率与它所表示的直线的斜率相反，即，越往右斜率越小，越往左斜率越大，斜率的绝对值永远小于1。
（4）八年级反比例函数的开口方向是朝下的，在它的两端点（即，x=0，y无穷大；x无穷大，y=0）上方约匀曲率，且在这种情况下它的极点坐标为（0，0）。
第二章解析几何2.1 图形图1-1 八年级反比例函数的图形图1-1是八年级反比例函数y=1/x的图形，图形是一条抛物线，其中x和y分别表示横坐标和纵坐标。
图中x轴上的点处于y轴上，因此函数的定义域是正数区间，而它的值域是所有实数，其图形与正比例函数的图形相反。
2.2 极值八年级反比例函数的极值坐标是（0，0），而且它的开口方向是朝下的，在它的两端点（即，x=0，y无穷大；x无穷大，y=0）上方约匀曲率。
2.3 斜率八年级反比例函数的斜率与它所表示的直线的斜率相反，即，越往右斜率越小，越往左斜率越大，斜率的绝对值永远小于1。
第三章导数八年级反比例函数的导数为：y'=-1/x^2结论通过本章的学习，我们可以了解到：八年级反比例函数的定义是：y=1/x，它的图形是一条抛物线，它的极值坐标是（0，0），它的斜率的绝对值永远小于1，它的导数为：y'=-1/x^2以上就是本文关于八年级反比例函数的介绍，希望能够帮助到大家。
八年级数学反比例函数的图解和性质
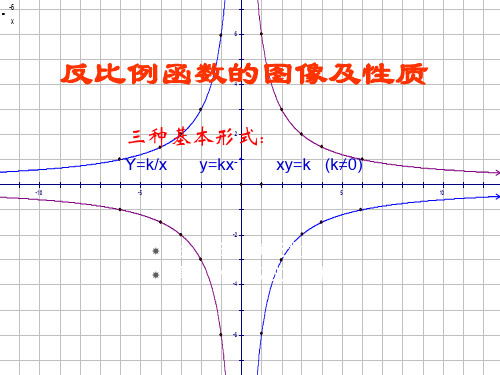
象
限。
（二）根据图象完成下列填空
1、已知反比例函数y=(1-2m)/x的图象如图1所示，则
m
。如图2时，则m
。
y
y
ox
o
x
ቤተ መጻሕፍቲ ባይዱ
图1
图2
２、已知点A(x1,y1)、B (x2,y2)、 C(x3,y3)在反比例 函数y=-5/x的图象上，并且x1＜x2＜0＜x3，则y1、 y2、y3的大小关系是：
（三）根据图象选择：
例1： 已知Y与X的平方成反比例，并 且当X=3时，Y=4；求X=6时， Y的值.
例2：完成某项工程的时间y（天） 与参加施工的人数x（个）成反比
例关系。如果参加这项工程施工 工人数为4人时，10天能完成这项 工程。现要求8天完成这项工程， 需要多少人参加 施工？
二、新课 反比例函数的图像和性质
三象限内；在每个象限内Y随X的增大而减小。 3、当K〈 0时，图象的两个分支分布在第二、
四象限内；在每个象限内Y随X的增大而增大。 (囗诀：K大一三减，K小二四增） 4、反比例函数图像关于原点对称，且关于直
线y=x和y=-x对称。 思考：反比例函数、正比例、一次函数的性
质有何异同？（课后填充表格）
Y=6/x … -1.5 -2 -3 -6 6 3 2 1.5 …
Y=-6/x … 1.5 2 3 6 -6 -3 -2 -1.5 …
Y=3/x … -0.75 -1 -1.5 -3 3 1.5 2 0.75 …
Y=-3/x … 0.75 1 1.5 3 -3 -1.5 -2 -0.75 …
y y﹦6∕x
下列（ ）是函数y=kx-k和y=k/x的大致图象
y ox
y ox
八年级数学反比例函数的图象与性质
对于反比例函数图象上点的坐标特征问题，可以通过分析函数性质或利用已知条件 进行推理判断。
对于反比例函数与一次函数的交点问题，可以通过联立两个函数的解析式求解交点 坐标。在解题过程中需要注意分类讨论和数形结合的思想应用。
06 课堂小结与课后作业布置
2)$，求该函数的解析式，并判断点 $Q(-2, 3)$ 是否在该函数的图象上。
02 03
拓展题2
已知反比例函数 $y = frac{m}{x}$ 与一次函数 $y = ax + b$ 的图象交 于点 $M(4, -1)$ 和 $N(1, -4)$，求这两个函数的解析式，并求出它们 的另一个交点坐标。
无论 $k$ 取何值（$k neq 0$），反 比例函数的图象总是无限接近于坐标 轴，但永远不会与坐标轴相交。
02 反比例函数图象绘制
列表法绘制步骤
确定自变量的取值范围
根据题目要求或实际情况，确 定自变量$x$的取值范围。
绘制坐标点
在坐标系中，以自变量$x$的值 为横坐标，函数值$y$的值为纵 坐标，绘制出对应的坐标点。
易错难点剖析指导
忽略反比例函数定义中 $k neq 0$ 的条件，导致错误地认为当 $x = 0$ 时，$y$ 也有定义。
在绘制反比例函数图象时，未注 意到双曲线关于原点对称的性质，
导致图象绘制不准确。
在分析反比例函数性质时，未注 意到 $k$ 的正负对函数图象和 性质的影响，导致分析错误。
课后作业布置及要求
解析法
对于反比例函数y=k/x (k≠0)，当k>0时，函数图象在第一、三象限，且y随x的增大而减小（即减函数）； 当k<0时，函数图象在第二、四象限，且y随x的增大而增大（即增函数）。
八年级数学反比例函数的图解和性质
声速
声速与频率和介质有关，在一定 介质中，声速与频率成反比关系。
磁场
在磁场中，磁感应强度与电流成 正比，与导线长度成反比，这是
电磁感应现象的基础。
在经济中的应用
供需关系
01
在市场经济中，商品的价格与供应量成反比关系，当需求量一
定时，供应量增加会导致价格下降。
投资回报
02
投资回报率与投资额成反比关系，当风险一定时，投资额越大，
中心对称
分布在第二和第四象限
由于k的正负性，反比例函数的图像分 布在第二和第四象限。
反比例函数的图像关于原点中心对称。
反比例函数图像的变换
k值变化
改变k的值会影响反比例函 数图像的形状和位置。
x轴和y轴的变换
通过伸缩x轴和y轴，可以 改变反比例函数图像的形 状。
图像的旋转
通过旋转反比例函数图像， 可以观察其在不同角度下 的形态。
01
02
03
确定函数表达式
首先确定反比例函数的表
达式，例如$y
=
frac{k}{x}$（其中k为常
数）。
ห้องสมุดไป่ตู้
确定坐标轴
在平面直角坐标系中，选 择适当的x和y轴范围。
绘制图像
根据反比例函数的表达式， 在坐标系中逐点绘制函数 图像。
反比例函数图像的特性
无限接近x轴和y轴
反比例函数的图像会无限接近x轴和y 轴，但不会与它们相交。
反比例函数可以看作是幂函数的一种特殊情况，即当n=-1时 的幂函数。因此，反比例函数与幂函数在性质上有一定的相 似性，例如它们的导数都与自身有关。
THANKS FOR WATCHING
感谢您的观看
八年级反比例函数
已知矩形的面积为8, 那么它 的长y与宽x之间的关系用图 像大致可表示为 ( )．
y y y y
O O (A) x O (B) x (C)
x
O (D)
x
思维慎密
2.函数y=ax-a 与 角坐标系中的图象可能是
y o (1) x y o (2) x
a y a 0 x
在同一条直 :
已知y＝y1＋y2，
y1与x成正比例，y2 反比例，
2成 与x
且x＝2与x＝3时，y的值 都等于19．
求y与x间的函数关系式．
m3 .已知反比例函数 y x 经过点A(2,－m)和B(n,2n)， 求：
(1)m和n的值； (2)若图象上有两点P1(x1,y1) 和P2(x2,y2)，且x1＜0＜ x2， 试比较y1和 y2的大小．
2 y x
y (3n 9) x 若反比例函数
n 2 13
的图象在所在象限内，y 随x的增大而增大，求n的 值．
已知一个长方体的体积是100立 方厘米，它的长是ycm，宽是 5cm，高是xcm． (1)写出用高表示长的函数式； (2)写出自变量x的取值范围； (3)当x＝3cm时，求y的值．
反 比 例 函 数 （ 复 习 ）
y
o
x
忆一忆
什么是反比例函数？其图象是什么？反比例 函数的性质？
k 形如y= x (k为常数，k≠0）的函数称为反比例函数），其 中x是自变量，y是函数，k是比例系数。
k 反比例函数 y （k为常数，k≠0）的图象是 x 双曲线.
当k＞0时，双曲线的两支分别在第一、三象限， 在每个象限内，y随x的增大而减少；
如图，点P是一个反比例函数与正比例 函数的图象的交点，PQ垂直于x轴,垂足 Q的坐标为(2,0)． (1) 求这个反比例函数的解析式. (2) 如果点M在这个反比例函数的图象上, 且△MPQ的面积为6,求点M的坐标.
八年级秋季班-第11讲：反比例函数
反比例函数是八年级数学上学期第十八章第二节内容，主要对反比例函数的图像及性质进行讲解，重点是反比例函数的性质的理解，难点是反比例函数表达式的归纳总结．通过这节课的学习为我们后期学习反比例函数的应用提供依据．一、反比例函数的概念1、如果两个变量的每一组对应值的乘积是一个不等于零的常数，我们就说这两个变量成反比例．用数学式子表示两个变量x 、y 成反比例，就是xy k =，或表示为ky x =，其中k是不等于0的常数．2、解析式形如ky x=（k 是常数，0k ≠）的函数叫做反比例函数，其中k 叫做比例系数．3、反比例函数ky x=的定义域是不等于零的一切实数．反比例函数知识结构模块一：反比例函数的概念知识精讲内容分析【例1】下列变化过程中的两个变量成反比例的是（）A ．圆的面积和半径B ．矩形的面积一定，它的长与宽C ．完成一项工程的工效与完成工期的时间D ．人的身高及体重【难度】★【答案】【解析】【例2】（1）已知：y 与x 成反比例，且1x =-时，2y =，则它的函数解析式是_________;（2）已知y 与2x 成反比例，且当2x =-时，14y =-，则当13x =时，y =_________.【难度】★【答案】【解析】【例3】下列函数（其中x 是自变量）中，哪些是反比例函数?哪些不是，为什么?（1）3x y =；（2）12y x -=；（3）1(0)y k kx =≠；（4）2xy =-；（5）21y x=+．【难度】★【答案】【解析】【例4】（1）如果21(1)kk y k x --=-是反比例函数，则k 的值是_________；（2）已知函数210(3)my m x -=-是反比例函数，则m =_________.【难度】★★【答案】【解析】例题解析【例5】下列说法中正确的有（）个．（1）当10k y kx≠=时，是反比例函数；（2）如果2213y y x x=，那么与成反比例；（3）如果211m y m x-=+-是反比例函数，则1m =±；（4）如果x 、y 成正比例，y 与z 成反比例，则x 与z 成反比例．A ．1B ．2C ．3D ．4【难度】★★【答案】【解析】【例6】已知某反比例函数，且当1x =时，2y =-，当3x y m =-=时，求m 的值．【难度】★★【答案】【解析】【例7】已知21y x +-与成反比例，且当13x y =-=-时，当3x =时，y 的值．【难度】★★【答案】【解析】【例8】已知一梯形的面积是30，上底长是下底长的12，设下底长为x ，高为y ，求y 关于x 的函数关系式并写出这个函数的定义域．【难度】★★【答案】【解析】【例9】已知反比例函数ky x=的图像上有一点A ，它的横坐标x 和纵坐标y 是方程2280x x --=的两个根，求：（1）k 的值；（2）点A 到y 轴的距离．【难度】★★【答案】【解析】【例10】设1212k ky y x x==和，当2x =时，121213y y y y +=-=，，求12k k 、的值．【难度】★★★【答案】【解析】【例11】已知122y y y =-，若1y 与x 成反比例，2y 与3x +成正比例，且当1x =时10y =，当1x =-时2y =；（1）求y 与x 间的函数关系式；（2）求当12y =时，x 的值．【难度】★★★【答案】【解析】师生总结1.反比例函数的定义域有限制吗？请说明二、反比例函数的图像1、反比例函数ky x=（k 是常数，0k ≠）的图像叫做双曲线，它有两支．三、反比例函数的性质1、当0k >时，函数图像的两支分别在第一、三象限；在每个象限内，当自变量x 的值逐渐增大时，y 的值随着逐渐减小．2、当0k <时，函数图像的两支分别在第二、四象限；在每个象限内，当自变量x 的值逐渐增大时，y 的值随着逐渐增大．3、图像的两支都无限接近于x 轴和y 轴，但不会与x 轴和y 轴相交．【例12】（1）已知反比例函数2a y x-=图像在第二、四象限，则a 的取值范围是_______；（2）已知(0)ky k x=≠图像上有一点P （3，2），那么这个反比例函数的解析式为_________.【难度】★【答案】【解析】【例13】已知反比例函数(0)ky k x=≠的图像经过经过点（1，2-），则这个函数解析式是______________；当x ＜0时，y 的值随着x 的增大而________．【难度】★【答案】【解析】知识精讲例题解析模块二：反比例函数的图像及性质【例14】当m =_______时函数231(2)mm y m x --=-是反比例函数，且当0x >时，y 值随x的值增大而减小．【难度】★【答案】【解析】【例15】已知（3，4）是反比例函数221m m y x+-=图像上的一点，则函数图像必过点（）．A ．（2，6-）B ．（6-，2）C ．（3，4-）D ．（3-，4-）【难度】★【答案】【解析】【例16】（1）已知函数1y x -=是反比例函数，则k 的取值范围是________；（2）已知反比例函数1k y x+=，点1122()()x y x y ，、，为其图像上的两点，若当12120x x y y <<>时，，则k 的取值范围是___________．【难度】★★【答案】【解析】【例17】下列函数1135y x y x y y x x=-===-，，，中，每个象限内y 的值随x 的增大而减小的有（）个A ．0个B ．1个C ．2个D ．3个【难度】★★【答案】【解析】【例18】下列函数21()a y a x--=是常数的图像上有三点A 13y （-，）、B 21y （-，）、C 32y （，），则1y 、2y 、3y 的大小关系是（）A ．231y y y <<B ．321y y y <<C ．123y y y <<D ．312y y y <<【难度】★★【答案】【解析】【例19】（1）已知P （1，2+1m ）在双曲线ky x=上，则双曲线的图像在第_______象限内，当x <0时，y 的值随x 的减小而________；（2）设反比例函数15510y x x -=-≤≤，当时，函数的最大值是______________．【难度】★★【答案】【解析】【例20】（1）平面直角坐标系中，点A (725)m m --，在第二象限，且m 为整数，求过点A 的反比例函数解析式；（2）若反比例函数3k y x -=的图像位于第二、四象限内，正比例函数2(1)3y k x =-过一、三象限，求整数k 的值．【难度】★★【答案】【解析】【例21】函数122(4)m y m m x=+可能是正比例函数或者是反比例函数吗?为什么?【难度】★★★【答案】【解析】【例22】已知反比例函数(0)ky k x=≠，当自变量x 的取值范围为84x ≤≤--时，相应的函数取值范围是12y ≤≤--1，求这个反比例函数解析式．【难度】★★★【答案】【解析】师生总结2.反正比例函数的性质是什么？反比例函数和几何图形的综合【例23】已知反比例函数图像上有一点P ，过P 作y 轴的垂线，垂足为H ，如果△POH的面积为6，则反比例函数的解析式为_____________.【难度】★【答案】【解析】【例24】如图，x 轴上一点C 的坐标是（-3，0）．点P 从原点出发，沿y 轴向上运动，过点P 作x 轴的平行线，分别与反比例函数42y y x x =-=和的图像交于点A 、B ，在点P 从下向上移动过程中，三角形ABC 的面积（）A ．逐渐增大B ．逐渐减小C ．保持不变D ．先增大，到一定程度后减小【难度】★★【答案】【解析】知识精讲例题解析ABC OPxy模块三：反比例函数的综合【例25】如图，矩形ABCD 的边CD 在x 轴上，顶点A 在双曲线1y x=上，顶点B 在双曲线3y x=上，求矩形ABCD 的面积．【难度】★★【答案】【解析】【例26】过原点作直线交双曲线(0)ky k x=>于点A 、C ，过A 、C 两点分别作两坐标轴的平行线，围成矩形ABCD ，如图所示．（1）已知矩形ABCD 的面积等于8，求双曲线的解析式；（2）若已知矩形ABCD 的周长为8，能否由此确定双曲线的解析式?如果能，请予求出；如果不能，说明理由．【难度】★★【答案】【解析】A B CDE OxyyABCDOx【例27】正方形OAPB 、ADFE 的顶点A 、D 、B 在坐标轴上，点E 在AP 上，点P 、F 在函数(0)ky k x =>的图像上，已知正方形OAPB 的面积是16．（1）求k 的值和直线OP 的函数解析式；（2）求正方形ADEF 的边长．【难度】★★★【答案】【解析】【例28】如图，已知正方形OABC 的面积是9，点O 为坐原点，A 在x 轴上，C 在y 轴上，B 在函数(00)k y k x x =>>，的图像上，点P （m ，n ）在(00)ky k x x =>>，的图像上异于B 的任意一点，过点P 分别作x 轴，y 轴的垂线，垂足分别是E 、F ．设矩形OEPF 和正方形OABC 不重合部分的面积是S ．（1）求点B 的坐标；（2）当92S =时，求点P 的坐标；（3）写出S 关于m 的函数解析式．【难度】★★★【答案】【解析】A BC PE FyOxyABPFOxE【习题1】下列函数（其中x 是自变量）中，哪些是反比例函数?哪些不是?为什么?（1）13y x =-；（2）4xy =；（3）15y x=-；（4）2(0)ay a a x =≠为常数，；（5）1y xπ=；（6）21y x =.【难度】★【答案】【解析】【习题2】已知1y x -与成反比例，当x =1时，y =3；当x =8时，y =________．【难度】★【答案】【解析】【习题3】（1）反比例函数22(2)my m x -=-的图像在第二、四象限，则m =________；（2）若反比例函数230k y x x-+=<，当时，y 随x 的增大而增大，则k 的取值范围是____________．【难度】★【答案】【解析】随堂检测【习题4】在函数(0)ky k x=>图像上有三点112233()()()A x y B x y C x y ，，，，，，如果1230x x x <<<，试比较123y y y ，，大小关系___________.【难度】★★【答案】【解析】【习题5】反比例函数2121k y k x+=+-的图像经过第二、四象限，求这个函数的解析式.【难度】★★【答案】【解析】【习题6】作出反比例函数12y x=的图像，并根据图像解答下列问题：（1）当4x =时，求y 的值；（2）当2y =-时，求x 的值；（3）当2y >时，求x 的范围．【难度】★★【答案】【解析】【习题7】点P 在反比例函数1y x=(x ＞0)的图像上，且横坐标为2．若将点P 先向右平移两个单位，再向上平移一个单位后得到点'P ．求在第一象限内，经过点'P 的反比例函数图像的解析式．【难度】★★【答案】【解析】【习题8】已知函数12y y y =+，1y 与x 成反比例，2y 与(2)x -成正比例，当1x =时，1y =-；当3x =时，5y =，求当6x =时，y 的值．【难度】★★【答案】【解析】【习题9】（1）若P 是反比例函数3ky x=图像上的一点，PQ ⊥y 轴，垂足为点Q ，若2POQ s ∆=，求k 的值；（2）已知反比例函数ky x=的图像上有一点A ，过A 点向x 轴，y 轴分别做垂线，垂足分别为点B C ，，且四边形ABOC 的面积为15，求这个反比例函数解析式．【难度】★★【答案】【解析】【习题10】如图，点A 、B 在反比例函数(0)ky k x=>的图像上，且A 、B 横坐标分别是a 、2a (0)a >．AC ⊥x 轴，垂足为C ，三角形AOC 的面积为2．（1）求反比例函数的解析式；（2）若点12(2)a y a y (-，)、-，也在反比例函数的图像上，试比较12y y ，的大小．【难度】★★★【答案】【解析】A BG D EFCOxy【习题11】如图，在平面直角坐标系中，正比例函数3y x =与反比例函数图像交于第一象限内的点A ，AB ⊥x 轴于点B ，AB =6．（1）求反比例函数的解析式；（2）在直线AB 上是否存在点P ，使点P 到正比例函数直线OA 的距离等于点P 到点B 的距离?若存在，求点P 坐标，若不存在，请说明理由．【难度】★★★【答案】【解析】【习题12】已知反比例函数4y x=与正比例函数相交与点A ，点A 的坐标是（1，m ）．（1）求此正比例函数解析式；（2）若正比例函数14y x =与反比例函数4y x=的图像在第一象限内相交与点B ，过点A 和点B 分别做x 轴的垂线，分别交x 轴与点C 和点D ，AC 和OB 相交与点P ，求梯形PCDB 的面积；（3）联结AB ，求AOB ∆面积．【难度】★★★【答案】【解析】ABOxy【习题13】如图，在反比例函数2(0)y x x=>的图像上，有点1234P P P P ，，，，他们的横坐标为1，2，3，4．分别过这些点往x 轴和y 轴上作垂线，图中所构成的阴影部分的面积从左向右依次是123123S S S S S S ++，，，求的值．【难度】★★★【答案】【解析】【作业1】判断下列问题中两个变量是不是反比例函数关系?为什么?（1）三角形的面积S 一定时，它的一条边长a 和这条边长上的高h ；（2）存煤量Q 一定时，平均每天的用煤量m 与可用天数t ；（3）货物的总价A 一定时，货物的单价a 与货物的数量x ；（4）车辆所行使的路程S 一定时，车轮的直径d 和车轮的旋转周数n ．【难度】★【答案】【解析】【作业2】已知反比例函数(0)ky k x=<，当0x <时，它的图像在第______象限．【难度】★【答案】【解析】课后作业1234xyO 1P 2P 3P 4P 3S 2S 1S【作业3】（1）已知函数63k y x-=，如果在每个象限内y 随x 的增大而减小，那么k 的取值范围是______________；（2）如果双曲线2m y x +=位于第一，三象限，那么m 的取值范围是______________．【难度】★【答案】【解析】【作业4】已知点11()x y ，，22()x y ，在反比例函数2k y x-=图像上，当120x x >>时，12y y <，求k 的取值范围．【难度】★【答案】【解析】【作业5】作出反比例函数xy 4-=的图像，结合图像回答：（1）当2x =时，y 的值；（2）当14x <≤时，y 的取值范围；（3）当14y ≤<时，y 的取值范围．【难度】★★【答案】【解析】【作业6】已知反比例函数ky x=的图像上有一点A ，过A 点向x 轴做垂线，垂足分别为点B ，且AOB ∆的面积为15，求这个反比例函数解析式．【难度】★★【答案】【解析】【作业7】已知函数12y y y =-，且1y 为x 的反比例函数，2y 为x 的正比例函数，且312x x =-=，时，y 的值都是1．求y 关于x 的函数关系式．【难度】★★【答案】【解析】【作业8】在反比例函数ky x=的图像上有一点A ，它的横坐标x 和纵坐标y 是方程290x -=的两个根．求：（1）k 的值；（2）点A 到y 轴的距离；（3）点1(27)3P -，是否在该反比例函数图像上?【难度】★★【答案】【解析】【作业9】等腰直角POA 的直角顶点P 在反比例函数4y x=(0)x >的图像上，A 点在x 轴正半轴上，求A 点坐标．【难度】★★【答案】【解析】【作业10】已知，如图点P 是双曲线24y x=上的一点，PA ⊥x 轴于点A ，PB ⊥y 轴于点B ，PA 、PB 分别交双曲线11y x=于点D 、C ．求△PCD 的面积．【难度】★★★【答案】【解析】【作业11】如图已知在平面直角坐标系中，正方形ABCD 顶点A 、B 的坐标分别为（1，0）和（0，2）．双曲线(0)ky x x=>经过点D ．（1）求双曲线的函数解析式；（2）将正方形ABCD 沿x 轴向左平移多少个单位长度，可以使点C 正好落在双曲线上．【难度】★★★【答案】【解析】A BCDOP yxyABCDEF Ox。
初二数学《反比例函数》说课稿（通用5篇）
初二数学《反比例函数》说课稿初二数学《反比例函数》说课稿（通用5篇）作为一无名无私奉献的教育工作者，常常要根据教学需要编写说课稿，编写说课稿助于积累教学经验，不断提高教学质量。
写说课稿需要注意哪些格式呢？下面是小编为大家收集的初二数学《反比例函数》说课稿（通用5篇），仅供参考，大家一起来看看吧。
初二数学《反比例函数》说课稿1各位评委：大家好！今天我要说的课题是义务教育人教版初中八年级十七章第一节“反比例函数”。
我将从如下步骤进行。
一、说教材1、内容分析：本节课是“反比例函数”的第一节课，是继正比例函数、一次函数之后，二次函数之前的又一类型函数，本节课主要通过丰富的生活事例，让学生归纳出反比例函数的概念，并进一步体会函数是刻画变量之间关系的数学模型，从中体会函数的模型思想。
因此本节课重点是理解和领悟反比例函数的概念，所渗透的数学思想方法有：类比，转化，建模。
2、学情分析：对八年级学生来说，虽然他们已经对函数，正比例函数，一次函数的概念、图象、性质以及应用有所掌握，但他们面对新的一次函数时，还可能存在一些思维障碍，如学生不能准确地找出变量之间的自变量和因变量，以及如何从事例中领悟和总结出反比例函数的概念，因此，本节课的难点是理解和领悟反比例函数的概念。
二、说教学目标根据本人对《数学课程标准》的理解与分析，考虑学生已有的认知结构、心理特征，我把本课的目标定为：1、从现实的情境和已有的知识经验出发，讨论两个变量之间的相依关系，加深对函数概念的理解。
2、经历抽象反比例函数概念的过程，领会反比例函数的意义，理解反比例函数的概念。
三、说教法本节课从知识结构呈现的角度看，为了实现教学目标，我建立了“创设情境→建立模型→解释知识→应用知识”的学习模式，这种模式清晰地再现了知识的生成与发展的过程，也符合学生的认知规律。
于是，从教学内容的性质出发，我设计了如下的课堂结构：创设出电流、行程等情境问题让学生发现新知，把上述问题进行类比，导出概念，获得新知，最后总结评价、内化新知。
人教版初中数学八上反比例函数定义和性质
反比例函数定义和性质一、反比例函数的定义一般地，形如xky =（k 为常数，0k ≠）的函数称为反比例函数，它可以从以下几个方面来理解：⑴x 是自变量，y 是x 的反比例函数；⑵自变量x 的取值范围是0x ≠的一切实数，函数值的取值范围是0y ≠；⑶比例系数0k ≠是反比例函数定义的一个重要组成部分；⑷反比例函数有三种表达式：①xky =（0k ≠），②1kx y -=（0k ≠），③k y x =⋅（定值）（0k ≠）；⑸函数xky =（0k ≠）与y k x =（0k ≠）是等价的，所以当y 是x 的反比例函数时，x 也是y 的反比例函数。
（k 为常数，0k ≠）是反比例函数的一部分，当k=0时，xky =，就不是反比例函数了，由于反比例函数xky =（0k ≠）中，只有一个待定系数，因此，只要一组对应值，就可以求出k 的值，从而确定反比例函数的表达式。
至于这一组对应值给出的方式一般有以下几种：①当x= 时,y= ②从列表中找 ③点坐标 ④图像上的一个能看出坐标的点。
二、反比例函数的图像及画法反比例函数的图像是双曲线，它有两个分支，这两个分支分别位于第一、第三象限或第二、第四象限，它们关于原点对称，由于反比例函数中自变量函数中自变量0x ≠，函数值0y ≠，所以它的图像与x 轴、y 轴都没有交点，即双曲线的两个分支无限接近坐标轴，但永远达不到坐标轴。
反比例的画法分三个步骤：⑴列表；⑵描点；⑶连线。
再作反比例函数的图像时应注意以下几点：①列表时选取的数值宜对称选取；②列表时选取的数值越多，画的图像越精确；③连线时，必须根据自变量大小从左至右（或从右至左）用光滑的曲线连接，切忌画成折线；④画图像时，它的两个分支应全部画出，但切忌将图像与坐标轴相交。
三、反比例函数的性质☆关于反比例函数的性质，主要研究它的图像的位置及函数值的增减情况，如下表：反比例函数xky =（0k ≠）k 的符号k >0k <图像性质①x 的取值范围是0x ≠，y 的取值范围是0y ≠②当0k >时，函数图像的两个分支分别在第一、第三象限，在每个象限内，y 随x 的增大而减小。
八年级数学反比例函数知识点
反比例函数具有中心对称和轴对称的性质。通过分析这些 性质，可以进一步确认图像是否为反比例函数的图像。
利用特殊点进行验证
在反比例函数的图像上，存在一些特殊的点，如与坐标轴 的交点、顶点等。通过计算这些特殊点的坐标，并与图像 上的点进行比较，可以验证图像的正确性。
03
反比例函数在实际问题中应用举例
物理问题
在物理问题中，也有一些量与另一些 量成反比例关系的情况。例如，在力 学中，当物体受到恒力作用时，其加 速度与质量成反比例关系；在电学中 ，电阻与电流成反比例关系等。这时 可以用反比例函数来描述这种关系， 并求出相关物理量。
04
方程与不等式在反比例函数中运用
方程求解技巧分享
观察法
通过观察方程的特点， 直接得出方程的解。
对于反比例函数 y = k/x，当 x 增大 时，y 减小；当 x 减小时，y 增大。 即 x 与 y 成反比关系。
增减性质
在第一、三象限内，随着 x 的增大， y 的值逐渐减小；在第二、四象限内 ，随着 x 的增大，y 的值逐渐增大。
对称性质
反比例函数的图像关于原点对称，即 如果点 (x, y) 在双曲线上，那么点 (x, -y) 也在双曲线上。
工程问题
经济问题
在工程问题中，经常遇到工作总量与 工作时间成反比例的情况。例如，一 项工程需要在规定时间内完成，如果 增加工人数量，则每个工人完成的工 作量将减少，但总工作量不变。这时 可以用反比例函数来描述这种关系， 并求出所需工人数量或完成工程所需 时间等。
在经济问题中，价格与需求往往成反 比例关系。例如，某种商品的价格上 涨，则其需求量将减少；反之，价格 下降则需求量增加。这时可以用反比 例函数来描述这种关系，并求出均衡 价格或均衡数量等。
初二数学重要知识点整理反比例函数的性质
对称变换规律
原点对称
反比例函数的图像关于原点对称，即图像上的任意一点关于 原点对称的点也在图像上。
轴对称
反比例函数的图像不具有轴对称性质，但可以通过平移和伸 缩变换得到具有轴对称性质的图像。例如，将反比例函数图 像沿y=-x方向平移后，可以得到关于直线y=-x对称的图像。
03
反比例函数与直线交点问题
三角形，且两直角边之积为定值（即比例系数k的绝对值）。
02
通过作垂线构造相似三角形
在反比例函数图象上作垂线，可以构造出与给定三角形相似的三角形，
进而利用相似三角形的性质解决问题。
03
利用平行线截线段成比例定理
在反比例函数图象中，如果有一条平行于坐标轴的直线与双曲线相交，
那么这条直线截得的线段长度之比等于对应点的横（或纵）坐标之比。
当 $k < 0$ 时，双曲线在第二、 四象限内，且随着 $x$ 的增大（ 或减小），$y$ 值逐渐增大（或 减小）。
比例系数 $k$ 的意义：在反比例 函数 $y = frac{k}{x}$ 中，$k$ 是 一个非零常数，称为比例系数。 它决定了双曲线的形状和位置。
当 $k > 0$ 时，双曲线在第一、 三象限内，且随着 $x$ 的增大（ 或减小），$y$ 值逐渐减小（或 增大）。
思路拓展
对于反比例函数与相似三角形的综合题，首先要熟练掌握反比例函数的基本性质和相似三角形的基本性质。其次 要善于利用反比例函数图象上点的坐标特征和相似三角形的构造方法。最后要注意总结归纳解题方法和思路，以 便在遇到类似问题时能够迅速找到解题方向。
06
复习总结与提高训练
关键知识点回顾总结
反比例函数的概念
面积、体积问题中的应用
八年级数学反比例函数2
y
y
(A)
0
x
Байду номын сангаас
(B)
0
x
y
y x (D)
0
(C)
0
x
问题探讨 在平面直角坐标系内，从反比例函数y=k/x （k＞0））的图象上的一点分别作坐标轴的垂 线段，与坐标轴围成的矩形的面积是12，请你 求出该函数的解析式。
y
y
B
P(m,n) A
B
P(m,n) A
o
x
S矩形= k
o
x
课堂小结
①能正确画出反比例函数的图象 ②反比例函数的性质 及应用 ③反比例函数的图象的分布与比例系数k的 符号的关系
的图象上，• 试判断
点（-2，-5）是否也在此图象 上．”题中的“？• ”是被一个 同学不小心擦掉的一个数字，请 你分析一下“？”
例1 已知反比例函数的图象经过点A（2，6） （1）这个函数的图象分布在哪些象限？ y随x的增大而如何变化？ (2) 点 B(3 ， 4),C(-2.5 ， -4.8) 和 D(2 ， 5) 是否在 这个函数的图象上？ 1、已知反比例函数的图象经过点A(3，－4)． (1)这个函数的图象分布在哪些象限?在图象的 每一支上，y随x的增大如何变化? (2)点B(－3，4)，点C(－2，6)和点D(3，4) 是否在这个函数的图象上?
图象的一支，根据图象回答下列问题： (1) 图象的另一支在哪个象限 ? 常数 n 的 取值范围是什么? (2)在图象上任取一点A(a，b)和 B(a' ， b') ，如果 a ＜ a' ，那么 b 和 b' 有 怎样的大小关系?
n7 y 2．如下图是反比例函数 x
八年级反比例函数
（一）反比例函数的概念： 知识要点：1、一般地，形如 y =xk( k 是常数, k = 0 ) 的函数叫做反比例函数。
注意：（1）常数 k 称为比例系数，k 是非零常数；（2）解析式有三种常见的表达形式： （A ）y =xk（k ≠ 0） ， （B ）xy = k （k ≠ 0） （C ）y=kx -1（k ≠0） 例题讲解：有关反比例函数的解析式 （1）下列函数，① 1)2(=+y x ②. 11+=x y ③21x y = ④.x y 21-=⑤2x y =-⑥13y x = ；其中是y关于x 的反比例函数的有：_________________。
（2）函数22)2(--=ax a y 是反比例函数，则a 的值是（ ）A ．－1B ．－2C ．2D ．2或－2 （3）若函数11-=m xy (m 是常数)是反比例函数，则m ＝________，解析式为________．（4）如果y 是m 的反比例函数，m 是x 的反比例函数，那么y 是x 的（ ）A ．反比例函数B ．正比例函数C ．一次函数D ．反比例或正比例函数 练习：（1）如果y 是m 的正比例函数，m 是x 的反比例函数，那么y 是x 的（ ） （2）如果y 是m 的正比例函数，m 是x 的正比例函数，那么y 是x 的（ ） （5）反比例函数(0ky k x=≠）的图象经过（—2，5）和（2， n ）， 求1）n 的值； 2）判断点B （24，2-）是否在这个函数图象上，并说明理由（6）已知y 与2x －3成反比例，且41=x 时，y ＝－2，求y 与x 的函数关系式．（7）已知函数12y y y =-，其中1y 与x 成正比例, 2y 与x 成反比例，且当x ＝1时，y ＝1；x ＝3时，y ＝5．求：（1）求y 关于x 的函数解析式； （2）当x ＝2时，y 的值．(二)反比例函数的图象和性质： 知识要点：1、形状：图象是双曲线。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
初二数学反比例函数的综合复习一选择题1、 已知点),1(1y -，),2(2y ，),3(3y 在反比例函数xk y 12--=的图像上. 下列结论中正确是（B ）A ．321y y y >>B ．231y y y >>C ．213y y y >>D ． 132y y y >>2、 已知点A （11x y ，）、B （22x y ，）是反比例函数xky =（0>k ）图象上的两点，若210x x <<，则有（ A ）A ．210y y << B ．120y y << C ．021<<y y D ．012<<y y3、 下列四个点中，有三个点在同一反比例函数x ky =的图象上，则不在这个函数图象上的点是 (B ) A ．(5，1) B ．(－1，5) C ．(35，3) D ．(－3，35-)4反比例函数ky x=在第一象限的图象如图所示，则k 的值可能是（ C ）DBAyxOC第4题 第5题 第6题 第8题 A ．1 B ．2 C ．3 D ．4 5、 如图，A 、B 是函数2y x=的图象上关于原点对称的任意两点，BC ∥x 轴，AC ∥y 轴，△ABC 的面积记为S ，则（ B ）A ． 2S =B ． 4S =C ．24S <<D ．4S >6、如图，已知双曲线(0)ky k x=<经过直角三角形OAB 斜边OA 的中点D ，且与直角边AB 相交于点C ．若点A 的坐标为（6-，4），则△AOC 的面积为（ B ）A ．12B ．9C ．6D ．4 7120a b -+=，点M （a ，b ）在反比例函数ky x=的图象上，则反比例函数的解析式为( D ) .A ．2y x= B ．1y x=-C ．1y x =D ．2y x=-8、 一块蓄电池的电压为定值，使用此蓄电池为电源时，电流I （A ）与电阻R （Ω）之间的函数关系如图所示，如果以此蓄电池为电源的用电器限制电流不得超过10A ，那么此用电器的可变电阻应（ A ）． A ．不小于4.8ΩB ．不大于4.8ΩC ．不小于14ΩD ．不大于14Ω9、一次函数y =kx+b与反比例函数y=k/x的图象如图所示，则下列说法正确的是（ C ）A．它们的函数值y随着x的增大而增大B．它们的函数值y随着x的增大而减小C．k＜0D．它们的自变量x的取值为全体实数第9题第11题11、如图，是一次函数y=kx+b与反比例函数y=2x的图像，则关于x的方程kx+b=2x的解为（C ）（A）x l=1，x2=2 （B）x l=－2，x2=－1 （C）x l=1，x2=－2 （D）x l=2，x2=－1二、填空题第12题第13题12、如图，在反比例函数2yx=（0x>）的图象上，有点1234P P P P，，，，它们的横坐标依次为1，2，3，4．分别过这些点作x轴与y轴的垂线，图中所构成的阴影部分的面积从左到右依次为123S S S，，，则123S S S++=1.5 ．13、反比例函数kyx=)0(<k的图象与经过原点的直线l相交于A、B两点，已知A点坐标为)1,2(-，那么B点的坐标为（2，-1 ）三、解答题1、如图，一次函数2y kx=+的图象与反比例函数myx=的图象交于点P，点P在第一象限．P A⊥x轴于点A，PB⊥y 轴于点B．一次函数的图象分别交x轴、y轴于点C、D，且S△PBD= 4, OC:OA:BD=1:2:4．（1）求点D的坐标；（2）求一次函数与反比例函数的解析式；（3）根据图象写出当0x>时，一次函数的值大于反比例函数的值的x的取值范围.2yx=xyOP1P2P3P41 2 3 42、如图，已知反比例函数12kyx=的图象与一次函数2y k x b=+的图象交于A B，两点，(1)A n，，122B⎛⎫--⎪⎝⎭，．（1）求反比例函数和一次函数的解析式；（2）当x为何值时，一次函数的值大于反比例函数的值？（3）求△AOB的面积。
（4）在x轴上是否存在点P，使AOP△为等腰三角形？若存在，请你直接写出P点的坐标；若不存在，请说明理由。
3、如图1，已知双曲线y=（k1＞0）与直线y=k2x交于A、B两点，点A在第一象限．试解答下列问题：（1）若点A坐标为（4，2），则B点坐标为若点A的横坐标为m，则B点坐标为（用含m和k1或k2的式子表示）；（2）如图2，过原点作另一条直线l，交双曲线y=（k1＞0）于P、Q两点，说明四边形APBQ是平行四边形；k1xk1xyxPBDAOC（3）设点A 、P 的横坐标分别为m 、n ，四边形APBQ 可能是矩形吗？可能是正方形吗？若可能，直接写出m 、n 应满足的条件；若不可能，请说明理由．（1）（－4，－2） （－m ，－k′m ）或（－m ，－k/m ） （2）①由勾股定理OA= √[m^2+(k′m)^2]， OB=√[(-m)^2+(-k′m)^2] = √[m^2+(k′m)^2] ∴OA=OB ．同理可得OP=OQ ，∴四边形APBQ 一定是平行四边形．②四边形APBQ 可能是矩形， m ，n 应满足的条件是mn=k ．四边形APBQ 不可能是正方形．理由：点A ，P 不可能达到坐标轴，即∠POA≠90°．5、 如图所示，已知：正方形OABC 的面积为9 ，点O 为坐标原点，点A 在x 轴上，点C 在y轴上, 点B 在函数)0,0(>>=x k x k y 的图象上,点P(m ，n)是函数)0,0(>>=x k xky 的图象上动点，过点P 分别作x 轴、y 轴的垂线，垂足分别为E 、F ，若设矩形OEPF 和正方形OABC不重合的部分面积为S. (1)求B 点坐标和k 的值；(2)当29=S 时，求点P 的坐标；(3)写出S 关于m 的函数关系式．解：（1）依题意：设B 点坐标为()x y 00，， 所以S x y x y OABC 正方形，====000093即B x y k k ()33900，，所以，==；（2）①P （m ，n ）在y x =9上，S mn OEP F 矩形19==，所以S nOAGF 矩形=3由已知可得S n =-=9392解得n m P ==3266321，，所以，()②如图（a ）所示，同理可求得P 2326()，（3）如图（b ）所示，当03<<m 时，因为点P 坐标为（m ，n ） 所以S mOEGC 矩形=3S S S OEPF OEGC=-矩形矩形所以S m m =-<<9303()如图（c ）所示，当m ≥3时，因为P 点坐标为（m ，n ）所以S n mn n m OAGP 矩形，，===399所以S n m =-=-939276、如图，一次函数的图象与反比例函数y 1＝－3x(x <0)的图象相交于正A 点，与y 轴、x 轴分别相交于B 、C 两点，且C(2，0)．当x <－1时，一次函数值大于反比例函数值；当x >－1时，一次函数值小于反比例函数值．(1)求一次函数的解析式；(2)设函数y 2＝a x (x >0)的图象与y 1＝－3x (x <0)的图象关于y 轴对称，在y 2＝ax(x >0)的图象上取一点P(P点的横坐标大于2)，过P 作PQ ⊥x 轴，垂足是Q ，若四边形BCQP 的面积等于2，求P 点的坐标．20、（10分）某单位为响应政府发出的全民健身的号召，打算在长和宽分别为20米和11米的矩形大厅内修建一个60平方米的矩形健身房ABCD。
该健身房的四面墙壁中有两侧沿用大厅的旧墙壁（如图为平面示意图），已知装修旧墙壁的费用为20元/平方米，新建（含装修）墙壁的费用为80元/平方米。
设健身房的高为3米，一面旧墙壁AB的长为x米，修建健身房的总投入为y元。
（1）求y与x的函数关系式；（2）为了合理利用大厅，要求自变量x必须满足8≤x≤12.当投入资金为4800元时，问利用旧墙壁的总长度为多少米？解：（1）根据题意，AB=x，AB•BC=60，所以BC=60/x．y=20×3（x+60/x）+80×3（x+60/x），即y=300（x+60/x）．（2）把x=10代入y=300（x+60/x），得y=300(10+6)=1800答：需投入的资金为1800元。
CD11米20米。