【高考数学】集合与函数典型例题整合
集合与函数基本概念例题和知识点总结

集合与函数基本概念例题和知识点总结在数学的学习中,集合与函数是非常重要的基础知识。
它们不仅是后续数学学习的基石,也在实际生活和其他学科中有着广泛的应用。
下面我们将通过一些例题来深入理解集合与函数的基本概念,并对相关知识点进行总结。
一、集合的基本概念集合是把一些确定的、不同的对象作为一个整体来考虑。
集合中的对象称为元素。
例如,“所有小于 10 的正整数”就可以构成一个集合,记为 A ={1, 2, 3, 4, 5, 6, 7, 8, 9} 。
集合的表示方法通常有列举法、描述法和图示法。
列举法就是将集合中的元素一一列举出来,如上面的例子。
描述法是用集合中元素所具有的共同特征来描述集合,比如 B ={x | x 是大于 5 小于 15 的整数} 。
图示法常用的有韦恩图,能直观地表示集合之间的关系。
集合之间的关系有子集、真子集、相等。
如果集合 A 的所有元素都是集合 B 的元素,就说 A 是 B 的子集,记作 A ⊆ B 。
如果 A 是 B 的子集,且 B 中至少有一个元素不属于 A ,则 A 是 B 的真子集,记作 A ⊂ B 。
如果 A 和 B 的元素完全相同,那么 A 和 B 相等,记作 A = B 。
来看一个集合的例题:已知集合 A ={1, 2, 3} ,集合 B ={x |x² 6x + 8 = 0} ,判断 A 和 B 的关系。
首先求解集合 B 中的方程 x² 6x + 8 = 0 ,即(x 2)(x 4) = 0 ,解得 x = 2 或 x = 4 ,所以集合 B ={2, 4} 。
可以看出集合 A 中的元素 1 和 3 不在集合 B 中,集合 B 中的元素 2 和 4 也不在集合 A 中,所以 A 和 B 没有包含关系。
二、函数的基本概念函数是一种特殊的对应关系。
设 A 、 B 是非空的数集,如果按照某个确定的对应关系 f ,使对于集合 A 中的任意一个数 x ,在集合 B 中都有唯一确定的数 f(x) 和它对应,那么就称 f :A → B 为从集合 A 到集合 B 的一个函数。
高中集合题型和例题大全

高中集合的题型和例题有很多种,以下是一些常见的类型和示例:
1. 集合的表示方法
例题:用列举法表示下列集合:
(1){x|x是小于10的正整数}
(2){y|y是5的正整数倍}
(3){x|x是4除以3的余数}
(4){y|y是9的平方数}
2. 集合之间的关系
例题:已知集合A={x|x=2k+1,k∈Z},B={x|x=4k+1,k∈Z},求证:A∩B=
{x|x=8k+1,k∈Z}。
3. 集合的运算
例题:已知集合A={1,2,3,4},B={3,4,5,6},求:
(1)A∪B;
(2)A∩B;
(3)A-B;
(4)B-A。
4. 集合的元素与集合的关系
例题:已知集合A={a,b,c,d},B={e,f},且集合C满足A∩C≠∅,B∩C≠∅,求C的可能情况。
5. 集合的子集与真子集
例题:已知集合A={1,2,3},求A的所有子集和真子集。
6. 集合的交集、并集、补集运算
例题:已知集合A={1,2,3},集合B={2,3,4},求:
(1)A∩B;
(2)A∪B;
(3)C∪A;
(4)C∪B。
7. 含参数的集合问题
例题:已知集合A={x|ax+b=0},若A=∅时a、b应满足什么条件?如果A≠∅时a、b 应满足什么条件?。
【名师同步】高中数学 必修1 集合与函数 1.2.2 函数解析式 知识点+例题+练习题(含答案)

高中数学必修1 集合与函数 1.2.2 函数解析式知识点+例题+练习题1.常见函数解析式:(1)一次函数: ;(2)反比例函数: ;(3)二次函数: .2.抽象函数解析式:f(ax+b)=g(x);步骤:第一步:;第二步:;第三步:;第四步: .【例1】已知f(x)是一次函数,且满足3f(x+1)-f(x)=2x+9,求f(x).【例2】已知f(x+1)=x2+4x+1,求f(x)的解析式.【例3】已知f(x)是一次函数,且f[f(x)]=4x+3,则f(x)= .【例4】求下列函数解析式.(1)已知2f(x1)+f(x)=x(x ≠0),求f(x); (2)已知f(x)+2f(-x)=x 2+2x ,求f(x).【例5】设二次函数f(x)满足f(2+x)=f(2-x),且f(x)=0的两个实根的平方和为10,f(x)的图象过点(0,3),求f(x)的解析式.1.已知函数f(2x +1)=3x +2,且f(a)=2,则a 的值等于( )A.8B.1C.5D.-1 2.已知f(x +1)=x 2-4,那么f(6)的值是( )A.32B.21C.12D.45 3.已知f(x -1)=x 2+4x -5,则f(x +1)=( )A.x 2+6x B.x 2+8x +7 C.x 2+2x -3 D.x 2+6x -10 4.已知f(121-x )=2x -5,且f(a)=6,则a 等于( ) A.-47 B.47 C.34 D.-34 5.如果f(x 1)=xx-1,则当x ≠0,1时,f(x)等于( ) A.x 1 B.11-x C.x -11 D.x1-1 6.若函数f(x)满足f(2x-1)=x+1,则f(x)=_______________. 7.若f(2x +1)=4x 2+4x ,则f(x)的解析式为____________. 8.已知f(x)=x 2+1,g(x)=2x +1,则f[g(x)]=________. 9.已知f(x -x 1)=x 2+21x,则函数f(x +1)的表达式为________________. 10.已知f(x)=ax 2+bx+c ,若f(0)=0,且f(x+1)=f(x)+x+1,求f(x)的表达式.11.求下列函数解析式.(1)已知f(x)是一次函数,且满足3f(x +1)-2f(x -1)=2x +17,求f(x); (2)已知f(x)满足2f(x)+f(x1)=3x ,求f(x)12.设二次函数f(x)=ax 2+bx+c ,当x=3时取得最大值10,并且它的图象在x 轴上截得的线段长为4,求a 、b 、c 的值.1.已知f(x x +-11)=2211xx +-,则f(x)的解析式可能为( ) A.21x x + B.-212x x + C.212x x + D.-21xx+ 2.若g(x)=1-2x,f[g(x)]=221xx -,则f(0.5)的值为( ) A.1 B.15 C.4 D.30 3.已知f(x-1)=2x 2-1,则f(x)= ,f(x)=x 2+2x,则f(2x+1)= . 4.若f(x)=ax 2-2,a 为一个正的常数,且f(f(2))=-2,则a=________.5.已知f(x +1)=x +2x ,则f(x)的解析式为______________________.6.已知函数f(x +1)=x 2-2. (1)求f(2)的值; (2)求函数f(x)的解析式.7.若3f(x -1)+2f(1-x)=2x ,求f(x).8.设f(x)是R 上的函数,且满足f(0)=1,并且对任意实数x ,y ,有f(x -y)=f(x)-y(2x -y +1),求f(x)的解析式.9.已知二次函数f(x)的二次项系数为a,且不等式f(x)>-2x的解集为(1,3).(1)若方程f(x)+6a=0有两个相等的根,求f(x)的解析式;(2)若f(x)的最大值为正数,求a的取值范围.知识点 参考答案 1.(1)y=kx+b ;(2)y=kx-1;(3)y=ax 2+bx+c. 2.设t=ax+b ;注意t 的取值范围;求出x(用含t 的代数式表示出x);将含t 的代数式代入到g(x)中; 整理并将t 转化为x ,即可得到f(x)的表达式.例题参考答案例1.解:由题意,设函数为f(x)=ax +b(a ≠0),∵3f(x +1)-f(x)=2x +9,∴3a(x +1)+3b -ax -b=2x +9,即2ax +3a +2b=2x +9, 由恒等式性质,得2a=2,3a+2b=9,∴a=1,b=3. ∴所求函数解析式为f(x)=x +3.例2.解:设x +1=t ,则x=t -1,f(t)=(t -1)2+4(t -1)+1,即f(t)=t 2+2t -2.∴所求函数为f(x)=x 2+2x -2. 例3.答案为:2x +1或-2x -3.解析:设f(x)=ax +b(a ≠0),则f[f(x)]=f(ax +b)=a(ax +b)+b=a 2x +ab +b=4x +3,∴a 2=4,ab+b=3解得a=2,b=1或a=-2,b=-3.故所求的函数为f(x)=2x +1或f(x)=-2x -3.例4.解:(1)∵f(x)+2f(x 1)=x ,将原式中的x 与1x 互换,得f(x 1)+2f(x)=x1.于是得关于f(x)的方程组,解得f(x)=332xx (x ≠0). (2)∵f(x)+2f(-x)=x 2+2x ,将x 换成-x ,得f(-x)+2f(x)=x 2-2x , ∴将以上两式消去f(-x),得3f(x)=x 2-6x ,∴f(x)=31x 2-2x. 例5.解:∵f(2+x)=f(2-x),∴f(x)的图象关于直线x=2对称.于是,设f(x)=a(x-2)2+k(a ≠0),则由f(0)=3,可得k=3-4a ,∴f(x)=a(x-2)2+3-4a=ax 2-4ax+3.∵ax 2-4ax+3=0的两实根的平方和为10, ∴10=x 12+x 22=(x 1+x 2)2-2x 1x 2=16-a6. ∴a=1. ∴f(x)=(x-2)2-1=x 2-4x+3. 课堂练习 参考答案1.答案为:B2.答案为:B ;3.答案为:B ;解析:令x -1=t ,∴x=t +1,∴f(t)=(t +1)2+4(t +1)-5=t 2+6t ,∴f(x)=x 2+6x.∴f(x +1)=(x +1)2+6(x +1)=x 2+8x +7. 4.答案为:B ; 5.答案为:B ;6.答案为:0.5x+1.5;7.答案为:f(x)=x 2-1;8.答案为:4x 2+4x +2;9.答案为:f(x +1)=x 2+2x +3;10.解:∵f(0)=0,∴c=0.又∵f(x+1)=a(x+1)2+b(x+1)=ax 2+2ax+a+bx+b ,f(x)+x+1=ax 2+bx+x+1,∴ax 2+2ax+a+bx+b=ax 2+bx+x+1.解得2ax+a+b=x+1.∴2a=1,a+b=1,得a=0.5,b=0.5.∴f(x)的解析式为f(x)=0.5x 2+0.5x.11.解:(1)设f(x)=ax +b(a ≠0),则3f(x +1)-2f(x -1)=3ax +3a +3b -2ax +2a -2b=ax +b +5a=2x +17,∴a=2,b=7,∴f(x)=2x +7.(2)2f(x)+f(x 1)=3x,①把①中的x 换成1x ,得2f(x 1)+f(x)=x3,②①×2-②得3f(x)=6x -x 3,∴f(x)=2x -x1. 12.解:当x=3时,取得最大值10的二次函数可写成:f(x)=a(x-3)2+10,且a <0.因为抛物线的对称轴是x=3,又因为图象在x 轴上截得的线段长是4,所以由对称性,图象与x 轴交点的横坐标分别是1、5.因此,二次函数又可写成f(x)=a(x-1)(x-5)的形式,从而a(x-3)2+10=a(x-1)(x-5),a=-2.5,所以f(x)=- 2.5(x-3)2+10=-2.5x 2+15x-12.5. 因此,a=-2.5,b=15,c=-12.5.课后练习 参考答案1.答案为:C ;2.答案为:B ;3.答案为:2x 2-4x+1,4x 2+6x+1. 4.答案为:22; 解析:f(2)=a(2)2-2=2a -2, ∴f(f(2))=f(2a -2)=a(2a -2)2-2=-2,∴a(2a -2)2=0.∵a>0,∴2a -2=0,即a=22.5.答案为:f(x)=x 2-1(x ≥1) 解析:∵f(x +1)=x +2x =(x )2+2x +1-1=(x +1)2-1,∴f(x)=x 2-1.由于x +1≥1,所以f(x)=x 2-1(x ≥1).6.解:(1)令x=1,则f(2)=12-2=-1.(2)令x +1=t ,∴x=t -1.∴f(t)=(t -1)2-2=t 2-2t -1.∴f(x)=x 2-2x -1. 7.解:令t=x -1,则1-x=-t ,原式变为3f(t)+2f(-t)=2(t +1),①以-t 代t ,原式变为3f(-t)+2f(t)=2(1-t),② 由①②消去f(-t),得f(t)=2t +0.4.即f(x)=2x +0.4. 8.解:因为对任意实数x ,y ,有f(x -y)=f(x)-y(2x -y +1),所以令y=x ,有f(0)=f(x)-x(2x -x +1), 即f(0)=f(x)-x(x +1).又f(0)=1,∴f(x)=x(x +1)+1=x 2+x +1.9.解:(1)∵f(x)+2x>0的解集为(1,3),f(x)+2x=a(x-1)(x-3),且a<0,因而f(x)=a(x-1)(x-3)-2x=ax 2-(2+4a)x+3a.①由方程f(x)+6a=0,得ax 2-(2+4a)x+9a=0.②因为方程②有两个相等的根,所以Δ=[-(2+4a)]2-4a\59a=0,即5a 2-4a-1=0. 解得a=1或a=-0.2.由于a<0,舍去a=1.将a=-0.2代入①得f(x)的解析式为f(x)=-0.2x 2-1.2x-0.6.(2)由f(x)=ax 2-2(1+2a)x+3a=a(x-a a 21+)2-aa a 142++及a<0,可得f(x)的最大值为-aa a 142++.由⎪⎩⎪⎨⎧<>++-0142a a a a , 解得a<-2-3或-2+3<a<0.故当f(x)的最大值为正数时,实数a 的取值范围是(-∞,-2-3)∪(-2+3,0).。
【高中数学】《集合》高考常考题型(后附解析)

《集合》常考题型题型一.通过集合的关系求参数范围1.已知集合2{|320}A x x x =−+=,22{|2(1)(5)0}B x x a x a =−++−=,A B A =,实数a 的取值范围是 . 2.已知全集U R =,集合{|25}A x x =−,{|121}B x a x a =+−,且U A B ⊆,实数a 的取值范围是 . 3.已知集合2{|10}A x R x ax =∈++=和{1B =,2},且A B ⊆,则实数a 的取值范围是 . 题型二.子集个数问题4.用d (A )表示集合A 中的元素个数,若集合22{|()(1)0}A x x ax x ax =−−+=,{0B =,1},且|d (A )d−(B )|1=.设实数a 的所有可能取值构成集合M ,则()(d M = )A .3B .2C .1D .4 题型三.集合与元素的关系5.设A 是非空数集,0A ∉,1A ∉,且满足条件:若a A ∈,则11A a∈−. 证明:(1)若2A ∈,则A 中必还有另外两个元素;(2)集合A 不可能是单元素集;(3)集合A 中至少有三个不同的元素.参考答案1.已知集合2{|320}A x x x =−+=,22{|2(1)(5)0}B x x a x a =−++−=,AB A =,求实数a 的取值范围.【解答】解:由2320x x −+=解得1x =,2.{1A ∴=,2}.A B A =,B A ∴⊆. 1B ︒=∅,△8240a =+<,解得3a <−.2︒若{1}B =或{2},则△0=,解得3a =−,此时{2}B =−,不符合题意.3︒若{1B =,2},∴2122(1)125a a +=+⎧⎨⨯=−⎩,此方程组无解. 综上:3a <−.∴实数a 的取值范围是(,3)−∞−.2.已知全集U R =,集合{|25}A x x =−,{|121}B x a x a =+−,且U A B ⊆,求实数a 的取值范围. 【解答】解:{|121}B x a x a =+−,且U A B ⊆,B ∴=∅,或211a a −>+,解得2a >, ①{|1U B x x a =<+,或21}x a >−,∴251a a ⎧⎨<+⎩或2212a a ⎧⎨−<−⎩, 解得4a >或a ∈∅.此时实数a 的取值范围为4a >.②当B =∅,U B R =,满足U A B ⊆,121a a ∴+>−,解得2a <.综上可得:实数a 的取值范围为4a >或2a <.3.已知集合2{|10}A x R x ax =∈++=和{1B =,2},且A B ⊆,则实数a 的取值范围是[2−,2). 【解答】解:因为A B ⊆,所以A =∅或{1}A =,{2}A =或{1A =,2}. 若A =∅,则△240a =−<,解得22a −<<.若{1}A =应有△240a =−=且110a ++=,解得2a =−.若{2}A =时,应有△240a =−=且4210a ++=,此时无解. 若{1A =,2},则1,2是方程210x ax ++=的两个根,所以由根与系数的关系得121⨯=,显然不成立.综上满足条件的实数a 的取值范围是22a −<.故答案为:[2−,2).4.用d (A )表示集合A 中的元素个数,若集合22{|()(1)0}A x x ax x ax =−−+=,{0B =,1},且|d (A )d−(B )|1=.设实数a 的所有可能取值构成集合M ,则()(d M = )A .3B .2C .1D .4【解答】解:由题意,d (B )2=,|d (A )d −(B )|1=,d ∴(A )1=或3, 方程22()(1)0x ax x ax −−+=可化为20x ax −=或210x ax −+=, 即0x =或x a =或210x ax −+=,①若d (A )1=,则方程22()(1)0x ax x ax −−+=有且只有一个解,故0a =,此时方程22(1)0x x +=有且只有一个解;②若d (A )3=,则方程22()(1)0x ax x ax −−+=有三个不同的解,则2040a a ≠⎧⎨−=⎩,解得,2a =±, 经检验,2a =±时,方程22()(1)0x ax x ax −−+=有三个不同的解,综上所述,{0M =,2−,2},故()3d M =, 故选:A .5.设A 是非空数集,0A ∉,1A ∉,且满足条件:若a A ∈,则11A a ∈−. 证明:(1)若2A ∈,则A 中必还有另外两个元素;(2)集合A 不可能是单元素集;(3)集合A 中至少有三个不同的元素.【解答】解:(1)若2A ∈,则1112A =−∈−,于是()11112A =∈−−, 故集合A 中还含有1−,12两个元素. (2)若A 为单元素集,则11a a =−,即210a a −+=,此方程无实数解,∴11a a≠−, ∴a 与11a−都为集合A 的元素,则A 不可能是单元素集. (3)由A 是非空集合知存在1111111a a A A A a a a−∈⇒∈⇒=∈−−−−. 现只需证明a 、11a −、1a a−−三个数互不相等. ①若21101a a a a =⇒−+=−,方程无解,∴11a a≠−; ②若2110a a a a a −=⇒−+=−,方程无解;∴1a a a−≠−; ③若211101a a a a a −=⇒−+=−−,方程无解,∴111a a a −≠−−, 故集合A 中至少有三个不同的元素.。
集合和函数练习题集(附答案解析)

集合与函数综合练习一、填空题:1.设函数x xx f =+-)11(,则)(x f 的表达式为 2.函数)(x f 在区间]3,2[-是增函数,则)5(+=x f y 的递增区间是 3. 函数f(x)=)24(log 122x x -+-的定义域为4.已知集合}023|{2=+-=x ax x A 至多有一个元素,则a 的取值范围 .5.函数||2x x y +-=,单调递减区间为6.构造一个满足下面三个条件的函数实例,①函数在)1,(--∞上递减;②函数具有奇偶性;③函数有最小值为0; .7.=+34-3031-]2-[54-0.064)()(___________ ____; 8.已知)(x f =x x +1,则111(1)(2)()(3)()(4)()234f f f f f f f ++++++= 。
9.已知函数()y f x =为奇函数,若(3)(2)1f f -=,(2)(3)f f ---=_______ 10.)(x f =21(0)2(0)x x x x ⎧+≤⎨->⎩,若)(x f =10,则x = .11.若f (x )是偶函数,其定义域为R 且在[0,+∞)上是减函数,则f (-43)与f (a 2-a +1)的大小关系是____.12.log 7[log 3(log 2x )]=0,则21-x等于= 13.函数y=log 21(x 2-5x+17)的值域为 。
14.函数y=lg(ax+1)的定义域为(-∞,1),则a= 。
二、解答题:15.已知集合A 的元素全为实数,且满足:若a A ∈,则11a A a+∈-。
(1)若3a =-,求出A 中其它所有元素;(2)0是不是集合A 中的元素?请你设计一个实数a A ∈,再求出A 中的所有元素?16.已知函数[]5,5,22)(2-∈++=x ax x x f .(1)求实数a 的范围,使)(x f y =在区间[]5,5-上是单调递增函数。
专题02:集合知识点与典型例题(解析版)-2022年高考数学一轮复习

故选:C
12.已知集合U 1, 2,3, 4,5, 6,A 1, 2,3 ,集合 A 与 B 的关系如图所示,则集合 B 可
能是( )
A.2, 4,5
B.1, 2,5
【答案】D 【分析】
由图可得 B A ,由选项即可判断.
【详解】
解:由图可知: B A ,
A 1, 2,3 ,
C. 1, 6
故选:D.
5.设 A={y|y=﹣1+x﹣2x2},若 m∈A,则必有( )
A.m∈{正有理数} 【答案】D 【分析】
B.m∈{负有理数}
C.m∈{正实数}
D.m∈{负实数}
求出函数 y 1 x 2x 2 的值域,就是集合 A,进而可判断结果
【详解】
解:因为 y 1 x 2x2 2(x 1 )2 7 7 , 488
∪A.
4、全集与补集
(1)全集:如果集合 S 含有我们所要研究的各个集合的全部元素,这个集合就可以看作一
个全集。通常用 U 来表示。
(2)补集:设 S 是一个集合,A 是 S 的一个子集(即 A S),由 S 中
S
所有不属于 A 的元素组成的集合,叫做 S 中子集 A 的补集(或余集)。
记作: CSA ,即 CSA ={x | xS 且 x A}
对于 B:{(x, y}) | x 2, y 3},表示的是点集,故不相等;
对于 C: x | x2 5x 6 0 ,表示方程 x2 5x 6 0 的解集,因为 x2 5x 6 0 的解 为 x 2 ,或 x 3 ,所以 x | x2 5x 6 0 2,3
对于 D: x N x2 9 0 3,2,1, 0,1, 2,3 ,故不相等
B. {1, 3}
高中数学高考总复习-集合与函数概念知识点及习题
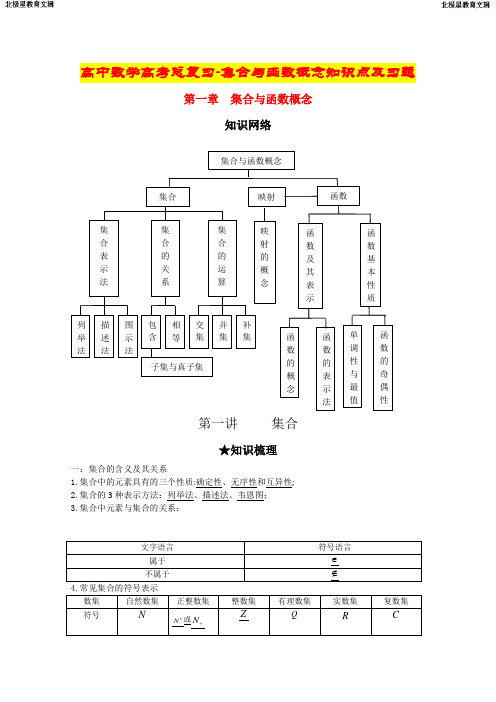
高中数学高考总复习-集合与函数概念知识点及习题第一章 集合与函数概念知识网络第一讲 集合★知识梳理一:集合的含义及其关系1.集合中的元素具有的三个性质:确定性、无序性和互异性;2.集合的3种表示方法:列举法、描述法、韦恩图;3.集合中元素与集合的关系: 文字语言 符号语言属于 ∈不属于∉4.常见集合的符号表示数集 自然数集正整数集整数集有理数集实数集 复数集符号N *N 或+NZQR C集合 集 合 表 示 法 集 合 的 运 算集 合 的 关 系 列 举 法 描 述 法 图 示 法包 含 相 等 子集与真子集交 集 并 集 补 集函数函数 及其表示 函数基本性质单调性与最值 函数的概念函数 的 奇偶性函数的表示法映射 映射的概念集合与函数概念表示关系文字语言符号语言相等集合A与集合B中的所有元素都相同BA⊆且A⊆B⇔BA=子集A中任意一元素均为B中的元素BA⊆或AB⊇真子集A中任意一元素均为B中的元素,且B中至少有一元素不是A的元素A B空集空集是任何集合的子集,是任何非空集合的真子集A⊆φ,φB(φ≠B)三:集合的基本运算①两个集合的交集:A BI= {}x x A x B∈∈且;②两个集合的并集: A BU={}x x A x B∈∈或;③设全集是U,集合A U⊆,则UC A={}x x U x A∈∉且交并补I U{|,}A B x x A x B=∈∈I且{|,}A B x x A x B=∈∈U或UC A={}x x U x A∈∉且方法:常用数轴或韦恩图进行集合的交、并、补三种运算.★重、难点突破重点:集合元素的特征、集合的三种表示方法、集合的交、并、补三种运算。
难点:正确把握集合元素的特征、进行集合的不同表示方法之间的相互转化,准确进行集合的交、并、补三种运算。
重难点:1.集合的概念掌握集合的概念的关键是把握集合元素的三大特性,要特别注意集合中元素的互异性,在解题过程中最易被忽视,因此要对结果进行检验;2.集合的表示法(1)列举法要注意元素的三个特性;(2)描述法要紧紧抓住代表元素以及它所具有的性质,{})(x fyx=如、{})(x fyy=、{})(),(xfyyx=等的差别,如果对集合中代表元素认识不清, 将导致求解错误:问题:已知集合221,1,9432x y x y M xN y ⎧⎫⎧⎫=+==+=⋂⎨⎬⎨⎬⎩⎭⎩⎭则M N=( ) A. Φ;B. {})2,0(),0,3(;C. []3,3-;D. {}3,2(3)Venn 图是直观展示集合的很好方法, 在解决集合间元素的有关问题和集合的运算时常用Venn 图。
集合典型例题(含解析)

第一章集合一、选择题1.(2012·湖南高考理科·T1)设集合M={-1,0,1},N={x|x2≤x},则M∩N=( )(A){0} (B){0,1} (C){-1,1} (D){-1,0,1}【解题指南】求出集合N中所含有的元素,再与集合M求交集.【解析】选B. 由…2x x,得…2x x0-,…x(x1)0-,剟0x1,所以N=剟{x0x1},所以M I N={0,1},故选B.2.(2012·浙江高考理科·T1)设集合A={x|1<x<4},集合B ={x|x2-2x-3≤0}, 则A∩(C R B)=()(A)(1,4) (B)(3,4) (C)(1,3) (D)(1,2)∪(3,4)【解题指南】考查集合的基本运算.【解析】选B.集合B ={x|x2-2x-3≤0}={}13x x-≤≤,{}1,3RB x x x=<->或ð,∴A∩(C R B)=(3,4)3.(2012·江西高考理科·T1)若集合{}{}1,1,0,2A B=-=,则集合{}|,,z z x y x A y B=+∈∈中的元素的个数为()(A)5 (B)4 (C)3 (D)2【解题指南】将x y+的可能取值一一列出,根据元素的互异性重复元素只计一次,可得元素个数.【解析】选C.由已知得,{}|,,z z x y x A y B=+∈∈{}1,1,3=-,所以集合{}|,,z z x y x A y B=+∈∈中的元素的个数为3.4.(2012·新课标全国高考理科·T1)已知集合{}1,2,3,4,5A=,(){},|,,,B x y x A y A x y A =∈∈-∈则B 中所含元素的个数为( )(A)3 (B)6 (C)8 (D)10【解题指南】将x y -可能取的值列举出来,然后与集合A 合到一起,根据元素的互异性确定元素的个数.【解析】选D.由,x A y A ∈∈得0x y -=或1x y -=±或2x y -=±或3x y -=±或4x y -=±,故集合B 中所含元素的个数为10个.5. (2012·广东高考理科·T2)设集合U={1,2,3,4,5,6},M={1,2,4 },则=ðU M ( )(A)U (B){1,3,5} (C){3,5,6} (D){2,4,6}【解题指南】掌握补集的定义:{|,}U M x x U x M =∈∉且ð,本题易解.【解析】选C. {3,5,6}U M =ð.6.(2012·山东高考文科·T2)与(2012·山东高考理科·T2)相同 已知全集{}0,1,2,3,4U =,集合{}{}1,2,3,2,4A B ==,则U (A)B ð为( ) (A ){}1,2,4 (B ){}2,3,4 (C ){}0,2,4 (D ){}0,2,3,4【解题指南】 先求集合A 关于全集U 的补集,再求它与集合B 的并集即可.【解析】选C.{}{}{}U (A)B 0,42,40,2,4==ð. 7.(2012·广东高考文科·T2)设集合U={1,2,3,4,5,6},M={1,3,5},则U M ð=( )(A){2,4,6} (B){1,3,5} (C){1,2,4} (D)U【解题指南】根据补集的定义:{|,}U M x x U x M =∈∉且ð求解即可.【解析】选A. {2,4,6}U M =ð.8.(2012·辽宁高考文科·T2)与(2012·辽宁高考理科·T1)相同 已知全集U={0,1,2,3,4,5,6,7,8,9},集合A={0,1,3,5,8},集合B={2,4,5,6,8},则()()U U A B ⋂=痧(A){5,8} (B){7,9} (C){0,1,3} (D){2,4,6}【解题指南】据集合的补集概念,分别求出,痧U U A B ,然后求交集.【解析】选B. 由已知C U A={2,4,6,7,9},U B ð={0,1,3,7,9},则(U A ð)⋂(U B ð)={2,4,6,7,9}⋂{0,1,3,7,9}={7,9}.9.(2012·新课标全国高考文科·T1)已知集合A={x|x 2-x -2<0},B={x|-1<x<1},则( )(A )A B Ü (B )B A Ü (C )A=B (D )A ∩B=∅【解题指南】解不等式x 2-x -2<0得集合A ,借助数轴理清集合A 与集合B 的关系.【解析】选B. 本题考查了简单的一元二次不等式的解法和集合之间的关系,由题意可得{}|12A x x =-<<,而{}|11B x x =-<<,故B A Ü.10.(2012·安徽高考文科·T2)设集合A={3123|≤-≤-x x },集合B 为函数)1lg(-=x y 的定义域,则A ⋂B=( )(A )(1,2) (B )[1,2] (C )[ 1,2) (D )(1,2 ]【解题指南】先求出集合,A B ,再求交集.【解析】选D .∵{3213}[1,2]A x x =-≤-≤=-,(1,)(1,2]=+∞=B A B ,∴.11.(2012·福建高考文科·T2)已知集合{1,2,3,4}M =,{2,2}N =-,下列结论成立的是( )(A)N M ⊆ (B)M N M = (C)M N N = (D){2}M N =【解题指南】通过观察找出公共元素,即得交集,结合子集,交、并、补各种概念进行判断和计算.【解析】选D .N 中元素-2不在M 中,因此,A 错,B 错; {2}M N N =≠,因此C错,故选D .12.(2012·浙江高考文科·T1)设全集U={1,2,3,4,5,6} ,集合P={1,2,3,4} ,Q={3,4,5},则P∩(ðU Q)=()(A){1,2,3,4,6} (B){1,2,3,4,5}(C){1,2,5} (D){1,2}【解题指南】考查集合的基本运算.【解析】选D. C U Q={}1,2,6,则P∩(CU Q)={}1,2.13.(2012·北京高考文科·T1)与(2012·北京高考理科·T1)相同已知集合A={x∈R|3x+2>0},B={x∈R|(x+1)(x-3)>0},则A∩B=()(A)(-∞,-1)(B)(-1,-23)(C)(-23,3)(D)(3,+∞)【解题指南】通过解不等式先求出A,B两个集合,再取交集.【解析】选D.集合A=2{|}3x x>-,{|13}B x x x=<->或,所以{|3}A B x x=>.14.(2012·湖南高考文科·T1)设集合M={-1,0,1},N={x|x2=x},则M∩N=()(A){-1,0,1} (B){0,1} (C){1} (D){0}【解题指南】先求出集合N中的元素,再求集合M,N的交集.【解析】选B. N={0,1},∴M∩N={0,1},故选B.15. (2012·江西高考文科·T2)若全集U={x∈R|x2≤4},则集合 A={x∈R||x+1|≤1}的补集C u A为( )(A){x∈R |0<x<2} (B){x∈R |0≤x<2}(C){x∈R |0<x≤2} (D){x∈R |0≤x≤2}【解题指南】解不等式得集合U和A,在U中对A取补集.【解析】选C.{|22}U x x =-≤≤,{|20}A x x =-≤≤,则ðU A={|02}U C A x x =<≤. 16.(2012·湖北高考文科·T1)已知集合A={x|2x -3x +2=0,x ∈R } , B={x|0<x <5,x ∈N },则满足条件A ⊆C ⊆B 的集合C 的个数为(A) 1 (B)2 (C) 3 (D)4【解题指南】根据集合的性质,先化简集合A,B.再结合集合之间的关系求解.【解析】选D. 由题意知:A= {1,2} ,B={1,2,3,4}.又A C B ⊆⊆,则集合C 可能为{1,2},{1,2,3},{1,2,4},{1,2,3,4}. 二、填空题17.(2012·上海高考理科·T2)若集合}012|{>+=x x A ,}2|1||{<-=x x B ,则=B A .【解题指南】本题考查集合的交集运算知识,此类题的易错点是临界点的大小比较. 【解析】集合1{2+10}{|}2A x x x x =>=>-,集合{}{12}{|212}13B x x x x x x =-<=-<-<=-<<,所以1{|3}2A B x x =-<<. 【答案】1{|3}2x x -<< 18.(2012·江苏高考·T1)已知集合{}{}1,2,4,2,4,6A B ==,则A B = .【解题指南】从集合的并集的概念角度处理.【解析】{1,2,4,6}=A B .【答案】{1,2,4,6}。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
概念、方法、题型、易误点及应试技巧总结一、集合与简易逻辑一.集合元素具有确定性、无序性和互异性. 在求有关集合问题时,尤其要注意元素的互异性,如(1)设P 、Q 为两个非空实数集合,定义集合P+Q={|,}a b a P b Q +∈∈,若{0,2,5}P =,}6,2,1{=Q ,则P+Q 中元素的有________个。
(答:8)(2)设{(,)|,}U x y x R y R =∈∈,{(,)|20}A x y x y m =-+>,{(,)|B x y x y n =+-0}≤,那么点)()3,2(B C A P u ∈的充要条件是________(答:5,1<->n m );(3)非空集合}5,4,3,2,1{⊆S ,且满足“若S a ∈,则S a ∈-6”,这样的S 共有_____个(答:7)二.遇到A B =∅时,你是否注意到“极端”情况:A =∅或B =∅;同样当A B ⊆时,你是否忘记∅=A 的情形?要注意到∅是任何集合的子集,是任何非空集合的真子集。
如 集合{|10}A x ax =-=,{}2|320B x x x =-+=,且A B B =,则实数a =___.(答:10,1,2a =)三.对于含有n 个元素的有限集合M ,其子集、真子集、非空子集、非空真子集的个数依次为,n 2,12-n ,12-n .22-n 如 满足{1,2}{1,2,3,4,5}M ⊂⊆≠集合M 有______个。
(答:7)四.集合的运算性质: ⑴A B A B A =⇔⊆; ⑵A B B B A =⇔⊆;⑶A B ⊆⇔B C A C U U ⊇;⑷∅=B C A U B A ⊆⇔; ⑸B A U B A C U ⊆⇔= )(; ⑹()U C A B U U C A C B =; ⑺()U U U C A B C A C B =.如:设全集}5,4,3,2,1{=U ,若}2{=B A ,}4{)(=B A C U ,}5,1{)()(=B C A C U U , 则A =_____,B =___.(答:{2,3}A =,{2,4}B =)五.研究集合问题,一定要理解集合的意义――抓住集合的代表元素。
如:{}x y x lg |=—函数的定义域;{}x y y lg |=—函数的值域;{}x y y x lg |),(=—函数图象上的点集,如(1)设集合{|M x y ==,集合N ={}2|,y y x x M =∈,则MN =___(答:[4,)+∞);(2)设集合{|(1,2)(3,4),M a aR λλ==+∈,{|(2,3)(4,5)N a a λ==+,}R λ∈,则=N M _____(答:)}2,2{(--)六.数轴和韦恩图是进行交、并、补运算的有力工具,在具体计算时不要忘了集合本身和空集这两种特殊情况,补集思想常运用于解决否定型或正面较复杂的有关问题。
如:已知函数12)2(24)(22+----=p p x p x x f 在区间]1,1[-上至少存在一个实数c ,使0)(>c f ,求实数p 的取值范围。
(答:3(3,)2-)七.复合命题真假的判断。
“或命题”的真假特点是“一真即真,要假全假”;“且命题”的真假特点是“一假即假,要真全真”;“非命题”的真假特点是“真假相反”。
如: 在下列说法中:⑴“p 且q ”为真是“p 或q ”为真的充分不必要条件; ⑵“p 且q ”为假是“p 或q ”为真的充分不必要条件; ⑶“p 或q ”为真是“非p ”为假的必要不充分条件; ⑷“非p ”为真是“p 且q ”为假的必要不充分条件。
其中正确的是__________(答:⑴⑶)八.四种命题及其相互关系。
若原命题是“若p 则q ”,则逆命题为“若q 则p ”;否命题为“若﹁p 则﹁q ” ;逆否命题为“若﹁q 则﹁p ”。
提醒:(1)互为逆否关系的命题是等价命题,即原命题与逆否命题同真、同假;逆命题与否命题同真同假。
但原命题与逆命题、否命题都不等价; (2)在写出一个含有“或”、“且”命题的否命题时,要注意“非或即且,非且即或”; (3)要注意区别“否命题”与“命题的否定”:否命题要对命题的条件和结论都否定,而命题的否定仅对命题的结论否定;(4)对于条件或结论是不等关系或否定式的命题,一般利用等价关系“A B B A ⇒⇔⇒”判断其真假,这也是反证法的理论依据。
(5)哪些命题宜用反证法? 如:(1)“在△ABC 中,若∠C=900,则∠A 、∠B 都是锐角”的否命题为__________(答:在ABC ∆中,若90C ∠≠,则,A B ∠∠不都是锐角);(2)已知函数2(),11x x f x a a x -=+>+,证明方程0)(=x f 没有负数根。
九.充要条件。
关键是分清条件和结论(划主谓宾),由条件可推出结论,条件是结论成立的充分条件;由结论可推出条件,则条件是结论成立的必要条件。
从集合角度解释,若B A ⊆,则A 是B 的充分条件;若B A ⊆,则A 是B 的必要条件;若A=B ,则A 是B 的充要条件。
如: (1)给出下列命题:① 实数0=a 是直线12=-y ax 与322=-y ax 平行的充要条件;② 若0,,=∈ab R b a 是b a b a +=+成立的充要条件;③ 已知R y x ∈,,“若0=xy ,则0=x 或0=y ”的逆否命题是“若0≠x 或0≠y 则0≠xy ”; ④“若a 和b 都是偶数,则b a +是偶数”的否命题是假命题 。
其中正确命题的序号是_______(答:①④);(2)设命题p :|43|1x -≤;命题q:0)1()12(2≤+++-a a x a x 。
若┐p 是┐q 的必要而不充分的条件,则实数a 的取值范围是(答:1[0,]2)十.一元一次不等式的解法:通过去分母、去括号、移项、合并同类项等步骤化为ax b >的形式,若0a >,则b x a >;若0a <,则bx a<;若0a =,则当0b <时,x R ∈;当0b ≥时,x ∈∅。
如已知关于x 的不等式0)32()(<-++b a x b a 的解集为)31,(--∞,则关于x 的不等式0)2()3(>-+-a b x b a 的解集为_______(答:{|3}x x <-)十一.一元二次不等式的解集(联系图象)。
尤其当0∆=和0∆<时的解集你会正确表示吗?设0a >,,x x 是方程20ax bx c ++=的两实根,且x x <,则其解集如下表:如解关于x 的不等式:01)1(<++-x a ax 。
(答:当0a =时,1x >;当0a <时,1x >或1x a <;当01a <<时,11x a<<;当1a =时,x ∈∅;当1a >时,11x a<<) 十二.对于方程02=++c bx ax 有实数解的问题。
首先要讨论最高次项系数a 是否为0,其次若0≠a ,则一定有042≥-=∆ac b 。
对于多项式方程、不等式、函数的最高次项中含有参数时,你是否注意到同样的情形?如:(1)()()222210a x a x -+--<对一切R x ∈恒成立,则a 的取值范围是_______(答:(1,2]); (2)关于x 的方程()f x k =有解的条件是什么?(答:k D ∈,其中D 为()f x 的值域),特别地,若在[0,]2π内有两个不等的实根满足等式cos 221x x k =+,则实数k 的范围是_______.(答:[0,1))十三.一元二次方程根的分布理论。
方程2()0(0)f x ax bx c a =++=>在),(+∞k 上有两根、在(,)m n 上有两根、在),(k -∞和),(+∞k 上各有一根的充要条件分别是什么?0()0()02f m f n b m an ∆≥>><-<⎧⎪⎪⎨⎪⎪⎩、()0f k <)。
根的分布理论成立的前提是开区间,(0()02f k bk a∆≥>->⎧⎪⎪⎨⎪⎪⎩、若在闭区间[m 有实数解的情况,可先利用在开区间),(n m 上实根分布的情况,得出结果,再令n x =和m x =检查端点的情况.如实系数方程220x ax b ++=的一根大于0且小于1,另一根大于1且小于2,则12--a b 的取值范围是_________(答:(41,1))十四.二次方程、二次不等式、二次函数间的联系你了解了吗?二次方程20ax bx c ++=的两个根即为二次不等式20(0)ax bx c ++><的解集的端点值,也是二次函数2y ax bx c =++的图象与x 轴的交点的横坐标。
如(1)32ax >+的解集是(4,)b ,则a =__________(答:18);(2)若关于x 的不等式02<++c bx ax 的解集为),(),(+∞-∞n m ,其中0<<n m ,则关于x 的不等式02<+-a bx cx 的解集为________(答:),1()1,(+∞---∞nm ); (3)不等式23210x bx -+≤对[1,2]x ∈-恒成立,则实数b 的取值范围是_______(答:∅)。
二、函数一.映射f : A →B 的概念。
在理解映射概念时要注意:㈠中元素必须都有象且唯一;㈡B 中元素不一定都有原象,但原象不一定唯一。
如:(1)设:f M N →是集合M 到N 的映射,下列说法正确的是 A 、M 中每一个元素在N 中必有象 B 、N 中每一个元素在M 中必有原象 C 、N 中每一个元素在M 中的原象是唯一的 D 、N 是M 中所在元素的象的集合(答:A );(2)点),(b a 在映射f 的作用下的象是),(b a b a +-,则在f 作用下点)1,3(的原象为点________(答:(2,-1));(3)若}4,3,2,1{=A ,},,{c b a B =,,,a b c R ∈,则A 到B 的映射有 个,B 到A 的映射有 个,A 到B 的函数有 个(答:81,64,81);(4)设集合{1,0,1},{1,2,3,4,5}M N =-=,映射:f M N →满足条件“对任意的x M ∈,()x f x +是奇数”,这样的映射f 有____个(答:12);(5)设2:x x f →是集合A 到集合B 的映射,若B={1,2},则B A 一定是_____(答:∅或{1}).二.函数f : A →B 是特殊的映射。
