平面开链机械臂动力系统及其控制的向量键合图建模与分析
平面机械手的建模与优化设计

平面机械手的建模与优化设计随着工业的不断发展和进步,人们对于机械自动化技术的需求也越来越高。
平面机械手作为一种高效的自动化机械,广泛应用于各个领域,如物流、生产线、汽车制造等。
平面机械手的建模和优化,对于提高机械手的灵活性、稳定性和效率至关重要。
本文将主要探讨平面机械手的建模与优化设计。
一、平面机械手的建模平面机械手的建模是指通过对机械手的运动学、动力学性质进行分析和计算,得出机械手在不同工作状态下的运动轨迹、速度和加速度。
平面机械手的建模可以使用数学模型和计算机仿真等方法实现。
1.1. 数学模型数学模型是通过对平面机械手的结构和运动规律进行分析,得出精确的数学公式,用于计算机操作和控制机械手的轨迹、速度、加速度和力学性质。
数学模型主要包括:几何学模型、运动学模型和动力学模型。
1.1.1 几何学模型几何学模型是根据机械手的基本结构和运动连接,通过几何关系推导出机械手的位置坐标和各个工具执行器的运动轨迹。
几何学模型通常使用欧拉角和轴角等方法进行计算。
1.1.2 运动学模型运动学模型是通过对机械手的位置和方向进行分析,得出机械手的运动轨迹、速度和加速度。
运动学模型通常使用逆向运动学和正向运动学等方法进行计算。
1.1.3 动力学模型动力学模型是通过对机械手受力和力矩的计算,得出机械手的运动学性质和输入输出关系。
动力学模型通常使用拉格朗日方程和牛顿-欧拉方程等方法进行计算。
1.2 计算机仿真计算机仿真是通过对平面机械手进行虚拟建模和实验,模拟机械手在不同工作状态下的运动轨迹、速度和加速度。
计算机仿真可以帮助优化机械手的设计,提高效率和精度。
二、平面机械手的优化设计平面机械手的优化设计是指通过对机械手的结构、工具和控制系统等进行改进,提高机械手的灵活性、稳定性和效率。
平面机械手的优化设计可以使用多目标优化和仿生优化等方法实现。
2.1 多目标优化多目标优化是通过对机械手的多个目标进行分析和权衡,寻找机械手的最优设计方案。
管理学机械设计基础第五版杨可桢版第一章平面机构的自由度和速度分析

两构件组成的运动副,不外乎通过点、线或面 的接触来实现。按照接触特性,通常把运动副分为 高副和低副。
1.低副:凡两构件以面接触构成的运动副称为低副, 平面机构中的低副有转动副和移动副两种。 (1)转动副:组成运动副的两构件只能在一个平面 内相对转动,这种运动副称为转动副,或称铰链。
讲授方法:
多媒体课件。
§1-1 运动副及其分类
1.1 自由度
y
O
x
如图,处于xoy坐标系中的一个作平面运动的自由 自由构件S具有三个独立的运动,即沿x轴、y轴方向的 移动和绕A点的转动。这种相对于参考系构件所具有的 独立运动称为构件的自由度。
一个作平面运动的自由构件有三个自由度。
1.2 运动副及其分类
下面通过具体的例子说明机构运动简图的绘 制方法。
四、绘制机构运动简图的步骤
机构运动简图必须与原机构具有完全相同的运 动特性,忽略对运动没有影响的构件的外形和运动 副具体构造。只有这样我们才可以根据运动简图对 机构进行运动分析和受力分析。为了达到这一要求, 绘制运动简图要遵循以下步骤:
⑴.根据机构的实际结构和运动情况,找出机构的原动件(即作独立运 动的构件)及工作执行构件(即输出运动的构件); ⑵.确定机构的传动部分,即确定构件数、运动副、类型和位置; ⑶.确定机架,并选定多数机构的运动平面作为绘制简图的投影面; ⑷.选择合适的比例尺,用构件和运动副的符号正确绘制出运动简图。
教学目标:
1.了解机构的组成,搞清运动副、运动链、约束和 自由度、速度瞬心的概念; 2.能绘制常用平面机构的运动简图; 3.能计算平面机构的自由度; 4.平面机构具有确定运动的条件; 5. 应用瞬心法进行机构的速度分析。
教学重点和难点 :
基于平面几何的机械手臂动力学分析

基于平面几何的机械手臂动力学分析机械手臂是一种能够对物体进行精确操控的机械装置。
它结合了力学、电机、计算机控制等多种技术,具有广泛的应用前景。
本文将基于平面几何,对机械手臂的动力学进行分析,并探讨其工作原理及应用。
一、机械手臂的工作原理机械手臂的工作原理类似于人的手臂,由基座、关节、连杆和执行器等部分组成。
其中,关节是连接连杆的部件,允许其在空间中运动。
执行器则是用于接触物体、抓取或释放物体的组件。
机械手臂的运动轨迹可以通过控制关节的角度来实现。
在机械手臂的运动中,关节的角度变化会引起连杆的运动,从而改变机械臂的位置和姿态。
根据运动学原理,机械手臂的位置和姿态可以用坐标系来表示。
其中,位置用三维坐标系,姿态用欧拉角或四元数表示。
这种表示方式可以大大简化机械手臂的运动控制,提高其精准度和稳定性。
二、机械手臂的动力学分析机械手臂的动力学分析是指研究机械臂运动过程中的力学特性,包括运动学、动力学和控制等方面。
其中,运动学主要研究机械臂的运动轨迹和速度、加速度等动态特性。
动力学则是研究机械臂运动过程中的力、力矩和惯性等物理量,以及它们之间的相互作用。
控制方面则是通过电机和控制器等设备,对机械臂的运动进行精确控制。
在机械手臂的运动过程中,会涉及到许多力学问题。
例如,机械臂的重心变化会影响其稳定性;机械臂在变速运动中,惯性力会影响加速度和力矩的计算;机械手臂在接触物体时,需要考虑摩擦力和接触压力等问题。
这些问题都需要通过数学模型进行建模,从而实现对机械臂的控制和优化。
三、机械手臂的应用机械手臂广泛应用于制造业、军事、医疗等领域。
例如,制造业中的自动化生产线、工业机器人等,都需要机械手臂的操控和控制;军事领域则需要机械手臂进行侦查、拆弹、物资运输等任务;医疗领域则将机械手臂用于手术、治疗等方面。
其中,工业机器人是机械手臂应用最为广泛的领域之一。
工业机器人主要用于自动化生产线上的物料搬运、零件加工、装配等工艺。
(完整word版)平面双连杆机械臂动态模型 (2)(word文档良心出品)
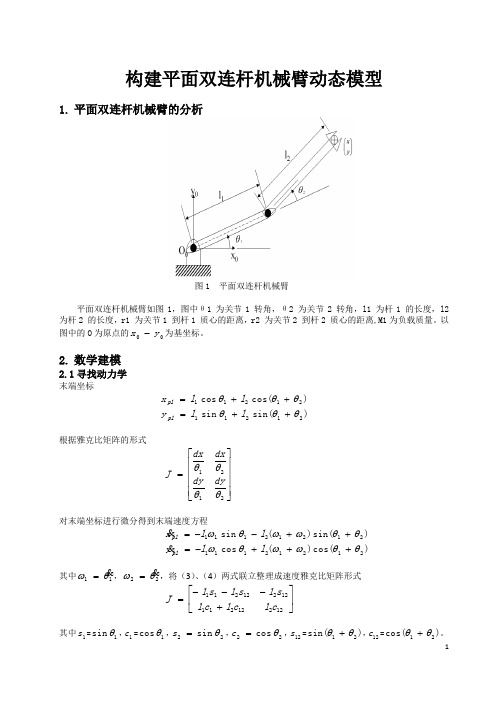
构建平面双连杆机械臂动态模型1. 平面双连杆机械臂的分析图1 平面双连杆机械臂平面双连杆机械臂如图1,图中θ1 为关节1 转角,θ2 为关节2 转角,l1 为杆1 的长度,l2为杆2 的长度,r1 为关节1 到杆1 质心的距离,r2 为关节2 到杆2 质心的距离,M1为负载质量。
以图中的O 为原点的00y x -为基坐标。
2. 数学建模2.1寻找动力学末端坐标)cos(cos 21211θθθ++=l l x pl )sin(sin 21211θθθ++=l l y pl根据雅克比矩阵的形式⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=2121θθθθdy dy dx dx J对末端坐标进行微分得到末端速度方程)sin()(sin 21212111θθωωθω++--=l l x pl & )cos()(cos 21212111θθωωθω+++-=l l y pl &其中11θω&=,22θω&=,将(3)、(4)两式联立整理成速度雅克比矩阵形式 ⎥⎦⎤⎢⎣⎡+---=1221221112212211c l c l c l s l s l s l J其中1s =1sin θ,1c =1cos θ,22sin θ=s ,22cos θ=c ,12s =)sin(21θθ+,12c =)cos(21θθ+。
在机器人基础坐标系中的速度与各关节速度间的关系以及手部与外界接触力与对应各关节间的关系可以利用雅克比矩阵来建立。
对机械臂末端速度方程(3) 、方程(4) 进行求导得到末端加速度方程如下[]1221222122211221121221122112)()(c l c l c l c l s l s l s l x pl ωωωωαα+++-=+++&& []1221222122211221121221122112)()(s l s l s l sl s l s l s l y pl ωωωωαα+++-=+++&&其中1α=1θ&&,2α=2θ&&,上述推导的方程构成了进行动力学仿真的基础,它们表明了有效负荷的加速度与 两节点处电动机的角速度和角加速度之间的关系。
机械原理4-23MATLAB平面连杆机构动力学分析

基于MATLAB/Solidworks COSMOSMotion的平面连杆机构动力学分析07208517王锡霖4-23在图示的正弦机构中,已知l AB =100 mm,h1=120 mm,h2 =80 mm,W1 =10 rad/s(常数),滑块2和构件3的重量分别为G2 =40 N和G3 =100 N,质心S2 和S3 的位置如图所示,加于构件3上的生产阻力Fr=400 N,构件1的重力和惯性力略去不计。
试用解析法求机构在Φ1=60°、150°、220°位置时各运动副反力和需加于。
构件1上的平衡力偶Mb分别对三个构件进行受力分析如图:构件3受力图构件2受力图构件1受力图(1)滑块2:V S2 =L AB W1 ①a s2 = L AB W12②构件3:S=L AB sinΦ1 ③V3=L AB W1 COSΦ1 ④a3=-L AB W12 sinΦ1 ⑤(2)确定惯性力:F12=m2as2=(G2/g)LABW12 ⑥F13=m3a3=(G3/g)LABW12sinΦ1 ⑦(3)各构件的平衡方程:构件3:∑Fy=0,FR23 =Fr-F13∑Fx=0,FR4’=FR4∑MS3 =0,FR4=FR23LAcosΦ1/h2构件2:∑Fx=0,FR12x=F12cosΦ1∑Fy=0,FR12y=FR32-F12sinΦ1构件1:∑Fx=0,FR41x=FR12x∑Fy=0,FR41y=FR12y∑MA =0,Mb=FR32LABcosΦ1总共有八个方程,八个未知数。
归纳出一元八次方程矩阵:1 0 0 0 0 0 0 0 FR23 Fr-F130 1 -1 0 0 0 0 0 FR4’ 0-LAB COSΦ1/h20 1 0 0 0 0 0 FR40 0 0 1 0 0 0 0 FR12x = F12cosΦ1-1 0 0 0 1 0 0 0 FR12y -F12sinΦ10 0 0 -1 0 1 0 0 FR41x 00 0 0 0 -1 0 1 0 FR41y 0-LABCOSΦ1 0 0 0 0 0 0 1 Mb 0 AX=B进而可得:X=A\B。
机械臂模型及旋转矩阵探究ppt课件
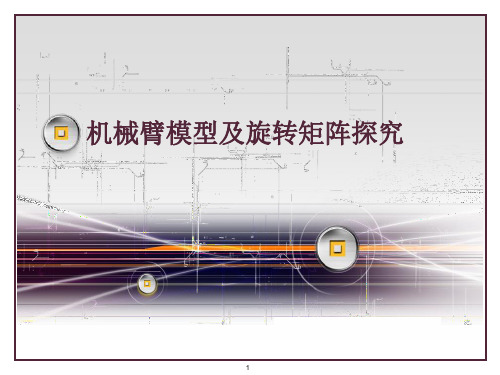
c1 s1 0 0
0 1
T
s1
0
c1 0
0
0
1 0
0
0
0
1
c2 s2 0 0
1 2
T
0
s
2
0 c2
0 1
0
0
0 0 0 1
c3 s3 0 a2
2 3
T
s3 0
0
c3 0 0
机械臂的模型?2旋转矩阵的一种理解已知向量op有矩阵cossinsincos???????????xy??????11cossinsincosxxyy????????????????????????有cossinsincosxyxy?????????????xyp?o设op的长度为r辐角为?cosxr??sinyr??coscossinsincossinsincosrrrr?????????????????cossinrr??????????????机械臂的模型axayazbxbybzpboaooabpp点在b系中为bpb系原点在a系中可表示为oabpoaabbppp??机械臂的模型?cossin0sincos0001rz?????????????????cossin0cossin0cossincos0sincos0sin00100010axrpyr??????????????????????????????????????????????????????pxy0xayazaxbybzb绕z轴旋转的旋转矩阵如下
9
机械臂的模型 1、自由度
Z
Y X
如图只沿X、Y、Z轴运动的机械臂是三自由度的。如果还能绕X、 Y、Z轴旋转那么就是六自由度的。
机械臂动力学建模与优化控制

机械臂动力学建模与优化控制1.引言机械臂作为一种高度灵活、多功能的机器人系统,在工业生产中起着重要作用。
机械臂的动力学建模和优化控制是实现其高效运动的关键。
本文将介绍机械臂动力学建模的基本原理以及优化控制方法,并探讨在实际应用中的一些挑战和解决方案。
2.机械臂动力学建模机械臂的动力学建模是对机械臂系统进行描述和分析的基础。
动力学建模的核心是建立机械臂的运动学和动力学方程。
2.1 运动学方程机械臂的运动学描述了机械臂末端执行器的位置、速度和加速度与关节的运动学参数之间的关系。
运动学方程可以通过解析解或数值解的方式得到。
常用的数值解法有迭代法和雅可比矩阵法。
2.2 动力学方程机械臂的动力学是研究力和加速度之间的关系。
动力学方程可以通过拉格朗日方程、牛顿-欧拉方程或D'Alembert原理等方法推导得到。
动力学方程的求解可以用来预测机械臂的运动轨迹和反馈控制。
3.机械臂优化控制机械臂的优化控制旨在通过调整机械臂的控制参数,使机械臂的性能达到最佳。
优化控制可以通过不同的方法实现,例如PID控制、模型预测控制和自适应控制等。
3.1 PID控制PID控制是一种经典的控制方法,通过对机械臂的位置、速度和加速度进行测量和反馈,在控制器中计算出合适的控制信号,调整机械臂的运动。
PID控制的优点是简单易实现,但对非线性系统的控制效果有限。
3.2 模型预测控制模型预测控制是一种基于动态模型的控制方法,通过对机械臂的运动进行建模和预测,计算出最佳的控制信号。
模型预测控制的优点是可以考虑系统的非线性和时变性,对不确定性具有较好的鲁棒性。
3.3 自适应控制自适应控制是一种能够根据系统的变化自动调整控制策略的方法。
自适应控制能够根据机械臂系统的输入和输出数据,自动调整控制参数,提高控制精度和稳定性。
4.挑战与解决方案在实际应用中,机械臂的动力学建模和优化控制面临一些挑战。
一方面,机械臂系统的非线性和耦合性使得动力学建模变得复杂。
(完整word版)平面双连杆机械臂动态模型(word文档良心出品)

构建平面双连杆机械臂动态模型1. 平面双连杆机械臂的分析图1 平面双连杆机械臂平面双连杆机械臂如图1,图中θ1 为关节1 转角,θ2 为关节2 转角,l1 为杆1 的长度,l2为杆2 的长度,r1 为关节1 到杆1 质心的距离,r2 为关节2 到杆2 质心的距离,M1为负载质量。
以图中的O 为原点的00y x -为基坐标。
2. 数学建模2.1寻找动力学末端坐标)cos(cos 21211θθθ++=l l x pl )sin(sin 21211θθθ++=l l y pl根据雅克比矩阵的形式⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=2121θθθθdy dy dx dx J对末端坐标进行微分得到末端速度方程)sin()(sin 21212111θθωωθω++--=l l x pl & )cos()(cos 21212111θθωωθω+++-=l l y pl &其中11θω&=,22θω&=,将(3)、(4)两式联立整理成速度雅克比矩阵形式 ⎥⎦⎤⎢⎣⎡+---=1221221112212211c l c l c l s l s l s l J其中1s =1sin θ,1c =1cos θ,22sin θ=s ,22cos θ=c ,12s =)sin(21θθ+,12c =)cos(21θθ+。
在机器人基础坐标系中的速度与各关节速度间的关系以及手部与外界接触力与对应各关节间的关系可以利用雅克比矩阵来建立。
对机械臂末端速度方程(3) 、方程(4) 进行求导得到末端加速度方程如下[]1221222122211221121221122112)()(c l c l c l c l s l s l s l x pl ωωωωαα+++-=+++&& []1221222122211221121221122112)()(s l s l s l sl s l s l s l y pl ωωωωαα+++-=+++&&其中1α=1θ&&,2α=2θ&&,上述推导的方程构成了进行动力学仿真的基础,它们表明了有效负荷的加速度与 两节点处电动机的角速度和角加速度之间的关系。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
平面开链机械臂动力系统及其控制的向量键合图建模与分析易仲庆;谢进;张建奇【摘要】平面开链机械臂是由一系列电机驱动单臂串联而成.利用这种串联式的结构特性,建立了电机驱动单臂的子系统机电耦合向量键合图模型以及等价动力学一阶微分方程,并利用模块化的方式建立出整个平面开链机械臂系统的键合图动力学模型.模型中通过考虑电机输出轴以及机械臂的挠性,实现微分因果关系的消除.以平面2R机械臂为例,通过对含有PD控制器的机电耦合系统动力学模型进行键合图仿真与Matlab仿真的结果对比,以及容性元件取值对系统动态响应影响的分析,验证了所提出方法的正确和有效性.%A planar open chain manipulator is composed of a series of single arm actuated by a motor.This serial chain nature make it possible to establish the vector bond graph model and equivalent dynamic first order differential equation of electromechanical coupling for the single arm actuated by a motor firstly,and then to establish the vector bond graph and dynamics modeling for the whole manipulator by the modular method.The differential causality is solved by considering the flexible of the motor output shaft and manipulator.A planar 2R manipulator is taken as an example to demonstrate the method proposed in it and its effectiveness and correctness as well,by comparing the simulation results from Bond Graph and Matlab simulation of the system with the PD controller and analysing the influence of the value of the capacitive element on dynamic response of the system.【期刊名称】《机械设计与制造》【年(卷),期】2017(000)003【总页数】5页(P60-63,67)【关键词】向量键合图;机电耦合;开链机械臂【作者】易仲庆;谢进;张建奇【作者单位】西南交通大学机械工程学院,四川成都610031;西南交通大学机械工程学院,四川成都610031;西南交通大学机械工程学院,四川成都610031【正文语种】中文【中图分类】TH16机电一体化是机械工业的一个重要发展方向。
在机电一体化中,机电之间的耦合关系是机械学科新的研究课题。
建立机电系统耦合动力学模型、对机电系统的耦合效应进行定量分析是复杂机电系统动力学分析、动态特性分析、故障诊断等所必须解决的关键问题[1-2]。
键合图[3]理论以能量守恒原理为基础,将多种物理参量用统一的势、流、变位和动量4种状态变量表示,可以直观地描述系统内部状态的变化过程,是一种用统一的方式处理多种能量范畴的工程系统的动态分析方法[4],与其他理论和方法结合在一起,可以成为机电系统分析及控制的有效工具[5-7]。
文献[8,9]研究了利用键合图的方法建立各种机电系统动力学分析模型的问题;文献[10]应用敏感性键合图对机电系统中的控制问题进行了分析;文献[11]在利用键合图建立了摄像机仰俯系统的动力学模型的基础上,对控制器的设计进行了深入的研究。
然而,利用键合图对机电系统中的电机、机构以及控制器进行全面的分析和研究仍然需要探索出有效的方法[12]。
相比于传统标量键合图,向量键合图(Vector of Bond Graph)方法具有表达形式简明紧凑,包含信息量大的特点[13],在多能域特别是复杂多体系统多能域分析时具有明显的优势。
平面开链机械臂是一种主要的工业机器人机构,其动力学性能直接影响到机器人的性能及其控制系统的设计。
常用的工业机器人动力学建模理论和方法是Newton-Euler方法[14]和Lagrangian方法和基于文献[15]。
这些方法重点研究的是机械臂本体的动力学问题,很少涉及到驱动电机的动力学问题。
Lagrange-Maxwell 方法[16]综合考虑了电机和机械系统的动力分析问题,但是所建立的方程式还是二阶的微分方程,并且不能直观地描述机电系统的能量传递和变化等方面的信息。
以永磁同步电机驱动的平面开链机械臂为研究对象,研究向量键合图方法在机械臂动力学方程的建立及控制系统中的应用,以探索出考虑驱动电机的机器人机构动力学和控制分析、设计的有效方法。
2.1 平面开链机械臂的结构一个平面nR开链机械臂物理模型,如图1所示。
机械臂由n个活动构件和n个转动副组成。
当机构为全驱动机构时,在每个转动副处应安装一个驱动器。
在研究中,驱动器为永磁同步电机(PMSM),则驱动器与其驱动杆件之间形成了一个机电耦合的子系统,其控制原理图,如图2所示。
显然,图1所示的平面nR开链机械臂应包含有n个图2所示的子系统。
2.2 平面开链机械臂子系统的键合图及动力学模型子系统中主要的物理部件包括驱动电动机及其直接驱动的机械臂。
2.2.1 驱动电动机的动力学建模永磁同步电动机的工作原理图,如图3所示。
根据电动机工作原理和功率流向,可以建立电机的键合图模型,如图4所示。
设电机转子两极之间的中心线为q轴。
键合图模型,如图4所示。
可得电机状态方程。
式中:I2—定子在q轴上的电感Lq;I6—转子转动惯量Jm;R3—定子电枢电阻Rs;R7—摩擦阻尼Cm;KT—d轴磁链Ψds;e1—定子电压q轴分量uq;e8—负载转矩TL;p2=iqLq(iq—q轴电流),p6=ωJm(ω—转子转速)。
2.2.2 机械臂的运动分析与建模机械臂的物理模型,如图5所示。
采用D-H方法[14]建立坐标系。
令机械臂i的质心Ci及末端在全局坐标系下的线速度分别为0viC、0vi+1,角速度为iωi,则由图5可以得到构件速度转换关,如式(2)所示。
2.2.3 电动机驱动机械臂子系统的动力学建模根据机械臂子系统中电机与机械臂之间的耦合关系,建立消除微分因果关系的机电耦合子系统的向量键合图模型,如图7所示。
结合图5和式(2)建立构件i的向量键合图模型,如图6所示。
图中:键13—机械臂与电机之间的耦合键;键14、20—机械臂i与机械臂i-1之间的接口键;键25、28—与机械臂i+1之间的接口键,这些键所代表的物理含义分别为:为避免模型中微分因果关系导致的状态变量不独立,采用了将电机输出轴设为挠性轴、机械臂设为弹性杆,而在模型中增加两个容性元件的方法[3],如图7所示。
显然,这样的处理方法更加便于考虑系统中部件的弹性变形。
然而,容性元件的取值对系统的运动却有重要的影响。
这一点将在第2节中通过具体示例进行说明。
图中变换器TF、MTF模数的具体表达式为:从图7的机械臂i子系统键合图模型可以看出:构件模块含有3个状态变量,电机模块也含3个状态变量,即每个机械臂子系统含6个状态变量。
设状态变量X=[p2,p6,q9,p16,q21,p24]T,列出系统i的状态方程,如式4所示。
式中:e1=uqi,e23=[0,-mig,0],R3=Rsi,R7=Cmi,I2=Lqi,I6=ji,I16= diag(0,0,J1),I24=diag(mi,mi,mi),c9=1/k(2i-1),c21=diag(1/ k2i,1/k2i,0)由以上分析可以看出,由键合图可以直接得到一阶微分方程表示的机电耦合系统的动力学方程式。
这就非常有利于直接利用数值计算的方法对系统进行仿真分析。
2.3 平面开链机械臂的键合图及动力学模型利用2.2节中电机驱动机械臂子系统的模型,并注意到子系统i与子系统i-1及子系统i+1之间运动和动力的相互影响,在图7所示模型的基础上采用模块化的方式扩展。
利用式2可计算出机械臂i的质心Ci及末端在全局坐标系下的线速度、角速度;利用式(3)可计算出与i所对应的4个变换器的模数;利用式(4)便可以推导出平面nR开链机械臂机电耦合动力学方程式。
显然,平面nR开链机械臂机电耦合的动力学方程中有6n个状态变量。
本节以2R机械臂为例,说明利用向量键合图以模块化的方式建立平面开链机械臂机电系统耦合动力学方程、进行控制分析的思想。
3.1 2R机械臂的机电系统耦合动力学方程平面2R机械臂的物理模型,如图8所示。
设l11=l1/2,l21=l2/ 2。
由式(2)写出构件质心与末端在全局坐标系下的速度。
根据2.3节中的方法建立平面2R机械臂系统机电耦合向量键合图模型,如图9所示。
设图9中系统状态变量X=[p2,p6,q9,p14,q18,p21,p24,p28,q31,p37,q44,p47]T。
根据式(4)进行推理,可以得到平面2R机械臂系统的动力学状态方程,如式(5)所示。
其中,e1=uq1,e20=[0,-m1g,0],e23=uq2,e46=[0,-m2g,0],I2=Lq1,I6=j1,I14=diag(0,0,J1),I21=diag(m1,m1,m1),I24=Lq2,I28= j2,I37=diag(0,0,J2),I47=diag(m2,m2,m2),R3=Rs1,R7=Cm1,R25=Rs2,R29=Cm2,c9=1/k1,c18=diag(1/k2,1/k2,0),c31=1/ k3,c44=diag(1/k4,1/k4,0)3.2 平面2R机械臂的运动控制采用具备渐进稳定性的PD控制方法对平面2R机械臂驱动电机进行控制,控制对象为电机的输入电压。
将PD控制器的输出作为势源的输入加在键合图模型之中。
电机的输入电压为:式中:e(t)—机械臂实时角速度与期望值的误差。
设构件1、2在关节空间中的期望运动规律分别为:平面2R机械臂结构参数和驱动电机的参数分别,如表1、表2所示。
取ω=1,kP1=400,kD1=40,kP2=330,kD2=45,仿真得到的关节1和关节2的时域波形图,如图10所示。
关节1和关节2的相图,如图11所示。
