函数的单调性导学案
函数的单调性与最值导学案
学案5 函数的单调性与最值导学目标： 1.理解函数的单调性、最大值、最小值及其几何意义.2.会用定义判断函数的单调性，会求函数的单调区间及会用单调性求函数的最值．自主梳理1．单调性(1)定义：一般地，设函数y ＝f (x )的定义域为I ，如果对于定义域I 内某个区间D 上的任意两个自变量x 1，x 2，当x 1<x 2时，都有f (x 1)<f (x 2)(f (x 1)>f (x 2))，那么就说f (x )在区间D 上是______________．(2)单调性的定义的等价形式：设x 1，x 2∈[a ，b ]，那么(x 1－x 2)(f (x 1)－f (x 2))>0⇔f (x 1)－f (x 2)x 1－x 2>0⇔f (x )在[a ，b ]上是________；(x 1－x 2)(f (x 1)－f (x 2))<0⇔f (x 1)－f (x 2)x 1－x 2<0⇔f (x )在[a ，b ]上是________． (3)单调区间：如果函数y ＝f (x )在某个区间上是增函数或减函数，那么说函数y ＝f (x )在这一区间具有(严格的)单调性，区间D 叫做y ＝f (x )的__________．(4)函数y ＝x ＋a x(a >0)在 (－∞，－a )，(a ，＋∞)上是单调________；在(－a ，0)，(0，a )上是单调______________；函数y ＝x ＋a x(a <0)在______________上单调递增． 2．最值一般地，设函数y ＝f (x )的定义域为I ，如果存在实数M 满足：①对于任意的x ∈I ，都有f (x )≤M (f (x )≥M )；②存在x 0∈I ，使得f (x 0)＝M .那么，称M 是函数y ＝f (x )的____________．自我检测1．若函数y ＝ax 与y ＝－b x在(0，＋∞)上都是减函数，则y ＝ax 2＋bx 在(0，＋∞)上是 ) A ．增函数 B ．减函数C ．先增后减D ．先减后增2．设f (x )是(－∞，＋∞)上的增函数，a 为实数，则有 ( )A ．f (a )<f (2a )B ．f (a 2)<f (a )C ．f (a 2＋a )<f (a )D ．f (a 2＋1)>f (a )3．下列函数在(0,1)上是增函数的是 ( )A ．y ＝1－2xB ．y ＝x －1C ．y ＝－x 2＋2xD ．y ＝54．设(a ，b )，(c ，d )都是函数f (x )的单调增区间，且x 1∈(a ，b )，x 2∈(c ，d )，x 1<x 2，则f (x 1)与f (x 2)的大小关系是 ( )A ．f (x 1)<f (x 2)B ．f (x 1)>f (x 2)C ．f (x 1)＝f (x 2)D ．不能确定5．当x ∈[0,5]时，函数f (x )＝3x 2－4x ＋c 的值域为 ( )A ．[c,55＋c ]B ．[－43＋c ，c ] C ．[－43＋c,55＋c ] D ．[c,20＋c ] 探究点一 函数单调性的判定及证明例1 设函数f (x )＝x ＋a x ＋b(a >b >0)，求f (x )的单调区间，并说明f (x )在其单调区间上的单调性．变式迁移1 已知f (x )是定义在R 上的增函数，对x ∈R 有f (x )>0，且f (5)＝1，设F (x )＝f (x )＋1f (x )，讨论F (x )的单调性，并证明你的结论．探究点二 函数的单调性与最值例2 已知函数f (x )＝x 2＋2x ＋ax ，x ∈[1，＋∞)．(1)当a ＝12时，求函数f (x )的最小值；(2)若对任意x ∈[1，＋∞)，f (x )>0恒成立，试求实数a 的取值范围．变式迁移2 已知函数f (x )＝x －a x ＋a2在(1，＋∞)上是增函数，求实数a 的取值范围．探究点三 抽象函数的单调性例3 已知函数f (x )对于任意x ，y ∈R ，总有f (x )＋f (y )＝f (x ＋y )，且当x >0时，f (x )<0，f (1)＝－23.(1)求证：f (x )在R 上是减函数；(2)求f (x )在[－3,3]上的最大值和最小值．变式迁移3 已知定义在区间(0，＋∞)上的函数f (x )满足f (x 1x 2)＝f (x 1)－f (x 2)，且当x >1时，f (x )<0.(1)求f (1)的值；(2)判断f (x )的单调性；(3)若f (3)＝－1，解不等式f (|x |)<－2.分类讨论及数形结合思想 例 (12分)求f (x )＝x 2－2ax －1在区间[0,2]上的最大值和最小值．【(满分：75分)一、选择题(每小题5分，共25分)1“a ＝1”是“函数f (x )＝x 2－2ax ＋3在区间[1，＋∞)上为增函数”的( )A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件2已知函数f (x )＝⎩⎪⎨⎪⎧x 2＋4x ， x ≥0，4x －x 2， x <0，若f (2－a 2)>f (a )，则实数a 的取值范围是 ) A ．(－∞，－1)∪(2，＋∞) B ．(－1,2)C ．(－2,1)D ．(－∞，－2)∪(1，＋∞)3．用min{a ，b ，c }表示a ，b ，c 三个数中的最小值．设f (x )＝min{2x ，x ＋2,10－x }(x ≥0)，则f (x )的最大值为( )A ．4B ．5C ．6D ．74．若f (x )＝－x 2＋2ax 与g (x )＝a x ＋1在区间[1,2]上都是减函数，则a 的取值范围是 A ．(－1,0)∪(0,1) B ．(－1,0)∪(0,1]C ．(0,1)D ．(0,1]5．已知定义在R 上的增函数f (x )，满足f (－x )＋f (x )＝0，x 1，x 2，x 3∈R ，且x 1＋x 2>0，x 2＋x 3>0，x 3＋x 1>0，则f (x 1)＋f (x 2)＋f (x 3)的值 ( )A ．一定大于0B ．一定小于0C ．等于0D ．正负都有可能题号 1 2 3 4 5答案 6．函数y ＝－(x －3)|x |的递增区间是________．7．设f (x )是增函数，则下列结论一定正确的是________(填序号)．①y ＝[f (x )]2是增函数；②y ＝1f (x )是减函数； ③y ＝－f (x )是减函数；④y ＝|f (x )|是增函数．8．设0<x <1，则函数y ＝1x ＋11－x的最小值是________． 三、解答题(共38分)9．(12分)(湖州模拟)已知函数f (x )＝a －1|x |.(1)求证：函数y ＝f (x )在(0，＋∞)上是增函数；(2)若f (x )<2x 在(1，＋∞)上恒成立，求实数a 的取值范围．10．(12分)已知f (x )＝x 2＋ax ＋3－a ，若x ∈[－2,2]时，f (x )≥0恒成立，求a 的取值范围．11．)已知f (x )是定义在[－1,1]上的奇函数，且f (1)＝1，若a ，b ∈[－1,1]，a ＋b ≠0时，有f (a )＋f (b )a ＋b >0成立．(1)判断f (x )在[－1,1]上的单调性，并证明它；(2)解不等式：f (x ＋12)<f (1x －1)；(3)若f (x )≤m 2－2am ＋1对所有的a ∈[－1,1]恒成立，求实数m 的取值范围．。
高三理科数学导学案函数的单调性
富县高级中学高三理科数学导学案 班级： 姓名： 小组： 备写人： 课题函数的单调性与最值 课型 复习课 编号 20140919 使用时间第 周 星期复习目标1、能从数、形两个角度理解、认识函数的单调性；2、会根据具体题目选择合适的方法判断函数的单调性、求函数的单调区间，特别要求会用求导的方法判断函数的单调性、求函数的单调区间；3、能会用函数的单调性求参数的取值范围。
． 重 点选择合适的方法判断函数的单调性、求函数的单调区间。
难点 利用单调性求参数的取值范围。
学 习 过 程 师生笔记一、知识梳理1、 判断函数单调性的方法：（1）定义法（取值、作差、变形、定号、下结论）；（2）图像法（从图像上观察函数的单调性）；（3）利用已知函数的单调性法（增+增=增，减+减=减，增-减=增，减-增=减）；（4）利用导数（根据导数的正负来判断原函数的单调性）；（5）复合函数的单调性（同增异减）2．函数的最值若)()(0x f x f ≥，则)(0x f 为函数)(x f 的最小值； 若)()(0x f x f ≤，则)(0x f 为函数)(x f 的最大值。
二、学情自测1．下列函数中既是奇函数又是增函数的是：（ ）A ．1+=x yB ．2-x y =C ．xy 1= D ．x x y = 2．函数b x k y ++=)12（在），（∞+∞-是减函数，则( )A.21>kB. 21<kC. 21->kD.21-<k 3．函数)1(-11)(x x x f -=的最大值是（ ）A.54B. 45C. 43D.344、函数11)(-=x x f 在[]3,2上的最小值是 ，最大值是 。
三、课堂探究题型一：判断函数的单调性 【例1】讨论函数1)(2+=x x x f 的单调性。
题型二：求函数的单调区间【例2】求出下列函数的单调区间：(1)f (x )＝x 2－4|x |＋3；(2)f (x )＝|x 2－4x ＋3|；(3)f (x )＝log 2(x 2－1)．题型三：利用单调性求参数范围【例3】若函数f (x )＝ax －1x ＋1在(－∞，－1)上是减函数，求实数 a 的取值范围．四、复习检测1．下列函数中，既是偶函数又是在），（∞+0单调递增的是（ ）A ．3x y =B ．1+=x yC ．1-2+=x yD ．x y -2= 2．若函数a x x f +=2)(在[]∞+，3上是单调递增函数，则a =（ ）3．已知函数x a x x x f ++=2)(2，若对于任意[)∞+∈，1x ， 0)(>x f 恒成立，则实数ａ的取值范围是 。
函数的单调性与导数教案
函数的单调性与导数教案函数的单调性与导数教案一、目标知识与技能：了解可导函数的单调性与其导数的关系；能利用导数研究函数的单调性，会求函数的单调区间。
过程与方法：多让学生举命题的例子，培养他们的辨析能力；以及培养他们的分析问题和解决问题的能力；情感、态度与价值观：通过学生的参与，激发学生学习数学的兴趣。
二、重点难点教学重点：利用导数研究函数的单调性，会求不超过4次的多项式函数的单调区间教学难点：利用导数研究函数的单调性，会求不超过4次的多项式函数的单调区间三、教学过程：函数的赠与减、增减的快与慢以及函数的最大值或最小值等性质是非常重要的．通过研究函数的这些性质，我们可以对数量的变化规律有一个基本的了解．我们以导数为工具，对研究函数的增减及极值和最值带来很大方便．四、学情分析我们的学生属于平行分班，没有实验班，学生已有的知识和实验水平有差距。
需要教师指导并借助动画给予直观的认识。
五、教学方法发现式、启发式新授课教学基本环节：预习检查、总结疑惑→情境导入、展示目标→合作探究、精讲点拨→反思总结、当堂检测→发导学案、布置预习六、课前准备1．学生的学习准备：2．教师的教学准备：多媒体课件制作，课前预习学案，课内探究学案，课后延伸拓展学案。
七、课时安排：1课时八、教学过程(一)预习检查、总结疑惑检查落实了学生的预习情况并了解了学生的疑惑，使教学具有了针对性。
提问1．判断函数的单调性有哪些方法？（引导学生回答“定义法”，“图象法”。
）2．比如，要判断y=x2的单调性，如何进行？（引导学生回顾分别用定义法、图象法完成。
）3．还有没有其它方法？如果遇到函数：y=x3－3x判断单调性呢？（让学生短时间内尝试完成，结果发现：用“定义法”，作差后判断差的符号麻烦；用“图象法”,图象很难画出来。
）4．有没有捷径？（学生疑惑,由此引出课题）这就要用到咱们今天要学的导数法。
以问题形式复习相关的旧知识，同时引出新问题：三次函数判断单调性，定义法、图象法很不方便，有没有捷径？通过创设问题情境，使学生产生强烈的问题意识，积极主动地参与到学习中来。
郑006 3.1函数的单调性与导数006导学案2013-14高二下数学2-2
当x1＜x2时，都有＝，那么函数f(x)就是区间I上的函数.
2：函数f(x)在 处的导数的几何意义？
：自主学习
【学法指导】：预习教材22页-23页完成下面内容：
我们知道，曲线 的切线的斜率就是函数 的导数.
函数的单调性与其导函数正负的关系:
结论：一般地，设函数 在某个区间内有导数，
如果在这个区间内 ，那么函数 在这个区间内的增函数；
如果在这个区间内 ，那么函数 在这个区间内的减函数.
：独立思考
【思路点拨】：预习教材24页-25页完成下面内容：
例1：判断下列函数的的单调性，并求出单调区间：
（1） ；
（2） .
★例2：求证：函数 在 内是减函数.
(2)是否存在实数a，使f(x)在(－1,1)上单调递减？若存在，求出a的取值范围；若不存在，说明理由．
【思路点拨】：
：独立完成
1.若 为增函数，则一定有（）
A． B．
C． D．
2.函数 在下面哪个区间内是增函数（）
A． B．
C． D．
3.若在区间 内有 ，且 ，则在 内有（）
A． B．
C． D．不能确定
问题1：用导数求函数单调区间的三个步骤：
①
②
③
问题2：如果在某个区间内恒有 ，那么函数 有什么特性？
例3：已知导函数的下列信息：
当 时， ；
当 ，或 时， ；
当 ，或 时， .试画出函数 图象的大致形状.
：合作探究
★★例3：已知函数f(x)＝x3－a求实数a的取值范围．
(1)若a≤0，则f′(x)＝ex－a≥0，
即f(x)在R上递增，
函数的单调性导学案
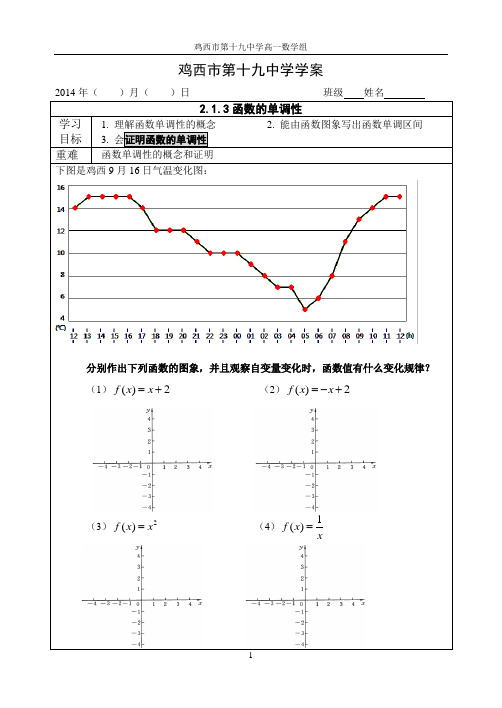
鸡西市第十九中学学案2014年（ ）月（ ）日 班级 姓名2.1.3函数的单调性学习 目标 1. 理解函数单调性的概念 2. 能由函数图象写出函数单调区间 3. 会证明函数的单调性 重难函数单调性的概念和证明下图是鸡西9月16日气温变化图：分别作出下列函数的图象，并且观察自变量变化时，函数值有什么变化规律？ （1）()2f x x =+（2）()2f x x =-+（3）2()f x x =（4）1()f x x=1x 2x )(1x f )(2x f )(x f 图3yx1x 2x )(1x f )(2x f )(x f 图4yx从直观上看，函数图象从左向右看，在某个区间上，图象是上升的，则此函数是______，若图象是下降的，则此函数是_____________ 增函数减函数前提一般地,设函数()f x 的定义域为I :如果对于定义域内某个区间D 上的任意两个自变量的值12,x x ,定义当12x x <时,都有12()()f x f x <,那么就说函数()f x 在区间D 上是增函数.如右图所示.当12x x <时,都有12()()f x f x >,那么就说函数()f x 在区间D 上是减函数.如右图所示.图象描述自左向右看图象是___________自左向右看图象是__________【注意】函数的单调性是一个局部概念单调区间：如果函数f (x )在某个区间D 上是增函数或减函数，就说f (x )在这一区间上具有（严格的）单调性，区间D 叫f (x )的单调区间.例1、如图，定义在[-5,5]上的f (x )，根据图象说出单调区间及单调性.xx f 1)(=在),0(+∞和(-∞上均为减函数，)(x f 在整个定义域上是否为减函数？例2、如何从解析式的角度说明2)(x x f =在),0[+∞上为增函数？。
导学案007(函数的单调性)
函数的单调性编号:007一、考纲要求：函数的基本性质二、复习目标：1.理解函数的单调性2.能判断或证明函数的单调性三、重点难点：判断或证明函数的单调性四、要点梳理：1．函数的单调性(1)单调函数的定义若函数f(x)在区间D上是增函数或减函数，则称函数f(x)在这一区间上具有(严格的)单调性，区间D叫做f(x)的单调区间．2．函数的最值一个防范函数的单调性是对某个区间而言的，所以要受到区间的限制．例如函数y ＝1x分别在(－∞，0)，(0，＋∞)内都是单调递减的，但不能说它在整个定义域即(－∞，0)∪(0，＋∞)内单调递减，只能分开写，即函数的单调减区间为(－∞，0)和(0，＋∞)，不能用“∪”连接． 两种形式设任意x 1，x 2∈[a ，b ]且x 1＜x 2，那么 ①f x 1－f x 2x 1－x 2＞0⇔f (x )在[a ，b ]上是增函数；f x 1－f x 2x 1－x 2＜0⇔f (x )在[a ，b ]上是减函数．②(x 1－x 2)[f (x 1)－f (x 2)]＞0⇔f (x )在[a ，b ]上是增函数；(x 1－x 2)[f (x 1)－f (x 2)]＜0⇔f (x )在[a ，b ]上是减函数． 两条结论(1)闭区间上的连续函数一定存在最大值和最小值．当函数在闭区间上单调时最值一定在端点取到．(2)开区间上的“单峰”函数一定存在最大(小)值． 四种方法 函数单调性的判断(1)定义法：取值、作差、变形、定号、下结论．(2)复合法：同增异减，即内外函数的单调性相同时，为增函数，不同时为减函数． (3)导数法：利用导数研究函数的单调性． (4)图象法：利用图象研究函数的单调性．五、基础自测：1．判断下列说法是否正确：（1）若定义在R 上的函数()f x 满足(2)(1)f f >，则函数()f x 是R 上的单调增函数； （2）若定义在R 上的函数()f x 满足(2)(1)f f >，则函数()f x 在R 上不是单调减函数； （3）若定义在R 上的函数()f x 在区间(,0]-∞上是单调增函数，在区间[0,)+∞上是单调增函数，则函数()f x 在R 上是单调增函数；（4）若定义在R 上的函数()f x 在区间(,0]-∞上是单调增函数，在区间(0,)+∞上是单调增函数，则函数()f x 在R 上是单调增函数．2、下列函数 （1）2()(1)f x x =- （2）()x f x e = （3）()ln(1)f x x =+ （4） 111y x =-- （5）||y x x =在(,0)x ∈-∞是减函数的序号是_________________ 4．六、典例精讲:例1 （1）判断函数()f x = （2）判断函数1()ln 1xf x x-=+的单调性，并证明你的结论．例2(1) 函数32()15336f x x x x =--+的单调递增区间为 ． (2) 函数20.7log (32)y x x =-+的单调减区间是____________________例3．已知函数()f x 对任意x ，y ∈R ，总有()()()f x f y f x y +=+，且当0x >时，()0f x <， ，求证：()f x 是R 上的减函数．七、千思百练：1．函数1()f x x x=-的单调增区间为 ． 2、设函数()f x 是减函数，且()0f x >，下列函数中为增函数的是_________(1)1()y f x =-(2)12log ()y f x = (3)()2f x y = (4)[]2()y f x =(5)32()y x f x =-3．函数()f x 是R 上的减函数，a ∈R ，记2()m f a =，(1)n f a =-，则m ，n 的大小关系是 ．4、（必修1第37页第7题）函数21()21x x f x -=+的单调区间是_______________________5、（必修1第55页第12题）对于任意的12,,x x R ∈若函数1()()2xf x =，则1212()()()22f x f x x xf ++与的大小关系是__________________八、反思感悟：1、判断函数单调性的常见方法：（1）图像法 （2）定义法 （3）导数法2、复合函数单调性的判断：同增异减法。
北师大版必修一数学3.1函数的单调性 导学案
安边中学 高一 年级 上 学期 数学 学科导学稿 执笔人：王广青 总第 课时 一、课题：3函数的单调性
二、学习目标
1.熟记函数单调性的定义；
2、能用数学语言描述函数的单调性；
3、会用函数单调性的定义证明或判断简单函数的单调性。
三、教学过程
【温故知新】
问题1、映射的概念是什么？
【导学释疑】
依据学习内容认真研究课本3836P P -的内容，完成并理解下面的问题。
1、增函数的定义：
一般地，设函数的定义域为A:如果对于定义域A 内某个 上的 两个自变量的值x1,x2，当x1< x2时，都有_______ 那么就说函数f(x)在 上是增函数。
这个区间 叫做这个函数的
单调增区间。
2、减函数的定义：
一般地，设函数的定义域为A:如果对于定义域A 内某个 上的 两个自变量的值x1,x2，当x1< x2时，都有_________ 那么就说函数f(x)在 上是减函数。
这个区间 叫做这个函数
的单调减区间。
3、 和 ，统称为单调函数。
【巩固提高】
例题1：画出函数23)(+=x x f 的图像，判断它的单调性，并加以证明
例题2：求证：函数11)(--
=x
x f 在区间(－∞,0)上是单调增函数。
单调性(1)—导学案
检 查
答： （2）定义中的 x1, x 2 能否取特值代替来判断单调性？ 答： （3）函数 y=x-1, 在 x {1、2、3、4}是否存在单调性？
展 示
答： 2、画出函数 y= 1 的图像，说出单调 x
区间，并指明在该区间上的单调性.
神木中学“352”高效课堂高一数学
1、判断并证明函数 f(x)=4x-3 的单调性.
神木中学“352”高效课堂高一数学
导学案
课
主备老师:张亚坤
题：函数的单调性（1）
班级： 姓名_____ 组别：
达 标要 求
对于
知识目标 能力目标 重点知识
1、理解函数单调性的概念，会写函数的单调区间， 2、学会运用函数单调性的定义来判断函数的单调性. 培养运用“数形结合思想”解决数学问题能力 函数单调性的定义和函数单调性的证明
）
目
A. y 3x 1
B. y x 2
C. y x 2 4 x 3
3、 已知函数 f ( x) ax 和 g ( x ) 在 (, 0) 上
b 在 (0, ) 上都是减少的， 则 h( x) ax2 bx c x
（
( B ) 是减少的 ( D) h( x) 的单调性不能确定
导学案
深 化
2、证明函数 y x
1 在[1，+ ）上是增加的. x
选
讲
1、下列函数中,在区间 0,1 上是增加的是 A． y x B． y 3 x C． y
1 x
（
）
D． y x 2 4 （ D. y
4 x
2、下列函数中，在区间（0，2）上为增加的是
1 ，在区间 (,0)和(0, ) 上分别是减少的. x
8函数的单调性学生版
函数的单调性一、单调性的理解 (注意定义域)1. (1)122121,,,()()x x D x x f x f x ∀∈>> (2) 211221()(),,0f x f x x x D x x >∀∈>- (3) 122121,,[()()]()0x x D f x f x x x ∀∈>->(4)'()0f x >2. 函数单调性的理解 1y x = t a n y x = 2(0)(0)x a x y x x + ≥⎧=⎨- <⎩ 二. 单调性的证明（ 定义法 复合函数法 导数法 ）1．求证：函数x x f -=)(在定义域上是减函数.2.函数f(x)对任意的a 、b ∈R,都有f(a+b)=f(a)+f(b)-1,并且当x ＞0时，f(x)＞ 1.（1）求证：f(x)是R（2）若f(4)=5,解不等式f(3m 2-m-2)＜ 3.三、求单调区间3.函数11x y x-=+的递减区间是 4..函数y ＝log 12(4＋3x －x 2)的一个单调递增区间是 5.函数x x x f ln 2)(2-=的增区间是6.函数22||1y x x =-++的单调增区间四、单调性的应用(1).求参数范围7．f (x )＝⎩⎪⎨⎪⎧ a x (x >1)⎝⎛⎭⎫4－a 2x ＋2 (x ≤1)是R 上的单调递增函数，则实数a 的取值范围为 8. 若函数f (x )＝|log a x |(0<a <1)在区间(a,3a －1)上单调递减，则实数a 的取值范围_______． 9. 已知函数f (x )＝3－ax a －1(a ≠1)．(1)若a >0，则f (x )的定义域是____ ____； (2)若f (x )在区间(0,1]上是减函数，则实数a 的取值范围是____ ____．10. 函数y ＝x －5x －a －2在(－1，＋∞)上单调递增，则a 的取值范围是_____ __． 11.已知函数f (x )＝⎩⎪⎨⎪⎧ x 2＋4x ，x ≥0，4x －x 2，x <0.若f (2－a 2)>f (a )，则实数a 的取值范围是_ ____12．函数9()log (8)a f x x x=+-在[1,)+∞上是增函数，求a 的取值范围____ __．(2)比较大小13．已知函数()f x 在[0, π)上是递减函数，且周期是3，那么下列三个数 (lg100)f , f (2π), f (23π)，从大到小的顺序是（3）.求值域14.求函数y=-+2x x -6的值域 （4）.解方程15.求解方程03x 8x )3x 7(55=++++。
高中数学选择性必修二 5 3 1函数的单调性新 导学案
5.3.1函数的单调性(2) 导学案1．掌握利用导数判断函数的单调性的一般步骤．2．探究函数增减的快慢与导数的关系．3.学会处理含参函数的单调性问题重点：导数判断函数的单调性的一般步骤难点：含参函数的单调性问题1.函数f (x)的单调性与导函数f ′(x)正负的关系定义在区间(a，b)内的函数y＝f (x)：f ′(x)的正负 f (x)的单调性f ′(x)＞0单调递____f ′(x)＜0单调递____增;减2．判断函数y＝f (x)的单调性第1步：确定函数的______；第2步：求出导数f ′(x)的____；第3步：用f ′(x)的____将f (x)的定义域划分为若干个区间，列表给出f ′(x)在各区间上的____，由此得出函数y＝f (x)在定义域内的单调性．定义域 ;零点 ;零点 ;正负3.函数图象的变化趋势与导数值大小的关系一般地，设函数y ＝f (x )，在区间(a ，b )上：导数的绝对值函数值变化函数的图象 越大 __ 比较“____”(向上或向下) 越小__比较“____”(向上或向下)快;陡峭 ;慢;平缓探究1. 形如f(x)=ax 3+bx 2+cx+d(a≠0)的函数应用广泛，下面我们利用导数来研究这类函数的单调性。
例3. 求函数f (x )=13x 3−12x 2−2x +1的单调区间.如果不用导数的方法，直接运用单调性的定义，你如何求解本题？用解不等式法求单调区间的步骤 1确定函数f x 的定义域； 2求导函数f ′x ；3解不等式f ′x ＞0或f ′x ＜0，并写出解集； 4根据3的结果确定函数f x 的单调区间. 跟踪训练1.求下列函数的单调区间： (1)f (x )＝3x 2－2ln x ；(2)f (x )＝x 2e －x .探究2：研究对数函数y =lnx 与幂函数y =x 3在区间(0,+∞)上增长快慢的情况.例4.设x>0,f(x)=lnx,g(x)=1−1x,两个函数的图像如图所示。
2014—2015学年高一数学必修一导学案：2.2.1函数的单调性(2)
3 （2）已知 y f ( x) ，在 [0 , ) 上是减函数，试比较 f ( ) 与 f (a 2 a 1) 的大小 4 关系 ．
3、已知函数 f ( x) 2x 2 mx 1 ，在 [2,) 上是增函数，在 (,2] 上是减函数， 则 f ( 2) 是函数 f ( x) 的最 值。
4 、 函 数 f ( x) 2 x 2 mx 1 ， 当 x (2,) 时 是 减 函 数， 则 m 的 取 值 范 围 是 。
y 3 2 -1.5 1 -4 -3 -2 -1 O
7 1 2 3 4 5 6 -1 -2 x
三、课堂研讨
例 1. 求下列函数的最值： （1） y x 2 x
2
（2） y
1 , x [1,3] x
2 例 2、已知函数 f ( x) x mx 1, 且 f (1) 3 ，求函数 f ( x) 在区间[2，3]内的最 值。
四、学后反思
2
函数的单调性：第 2 课时 检测案 班级： 【课堂检测】
1、函数 y 2 x 1 在 [1,2] 上的最大值和最小值分别是____ 2、函数 y x 2 x 在 [3,0] 上的最大值和最小值分别是_______ 3、函数 y _____。 ___。
姓名：
学号：
第
学习小组
2 1 在 [1,3] 上的最大值为__________，最小值为_________。 x
4、求函数 f ( x) 2 x 2 3x 1 在 [2,1] 上的最值。
5、已知函数 y f ( x) 在定义 R 域上是单调减函数，且 f (a 1) f (2a) ，求 a 的取 值范围。
1.3 1函数单调性与导数 导学案 (教师版)
§1.3导数在研究函数中的应用1.3.1函数的单调性与导数内容要求 1.结合实例，借助几何直观探索并了解函数的单调性与导数的关系.2.能利用导数研究函数的单调性.3.会求不超过三次的多项式函数的单调区间.知识点1函数的单调性与导数的关系(1)在区间(a，b)内函数的导数与单调性有如下关系：导数函数的单调性f′(x)>0单调递增f′(x)<0单调递减f′(x)＝0常函数(2)在区间(a，b)函数的单调性导数单调递增f′(x) ≥0单调递减f′(x)≤0常函数f′(x)＝0【预习评价】思考在区间(a，b)内，函数f(x)单调递增是f′(x)>0的什么条件？提示必要不充分条件.知识点2利用导数求函数的单调区间求可导函数单调区间的基本步骤：(1)确定定义域；(2)求导数f′(x)；(3)解不等式f′(x)＞0，解集在定义域内的部分为单调递增区间；(4)解不等式f′(x)＜0，解集在定义域内的部分为单调递减区间.【预习评价】函数f(x)＝13－x2－3x＋2的单调增区间是________.3x解析 f ′(x )＝x 2－2x －3，令f ′(x )＞0，解得x ＜－1或x ＞3，故f (x )的单调增区间是(－∞，－1)，(3，＋∞). 答案 (－∞，－1)，(3，＋∞)题型一 利用导数判断(或证明)函数的单调性【例1】 证明：函数f (x )＝sin x x 在区间⎝ ⎛⎭⎪⎫π2，π上单调递减.证明 f ′(x )＝x cos x －sin x x 2，又x ∈⎝ ⎛⎭⎪⎫π2，π，则cos x <0，∴x cos x －sin x <0， ∴f ′(x )<0，∴f (x )在⎝ ⎛⎭⎪⎫π2，π上单调递减.规律方法 关于利用导数证明函数单调性的问题：(1)首先考虑函数的定义域，所有函数性质的研究必须保证在定义域内这个前提下进行.(2)f ′(x )>0(或<0)，则f (x )为单调递增(或递减)函数；但要特别注意，f (x )为单调递增(或递减)函数，则f ′(x )≥0(或≤0).【训练1】 证明：函数f (x )＝ln xx 在区间(0，e)上是增函数. 证明 ∵f (x )＝ln xx ，∴f ′(x )＝x ·1x －ln x x 2＝1－ln x x 2.又0<x <e ，∴ln x <ln e ＝1. ∴f ′(x )＝1－ln xx 2>0，故f (x )在区间(0，e)上是增函数.题型二 利用导数求函数的单调区间 【例2】 求下列函数的单调区间：(1)f (x )＝2x 3＋3x 2－36x ＋1； (2) f (x )＝sin x －x (0<x <π)； (3)f (x )＝3x 2－2ln x ； (4) f (x )＝x 3－3tx .解 (1) f ′(x )＝6x 2＋6x －36.由f ′(x )＞0得6x 2＋6x －36>0，解得x <－3或x >2； 由f ′(x )＜0解得－3<x <2.故f (x )的增区间是(－∞，－3)，(2，＋∞)；减区间是(－3，2). (2)f ′(x )＝cos x －1.因为0<x <π，所以cos x －1＜0恒成立， 故函数f (x )的单调递减区间为(0，π). (3)函数的定义域为(0，＋∞)， f ′(x )＝6x －2x ＝2·3x 2－1x . 令f ′(x )>0，即2·3x 2－1x >0， 解得－33<x <0或x >33. 又∵x >0，∴x >33. 令f ′(x )<0，即2·3x 2－1x <0， 解得x <－33或0<x <33. 又∵x >0，∴0<x <33.∴f (x )的单调递增区间为(33，＋∞)，单调递减区间为(0，33).(4)f′(x)＝3x2－3t.令f′(x) ＞0，得3x2－3t＞0，即x2＞t，∴当t≤0时，f′(x)＞0恒成立，函数的增区间是(－∞，＋∞)；当t>0时，由x2＞t解得x＞t或x＜－t；由f′(x)＜0解得－t＜x＜t，函数f(x)的增区间是(－∞，－t)和(t，＋∞)，减区间是(－t，t).综上，当t≤0时，f(x)的增区间是(－∞，＋∞)；当t＞0时，f(x)的增区间是(－∞，－t)，(t，＋∞)，减区间是(－t，t).规律方法求函数的单调区间的具体步骤：(1)优先确定f(x)的定义域；(2)计算导数f′(x)；(3)解f′(x)>0和f′(x)<0；(4)定义域内满足f′(x)>0的区间为增区间，定义域内满足f′(x)<0的区间为减区间.【训练2】求函数f(x)＝x3＋3x的单调区间.解方法一函数f(x)的定义域为(－∞，0)∪(0，＋∞).f′(x)＝3x2－3x2＝3⎝⎛⎭⎪⎫x2－1x2.由f′(x)＞0，解得x＜－1或x＞1.由f′(x)＜0，解得－1＜x＜1，且x≠0.所以函数f(x)的单调递增区间为(－∞，－1)，(1，＋∞)；单调递减区间为(－1，0)，(0，1).方法二函数f(x)的定义域为(－∞，0)∪(0，＋∞).f′(x)＝3x2－3x2＝3(x2－1x2)；令f′(x)＝0，得x＝±1.当x 变化时，f ′(x )与f (x )的变化情况如下表： x (－∞，－1)－1 (－1，0) (0，1) 1 (1，＋∞)f ′(x )＋0 －－0 ＋ f (x ) 单调递增Z －4单调递减] 单调递减]4单调递增Z0)，(0，1).方向1 已知函数的单调性求参数的取值范围【例3－1】 已知函数f (x )＝x 2＋ax (x ≠0，常数a ∈R ).若函数f (x )在x ∈[2，＋∞)上是单调递增的，求a 的取值范围.解 f ′(x )＝2x －a x 2＝2x 3－ax 2.要使f (x )在[2，＋∞)上是单调递增的，则f ′(x )≥0在x ∈[2，＋∞)时恒成立， 即2x 3－ax 2≥0在x ∈[2，＋∞)时恒成立. ∵x 2>0，∴2x 3－a ≥0，∴a ≤2x 3在x ∈[2，＋∞)上恒成立. ∴a ≤(2x 3)min .∵x ∈[2，＋∞)时，y ＝2x 3是单调递增的， ∴(2x 3)min ＝16，∴a ≤16.当a ＝16时，f ′(x )＝2x 3－16x 2≥0(x ∈[2，＋∞))有且只有f ′(2)＝0，∴a 的取值范围是(－∞，16].方向2利用函数的单调性证明不等式【例3－2】已知a，b为实数，且b＞a＞e，其中e为自然对数的底，求证：a b＞b a.证明当b＞a＞e时，要证a b＞b a，只要证b ln a＞a ln b，即只要证ln aa＞ln bb.构造函数y＝ln xx(x＞0)，则y′＝1－ln xx2.因为当x＞e时，y′＝1－ln xx2＜0，所以函数y＝ln xx在(e，＋∞)内是减函数.又因为b＞a＞e，所以ln aa ＞ln bb.故a b＞b a.规律方法(1)已知函数的单调性，求函数解析式中参数的取值范围，可转化为不等式恒成立问题，一般地，函数f(x)在区间I上单调递增(或减)，转化为不等式f′(x)≥0(f′(x)≤0)在区间I上恒成立，再用有关方法可求出参数的取值范围.(2)“构造”是一种重要而灵活的思维方式，应用好构造思想解题的关键是：一要有明确的方向，即为什么目的而构造；二是要弄清条件的本质特点，以便重新进行逻辑组合.【训练3】若函数f(x)＝x3＋x2＋mx＋1是R上的单调函数，求实数m的取值范围.解f′(x)＝3x2＋2x＋m.因为f(x)是R上的单调函数，所以f′(x)≥0恒成立或f′(x)≤0恒成立.因为二次项系数3＞0，所以只能有f′(x)≥0恒成立.因此Δ＝4－12m≤0，故m≥13.当m ＝13时，使f ′(x )＝0的点只有一个x ＝－13，也符合题意.故实数m 的取值范围是⎣⎢⎡⎭⎪⎫13，＋∞.课堂达标1.函数f (x )＝x ＋ln x 在(0，6)上是( ) A.增函数 B.减函数C.在⎝ ⎛⎭⎪⎫0，1e 上是减函数，在⎝ ⎛⎭⎪⎫1e ，6上是增函数D.在⎝ ⎛⎭⎪⎫0，1e 上是增函数，在⎝ ⎛⎭⎪⎫1e ，6上是减函数解析 ∵f ′(x )＝1＋1x >0， ∴函数在(0，6)上单调递增. 答案 A2.f ′(x )是函数y ＝f (x )的导函数，若y ＝f ′(x )的图象如图所示，则函数y ＝f (x )的图象可能是( )解析 由导函数的图象可知，当x <0时，f ′(x )>0，即函数f (x )为增函数；当0<x <2时，f ′(x )<0，即f (x )为减函数；当x >2时，f ′(x )>0，即函数f (x )为增函数.观察选项易知D 正确. 答案 D3.若函数f (x )＝x 3－ax 2－x ＋6在(0，1)内单调递减，则实数a 的取值范围是( )A.[1，＋∞)B.a ＝1C.(－∞，1]D.(0，1)解析 ∵f ′(x )＝3x 2－2ax －1，又f (x )在(0，1)内单调递减，∴不等式3x 2－2ax －1≤0在(0，1)内恒成立，∴f ′(0)≤0，且f ′(1)≤0，∴a ≥1. 答案 A4.函数y ＝x 2－4x ＋a 的增区间为______，减区间为______. 解析 y ′＝2x －4，令y ′>0，得x >2；令y ′<0，得x <2， 所以y ＝x 2－4x ＋a 的增区间为(2，＋∞)，减区间为(－∞，2). 答案 (2，＋∞) (－∞，2)5.若函数f (x )＝ln x －12ax 2－2x 存在单调递减区间，则实数a 的取值范围是________.解析 f ′(x )＝1x －ax －2＝－ax 2＋2x －1x.因为函数f (x )存在单调递减区间，所以f ′(x )≤0有解.又因为函数f (x )的定义域为(0，＋∞)，所以ax 2＋2x －1≥0在(0，＋∞)内有解. ①当a ＞0时，y ＝ax 2＋2x －1为开口向上的抛物线，ax 2＋2x －1≥0在(0，＋∞)内恒有解；②当a ＜0时，y ＝ax 2＋2x －1为开口向下的抛物线， 若ax 2＋2x －1≥0在(0，＋∞)内恒有解，则⎩⎨⎧Δ＝4＋4a ≥0，x ＝－1a ＞0，解得－1≤a ＜0， 而当a ＝－1时，f ′(x )＝x 2－2x ＋1x ＝（x －1）2x ≥0，不符合题意，故－1＜a ＜0；③当a ＝0时，显然符合题意.综上所述，a 的取值范围是(－1，＋∞). 答案 (－1，＋∞)课堂小结1.导数的符号反映了函数在某个区间上的单调性，导数绝对值的大小反映了函数在某个区间或某点附近变化的快慢程度.2.利用导数求函数f (x )的单调区间的一般步骤： (1)确定函数f (x )的定义域； (2)求导数f ′(x )；(3)在函数f (x )的定义域内解不等式f ′(x )>0和f ′(x )<0； (4)根据(3)的结果确定函数f (x )的单调区间.基础过关1.函数f (x )＝(x －3)e x 的单调递增区间是( ) A.(－∞，2) B.(0，3) C.(1，4)D.(2，＋∞)解析 f ′(x )＝(x －3)′e x ＋(x －3)(e x )′＝(x －2)e x ，令f ′(x )＞0，即(x －2)e x ＞0，解得x ＞2，故选D. 答案 D2.y ＝x ln x 在(0，5)内的单调性是( ) A.单调递增 B.单调递减C.在⎝ ⎛⎭⎪⎫0，1e 内单调递减，在⎝ ⎛⎭⎪⎫1e ，5内单调递增D.在⎝ ⎛⎭⎪⎫0，1e 内单调递增，在⎝ ⎛⎭⎪⎫1e ，5内单调递减解析 函数的定义域为(0，＋∞).y ′＝ln x ＋1，令y ′＞0，得x ＞1e ；令y ′＜0，得0＜x ＜1e .所以函数y ＝x ln x 在⎝ ⎛⎭⎪⎫0，1e 内单调递减，在⎝ ⎛⎭⎪⎫1e ，5内单调递增.答案 C3.函数f (x )＝x 3＋ax 2＋bx ＋c ，其中a ，b ，c 为实数，当a 2－3b <0时，f (x )是( ) A.增函数 B.减函数 C.常数D.既不是增函数也不是减函数解析 求函数的导函数f ′(x )＝3x 2＋2ax ＋b ，导函数对应方程f ′(x )＝0的Δ＝4(a 2－3b )<0，所以f ′(x )>0恒成立，故f (x )是增函数. 答案 A4.函数y ＝f (x )在其定义域⎝ ⎛⎭⎪⎫－32，3内可导，其图象如图所示，记y ＝f (x )的导函数为y ＝f ′(x )，则不等式f ′(x )≤0的解集为________.解析 函数y ＝f (x )为减函数的区间，反映在图象上图象是下降的. 答案 ⎣⎢⎡⎦⎥⎤－13，1∪[2，3)5.当x >0时，f (x )＝x ＋2x 的单调递减区间是________.解析 f ′(x )＝1－2x 2＝x 2－2x 2＝（x －2）（x ＋2）x 2.由f ′(x )<0且x >0得0<x < 2. 答案 (0，2)6.已知函数f (x )＝x 3＋bx 2＋cx ＋d 的图象经过点P (0，2)，且在点M (－1，f (－1))处的切线方程为6x －y ＋7＝0. (1)求函数y ＝f (x )的解析式； (2)求函数y ＝f (x )的单调区间.解 (1)由y ＝f (x )的图象经过点P (0，2)，知d ＝2，∴f (x )＝x 3＋bx 2＋cx ＋2，f ′(x )＝3x 2＋2bx ＋c .由在点M (－1，f (－1))处的切线方程为6x －y ＋7＝0，知－6－f (－1)＋7＝0，即f (－1)＝1，f ′(－1)＝6.∴⎩⎪⎨⎪⎧3－2b ＋c ＝6，－1＋b －c ＋2＝1，即⎩⎪⎨⎪⎧2b －c ＝－3，b －c ＝0，解得b ＝c ＝－3. 故所求的解析式是f (x )＝x 3－3x 2－3x ＋2.(2)f ′(x )＝3x 2－6x －3.令f ′(x )>0，得x <1－2或x >1＋2；令f ′(x )<0，得1－2<x <1＋ 2.故f (x )＝x 3－3x 2－3x ＋2的单调递增区间为(－∞，1－2)和(1＋2，＋∞)，单调递减区间为(1－2，1＋2).7.已知向量a ＝(x 2，x ＋1)，b ＝(1－x ，t ).若函数f (x )＝a ·b 在区间(－1，1)上是增函数，求t 的取值范围.解 由题意得f (x )＝x 2(1－x )＋t (x ＋1)＝－x 3＋x 2＋tx ＋t ，则f ′(x )＝－3x 2＋2x ＋t .若f (x )在(－1，1)上是增函数，则在(－1，1)上f ′(x )≥0恒成立.即t ≥3x 2－2x 在区间(－1，1)上恒成立.令函数g (x )＝3x 2－2x ，由于g (x )的图象是对称轴为x ＝13，开口向上的抛物线，故t ≥3x 2－2x 在区间(－1，1)上恒成立⇔t ≥g (－1)，即t ≥5.故t的取值范围是[5，＋∞).能力提升8.已知函数f(x)在定义域R上为增函数，且f(x)＜0，则g(x)＝x2f(x)在(－∞，0)内的单调情况一定是()A.单调递减B.单调递增C.先增后减D.先减后增解析因为函数f(x)在定义域R上为增函数，所以f′(x)≥0.又因为g′(x)＝2xf(x)＋x2f′(x)，所以当x∈(－∞，0)时，g′(x)＞0恒成立，所以g(x)＝x2f(x)在(－∞，0)内单调递增.答案 B9.已知函数y＝xf′(x)的图象如图所示，选项中的四个图象中能大致表示y＝f(x)的图象的是()解析由题图可知，当x＜－1时，xf′(x)＜0，所以f′(x)＞0，此时原函数为增函数，图象应是上升的；当－1＜x ＜0时，xf ′(x )＞0，所以f ′(x )＜0，此时原函数为减函数，图象应是下降的；当0＜x ＜1时，xf ′(x )＜0，所以f ′(x )＜0，此时原函数为减函数，图象应是下降的；当x ＞1时，xf ′(x )＞0，所以f ′(x )＞0，此时原函数为增函数，图象应是上升的.由上述分析可知选C.答案 C10.若函数f (x )＝kx －ln x 在区间(1，＋∞)上单调递增，则k 的取值范围是________.解析 由于f ′(x )＝k －1x，f (x )＝kx －ln x 在区间(1，＋∞)上单调递增，故f ′(x )＝k －1x ≥0在(1，＋∞)上恒成立.由于k ≥1x ，而0＜1x ＜1，故k ≥1，即k 的取值范围是[1，＋∞).答案 [1，＋∞)11. 已知函数f (x )＝x 3－2x ＋e x －1e x ，其中e 是自然对数的底数，若f (a －1)＋f (2a 2)≤0，则实数a 的取值范围是________．解析 f ′(x )＝3x 2－2＋e x ＋1e x ≥3x 2－2＋2e x ·1ex ＝3x 2≥0且f ′(x )不恒为0，所以f (x )为单调递增函数．又f (－x )＝(－x )3－2(－x )＋e －x －1e －x ＝－⎝ ⎛⎭⎪⎫x 3－2x ＋e x －1e x ＝－f (x )，故f (x )为奇函数．由f (a －1)＋f (2a 2)≤0得，f (2a 2)≤－f (a －1)＝f (1－a )，所以2a 2≤1－a ，解得－1≤a ≤12，故实数a 的取值范围为⎣⎢⎡⎦⎥⎤－1，12. 答案 ⎣⎢⎡⎦⎥⎤－1，12 12.已知函数f (x )＝ln x －f ′(1)x ＋1－ln 2，试求f (x )的单调区间.解 由f (x )＝ln x －f ′(1)x ＋1－ln 2，x ∈(0，＋∞)，得f ′(x )＝1x －f ′(1).令x ＝1，则f ′(1)＝1－f ′(1)，∴f ′(1)＝12，f ′(x )＝1x －12.由f ′(x )＞0，即1x －12＞0，得0＜x ＜2；由f ′(x )＜0，即1x －12＜0，得x ＞2.故f (x )的单调递增区间为(0，2)，单调递减区间为(2，＋∞).创新突破13.已知函数f (x )＝x 3＋ax 2＋x ＋1，a ∈R .(1)讨论函数f (x )的单调区间；(2)设函数f (x )在区间⎝ ⎛⎭⎪⎫－23，－13内是减函数，求a 的取值范围. 解 (1)f ′(x )＝3x 2＋2ax ＋1，Δ＝4(a 2－3).当Δ＞0，即a ＞3或a ＜－3时，令f ′(x )＞0，即3x 2＋2ax ＋1＞0，解得x ＞－a ＋a 2－33或x ＜－a －a 2－33；令f ′(x )＜0，即3x 2＋2ax ＋1＜0， 解得－a －a 2－33＜x ＜－a ＋a 2－33. 故函数f (x )的单调递增区间是⎝ ⎛⎭⎪⎫－∞，－a －a 2－33，⎝ ⎛⎭⎪⎫－a ＋a 2－33，＋∞； 单调递减区间是⎝ ⎛⎭⎪⎫－a －a 2－33，－a ＋a 2－33. 当Δ＜0，即－3＜a ＜3时，对所有的x ∈R 都有f ′(x )＞0，故f (x )在R 上单调递增.当Δ＝0，即a ＝±3时，f ′⎝ ⎛⎭⎪⎫－a 3＝0，且对所有的x ≠－a 3都有f ′(x )＞0，故f (x )在R 上单调递增.(2)由(1)，知只有当a ＞3或a ＜－3时，f (x )在⎝ ⎛⎭⎪⎫－a －a 2－33，－a ＋a 2－33内是减函数， 所以⎩⎪⎨⎪⎧－a －a 2－33≤－23，－a ＋a 2－33≥－13.解得a ≥2.故a 的取值范围是[2，＋∞).。
导数与函数单调性导学案
主备人： 审核： 包科领导： 年级组长： 使用时间：3.1.1导数与函数的单调性【学习目标】1.了解可导函数的单调性与其导数的关系。
2.能利用导数研究函数的单调性，会求函数的单调区间。
3.会求不超过三次的多项式函数的单调区间。
【重点】利用导数研究函数的单调性，会求不超过三次的多项式函数的单调区间。
【难点】利用导数研究函数的单调性，会求不超过三次的多项式函数的单调区间。
【使用说明与学法指导】1.通过阅读教材，自主学习，思考，交流，讨论和概括，完成本节课的学习目标。
2.用红笔勾勒出疑点，合作学习后寻求解决方案。
3.带*号的为选做题。
【自主探究】1.函数的单调性与导数的关系在某个区间),(b a 内，如果0)(>'x f ，那么函数)(x f y =在这个区间内_____________：如果0)(<'x f ，那么函数)(x f y =在这个区间内_____________。
说明：特别的，如果0)(='x f ，那么函数)(x f y =在这个区间内是_____________。
2.函数)(x f 的单调增区间，可通过解不等式_____________求得，而单调减区间可由不等式_____________解得。
3.求可导函数)(x f 单调区间的步骤（1）____________________________（2）____________________________（3）____________________________【合作探究】1. 求下列函数的单调区间.62)1(24+-=x x y ；22ln )2(x x y +-= ；2. 函数x axx f -=3)(在R 上为减函数，求a 的取值范围.3. 求证：函数3223121y x x x =+-+在区间()2,1-内是减函数.4. 已知曲线106323-++=x x x y ，点),(y x P 在该曲线上移动，过点P 的切线设为l ，(1)求证：此函数在R 上单调递增；(2)求l 的斜率的范围.【巩固提高】1. 求下列函数的单调区间.(1)),0(,sin )(π∈-=x x x x f ； (2)x x x f 9)(+=；(3)x x x f ln )(=. 2. 已知函数)0(1)1(3)(223>+-+-=k k x k kx x f ，若)(x f 的单调减区间是)4,0(，求k 的值.3.已知函数32324)(x axx x f -+=在区间]1,1[-上是增函数，求实数a 的取值范围.★4.若函数x ax x f +=3)((1)求实数a 的取值范围，使)(x f 在R 上是增函数.(2)求实数a 的取值范围，使)(x f 恰好有三个单调区间. ★ 5.偶函数e dx cx bx ax x f ++++=234)(的图像过点)1,0(P ，且在1=x 处的切线方程为2-=x y ，求)(x f 的解析式.。
函数的单调性导学案
函数的单调性导学案编撰人：李斌审定：阜阳四中高一数学组一、【学习目标】（自学引导：这节课我们主要任务就是通过对单调性的研究，然后会运用函数单调性解决题目.这节课的特点是符号较多，希望同学们课下做好预习.）1、理解函数单调性的本质内容和函数单调性的几何意义；2、掌握判断函数单调性的判断方法：定义法和图象法；3、熟练的掌握用定义法证明函数单调性及其步骤.课前引导：函数图象上任意点P(x,y)的坐标有什么意义？二、【自学内容和要求及自学过程】观察教材第27页图1.3-2，阅读教材第27-28页“思考”上面的文字，回答下列问题（自学引导：理解“上升”、“下降”的本质内涵，归纳出增函数的定义）<1>你能描述上面函数的图像特征吗？该怎样理解“上升”、“下降”的含义？<2>对于二次函数y=x2，列出表(1)，完成表(1)并体会图象在y轴右侧上升；x …-3 -2 -1 0 1 2 3 4 …f(x)=x2……结论：<1>函数y=x的图象，从左向右看是＿＿＿（上升、下降）的；函数y=x2的图象在y轴左侧是＿＿＿的，在y轴右侧是＿＿＿的；函数y=-x2的图象在y轴左侧是＿＿＿的，在y轴右侧是＿＿＿的；按从左向右的方向看函数的图象，意味着图象上点的横坐标逐渐增大即函数的自变量逐渐增大；图象是上升的意味着图象上点的＿＿＿（横、纵）坐标逐渐变大，也就是对应的函数值随着逐渐增大.也就是说从左向右看图象上升，反映了函数值随着自变量的增大而＿＿＿；“下降”亦然；<2>在区间(0，+∞)上，任取x1、x2，且x1<x2,那么就有y1＿＿y2(<,>),也就是有f(x1) ＿＿＿f(x2).这样可以体会用数学符号刻画图象上升.阅读教材第28页“思考”下面的内容，然后回答下列问题（自学引导：同学们要理解增函数的定义，符号比较多，要一一的理解）<3>数学上规定：函数y=x2在区间(0,+∞)上是增函数.请给出增函数定义.<4>增函数的定义中，把“当x1<x2时，都有f(x1)<f(x2)”改为“当x1>x2时，都有f(x1)>f(x2)”，这样行吗?增函数的定义中，“当x1<x2时，都有f(x1)<f(x2)”反映了函数值有什么变化趋势?函数图象有何特点?<5>增函数的几何意义是什么？结论：<3>一般地，设函数f(x)的定义域为I:如果对于定义域I内某个区间D上的任意两个自变量的值x1、x2，当＿＿＿时，都有＿＿＿，那么就说函数f(x)在区间D上是增函数；<4>增函数的定义：由于当x1<x2时，都有f(x1)<f(x2)，即都是相同的不等号“<”，也就是说前面是“<”，后面也是“<”,步调一致；“当x1>x2时，都有f(x1)>f(x2)”都是相同的不等号“>”，即前面是“>”，后面也是“>”,步调一致.因此我们可以简称为：步调一致增函数；增函数反映了函数值随自变量的增大而增大；从左向右看,图象是上升的；<5>增函数几何意义是从左向右看,图象是＿＿＿（上升、下降）的；（自学引导：类比增函数的定义，切实理解减函数的含义.）思考：<1>类比增函数的定义，请你给出减函数的定义；<2>函数y=f（x）在区间D上具有单调性，说明了函数y=f（x）在区间D上的图象有什么变化趋势？结论：<1>一般地，设函数f(x)的定义域为I，如果对于定义域I内某个区间D上的任意两个自变量的值x1、x2，当＿＿＿时，都有＿＿＿，那么就说函数f(x)在区间D上是减函数.简称为：步调不一致减函数.减函数的几何意义：从左向右看,图象是＿＿＿的.函数值变化趋势：函数值随着自变量的增大而减小；<2>函数y=f（x）在区间D上，函数值的变化趋势是随自变量的增大而增大（减小），几何意义：从左向右看,图象是＿＿＿（＿＿＿）（上升、下降）的；阅读教材第29页第一段，然后回答下列问题<7>你能理解“严格的单调性”所包含的含义吗？试述之.三、讲授新课1.引例：观察y=x2的图象，回答下列问题（投影1）问题1：函数y=x2的图象在y轴右侧的部分是上升的，说明什么？⇒随着x的增加，y值在增加。
函数单调性教案函数单调性教学设计(6篇)
函数单调性教案函数单调性教学设计（6篇）为你细心整理了6篇《函数的单调性教学设计》的范文，但愿对你的工作学习带来帮忙，盼望你能喜爱！固然你还可以在搜寻到更多与《函数的单调性教学设计》相关的范文。
《函数的单调性》教学设计【教材分析】《函数单调性》是高中数学新教材必修一其次章第三节的内容。
在此之前，学生已学习了函数的概念、定义域、值域及表示法，这为过渡到本节的学习起着铺垫作用。
本节内容是高中数学中相当重要的一个根底学问点，是讨论和争论初等函数有关性质的根底。
把握本节内容不仅为今后的函数学习打下理论根底，还有利于培育学生的抽象思维力量及分析问题和解决问题的力量.【学生分析】从学生的学问上看，学生已经学过一次函数，二次函数，反比例函数等简洁函数，函数的概念及函数的表示，接下来的任务是对函数应当连续讨论什么,从各种函数关系中讨论它们的共同属性，应当是顺理成章的。
从学生现有的学习力量看，通过初中对函数的熟悉与试验，学生已具备了肯定的观看事物的力量，积存了一些讨论问题的阅历，在肯定程度上具备了抽象、概括的力量和语言转换力量。
从学生的心理学习心理上看，学生头脑中虽有一些函数性质的实物实例，但并没有上升为“概念”的水平，如何给函数性质以数学描述?如何“定性”“定量”地描述函数性质是学生关注的问题，也是学习的重点问题。
函数的单调性是学生从已经学习的函数中比拟简单发觉的一共性质，学生也简单产生共鸣，通过比照产生顿悟，渴望获得这种学习的.积极心向是学生学好本节课的情感根底。
【教学目标】1．使学生从形与数两方面理解函数单调性的概念.2．通过对函数单调性定义的探究，渗透数形结合数学思想方法，培育学生观看、归纳、抽象的力量和语言表达力量.3．通过学问的探究过程培育学生细心观看、仔细分析、严谨论证的良好思维习惯，让学生经受从详细到抽象，从特别到一般，从感性到理性的认知过程．【教学重点】函数单调性的概念.【教学难点】从形与数两方面理解函数单调性的概念.【教学方法】教师启发讲授，学生探究学习．【教学手段】计算机、投影仪．【教学过程】教学根本流程1、视频导入------营造气氛激发兴趣2、直观的熟悉增（减）函数-----问题探究3、定量分析增（减）函数）-----归纳规律4、给出增（减）函数的定义------展现结果5、微课教学设计函数的单调性定义重点强调 ------ 稳固深化 7、课堂收获 ------提高升华（一）创设情景，提醒课题1．钱江潮，自古称之为“天下奇观”。
函数的单调性教学设计(教案)
2.3 《函数的单调性》教学设计(第一课时)一、教材分析(一)本节内容的地位与作用中学生对函数单调性的学习分为三个阶段，分别为初中通过简单函数的感性认识、高一的严格定义及高二利用导数解决函数的单调性.因此，高一函数单调性概念的学习，起到了承前启后的作用.函数的单调性是学生学习的第一个函数性质，也是第一个用数学符号语言刻画的概念.因此，单调性的研究方法非常重要，它为以后函数奇偶性、周期性等其它性质的学习提供了方法依据.它是解决函数定义域、值域、数列、不等式、三角函数等问题的有力工具，是高考重点考查的内容之一，同时也是培养学生逻辑推理能力的绝佳素材.(二)教学目标1、知识目标：理解函数单调性的概念，掌握判别函数单调性的方法．2、能力目标：培养学生自主探索能力、分析归纳能力及逻辑推理能力．3、情感目标：通过层层设问，激发学生的好奇心和求知欲，培养学生的自信心，提高学生学习数学的兴趣.(三)教学重难点重点：函数单调性的概念.难点：（1）函数单调性概念的生成中，如何从图象的直观认识过渡到用符号语言表述；（2）运用定义证明函数的单调性．二、学情分析（一）认知水平1、知识学生通过初中的学习对函数的升、降有了初步的感知；函数的概念及表示的学习为本节内容做好了知识铺垫．2、技能他们初步具备了分析概括能力，但科学的思维方法尚未形成．（二）心理特征他们好奇心强，追求成功的愿望强烈．他们渴望老师给他们提供自主探索的时间及展示自我的空间．但他们抽象思维能力相对薄弱．三、教法分析本着新课改下以学生为主体，教师为主导的教学理念，结合本节课的知识特点及学情分析，决定采用问题式、启发式、探究式相结合的教学法．主要体现在新课引入时的层层设问，概念生成时的启发引导，总结证明步骤时的探究发现等．因幻灯片直观形象且教学容量大，故决定采用多媒体辅助教学．四、学法分析新课标要求学生不仅仅要“学会”，还应当让学生“会学”、“乐学”.在这种理念的指引下，我在教学设计上强调了让学生主动参与，积极探究，同时让学生相互交流与合作．让学生在与老师、同学之间的交流、讨论中完成知识的构建及难点的突破.五、教学过程教学环节教学内容设计思路创设情境引入新课(1)生活常识“糖水加糖味更甜”(2)焦作市某日全天气温图像问题：（1）观察图像，能得出哪些信息？（2）说说一天中气温的变化趋势？由生活情境引入新课，以此激发学生的学习兴趣。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
例1、判断一次函数 反比例函数 ，二次函数 的单调性。
例2、求证:函数 上是增函数。(在下面证明过程中填空)
证明：取 ,且______________.
则 ,
因 且 ,所以_________________________,
所以 即________________,
所以函数 上_______________.
例3、已知函数 .
①当 时，求函数的最大值和最小值；
②求实数 的取值范围，使 在区间 上是单调函数。
例4、知函数 在[1,3]有最大值5和最小值2，求a、b的值。
三、当堂反馈
1、下列函数中，在区间(0，2)上为增函数的是( )
A． B． C． D．
2、函数 在实数集上是增函数，则（）
A． B． C． D．
（1）、都有f(x1)f(x2)，那么我们就说函数 在区间D上是减函数；
（2）、都有f(x1)f(x2)，那么我们就说函数 在区间D上是增函数。
2．函数的单调性：如果一个函数在某个区间M上是或者，就说这个函数在这个区间M上具有（区间M称为）
3．最大值：一般地，设函数y=f(x)的定义域为I，如果存在实数M满足：
A． B． C． D．无法确定
2、若函数f(x)=∣x-a∣在区间 内为减函数，则a的范围是 （ ）
A、a≥1 B、a=1 C、a≤1 D、0≤a≤1
3、已知函数f(x)在R上是增函数，若a+b>o,则有：
A、f(a)+f(b)>f(-a)+f(-b); B、f(a)+f(b)>f(-a)-f(-b);
（1）对于任意的x∈I，都有；
（2）存在，使得，那么我们称M是函数y=f(x)的。
最小值：一般地，设函数y=f(x)的定义域为I，如果存在实数M满足：
（1）对于任意的x∈I，都有；
（2）存在，使得，那么我们称M是函数y=f(x)的。
4．如何判断和证最值的步骤是什么？
3、已知函数 在区间 上是减函数，则实数 的取值范围是（）
A． B． C． D．
4、用定义证明：函数 在 上是增函数。
5、已知
（1）当 时，求函数的最大值和最小值；（2）求 的取值范围，使得函数在区间 上具有单调性；（3）试求函数在区间 上的最小值。
四、课后作业
1、函数 在 和 都是增函数，若 ，且 那么（）
（2）若函数f(x)在区间 内是增函数，求a的范围；
（教师“复备”栏或学生笔记栏）
学校乐从中学年级高二学科数学导学案
主备审核授课人授课时间班级姓名小组
课题：函数的单调性及最值课型：复习课课时：一
【学习目标】
理解函数的单调性、最大（小）值及其几何意义
【学习过程】
一、知识要点
1．函数单调性的定义：设函数 的定义域为I,如果对于定义域I内某个区间D上的任意两个自变量的值 ， ，当 < 时，
C、f(a)+f(-a)>f(b)+f(-b); D、f(a)+f(-a)>f(b)-f(-b);
4、函数f(x)是定义在（-1，1）上的增函数，且f(a-2)-f(4-a2)<0, 那么a的取值范围为____________;
5、设二次函数f(x)=x2-(2a+1)x+3
（1）若函数f(x)的单调增区间为 ，求实数a的值；