电路基本定律相量形式

当 C一定时,电容的容抗与频率f 成反比。频率越高， 感抗越小，在直流电路中容抗为无限大，可视为开路。
2. 电压电流的相位关系
uUms iω nt
iImsiω nt (90 )
U mUm00 ImIm900
i uC
i 超前u
2
3. 电压电流的相量关系
ui u
i
UImm
p
（1）瞬时功率
p u U i( 1 c I2 o t)s
（2）平均功率
（有功功率）
0
PT 10 TpdtU IU R 2I2R
t
P=U I
t
四、电感元件的电压电流关系的相量式
设在电感元件的交流电路中
，电压、电流参考方向如图示。
+
1.电压电流的数值关系
ui L
瞬时值 设： iImsi nt
2. 电压电流的相位关系
iImsi nt ImIm00U mUm900 u+
u L I m co t U m s sit n 9 )( 0
u 超前i
eu 2 e滞后i
ui
u
i
–
e
i
e
L
2
3. 电压电流的相量关系
0
t

U Im mUIm m 09000U Im m900jXL

Um00 Im900
jXC
I
0
2
•
UjIXC
U
CHale Waihona Puke ItU• 相量图
3、功率
设：uU m sin t
iu
iIm si n t(90 ) 0
t
其波形图如右：
p
（1）瞬时功率
p u U i sI 2 i n t
+
+
（2）平均功率 P0
0
–
– t
电容不消耗功率， 是储能元件。
2
U•
U jIXL
+
U I
–
E
L 相量图
•
I E•
4. 功率
设：iIm sin t
ui
uU m si n t9 ()0
其波形图如右：
0
t
（1）瞬时功率
p
p u iU sI i2 n t +
+
（2）平均功率
P0
0
–
– t
（3Q）无U功I功X率LI2U XL 2
–
则 u L di
U 最 u m U 大 值 L Im I、 I m L 有L c 效II值m X o t L X L dU tm s s X感L抗it ( n L )9 )( 0 电最姆电流大定感有值律的效满形电值足式压、欧。与
感感抗抗当的越L大倒一，数定在称时直,为线流感圈电的纳路感中，抗感即与抗：频为B L率零f，X成1可L 正单视比为位。短：频路率西。越[门高子，]
因此，相量形式的KVL为:
对任一闭合回路满足

U 0
正弦电流用相量表示后，KCL仍然适用。
三、电阻元件电压电流关系的相量形式
设在电阻元件的交流电路中 ，电压、电流参考方向如图示。
1.电压电流的数值关系
+
ui R
–
则瞬值u 时 R 设 ：R im i s ImsI i t i n U n tm sImi t In m00
电感不消耗功率， 是储能元件。
电感与电源之间能量交换的规模称为无功功
率。其值为瞬时功率的最大值，单位为(var) 乏。
五、电容元件的电压电流关系的相量形式
设在电容元件的交流电路中 ，电压、电流参考方向如图示。
1.电压电流的数值关系
i uC
瞬时值 设：uUms iω nt
则 i C du U 最m i大 值C Im ω 、CU 1有ωm 效c 值Im ω o XtC dt I s m s X容C抗ω i(t n 1C)9 ) (电最姆0 电流大定容有值律的效满形电值足式压、欧。与
第三节 电路基本定律的相量形式
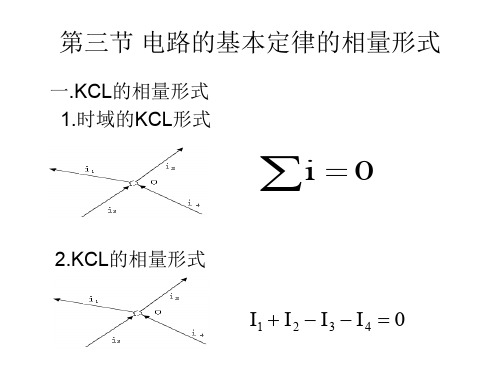
一、KCL的相量形式
时域内KCL为 i 0
在正弦交流电路中，上式各项电流均为同频 率的正弦量。
因此，相量形式的KCL为: 对任一节点满足

I 0
正弦电流用相量表示后，KCL仍然适用。
二、KVL的相量形式
时域内的KVL为: u0
在正弦交流电路中，上式各项电压均为同频 率的正弦量。
电阻的电压 与电流瞬时
最大值、有效值 UmRIm 或
Um

U

U mUm00
R
值、有效值 、最大值都
Im I
满足欧姆定
2. 电压电流的相位关系
u 、i 同相
3. 电压电流的相量关系
律。
ui
u i
+
U I
–
R
U m I m

R

I 0 U
相量图
t
3、功率
u
i
+
u
R
0
–
i
u i U Im m ssi i n tn t
（3）无功功率
Q U IX C I2
电容与电源之间能量交换的规模称为无功功 率。其值为瞬时功率的最大值，单位为(var) 乏。