电路之电路定律的相量形式
合集下载
电路相量法
等于初相位之差
规定： |j | ( 180°)。
• j >0， u 超前 i，或 i 滞后u (u 比 i 先到达最大值)；
u, i u i
O
wt
u i
j
• j <0， i 超前 u ，或u 滞后 i (i 比 u 先到达最大值)。
特殊相位关系：
j = (180o ) ，u与 i 反相
j = 0 ，u与 i 同相
解 547 10 25 (3.41 j3.657) (9.063 j4.226)
12.47 j0.569 12.48 2.61
例2
220 35 (17 j9) (4 j6) ?
20 j5
解
原式
180.2
j126.2
19.2427.9 7.21156.3 20.6214.04
考虑。
（2）测量中，电磁式交流电压、电流表读数均为有效值。 （3）电压、电流的瞬时值、最大值、有效值的符号。
i , Im , I
4. 同频率正弦量的相位差
设 u(t)=Umcos(w t+ u), i(t)=Imcos(w t+y i)
则 相位差 ：j = (w t+ u) - (w t+ i) = u- i
相量法是分析求解正弦电流电路稳态响应的一种 有效工具。
1. 正弦量的相量表示
两个正弦量的相加
i1 2 I1 cos(w t 1 ) i2 2 I2 cos(w t 2 )
角频率： 有效值： 初相位：
ui1, i
w
i1
i2
w
i2
I1 0
I2
1
2
i1+ii23wi3
最新电工学电力学课程第八章《电路定律的相量形式》
由相量形式KVL有 : V V 1 V 2 600 8090 (V)
（2）相量图解法
60 j80 10053.1 (V) 故 : |V | 100(V)
相量法的三个基本公式
UR RIR
U L jL IL
1
UC
j
C
IC
以上公式是在电压、电流关联参考方向的条件
错误的写法
1 u
C i
1
C
U I
(2) 容抗的绝对值和频率成反比。
0, XC , 直流开路( 隔直作用) ;
XC
, XC 0, 高频短路（旁路作用）;
(3) 由于容抗的存在使电流领先电压。
4、受控源 如果受控源（线性）的控制电压或电流是正弦量， 则受控源的电压或电流将是同一频率的正弦量。
i 超前u 90° I
0
所示，反映电压电流瞬时 值关系的波形图如图(b)所示。由此图可以看出电容电流超 前于电容电压90°，当电容电压由负值增加经过零点时，其 电流达到正最大值。
容抗
I= CU
U 1
I C
容抗的物理意义：
X
C
定义
1
C
(1) 表示限制电流的能力；
相量关系
+
U R R I
U R
-
有效值关系：UR = RI 相位关系：u , i 同相
I
R
U
相量图
相量模型
2. 电感
时域
频域
i(t)
i(t) 2I cost
+ u (t)
u(t) L di(t)
电工基础5.3 电路基本定律的相量形式
结论：①电容元件电压电流大小关系为：
U 1 I
C
②电容元件电压电流相量关系为：
i
u
2
或i
u
2
即电流I超前电压U π/2.
3、容抗与容纳
（1）容抗Xc：表示电容对正弦电流得
1 单位为欧【姆】()
2f C
① ω＝0，Xc→∞ 电容元件相当于开路 ② ω →∞ ，Xc＝0 电容元件相当于短路
3、KVL在相量图上体现为——封闭多 边形。 三、电阻元件电压电流关系的相量形式： 1、电阻元件 （1）电阻元件时域 形式的电压与电流 关系：
u = Ri
图4-18电阻元件电压电流瞬时值关系
（2）电阻元件的相量形式：
U RI
结论：①电阻元件的电压与电流关系
U=RI 或 I=GU(G=1/R)
①
电感相当于短路
② 0, X L 0 电感相当于开路
（2)感纳： 表示电, X感L 对正弦电流的导通能力。
单位西【门子】（S）
BL
1 XL
故又得：
U jX L I
I jBL U
例4－6：已知0.5H的电感两端电压为
uL 220 2 sin(314t 30)V ，求：XL、BL和IL， 并画出相量图。
2、电容元件的相量形式
I jCU
U
1
jC
或U
1
I j
1
I
jC
C
证：2I
sin(t
i )
d dt
[
电路基本定律相量形式
当 C一定时,电容的容抗与频率f 成反比。频率越高， 感抗越小，在直流电路中容抗为无限大，可视为开路。
2. 电压电流的相位关系
uUms iω nt
iImsiω nt (90 )
U mUm00 ImIm900
i uC
i 超前u
2
3. 电压电流的相量关系
ui u
i
UImm
p
（1）瞬时功率
p u U i( 1 c I2 o t)s
（2）平均功率
（有功功率）
0
PT 10 TpdtU IU R 2I2R
t
P=U I
t
四、电感元件的电压电流关系的相量式
设在电感元件的交流电路中
，电压、电流参考方向如图示。
+
1.电压电流的数值关系
ui L
瞬时值 设： iImsi nt
2. 电压电流的相位关系
iImsi nt ImIm00U mUm900 u+
u L I m co t U m s sit n 9 )( 0
u 超前i
eu 2 e滞后i
ui
u
i
–
e
i
e
L
2
3. 电压电流的相量关系
0
t
U Im mUIm m 09000U Im m900jXL
Um00 Im900
jXC
I
0
2
•
UjIXC
U
CHale Waihona Puke ItU• 相量图
3、功率
设：uU m sin t
iu
iIm si n t(90 ) 0
t
其波形图如右：
电路原理 第八章_相量法
复数 复数
—
孙惠英 shy@
上页
下页
返回
第8章
4、正弦量的相量表示法(续）
—
已知正弦量 220√ 2 cos ( ω t－35° ) 有效值相量 最大值相量 220/ －35° — 220√ 2 /－35°
已知 相量 10/45° and 正弦量的角频率ω 相应的正弦量 — 10 √ 2 cos( ωt + 45° )
0 ωt1
ωt2
ωt
φ
图8-5 用旋转矢量表示的正弦量
孙惠英 shy@
上页
下页
返回
第8章
4、正弦量的相量表示法 F = ⎪F⎪e j(ω t + ϕ )
ejθ = cosθ + jsinθ
设：有一复数
欧拉公式
F = ⎪F⎪ej(ωt + ϕ ) = ⎪F⎪cos(ωt + ϕ) + j⎪F⎪sin(ωt +ϕ) Re [F] = ⎪F⎪cos(ωt + ϕ ) Im [F] = ⎪F⎪sin(ωt + ϕ )
返回
第8章
三、旋转因子
/ϕ 旋转因子: e jϕ = 1 — A = ⎪A⎪ejα Aejϕ = ⎪A⎪ejαejϕ = ⎪A⎪ej(α+ϕ ) ejπ/2 = j1 e－jπ/2 = − j1
+j
Aejϕ
ϕ α
0
A
+1
e－jπ = − 1
孙惠英 shy@
上页
下页
返回
第8章
ϕ 12 = ϕ 1－ ϕ 2 —— u1 超前于 u2 的相角 ϕ 21 = ϕ 2－ ϕ 1 —— u2 超前于 u1 的相角
电路定律的相量形式
滞后于电源电压/3，问R、C应如何选择。
解1 Us RI jXC I
I Us ,
U s U C
R jXC
jCR 1
UC
jX C
R
Us jXC
CR tan 60
解2 画相量图计算。
tan 60 3 UR RI CR UC I /C
I+
U _
R+
jXC
U C -
3 U R
I
U C
60
I
jBLU
j 1U
L
1 U
jL
返回 上页 下页
波形图及相量图
uL pL
U L
i
O
2 t
电压超前 电流90°
I
i
功率 pL uLi ULmIm cos(t i )sin(t i ) ULI sin 2(t i )
瞬时功率以2交变，有正有负，一周期内刚
好互相抵消，表明电感只储能不耗能。
返回 上页 下页
i(t)
+ u-L(t)
I
+
•
U-L
时域形式 i(t) 2I cos( t i )
L
uL (t) L
相量形式
di(t)
dt
2
2L
LIc
I sin( t os( t
i
i
) π 2
)
I I i UL LI i π 2
jL
相量关系
UL jL I jX LI
相量模型
有效值关系 UL= L I 相位关系 u=i +90°
3. 电容元件VCR的相量形式
iC(t) + u(t) -
电路(第五版).-邱关源原著-电路教案--第8章相量法
电路(第五版).-邱关源原著-电路教案--第8章相量法第8章 相量法● 本章重点1、正弦量的两种表示形式；2、相量的概念；3、KVL 、KCL 及元件VCR 的相量形式。
● 本章难点1、 正确理解正弦量的两种表示形式的对应关系；2、 三种元件伏安关系的相量形式的正确理解。
● 教学方法本章是相量法的基础，对复数和正弦量两部分内容主要以自学为主，本章主要讲授相量法的概念、电路定律的相量形式以及元件V AR 的相量形式。
讲述中对重点内容不仅要讲把基本概念讲解透彻，而且要讲明正弦量的相量与正弦时间函数之间的对应关系；元件V AR 的相量形式与时域形式之间的对应关系，使学生加深对内容的理解并牢固掌握。
本章对元件的功率和能量这部分内容作了简单讲解，以便为下一章的学习打下基础。
本章共用4课时。
● 授课内容8.1复数1. 复数的三种表示bj a A += 直角坐标=θ∠r 极坐标 =θj re 指数形式θθθsin cos 22r b r a ab arctgb a r ==⇒=+=⇒直极极直θθsin cos jr r A += 三角表示形式欧拉公式：θθθsin cos j e j +=2. 复数的运算已知：11111θ∠=+=r jb a A ，22222θ∠=+=r jb a A求：212121,,A AA A A A ⋅±i()()212121b b j a a A A ±+±=±212121212121θθθθ+∠=+∠=⋅r r A A r r A A 8.2正弦量一、正弦量：随时间t 按照正弦规律变化的物理量，都称为正弦量，它们在某时刻的值称为该时刻的瞬时值，则正弦电压和电流分别用小写字母i 、u 表示。
周期量：时变电压和电流的波形周期性的重复出现。
周期T ：每一个瞬时值重复出现的最小时间间隔，单位：秒（S ）； 频率f ： 是每秒中周期量变化的周期数，单位：赫兹（Hz ）。
电路分析课件第八章相量法
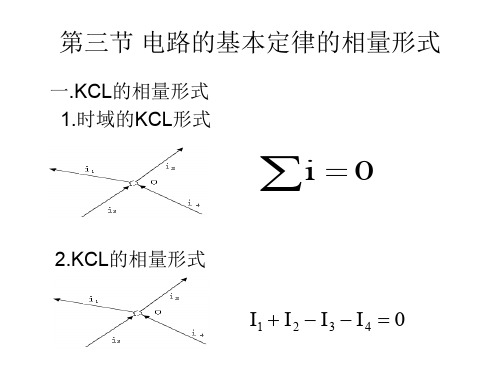
KVL：任意时刻，任一回路，U=0
三、受控源的相量形式
i1
I1
R
正弦电流
i 1 电路时：
R
1I1
本章小结：
所谓相量法，就是电压、电流用相量表示， RLC元件用阻抗、感抗、容抗表示，画出电路的相 量模型，利用KCL、KVL和欧姆定律的相量形式写 出未知电压、电流相量的代数方程加以求解，因此， 应用相量法应熟练掌握:
∴ i =46.2 2cos(314t–27º)A j I1
+1 I
相量图
I2
注意：
在分析正弦交流电路时字母的写法：
i — 瞬时值 I — 有效值 Im — 最大值 I — 有效值相量 Im— 最大值相量
三、不同频率的正弦量不能用相量法运算。
相量只含有正弦量的有效值(最大值)和初相 位的信息，不包含频率的信息，即：在运用相量 法分析正弦量时，默认为同频率。
将 I (或 U)定义为电流i (或电压u) 的相量，它含有 正弦量的振幅和相位的信息。
注意：
有一个正弦量便可以得到一个相量； 有一个相量也可以写出对应的正弦
量。两者是一一对应的关系，决不
是相等的关系。
u=220 2 cos(314t+45º)V
U=220 45ºV u U
I=50 –30ºA 一一对应 i =50 2 cos(ωt–30º)A i I
U 相量形式电路图
相量关系既反映了u、i 的有效 值关系又反映了相位的关系。
I U 相量图
2、电感
iL
u
若：i = 2 Icos(ωt+ψi )
则：u=L
di dt
=–
2 IωLsin(ωt+ψi )
电路分析相量法
量的相量乘以 jω ，即表示di/dt 的相量为
j I I( i 90o )
该相量的模为ωI ，辐角则超前原相量π/2 。
对 i 的高阶导数 dni/dtn ，其相量为 ( j )。n I
3)正弦量的积分
设 i 2I cos( t i )，则
idt Re[ 2Ie j t ] dt Re[ (
F1F2 | F1 | 1 | F2 | 2 | F1 || F2 | (1 2 )
可见复数的乘法运算使用指数形式或极坐标形式较为简便。
3)除法运算
a)代数形式
F1 F2
a1 a2
jb1 jb2
(a1 (a2
jb1 )(a2 jb2 )(a2
jb2 ) jb2 )
(a1a2
b1b2 ) j(a2b1 a22 b22
设 F1 a1 jb1 ， F2 a2 jb2 ，则
F1 F2 (a1 jb1 ) (a2 jb2 ) (a1 a2 ) j(b1 b2 )
平行四边形法则：
+j F1 +F2 F1
F2 o
+1
+j F1
F2 o
F1－F2 +1
2)乘法运算 a)代数形式
F1F2 (a1 jb1 )(a2 jb2 ) (a1a2 b1b2 ) j(a1b2 a2b1 )
di d Re[ 2Ie j t ] Re[ d ( 2Ie j t )] Re[ 2( j I)e j t ]
dt dt
dt
Re[ 2 Ie ] j( ti 90o ) 2 I cos( t i 90o )
上式表明：
复指数函数实部的导数等于复指数函数导数的实部；
84 电路定律的相量形式
§8.4 电路定律的相量形式
一. 基尔霍夫定律的相量形式 正弦电流电路中的各支路电流和支路电压都
是同频正弦量，所以可以用相量法将KCL和KVL转 换为相量形式。
•
i(t) 0 I 0
•
u(t) 0 U 0
注：但一般 I 0 ， U 0
二、电阻、电感和电容元件的VCR相量形式
1. 电阻
相量模型
IL IC IR
jLIL
1
jC
IC
U S
RIR
1
jC
IC
相量形式代数方程
相量模型：电压、电流用相量；元件用复数阻抗或导纳。
例8-6：正弦电流源的电流，其有效值IS=5A，角频率 ω=103rad/s， R=3Ω，L=1H，C=1μF。求电压uad和ubd。
ai
b
c
iS
+ uR - + uL - +
i(t)
+ uR(t) -
已知 i(t) 2I cos(t ) 则 uR (t) Ri(t) 2RI cos(t )
R
相量形式：
I I
U R RI I
相量关系
U R R I
+
U R
-
有效值关系：UR = RI
相位关系：u , i 同相
I
R
U
相量图
相量模型
2. 电感
时域
频域
i(t)
i(t) 2I cost
= 15 /0 °V
•
•
U L jL I = 5000 / 90°V
•
UC j
1
•
I
= 5000 / - 90 °V
C
•
一. 基尔霍夫定律的相量形式 正弦电流电路中的各支路电流和支路电压都
是同频正弦量，所以可以用相量法将KCL和KVL转 换为相量形式。
•
i(t) 0 I 0
•
u(t) 0 U 0
注：但一般 I 0 ， U 0
二、电阻、电感和电容元件的VCR相量形式
1. 电阻
相量模型
IL IC IR
jLIL
1
jC
IC
U S
RIR
1
jC
IC
相量形式代数方程
相量模型：电压、电流用相量；元件用复数阻抗或导纳。
例8-6：正弦电流源的电流，其有效值IS=5A，角频率 ω=103rad/s， R=3Ω，L=1H，C=1μF。求电压uad和ubd。
ai
b
c
iS
+ uR - + uL - +
i(t)
+ uR(t) -
已知 i(t) 2I cos(t ) 则 uR (t) Ri(t) 2RI cos(t )
R
相量形式：
I I
U R RI I
相量关系
U R R I
+
U R
-
有效值关系：UR = RI
相位关系：u , i 同相
I
R
U
相量图
相量模型
2. 电感
时域
频域
i(t)
i(t) 2I cost
= 15 /0 °V
•
•
U L jL I = 5000 / 90°V
•
UC j
1
•
I
= 5000 / - 90 °V
C
•
电路原理课件 第8章 相量法
三. 相位差 ：
两个同频率正弦量相位角之差。
i(t) 0
Im um
设 u(t)=Umcos(w t+ u)
2
i(t)=Imcos(w t+ i)
0
wt
则 相位差j : j = (w t+ u)- (w t+ i)
u- i
同频率正弦量的相位差等于它们的初相之差。 不同频率的两个正弦量之间的相位差不再是一个常数，而是 随时间变动。
j u与i正交; j u与i反相;
2
§8 - 3相量法的基础
1. 正弦量的相量表示
复函数 F F ej(wt)
没有物理意义
F cos(wt ) j F sin(wt Ψ )
若对F取实部：
Re[F] F cos(ωt Ψ ) 是一个正弦量，有物理意义。
对于任意一个正弦时间函数都可以找到唯一的与其对应的 复指数函数：
F e j
4、极坐标形式：
F F ej
=|F|
二 复数运算
(1)加减运算——代数形式
+j F2
若 F1=a1+jb1
F2=a2+jb2 O
则 F1±F2= (a1±a2) +j (b1±b2)
F= F1 +F1
F1 +1
+j
O - F2
F2 F1
F= F1 - F2 +1
(2) 乘除运算——指数形式或极坐标形式
⑶∫i2dt。
解： ⑴设 i i1 i2 2I cos(wt i ), 其相量为 I=I/Ψi
I I1 I2 10/600A+22/-1500A=（5+j8.66）A+（-19.05-j11）A
第20讲 电路定律的相量形式、阻抗与导纳
频域
&L = I L∠φi I
& UL
有效值关系 UL=ω L IL
UL = ωLIL π φu = φi + 2
& IL
& U
+ L
π φ + = ωL I L∠ i 2
相位关系 uL 超前 iL 90° °
& U
jω L
L
相量模型
相量图
& IL
感抗 U=ω L I XL= U/I =ω L= 2π f L， 单位 欧 π ， 单位: 感抗的物理意义： 感抗的物理意义： (1) 表示限制电流的能力； 表示限制电流的能力； (2) 感抗和频率成正比。 感抗和频率成正比。 XL
& U
φ = U∠ u
π φ + & I = ω C U∠ u 2
有效值关系 I=ω C U
+
I&
U&
1 jω C
& I
& U
相位关系 i 超前 90° 超前u °
-
相量模型
相量图
容抗 I=ω CU
U 1 = I ωC 容抗的物理意义： 容抗的物理意义：
1 XC = ωC
def
错误的写法 1 u = ωC i
θ = φu - φi
θ
R 阻抗三角形
X
具体分析一下 R-L-C 串联电路 Z=R+j(ω L-1/ω C)=|Z|∠
ω L > 1/ω C ，X>0， >0，u领先 ，电路呈感性； 领先i， ， ， 领先 电路呈感性； ω L<1/ω C ，X<0， <0，u落后 ，电路呈容性； 落后i， ， ， 落后 电路呈容性； ω L=1/ω C ，X=0， =0，u与i同相，电路呈电阻性。 同相， ， ， 与 同相 电路呈电阻性。
电路基本定律的相量形式
U
i
L
u
U IX L di jX L 则 uL X L L dt jL u 2 IL sin(t 90 )
jX C
i 2 I sin t
UI
I
u领先 i 90°
U I jX L
0
I2XL
设
i
C
u
iC
du dt
1 j C 1 j C
？
？
单一参数正弦交流电路的分析计算小结
电路 电路图 基本 参数 （正方向） 关系
i 复数 阻抗 设 电压、电流关系 瞬时值 有效值 相量图 相量式 功率 有功功率 无功功率
u 2U sin t
I
U IR
U
R
u
u iR
R
则
U IR
UI
0
i 2 I sin t
设
u、 i 同相
图 KVL的相量形式
回路的电压方程： 其KVL相量表达式为：
u1 u 2 u 3 u 4 0
U1 U 2 U 3 U 4 0
小 结
电路参数
R L
基本关系 复阻抗
u iR
R
I
U
U
电路参数
基本关系
复阻抗
电路参数
jX L j L
di uL dt
项目十九 电路基本定律的相量形式
电压、电流瞬时值的关系符合欧姆定律、基尔霍 夫定律 。
i
R
u
L
uR uL
u uR uL di iR L dt
电流、电压相量符合相量形式的欧姆定律、 基尔霍夫定律。
I
i
L
u
U IX L di jX L 则 uL X L L dt jL u 2 IL sin(t 90 )
jX C
i 2 I sin t
UI
I
u领先 i 90°
U I jX L
0
I2XL
设
i
C
u
iC
du dt
1 j C 1 j C
？
？
单一参数正弦交流电路的分析计算小结
电路 电路图 基本 参数 （正方向） 关系
i 复数 阻抗 设 电压、电流关系 瞬时值 有效值 相量图 相量式 功率 有功功率 无功功率
u 2U sin t
I
U IR
U
R
u
u iR
R
则
U IR
UI
0
i 2 I sin t
设
u、 i 同相
图 KVL的相量形式
回路的电压方程： 其KVL相量表达式为：
u1 u 2 u 3 u 4 0
U1 U 2 U 3 U 4 0
小 结
电路参数
R L
基本关系 复阻抗
u iR
R
I
U
U
电路参数
基本关系
复阻抗
电路参数
jX L j L
di uL dt
项目十九 电路基本定律的相量形式
电压、电流瞬时值的关系符合欧姆定律、基尔霍 夫定律 。
i
R
u
L
uR uL
u uR uL di iR L dt
电流、电压相量符合相量形式的欧姆定律、 基尔霍夫定律。
I
第8章 相量法
o
j ＝ 0， 同相
u i o o
u i wt
wt
u
j= /2：u 领先 i /2
i o
wt
同样可比较两个电压或两个电流的相位差。
例
解
计算下列两正弦量的相位差。
(1) i1 (t ) 10 cos( π t 3π 4) 100 i2 (t ) 10 cos( π t π 2) 100
j π 2
F
0
Re
jF
π j π π π 2 , e cos( ) jsin( ) j 2 2 2
F
π , e
j π
cos( π) jsin( π) 1
注意 +j, –j, -1 都可以看成旋转因子。
8.2
1. 正弦量
瞬时值表达式
180.2 j126.2 2.238 j6.329
182.5 j132.5 225.536
③旋转因子 复数
ej =cos +jsin =1∠
Im F• ej
F• ej
旋转因子 0
F Re
特殊旋转因子
jF
Im
π , 2 π π e cos jsin j 2 2
若交流电压有效值为 U=220V ，
注意
U=380V 其最大值为 Um311V Um537V
① 工程上说的正弦电压、电流一般指有效值，如 设备铭牌额定值、电网的电压等级等。但绝缘水平、 耐压值指的是最大值。因此，在考虑电器设备的耐 压水平时应按最大值考虑。
②测量中，交流测量仪表指示的电压、电流读 数一般为有效值。
o
j ＝ 0， 同相
u i o o
u i wt
wt
u
j= /2：u 领先 i /2
i o
wt
同样可比较两个电压或两个电流的相位差。
例
解
计算下列两正弦量的相位差。
(1) i1 (t ) 10 cos( π t 3π 4) 100 i2 (t ) 10 cos( π t π 2) 100
j π 2
F
0
Re
jF
π j π π π 2 , e cos( ) jsin( ) j 2 2 2
F
π , e
j π
cos( π) jsin( π) 1
注意 +j, –j, -1 都可以看成旋转因子。
8.2
1. 正弦量
瞬时值表达式
180.2 j126.2 2.238 j6.329
182.5 j132.5 225.536
③旋转因子 复数
ej =cos +jsin =1∠
Im F• ej
F• ej
旋转因子 0
F Re
特殊旋转因子
jF
Im
π , 2 π π e cos jsin j 2 2
若交流电压有效值为 U=220V ，
注意
U=380V 其最大值为 Um311V Um537V
① 工程上说的正弦电压、电流一般指有效值，如 设备铭牌额定值、电网的电压等级等。但绝缘水平、 耐压值指的是最大值。因此，在考虑电器设备的耐 压水平时应按最大值考虑。
②测量中，交流测量仪表指示的电压、电流读 数一般为有效值。
o
电路课件 电路08 相量法32页PPT
工程中以频率区分，如音频、高频、甚高频电路。
φi是在t=0时刻相位，称初相位(角)，简称初相：
(ωt+φi)|t=0 =φi 单位用弧度或度，主值范围内取值，|φi|≤180°
初相与计时零点有关。任一正弦量初相允许任意指定， 但一个电路许多相关正弦量，只能相对共同计时零点 确定各自相位。
正弦量三要素是正弦量间进行比较和区分的依据。
图8-4正弦电流i，在参考方向下，数学表达式定义：
i=Imcos(ωt+φi)
(8-1)
3个常数Im、ω和φi称正弦量三要素。
Im称正弦量振幅，是正弦量在整个振荡过程中达到最
大值，即cos(ωt+φi)=1时，有 imax=Im
也是正弦量极大值。
cos(ωt+φi)=-1时，
有最小值(也是极小值)：
复数相加和相减运算可按平行四边形法在复平面 上用向量相加和相减求得，图8-2。
19.04.2020
第八章 相量法
8-1 复 数
4
两个复数相乘
复数相乘用指数形式方便： F1F2 =|F1|ejθ1|F2|ejθ2 =|F1||F2|ej(θ1+θ2)
所以： |F1F2|=|F1||F2|
arg(F1F2)＝arg(F1)+arg(F2) 两个复数相乘的代数形式：
F 13 j4 5 5.1 3 0 .5 1.1 8 0 8 .5 1.9 7 1 F 2 1 1 0 31 5 1 0 35
19.04.2020
第八章 相量法
8-1 复 数
9
8-2 正弦量
电路中按正弦规律变化的电压或电流，统称正弦量。
正弦量数学描述，可用sine函数，也可用cose函数。 本书用cose函数。
第8章 相量法
12.47 j 0.569 12.48 2.61
(17 j 9) (4 j 6) 220 35 ? 20 2 ： j5 例
19.24 27.9 7.21156.3 原式 180.2 j126.2 20.6214.04
180.2 j126.2 6.72870.16
我国国家标准规定的电力网额定电压有 10KV、35 kV、110 kV、220 kV、330 kV、500 kV，目前大力研究750KV,1000KV，已经有线路 试运行。 市区一般输电电压为 10 kV 左右（江苏在 试点 20KV）电压等级，通常需要设臵降压变电 所， 经配电变压器将电压降为 380/ 220 V， 再引出若干条供电线到各用电点的配电箱上， 配电箱将电能分配给各用电设备。
第8章
相量法
本章重点
8.1 8.2 8.3 8.4 复数 正弦量 相量法的基础
电路定律的相量形式
目的：交流电路的分析基础!
日常生活，交流电应用广泛!
回顾：直流电路中学习了哪些定理与方法？
i1
20
5
i2
u 1
140V
6
u 2
i3
u3
90V
三个基本工具：欧姆定理，(a) KCL,
几种不同值时的旋转因子：
Im
jI
0
I cos j sin j 2 2
Re
jI
j 2 , e cos( ) j sin( )j 2 2 2
I
, e j cos( ) j sin( ) 1
交流情况下电容如何处理？
i +
(17 j 9) (4 j 6) 220 35 ? 20 2 ： j5 例
19.24 27.9 7.21156.3 原式 180.2 j126.2 20.6214.04
180.2 j126.2 6.72870.16
我国国家标准规定的电力网额定电压有 10KV、35 kV、110 kV、220 kV、330 kV、500 kV，目前大力研究750KV,1000KV，已经有线路 试运行。 市区一般输电电压为 10 kV 左右（江苏在 试点 20KV）电压等级，通常需要设臵降压变电 所， 经配电变压器将电压降为 380/ 220 V， 再引出若干条供电线到各用电点的配电箱上， 配电箱将电能分配给各用电设备。
第8章
相量法
本章重点
8.1 8.2 8.3 8.4 复数 正弦量 相量法的基础
电路定律的相量形式
目的：交流电路的分析基础!
日常生活，交流电应用广泛!
回顾：直流电路中学习了哪些定理与方法？
i1
20
5
i2
u 1
140V
6
u 2
i3
u3
90V
三个基本工具：欧姆定理，(a) KCL,
几种不同值时的旋转因子：
Im
jI
0
I cos j sin j 2 2
Re
jI
j 2 , e cos( ) j sin( )j 2 2 2
I
, e j cos( ) j sin( ) 1
交流情况下电容如何处理？
i +
7向量法-电路定律的相量形式
7电路定律的相量形式1. 电阻元件 VCR 的相量形式设图8.13（a）中流过电阻的电流为则电阻电压为：其相量形式：图8.13（a）以上式子说明：（1）电阻的电压相量和电流相量满足复数形式的欧姆定律：，图8.13（b）为电阻的相量模型图。
图 8.13（ b ）（2）电阻电压和电流的有效值也满足欧姆定律：U R = RI（3）电阻的电压和电流同相位，即：ψu = ψi电阻电压和电流的波形图及相量图如图8.14（a）和（b）所示。
图 8.14（a）（b）电阻的瞬时功率为：即瞬时功率以2ω交变，且始终大于零，如图8.14（a）所示，表明电阻始终吸收功率。
2. 电感元件 VCR 的相量形式设图 8.15（a）中流过电感的电流为则对应的相量形式分别为：图 8.15 （ a ）（ b ）以上式子说明：（1）电感的电压相量和电流相量满足关系：，其中X L=ωL=2πfL ，称为感抗，单位为Ω(欧姆)，图8.16（b）为电感的相量模型图。
（2）电感电压和电流的有效值满足关系：，表示电感的电压有效值等于电流有效值与感抗的乘积。
（3）电感电压超前电流相位，即：电感电压和电流的波形图及相量图如图8.16（a）和（b）所示。
注意:（1）感抗表示限制电流的能力；（2）感抗和频率成正比如图8.16（c）所示，当；电感电压和电流的波形图及相量图如图8.16（a）和（b）所示。
图 8.16 （a）（b）（c）电感的瞬时功率为：即电感的瞬时功率以 2ω交变，有正有负，如图8.16（a）所示。
电感在一个周期内吸收的平均功率为零。
3. 电容元件 VCR 的相量形式图 8.17 （ a ）（ b ）设图8.17（a）中电容的电压为：则对应的相量形式分别为：以上式子说明：（1）电容的电压相量和电流相量满足关系：其中X C =1/ωC ，称为容抗，单位为Ω(欧姆)，图8.17（b）为电容的相量模型图。
（2）电容电压和电流的有效值满足关系：，表示电容的电压有效值等于电流有效值与容抗的乘积。
电路基本定律的相量形式
uC －
RI 100 0.5 245 50 245 U R
jX I U C C j100 0.5 245 50 2 45
i sin( 100t 45) A u R 100 sin( 100t 45) V u C 100 sin( 100t 45) V
i
2
解：
1000V U s 1 1 XC 100 6 C 100 100 10
+
us －
+
R C uR －
+
U U U s R C
RI U R U U RI jX I U s R C C ( R jX C ) I jX I U C C U 1000 1000 s I 0.5 245A R jX C 100 j100 100 2 45
2、电感元件
di 电感元件伏安关系： u L dt 根据相量运算的规则1、规则3和规则4 ，有：
jLI jX I U L
U 、 I I 代入，得： 将U u i U u j LI i LI ( i 90)
U LI X L I
u i 90
i
L
+ u － (a) 电感元件
U
θ u θ i
I
感抗：XL=ωL，与频率成正比。
(b) 相量图
du 电感元件伏安关系： i C dt 根据相量运算的规则1、规则3和规则4 ，有：
3、电容元件
jCU I
U 、 I I 代入上式，得： 将U u i I i j CU u CU ( u 90)
电工与电子技术电路定理的相量形式
i(t) =10 2 cos(5t + 36.90 )A
ɺ U _ ɺ I
+
ɺ I
1
-j10Ω 15Ω j20Ω
ɺ I2
返 回
ɺ I3
上 页 下 页
jω L 相量关系： 相量关系：
ɺ ɺ ɺ UL = jωL IL = jXL IL
Ψu=Ψi +90°
返 回 上 页 下 页
相量模型
有效值关系： UL=ω L IL 相位关系： 相位关系：
感抗和感纳
XL=ωL=2πfL，称为感抗，单位为 (欧姆) 称为感抗，单位为Ω 欧姆) BL=1/ω L =1/2πfL， 称为感纳，单位为 S 称为感纳 感纳，
ɺ IC
Ψu
ɺ UC
ωt
pC = uCiC = 2UC IC cos(ω t +Ψu ) sin( ω t +Ψu ) = UC IC sin 2(ω t +Ψu )
瞬时功率以2ω交变，有正有负， 瞬时功率以 交变，有正有负，一周期 交变 内刚好互相抵消，表明电容只储能不耗能。 内刚好互相抵消，表明电容只储能不耗能。 有功功率P 有功功率 P=0
1 ωC
ɺ IC
+ ɺ UC -
−j
相量模型
ɺ ɺ 相量关系： 相量关系： ɺC = 1 IC = −j 1 IC U jωC ωC 1 IC 有效值关系： UC = 有效值关系： ωC 相位关系： 相位关系： Ψu=Ψi -90°
返 回 上 页 下 页
容抗与容纳
XC=1/ω C， 称为容抗，单位为 Ω(欧姆) 称为容抗， (欧姆) Β C = ω C， 称为容纳，单位为 S 称为容纳，
返 回 上 页 下 页