疑难释义4.2如何评价分层总和法
层次分析法步骤解析—根法、和法、幂法

层次分析法(AHP)AHP(Analytic Hierarchy Process)方法,是由20世纪70年代由美国著名运筹学学家T.L.Satty提出的。
它是指将决策问题的有关元素分解成目标、准则、方案等层次,在此基础上进行定性分析和定量分析的一种决策方法。
这一方法的特点,是在对复杂决策问题的本质、影响因素及其内在关系等进行深入分析之后,构建一个层次结构模型,然后利用较少的定量信息,把决策的思维过程数学化,从而为求解多准则或无结构特性的复杂决策问题提供了一种简便的决策方法。
AHP十分适用于具有定性的,或定性定量兼有的决策分析。
这是一种十分有效的系统分析和科学决策方法,现在已广泛地应用在企业信用评级、经济管理规划、能源开发利用与资源分析、城市产业规划、企业管理、人才预测、科研管理、交通运输、水资源分析利用等方面。
一、递阶层次结构的建立一般来说,可以将层次分为三种类型:(1)最高层:只包含一个元素,表示决策分析的总目标,因此也称为总目标层。
(2)中间层:包含若干层元素,表示实现总目标所涉及的各子目标,包含各种准则、约束、策略等,因此也称为目标层。
(3)最低层:表示实现各决策目标的可行方案、措施等,也称为方案层。
典型的递阶层次结构如下:总目标m一个好的递阶层次结构对解决问题极为重要,因此在建立递阶层次结构时,应注意到:(1)从上到下顺序地存在支配关系,用直线段(作用线)表示上一层次因素与下一层次因素之间的关系,同一层次及不相邻元素之间不存在支配关系。
(2)整个结构不受层次限制。
(3)最高层只有一个因素,每个因素所支配元素一般不超过9个,元素过多可进一步分层。
(4)对某些具有子层次结构可引入虚元素,使之成为典型递阶层次结构。
二、构造比较判断矩阵设有m个目标(方案或元素),根据某一准则,将这m个目标两两进行比较,把第i个目标(i=1,2,…,m)对第j个目标的相对重要性记为a ij,(j=1,2,…,m),这样构造的m阶矩阵用于求解各个目标关于某准则的优先权重,成为权重解析判断矩阵,简称判断矩阵,记作A=(a ij)m×m。
教学质量评估中应用的层次分析法
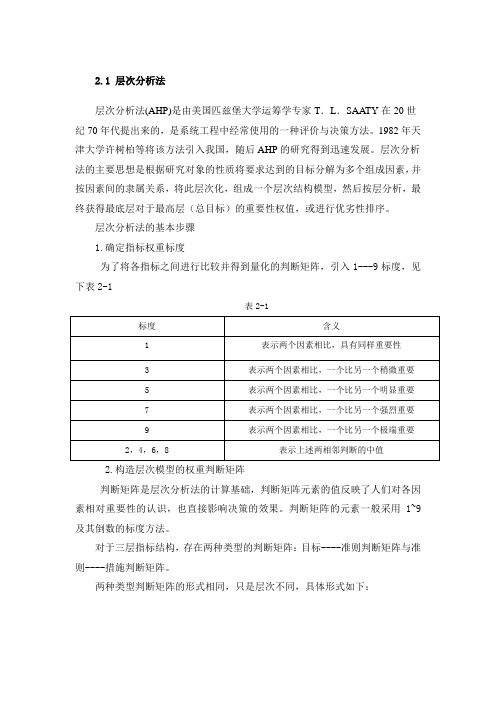
2.1 层次分析法层次分析法(AHP)是由美国匹兹堡大学运筹学专家T.L.SAATY在20世纪70年代提出来的,是系统工程中经常使用的一种评价与决策方法。
1982年天津大学许树柏等将该方法引入我国,随后AHP的研究得到迅速发展。
层次分析法的主要思想是根据研究对象的性质将要求达到的目标分解为多个组成因素,并按因素间的隶属关系,将此层次化,组成一个层次结构模型,然后按层分析,最终获得最底层对于最高层(总目标)的重要性权值,或进行优劣性排序。
层次分析法的基本步骤1.确定指标权重标度为了将各指标之间进行比较并得到量化的判断矩阵,引入1---9标度,见下表2-1表2-1标度含义1 表示两个因素相比,具有同样重要性3 表示两个因素相比,一个比另一个稍微重要5 表示两个因素相比,一个比另一个明显重要7 表示两个因素相比,一个比另一个强烈重要9 表示两个因素相比,一个比另一个极端重要2,4,6,8 表示上述两相邻判断的中值2.构造层次模型的权重判断矩阵判断矩阵是层次分析法的计算基础,判断矩阵元素的值反映了人们对各因素相对重要性的认识,也直接影响决策的效果。
判断矩阵的元素一般采用1~9及其倒数的标度方法。
对于三层指标结构,存在两种类型的判断矩阵:目标----准则判断矩阵与准则----措施判断矩阵。
两种类型判断矩阵的形式相同,只是层次不同,具体形式如下:⎪⎪⎪⎪⎪⎭⎫ ⎝⎛n n n n n n a a a a a a a a a ,2,1,.22,21,2,1.....,211,1................ 式中,j i a ,表示指标i a 相对于指标j a 的相对权重。
3.指标权重计算与一致性检验层次分析法的指标权重计算问题,可归结为判断矩阵的特征向量和最大特征值的计算,常用的方法是方根法,计算步骤如下:步骤一:计算判断矩阵R 的每一行元素的乘积,∏===nj n i ij i B M 1,.....2,1,步骤二:计算i M 的n 次方根, n i M w ni i,......2,1,)(1==步骤三:对i w 进行归一化处理,即n i w w w n i ii i ......2,1,1=∑==则所求权向量Tw w w w ]...,[4,2,1=。
层次分析法详解

构建风险层次结构通过选取的指标可以看出这是一个多目标的且问题涉及到许多因素,各种因素的作用相互,情况复杂。
依据层次分析法处理这类复杂的问题就需要对所涉及的因素指标进行分析:哪些是需相互比较的;哪些是需相互影响的。
把那些需相互比较的因素归成同一类,构造出一个各因素类之间相互联结的层次结构模型。
各因素类的层次级别由其与目标的关系而定:第一层是目标层,也就是国家风险的评价排序第二层是准则层,这一层中是国家风险排序所涉及的国家风险类型,即政治风险、经济风险、社会风险。
第三层是子准则层,这一层是评价衡量准则层中各要素的影响因素及评价指标,即政权凝聚力、腐败状况、相关法律政策、国际关系、官僚主义、经济政策、汇率稳定性、金融环境、内部冲突、外部冲突、民族差异等。
第四层也就是我们要选择的方案即所要选择的并购方案国家。
图5.1风险层次结构模型Fig.5.1 The hierarchical structure model of country risk为了方便计算以及模型的理解,层次结构中各层次均用字母代替,目标层为iA ,准则层为B i ,子准则层为C i ,方案层为D i 。
5.2.2 重要性程度描述为了将上述复杂的多因素综合比较问题转化为简单的两因素相对比较问题。
首先找出所有两两比较的结果,并且把它们定量化;然后再运用适当的数学方法从所有两两相对比较的结果之中求出多因素综合比较的结果。
进行定性的成对比较时,我们将比较结果分为5种等级:相同、稍强、强、明显强、绝对强并将我们所做出的比较结果应用1~9个数字尺度来进行定量化,比较具体含义及相应数字对应如下表:表5.2 AHP重要程度描述表Table 5.2 Described table of AHP important degree 定性比较结果数字定量因素1相较于因素2具有相同的重要性 1因素1与因素2相比,前者重要性稍强 3因素1与因素2相比,前者重要性强 5因素1与因素2相比,前者重要性明显强7因素1与因素2相比,前者重要性绝对强9因素1与因素2相比,相对重要性处于上述等级之间2、4、6、8(续表5.2)定性比较结果数字定量因素1与因素2相比,后者的重要性要稍强、强、明显强、绝对强于前者1/3、1/5、1/7、1/9例如:在准则层中有三个因素政治风险B1、经济风险B2以及社会风险B3,假设如果政治风险B1相较于经济风险B2在风险中的重要性稍强那么就是B1:B2=3:1也就是3。
分层总和法

基础最终沉降量计算 (1)定义地基土层在建筑物荷载作用下,不断产生压缩,直至压缩稳定后地基表面的沉降量称为地基的最终沉降量。
原因其外因主要是建筑物荷载在地基中产生附加应力;内因是土的碎散性,孔隙发生压缩变形,引起地基沉降。
目的判断地基变形值是否超出允许的范围,以便在建筑物设计时,采取相应的工程措施,保证建筑物的正常使用。
方法有关地基沉降量的方法很多,工业与民用建筑中常见的有分层总和法和《规范》法,还有弹性理论法和数值计算法。
基础最终沉降量计算 (2)分层总和法简介工程上计算地基的沉降时,在地基可能产生压缩的土层深度内,按土的特性和应力状态的变化将地基分为若干(n)层,假定每一分层土质均匀且应力沿厚度均匀分布,然后对每一分层分别计算其压缩量s i,最后将各分层的压缩量总和起来,即得地基表面的最终沉降量s,这种方法称为分层总和法。
分层总和法的基本思路是:将压缩层范围内地基分层,计算每一分层的压缩量,然后累加得总沉降量。
分层总和法有两种基本方法:e~p曲线法和e~lgp 曲线法。
基础最终沉降量计算 (3)计算原理一般取基底中心点下地基附加应力来计算各分层土的竖向压缩量,认为基础的平均沉降量s 为各分层上竖向压缩量D s i 之和,即几点假设地基土为一均匀的、等向的半无限空间弹性体;计算部位为基础中心点O 下土柱所受附加应力s z 进行计算;地基土的变形条件为侧限条件;计算深度因工程上附加应力扩散随深度而减少,计算到某一深度(受压层)即可。
分层总和法是目前最常用的地基沉降计算方法1nii s s ==D ∑计算步骤1、绘制基础中心下地基的自重应力、附加应力分布曲线,求2、确定沉降计算深度(压缩下限深度)如压缩下限下部还有更软的土层,则计算至该土层底面为止;如压缩层内部有基岩,则受压层深度计算至新鲜岩土为为止;3、分层厚度的确定,天然土层交界面及地下水面为特定的分界面。
c s zs 0.20.1z c z c s s s s ≤⎧⎨≤⎩一般土软土0.4(4)i h b or m ≤基础最终沉降量计算 (4)基础最终沉降量计算 (5)4、计算分层沉降量s i5、最终变形量1211i i i i i iie e s h h e ε-D ==+1112ci ci i ip e s s -+=⇒21212i i i izi zi i p p p e p s s -=+D ⎫⎪⇒+⎬D =⎪⎭查e ~p 曲线1nii s s ==D ∑计算中的几个问题1、有相邻荷载作用时,应将相临荷载引起的附加应力叠加到基础自身引起的附加应力中去;2、有相邻荷载时,我国《建筑地基基础设计规范》规定采用下式确定沉降计算深度:式中,—由计算深度向上取厚度为的土层沉降计算值;s —计算深度范围内各个分层土的沉降计算值的总和。
分层总和法与规范法的区别

hi
∑ S = Si ≈ 53.4mm
Si
=
e1 − e2 1+ e1
⋅ hi
1、规范法计算地基变形的公式
∑ ( ) S = ψs S′ = ψs
n i =1
p0 Esi
zi ai − zi−1 ai−1
2
2、经验修正系数 ψ s
ψs
=
S∞ S′
S∞ —根据地基沉降量观测资料得到的最终沉降量 S ′ —按规范方法计算的地基压缩量
⋅ hi
Si
=
σ zi E si
hi
Si
=
ai 1 +e1i
σ zi hi
(7) 计算地基沉降量 S=∑Si
【例题 3.2】某厂房, 柱基正方形, 边长L=b=4m。埋深d=1.0m。荷重 P=1440KN。地基粉质粘土, γ= 16.0KN/m3, e =0.97。 a1=0.30MPa-1。地下
2.0616
5.5
35.23
35.23
7.8 1.0 z2 = 3.9 0.455 3.5490 1.4874 6.5 21.51 56.77
b
Z1
计算 ψ s
计算沉降量
∑ ( ) Si =
n i =1
p0 Esi
zi ai −zi−1 ai−1
列表
Zn
∑∑ Es =
Ai = A1 + A2
Ai Esi
【例题 3.4】
某厂房为框架结构, 柱基底面为正方形, 边长L=b=4m。基础 埋置深度d=1.0m。上部结构传至基础顶面荷重P=1440KN。 地基为粉质粘土, 土的天然重度γ= 16.0KN/m3, 地下水位深 3.4m, 地下水位以上土的Es1=5.5MPa,地下水位以下土的 Es2=6.5MPa。地基承载力标准值fK=94kPa, 计算柱基中点 的沉降量。
层次分析及综合评价方法

1/3(a12)
1/5(a13)
1(a22)
1/3(a23)
3(a23)
1(a33)
4.4 计算权重系数(续1)
(2)按公式 Wi m a i1ai 2 aim 计算初始权重系数 Wi 得
W1 3 1 3 5 2.4662同理得W2 1.0000,W3 0.4055
指标 权重 甲学生 乙学生
指标 权重 甲学生 乙学生
指标 权重 甲学生 乙学生
德育总分 0.3 90 70
德育总分 0.1 90 70
德育总分 0.3 90 70
智育总分 0.6 70 80
智育总分 0.8 70 80
智育总分 0.6 70 80
体育总分 0.1 80 70
体育总分 0.1 80 70
1)专家个人判断 即分别征求专家个人意见,在专家各自单独给 评价指标的相对重要性打分的基础上,进行统计处理,以确定 各指标的权重。 优点:专家打分时不受外界影响,没有心理压力,可以最 大限度地发挥个人创造能力。
缺点:仅凭个人判断,易受专家知识深度与广度的影响, 难免带有片面性。
2)专家会议 即召开所有被挑选专家,以集体讨论的方式进行 评分,然后再以统计手段确定各指标的权重。 优点:可以交换意见,相互启发,弥补个人之不足。 缺点:主要表现在易受心理因素的影响,如屈从于权威和 大多数人的意见,受劝说性意见的影响,不愿公开修正已发表 的意见等等。
选 择 综 合 评 价 指 标
3.2 系统分析法及文献资料 分析优选法筛选指标
缺乏 有关 历史 资料, 或指 标难 以数 量化 时
系统分析法(systematic analysis method): 是一种常用的凭经验挑选指标的方法, 首先将所有备选指标按系统(或属性、 类别)划分,再通过座谈或填调查表的 方法获得对各指标的专家评分,确定主 次,再从各系统内挑选主要的指标作为 评价指标。 文献资料分析优选法:即全面查阅有关 评价指标设置的文献资料,分析各指标 的优缺点并加以取舍。
分层总和法
2.0
− 1.2 ×17.6
=
52.9kPa
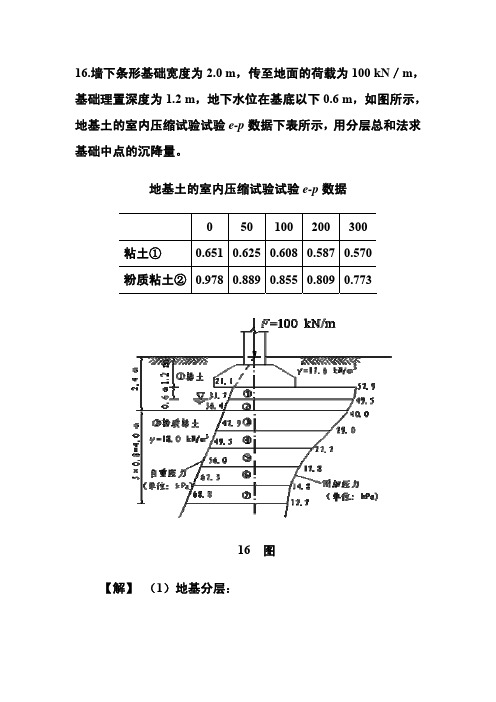
查条形基础竖向应力系数表,可得应力系数 au 及计算 各分层点的竖向附加应力,并计算各分层上下界面处附加应力的 平均值,见图及下表。
(4)将各分层自重应力平均值和附加应力平均值之和作为该 分层受压后的总应力 p2i。
(5)确定压缩层深度:
一般可按 z/c=0.2 来确定压缩层深度,在 z=4.4 m 处, z/c =14.8/62.5=0.237>0.2,在 z=5.2 m 处, z/c=12.7/69.0=0.184< 0.2,所以压缩层深度可取为基底以下 5.2 m。
4 2.8 49.5 22.2 ④ 0.8 46.2 25.6 71.8 08 ⑤ 0.8 52.8 20.0 72.8 0.887 0.874 5.5 6 4.4 62.6 14.8 ⑥ 0.8 59.3 16.3 75.6 0.883 0.872 4.7 7 5.2 68.8 12.7 ⑦ 0.8 65.7 13.8 79.4 0.878 0.869 3.8
(6)计算各分层的压缩量
如第③层
Δs3
=
e1i − e2i 1+ e1i
Hi
=
0.901− 0.872 1+ 0.901
× 800mm
= 11.8mm
各分层的压缩量列于下表中。
(7)计算基础平均最终沉降量
7
s = ∑ si = 7.7 + 6.6 +11.8 + 9.3 + 5.5 + 4.7 + 3.8 = 49.4mm i =1 表 分层总和法计算地基最终沉降
分 层 点
深 自重 附加 度 应力 应力 层 zi c c 号 m kPa kPa
分层总和法计算步骤

分层总和法计算步骤
分层总和法是一种层次分析法(AHP)的求解过程。
它的计算步骤如下:
1、建立层次结构。
将问题分解成不同的层次结构,从大范围到小范围逐级划分。
例如,可以将问题划分为目标层、准则层和方案层。
2、设定判断矩阵。
在每个层次下,建立判断矩阵。
判断矩阵由两两比较各元素的重要性所得,元素之间的重要性用1-9的数字表示。
根据判断矩阵的特性,它是一个对称矩阵,对角线元素为1,上下对称元素相乘之积为1。
3、归一化判断矩阵。
对每个判断矩阵的列向量进行归一化处理,使得每列向量的和等于1。
4、计算权重向量。
根据归一化判断矩阵的每列向量求平均值,得到该层次下各元素的权重。
5、一致性检验。
对每个判断矩阵进行一致性检验,通过计算一致性比例(CR)来判断判断矩阵的一致性。
CR的计算公式为CR=(最大特征值-n)/(n-1)*RI,其中n为判断矩阵的阶数,RI为随机一致性指标,根据判断矩阵的阶数查表得到。
若CR小于0.1,则认为判断矩阵通过一致性检验。
6、重构目标层次到方案层次。
将目标层次的权重向量与准则层次的权重向量相乘,得到重构的权重向量。
同理,将准则层次的权重向量与方案层次的权重向量相乘,得到最终的权重向量。
7、计算综合得分。
将方案层次的得分乘以其对应的权重值,再对所有方案的得分进行相加,得到每个方案的综合得分。
根据得分的大小排序,确定最优方案。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
土力学
S o i l M e c h a n i c s
第四章Chapter 4 疑难释义4.2
如何评价分层总和法
当前建筑地基基础设计规范提出的计算最终沉降量的方法是以分层总和法为基础的。
分层总和法采用了如下假定:基底压力为线性分布;附加应力用弹性理论计算;只发生单向沉降,即侧限应力状态;只计算固结沉降,不计瞬时沉降和次固结沉降。
该方法具有如下优点: 可计算成层地基;可计算不同形状的基础,包括条性、矩形和圆形等;可计算不同基底压力分布,包括均匀、三角形和梯形分布;参数的试验测定方法简单。
1 / 1。
