Excel在数模解题中的应用(董)
Excel在数学建模中的应用

环境系统分析
Excel规划求解 (四)Excel规划求解
的规划求解, 用Excel的规划求解,解农药管理问题。 的规划求解 解农药管理问题。
LP: S.t. Max Z=140X1+ 100X2 0.9X1+ 0.5X2 ≤632.5 X1+ X2 ≤1000 X1,X2≥0
环境系统分析
Excel的规划求解操作过程 的规划求解操作过程
ISCST3模型是由美国环保局开发并推广使用的一个城 ISCST3模型是由美国环保局开发并推广使用的一个城 市尺度的大气扩散模型, 市尺度的大气扩散模型,该模型是基于统计理论的正态 烟流模式,使用的公式为目前广范应用的稳态密封型高 烟流模式, 斯扩散方程。 斯扩散方程。
环境系统分析
气象参数预处理程序界面
环境系统分析
(一)多元回归模型的建立
环境系统分析
(一)多元回归模型的建立
环境系统分析
(二)模型参数估值
已 知 河 流 平 均 流 速 为 4.0km/h , 饱 和 溶 解 氧 (DO) 为 10.0mg/L,河流起点的 ,河流起点的BOD(L0)浓度为 浓度为20mg/L,沿程 浓度为 , 的溶解氧(DO)的测定数据在文件 的测定数据在文件BOD-DO.xls 给出。 给出。 的溶解氧 的测定数据在文件 试根据河流溶解氧的变化规律,确定耗氧速度常数K 试根据河流溶解氧的变化规律,确定耗氧速度常数 d 和复氧速度常数Ka。已知数学模型为: 已知数学模型为: 和复氧速度常数
工具”菜单中,单击“规划求解” 1 在“工具”菜单中,单击“规划求解”命令 目标单元格”编辑框中, 2 在“ 目标单元格 ”编辑框中 ,键入单元格引用或目标单元格 的名称。目标单元格必须包含公式。 的名称。目标单元格必须包含公式。 最大值” 、、“ 最小值” 3 目标单元格中数值可选 “ 最大值 ” 、、 “ 最小值 ” 或指定 “目标值” 。 目标值” 可变单元格”编辑框中, 4 在“ 可变单元格 ”编辑框中 ,键入每个可变单元格的名称或 引用,用逗号分隔不相邻的引用。 引用 ,用逗号分隔不相邻的引用。可变单元格必须直接或间 接与目标单元格相联系。 接与目标单元格相联系。
Excel在数学建模中的应用(例题+练习)
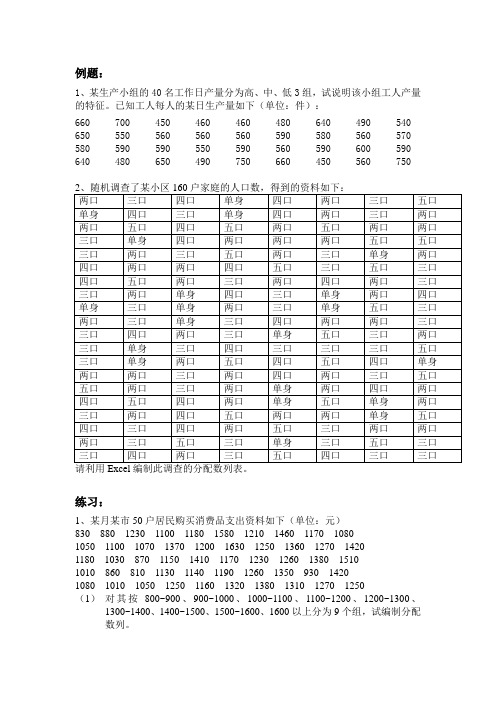
例题:
1、某生产小组的40名工作日产量分为高、中、低3组,试说明该小组工人产量的特征。
已知工人每人的某日生产量如下(单位:件):
660 700 450 460 460 480 640 490 540 650 550 560 560 560 590 580 560 570 580 590 590 550 590 560 590 600 590 640 480 650 490 750 660 450 560 750
练习:
1、某月某市50户居民购买消费品支出资料如下(单位:元)83088012301100118015801210146011701080 1050110010701370120016301250136012701420 118010308701150141011701230126013801510 1010860810113011401190126013509301420 1080101010501250116013201380131012701250
(1)对其按800~900、900~1000、1000~1100、1100~1200、1200~1300、1300~1400、1400~1500、1500~1600、1600以上分为9个组,试编制分配数列。
(2)根据编制的分配数列绘制折线图,直方图。
2、某银行为了提高客户满意度,在客户办完业务后,柜员会让客户在他的“客户满意度调查终端”上按一下,客户可以在“很满意”、“满意”、“比较满意”、“不满意”、“很不满意”几个按钮中选择一个,对这个柜员的服务进行即时评价。
Excel在数学建模中的应用实例

Excel在数学建模中的应用实例一、Excel 基础1、自动填充公式函数等例1.1:自动填充编号:病例数据的统一编号例1.2:自动填充实现复制例1.3:自动填充生成序列:等差、等比例1.4:利用函数计算2e-ln3.例1.5:利用函数求逆矩阵及矩阵转置、数乘矩阵、矩阵和、积、行列式等运算如已知1101122222213153A⎡⎤⎢⎥⎢⎥=⎢⎥-⎢⎥-⎣⎦,求A’,A-1解:A’:选择性粘贴,或用transpose()函数(可在名称框中输入范围以选中结果区域,然后填入公式=transpose(原矩阵区域),再按Ctrl+Shift+Enter即可)A-1:Excel中输入矩阵,在结果矩阵第一行一列处输入=MINVERSE(原矩阵区域),结果只显示一个数字,用鼠标选中结果区域,先F2,后Ctrl+Shift+ Enter.A+B:用自动填充,或选中结果区域,在第一格输入公式后Ctrl+Entern*A:用自动填充+绝对引用,也可同上A/n:用自动填充+绝对引用,也可同上A*B:选中结果区域,用MMult函数后Ctrl+Shift+ Enter求矩阵行列式的值:用MDETERM函数用矩阵运算解方程组:未知数X等于系数矩阵的逆矩阵和Y向量的乘积.例1.6:用公式计算11212312341...23353573579π=+++++计算π的近似值,使误差小于10-14解:令n=1; m=3; t=1; p=1,然后n=n+1; m=m+2; t=t*n/m; p=p+t; pi=p*2 10-14即计算出的前后两项相差小于10-14例1.7:利用公式及函数计算:当x=3,2,1,0,-1,-2,-3时分段函数sin,0cos,0xx x xye x x>⎧=⎨≤⎩的值。
解:先输入列x,后用if和三角函数解决。
例1.8:求连续复利问题假设银行活期存款年利率为r(如r=3.25%),若某储户存20000元活期存款,那么一年后,他可以得到利息20000r,本息合计20000(1+r)元,因活期可以随便什么时候支取,如果满半年就结算一次,此时的本息合计为20000(1+r/2),把本息取出后立即再存入的话可得复利,即半年后再次结算,则全年的本息合计为20000(1+r/2)2,因为(1+r/2)2=1+r+r 2/4>1+r ,如此可发现每半年结算一次获利比一年结算一次多,某储户就想是不是每季度、每月、每半月。
利用Excel进行数据建模实现与

利用Excel进行数据建模实现与让我来为您撰写一篇关于利用Excel进行数据建模实现与分析的文章。
Excel是一款功能强大的电子表格软件,广泛应用于数据处理、分析和建模等领域。
通过Excel,我们可以对大量数据进行整理、计算和可视化,并通过建模分析来揭示数据背后的规律和趋势。
本文将探讨如何利用Excel进行数据建模和分析,为读者提供一些实用的技巧和方法。
I. 数据输入与整理(字数限制:200字)在进行数据建模之前,首先需要将数据导入Excel,并进行整理和清洗。
通过Excel的数据导入功能,我们可以将外部数据源(例如数据库、文本文件等)导入到工作表中,然后使用Excel的数据整理功能(如筛选、排序、条件格式等)对数据进行清洗和整理,以确保数据的准确性和一致性。
II. 数据计算与分析(字数限制:300字)在进行数据建模之前,需要对数据进行计算和分析,以获取有价值的信息和洞察。
Excel提供了丰富的函数和工具,可用于数据计算和分析。
例如,通过使用SUM、AVERAGE、COUNT等函数,我们可以计算数据的总和、平均值和数量。
通过使用PivotTable和PivotChart功能,我们可以对数据进行交叉分析和可视化呈现,以揭示不同维度的数据关系和趋势。
III. 数据建模与预测(字数限制:400字)数据建模是利用Excel进行数据分析的重要环节,它通过建立数学模型来揭示数据背后的规律和趋势。
在Excel中,我们可以使用线性回归、多元回归、时间序列等统计方法进行数据建模。
通过将数据和模型进行拟合,可以得到拟合度高的模型,并进行数据预测和趋势分析。
IV. 数据可视化与呈现(字数限制:300字)数据可视化是将数据以图表等形式进行呈现,以便更好地理解和传达数据分析的结果。
Excel提供了各种图表类型(如柱状图、折线图、散点图等),方便我们根据需要创建不同类型的图表。
通过调整图表的样式、颜色和标签等属性,可以使图表更加美观和易读。
Excel在数学建模教学中的应用

Excel在数学建模教学中的应用背景数学建模是现代教育和科研中重要的一环,它将现实生活中的实际问题转化为数学问题,并通过数学模型进行分析和解决。
在学习过程中,学生需要提高模型构建和求解问题的能力,这就需要使用工具来支持学生的学习。
其中,Excel是一种应用广泛、易于上手的工具,因此在数学建模教学中,Excel的应用也越来越多。
Excel在数学建模教学中的优势数据处理和分析Excel具有数据处理和分析的能力,这使得学生可以通过Excel来处理数据,绘制各种统计图表,进行数据分析和预测。
这些能力可以帮助学生更好地理解模型和现实问题的关系,并进一步提高他们的模型构建和分析能力。
运算和求解Excel也具有强大的运算和求解能力。
无论是线性回归、非线性方程、优化问题,Excel都能够提供相关的函数和工具,帮助学生求解数学建模中的实际问题。
这些能力可以帮助学生掌握数学建模的基本技能,提高他们的数学思维和解决问题的能力。
可视化呈现Excel可以将复杂的数据和分析结果以图形和表格的形式直观地呈现出来,这对于学生理解和分析问题非常重要。
学生可以使用Excel绘制求解结果的各种图表,从而更好地理解模型和问题之间的关系。
灵活性和易用性Excel具有灵活和易用的特点,不需要编写复杂的代码就能够完成许多数学建模的任务。
学生可以通过自己的理解和创造力来使用Excel完成各种数学建模的任务,这也有助于培养学生的创新精神和动手能力。
Excel在数学建模教学中的实际应用数据处理和分析在数学建模教学中,学生经常需要使用实际数据进行建模和分析,这时候Excel就可以发挥它的优势了。
学生可以使用Excel进行数据预处理和清洗,处理缺失值和异常值,绘制各种数据图表。
在此基础上,学生可以通过Excel进行各种数据分析,比如拟合曲线、计算统计量、构建回归模型等等。
模型的求解在数学建模中,模型的求解是一个非常重要的步骤,也是学生需要掌握的一个基本技能。
Excel在数学建模中的应用在数学建模中的应用

Excel在数学建模中的应⽤在数学建模中的应⽤Excel 在数学建模中的应⽤在数学建模中的应⽤Excel 是Microsoft Office套件中的电⼦表格软件,它的应⽤很⼴泛,许多⼈把它当作⼀般的制作表格和图表的软件,⽽不清楚它的强⼤数据运算能⼒。
其实,Excel 内置了数百个函数供⽤户调⽤,还允许⽤户根据⾃⼰的需要随意定义⾃⼰的函数,Excel ⽆需编程就能够实现其他软件需要编程才能完成的复杂计算,能进⾏各种数据的统计、运算、处理和绘制统计图形,只要善于开发,Excel ⼀定能够在数学建模中发挥出更⼤的作⽤。
第⼀章 Excel 基本知识1. Excel的安装、启动和退出2. Excel⼯作界⾯简介Excel 以⼯作簿(book)的形式构成⽂件。
⼀个⼯作簿⽂件可包含多个⼯作表(⾄多255 张,⼀个⼯作表最多可容纳65536 个观察个体(记录)和256个变量(或字段名))、图表、宏指令表,这些都可以同时存在于同⼀个⼯作簿⽂件内。
当保存⼯作簿时,会把⼯作簿中的⼯作表、图表、宏指令表⼀并保存。
Excel ⼯作界⾯包括如下⼏项内容:标题栏、菜单栏、⼯具栏、编辑栏、⼯作表、⼯作表名称、滚动条、状态栏等。
3.单元格的命名4.配合⿏标操作的键:Shift 键、Ctrl键、Alt键。
5.宏的录制与使⽤第⼆章数据⽂件的建⽴与利⽤除直接输⼊数据或调⽤数据⽂件的⼀般功能外,Excel 还可由公式或⼀般数据快速填充⽅式产⽣新的数据,数据的复制、移动、插⼊、删除、排序、筛选等编缉操作⾮常灵活,经格式化后的数据⼯作表美观好看,使得Excel成为⽬前建⽴中⼩型数据⽂件最常⽤、最优秀软件之⼀。
Excel 数据与世界最优秀的统计软件SAS、SPSS等的数据可相互导⼊,⽅便处理。
本章将介绍如何利⽤录⼊、导⼊数据来建⽴Excel 数据⽂件。
1.单元格格式:数字、对齐、字体、边框、图案、保护。
2.数据的有效性设置3.建⽴数据清单4.数据“记录单”的作⽤5.数据的⾃动填充:填充柄、Ctrl+Enter复合键、填充序列对话框、等⽐数列数据的填充(编辑-填充-序列)、公式的⾃动填充(相对引⽤A1,绝对引⽤$A$1)6.公式与函数(例九九乘法⼝诀表的编制)7.数据的分列(数据-分列)8.添加与编辑批注(插⼊-批注)9.数据的导⼊与导出第三章数据的编缉与查询数据清单建⽴后,可能需要继续对部分数据进⾏剪切、复制、移动、删除、替换、产⽣新数据等。
Excel在数学建模中的应用

第四步:将条形图转换成标准直方图
(如图所示)
35
二、用Excel绘制图表 (以文件“图表”为例)
图表是数据表现的另一种形式。数据的图表化就是将单 元格中的数据以各种统计图的形式显示。
1.图表种类 (1)独立的图表:单独占据一个工作表,打印时也将与数据 表分开打印。 (2)附属于工作表的嵌入式图表:它和数据源放置在同一张 工作表中,同时打印。
39
绘图实例: 用Excel绘制任意一元函数的图像
以 y 2sin x ln(1 x2 ) 为例介绍:
40
三、用Excel进行相关与回归分析 1、用Excel计算描述统计量 2、用Excel进行相关分析 3、用Excel进行回归分析
41
三-1、用Excel计算描述统计量 (1)用函数计算描述统计量 (2)描述统计菜单项的使用
6
函数的引用
手工输入:在编辑栏或单元格内输入 引用单元格地址:
7
相对引用
利用单元格间的相对位置关系引用单元格内容。公式中 的相对引用随单元格的移动而修改,但原来的位置不变。
例:打开文件“数据编辑”,在工作表“电视机的销售 统计表” 的G3中输入“=E3*F3,则可在G4、G5、G6、 G7、G8中填入相应公式来计算商品的销售金额。 绝对引用
3
自动输入数据
自动填充鼠标拖动填充柄向下、右拖数字 增量为1,向上、左拖增量为-1 .
自定义序列 ① 工具——选项——新序列——输入序列 内容,每个序列间按回车键——添加 ② 选中序列区域——工具——选项——导 入——确定
4
5
公式的使用
用公式计算 所有的公式运算均以“=”开头。错误的公式以#开头。 (1)数学运算符: +、-、*、/、^、%(计算准则:先乘方,再乘、除,
数学建模——excel
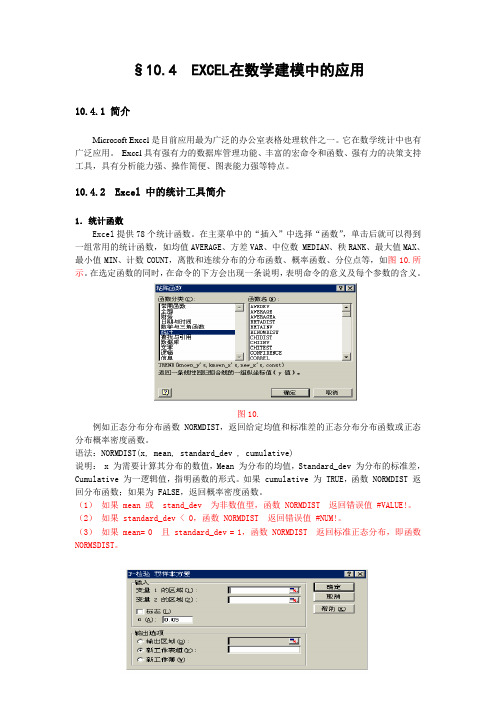
§10.4 EXCEL在数学建模中的应用10.4.1 简介Microsoft Excel是目前应用最为广泛的办公室表格处理软件之一。
它在数学统计中也有广泛应用。
Excel具有强有力的数据库管理功能、丰富的宏命令和函数、强有力的决策支持工具,具有分析能力强、操作简便、图表能力强等特点。
10.4.2 Excel 中的统计工具简介1.统计函数Excel提供78个统计函数。
在主菜单中的“插入”中选择“函数”,单击后就可以得到一组常用的统计函数,如均值AVERAGE、方差VAR、中位数 MEDIAN、秩RANK、最大值MAX、最小值MIN、计数COUNT,离散和连续分布的分布函数、概率函数、分位点等,如图10.所示。
在选定函数的同时,在命令的下方会出现一条说明,表明命令的意义及每个参数的含义。
图10.例如正态分布分布函数 NORMDIST,返回给定均值和标准差的正态分布分布函数或正态分布概率密度函数。
语法:NORMDIST(x, mean, standard_dev , cumulative)说明: x 为需要计算其分布的数值,Mean 为分布的均值,Standard_dev 为分布的标准差,Cumulative 为一逻辑值,指明函数的形式。
如果 cumulative 为 TRUE,函数 NORMDIST 返回分布函数;如果为 FALSE,返回概率密度函数。
(1)如果 mean 或 stand_dev 为非数值型,函数 NORMDIST 返回错误值 #VALUE!。
(2)如果 standard_dev < 0,函数 NORMDIST 返回错误值 #NUM!。
(3)如果 mean= 0 且 standard_dev = 1,函数 NORMDIST 返回标准正态分布,即函数NORMSDIST。
图10.2.统计宏Excel 为统计分析提供了一个功能很强的统计软件包。
它是一个外挂的开发产品。
在安装时可以有选择地将它加载到Excel 系统环境中去,在主菜单“工具”菜单的最下面一栏,如果已存在“数据分析”命令,则直接调用该软件包。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
此题可列出微分方程并解出纯理论解, 但这里我们采用数值解法。
模型假设及构建
以坦克初始点为坐标原点,正东方向为x轴正方 向建立直角坐标系。假定在每个0.1秒时间间隔内, 坦克先向北行驶1.5米,然后导弹朝着对准坦克的方 向行驶6米。 Tk ~坦克第k个0.1秒末的纵坐标值 xk~导弹第k个0.1秒末的横坐标值 yk~导弹第k个0.1秒末的纵坐标值 Tk=1.5k; k=1,2, 0≤ xk ≤3000 ; 0≤ yk; k=1,2,
为解决此题,首先必须建立从k时刻到k+1时刻的 导弹轨迹坐标关系式:
(xk+1,yk+1)
由此可得出从k时刻到k+1时刻的导弹轨迹坐标关系式:
yk 1 yk Tk 1 yk xk 1 xk xk
xk 1 xk yk 1 yk
2
2
6
模型求解:
循环计算,直到可以覆盖整个轨道即可。
对于椭圆轨道:最少需要多少个测控站?
进一步讨论: 有必要求解β2吗? 假如将(θ+β1) 视为任意初始角θ, 从P1开始作为第一 个测控站,往下递 推,如何? 飞船最少测控站数
建模案例3:
如何预报人口的增长
•已知近200多年来美国人口数据(见上图) •问:如何预测2000年和2010年美国的人口数?
根据以上导弹坐标关系式,可推导出以下递推关系式
xk 1 xk
6 xk
Tk 1 yk
2
xk
2
yk 1 yk 36 xk 1 xk
2
有了这个导弹坐标递推公式,就可借助Excel表格软 件上机逐步计算出导弹运行轨迹。当: xk+1≤ 0且xk >0 时,即可近似确认导弹击中了坦克。追迹题解 所得结果为:当k≈533.3(即导弹运行53.3秒)时, 在Tk+1 ≈ 800(即坦克约向北行驶了800米)处,导弹 击中坦克。
此问题可归结为d1~d6共6种切割厚度的排序优化。 采用枚举法,有多少种可能的方案? P6=6×5×4×3×2×1=720? 还能减少吗?
图1
由于同方向两次切割有必然的顺序, 先选废料尺寸较长的切割。
所以枚举方案数为: P6/23 = 90 换一种思维,枚举数为:
2 2 C6 C4 90
•解决这一问题,先要探索人口增长的规律,然后要掌握 用线性回归拟合参数的方法。
指数增长模型
离散型的计算公式
k年后人口 今年人口 x0, 年增长率 r
xk x0 (1 r )
k
马尔萨斯于1798年提出如下连续型的指数增长模型
x(t) ~时刻t人口
r ~ 人口(相对)增长率(常数)
x(t t ) x(t ) r x(t ) t
截断切割
图1
建模案例5:基尼系数的计算
• 基尼系数是由意大利罗马大学教授基尼(Corrado Gini, 1884-1965)根据洛伦茨曲线(Lorenz Curve)提出的 对社会收入不公平等度的一种度量。
G A / A B 2 A 1 2 B
G 1 2 L x dx
0.641
• 借助Maple或其他数学软件可计算得:
G 1 2 x 0.78 x1.04 1 x
0 1
0.641
dx 0.3497
建模案例6:城市街道长度计算(2011年赛题B)
• 已知: 某城市街区的交通网络示意图。 该市街区各节点之间街道编号及坐标数据表。 • 要求:计算全部各条街道的长度。 思考:此题的难度在哪里?
• • •
需要统计分析那些数据?(平均分、标准差、……) 问题是数据比较杂乱,难以给出合理的评价方法。 关键是熟练运用: Excel表格中统计函数的运用; Excel表格的排序功能。 12年A题解
dx x r ( x) x r x (1 ) 可以得出其差分形式 dt xm
x 1 r r xt r s xt t x t xm
于是根据现有的历年人口xt数值,采用“最小二乘法”作 拟合,可以计算得出参数r、s值,进一步得出xm值。 人口预测模型参数拟合
• • • •
其实计算公式并不涉及高深的数学理论。 问题是计算量太大,难以很快得出结果。 关键是熟练运用Excel的查询和引用功能。 某市各条街道长度计算结果
建模案例7:NBA赛程分类统计(2008年赛题D)
• 已知2008~2009赛季NBA常规赛的赛程安排。 • 要求分别统计出每个球队全部82场比赛的赛程表。 思考:此题的难度在哪里?
0
1
L x x c x 1 x
•
基尼系数的求解步骤: 根据统计数据,适当分段; 计算各段相关数据; 拟合L(x)函数的待定参数; 计算基尼系数。
• 例题:根据国家统计局的抽样调查,我国在1999年城 镇人口的分组收入情况数据如下表显示,试拟合对应 的洛伦兹曲线并计算基尼系数。
对三角形OP1A,由正弦定理得, OP OA 1 , sin sin 2 2 R cos( ) p 即 , cos 1 e cos 1 cos R cos( ) 1 e cos 1 p ,
p OA 1 e cos 1 a, b为长,短半轴
OB a 2 b2 , e a sin 2 sin 2 2 R cos( ) p b2 即 , p cos 2 1 e cos 2 a
Excel在数学建模 解题中的应用
董哲生
建模案例1: 导弹追迹问题
一辆坦克以 15m/s 速度向北行驶,同一时刻在 坦克正东方向3000m处一枚反坦克导弹以60m/s速度 对准它射出。假定坦克和导弹均为匀速运动,坦克 运动方向不变,导弹运动方向始终为对准坦克。问 经过多少秒钟?导弹在何处击中坦克?
建模案例4:最优截断切割问题
• 从一个长方体中加工出一个已知尺寸、位置预定的长方 体(这两个长方体的对应表面是平行的),通常要经过 6 次截断切割。设水平切割单位面积的费用是垂直切割 单位面积费用的r倍,试设计一种安排各面加工次序 (称“切割方式”)的方法,使加工费用最少。 • 有人提出如下切割方案准则:每次选择一个加工费用最 少的待切割面进行切割。你认为正确吗? • 以下实例验证你的方法:待加工长方体和成品长方体的 长、宽、高分别为10、14.5、19和3、2、4,二者左侧 面、正面、底面之间的距离分别为6、7、9(单位均为 厘米)。垂直切割费用为每平方厘米1元,r的数据分别 考虑三种情况:①r =1;②r =1.5;③r=8。
• 不符合19世纪后多数地区人口增长规律; •不能预测较长期的人口增长过程。
原因何在?
19世纪后多数地区的人口数据显示: 人口增长率r并不是常数,而是逐渐下降的。
阻滞增长模型 (Logistic模型)
人口增长到一定数量后,增长率下降的原因: 资源、环境等因素对人口增长的阻滞作用 且阻滞作用随人口数量增加而变大 r是x的减函数
• • • 其实分类统计方法并不涉及高深的数学理论。 问题是统计量太大,难以很快得出结果。 关键是熟练运用: Word文档字符的表格化; Word文档表格转化为Excel文档; Excel表格的排序功能。 NBA各队赛程表
建模案例8:葡萄酒的品质评价(2012年赛题A)
• 已知两组评酒员对红、白两类,各数十个品种葡萄酒的 评分表。 • 问题:①两组评酒员的评价结果有无显著性差异,哪一 组的评价结果更可信?②如何给这些葡萄酒的品质排序?
多少个测控站能进行全程跟踪测控?
• 对于圆轨道
sin( / 2 ) sin( / 2 ) , hR R cos( ) cos( ) hR R R cos( ) arccos hR 2 所需要站点数目 1 2 所需要站点数随高度减少
由此可以确定下一个观测站的位置 : 1 1
计算步骤 : 给定近地点、远地点,求a, b, e, p 给定一个初始角度 ,由方程 R cos( ) p cos 1 1 e cos 1 R cos( ) p 和 分别求出1和 2, cos 2 1 e cos 2 再由 cos R cos( ) 1 e cos 1 p 求出,
飞船最少测控站数
对于椭圆轨道:最少需要多少个测控站?
对于椭圆轨道, 其极坐标方程为: OA p 1 e cos 1
a, b为长,短半轴 a 2 b2 e a b2 p a
对三角形OPA,由正弦定理得, OA , sin 1 sin 2 2 R cos( ) p 即 , cos 1 1 e cos 1 对三角形OPB,由正弦定理得, OP OP
对洛伦兹函数 L x x c x 1 x
两边取对数,得 ln x L ln c ln x ln 1 x
接下来就可运用Excel拟合参数了。基尼系数计算
• 根据Excel拟合结果 • 洛伦兹函数为:
L x x ቤተ መጻሕፍቲ ባይዱ0.78 x1.04 1 x
x(t ) x 0 e
r t
rt
dx r x, x(0) x0 dt
x0 (e ) x0 (1 r )
t
结果表明:随着时间增加人口总数将无限增长!?
指数增长模型的应用及局限性
•与19世纪以前欧洲一些地区人口统计数据吻合; •也适用于19世纪后迁往加拿大的欧洲移民后代; •可用于短期人口增长预测。
