4.4梁的正应力及其强度条件
工程力学梁的正应力强度条件及其应用1
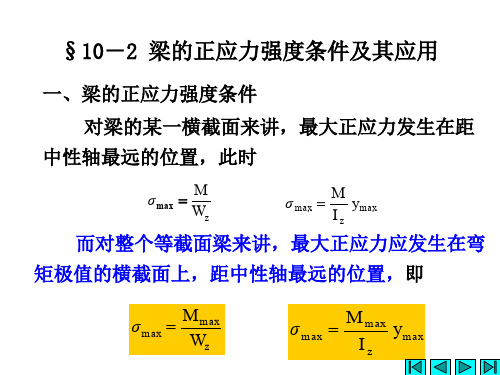
ymax
对矩形截面
Wz
bh3 12 h2
bh2 6
Wz
bh2 6
对圆形截面
Wz
d 4
d
64 2
d 3
32
Wz
d 3
32
各种型钢的截面惯性矩Iz和弯曲截面系数Wz的 数值,可以在型钢表中查得。
为了保证梁能安全的工作,必须使梁横截面上的
最大正应力不超过材料的许用应力,所以梁的正应力
强度条件为
σmax
M max Wz
σ
二、三种强度问题的计算
σmax
M max Wz
σ
(1)强度校核 (2)选择截面 (3)确定许用荷载
σmax
M max Wz
σ
Wz
M max σ
M max Wz σ
例题10-2 一矩形截面简支木梁如图所示,已知l=4m, b=140mm,h=210mm,q=2kN/m,弯曲时木材的许 用正应力[σ]=10MPa,校核该梁的强度。
σc,max
MC Iz
y1
2.7 103 0.072 0.573105
33.9 106 Pa
33.9MPa [σc]
由以上分析知该梁满足强度要求。
例题10−4 如图所示的简支梁由工字钢制成,钢的 许用应力[σ ]=150MPa,试选择工字钢的型号。
解:先画出弯矩图如图b所示。 梁的最大弯矩值为
y1
1.8103 0.072 0.573105
22.5106 Pa
22.5MPa
材料力学-第三章正应力强度条件

解: 由公式
max
M max Wz
M max bh 2
6
可以看出, 该梁的承载能力将是原来的 2 倍。
例:主梁AB,跨度为l,采用加副梁CD的方 法提高承载能力,若主梁和副梁材料相同,截面 尺寸相同,则副梁的最佳长度a为多少?
a Pa
C2 A
2D B
l
l
2
2
CL8TU8
解:
主梁AB的最大弯矩
P M max AB 4 (l a)
y1
Wy1tzy2ycImzayxmamxax抗弯截面模y 量CL8TU4
max
M ymax IZ
M WZ
横截面上的应力分布图:
z
z
M 0
M 0 CL8TU5
bh3
bh2
I Z 12 , WZ 6
d4
I Z 64
d3
, WZ 32
IZ
(D4 d 4)
64
D4
64
(1 4 )
P
A
x
dx C
2m
2m
300 B
200
例:我国营造法中,对矩形截面梁给出的尺 寸比例是 h:b=3:2。试用弯曲正应力强度证明: 从圆木锯出的矩形截面梁,上述尺寸比例接近 最佳比值。
解: b2 h2 d 2
bh2 b(d 2 b2 )
Wz 6
6
Wz d 2 b2 0 b 6 2
CL8TU3
梁在纯弯曲时的平面假设:
梁的各个横截面在变形后仍保持为平 面,并仍垂直于变形后的轴线,只是横截 面绕某一轴旋转了一个角度。
中性轴过截面形心
中性层的曲率公式: 1 M
EIz 正应力计算公式: M y
梁的应力
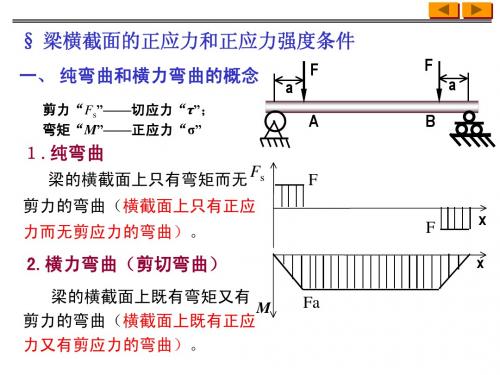
384 MPa
t max 178 MPa , c max 384 MPa
5. C 截面曲率半径ρ
30
A
1m
FAY
B C
l = 3m
x
K
C 截面弯矩
M C 60kN m
z y
FBY
I Z 5.832 10 m
1 M EI
9
5
4
FS 90kN
x 90kN
C
EI Z MC
200 10 5.832 10 60 10
3
5
q=60kN/m
180
3. C 截面最大正应力
120
A
1m
FAY
B C
l = 3m
30
C 截面弯矩
M C 60kN m
x
K
z y
Cmax
FBY
I Z 5.832 10 m
M C ymax IZ
3
5
4
FS 90kN
x 90kN x
60 10
180
二 、纯弯曲梁横截面上的正应力公式
(一)变形几何关系: 由纯弯曲的变形规律→纵向线应变的变化规律。 1、观察实验:
2、变形规律: ⑴、横向线:仍为直线, 只是相对转动了一个角度 且仍与纵向线正交。
⑵、纵向线:由直线变为 曲线,且靠近上部的纤维 缩短,靠近下部的纤维伸 长。 3、假设: M
a
c
b
a
§ 梁横截面的正应力和正应力强度条件
一、 纯弯曲和横力弯曲的概念
剪力“Fs”——切应力“τ”; 弯矩“M”——正应力“σ”
梁的应力和强度计算

z dA dM z y dA
dM y
( Stresses in Beams) 将应力表达式代入(1)式,得
FN
A
E
y
dA 0
E
A
ydA 0
待解决问题:
中性轴的位置
中性层的曲率半径ρ
S z ydA 0 A
y M y zE dA 0 A
中性轴通过横截面形心
伽利略(G.Galiieo, 1564-1642)的研究中认为: 弯曲应力是均匀分布的 (《两门新科学的对话》1638 年出版 ) , 因而得不到正确的公式,大科学家有时 也弄错。
( Stresses in Beams)
C C
Z 中性轴
Z
y
压
C M M
y 拉
C
Z
Z 两部分。
?
( Stresses in Beams)
横截面的 对称轴
横截面
y σ Eε E ρ
M
中性层
中性轴
1、中性轴的位置(Location of the neutral axis) 2、中性层的曲率半径 (Curvature radius of the neutral surface)
?
中性轴
( Stresses in Beams)
强度条件(strength condition):
梁内的最大工作应力不超过材料的许用应力
1、数学表达式(mathematical formula)
max
M max [ ] W
2、强度条件的应用(application of strength condition)
M max (1) 强度校核 [ ] W M max (2)设计截面 W [ ] (3)确定许可核载 M max W [ ]
四梁的正应力强度条件
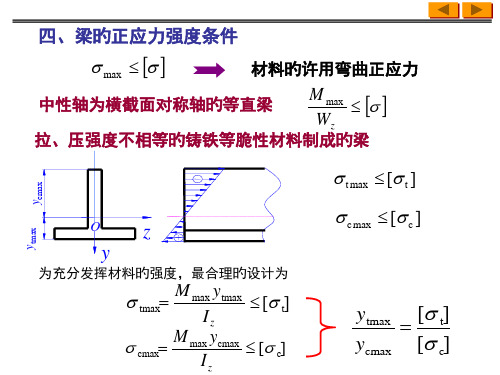
Iz
1 2
Ip
πr03
S
* z
(πr0
)
2r0 π
2r02
max
FS
S
* z
I z (2 )
FS (2r02 ) πr03 (2 )
FS 2 FS
πr0
A
例 FS = 15 kN,Iz = 8.8410-6 m4,b
= 120 mm, 20 mm, yC = 45 mm。试求 :max ;腹板与翼缘交 接处切应力 a
需要校核剪应力旳几种特殊情况: (1)梁旳跨度较短,M 较小,而 Q 较大时,要校核剪应力。 (2)铆接或焊接旳组合截面,其腹板旳厚度与高度比不大于型钢
旳相应比值时,要校核剪应力 (3)各向异性材料(如木材)旳抗剪能力较差,要校核剪应力。
§6-3 薄壁截面梁弯曲切应力旳进一步分析
切应力公式旳应用-弯曲中心
B截面:
max
MB WzB
Fa
d13
62.5 267 32
0.163
32
41.5106 Pa 41.5MPa
C截面:
max
MC WzC
Fb
d
3 2
62.5 160
0.133
32
32 46.4106 Pa 46.4MPa
(5)结论:轮轴安全
Fa
Fb
例、T 字形截面旳铸铁梁受力如图,铸铁旳[t]=30 M Pa,
E mG C mH D l/2 l
E max
F max
F
梁旳切应力强度条件为
max
对等直梁,有
F S* Smax z max
Izb
材料在横力弯曲时旳许用切应力
弯曲正应力、切应力与强度条件

M
C
拉
Z
C
Z
中性轴
拉
y
中性轴
y
压
中性轴将横截面分为 受拉 和 受压 两部分。
M yAz(
d)A E
Az
y dA
E
I
yz
0
Iyz0
因为 y 轴是横截面的对称轴,所以 Iyz 一定为零。 该式自动满足
中性轴是横截面的形心主惯性轴
M ZAy(
d)A E
A
y2 dA
E
Iz
M
1M
EI z
基本假设2: 纵向纤维无挤压假设
纵向纤维间无正应力。
公式推导
d
用两个横截面从梁中假想地截取 长为 dx 的一段 。
由平面假设可知,在梁弯曲时,
这两个横截面将相对地旋转一个
角度 d 。
横截面的转动将使梁的凹边的纵 向线段缩短,凸边的纵向线段伸 长。由于变形的连续性,中间必 有一层纵向线段 O1O2 无长度改 变。此层称为 中性层 。
m M
FS m
m
m
M
FS
m
m
只有与切应力有关的切向内力元素 dFS = dA 才能合成剪力 只有与正应力有关的法向内力元素 dFN = dA 才能合成弯矩 所以,在梁的横截面上一般既有 正应力,又有 切应力
一,纯弯曲梁横截面上的正应力
RA
P
P RB
C a
P
+
D a
+
P
+
Pa
推导 纯弯曲 梁横截面上正应力的计算公式。 几何 物理 静力学
2 假想地从梁段上截出体积元素 mB1
m'
m z
梁应力强度计算

第五章 平面弯曲梁的强度
内容: 梁的应力、强度计算
τ→FS
z
dA
FS y
σ→M
M
z
dA
dA
y
M =∫yσσd
A
§5.1 梁的正应力
一、纯弯曲梁横截面上的正应力
F
F
a
l
a
FS F
M
x
F Fa
x
FS M
纯弯曲梁
Me
l
x
Me
450×0.03 2×45×10-9
=150
MPa
(-)
习题5-13 当20号槽钢受纯弯曲变形时,测出A、B两点间长度
Δl=27×10-3mm,材料的E=200GPa。试求梁截面上的弯矩M。
解:
50
5
M
AB
M
●
●
ε=
Δl l
=
27×10-3 50
=5.4×10-4
σ=Eε=200×109×5.4×10-4=108MPa
BC段: d2 ≥ 3
32×455×103 π140×106
= 321 mm
取: d1=250mm d2=322mm
例11. 已知:[σ]=160MPa,[τ]=100MPa,
试选工字钢梁的型号。
解: Fsmax=6kN
1.σ计算:
σmax =
M max Wz
≤ [σ]
M max = 8 kN • m
=
1 2
qab+
1 8
qb2
=
0.02375q
N
•
m
梁的正应力强度条件

梁的正应力强度条件
梁的正应力强度条件是指在梁受到载荷作用时,梁内部所产生的正应力不能超过材料的承载能力。
这是保证梁结构不会发生破坏的重要条件之一。
一、梁的正应力
在静力学中,梁是指一种长条形结构,在两端支撑下承受外部载荷。
当外部载荷作用于梁上时,会在梁内部产生正应力。
正应力是指垂直于截面的单位面积上所受到的拉伸或压缩作用。
二、强度条件
为了保证梁结构的安全可靠,需要满足强度条件。
强度条件是指在外部载荷作用下,材料内部所产生的应力不能超过其承载能力,即:
σ≤σmax
其中,σ为材料所受到的应力;σmax为材料允许承受的最大应力。
三、正应力强度条件
对于梁而言,其内部产生的正应力必须满足以下强度条件:
σx≤f
其中,σx为沿着x轴方向产生的正应力;f为材料允许承受的最大正应力。
四、梁的截面形状对强度条件的影响
梁的截面形状对其正应力强度条件有重要影响。
一般来说,截面形状越大,正应力强度条件就越好。
例如,在相同载荷作用下,矩形截面的梁比圆形截面的梁更加稳定。
五、应力集中
应力集中是指在梁结构中存在某些地方的应力异常集中现象。
这种现象可能会导致材料发生裂纹或破坏。
为了避免应力集中,可以通过改变梁的截面形状或采用合适的支撑方式来解决。
六、总结
梁的正应力强度条件是保证其结构安全可靠的重要条件之一。
在设计
和使用梁结构时,需要考虑其截面形状和支撑方式等因素,并避免出现应力集中现象,以确保其正应力不超过材料承载能力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《梁的正应力及其强度条件》教学设计
课题 4.4梁的正应力及其强度条件教学时间4课时
教学目标
知识与技能
1、通过实验,理解对称截面上的正应力分布规律;
2、理解非对称截面上的正应力分布规律;
3.了解矩形和圆形截面二次矩、抗弯截面系数,了解正
应力计算公式;
4.能运用正应力强度条件解决工程实际中基本构件的强
度校核;
5.能运用正应力强度条件解决工程实际中的截面设计和
确定许用荷载
过程与方法
1、能通过实验,观察称截面梁的变形特点,分析得出对称
截面上的正应力分布规律;
2、探究正应力强度条件在工程中的三种应用的解题方法。
情感、态度、价值观
1、通过探究梁的变形特点,体验分析出梁的内力分布规
律,培养学生开拓创新精神,增强理解能力,分析能力;
2、通过分析梁的正应力强度条件在工程中的三种应用,
增强学生的安全、经济、适用意识。
教学重点梁的正应力分布规律和梁的正应力强度条件在工程中的三种应用。
教学难点此节概念较抽象,重在理解和熟悉。
教学内容及其过程学生活动教师导学
一、引入
1、如图一、二所示,用一矩形橡胶棒(建议力学教师常备),在其表面画上一些均匀分布的小方格,在力偶(均布线荷载或力)的作用下,观察其横向线和纵向线的变化。
那么,是什么原因引起的变化呢?变化大小又与什么因素有关呢?
图一图二
二、导学提纲
1.梁的正应力
(1)上述实验中,通过观察可得出:各横向线代表的横截面变形后为面,在梁的下部的纵向线,而上部的纵向线则,说明了梁的下部受,下让两位同学上
来做图一、图二
的实验,橡胶棒
两端作用两个
力偶,其它同学
通过观察纵向
与横向线的变
化情况来回答
问题。
通过图二的实
验,让学生亲
身体验或观察
变形特点,提
出问题,从而
引入课题。
解:( 1)绘制M 图(图4-16b)。
M max 发生在跨中截。
