初三数学练习2
图形与证明(二)复习(1)练习2

DCBAD九年级数学 作业1、如图,设M ,N 分别是直角梯形ABCD 两腰AD ,CB 的中点,DE 上AB 于点E ,将△ADE 沿DE 翻折,M 与N 恰好重合,则AE :BE 等于( ) A .2:1 B .1:2 C .3:2 D .2:32、小宇同学在一次手工制作活动中,先把一张矩形纸片按图1的方式进行折叠,使折痕的左侧部分比右侧部分短1cm ;展开后按图2的方式再折叠一次,使第二次折痕的左侧部分比右侧部分长1cm ,再展开后,在纸上形成的两条折痕之间的距离是( )A .0.5cmB .1cmC .1.5cmD .2cm3、如图,若将四根木条钉成的矩形木框变为平行四边形ABCD 的形状,并使其面积为矩形面积的一半,则这个平行四边形的一个最小内角的值等于 。
4、矩形ABCD 中,22=AB ,将角D 与角C 分别沿过A 和B 的直线AE 、BF 向内折叠,使点D 、C 重合于点G ,且AGB EGF ∠=∠,则=AD .5、已知平行四边形A B C D ,AD a AB b ABC α===,,∠.点F 为线段B C 上一点(端点B C ,除外),连结A F A C ,,连结D F ,并延长D F 交A B 的延长线于点E ,连结C E .(1)当F 为B C 的中点时,求证E F C △与A B F △的面积相等;(2)当F 为B C 上任意一点时,E F C △与A B F △的面积还相等吗?说明理由.左右左右第二次折叠 第一次折叠图1图26、在一次数学实践探究活动中,小强用两条直线把平行四边形ABCD 分割成四个部分,使含有一组对顶角的两个图形全等; (1)根据小强的分割方法,你认为把平行四边形分割成满足以上全等关系的直线有 组;(2)请在图中的三个平行四边形中画出满足小强分割方法的直线; (3)由上述实验操作过程,你发现所画的两条直线有什么规律?7、如图:把一个矩形如图折叠,使顶点B 和D 重合,折痕为EF 。
2022年人教版中考数学一轮复习:四边形综合 专项练习题2(Word版,含答案)

2022年人教版中考数学一轮复习:四边形综合专项练习题21.如图,已知四边形ABCD是平行四边形,从①AB=AD,②AC=BD,③∠ABC=∠ADC中选择一个作为条件,补充后使四边形ABCD成为菱形,则其选择是(限填序号).2.如图1,平行四边形纸片ABCD的面积为120,AD=15.今沿两对角线将四边形ABCD剪成甲、乙.丙、丁四个三角形纸片.若将甲、丙合并(AD、CB重合)形成一个对称图形戊,如图2所示.则图形戊的两条对角线长度之和为.3.如图,菱形ABCD的两条对角线AC,BD交于点O,BE⊥AD于点E,若AC=8,BD=6,则BE的长为.4.如图,在▱ABCD中,∠A=70°,DB=DC,CE⊥BD于E,则∠BCE=.5.如图,在菱形ABCD中,AB=BD,点E、F分别在AB、AD上,且AE=DF,连接BF与DE交于点H,若CG=1,则S=.四边形BCDG6.如图,正方形瓷砖图案是四个全等且顶角为45°的等腰三角形.已知该瓷砖的面积是1m2,则中间小正方形的面积为m2.7.如图所示,在Rt△ABC外作等边△ADE,点E在AB边上,AC=5,∠ABC=30°,AD=3.将△ADE沿AB方向平移,得到△A′D′E′,连接BD′.给出下列结论:①AB=10;②四边形ADD′A′为平行四边形;③AB平分∠D′BC;④当平移的距离为4时,BD′=3.其中正确的是(填上所有正确结论的序号).8.如图,菱形ABCD的对角线AC,BD相交于点O,P为AB边上一动点(不与点A,B重合),PE⊥OA于点E,PF⊥OB于点F,若AB=4,∠BAD=60°,则EF的最小值为.9.如图,在正方形ABCD中,点E为BC边上一点,且CE=2BE,点F为对角线BD上一点,且BF=2DF,连接AE交BD于点G,过点F作FH⊥AE于点H,若HG=2cm,则正方形ABCD 的边长为cm.10.把图1中的菱形沿对角线分成四个全等的直角三角形,将这四个直角三角形分别拼成如图2,图3所示的正方形,则图1中菱形的面积为.11.如图,在正方形ABCD内有一点P,若AP=4,BP=7,DP=9,则∠APB的度数为.12.如图是两个边长分别为2a,a的正方形,则△ABC的面积是.13.如图,点P是正方形ABCD内一点,连接AP、BP、DP,若AP=1,PD=,∠APB=135°,则正方形ABCD的面积为.14.如图,正三角形ABC与正方形CDEF的顶点B,C,D三点共线,动点P沿着CA由C向A 运动.连接EP,若AC=10,CF=8.则EP的最小值是.15.如图,正方形ABCD中,H为CD上一动点(不含C、D),连接AH交BD于G,过点G作GE⊥AH交BC于E,过E作EF⊥BD于F,连接AE,EH.下列结论:①AG=EG;②∠EAH=45°;③BD=2GF;④GE平分∠FEC.正确的是(填序号).16.如图,平面内三点A、B、C,AB=4,AC=3,以BC为对角线作正方形BDCE,连接AD,则AD的最大值是.17.如图,在正方形ABCD中,点E在对角线AC上,EF⊥AB于点F,EG⊥BC于点G,连接FG,若AB=8,则FG的最小值为.18.如图,正方形ABCD的边长为2,点E是BC的中点,连接AE与对角线BD交于点G,连接CG并延长,交AB于点F,连接DE交CF于点H,连接AH.以下结论:①CF⊥DE;②=;③GH=;④AD=AH,其中正确结论的序号是.19.如图,矩形ABCD中,对角线AC、BD交于点O,AE⊥BD于E,若∠DAE=3∠BAE.则的值为.20.将矩形ABCD按如图所示的方式折叠,BE、EG、FG为折痕,若顶点A、C、D都落在点O 处,且点B、O、G在同一条直线上,同时点E、O、F在另一条直线上.(1)的值为.(2)若AD=4,则四边形BEGF的面积为.参考答案1.解:①∵四边形ABCD是平行四边形,AB=AD,∴平行四边形ABCD是菱形;②∵四边形ABCD是平行四边形,AC=BD,∴平行四边形ABCD是矩形;③∵四边形ABCD是平行四边形,∴∠ABC=∠ADC,因此∠ABC=∠ADC时,四边形ABCD还是平行四边形;故答案为:①.2.解:如图,连接AD、EF,则可得对角线EF⊥AD,且EF与平行四边形的高相等.∵平行四边形纸片ABCD的面积为120,AD=1520,∴BC=AD=15,EF×AD=×120,∴EF=8,又BC=15,∴则图形戊中的四边形两对角线之和为20+3=23,故答案为23.3.解:∵四边形ABCD是菱形,∴AO=CO=4,BO=DO=3,AC⊥BD,∴AD===5,=AD×BE=×AC×BD,∵S菱形ABCD∴BE=,故答案为:.4.解:∵四边形ABCD是平行四边形,∴∠BCD=∠A=70°,∵DB=DC,∴∠DBC=∠BCD=70°,∵CE⊥BD,∴∠CEB=90°,∴∠BCE=20°.故答案为:20°.5.解:过点C作CM⊥GB于M,CN⊥GD,交GD的延长线于N.∵四边形ABCD为菱形,∴AB=AD=CD=BC,∵AB=BD,∴AB=BD=AD=CD=BC,∴△ABD为等边三角形,△BCD是等边三角形,∴∠A=∠BDF=60°,∠ADC=60°,在△ADE和△DBF中,,∴△ADE≌△DBF(SAS),∴∠ADE=∠DBF,∵∠FBC =60°+∠DBF ,∠NDC =180°﹣(120°﹣∠ADE )=60°+∠ADE ,∴∠NDC =∠FBC ,在△CDN 和△CBM 中,,∴△CDN ≌△CBM (AAS ),∴CM =CN ,在Rt △CBM 与Rt △CDN 中,,∴Rt △CBM ≌Rt △CDN (HL ),∴S 四边形BCDG =S 四边形CMGN .S 四边形CMGN =2S △CMG ,∵∠CGM =60°,∴GM =CG =,CM =CG =,∴S 四边形BCDG =S 四边形CMGN =2S △CMG =2×××=, 故答案为:.6.解:如图,作大正方形的对角线,作小正方形的对角线并延长交大正方形各边于中点, 设小正方形的边长为xm , 则大正方形的边长为x +x x =(1)xm , ∵瓷砖的面积是1m 2,∴大正方形的边长为1m ,即(1)x =1, 解得x =﹣1, ∴中间小正方形的面积为()2=3﹣2, 故答案为:3﹣2.7.解:∵∠ACB=90°,AC=5,∠ABC=30°,∴AB=2AC=10,故①正确;由平移的性质得:A'D'=AD,A'D'∥AD,∴四边形ADD′A′为平行四边形,故②正确;当平移的距离为4时,EE'=4,∴BE'=AB﹣AE﹣EE'=10﹣3﹣4=3,由平移的性质得:∠A'D'E'=∠A'E'D'=∠AED=60°,A'D'=D'E'=DE=AD=3,∴BE'=D'E',∴∠E'BD'=∠E'D'B=∠A'E'D'=30°,∴∠A'D'B=60°+30°=90°,∴BD'=A'D'=3,故④正确;由④得:当平移的距离为4时,∠E'BD'=∠ABC=30°,故③错误;故答案为:①②④.8.解:连接OP,∵四边形ABCD是菱形,∴AC⊥BD,∠CAB=DAB=30°,∵PE⊥OA于点E,PF⊥OB于点F,∴∠EOF=∠OEP=∠OFP=90°,∴四边形OEPF是矩形,∴EF=OP,∵当OP取最小值时,EF的值最小,∴当OP⊥AB时,OP最小,∵AB=4,∴OB=AB=2,OA=AB=2,∴S=OA•OB=AB•OP,△ABO∴OP==,∴EF的最小值为,故答案为:.9.解:如图,过F作FI⊥BC于I,连接FE,FA,∴FI∥CD,∵CE=2BE,BF=2DF,∴设BE=EI=IC=a,CE=FI=2a,AB=3a,∴则FE=FC=FA=a,∴H为AE的中点,∴AH=HE=AE=a,∴AG=AH+GH=a+2,∵四边形ABCD是正方形,∴BE∥AD,∴==,∴GE=AG=(a+2),∵GE=HE﹣GH=a﹣2,∴(a+2)=a﹣2,解得,a=,∴AB=3a=.故答案为:.10.解:设图1中分成的直角三角形的长直角边为a,短直角边为b,,得,∴图1中菱形的面积为:×4=48,故答案为48.11.解:∵四边形ABCD为正方形,∴∠ABC=90°,BA=BC,∴△BAP绕点A逆时针旋转90°可得△ADE,连接PE,由旋转的性质得,ED=BP=7,AE=AP=4,∠PBE=90°,∠AED=∠APB,∴△APE为等腰直角三角形,∴PE=AP=4,∠AEP=45°,在△PED中,∵PD=9,ED=7,PE=4,∴DE2+PE2=DP2,∴△PED为直角三角形,∠PED=90°,∴∠AED=90°+45°=135°,∴∠APB=135°,故答案为:135°.12.解:∵两个正方形的边长分别为2a,a,∴△ABC的的高为:2a+a,底边为:BC=a,∴△ABC的面积是:(2a+a)•a=a2.故答案为:a2.13.解:如图,将△APB绕点A逆时针旋转90°得到△AHD,连接PH,过点A作AE⊥DH交DH的延长线于E,∴△APB≌△AHD,∠PAH=90°,∴PB=DH,AP=AH=1,∠APB=∠AHD=135°,∴PH=AP=,∠APH=∠AHP=45°,∴∠PHD=90°,∴DH===2,∵∠AHD=135°,∴∠AHE=45°,∵AE⊥DH,∴∠AHE=∠HAE=45°,∴AE=EH,AH=AE,∴AE=EH=,∴DE=,∵AD2=AE2+DE2=13,∴正方形的面积为13,故答案为:13.14.解:如图,过点E作EP⊥AC,交FC于点G,当EP⊥AC时,EP取得最小值,∵正三角形ABC与正方形CDEF的顶点B,C,D三点共线,∴∠ACB=60°,∠FCD=90°,∴∠ACF=30°,∴∠CGP=∠EGF=60°,∵∠F=90°,∴∠FEG=30°,设PG=x,则CG=2x,∴FG=CF﹣CG=8﹣2x,∴EG=2FG=2(8﹣2x),∵FG=EF,∴8﹣2x=8×,∴x=4﹣,∴EP=EG+PG=2(8﹣2x)+x=16﹣3x=4+4.故答案为:4+4.15.解:连接GC,延长EG交AD于点L,∵四边形ABCD为正方形,∴AD∥CB,AD=CD,∠ADG=∠CDG=45°,∵DG=DG,∴△ADG≌△CDG(SAS),∴AG=GC,∠HCG=∠DAG,∵∠HCG+∠GCB=90°,∴∠DAG+∠GCB=90°,∵GE⊥AH,∴∠AGL=90°,∴∠ALG+∠LAG=90°,∵AD∥CB,∴∠ALG=∠GEC,∴∠GEC+∠LAG=90°,∴∠GEC=∠GCE,∴GE=GC,∴AG=EG,故①正确;∵GE⊥AH,∴∠AGE=90°,∵AG=EG,∴∠EAH=45°,故②正确;连接AC交BD于点O,则BD=2OA,∵∠AGF+∠FGE=∠GEF+∠EGF=90°,∴∠AGF=∠GEF,∵AG=GE,∠AOG=∠EFG=90°,∴△AOG≌△GFE(AAS),∴OA=GF,∵BD=2OA,∴BD=2GF,故③正确.过点G作MN⊥BC于点N,交AD于点M,交BC于点N,∵G是动点,∴GN的长度不确定,而FG=OA是定值,∴GE不一定平分∠FEC,故④错误;故答案为:①②③.16.解:将△ABD绕点D顺时针旋转90°,得△MCD,如图:由旋转不变性可得:CM=AB=4,AD=MD,且∠ADM=90°,∴△ADM是等腰直角三角形,∴AD=AM,AD最大,只需AM最大,而在△ACM中,AM<AC+CM,∴当且仅当A、C、M在一条直线上,即不能构成△ACM时,AM最大,且最大值为AC+CM =AC+AB=7,此时AD=AM=,故答案为:.17.解:连接BE,如图:∵四边形ABCD是正方形,∴∠ABC=90°,又EF⊥AB于点F,EG⊥BC,∴四边形FBGE是矩形,∴FG=BE,所以当BE最小时,FG就最小,根据垂线段最短,可知当BE⊥AC时,BE最小,当BE⊥AC时,在正方形ABCD中,△AEB是等腰直角三角形,在Rt△ABE中,根据勾股定理可得2BE2=AB2=64,解得BE=4,∴FG最小为4;故答案为4.18.解:∵四边形ABCD是边长为2的正方形,点E是BC的中点,∴AB=AD=BC=CD=2,BE=CE=,∠DCE=∠ABE=90°,∠ABD=∠CBD=45°,∴△ABE≌△DCE(SAS),∴∠CDE=∠BAE,DE=AE,∵AB=BC,∠ABG=∠CBG,BG=BG,∴△ABG≌△CBG(SAS),∴∠BAE=∠BCF,∴∠BCF=∠CDE,又∵∠CDE+∠CED=90°,∴∠BCF+∠CED=90°,∴∠CHE=90°,∴CF⊥DE,故①正确;∵CD=2,CE=,由勾股定理得,DE===5,=CD×CE=DE×CH,∵S△DCE∴CH=2,∵∠CHE=∠CBF,∠BCF=∠ECH,∴△ECH∽△FCB,∴=,∴=,∴CF=5,∴HF=CF﹣CH=3,∴=,故②正确;如图,过点A作AM⊥DE于点M,∵DC=2,CH=2,由勾股定理得,DH===4,∵∠CDH+∠ADM=90°,∠DAM+∠ADM=90°,∴∠CDH=∠DAM,又∵AD=CD,∠CHD=∠AMD=90°,∴△ADM≌△DCH(AAS),∴CH=DM=2,AM=DH=4,∴MH=DM=2,又∵AM⊥DH,∴AD=AH,故④正确;∵DE=5,DH=4,∴HE=1,∴ME=HE+MH=3,∵AM⊥DE,CF⊥DE,∴∠AME=∠GHE,∵∠HEG=∠MEA,∴△MEA∽△HEG,∴=,∴=,∴HG=,故③错误.综上,正确的有:①②④.故答案为:①②④.19.解:∵四边形ABCD是矩形,∴∠BAD=90°,OA=AC,OB=BD,AC=BD,∴OA=OB,∴∠OAB=∠OBA,∵∠DAE=3∠BAE,∴∠BAE=×90°=22.5°,∵AE⊥BD,∴∠OAB=∠OBA=90°﹣22.5°=67.5°,∴∠OAE=67.5°﹣22.5°=45°,∴△AOE是等腰直角三角形,∴OA=OE,设OE=a,则OB=OA=a,∴BE=OB﹣OE=(﹣1)a,BD=2OB=2a,∴DE=BD﹣BE=2a﹣(﹣1)a=(+1)a,∴==,故答案为:.20.解:(1)由折叠可得,AE=OE=DE,CG=OG=DG,∴E,G分别为AD,CD的中点,设CD=2a,AD=2b,则AB=OB=2a,DG=OG=CG=a,BG=3a,BC=AD=2b,∵∠C=90°,在Rt△BCG中,CG2+BC2=BG2,∴a2+(2b)2=(3a)2,∴b=a,∴===,由折叠可得:∠ABE=∠EBG,∠AEB=∠BEO,∠DEG=∠GEO,∵∠AEB=∠BEO+∠DEG=∠GEO=180°,∴∠BEG=90°,∵∠A=∠BEG=90°,∠ABE=∠EBG,∴△ABE∽△EBG,∴==,故答案为:;(2)∵AD=BC=2b=4,∴b=2,a=2,∴AB=OB=4,CG=2,AE=OE=2,∴BG=6,∵∠OBF =∠CBG ,由折叠可得∠BOF =∠BCG =90°, ∴△BOF ∽△BCG , ∴=, 即=,∴OF =,∴S 四边形EBFG =S △BEG +S △BFG =×6×2+×6×=9. 故答案为:9.。
九年级数学下册《30°,45°,60°角的三角函数值》综合练习2(含答案)

30°,45°,60°角的三角函数值一、请准确填空(每小题3分,共24分)1.如图1,在平面直角坐标系中,P 是∠α的边OA 上一点,且P 点坐标为(4,3)则sin α=______,cos α=______.2.已知α是锐角,且2cos α=1,则α=______;若tan(α+15°)=1,则tan α=______.3.如图2,B 、C 是河岸边两点,A 是对岸岸边一点,测得∠ABC=45°,∠ACB=45°,BC=60 m ,则点A 到对岸BC 的距离是_____m.ABC30ABC o图1图2 图34.要把5米长的梯子上端放在距地面3米高的阳台边沿上,猜想一下梯子摆放坡度最小为______.5.已知tan α·tan30°=1,且α为锐角,则α=______.6.设β为锐角,且x 2+2x+sin β=0的两根之差为2,则β=______.7.在△ABC 中,∠C=90°.若3AC=3BC ,则∠A 的度数是______,cosB 的值是______.8.如图3,某建筑物BC 直立于水平地面,AC=9米,要建造阶梯AB ,使每阶高不超过20 cm ,则此阶梯最少要建_____阶.(最后一阶的高度不足20 cm 时,按一阶算,3取1.732)二、相信你的选择(每小题3分,共24分)9.在△ABC 中,AB=AC=4,BC=2,则4cosB 等于( ) A.1B.2C.15D.41510.△ABC 中,∠A 、∠B 都是锐角,且sinA=21,cosB=23,则△ABC 的形状是( )A.直角三角形B.钝角三角形C.锐角三角形D.不能确定11.令a=sin60°,b=cos45°,c=tan30°,则它们之间的大小关系是( ) A.c<b<a B.b<c<a C.b<a<cD.a<c<b12.在Rt △ABC 中,∠C=90°,下列式子中不一定成立的是( ) A.tanA=AAcos sin B.sin 2A+sin 2B=1 C.sin 2A+cos 2A=1D.sinA=sinB13.在△ABC 中,若|sinA -23|+(1-tanB)2=0,则∠C 的度数是( ) A.45°B.60°C.75°D.105°14.已知△ABC 中,∠C=90°,∠A=60°,BC+AC=3+3,则BC 等于( ) A.3B.3C.23D. 3+115.若等腰三角形腰长为4,面积是4,则这个等腰三角形顶角的度数为( ) A.30° B.30°或150° C.60° D.60°或120°16.某人沿着坡度为1∶3的山坡前进了1000 m ,则这个人所在的位置升高了( )A.1000 mB.500 mC.5003 mD.331000 m 三、考查你的基本功(共24分) 17.(16分)计算或化简: (1)sin45°·cos60°-cos45°·sin30°; (2)5tan30°-2(cos60°-sin60°). (3)(23tan30°)2005·(22sin45°)2004; (4)2(2cos45°-tan45°)-(tan60°+sin30°)0-(2sin45°-1)-1.18.(8分)已知△ABC 中,∠C=90°,AC=m ,∠BAC=α(如图4),求△ABC 的面积.(用α的三角函数及m 表示)ABCm图4图5四、生活中的数学(共18分)19.(9分)“郑集中学”有一块三角形形状的花圃ABC ,现可直接测量到∠A=30°,AC= 40 m ,BC=25 m ,请求出这块花圃的面积.20.(9分)如图5,某货船以20海里/小时的速度将一批重要的物资由A 处运往正西方向的B 处,经16小时的航行到达,到达后便接到气象部门通知,一台风中心正由A 向北偏西60°方向移动,距台风中心200海里的圆形区域(包括边界)均会受到影响.在B 处的货船是否会受到台风的侵袭?说明理由.五、探究拓展与应用(共10分)21.(10分)(1)如图6中①、②,锐角的正弦值和余弦值都是随着锐角的确定而确定,变化而变化,试探索随着锐角度数的增大,它的正弦值及余弦值的变化规律.123(注:AB 1 =AB 2=AB 3 )① B 1B 2B 3 AC②图6(2)根据你探索到的规律,试分别比较18°、34°、50°、62°、88°这些锐角的正弦值的大小和余弦值的大小.参考答案一、1.53 54 2.60° 33 3.30 4.435.60°6.30°7.60° 238.26二、9.A 10.B 11.A 12.D 13.C 14.B 15.B 16.B 三、17.(1)0;(2)3338-;(3)21;(4)-22. 18.解:∵tan α=ACBC , ∴BC=AC·tan α=m·tan α.S △ABC =21AC·BC=21m 2tan α.四、19.解:作CD ⊥AB. ∵∠A=30°,∴CD=21AC=21×40=20(m),AD=22CD AC -=203(m), BD=22CD BC -=15(m).(1)当∠ACB 为钝角时,AB=AD+BD=203+15,∴S △ABC =21AB·CD=21(203+15)×20=(2003+150)(m 2).(2)当∠ACB 为锐角时,AB=AD -BD=203-15.∴S △ABC =21AB·CD=21(203-15)×20=(2003-150)(m 2).20.解:AB=16×20=320(海里), 作BD ⊥AC 垂足为D. ∵∠BAC=30°,∴sin30°=ABBD,BD=AB·sin30°=160. ∵160<200,∴B 处的货船会受到影响. 五、21.(1)由图①知 sinB 1AC 1=111AB C B ,sinB 2AC 2=222AB CB ,sinB 3AC 3=333AB C B . ∵AB 1=AB 2=AB 3且B 1C 1>B 2C 2>B 3C 3, ∴111AB C B >222AB C B >333AB C B . ∴sinB 1AC 1>sinB 2AC 2>sinB 3AC 3. 而∠B 1AC 1>∠B 2AC 2>∠B 3AC 3, 而对于cosB 1AC 1=11AB AC , cosB 2AC 2=22AB AC , cosB 3AC 3=33AB AC . ∵AC 1<AC 2<AC 3,∴cosB 1AC 1<cosB 2AC 2<cosB 3AC 3. 而∠B 1AC 1>∠B 2AC 2>∠B 3AC 3. 由图②知sinB 3AC=33AB CB , ∴sin 2B 3AC=2323AB C B . ∴1-sin 2B 3AC=1-2323AB C B =232323AB C B AB =232AB AC . 同理,sinB 2AC=22AB C B ,1-sin 2B 2AC=222AB AC , sinB 1AC=21AB C B ,1-sin 2B 1AC=212AB AC . ∵AB 3>AB 2>AB 1,∴232AB AC <222AB AC <212AB AC .∴1-sin 2B 3AC<1-sin 2B 2AC<1-sin 2B 1AC. ∴sin 2B 3AC>sin 2B 2AC>sin 2B 1AC. ∵∠B 3AC ,∠B 2AC ,∠B 1AC 均为锐角, ∴sinB 3AC>sinB 2AC>sinB 1AC. 而∠B 3AC>∠B 2AC>∠B 1AC. 而对于cosB 3AC=3AB AC, cosB 2AC=2AB AC, cosB 1AC=1AB AC. ∵AB 3>AB 2>AB 1,∴3AB AC <2AB AC <1AB AC. ∴cosB 3AC<cosB 2AC<cosB 1AC. 而∠B 3AC>∠B 2AC>∠B 1AC.结论:锐角的正弦值随角度的增大而增大,锐角的余弦值随角度的增大而减小.(2)由(1)知sin18°<sin34°<sin50°<sin62°<sin88°, cos18°>cos34°>cos50°>cos62°>cos88°.。
九年级数学:垂径定理练习(第2课时)(含答案)

九年级数学:垂径定理练习(第2课时)(含答案)1.平分弦(____________)的直径垂直于弦,并且平分弦所对的弧.2.平分弧的直径垂直平分弧所对的弦.3.垂径定理解读:(1)过圆心;(2)平分弦(不是直径);(3)垂直于弦;(4)平分弦所对的优弧;(5)平分弦所对的劣弧.若一条直线具备这五项中任意两项,则必具备另外三项.A组基础训练1.下列命题正确的有( )①垂直于弦的直径平分弦②平分弦的直径必垂直于弦,并且平分弦所对的两条弧③平分弦的直线必过圆心④弦所对的两条弧的中点连线垂直平分弦A.1个 B.2个 C.3个 D.4个2.如图,⊙O的弦AB=8,M是AB的中点,且OM=3,则⊙O的半径等于( )A.8 B.2 C.10 D.5第2题图3.如图,已知⊙O的半径为2cm,弦AB长23cm,则这条弦的中点C到弦所对劣弧的中点D 的距离为( )第3题图A .1cmB .2cm C.2cm D.3cm4.如图,一条公路弯道处是一段圆弧AB ︵,点O 是这条弧所在圆的圆心,C 是AB ︵的中点,OC 与AB 相交于点D.已知AB =120m ,CD =20m ,那么这段弯道的半径为( )第4题图A .200mB .2003mC .100mD .1003m5.如图,AB 为⊙O 的直径,CD 是弦,AB 与CD 相交于点E.若要得到结论AB⊥CD ,还需添加的条件是________________________________.(不添加其他辅助线)第5题图6.如图,AB ,CD 是⊙O 的直径,D 是AE ︵的中点,AE 与CD 交于点F ,若OF =3,则BE 的长为________.第6题图7.如图所示,AB 是半圆的直径,O 是圆心,C 是半圆上一点,E 是AC ︵的中点,OE 交弦AC 于点D.若AC =8cm ,DE =2cm ,则OD 的长为________.第7题图8.如图,在平面直角坐标系中,点A 的坐标是(10,0),点B 的坐标为(8,0),点C 、D 在以OA 为直径的半圆M 上,且四边形OCDB 是平行四边形,则点C 的坐标为________.第8题图9.如图,⊙O是△ABC的外接圆,且AB=AC=13,BC=24,求⊙O的半径.第9题图10.(绍兴中考)如图1,小敏利用课余时间制作了一个脸盆架,图2是它的截面图,垂直放置的脸盆与架子的交点为A,B,AB=40cm,脸盆的最低点C到AB的距离为10cm,求该脸盆的半径.第10题图B组自主提高11.如图所示,某游乐场的摩天轮⊙P的最高处A到地面l的距离是23m,最低处B到地面l的距离是3m,从B处乘摩天轮绕一周需3分钟,小明从B处乘摩天轮一周的过程中,当他到地面l的距离恰好是18m的时候应为第________分钟.第11题图11.如图,AB ,CD 是半径为5的⊙O 的两条弦,AB =8,CD =6,MN 是直径,AB ⊥MN 于点E ,CD ⊥MN 于点F ,P 为EF 上的任意一点,则PA +PC 的最小值为________.第12题图13.已知:如图,A 、B 、C 为⊙O 上三点,点D 、E 分别为AB ︵、AC ︵的中点,连结DE ,分别交AB 、AC 于点F 、G ,求证:AF =AG.第13题图C 组 综合运用14.如图,隧道的截面由圆弧AED 和矩形ABCD 构成,矩形的长BC 为12m ,宽AB 为3m ,隧道的顶端E (圆弧AED 的中点)高出道路(BC )7m.(1)求圆弧AED 所在圆的半径;(2)如果该隧道内设双行道,现有一辆超高货运卡车高6.5m ,宽2.3m ,问这辆货运卡车能否通过该隧道.第14题图3.3 垂径定理(第2课时)【课堂笔记】1.不是直径【课时训练】1-4.BDAC5.CE =DE 或AC ︵=AD ︵或BC ︵=BD ︵6.67.3cm8.(1,3)9.连结OA 交BC 于点D,连结OC,OB,∵AB =AC =13,∴AB ︵=AC ︵,∴∠AOB =∠AOC ,∵OB =OC,∴AO ⊥BC,CD =12BC =12.在Rt △ACD 中,AC =13,CD =12,所以AD =132-122=5,设⊙O 的半径为r,则在Rt △OCD 中,OD =r -5,CD =12,OC =r,所以(r -5)2+122=r 2,计算得出r =16.9.答:⊙O 的半径为16.9.第10题图10.如图,设圆的圆心为O,连结OA,OC,OC 与AB 交于点D,设⊙O 半径为R,∵OC ⊥AB,∴AD =DB =12AB =20,∠ADO =90°,在Rt △AOD 中,∵OA 2=OD 2+AD 2,∴R 2=202+(R -10)2,∴R =25,即该脸盆的半径为25cm.11.1或212.7 2第13题图13.连OD、OE,交AB、AC于M、N,∵OD=OE=r,∴∠ODE=∠OED,而D,E分别为弧AB,弧AC的中点,∴OD、OE分别垂直于AB、AC,则有∠DFB=∠EGC,∴∠AFG=∠AGF,∴AF=AG.14.(1)设圆心为点O,半径为R,连结OE交AD于F点,连结OA,OD,由垂径定理,得OF垂直平分AD,AF=6,OF=R-(7-3)=R-4,由勾股定理,得AF2+OF2=OA2,即:62+(R-4)2=R2,解得R=6.5米;(2)能通过,但要小心.车宽GH=2.3,圆的半径OH=6.5,由勾股定理,得OG= 6.52-2.32≈6.08,G点与BC的距离为7-6.5+6.08=6.58>6.5;能通过.第14题图。
21.3.2实际问题与一元二次方程(2)-人教版九年级数学上册练习

人教版九年级数学上册21.3.2实际问题与一元二次方程(2)一.选择题(共6小题)1.目前以5G等为代表的战略性新兴产业蓬勃发展.某市2019年底有5G用户2万户,计划到2021年底全市5G用户数累计达到8.72万户.设全市5G用户数年平均增长率为x,则x值为()A.20%B.30%C.40%D.50%2.某件羊毛衫的售价为1000元,因换季促销,商家决定降价销售,在连续两次降价x%后,售价降低了190元,则x为()A.5B.10C.19D.813.两个相邻自然数的积是132.则这两个数中,较大的数是()A.11B.12C.13D.144.在一次篮球邀请赛中,参赛的每两个队之间都要比赛一场,共比赛36场.则参赛的球队数为()A.6个B.8个C.9个D.12个5.某校“研学”活动小组在一次野外实践时,发现一种植物的1个主干上长出x个支干,每个支干上再长出x个小分支.若在1个主干上的主干、支干和小分支的数量之和是43个,则x等于()A.4B.5C.6D.76.如图,某中学计划靠墙围建一个面积为80m2的矩形花圃(墙长为12m),围栏总长度为28m,则与墙垂直的边x为()A.4m或10m B.4m C.10m D.8m二.填空题(共6小题)7.疫情期间居民为了减少外出时间,大家更愿意使用APP在线上买菜,某买菜APP今年一月份新注册用户为200万,三月份新注册用户为338万,则二、三两个月新注册用户每月平均增长率是.8.2019女排世界杯于9月14月至29日在日本举行,赛制为单循环比赛(即每两个队之间比赛一场),一共比赛66场,中国女排以全胜成绩卫冕世界杯冠军,为国庆70周年献上大礼,则中国队在本届世界杯比赛中连胜场.9.用一根20m长的绳子围成一个面积为24m2矩形,则矩形的长与宽分别是.10.九年级8班第一小组x名同学在庆祝2020年新年之际,互送新年贺卡,表达同学间的真诚祝福,全组共送出贺卡30张,则x的值是.11.如图,某小区规划在一个长34m、宽22m的矩形ABCD上,修建三条同样宽的通道,使其中两条与AB平行,另一条与AD平行,其余部分种花草.要使每一块花草的面积都为100m2,那么通道的宽应设计成m.12.如图,有一张矩形纸片,长10cm,宽6cm,在它的四角各剪去一个同样的小正方形,然后将四周突出部分折起,就能制作一个无盖的方盒,若方盒的底面积(图中阴影部分)是32cm2,则剪去的小正方形的边长为cm.三.解答题(共3小题)13.小张2019年末开了一家商店,受疫情影响,2020年4月份才开始盈利,4月份盈利6000元,6月份盈利达到7260元,且从4月份到6月份,每月盈利的平均增长率都相同.(1)求每月盈利的平均增长率.(2)按照这个平均增长率,预计2020年7月份这家商店的盈利将达到多少元?14.今年我国发生了较为严重的新冠肺炎疫情,口罩供不应求,某商店恰好年前新进了一批口罩,若按每个盈利1元销售,每天可售出200个,如果每个口罩的售价上涨0.5元,则销售量就减少10件,问应将每件涨价多少元时,才能让顾客得到实惠的同时每天利润为480元?15.如图,小华要为一个长3分米,宽2分米的长方形防疫科普电子小报四周添加一个边框,要求边框的四条边宽度相等,且边框面积与电子小报内容所占面积相等,小华添加的边框的宽度应是多少分米?人教版九年级数学上册21.3.2实际问题与一元二次方程(2)参考答案与一.选择题(共6小题)1.目前以5G等为代表的战略性新兴产业蓬勃发展.某市2019年底有5G用户2万户,计划到2021年底全市5G用户数累计达到8.72万户.设全市5G用户数年平均增长率为x,则x值为()A.20%B.30%C.40%D.50%【解答】解:设全市5G用户数年平均增长率为x,则2020年底全市5G用户数为2(1+x)万户,2021年底全市5G用户数为2(1+x)2万户,依题意,得:2+2(1+x)+2(1+x)2=8.72,整理,得:x2+3x﹣1.36=0,解得:x1=0.4=40%,x2=﹣3.4(不合题意,舍去).故选:C.2.某件羊毛衫的售价为1000元,因换季促销,商家决定降价销售,在连续两次降价x%后,售价降低了190元,则x为()A.5B.10C.19D.81【解答】解:依题意,得:1000(1﹣x%)2=1000﹣190,解得:x1=10,x2=190(不合题意,舍去).故选:B.3.两个相邻自然数的积是132.则这两个数中,较大的数是()A.11B.12C.13D.14【解答】解:设这两个数中较大的数为x,则较小的数为(x﹣1),依题意,得:x(x﹣1)=132,解得:x1=12,x2=﹣11(不合题意,舍去).故选:B.4.在一次篮球邀请赛中,参赛的每两个队之间都要比赛一场,共比赛36场.则参赛的球队数为()A.6个B.8个C.9个D.12个【解答】解:设有x个队参赛,根据题意,可列方程为:x(x﹣1)=36,解得:x=9或x=﹣8(舍去),故选:C.5.某校“研学”活动小组在一次野外实践时,发现一种植物的1个主干上长出x个支干,每个支干上再长出x个小分支.若在1个主干上的主干、支干和小分支的数量之和是43个,则x等于()A.4B.5C.6D.7【解答】解:依题意,得:1+x+x2=43,整理,得:x2+x﹣42=0,解得:x1=6,x2=﹣7(不合题意,舍去).故选:C.6.如图,某中学计划靠墙围建一个面积为80m2的矩形花圃(墙长为12m),围栏总长度为28m,则与墙垂直的边x为()A.4m或10m B.4m C.10m D.8m【解答】解:∵与墙垂直的边为xm,∴与墙平行的边为(28﹣2x)m.依题意,得:x(28﹣2x)=80,整理,得:x2﹣14x+40=0,解得:x1=4,x2=10.当x=4时,28﹣2x=20>12,不合题意,舍去;当x=10时,28﹣2x=8.故选:C.二.填空题(共6小题)7.疫情期间居民为了减少外出时间,大家更愿意使用APP在线上买菜,某买菜APP今年一月份新注册用户为200万,三月份新注册用户为338万,则二、三两个月新注册用户每月平均增长率是30%.【解答】解:设二、三两个月新注册用户每月平均增长率是x,依题意,得:200(1+x)2=338,解得:x1=0.3=30%,x2=﹣2.3(不合题意,舍去).故答案为:30%.8.2019女排世界杯于9月14月至29日在日本举行,赛制为单循环比赛(即每两个队之间比赛一场),一共比赛66场,中国女排以全胜成绩卫冕世界杯冠军,为国庆70周年献上大礼,则中国队在本届世界杯比赛中连胜11场.【解答】解:设中国队在本届世界杯比赛中连胜x场,则共有(x+1)支队伍参加比赛,依题意,得:x(x+1)=66,整理,得:x2+x﹣132=0,解得:x1=11,x2=﹣12(不合题意,舍去).故答案为:11.9.用一根20m长的绳子围成一个面积为24m2矩形,则矩形的长与宽分别是6m,4m.【解答】解:设矩形的长为xm,则宽为m,依题意,得:x•=24,整理,得:x2﹣10x+24=0,解得:x1=6,x2=4.∵x≥,∴x≥5,∴x=6,=4.故答案为:6m,4m.10.九年级8班第一小组x名同学在庆祝2020年新年之际,互送新年贺卡,表达同学间的真诚祝福,全组共送出贺卡30张,则x的值是6.【解答】解:依题意,得:x(x﹣1)=30,解得:x1=6,x2=﹣5(不合题意,舍去).故答案为:6.11.如图,某小区规划在一个长34m、宽22m的矩形ABCD上,修建三条同样宽的通道,使其中两条与AB平行,另一条与AD平行,其余部分种花草.要使每一块花草的面积都为100m2,那么通道的宽应设计成2m.【解答】解:设通道的宽应设计成xm,则种植花草的部分可合成长(34﹣2x)m,宽(22﹣x)m的矩形,依题意,得:(34﹣2x)(22﹣x)=100×6,整理,得:x2﹣39x+74=0,解得:x1=2,x2=37(不合题意,舍去).故答案为:2.12.如图,有一张矩形纸片,长10cm,宽6cm,在它的四角各剪去一个同样的小正方形,然后将四周突出部分折起,就能制作一个无盖的方盒,若方盒的底面积(图中阴影部分)是32cm2,则剪去的小正方形的边长为1cm.【解答】解:设剪去的小正方形的边长为xcm,依题意,得:(10﹣2x)(6﹣2x)=32,整理,得:x2﹣8x+7=0,解得:x1=1,x2=7(不合题意,舍去).故答案为:1.三.解答题(共3小题)13.小张2019年末开了一家商店,受疫情影响,2020年4月份才开始盈利,4月份盈利6000元,6月份盈利达到7260元,且从4月份到6月份,每月盈利的平均增长率都相同.(1)求每月盈利的平均增长率.(2)按照这个平均增长率,预计2020年7月份这家商店的盈利将达到多少元?【解答】解:(1)设每月盈利的平均增长率为x,依题意,得:6000(1+x)2=7260,解得:x1=0.1=10%,x2=﹣2.1(不合题意,舍去).答:每月盈利的平均增长率为10%.(2)7260×(1+10%)=7986(元).答:按照这个平均增长率,预计2020年7月份这家商店的盈利将达到7986元.14.今年我国发生了较为严重的新冠肺炎疫情,口罩供不应求,某商店恰好年前新进了一批口罩,若按每个盈利1元销售,每天可售出200个,如果每个口罩的售价上涨0.5元,则销售量就减少10件,问应将每件涨价多少元时,才能让顾客得到实惠的同时每天利润为480元?【解答】解:设应将每件涨价x元,则每天可售出(200﹣10×)个,依题意,得:(1+x)(200﹣10×)=480,化简,得:x2﹣9x+14=0,解得:x1=2,x2=7.又∵要让顾客得到实惠,∴x=2.答:应将每件涨价2元时,才能让顾客得到实惠的同时每天利润为480元.15.如图,小华要为一个长3分米,宽2分米的长方形防疫科普电子小报四周添加一个边框,要求边框的四条边宽度相等,且边框面积与电子小报内容所占面积相等,小华添加的边框的宽度应是多少分米?【解答】解:设小华添加的边框的宽度应是x分米,依题意,得:(3+2x)(2+2x)﹣3×2=3×2,整理,得:2x2+5x﹣3=0,解得:x1=,x2=﹣3(不合题意,舍去).答:小华添加的边框的宽度应是分米.。
苏科版九上 解直角三角形应用(2) 练习2
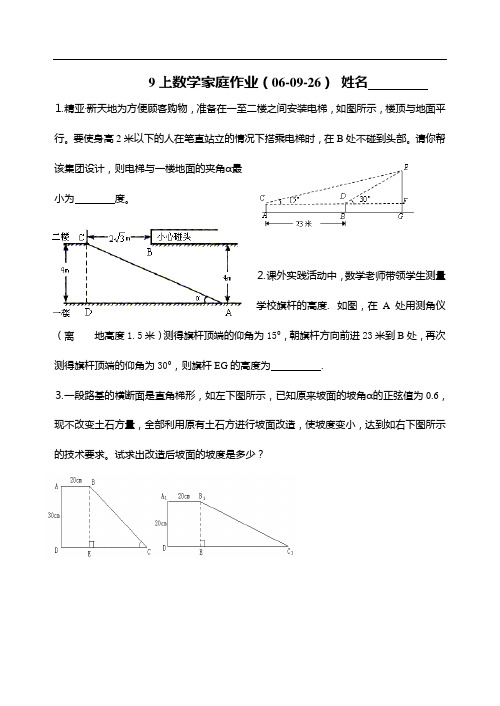
9上数学家庭作业(06-09-26) 姓名⒈精亚·新天地为方便顾客购物,准备在一至二楼之间安装电梯,如图所示,楼顶与地面平行。
要使身高2米以下的人在笔直站立的情况下搭乘电梯时,在B 处不碰到头部。
请你帮该集团设计,则电梯与一楼地面的夹角α最小为 度。
⒉课外实践活动中,数学老师带领学生测量学校旗杆的高度. 如图,在A 处用测角仪(离 地高度1.5米)测得旗杆顶端的仰角为15°,朝旗杆方向前进23米到B 处,再次测得旗杆顶端的仰角为30°,则旗杆EG 的高度为 .⒊一段路基的横断面是直角梯形,如左下图所示,已知原来坡面的坡角α的正弦值为0.6,现不改变土石方量,全部利用原有土石方进行坡面改造,使坡度变小,达到如右下图所示的技术要求。
试求出改造后坡面的坡度是多少?⒋如图,山脚下有一棵树AB ,小强从点B 沿山坡向上走50m 到达点D ,用高为1.5m 的测角仪CD 测得树顶的仰角为10°,已知山坡的坡角为15°,求树AB的高(精确到0.1m )BC PD A10°15°⒌如图,我校九(4)班的一个学习小组进行测量孤山高度的实践活动。
部分同学在山脚点A 测得山腰上一点D 的仰角为30°,并测得AD 的长度为180米;另一部分同学在山顶点B 测得山脚点A 的俯角为45°,山腰点D 的俯角为60°。
请你帮助他们计算出小山的高度BC (计算过程和结果都不取近似值)。
⒍如图,MN 表示某引水工程的一段设计路线,从M 到N 的走向为南偏东30°,在M 的南偏东60°方向上有一点A ,以A 为圆心、500m 为半径的圆形区域为居民区。
取MN 上的另一点B ,测得BA 的方向为南偏东75°。
已知MB =400m ,通过计算回答,如果不改变方向,输水管道是否会穿过居民区。
⒎如图,城市规划期间,要拆除一电线杆AB ,已知距电线杆水平距离14米的D 处有一大坝,背水坡的坡度i =1: 0.5,坝高CF 为2米,在坝顶C 处测得杆顶A 的仰角为30°,D 、E 之间是宽为2米的人行道.请问:在拆除电线杆AB 时,为确保行人安全,是否需要将此人行道封上?请说明理由(在地面上,以点B 为圆心,以AB 长为半径的圆形区域为危险区域)。
苏科版九上 解直角三角形应用(2) 练习2
九年级数学家庭作业(06-09-26) 姓名⒈精亚·新天地为方便顾客购物,准备在一至二楼之间安装电梯,如图所示,楼顶与地面平行。
要使身高2米以下的人在笔直站立的情况下搭乘电梯时,在B 处不碰到头部。
请你帮该集团设计,则电梯与一楼地面的夹角α最小为 度。
⒉课外实践活动中,数学老师带领学生测量学校旗杆的高度. 如图,在A 处用测角仪(离 地高度1.5米)测得旗杆顶端的仰角为15°,朝旗杆方向前进23米到B 处,再次测得旗杆顶端的仰角为30°,则旗杆EG 的高度为 .⒊一段路基的横断面是直角梯形,如左下图所示,已知原来坡面的坡角α的正弦值为0.6,现不改变土石方量,全部利用原有土石方进行坡面改造,使坡度变小,达到如右下图所示的技术要求。
试求出改造后坡面的坡度是多少?⒋如图,山脚下有一棵树AB ,小强从点B 沿山坡向上走50m 到达点D ,用高为1.5m 的测角仪CD 测得树顶的仰角为10°,已知山坡的坡角为15°,求树AB 的高(精确到0.1m )BC PD A10°15°⒌如图,我校九(4)班的一个学习小组进行测量孤山高度的实践活动。
部分同学在山脚点A 测得山腰上一点D 的仰角为30°,并测得AD 的长度为180米;另一部分同学在山顶点B 测得山脚点A 的俯角为45°,山腰点D 的俯角为60°。
请你帮助他们计算出小山的高度BC (计算过程和结果都不取近似值)。
⒍如图,MN 表示某引水工程的一段设计路线,从M 到N 的走向为南偏东30°,在M 的南偏东60°方向上有一点A ,以A 为圆心、500m 为半径的圆形区域为居民区。
取MN 上的另一点B ,测得BA 的方向为南偏东75°。
已知MB =400m ,通过计算回答,如果不改变方向,输水管道是否会穿过居民区。
⒎如图,城市规划期间,要拆除一电线杆AB ,已知距电线杆水平距离14米的D 处有一大坝,背水坡的坡度i =1: 0.5,坝高CF 为2米,在坝顶C 处测得杆顶A 的仰角为30°,D 、E 之间是宽为2米的人行道.请问:在拆除电线杆AB 时,为确保行人安全,是否需要将此人行道封上?请说明理由(在地面上,以点B 为圆心,以AB 长为半径的圆形区域为危险区域)。
北京市景山学校2022-2023学年九年级上学期数学期中基础练习2(含答案解析)
18.已知二次函数 y1 ax2 bx c a 0 与一次函数 y2 mx nm 0 的图象相交于点 A1, 6 和 B 7,3 ,如图所示,则使不等式 ax2 bx c mx n 成立的 x 的取值范围是
B. x1 1, x2 3
C. x1 4, x2 1
D.无法求解
8.通过平移 y x 12 3 的图象,可得到 y x2 的图象,下列平移方法正确的是( )
A.向左移动 1 个单位,向上移动 3 个单位 B.向右移动 1 个单位,向上移动 3 个单
位
C.向左移动 1 个单位,向下移动 3 个单位 D.向右移动 1 个单位,向下移动 3 个单
∴ x1 4, x2 1. 故选:C 【点睛】本题考查了一元二次方程的解,解题的关键是掌握能使一元二次方程左右两边相等 的未知数的值是一元二次方程的解. 8.C 【分析】根据平移前后两个抛物线的顶点坐标的变化来判定平移方法.
【详解】解:∵抛物线 y x2 的顶点坐标是 0,0 , 又∵抛物线 y x 12 3 的顶点坐标是 1,3 , ∴由二次函数 y x 12 3 的图象向左移动 1 个单位,向下移动 3 个单位,可得到 y x2
C. y a 1 x2
D. y a(1 x)2
7.关于 x 的方程 a (x + m)2 + b = 0 的解是 x1 2, x2 1 (a,m,b 均为常数,a≠0),则
方程 a (x + m + 2)2 +b = 0 的解是( )
北师大版九年级数学上册同步练习 第2章
北师大版数学九年级上册第二章第1节认识一元二次方程同步练习1.下列方程中是关于x 的一元二次方程的是( ) A .x 2+21x=0 B .ax 2+bx +c =0 C .(x -1)(x +2)=1 D .3x 2-2xy -5y 2=0 2.若方程(m +2)x ∣m ∣+3x -1=0是关于x 的一元二次方程,则m =______.3.下列数中:-1,2,-3,-2,3,是一元二次方程x 2-2x =3的解的有 ___________. 4.方程()45x x -=化为一般形式为( )A .2450x x =-+B .2450x x =++C .2450x x =--D .2450x x =+- 5.方程23740x x =-+中二次项的系数,一次项的系数及常数项分别是( )A .3、7、4B .3、7、﹣4C .3、﹣7、4D .3、﹣7、﹣4 6.将一元二次方程2514x x =-化成一般形式后,二次项系数和一次项系数分别为( )A .5、-4B .5、4C .5x 2、4xD .5x 2、-4x 、 7.一元二次方程x 2-4=0的根是( )A .-2B .±2C .2D .以上都不对 8.关于x 的方程x 2+x -a =0一个解是x =1,则a 为( )A .2B .-2C .1D .-19.下列方程中关于x 2203x =-;②21kx x =-3;③211x x x--=;④()210x x x -+=;⑤()2320k x kx +-=;⑥221x ax =-;是关于x 一元二次方程的个数有( )A .1B .2C .3D .4 10.把一元二次方程2(x 2+7)=x +2化成一般形式是 .11.下列数中-1,-2,1,2,是一元二次方程一元二次方程x 2-x -2=0的根是___________. 12.若0是一元二次方程22610x x m ++-=的一个根,则m 的取值为( )A .1B .-1C .±1D .以上都不是 13.已知关于x 的方程20x bx a =++有一个根是-a (a≠0),则a -b 的值为( )A .-1B .0C .1D .214.在一次聚会时,x 个人见面后每两人握一次手,共握手10次,则可列方程( )A .()110x x =-B .()2110x x =-C .()1102x x =⨯+D .()1102x x =⨯-15.某地区的消费品月零售总额持续增长,九月份为⒈2亿元,十月、十一月两个月一共为2.8亿元.设九月份到十一月份平均每月增长的百分率为x ,则可列方程( )A .()1.212 2.8x += B .()21.212.8x += C .()1.2.21 2.8x =+1+ D .()()21.21 1.212.8x x =+++16.已知m 是方程x 2-x -2=0的一个根,求代数式4m 2-4m -2的值. 17.若()1160m m x mx -+++2=是关于x 的一元二次方程,求m 的值.18.把下列一元二次方程化成一元二次方程的一般形式,并写出方程的二次项系数,一次项系数,常数项.(1)(3x -2)(2x -3)=x 2-5; (2)(x 2+7)=x +2.19.若方程x 2-2x +m =0的一个根是x =-1,求m 的值.20. 若关于x 的一元二次方程(m ﹣1)x 2+5x +m 2﹣3m +2=0有一个根为0,求m 的值.21. 已知x 2+3x +5的值为7,求代数式3x 2+9x ﹣2的值22.试判断:关于x 的方程(2a —4)x 2-2bx +c =0. (1)何时为一元二次方程?(2)何时为一元一次方程?答案:1.C2.m=23.-1,34.C5.C6.A7.B8.A9.B10.2x2-x+12=0;a=2,b=-1,c=12;11.2,-112.C13.A14.D15.D16.解:由已知,得m2-m-2=0∴m2-m=2∴4m2-4m-2=4(m2-m)-2=4×2-2=6.17.m=118.(1)3x2-5x+1=0;a=3,b=-5,c=1;(2)3x2-5x+1=0;a=3,b=-5,c=1;19.m=-320.m=221.解:由已知,得x2+3x+5=7∴x2+3x=2∴3x2+9x-2=3(x2+3x)-2=3×2-2=4.22.(1)a≠2;(2)a=2且b≠0;北师大版数学九年级上册第二章第2节用配方法解一元二次方程(第1课时)1.16的平方根是( )A .4B .-4C .±4D .±8 2.方程x 2=9的解是( )A .x 1=x 2=3B .x 1=x 2=-3C .x 1=3,x 2=-3D .x =33.方程x 2=3的解是( )A .12x x ==B .12x x ==C .1x 2x =D .x =34.方程()210x -=的解是( )A .x 1=1,x 2=-1B .x 1=x 2=1C . x 1=x 2=-1D . x 1=1,x 2=-25.方程()219x -=的解是( )A .x 1=1,x 2=-3B . x 1=4,x 2=-4C . x 1=4,x 2=-2D . x =36.若1是一元二次方程x 2+x -m 2=0的一个根,则m 为 . 7.直接写出方程的解:(1)()2190x -=+的解是__________;(2)()2316x -=的解是__________. 8.直接写出方程的解:(1)x 2+2x +1=9的解是 ; (2)x 2-2x -3=0的解是__________. 9.用直接开方法解方程.⑴9x 2=25 ⑵2x 2-98=0⑶3(x -2)2=0 ⑷3(x -1)2=2710.如果12x =是关于x 的方程22320x ax a -=+的根,求关于y 的方程23y a -=的解.11.一元二次方程2+2990x x -=变形正确的是( )A .()2+1100x =B .()21100x =﹣C .()2+2100x = D .()22100x -=12.将方程2250x x --=变形为()2+x m n =的形式正确的是( )A .()2+16x =B .()2+29x =C .()216x -= D .()229x -=13.方程3x 2=2的根是___________.14.一元二次方程22426x x -+=的根是___________.15.解下列方程:⑴()22510x +-= ⑵(x -2)2=9⑶()23175y -= ⑷2215x x -+=⑸()2531250x --= ⑹24415x x -+=16.用配方法解下列方程:⑴x 2+2x -3=0 ⑵x 2-6x -8=0⑶x 2-8x +7=0 (4)x 2-4x =1(5)x 2-4x -6=0, (6) x 2+12x +36=017.已知x 、y 、z 满足2246130++-=x x y y ,求代数式()zxy 的值.答案:1.C 2.C 3.C 4.B 5.C 6.±27.(1)4或-2;(2)7或-1; 8.(1)2或-4;(2)3或-1;9.(1)x 1=53,x 2=-53;(2)x 1=7,x 2=-7;(3)x 1=2+33,x 2=2-33;(4)x 1=4,x 2=-2; 10.y 1=2,y 2=-2; 11.A 12.C13.x 1=63,x 2=-63; 14.x 1=1+3,x 2=1-3; 15.(1)x 1=-2,x 2=-3;(2)x 1=5,x 2=-1;(3)y 1=6,y 2=-4; (4)x 1=1+5,x 2=1-5; (5)x 1=8,x 2=-2;(6)x 1=1+52,x 2=1-52;16.(1)x 1=1,x 2=-3;(2)x 1=3+17,x 2=3-17; (3)x 1=7,x 2=-1; (4)x 1=2+5,x 2=2-5;(5)x 1=2+10,x 2=2-10; (6)x 1=x 2=-6; 17.解:由已知,得x 2-4x +4+y 2+6y +9+z +2=0∴(x -2)2+(y +3)2+z +2=0 ∴x =2,y =-3,z =-2.∴(xy)z=[2×(-3)]-2=(-6)-2=1 36.北师大版数学九年级上册第二章第4节用因式分解法解一元二次方程同步练习1.方程x(x+3)=x的解是()A.x1=x2=﹣3 B.x1=1,x2=3 C.x1=0,x2=﹣3 D.x1=0.x2=﹣2 2.一元二次方程x2﹣5x+6=0的解为()A.x1=2,x2=﹣3 B.x1=﹣2,x2=3C.x1=﹣2,x2=﹣3 D.x1=2,x2=33.方程(x+1)(x﹣3)=﹣4的解是()A.x1=﹣1,x2=3 B.x1=1,x2=0 C.x1=1,x2=﹣1 D.x1=x2=14解方程(5x﹣3)2=2(5x﹣3),选择最适当的方法是()A..直接开平方法B.配方法C.公式法D.因式分解法5.方程x2-3x-4=0的所有根为( )A.x1=-1,x2=-4;B.x1=-1,x2=4 ;C.x1=1,x2=4 D.x1=1,x2=-46.方程(x-2)(x+3)=0的解是( )A.x=2 B.x=-3 C.x1=2,x2=-3 D.x1=-2,x2=37.方程x(x-2)=x-2的根是( )A.x=1 B.x1=2,x2=0 C.x1=1,x2=2 D.x=28.若菱形ABCD的一条对角线长为8,边CD的长是方程x2﹣10x+24=0的一个根,则该菱形ABCD的周长为()A.16 B.24 C.16或24 D.489.若一个三角形的两边长分别是2和6,第三边的边长是方程x2﹣10x+21=0的一个根,则这个三角形的周长为()A.7 B.3或7 C.15 D.11或15 10.将下列多项式分解因式(1)x2-5x==___________;(2)2x(x-3)-5(x-3) =___________;(3)x2+2x-8 =___________;(4)9x2-6x+1=0=___________;11.元二次方程x(x-1)=x的解是____ .12.小华在解一元二次方程x2-4x=0时,得出一个根是x1=4,则另一个根是x2=______.13.用适当解下列方程:(1)5x2-2x=0;(可提公因式)⑵9x2-4=0(平方差公式)(3)y2+2y=15.(4) (x-1)2-2(x-1)=02=3x(可移项再提公因式); (6)(x-2)(x+3)=0(5)x14.已知:m是关于x的一元二次方程mx2-2x+m=0的一个根,求m的值.15.阅读材料,解答问题:为解方程(x2-1)2-5(x2-1)+4=0,我们可以将x2-1视为一个整体,然后设x2-1=y,则(x2-1)2=y2,原方程化为y2-5y+4=0.解得y1=4,y2=1.①当y=4时,x2-1=4,∴x2=5,∴x=±5.②当y=1时,x2-1=1,∴x2=2,∴x=±2.∴原方程的解为x 1=2,x 2=-2,x 3=5,x 4=-5.在由原方程得到方程①的过程中,利用换元法达到了降次的目的,体现了转化的数学思想.利用上面的方法解方程x 4-x 2-6=0.16.已知:在平面直角坐标系中,点A 、B 分别在x 轴正半轴上,且线段OA 、OB (OA <OB )的长分别等于方程x 2﹣5x +4=0的两个根,点C 在y 轴正半轴上,且OB =2OC . (1)求A 、B 、C 三点坐标;(2)将△OBC 绕点C 顺时针旋转90°后得到△O ′B ′C ,求直线B ′C 的表达式.xy –1–2–3–41234–1–2–3–41234O答案: 1.D 2.D 3.D 4.D 5.B 6.C 7.C 8.B 9.C10.(1)x (x -5);(2)(x -3)(2x -5);(3)(x +4)(x -2);(4)(3x -1)2; 11.x 1=0,x 2=2; 12.013.(1)x 1=0,x 2=25; (2)x 1=23,x 2=-23; (3)y 1=-5,y 2=3;(4)x 1=1,x 2=3; (5)x 1=0,x 2=3; (6)x 1=2,x 2=-3; 14.m =0,-1,1; 15.x =± 316.解:(1)解方程x 2﹣5x +4=0得x 1=1,x 2=4, ∵OA <OB , ∴OA =1,OB =4,∵A 、B 分别在x 轴正半轴上, ∴A (1,0)、B (4,0);又∵OB =2OC ,且点C 在y 轴正半轴上 ∴OC =2,则C (0,2);(2)∵将△OBC 绕点C 顺时针旋转90°后得△O ′B ′C ,∴OB =O ′B ′=4,OC =O ′C ′=2,∠COB =∠C O′B ′=90°,∠OCO ′=∠BCB ′=90° ∴O ′(﹣2,2)、B ′(﹣2,﹣2), 设直线B ′C 的解析式为y =kx +b , 把B ′(﹣2,﹣2),C (0,2)代入得⎩⎨⎧-2k +b =-2b =2,解得⎩⎨⎧k =2b =2, ∴直线B ′C 的解析式为y =2x +2.xyA BCB'O'O北师大版数学九年级上册第二章第5节一元二次方程根与系数的关系同步练习1.若x 1、x 2是一元一次方程x 2-5x +6=0的两个根,则x 1+x 2的值是 ( ) A .1 B .5 C .-5 D .6 2.若x 1、x 2是一元一次方程x 2+x -2=0的两个根,则x 1·x 2的值是 ( ) A .-1 B .-2 C .1 D .2 3.以3和—2为根的一元二次方程是( )A .x 2+x -6=0 B .x 2+x +6=0 C .x 2-x -6=0 D .x 2-x +6=0 4.已知x 2-(m -1)x -(2m -2)=0两根之和等于两根之积,则m 的值为( ) A .1 B .—1 C .2 D .—2 5.已知方程3x 2-5x -7=0的两根为x 1、x 2,则下列各式中正确的是 ( ) A .x 1+x 2=5,x 1·x 2=7 B .x 1+x 2=-5,x 1·x 2=-7 C .x 1+x 2=53,x 1·x 2=-73 D .x 1+x 2=-53,x 1·x 2=-73 6.设方程x 2+x ﹣2=0的两个根为α,β,那么α+β﹣αβ的值等于( ) A .﹣3B .﹣1C .1D .37.关于x 的一元二次方程x 2+(a 2﹣3a )x +a =0的两个实数根互为倒数,则a 的值为( ) A .﹣3B .0C .1D .﹣3 或 08.关于x 的一元二次方程2x 2+kx ﹣4=0的一个根x 1=﹣2,则方程的另一个根x 2和k 的值为( ) A .x 2=1,k =2B .x 2=2,k =2C .x 2=1,k =﹣1D .x 2=2,k =﹣19.关于x 的一元二次方程x 2﹣5x +2p =0的一个根为1,则另一根为( ) A .﹣6B .2C .4D .110.已知m 、n 是一元二次方程x 2﹣3x ﹣1=0的两个实数根,则1m +1n =( ) A .3B .﹣3C .13D .﹣1311.一元二次方程x 2-4x -c =0的一个根是3,则c =_________,另一个根是_________. 12.一元二次方程x 2-x -3=0两根的倒数和等于__________.13.关于x 的方程x 2+px +a =0的根为x 1=1+2,x 2=1-2,则p =______,q =____. 14.若x 1、x 2是方程x 2-5x -7=0的两根,那么(1)x 2 1+x 2 2=________;(2)(x 1-x 2)2=__________;15.阅读材料:设一元二次方程ax 2+bx +c =0(a ≠0)的两根为x 1,x 2,则两根与方程系数之间有如下关系:x 1+x 2=-b a ,x 1·x 2=ca .根据该材料填空:已知x 1、x 2是方程x 2+6x +3=0的两实数根,则x 1x 2+ x 2x 1= .16.利用方程的根与系数的关系,求方程的两根之和、两根之积: (1)x 2-3x -5=0 (2)2x 2+5x -5=017.已知x 1、x 2是一元二次方程2x 2-2x +1-3m =0的两个实数根,且x 1·x 2+2(x 1+x 2)>0,求实数m 的取值范围.18.已知实数a 、b 满足等式a 2-2a -1=0,b 2-2b -1=0,求b a +ab 的值.19.已知关于x 的方程x 2-(k +1)x +14k 2+1=0的两根是一个长方形形两邻边的长.(1)k 为何值时,方程有两个实数根; (2)当该长方形形的对角线长为5时,求k . (3)当k 为何值时,矩形变为正方形?20.关于x 的一元二次方程x 2+2mx +m 2+m =0有两个不相等的实数根. (1)求m 的取值范围.(2)设出x 1、x 2是方程的两根,且x 12+x 22=12,求m 的值.21.已知:关于x 的一元二次方程x 2+πx ﹣2=0有两个实数根. (1)求m 的取值范围;(2)设方程的两根为x 1、x 2,且满足(x 1﹣x 2)2﹣17=0,求m 的值.22.已知x1,x2是一元二次方程x2﹣2x+k+2=0的两个实数根.(1)求k的取值范围.(2)是否存在实数k,使得等式1x1+1x2=k﹣2成立?如果存在,请求出k的值;如果不存在,请说明理由.答案: 1.B 2.B 3.C 4.A 5.C 6.C 7.C 8.A 9.C 10.B 11.-3;1 12.-13 13.-2;-1 14.39;53 15.10;16.(1)x 1+x 2=3,x 1•x 2=-5;(2)x 1+x 2=-52,x 1•x 2=-52. 17.解:∵x 1、x 2是一元二次方程2x 2﹣2x +1﹣3m =0的两个实数根, ∴x 1+x 2=1,x 1•x 2=1-3m2.又∵x 1﹣x 2+2(x 1+x 2)>0, ∴1-3m 2+2>0 解得:m <53 (4分),又∵原方程有实数根,∴b 2﹣4ac =(﹣2)2﹣4×2×(1﹣3m )=4﹣8+24m =﹣4+24m ≥0, ∴m ≥16 (7分) ∴16≤m <53 (8分)18解:当a =b 时,原式=1+1=2;当a ≠b 时,可以把a 、b 看作方程x 2﹣2x ﹣1=0的两个根, ∴a +b =2,ab =﹣1,∴b a +a b =a 2+b 2ab =(a +b )2-2ab ab =4+2-1=﹣6. 综上所述:b a +ab 的值为2或﹣6.19.解:(1)△=[﹣(k +1)]2﹣4×1×(14k 2+1)=2k ﹣3, ∵方程有两个实数根, ∴△≥0,即2k ﹣3≥0, 解得:k ≥32,∴当k ≥32时,方程有两个实数根. (2)设方程x 2﹣(k +1)+14k 2+1=0的两根分别为a 、b ,则a +b =k +1,ab =14k 2+1,∵矩形的对角线长为5,即a 2+b 2=5,∴a 2+b 2=(a +b )2﹣2ab =(k +1)2﹣2×(14k 2+1)=5, 整理得:k 2+4k ﹣12=0, 解得:k =2或k =﹣6(舍去).∴当矩形的对角线长为5时,k 的值为2. (3)当矩形为正方形时,方程两根相等, ∴△=2k ﹣3=0, 解得:k =32.∴当k 为32时,矩形变为正方形. 20.解:(1)根据题意得: △=(2m )2﹣4(m 2+m )>0, 解得:m <0.∴m 的取值范围是m <0.(2)根据题意得:x 1+x 2=﹣2m ,x 1x 2=m 2+m , ∵x 12+x 22=12, ∴(x 1+x 2)2﹣2x 1x 2=12,∴(﹣2m )2﹣2(m 2+m )=12,∴解得:m 1=﹣2,m 2=3(不合题意,舍去), ∴m 的值是﹣2.21.解:(1)∵关于x 的一元二次方程x 2+πx ﹣2=0有两个实数根,∴△=[π]2﹣4×1×(﹣2)=m +8≥0,且m ≥0, 解得:m ≥0.(2)∵关于x 的一元二次方程x 2+πx ﹣2=0有两个实数根x 1、x 2,∴x1+x2=﹣π,x1•x2=﹣2,∴(x1﹣x2)2﹣17=(x1+x2)2﹣4x1•x2﹣17=0,即m+8﹣17=0,解得:m=9.22.解:(1)∵一元二次方程x2﹣2x+k+2=0有两个实数根,∴△=(﹣2)2﹣4×1×(k+2)≥0,解得:k≤﹣1.(2)∵x1,x2是一元二次方程x2﹣2x+k+2=0的两个实数根,∴x1+x2=2,x1·x2=k+2.∵1x1+1x2=k﹣2,∴x1+x2x1·x2=2k+2=k﹣2,∴k2﹣6=0,解得:k1=﹣6,k2=6.又∵k≤﹣1,∴k=﹣6.∴存在这样的k值,使得等式1x1+1x2=k﹣2成立,k值为﹣6.(1);(2);(3);(4);(5);(6);(1)x1=,x2=;(2)x1=,x2=;(3)x1=,x2=;(4)x1=,x2=;(5)x1=,x2=;(6)x1=,x2=;北师大版数学九年级上册第二章第6节应用一元二次方程(第1课时)同步练习1.在长为100m,宽为80m的矩形场地上修建两条宽度相等且互相垂直的道路,剩余部分进行绿化,要使绿化面积为7644m2,则道路的宽应为多少米?设道路的宽应为xm,则可列方程为()A.100×80-100x-80x=7644 B.(100-x)(80-x)+x2=7644C.(100-x)(80-x)=7644 D.100x+80x=3562.一件商品的原价是100元,经过两次提价后的价格为121元,如果每次提价的百分率都是x,根据题意,下面列出的方程正确的是()A.100(1+x)=121 B.100(1-x)=121 C.100(1+x)2=121D.100(1-x)2=1213.某种品牌运动服经过两次降价,每件零售价由560元降为315元已知两次降价的百分率相同,求每次降价的百分率.设每次降价的百分率为x,下面所列的方程中正确的是()A.560(1+x)2=315 B.560(1-x)2=315 C.560(1-2x)2=315D.560(1+x2)=3154.某超市一月份的营业额为200万元,已知第一季度的总营业额共1000万元,如果平均每月增长率为x,则由题意列方程应为()A.200(1+x)2=1000 B.200+200×2x=1000C.200+200×3x=1000 D.200[1+(1+x)+(1+x)2]=10005.某厂今年一月的总产量为500吨,前三个月的总产量为720吨,平均每月增长率是x,根据题意可列方程___________ _____.6.市政府为了解决市民看病难的问题,决定下调药品的价格。
九年级(上)数学综合练习题(二)
九年级(上)数学综合练习题(二)数学选择题(本题共32分,每小题4分)1、如果两个相似三角形的相似比是1:2,那么这两个相似三角形的周长比是 A .2:1B.C . 1:4D .1:22、若将抛物线y=12x 2先向左平移2个单位,再向下平移1个单位得到新的抛物线,则新抛物线的解析式是A .21(2)12y x =+- B .21(2)12y x =-- C .2(2)1y x =+- D . 21(2)12y x =--3、在a 2□4a □4的空格□中,任意填上“+”或“-”,在所有得到的代数式中,能构成完全平方式的概率是A .14 B . 13 C .12 D . 1 4、如图4×4的正方形网格中,△MNP 绕某点旋转一定的角度,得到△M 1N 1P 1,则其旋转中心可能是A .点AB .点BC .点CD .点D5、如图,⊙B 的半径为4cm , 60=∠MBN ,点A ,C 分别是射线BM ,BN 上的动点,且直线BN AC ⊥.当AC 平移到与⊙B 相切时,AB 的长度是A .8cmB .6cmC .4cmD .2cm6、如图,每个小正方形边长均为1,则下列图中的三角形(阴影部分)与左图中ABC △相似的是7、两圆的圆心距为3,两圆半径分别是方程2430x x -+=的两根,则两圆的位置关系是 A .内切 B . 相交 C .外切 D . 外离A .B .C .D .ABC8、如图,,,,A B C D O 为的四等分点,动点P 从圆心O 出发,沿O C D O ---路线作匀速运动.设运动时间为(),()t s APB y ∠=︒,则下列图象中表示y 与t 之间函数关系最恰当的是二、填空题(本题共16分,每小题4分)9、边长为a 的正三角形的外接圆的半径为 .10、如图,,A C B D C D E A B E⊥⊥于点于点,且68AB DB ==,,则:ABC DBE S S =△△ .11、关于x 的一元二次方程01)1(22=-++-a x x a 的一个根是0,则a 的值为 .12、已知点A 的坐标为()a b ,,O 为坐标原点,连结OA ,将线段OA 绕点O 按逆时针方向旋转90°得1OA ,则点1A 的坐标为 . 三、解答题(本题共25分,每小题5分) 13、解方程:2326x x -=14、如图,在ABC △中,90C =∠,在AB 边上取一点D ,使BD BC =,过D 作DE AB ⊥交AC 于E ,86AC BC ==,.求DE 的长.15、如图,已知⊙O 是△ABC 的外接圆,AB 为直径,若PA ⊥AB ,PO 过AC 的中点M ,求证:PC 是⊙O 的切线.ED C B A16、如图,从一个半径为1m 的圆形铁皮中剪出一个圆心角为90︒的扇形,并将剪下来的扇形围成一个圆锥,求此圆锥的底面圆的半径.17、如图,一条河的两岸有一段是平行的,在河的南岸边每隔5米有一棵树,在北岸边每隔50米有一根电线杆.小丽站在离南岸边15米的点P 处看北岸,发现北岸相邻的两根电线杆A 、B ,恰好被南岸的两棵树C 、D 遮住,并且在这两棵树之间还有三棵树,求河的宽度.四、解答题(本题共10分,每小题5分)18、关x 的一元二次方程(x -2)( x -3)= m 有两个实数根x 1、x 2, (1)求m 的取值范围;(2)若x 1、x 2满足等式x 1x 2-x 1-x 2+1=0,求m 的值.19、如图,AB 为O 的直径,CD 是弦,且AB ⊥CD于点E .连接AC 、OC 、BC . (1)求证:∠ACO =∠BCD .(2)若EB =8cm ,CD =24cm ,求O 的直径.五、解答题(本题共10分,每小题5分)20、某校有A 、B 两个餐厅,甲、乙、丙三名学生各自随机选择其中的一个餐厅用餐. (1)请用列表或画树形图的方法求甲、乙、丙三名学生在同一个餐厅用餐的概率; (2)求甲、乙、丙三名学生中至少有一人在B 餐厅用餐的概率.21、如图,已知二次函数221y x x =--的图象的顶点为A .二次函数2y ax bx =+的图象与x 轴交于原点O 及另一点C ,它的顶点B 在函数221y x x =--的图象的对称轴上. (1)求点A 与点C 的坐标;(2)当四边形AOBC 为菱形时,求函数2y ax bx =+的关系式.COEDCB A六、解答题(本题共6分)22、阅读材料:为解方程()()22215140x x ---+=,我们可以将21x -视为一个整体,设21x y -=,则原方程可化为2540y y -+=,① 解得11y =,24y =.当1y =时,211x -=,22x ∴=即x = 当4y =时,214x -=,25x ∴=即x =.∴原方程的解为1x =2x =3x =4x =根据以上材料,解答下列问题.⑴填空:在原方程得到方程①的过程中,利用换元法达到降次的目的,体现了_____的数学思想.⑵解方程4260x x --=七、解答题(本题共21分,每小题7分) 23、如图,P 为正方形ABCD 内一点,若P A =a ,PB =2a ,PC =3a (a >0).(1) 求∠APB 的度数;(2) 求正方形ABCD 的面积.24、一开口向上的抛物线与x 轴交于A ,B 两点,C (m ,2-)为抛物线顶点,且AC ⊥BC . (1)若m 是常数,求抛物线的解析式; (2)设抛物线交y 轴正半轴于D 点,抛物线的对称轴交x 轴于E 点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初三数学练习2
1.(北京)如图,河旁有一座小山,从山顶A处测得河对岸点C的俯角为30°,测得岸边点D的俯角为45°,又知河宽CD为50米。
现需从山顶A到河对岸点C拉一条笔直的缆绳AC,求缆绳AC的长(答案可带根号)。
2.(东营市)如图:学校旗杆附近有一斜坡.小明准备测量学校旗杆AB的高度,他发现当斜坡正对着太阳时,旗杆AB的影子恰好落在水平地面和斜坡的坡面上,此时小明测得水平地面上的影长BC=20米,斜坡坡面上的影长CD=8米,太阳光线AD与水平地面成26°角,斜坡CD与水平地面BC成30°的角,求旗杆AB的高度(精确到1米).
(第21题)
19.(佛山)如图,从帐篷竖直的支撑竿AB的顶端A向地面拉出一条绳子AC固定帐篷.若地面固定点C到帐篷支撑竿底部B的距离是4.5米,∠ACB=35°,求帐篷支撑竿AB的高(精确到0.1米).备选数据:
sin35°≈0.57,cos35°≈0.82,tan35°≈0.70
3eud教育网 教学资源集散地。
可能是最大的免费教育资源网!
3eud 教育网 教学资源集散地。
可能是最大的免费教育资源网! 河水 B A C
D
4.(南安市)某市对一水库进行除险加固,加固后的拦水坝的横断面为梯形ABCD (如图所示),请你根据图中的数据,求出迎水面AB 的长度(精确到0.1米).
解:
5.(泉州)如图,一架梯子AB 斜靠在一面墙上,底端B 与墙角C 的距离BC 为1米,梯子与地面的夹角为70°,求梯子的长度(精确到0.1米)。
6.(荆门市)为了测量汉江某段河面的宽度,秋实同学设计了如下图所示的测量方案:先在河的北岸选一定点A ,再在河的南岸选定相距a 米的两点B 、C (如图),分别测得∠ABC =α,∠ACB =
β,请你根据秋实同学测得的数据,计算出河宽AD.(结果用含
a 和含α、β的三角函数表示)
3eud 教育网 教学资源集散地。
可能是最大的免费教育资源网!
21.(本题8分)如图,河对岸有一铁塔AB 。
在C 处测得塔顶A 的仰角为30°,向塔前进16米到达D ,在D 处测得A 的仰角为
45°,求铁塔AB 的高。
8.6月以来,我省普降大雨,时有山体滑坡灾害发生。
北峰小学教学楼后面紧邻着一个土坡,坡上面是一块平地,如图所示:AF ∥BC ,斜坡AB 长30米,坡角 ABC =65º。
为了防止滑坡,保障安全,学校决定对该土坡进行改造,经过地质人员勘测,当坡角不超过45º时,可以确保山体不滑坡。
(1)求坡顶与地面的距离AD 等于多少米?(精确到0.1米)
(2)为确保安全,学校计划改造时保持坡脚B 不动,坡顶A 沿AF 削进到E 点处,求AE 至少是多少米?(精确到0.1米)
(第21题)。
