第7章 角动量
合集下载
角动量定理与万有引力
1 S1 r1 v 1 2 1 S 2 r2 v 2 2
两个质点的孤立体系和角动量
而掠面速度对时间的微商为：
dS i 1 dri dv i 1 v i ri dt 2 dt 2 dt dv dv 1 1 1 v i v i ri i ri i 2 2 dt 2 dt
体系的角动量与质心的角动量
设在惯性系 K 中，体系相对原点的角动量为 L。在 质心系 KC 中，质心的角动量为 LC，则有： 令： L r m v 称为质心角动量 C C C C
LCM ( rC i mi v C i ) 称为体系相对于质心的角动量
i
则有：
L LC LCM
单质点孤立体系和掠面速度
单质点的孤立体系就是不 受外力作用的自由质点，它作 匀速直线运动（我们取惯性参 考系，且静止看成是匀速直线 运动的特例）。 如图，设该质点位于P点， 沿直线 AB 从 A 向 B 方向运动， 在相等的时间间隔 ⊿t的位移 是 ⊿s = v⊿t。 由于 OP 的方向（即 r 的方向）在不断改变，故 P 点相对于 O 点有转动。
单质点孤立体系和掠面速度
由图可见，各时间间隔 ⊿t 内矢径 r 扫过的那些小三角形具 有公共的高线 OH，因而有相等 的面积，于是我们找到的守恒量 是：矢径 r 在单位时间内扫过的 面积 S，我们称 该面积 S 为质点 P 的掠面速度。设矢径 r 与 AB 线的夹角为θ，故对单质点的孤 立体系有： 1 s 1 S r sin rv sin 常量 2 t 2
说明：
1. 角动量是矢量，单个质点的角动量是 r 和 p 的矢积， 因而既垂直于 r，又垂直于 p，即垂直于 r 和 p 所确 定的平面，其指向由右手定则决定。
两个质点的孤立体系和角动量
而掠面速度对时间的微商为：
dS i 1 dri dv i 1 v i ri dt 2 dt 2 dt dv dv 1 1 1 v i v i ri i ri i 2 2 dt 2 dt
体系的角动量与质心的角动量
设在惯性系 K 中，体系相对原点的角动量为 L。在 质心系 KC 中，质心的角动量为 LC，则有： 令： L r m v 称为质心角动量 C C C C
LCM ( rC i mi v C i ) 称为体系相对于质心的角动量
i
则有：
L LC LCM
单质点孤立体系和掠面速度
单质点的孤立体系就是不 受外力作用的自由质点，它作 匀速直线运动（我们取惯性参 考系，且静止看成是匀速直线 运动的特例）。 如图，设该质点位于P点， 沿直线 AB 从 A 向 B 方向运动， 在相等的时间间隔 ⊿t的位移 是 ⊿s = v⊿t。 由于 OP 的方向（即 r 的方向）在不断改变，故 P 点相对于 O 点有转动。
单质点孤立体系和掠面速度
由图可见，各时间间隔 ⊿t 内矢径 r 扫过的那些小三角形具 有公共的高线 OH，因而有相等 的面积，于是我们找到的守恒量 是：矢径 r 在单位时间内扫过的 面积 S，我们称 该面积 S 为质点 P 的掠面速度。设矢径 r 与 AB 线的夹角为θ，故对单质点的孤 立体系有： 1 s 1 S r sin rv sin 常量 2 t 2
说明：
1. 角动量是矢量，单个质点的角动量是 r 和 p 的矢积， 因而既垂直于 r，又垂直于 p，即垂直于 r 和 p 所确 定的平面，其指向由右手定则决定。
自主学习01 教材内容 第七章 自旋与角动量
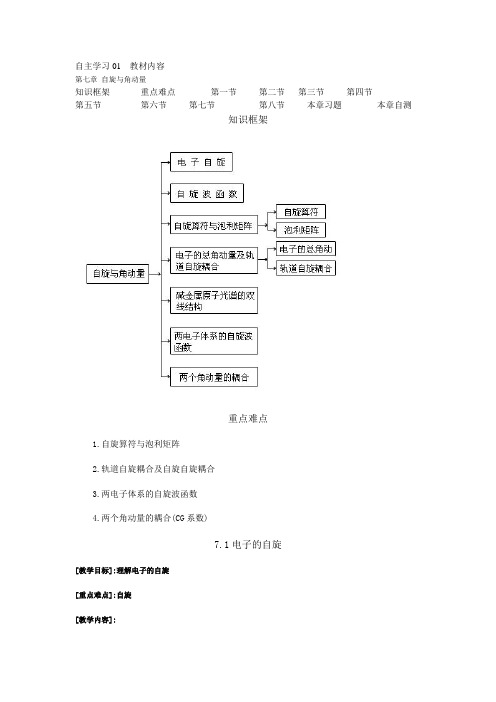
自主学习01 教材内容第七章自旋与角动量知识框架重点难点第一节第二节第三节第四节第五节第六节第七节第八节本章习题本章自测知识框架重点难点1.自旋算符与泡利矩阵2.轨道自旋耦合及自旋自旋耦合3.两电子体系的自旋波函数4.两个角动量的耦合(CG系数)7.1电子的自旋[教学目标]:理解电子的自旋[重点难点]:自旋[教学内容]:在较强的磁场下（∽T 10），我们发现一些类氢离子或碱金属原子有正常塞曼效应的现象，而轨道磁矩的存在，能很好的解释它但是，当这些原子或离子置入弱磁场（∽T 110-）的环境中，或光谱分辨率提高后，发现问题并不是那么简单，这就要求人们进一步探索。
大量实验事实证明，认为电子仅用三个自由度z ,y ,x 来描述并不是完全的。
我们将引入一个新的自由度—自旋，它是粒子固有的。
当然，自旋是Dirac 电子的相对论性理论的自然结果。
现在我们从实验事实来引入。
(1)电子自旋存在的实验事实（1）Stern-Gerlach 实验（1922年）当一狭窄的原子束通过非均匀磁场时，如果原子无磁矩，它将不偏转；而当原子具有磁矩μ，那在磁场中的附加能量为αμμcos B B U -=⋅-=如果经过的路径上，磁场在z 方向上有梯度，即不均匀，则受力dz dB U F αμcos =-∇=从经典观点看αcos 取值（从11--）,因此，不同原子（磁矩取向不同）受力不同，而取值dz dB μ-—dz dB μ所以原子分裂成一个带。
但Stern-Gerlach 发现，当一束处于基态的银原子通 过这样的场时，仅发现分裂成二束，即仅二条轨道（两个态）。
而人们知道，银原子（47z =）基 态0l =，所以没有轨道磁矩，而分成二个状态（二 个轨道），表明存在磁矩，而这磁矩在任何方向上的 投影仅取二个值。
这磁矩既然不是由于轨道运动产生的，因此，只能是电子本身的（核磁矩可忽），这磁矩称为内禀磁矩sμ，与之相联系的角动量称为电子自旋，它是电子的一个新物理量，也是一个新的动力学变量。
第七章角动量
（1）在无耦合表象中，J
2 1
,
J
2 2
,
J 1z
,
J
2z
均为对角矩阵；
（2）对于给定的 j1, j2 ，m1 可取(2 j1 1)个值 ，m2 可取 (2 j2 1)
个值，所以无耦合表象基矢有 (2 j1 1)(2 j2 1)个，各自
以量子数 m1, m2 的不同取值而体现，所以无耦合表象基
的共同本征矢写为
j1m1 j2m2 j1m1 j2m2
（3）
（在坐标表象，r j1m1 j2m2 Yj1m1 (1,1)Yj2m2 (2 ,2 )）
它们构成正交归一完备系
j1m1 j2m2 j1m1 j2m2 j1 j1 j2 j2 m1m1 m2 m2
称为无耦合基矢 以此为基矢的表象称为无耦合表象
（13）
2.2 矢量耦合系数 矢量耦合系数的明显表达式的推导十分复杂，有专门表
可查，有兴趣的话可以参考有关高等量子力学书籍，在此仅
给出 j1（任意）, j2 1/ 2 时的几个矢量耦合系数 ，并代入
（10）式得
• 3 光谱的精细结构 光谱的精细结构来自于能级的精细结构(以Na的D线为
例，精细结构是双线)。现在我们可以用考虑电子自旋后的 量子力学简并微扰理论加以解释。
j1 j2 jm
j1m1 j2m2 j1m1 j2m2 j1 j2 jm
m1 ,m2
（9）
展开系数 j1m1 j2m2 j1 j2 jm 是耦合表象基矢在无耦合表象基
矢上的分量，称为矢量耦合系数或称克来布希－高登系数
（Clebsch-Gorden）,简称C－G系数。
由J z J 1z J 2z可知 m m1 m2 故 m1 m m2 所以将（9）改
量子力学第七章习题解答
即
h h 2 2 2 λ − cos γ − (cos α + cos β ) = 0 4 4
2
h λ − = 0 (利用 cos 2 α + cos 2 β + cos 2 γ = 1) 4
2
2
⇒
a h 设对应于 S n = 的本征函数的矩阵表示为 χ 1 ( S n ) = ， b 2 2
由归一化条件，得
a 2 2 1 = χ 1 χ 1 = (a , b ) = a + b b 2 2 2 cos α + i cos β 2 2 a + a =1 1 + cos γ
+ * *
2 2 a =1 1 + cos γ
取
1 + cos γ a= 2
，得
b=
cos α + i cos β 2(1 + cos γ )
ˆ 在这些本征态中， 测量 S z 有哪些可能值？这些可 ˆ 能值各以多大的几率出现？ S z 的平均值是多少？
ˆ ˆ 解：在 S z 表象， S n 的矩阵元为
ˆ = h 0 1 cos α + h 0 − i cos β + h 1 0 cos γ Sn 1 0 i 0 0 − 1 2 2 2
⇒
b1 a1 = ⇒ a b 1 1
b1 = a1
χ 1+/ 2 χ 1 / 2 = 1 ，得 由归一化条件 a * * 1 (a1 , a1 ) = 1 a 1
即
2 a1 = 1
2
∴
a1 =
1 2
b1 =
2-(8)角动量
质点作圆周运动 L r mv 质点作直线运动
L r
2
mv
方向如图
L mvr sin rmv mr
Z Y O
ˆ L mvr sin mvd 或： L mvd k
L
r
X
mv
d
15 – 8 多普勒效应 质点系的角动量
1
此值为狄拉克h： h / 2
15 – 8
多普勒效应
4
第十五章 机械波
例3 一质量 m 1 . 20 10 kg 的登月飞船, 在离 月球表面高度 h 100 km 处绕月球作圆周运动.飞船 采用如下登月方式 : 当飞船位于点 A 时,它向外侧短 时间喷气 , 使飞船与月球相切地到达点 B , 且OA 与 OB 垂直 . 飞船所喷气体相对飞船的速度为 4 1 u 1 . 00 10 m s . 已知 v0 B vA 月球半径 R 1700 km ; vB 在飞船登月过程中,月球的 R 重力加速度视为常量 u v 2 g 1 . 62 m s . O A 试问登月飞船在登月过程 中所需消耗燃料的质量 h m 是多少?
i
第十五章 机械波 L Li r i p i
i
二 、力矩
中学时学过的力矩概念
二、力矩
M Fd Fr sin r F
o
d
r
M
F
定义：力对某点O的力矩等于力的 作用点的矢径r与力F的矢量积.
M
M r F
t2
Lz 2 z
M
t1
dt
dL
Lz 1
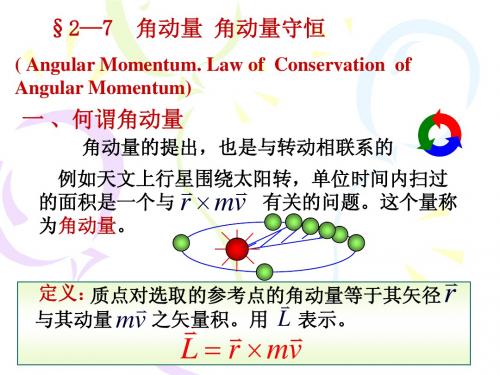
L r
2
mv
方向如图
L mvr sin rmv mr
Z Y O
ˆ L mvr sin mvd 或： L mvd k
L
r
X
mv
d
15 – 8 多普勒效应 质点系的角动量
1
此值为狄拉克h： h / 2
15 – 8
多普勒效应
4
第十五章 机械波
例3 一质量 m 1 . 20 10 kg 的登月飞船, 在离 月球表面高度 h 100 km 处绕月球作圆周运动.飞船 采用如下登月方式 : 当飞船位于点 A 时,它向外侧短 时间喷气 , 使飞船与月球相切地到达点 B , 且OA 与 OB 垂直 . 飞船所喷气体相对飞船的速度为 4 1 u 1 . 00 10 m s . 已知 v0 B vA 月球半径 R 1700 km ; vB 在飞船登月过程中,月球的 R 重力加速度视为常量 u v 2 g 1 . 62 m s . O A 试问登月飞船在登月过程 中所需消耗燃料的质量 h m 是多少?
i
第十五章 机械波 L Li r i p i
i
二 、力矩
中学时学过的力矩概念
二、力矩
M Fd Fr sin r F
o
d
r
M
F
定义：力对某点O的力矩等于力的 作用点的矢径r与力F的矢量积.
M
M r F
t2
Lz 2 z
M
t1
dt
dL
Lz 1
17第7章概念2-两个角动量的耦合
1 2
−1,1 + 2 2
1 2
1 2
, − 1 c 1 , − 1 + d − 1 , 1 2 2 2 2 2
=
1 2
(c + d ) = 0
0, 0 0, 0 = c*
2
1 2
, − 1 + d * − 1 , 1 c 1 , − 1 + d − 1 , 1 2 2 2 2 2 2 2
j1 + j2 , j1 + j2 − 1,L , jmin
因此，耦合表象基矢总数即空间维数为 因此， 1 首项+末项） ∑(2 j +1) = 2（首项+末项） 项数 j
×ቤተ መጻሕፍቲ ባይዱ
=
= ( jmax + jmin + 1)( jmax − jmin + 1)
(2 jmin + 1) + (2 jmax + 1) ( jmax − jmin + 1) 2
因此， ˆ 2 ˆ 2 ˆ 2 ˆ 也构成力学量完全集。 因此， J1 , J 2 , J , J z 也构成力学量完全集。 设它们的共同本征矢为 j1 j2 jm ，则
{
v v ˆ ˆ ˆ 2 = J 2 + J 2 + 2J ⋅ J ˆ ˆ J 1 2 1 2 ˆ ˆ ˆ ˆ ˆ ˆ2 [J 2 , J z ] = 0 [ J 2 , J12 ] = [ J 2 , J 2 ] = 0 且
j1 =1/ 2
,1 2
,1 2
m1 =1/ 2
j2 =1/ 2 m2 =1/ 2
=
( 1 − 1 + 1)( 1 + 1 ) 2 2 2 2
圆周运动：角动量和角动量守恒
角动量守恒在量子力学和粒子物理学中也有着重要的应用，对于理解微观世界的运动规律具有重要意义。
角动量守恒在未来的发展前景和影响将更加广泛，对于推动科学技术的发展和进步具有重要意义。
如何理解和掌握角动量守恒定律
6
学习角动量守恒定律的方法和技巧ຫໍສະໝຸດ 理解角动量守恒定律的难点和重点
角动量的定义：理解角动量的物理意义和数学表达式
角动量守恒可以帮助我们理解各种旋转运动现象，例如地球自转、陀螺旋转等。
角动量守恒还可以帮助我们解决一些实际问题，例如设计旋转机械、分析旋转物体的稳定性等。
角动量守恒在科技领域的应用价值
光学器件：利用角动量守恒原理，制造出高性能的光学器件，如光纤陀螺仪等
粒子加速器：利用角动量守恒原理，提高粒子加速器的性能和效率
角动量守恒定律
3
角动量守恒的条件
系统不受外力矩作用
系统的角动量守恒定律适用于旋转参考系和惯性参考系
系统的角动量变化率为零
系统内力矩之和为零
角动量守恒的证明方法
添加标题
添加标题
添加标题
添加标题
角动量守恒定律：L=mvr
牛顿第二定律：F=ma
角动量守恒的条件：系统不受外力矩作用
角动量守恒的证明：通过牛顿第二定律和角动量守恒定律，推导出角动量守恒的条件，从而证明角动量守恒定律。
角动量守恒定律：在圆周运动中，角动量保持恒定
角动量的大小：与物体的质量和速度成正比
角动量的变化：在圆周运动中，角动量不会发生变化，除非有外力作用
圆周运动中角动量守恒的证明
角动量守恒定律：在封闭系统中，系统内各物体的角动量之和保持不变
证明过程：假设物体在圆周运动中受到外力作用，根据牛顿第二定律，外力作用在物体上会产生加速度
第七章 第二讲
ˆ J ˆ 2J ˆ 2J ˆ 2, J x x y z
ˆ J ˆ 0 J y y,
ˆ 2, J ˆ Jx x
ˆ J ˆ 2, J x y
ˆ J ˆ 2, J x z
ˆ J ˆ J x z
ˆ J x
ˆ J ˆ , J x y
ˆ J ˆ ˆ ˆ J x y Jz Jz ,
1 1
上式与关系式
m1
j1 , j2 , j, m | j1 , m1 , j2 , m m1 j1 , m1 , j2 , m m1 | j1 , j2 , j , m jj
一起反映了C-G系数的么正性和实数性。
（3）j的取值范围（j与j1,j2的关系） 1.对给定j1 j2 ，求 jmax 因为m m1 m2 取值范围分别是：
Jmax = j1 + j2
等式两边基矢数应该相等
| j1 , j2 , j , m | j1 , m1 , j2 , m m1 j1 , m1 , j2 , m m1 | j1 , j2 , j , m
Jˆ ,
z
同理
Jˆ ,
z
ˆ 2 0 J 2
Jˆ
1z ,
ˆ 2 J ˆ , J 1 2z
ˆ 2 J 1
0
亦成立。 [证毕]
（二）耦合表象和无耦合表象
（1）本征函数
综合上述对易关系可 知：四个角动量算符
ˆ 2, J ˆ ,J ˆ 2, J ˆ 2 J z 1 2
两两 对易
jm
, j2 , m j1 , m1 2 |
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
对原子的同一组态而言，L和S都相同的状态，若不计及轨
道－自旋相互作用，且在没有外界磁场作用下，都具有完 全相同的能量。 将同一组态中，由相同L和S所构成的诸状态合称为一个 光谱项，每一个光谱项相当于一个能级。
24
对于一定的S，mS 可有S、S－1、…、－S共计2S＋1个取值，
分别对应总自旋角动量在外磁场方向的分量MSz的2S＋1种状态，
0
7
同样，我们还可以求得：
ˆ ˆ L2 , L y 0 ˆ ˆ L2 , Lz 0
根据各个算符间的对易关系，可以得出如下结
论：角动量大小的平方L2与任意一个分量可以同时
具有确定值，但是角动量的三个分量最多只有一个
有确定值，通常我们选取Lz 做为与L2 同时具有确定
5
ˆ f i y f z f Lx 同样： y z 2 2 2 2 f f f f 2 f ˆ L f 2 zy ˆ Ly x z xy 2 x xz xy z y zy xz
31
Hund规则
Hund第一规则
S最大时能量最低；S相同，则L最大时能量最低。
Hund第二规则
如L与S均相同，当电子壳层未达半充满时，J愈小能量愈低； 半充满后，则J愈大能量愈低。
32
S大，2S＋1大，即具有最大多重度的状态是最稳定的。
值的角动量分量。
8
注意：我们说角动量大小的平方L2具有确定值并
不是意味着角动量矢量 完全确定，因为 是个矢量，
要完全确定之，必须要知道其在各个方向上的分量， L L
这一点我们是做不到的，因为角动量各个分量的量
子力学算符间是不可对易的，最多只能有一个具有
确定的值。
9
7.2 电子自旋
1.自旋角动量算符的对易关系 单电子情况
2
所以：
2 f 2 f 其中用了下列关系式： zx xz
ˆ ˆ ˆ [ Lx , Ly ] i Lz
(这对于品优波 函数总是成立的)
6
同样，我们可以求得：
ˆ ˆ ˆ [ Ly , Lz ] i Lx
ˆ2 , L L ˆx
ˆ ˆ ˆ [ Lz , Lx ] i Ly
1D三个光谱项，而np1(n+1)p1 型组态具有这六个光
谱项。
29
光谱项1S
L＝0，S＝0；J＝0。光谱支项为：1S0。
光谱项1D
L＝2，S＝0；L＋S＝2，L－S＝2，J＝2。光谱支项
为：1D2。
三重态3P
L＝1，S＝1；L＋S＝2，L－S＝0，J＝2、1、0。三
个光谱支项分别为：3P2、3P1、3P0。
即自旋多重度为2S＋1。因此，在光谱学符号中通常将自旋多重
度写在L值符号的左上角，即：2S+1L。 又由于轨道和自旋的相互作用，不同的J所对应的能级会有微 小的差别。将J的数值记在L的右下角，即：2S+1LJ。称为光谱支 项。
25
几点结论
凡是充满壳层s2、p6、d10、f14等的总轨道角动量和总 自旋角动量均为0。
z z S
1 2
3 2
1 2
3 2
S
14
7.3 多电子原子的量子数和光谱项
R多电子原子的量子数 R光谱项及其应用
15
一、多电子原子的量子数
1.总轨道角量子数L
单电子轨道角动量
M l (l 1)
原子的总轨道角动量
总轨道角量子数
M L M L L( L 1)
L l1 l2 lN , l1 l2 lN 1, l1 l2 lN 2,
最小值为0或
l 的最小正值
i i
16
N
单电子轨道角动量在外磁场方向上的分量
Mz m
原子总轨道角动量在外磁场方向上的分量
M Lz mL
总轨道磁量子数
2 2 x 2 y 2 z
S S S S
2
(1) (2)
[S , Si ] 0 i x, y, z
[ S x , S y ] i S z
[ S y , S z ] i S x [ S z , S x ] i S y
(3)
12
2．单电子自旋算符的本征函数和本征值
对于单电子， 和 S z 的本征态只有两个，以和表示。 S
1 1 1 2 S s( s 1) ( 1) , s 2 2 2 1 1 1 2 2 2 S s( s 1) ( 1) , s 2 2 2
分量。
2
1 经典力学中的角动量
根据角动量定义(1)，可得：
L ypz zp y i zpx xpz j xp y ypx k Lx i Ly j Lz k
所以角动量的三个分量Lx，Ly，Lz等于
Lx ypz zp y ,
ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ 这样： [ Lx , Ly ] f [ Lx Ly Ly Lx ] f Lx Ly f Ly Lx f f f 2 y x y x f y y x x
Ly zpx xpz ,
L L L L
2 2 x 2 y 2 z
Lz xp y ypx
3
2.量子力学中的角动量
在量子力学中有两种角动量：轨道角动量和自旋角动量。轨道 角动量对应于经典力学中的角动量动量，在经典力学中没有对应的物理量。
根据量子力学的基本假设，轨道角动量的分量的算符为：
对电子而言
1 s 2
N N N 1 S , 1, 2, , , 0 2 2 2 2
18
总自旋角动量在外磁场方向的分量
M Sz mS
总自旋磁量子数
mS msi
i 1
N
共有2S＋1个取值：S、S－1、S－2、…、－S
19
3. 总角量子数J
原子中各电子的轨道角动量和自旋角动量相互作用，得到一个 总的角动量。两种耦合方式：
mL mi
i 1
N
共有2L＋1个取值：L，L－1，L－2，…，－L
17
2. 总自旋量子数S
原子的总自旋角动量 原子的总自旋量子数
M S M S S ( S 1)
S s1 s2 sN , s1 s2 sN 1, s1 s2 sN 2,
ˆ2 Lx
ˆ2 Ly
ˆ2 , L Lz ˆ x
ˆ2 , L L2 , L L2 , L Lx ˆ x ˆ y ˆ x ˆ z ˆ x ˆ2 , L L2 , L Ly ˆ x ˆ z ˆ x ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ L y L y , Lx L y , Lx L y Lz Lz , Lx Lz , Lx Lz ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ i L y Lz i Lz L y i Lz L y i L y Lz
自旋角动量本征方程
2 t 2
2 t
（6） (7)
1 3 S Y S (S 1) Y , (S 0, , 1, , 2, ) 2 2
(8)
Szt Y M s Y , (M s S , S 1, , S 1, S )
(9)
上式中S为多电子体系的总自旋量子数，Ms为S沿z轴的分量。
M Jz mJ
共有2J＋1个取值
mJ＝mL＋mS＝J，J－1，J－2，…，－J
22
二、光谱项及其应用
1. 光谱项与光谱支项 单电子轨道 l＝0 s 多电子原子 L＝0 S 1 p 1 P 2 d 2 D f 3 F … 3 … … …
23
根据原子光谱的实验数据及量子力学理论可以得出结论：
ˆ Lx i y z y z
ˆ ˆ i z x Lz i x y Ly x z x y
4
3.轨道角动量分量的算符间的对易关系
ˆ ˆ ˆ ˆ ˆ ˆ [ Lx , Ly ] Lx Ly Ly Lx
轨道和自旋的相互作用比各电子间的相互作用都要大，
故采用j－j耦合将会得到较好的结果。
对于Z≤40的轻原子，各电子间的相互作用要远大于每
个电子自身的轨道和自旋相互作用，于是L－S耦合将是 更好、更方便的近似方法。
21
多电子原子的总角动量 总角量子数
M J J ( J 1)
J＝L＋S，L＋S－1，L＋S－2，…，│L－S│ 总角动量在外磁场方向上的分量 总磁量子数
第七章 角动量
1
7.1 单粒子体系的角动量
经典力学中的角动量
p 的矢量积，即： 到原点的矢量 r 和质点的线动量 i j k Lr p x y z 1 px p y pz
在经典力学中角动量可以用一个矢量 L 来表示。它定义为质点
和 p 在x，y和z轴方向的 式中的x，y，z和px，py，pz分别是矢量 r
10
多电子体系
S S S S
S xt Sxj
j
2 t
2 xt
2 yt
2 zt
(4)
S yt S yj
j
(5)
S zt S zj
j