三垂直模型与全等综合之欧阳学文创编之欧阳家百创编
(完整版)三垂直模型与全等综合剖析

DPFEBC AF E CB A K 模型图与全等知识点 基本图形本题8分)如图,在等腰R t △ABC 中,∠ACB =90°,D 为BC 的中点,DE ⊥AB ,垂足为E ,过点B 作BF ∥AC 交DE 的延长线于点F ,连接CF . (1)求证:AD ⊥CF ;(2)连接AF ,求证:AF =CF .22.边长为1的正方形ABCD 中,E 是AB 中点,连CE ,过B 作BF ⊥CE 交AC 于F ,求AF.【例8】【例9】等腰Rt △ABC 中 ∠ACB =90°,AC=BC ;F 是BC 上的中点,连AF ,作CD ⊥AF 于E ,交AB 于D ; 连FD. 求证:AD =2BD ;【例3】已知△ABC 中,∠C=90 ,AC=BC,D 是AB 的中点,E 是BC 上任一点,EP ⊥CB,PF ⊥AC,E 、F 为垂足, 求证:△DEF 是等腰直角三角形.H B CFFEDC BAHFEDCBA【例4】如图,D为线段AB的中点,在AB上取异于D的点C,分别以AC、BC为斜边在AB 同侧作等腰直角三角形ACE与BCF,连结DE、DF、EF,求证:△DEF为等腰直角三角形。
【例5】如图,分别以△ABC的边AB、AC向外作等腰Rt△ABD,等腰Rt△ACE;连接DE。
AF是△ABC的中线,FA的延长线交DE于点H,求证:DE=2AF【例6】如图,在正方形ABCD中,点N是BC边上的点。
连接AN,MN⊥AN交∠DCB的外角平分线于点M。
求证:AN=MN9、如图,直线AB 交x 轴正半轴于点A (a ,0),交y 轴正半轴于点B (0, b ),且a 、b 满足4 a + |4-b |=0(1)求A 、B 两点的坐标;(2)D 为OA 的中点,连接BD ,过点O 作OE ⊥BD 于F ,交AB 于E ,求证∠BDO =∠EDA ;(3)如图,P 为x 轴上A 点右侧任意一点,以BP 为边作等腰Rt △PBM,其中PB=PM,直线MA交y轴于点Q,当点P在x轴上运动时,线段OQ的长是否发生变化?若不变,求其值;若变化,求线段OQ的取值范围.10ABOMPQx y24.(12分)如图,CODV等腰直角三角形,CA⊥x轴。
全等几何模型讲解之欧阳治创编

欧阳治创编 2021.03.10 欧阳治创编 2021.03.10常见的几何模型时间 2021.03.10创作:欧阳治一、旋转主要分四大类:绕点、空翻、弦图、半 角。
这四类旋转的分类似于平行四边形、矩形、菱形、 正方形的分类。
1.绕点型(手拉手模型)(1)自旋转:例题讲解:1. 如图所示,P 是等边三角形 ABC 内的一个点, PA=2,PB= ,PC=4,求△ABC 的边长。
2. 如图,O 是等边三角形 ABC 内一点,已知: ∠AOB=115°,∠BOC=125°,则以线段 OA、 OB、OC 为边构成三角形的各角度数是多少?欧阳治创编 2021.03.10 欧阳治创编 2021.03.10欧阳治创编 2021.03.10 欧阳治创编 2021.03.103.如图,P 是正方形 ABCD 内一点,且满足 PA: PD:PC=1:2:3,则∠APD=.4.如图(2-1):P 是正方形 ABCD 内一点,点 P 到 正方形的三个顶点 A、B、C 的距离分别为 PA=1, PB=2,PC=3。
求此正方形 ABCD 面积。
(2)共旋转(典型的手拉手模型)模型变形:例题讲解:1. 已知△ABC 为等边三角形,点 D 为直线 BC 上的 一动点(点 D 不与 B,C 重合),以 AD 为边作菱 形 ADEF( 按 A,D,E,F 逆 时 针 排 列 ) , 使 ∠DAF=60°,连接 CF.(1) 如图 1,当点 D 在边 BC 上时,求证: ① BD=CF ‚ ②AC=CF+CD.(2)如图 2,当点 D 在边 BC 的延长线上且其他条件 不变时,结论 AC=CF+CD 是否成立?若不成 立,请写出 AC、CF、CD 之间存在的数量关 系,并说明理由;欧阳治创编 2021.03.10 欧阳治创编 2021.03.10欧阳治创编 2021.03.10 欧阳治创编 2021.03.10(3)如图 3,当点 D 在边 BC 的延长线上且其他条件 不变时,补全图形,并直接写出 AC、CF、CD 之间存在的数量关系。
三垂直模型与全等综合剖析.docx
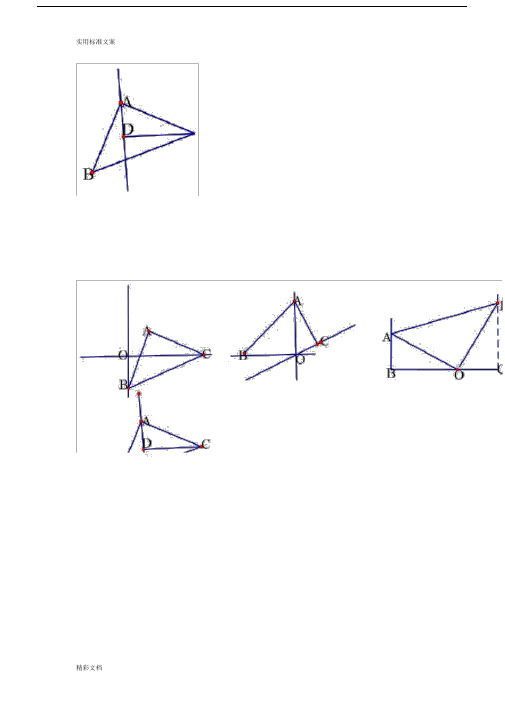
K模型图与全等知识点基本图形本题 8 分)如图,在等腰Rt △ABC中,∠ACB=90 °,D为BC的中点,DE⊥AB,垂足为E,过点 B 作 BF∥AC 交 DE 的延长线于点 F,连接 CF.(1)求证:AD⊥CF;(2)连接AF,求证:AF=CF.22 .边长为 1 的正方形 ABCD 中, E 是 AB 中点,连CE,过 B 作 BF⊥ CE 交 AC 于 F,求AF.D CFHA EB 【例 8】CFEA D B【例 9 】等腰 Rt △ABC 中∠ACB = 90 °,AC=BC ; F 是 BC 上的中点,连AF ,作 CD ⊥ AF 于 E,交 AB 于 D;连 FD. 求证: AD =2BD ;【例 3 】已知△ABC 中 ,∠C=90 ,AC=BC,D是AB的中点,E是BC上任一点,EP⊥ CB,PF⊥ AC,E、F为垂足 ,CFE求证 :△DEF 是等腰直角三角形.A D P B【例 4 】如图, D 为线段 AB 的中点,在AB 上取异于 D 的点 C,分别以 AC、BC 为斜边在AB 同侧作等腰直角三角形ACE 与 BCF,连结 DE、 DF、 EF,求证:△ DEF 为等腰直角三角形。
DFEHEAA C D BBFC【例 5 】如图,分别以△ ABC 的边 AB 、AC 向外作等腰Rt △ABD ,等腰 Rt △ACE;连接 DE。
AF 是△ABC 的中线,FA 的延长线交DE 于点 H ,求证: DE= 2AF【例 6 】如图,在正方形ABCD 中,点 N 是 BC 边上的点。
连接AN ,MN ⊥ AN 交∠DCB 的外角平分线于点M 。
求证: AN = MN9、如图,直线AB 交 x 轴正半轴于点 A(a,0),交 y 轴正半轴于点B(0, b),且 a 、b 满足 a 4+ |4 -b|=0(1)求A、B两点的坐标;(2)D为OA的中点,连接BD,过点O作OE⊥BD于F,交AB 于 E,求证∠BDO=∠EDA;yBEFO D A x(3)如图,P为x轴上A点右侧任意一点,以BP 为边作等腰Rt△PBM ,其中 PB= PM,直线 MA 交 y 轴于点 Q,当点 P 在 x轴上运动时,线段 OQ 的长是否发生变化?若不变,求其值;若变化,求线段 OQ 的取值范围.yM BO A PxQ 1024 .( 12分)如图, VCOD 等腰直角三角形, CA ⊥ x 轴。
三大国外离职模型之欧阳学文创编之欧阳家百创编

摘要:离职模型的构建是许多雇员离职研究学者研究的重点,主要从个体层面来研究雇员离职的决定因素,进而试图揭示雇员作出离职决策的过程。
雇员离职研究史上有三大主流离职模型,他们是Mobley(1979)扩展的中介链模型、Steers Mowday(1981)模型和Price-Mueller (2000)模型。
对三大主流离职模型进行了介绍和归纳,并总结了这些模型对我国雇员离职研究的启示。
关键词:雇员离职;主流模型;Price-Mueller模型1 三大主流离职模型简介1.1 扩展的Mobley中介链(1979)模型Mobley和他的同事在1979年构造出一个较为复杂和全面的雇员离职过程模型——扩展的莫布雷中介链模型(见图1),它将March和Simon模型、Price模型和Mobley中介链模型进行了结合,以尽可能地捕捉影响雇员离职的各种复杂因素。
该模型认为,雇员打算辞职继而从组织中真正流出,主要取决于四个因素:(1)工作满意与否。
企业雇员对其工作的满足感既是一个绝对概念又是一个相对概念。
前者是指一个工作由于符合某个员工的价值观,而给他的带来的满足程度。
如,一个热爱书籍、但不善交际的雇员可能对资料管理员的工作比较满意,而对公关部经理的工作却十分恐惧和厌恶;后者是指雇员在综合评价各种工作带给他的满足程度之后,所得到的感觉。
(2)对在组织内部改变工作角色及收益的预期。
雇员在对现有的工作感到绝对不满,或觉得其它企业具备更合适的工作而感到相对不满时,仍然有可能会从原有企业流失。
因为他会考虑自己将来在本企业的发展,是否还有比外界更大的空间,或者说是否会更加满足。
如果是,而且实现内部流动或晋升的机会比较大,那么他就不会从原企业流失。
而相反,如果一个雇员对现有的工作感到满意,但对企业内部未来的预期却不甚理想,则他也会积极在外界寻找新的机会,或者在本企业暂时停留,消极怠工,形成雇员的隐性流失。
(3)对在组织外部改变工作角色及收益的预期。
三垂直模型与全等综合

D P FE BCA K 模型图与齐等之阳早格格创做知识面基原图形原题8分)如图,正在等腰Rt △ABC 中,∠ACB=90°,D 为BC 的中面,DE ⊥AB ,垂脚为E ,过面B 做BF ∥AC 接DE 的延少线于面F ,对接CF .(1)供证:AD ⊥CF ;(2)对接AF ,供证:AF =CF .22.边少为1的正圆形ABCD 中,E 是AB 中面,连CE ,过B 做BF ⊥CE 接AC 于F ,供AF.【例8】【例9】等腰Rt △ABC 中 ∠ACB =90°,AC=BC ;F 是BC上的中面,连AF ,做CD ⊥AF 于E ,接AB 于D ; 连FD.供证:AD =2BD ;【例3】已知△ABC 中,∠C=90,AC=BC,D 是AB 的中面,E 是BC 上任一面,EP ⊥CB,PF ⊥AC,E 、F 为垂脚, 供证:△DEF 是等腰直角三角形.【例4】如图,D 为线段AB 的中面,正在AB 上与同于D的面C ,分别以AC 、BC 为斜边正在AB 共侧做等腰直角三角形ACE 与BCF ,连结DE 、DF 、EF ,供证:△DEF 为等腰直角三角形.【例5】如图,分别以△ABC 的边AB 、AC 背中做等腰Rt△ABD,等腰Rt△ACE;对接DE.AF是△ABC的中线,FA的延少线接DE于面H,供证:DE=2AF【例6】如图,正在正圆形ABCD中,面N是BC边上的面.对接AN,MN⊥AN接∠DCB的中角仄分线于面M.供证:AN=MN9、如图,直线AB接x轴正半轴于面A(a,0),接y 轴正半轴于面B(0,b),且a 、b谦脚4 a+ |4-b|=0(1)供A、B二面的坐标;(2)D为OA的中面,对接BD,过面O做OE⊥BD于F,接AB于E,供证∠BDO=∠EDA;(3)如图,P为x轴上A面左侧任性一面,以BP为边做等腰Rt△PBM,其中PB=PM,直线MA接y 轴于面Q,当面P正在x轴上疏通时,线段OQ的少是可爆收变更?若没有变,供其值;若变更,供线段OQ的与值范畴.1024.(12分)如图,COD 等腰直角三角形,CA ⊥x 轴.⑴若面C 的坐标是(—2,—4),供D 面的坐标.(4分) ⑵连结CD ,面E 为CD 的中面,供证:AE ⊥BE ;(4分) ⑶如图,面P 是y 轴正半轴是一面,OP=AB ,当面A 、B 正在x 轴上疏通时,∠APB+∠CPD 的值是可爆收变更?若并证明缘由.(4分)“K”为过二顶面做该直线垂线. 例:已知等腰RT △ABC 中,过面A △ABE ≌△CAF衍死:仄里直角坐标系中A (1,3),以OA 为边做正圆形OABC ,供B 、C 坐标.变式:仄里直角坐标系中,面A (4,1),过面O 做一条直线与OA 夹角为45°,供该直线剖析式.衍伸:仄里直角坐标系中直线3:2OA l y x =与单直线k y x=接于面A ,以OA 为边做等腰RT △OAB ,面B 刚刚佳降正在单直线上.供k.原题8分)如图,正在等腰Rt △ABC 中,∠ACB=90°,D 为BC 的中面,DE ⊥AB ,垂脚为E ,过面B 做BF ∥AC 接DE 的延少线于面F ,对接CF .(1)供证:AD ⊥CF ;(2)对接AF ,供证:AF =CF . ABC 的直角顶面C 正在x 轴上,面B 正在y 轴上.(1)如图1,若面C 的坐标为(2,0),A 的坐标为(-2,-2),供面B 的坐标.(2)如图2,直角边BC 正在坐标轴上疏通,使面A 正在第四象限内,过面A 做AD ⊥y 轴于D ,供CO AD BO -的值. 八年级数教每日一题(041-045)P —041如图,如图,正在仄里直角坐标系中,面A 战面B 的坐标分别是A (0,a ),B (b ,0),且a 、b 谦脚330a b -+=.(1)供面A 、面B 的坐标;(2)面C 是第三象限内一面,以BC 为直角边做等腰直角D yx A O C B O C B A△BCD,∠BCD=90º,过面A战面D分别做直线CO的垂线,垂脚分别是面E、F.试问线段AE、DF、CO之间是可存留某种决定的数量闭系?为什么?P—042 如图,正在仄里直角坐标系中,面A、面C分别正在y轴的正半轴战背半轴上,面B正在x轴正半轴上,∠ABC=90º.面E正在BC延少线上,过面E做ED∥AB,接y轴于面D,接x轴于面F,DO–AO=2CO.(1)供证:AB=DE;(2)若AB=2BC,供证:EF=EC;(3)正在(2)的条件下,若面B的坐标是(2,0),供面E 的坐标.9、如图,直线AB接x轴正半轴于面A(a,0),接y 轴正半轴于面B(0,b),且a 、b谦脚4 a+ |4-b|=0(1)供A、B二面的坐标;(2)D为OA的中面,对接BD,过面O做OE⊥BD于F,接AB于E,供证∠BDO=∠EDA;(3)如图,P为x轴上A面左侧任性一面,以BP为边做等腰Rt△PBM,其中PB=PM,直线MA接y 轴于面Q,当面P正在x轴上疏通时,线段OQ的少是可爆收变更?若没有变,供其值;若变更,供线段OQ的与值范畴.10如图,正在仄里直角坐标系xoy中,直线AP接x轴于面P (p,0),接y轴于面A(0,a),且a、b谦脚+(p+1)2=0.(1)供直线AP的剖析式;(2)如图1,面P 闭于y轴的对于称面为Q,R(0,2),面S正在直线AQ上,且SR=SA,供直线RS的剖析式战面S的坐标;(3)如图2,面B(-2,b)为直线AP上一面,以AB为斜边做等腰直角三角形ABC,面C正在第一象限,D为线段OP上一动面,对接DC,以DC为直角边,面D为直角顶面做等腰三角形DCE,EF⊥x轴,F为垂脚,下列论断:①2DP+EF的值没有变;②AO−EF的值没有变;其中惟有一个论断精确,请您采用出精确的论断,并供出其定值.如图,正在仄里直角坐标系xoy中,直线AP接x轴于面P (p,0),接y轴于面A(0,a),且a、b谦脚+(p+1)2=0.(1)供直线AP的剖析式;(2)如图1,面P 闭于y轴的对于称面为Q,R(0,2),面S正在直线AQ上,且SR=SA,供直线RS的剖析式战面S的坐标;(3)如图2,面B(-2,b)为直线AP上一面,以AB为斜边做等腰直角三角形ABC,面C正在第一象限,D为线段OP上一动面,对接DC,以DC为直角边,面D为直角顶面做等腰三角形DCE,EF⊥x轴,F为垂脚,下列论断:①2DP+EF的值没有变;②AO−EF的值没有变;其中惟有一个论断精确,请您采用出精确的论断,并供出其定值.。
三垂直模型精编版

⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯最新料介绍⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯一线三等角模型一 .一线三等角观点“一线三等角” 是一个常有的相像模型,指的是有三个等角的极点在同一条直线上组成的相像图形,这个角能够是直角,也能够是锐角或钝角。
不一样地域对此有不一样的称号,“K 形图”,“三垂直”,“弦图”等,以下称为“一线三等角”。
二 .一线三等角的分类全等篇CD CA P BA P锐角直角D DA AB PBC C相像篇CDCA PB A P锐角直角DDDDCBA PB 同侧钝角DAPP BC异侧D DCBA PB 同侧钝角DAPB AB C CABPCP异侧三、“一线三等角”的性质1.一般状况下,如图 3-1 ,由∠ 1=∠ 2=∠ 3,易得△ AEC∽△ BDE.2. 当等角所对的边相等时,则两个三角形全等. 如图 3-1 ,若 CE=ED,则△ AEC≌△ BDE.3.中点型“一线三等角”如图 3-2 ,当∠ 1=∠2=∠3,且 D 是 BC 中点时,△ BDE∽△ CFD∽△ DFE.4. “中点型一线三等角“的变式(认识)如图 3-3 ,当∠ 1=∠2 且BOC 90 1BAC 时,点O是△ABC的心里.能够考虑构2造“一线三等角”.如图 3- 4“中点型一线三等角”往常与三角形的心里或旁心有关,BOC 90 1BAC 这是心里的性质,反之未必是心里.在图 3-42BE 与 CF,交于点 P ,则点 D 是△ PEF 的旁心 . (右图)中,假如延伸5.“一线三等角”的各样变式(图 3-5 ,以等腰三角形为例进行说明)图 3-5其实这个第 4 图,延伸 DC 反而好理解 . 相当于双侧型的,不延伸理解,认为是一种新式的,同侧穿越型?不论怎么变,都是由三等角确立相像三角形来进行解题四、“一线三等角”的应用1.“一线三等角”应用的三种状况 .a.图形中已经存在“一线三等角”,直策应用模型解题;b.图形中存在“一线二等角”,不上“一等角”结构模型解题;c.图形中只有直线上一个角,不上“二等角”结构模型解题.领会:感觉最后一种状况出现比许多,特别是压轴题中,常常会有一个特别角或指导该角的三角函数值时,我常常结构“一线三等角”来解题.2.在定边对定角问题中,结构一线三等角是基本手段,特别是直角坐标系中的张角问题,在 x 轴或 y 轴(也能够是平行于 x 轴或 y 轴的直线)上结构一线三等角解决问题更是重要的手段 .3.结构一线三等角的步骤:找角、定线、构相像坐标系中,要讲究“线”的特别性如图 3-6 ,线上有一特别角,就考虑结构同侧型一线三等角自然只加这两条线往常是不够的,为了利用这个特别角导线段的关系,过 C 、D两点作直线 l 的垂线是必不行少的。
5第五章 三垂直全等模型

CD E BA图21图4图B A E C D 图3C D E BA C D EB AEDC B A 第五章 三垂直全等模型模型 三垂直全等模型如图,∠D=∠BCA=∠E=90°,BC=AC 。
结论:Rt △BCD ≌Rt △CAE 。
模型分析说到三垂直模型,不得不说一下弦图,弦图的运用在初中直角三角形中占有举足轻重的地位,很多利用垂直倒角,勾股定理求边长,相似求边长都会用到从弦图中支离出来的一部分几何图形去求解。
图①和图②就是我们经常会见到的两种弦图。
三垂直图形变形如下图③、图④,这也是由弦图演变而来的。
模型实例例1.如图,AB ⊥BC ,CD ⊥BC ,AE ⊥DE ,AE=DE 。
求证:AB+CD=BC 。
例2.如图,∠ACB-90°,AC=BC ,BE ⊥CE 于点D ,AD=2.5cm ,BE=0.8cm 。
求DE 的长。
A B C O x y (-1,0)(0,3)图21图(0,3)(-2,0)y x OC B A A B CDE F cb aAB C D E 例3.如图,在平面直角坐标系中,等腰Rt △ABC 有两个顶点在坐标轴上, 求第三个顶点的坐标。
热搜精练1.如图,正方形ABCD ,BE=CF 。
求证:(1)AE=BF ;(2)AE ⊥BF 。
2.直线l 上有三个正方形a 、b 、c ,若a 、c 的面积分别是5和11,则b 的面积是 。
P A BC EFE D C BA3.已知,△ABC 中,∠BAC-90°,AB=AC ,点P 为BC 上一动点(B P<CP ), 分别过B 、C 作BE ⊥AP 于点E 、CF ⊥AP 于点F 。
(1)求证:EF=CF-BE ;(2)若P 为BC 延长线上一点,其它条件不变,则线段BE 、CF 、EF 是否存在 某种确定的数量关系?画图并直接写出你的结论。
4.如图,在直角梯形ABCD 中,AD ∥BC ,AB ⊥BC ,AD=2,BC=3,设∠BCD=α, 以D 为旋转中心,将腰DC 绕点D 逆时针旋转90°至DE 。
三垂直模型证明过程

三垂直模型证明过程嘿,朋友们!今天咱们来唠唠那个超有趣的三垂直模型的证明过程,就像探索一个神秘的宝藏一样好玩。
你看啊,这三垂直模型就像是三个并肩作战的超级英雄。
首先,我们有三个角都是直角,这直角啊,就像是房子的墙角一样,方方正正,稳稳当当,一点儿也不歪。
那这三个直角的存在就像是给整个模型打了一个坚实的地基。
想象一下,我们有两条直角边就像两个小火车轨道,平行又笔直。
其中一条轨道上的一个点出发了一个线段,这个线段就像一个调皮的小猴子,蹦跶着去和另一条轨道上的某个点连线。
然后呢,我们要开始证明一些三角形全等啦。
这就好比是要找出这几个超级英雄之间隐藏的亲属关系一样。
我们通过角边角或者角角边这些规则来判断。
比如说,那几个直角肯定是相等的呀,这就像大家都知道太阳是圆的一样明显。
然后呢,还有那些锐角,就像是小饼干的碎角一样,通过一些巧妙的角度关系,发现它们也是相等的。
在这个证明过程中,那些线段的长度关系就像是一群小蚂蚁排着队,规规矩矩的。
一条线段和另一条线段相等,就像两个双胞胎小蚂蚁,长得一模一样。
我们利用已知条件的时候,就像是从一个装满魔法道具的口袋里掏出宝贝一样。
已知的角度、线段长度都是我们的宝贝,能帮助我们一步步解开这个三垂直模型的秘密。
当我们终于证明出三角形全等的时候,就像是找到了打开宝藏大门的钥匙。
那种感觉,就像是在黑暗的山洞里突然看到了闪闪发光的金子一样兴奋。
而且啊,这个三垂直模型证明出来之后,就像是掌握了一种魔法咒语,可以在好多几何问题里大显身手。
它就像一把万能钥匙,能打开许多看似复杂无比的几何迷宫的大门。
总之呢,三垂直模型的证明过程虽然有点小复杂,但就像一场有趣的冒险。
我们在这个充满直角、线段和三角形的世界里穿梭,像探险家一样不断发现惊喜,最后成功证明的时候,就像英雄凯旋而归,超有成就感的呢!。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
D P F
E B
C A K 模型图与全等
欧阳家百(2021.03.07)
知识点
基本图形
本题8分)如图,在等腰Rt △ABC 中,∠ACB=90°,D 为BC 的中
点,DE ⊥AB ,垂足为E ,过点B 作
BF ∥AC 交DE 的延长线于点F ,连接
CF .
(1)求证:AD ⊥CF ;
(2)连接AF ,求证:AF =CF .
22.边长为1的正方形ABCD 中,E 是
AB 中点,连CE ,过B 作BF ⊥CE 交AC 于F ,求AF.
【例8】
【例9】等腰Rt △ABC 中 ∠ACB =90°,AC=BC ;F 是BC 上的中
点,连AF ,作CD ⊥AF 于E ,交AB 于D ; 连FD.求证:AD =2BD ;
【例3】已知△ABC 中,∠C=90,AC=BC,D 是AB 的中点,E 是BC
上任一点,EP ⊥CB,PF ⊥AC,E 、F 为垂足,
求证:△DEF 是等腰直角三角形.
【例4】如图,D 为线段AB 的中点,在AB 上取异于D 的点C ,
分别以AC 、BC 为斜边在AB 同侧作等腰直角三角形ACE 与BCF ,连结DE 、DF 、EF ,求证:△DEF 为等腰直角三角形。
【例5】如图,分别以△ABC 的边AB 、AC 向外作等腰Rt △ABD ,
等腰Rt△ACE;连接DE。
AF是△ABC的中线,
FA的延长线交DE于点H,求证:DE=2AF
【例6】如图,在正方形ABCD中,点N是BC边上的点。
连接AN,MN⊥AN交∠DCB的外角平分线于点M。
求证:AN=MN
9、如图,直线AB交x轴正半轴于点A(a,0),交y 轴正半轴于点
B(0,b),且a 、b满足4
a+ |4-b|=0
(1)求A、B两点的坐标;
(2)D为OA的中点,连接BD,过点O作OE⊥BD于F,交AB 于E,求证∠BDO=∠EDA;
(3)如图,P为x轴上A点右侧任意一点,以BP为边作等腰Rt△PBM,其中PB=PM,直线MA交y 轴于点Q,当点P
在x轴上运动时,线段OQ的长是否发生变化?若不变,求
其值;若变化,求线段OQ的取值范围.
10
24.(12分)如图,COD 等腰直角三角形,CA ⊥x 轴。
⑴若点C 的坐标是(—2,—4),求D 点的坐标。
(4分) ⑵连结CD ,点E 为CD 的中点,求证:AE ⊥BE ;(4分)
⑶如图,点P 是y 轴正半轴是一点,OP=AB ,当点A 、B 在x 轴上运动时,∠APB+∠CPD 的值是否发生变化?若变化,请你指出“K”顶点作该直线垂线。
例:已知等腰RT △ABC 中,过点A 作直线。
衍生:平面直角坐标系中A (1,3),以OA 求B 、C 坐标。
变式:平面直角坐标系中,点A (4,1),过点O 作一条直线与OA 夹角为45°,求该直线解析式。
衍伸:平面直角坐标系中直线3:2OA l y x =与双曲线k y x
=交于点A ,以
OA 为边作等腰RT △OAB ,点B 刚好落在双曲线上。
求k 。
本题8分)如图,在等腰Rt △ABC 中,∠ACB=90°,D 为BC 的中
点,DE ⊥AB ,垂足为E ,过点B 作
BF ∥AC 交DE 的延长线于点F ,连接
CF .
(1)求证:AD ⊥CF ;
(2)连接AF ,求证:AF =CF .
5.已知等腰Rt ABC 的直角顶点C 在x 轴
上,点B 在y 轴上。
(1)如图1,若点C 的坐标为(2,0),A 的坐标为(-2,-2),求点B 的坐标。
(2)如图2,直角边BC 在坐标轴上运动,使点A 在第四象限内,过点A 作AD ⊥y 轴于D ,求
CO AD BO -的值。
八年级数学每日一
题(041-045)
P —041如图,如图,
在平面直角坐标系中,点A 和点B 的坐标分别是A (0,a ),B (b ,0),且a 、b 330a b -+=.
(1)求点A 、点B 的坐标;
(2)点C 是第三象限内一点,以BC 为直角边作等腰直角△BCD ,∠BCD=90º,过点A 和点D 分别作直线CO 的垂线,垂足分别是点E 、F.试问线段AE 、DF 、CO 之间是否存在某种确定的数量关系?为什么?
P —042 如图,在平面直角坐标系中,点A 、点C 分别在y 轴的正半D y x A
O C B O C B
A
轴和负半轴上,点B在x轴正半轴上,∠ABC=90º.点E在BC延长线上,过点E作ED∥AB,交y轴于点D,交x轴于点F,DO–AO=2CO.(1)求证:AB=DE;
(2)若AB=2BC,求证:EF=EC;
(3)在(2)的条件下,若点B的坐标是(2,0),求点E的坐标.
9、如图,直线AB交x轴正半轴于点A(a,0),交y 轴正半轴于点
B(0,b),且a 、b满足4
a+ |4-b|=0
(1)求A、B两点的坐标;
(2)D为OA的中点,连接BD,过点O作OE⊥BD于F,交AB 于E,求证∠BDO=∠EDA;
(3)如图,P为x轴上A点右侧任意一点,以BP为边作等腰Rt△PBM,其中PB=PM,直线MA交y 轴于点Q,当点P
在x轴上运动时,线段OQ的长是否发生变化?若不变,求
其值;若变化,求线段OQ的取值范围.
10
如图,在平面直角坐标系xoy中,直线AP交x轴于点P(p,0),交y轴于点A(0,a),且a、b满足
+(p+1)2=0.(1)求直线AP的解析式;(2)如图1,点P关于y 轴的对称点为Q,R(0,2),点S在直线AQ上,且SR=SA,求直线RS的解析式和点S的坐标;(3)如图2,点B(-2,b)为直线AP上一点,以AB为斜边作等腰直角三角形ABC,点C在第一象限,D为线段OP上一动点,连接DC,以DC为直角边,点D为直角顶点作等腰三角形DCE,EF⊥x轴,F为垂足,下列结论:①2DP+EF的值不变;②AO−EF
的值不变;其中只有一个结论正确,请你选择出正确的结论,并求
出其定值.
如图,在平面直角坐标系xoy中,直线AP交x轴于点P(p,0),交y轴于点A(0,a),且a、b满足
+(p+1)2=0.(1)求直线AP的解析式;(2)如图1,点P关于y 轴的对称点为Q,R(0,2),点S在直线AQ上,且SR=SA,求直线RS的解析式和点S的坐标;(3)如图2,点B(-2,b)为直线AP上一点,以AB为斜边作等腰直角三角形ABC,点C在第一象限,D为线段OP上一动点,连接DC,以DC为直角边,点D为直角顶点作等腰三角形DCE,EF⊥x轴,F为垂足,下列结论:①2DP+EF的值不变;②AO−EF
的值不变;其中只有一个结论正确,请你选择出正确的结论,并求出其定值.。
