多项式乘以多项式及乘法公式习题(终审稿)
多项式与多项式相乘例题

多项式与多项式相乘例题
当两个多项式相乘时,我们可以使用分配律和乘法原则来展开
计算。
下面我将给出一个例题来说明。
假设我们要计算多项式 (3x^2 + 2x + 1) 与 (2x + 1) 的乘积。
首先,我们可以使用分配律将每一项相乘,然后将结果相加。
具体步骤如下:
(3x^2 + 2x + 1) (2x + 1)。
= 3x^2 2x + 3x^2 1 + 2x 2x + 2x 1 + 1 2x + 1 1。
= 6x^3 + 3x^2 + 4x^2 + 2x + 2x + 1。
= 6x^3 + 7x^2 + 4x + 1。
所以,多项式 (3x^2 + 2x + 1) 与 (2x + 1) 相乘的结果是
6x^3 + 7x^2 + 4x + 1。
这是一个简单的例题,但是当多项式的项数较多时,计算会变得更加复杂。
在实际应用中,我们可以使用计算器或计算软件来进行多项式的乘法运算。
需要注意的是,多项式的乘法满足交换律和结合律,因此计算顺序不影响最终结果。
另外,当两个多项式相乘时,我们可以使用卡特兰恒等式、二项式定理等方法来简化计算,这些方法可以在具体的乘法运算中根据需要选择使用。
希望以上解答能够帮助到你,如果你还有其他问题,请继续提问。
多项式的乘法练习题

多项式的乘法练习题多项式乘多项式:(a+b)(c+d)=(x+a)(x+b)=平方差公式:(a+b)(a-b)=完整的平方公式:(a+b)2=(a-b)2=1。
简化a(B?C)?b(c?a)?C(a?B)的结果是()a.2ab?2bc?2ABC.2ab?2bcc。
2ab2。
以下公式中的计算误差为()a.2x?(2x3?3x?1)?4x4?6x2?2xc.?d.?2bcb、 b(b2?b?1)?b3?b2?屋宇署。
1x(2x2?2)??x3?x22332x(x?3x?1)?x4?2x2?X3233。
如果(8)×106)(5×102)(2×10)=m×10A,则m和a的值为()a.m=8,a=8b.m=8,a=10c.m=2,a=9d.m=5,a=104、若2x2+5x+1=a(x +1)2+b(x+1)+c,那么a,b,c应为()a.a=2,b=-2,c=-1c.a=2,b=1,c=-2b、 a=2,b=2,c=1d.a=2,b=1,c=25、.若(x?a)(x?b)的乘积中不含x的一次项,则a,b的关系是()a.互为倒数b.相等c.互为相反数d.a,b都为06、.下列各式中,不能用平方差公式计算的是()a、(4x?3y)(3y?4x)b.(2x2?y2)(2x2?y2)c.(a?b?c)(c?b?a)d.(x?y)(x?y)7、.下列各式中,相等关系一定成立的是()a、(x?y)2?(y?x)2b、(x?6)(x?6)?x2?6c、(x?y)?十、yd、6(x?2)?x(2?x)?(x?2)(x?6)8。
如果9x2+4y2=(3x+2Y)2+m,那么m是()a.6xyb.-6xyc。
12xyd.-12xy9。
下面的等式不成立,它是()a.(3x-y)2=9x2-6xy+y2b.(a+b-c)2=(c-a-b)2c.(0.5m-n)2=0.25m2-mn+n2d.(x-y)(x+y)(x2-y2)=x4-y410、已知(x+3)(x-2)=x+ax+b,则a、b的值分别是()a、 a=-1,b=-6b.a=1,b=-6c.a=-1,b=6d.a=1,b=611.观察下列算式:2=2,2=4,2=8,2=16,2=32,2=64,2=128,2=256,……根据其规律可知8的末位数是()a、2b、4c、6d、8一101234567822222.填空:1.(1.2?103)(2.5?1011)(4?109)?_______________.(3?102)2?(?103)?______-2ab (a2b+3ab2-1)=____________(4(?4x2?6x?8)?(?12x)?________;213?(?x)2?(?2x2y)3?2x2(x6y3?1)?2、(-2x+y)(-2x+y)=______(-x-3y)(-x-3y)=_______-(2x2+3y)(3y-2x2)=____________2121(m?n)(?m?n)=____________(a+b+2)(a+b-2)=__________22(1.5a?b)2=________(=_________322x?3y3y?2x=____________.233、(a+2b+3c)(a-2b-3c)=(______)2-(______)2;(2M?)(??)=____________ 三亿四千四百三十一万一千二百二十四(x+y)(_____)=y-x;(-5a-2b2)(______)=4b4-25a2.4164、2021-4010×2021+2021=____________二2壹仟玖佰玖拾玖元×2001=____________(1?x)(1?x)(1?x2)(1?x4)?______________(3x+2)(3x-2)(9x2+4)=____________(111x+y)(x-y)(x2+y2)=____________(y-3)2-2(y+2)(y-2)=___________3395、①(?x?3)(2)? 9? x2②(3x?2y)2?=(3x?2y)226.如果代数公式2x+3x+7的值为8,则代数公式4x+6x-9的值为;如果代数公式3x-4x+6的值是9,那么X-224x+1的值为(2),如果m2+m=1=0,则发现m3+2m2+2022=31=b7,即已知的A2+B2-2a+6b+10=0,然后是A2022~A2+B2的值。
七年级数学下册-第09讲 多项式乘多项式(6种题型+强化训练)(解析版)
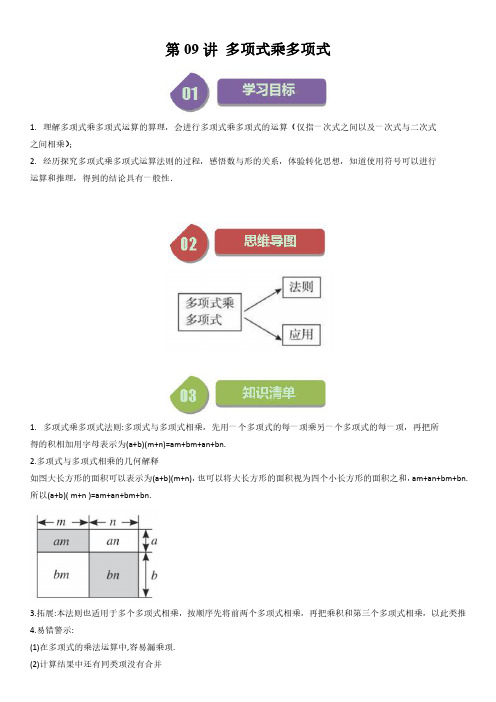
第09讲多项式乘多项式1.理解多项式乘多项式运算的算理,会进行多项式乘多项式的运算(仅指一次式之间以及一次式与二次式之间相乘);2.经历探究多项式乘多项式运算法则的过程,感悟数与形的关系,体验转化思想,知道使用符号可以进行运算和推理,得到的结论具有一般性.1.多项式乘多项式法则:多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加用字母表示为(a+b)(m+n)=am+bm+an+bn.2.多项式与多项式相乘的几何解释如图大长方形的面积可以表示为(a+b)(m+n),也可以将大长方形的面积视为四个小长方形的面积之和,am+an+bm+bn.所以(a+b)(m+n)=am+an+bm+bn.3.拓展:本法则也适用于多个多项式相乘,按顺序先将前两个多项式相乘,再把乘积和第三个多项式相乘,以此类推4.易错警示:(1)在多项式的乘法运算中,容易漏乘项.(2)计算结果中还有同类项没有合并题型一:利用多项式乘多项式法则计算1.(2023下·江苏·七年级专题练习)计算:()()43x y x y +-.【答案】2243x xy y +-【分析】根据多项式乘多项式的运算法则即可得.【详解】()()43x y x y +-224343x xy xy y =-+-2243x xy y =+-.【点睛】本题考查了整式的乘法运算,熟练掌握运算法则是解题关键.2.(2023下·江苏·七年级专题练习)计算:()()233x y x y +-.【答案】22673x xy y +-【分析】直接根据多项式乘以多项式的法则进行计算;先去括号,再合并同类项.【详解】解:()()233x y x y +-226293x xy xy y =-+-22673x xy y =+-【点睛】本题考查了多项式乘以多项式;根据乘法分配律,去括号,再合并同类项是关键.题型二:先化简再求值3.(2023下·江苏·七年级专题练习)先化简,再求值:()(2)(32)(3)a b a b a b a b -----,其中2,1a b ==-.【答案】22284a ab b -+-;28-【分析】根据多项式的乘法进行化简,然后将字母的值代入进行计算即可求解.【详解】解:原式()2222223926a ab ab b a ab ab b =--+---+()2222323116a ab b a ab b =-+--+2222323116a ab b a ab b =-+-+-22284a ab b =-+-;当2,1a b ==-时,原式222282(1)4(1)=-⨯+⨯⨯--⨯-8164=---28=-.【点睛】本题考查了多项式的乘法的化简求值,正确的去括号是解题的关键.题型三:利用多项式乘多项式的积中项的特征求待定字母的值4.(2023下·江苏·七年级专题练习)已知21()()x mx x n ++-的展开式中不含x 项,2x 项的系数为2-,求mn m n +-的值.【答案】1-8.(2023上·重庆·七年级校联考期中)小马虎做一道数学题“两个多项式A ,B ,已知2236B x x -=+,试求2A B -的值”.小马虎将2A B -看成2A B +,结果答案(计算正确)为2529x x -+.(1)当3x =-时,求多项式A 的值;(2)若多项式21C mx nx =-+,且满足A C -的结果不含2x 项和x 项,求m ,n 的值.【答案】(1)6-(2)1,4m n ==-【分析】本题考查整式的加减,解题的关键是掌握整式的加减法则.(1)将错就错,把B 与错误结果代入确定A 即可;(2)化简A C -,根据不含2x 项和x 项求出结果.【详解】(1)解:根据题意得:225292(236A x x x x =-+--+)22=5294612x x x x -+-+-243x x =+-,当3x =-时,原式2(3)1236=---=-;(2)解: 243A x x =-+,21C mx nx =-+,22(43)(1)A C x x mx nx ∴-=+---+22431x x mx nx =+--+-()()2144m x n x =-++-,结果不含x 2项和x 项,10,40m n ∴-=+=,∴1,4m n ==-.9.(2023下·江苏·七年级期中)在计算()()x a x b ++时,甲把b 错看成了6,得到结果是:2812x x ++;乙错把a 看成了a -,得到结果:26x x +-.(1)求出a ,b 的值;(2)在(1)的条件下,计算()()x a x b ++的结果.【答案】(1)2a =,3b =(2)256x x ++【分析】(1)根据题意可得出68a +=,1a b -+=,求出a 、b 的值即可;(2)把a 、b 的值代入,再根据多项式乘以多项式法则计算即可.【详解】(1)解:根据题意得:()()()22666812x a x a x x a x x ++++=++=+,()()()226x a x b x a b x ab x x -+=+-+-=+-,所以68a +=,1a b -+=,,解得:2a =,3b =;(2)解:把2a =,3b =代入,得()()()()22356x a x b x x x x ++=++=++.【点睛】本题考查了多项式乘以多项式,等式的性质,能正确运用多项式乘以多项式法则进行计算是解此题的关键.题型五:利用数形结合思想巧解整式的运算10.(2023下·江苏宿迁·七年级统考期中)阅读材料并解答问题:我们已经知道,完全平方公式可以用平面几何图形的面积来表示,实际上还有一些代数恒等式也可以用这种形式表示.例如:22(2)()23a b a b a ab b ++=++就可以用图(1)或图(2)等图形的面积表示.(1)请写出图(3)所表示的代数恒等式:________;(2)试画出一个几何图形,使它的面积能表示等式22()(3)43a b a b a ab b ++=++;(3)请仿照上述方法另写一个含有,a b 的代数恒等式,并画出与之对应的几何图形.【答案】(1)()()2222252a b a b a ab b++=++(2)见解析(3)()()22232a b a b a ab b ++=++,图见解析【分析】(1)图(3)中大长方形的长为()2a b +,宽为()2a b +,根据题意列出恒等式;(2)设计一个长方形的长为3a b +,宽为a b +的大长方形即可;(3)设计一个长方形的长为2+a b ,宽为a b +的大长方形即可.【详解】(1)解:()()2222252a b a b a ab b ++=++;(2)解:如图所示:;(3)解:恒等式()()22232a b a b a ab b ++=++,如图所示:.【点睛】本题主要考查了多项式乘法的几何背景,应从整体和部分两方面来理解多项式乘法的几何意义;主要围绕(1)图③可以解释为等式:_________;(2)请在虚线框中用图①中的基本图形若干块(每种至少用一次)拼成一个长方形,使拼出的长方形面积为22273a ab b ++,并标出此长方形的长和宽;(3)如图④,大正方形的边长为m ,小正方形的边长为n ,若用x y 、表示四个长方形的两边长指出以下关系式:①x y m +=;②()()x y x y m n +-= ;③()()2222x y x y m n ++-=+;④确的有().A .1个B .2个C .3个D .4个【答案】(1)22(2)(2)252a b a b a ab b ++=++(3)解:大正方形的边长为m ∴①x y m +=,故原命题正确;②∵x y m +=,x y n -=,∴()()x y x y m n +-= ,故原命题正确;(2)试用字母表示上述式子的规律,并说明结论的正确性.【答案】(1)55461⨯-⨯=;(2)()()2111n n n --+=,说明见解析.【分析】(1)根据题干中的等式找出规律,写出新的式子即可;(2)根据题干发现的规律,由特殊到一般,得出结论,再证明正确性即可.【详解】(1)解:通过观察,写出新的式子为55461⨯-⨯=,故答案为:55461⨯-⨯=;(2)解:()()2111n n n --+=,说明如下:左边()()()2221111n n n n n n n =--+=--+-==右边,∴结论成立.【点睛】本题考查了数字类规律探索,关键是由特殊到一般,得出一般规律,运用整式的运算进行验证.14.(2023下·江苏苏州·七年级苏州市立达中学校校考期中)阅读以下材料,回答下列问题:小明遇到这样一个问题:求计算()()()22334x x x +++所得多项式的一次项系数.小明想通过计算()()()22334x x x +++所得的多项式解决上面的问题,但感觉有些繁琐,他想探寻一下,是否有相对简洁的方法.他决定从简单情况开始,先找()()223x x ++所得多项式中的一次项系数.通过观察发现:也就是说,只需用2x +中的一次项系数1乘以23x +中的常数项3,再用2x +中的常数项2乘以23x +中的一次项系数2,两个积相加13227⨯+⨯=,即可得到一次项系数.延续.上面的方法,求计算()()()22334x x x +++所得多项式的一次项系数.可以先用2x +的一次项系数1,23x +的常数项3,34+x 的常数项4,相乘得到12;再用23x +的一次项系数2,2x +的常数项2,34+x 的常数项4,相乘得到16;然后用34+x 的一次项系数3,2x +的常数项2,23x +的常数项3,相乘得到18,最后将12,16,18相加,得到的一次项系数为46.参考小明思考问题的方法,解决下列问题:(1)计算()()2132x x ++所得多项式的一次项系数为______.(2)计算()()()13243x x x ++-所得多项式的一次项系数为______.(3)若计算()()()221321x x x x a x -+-+-所得多项式的一次项系数为0,则=a ______.(4)计算()51x +所得多项式的一次项系数为______,二次项系数为______.(5)计算()521x -所得多项式的一次项系数为______,二次项系数为______.【答案】(1)7(2)7-(3)1-(4)5,10(5)10,40-【分析】(1)结合已知可得(21)(32)x x ++所得多项式的一次项系数2213=⨯+⨯,即可求解;(2)结合已知可得(1)(32)(43)x x x ++-所得多项式的一次项系数1(3)231(3)412=⨯-⨯+⨯⨯-+⨯⨯,即可求解;(3)由22(1)(3)(21)x x x x a x ++-+-所得多项式中不含一次项,可得()()()()11311210a a -⨯⨯-+-⨯⨯-+⨯⨯=,即可求解;(4)(5)根据题目中提供的计算方法进行计算即可.【详解】(1)解:22137⨯+⨯=,故答案为:7;(2)1(3)231(3)4126987⨯-⨯+⨯⨯-+⨯⨯=--+=-,故答案为:7-;(3)由题意得,()()()()11311210a a -⨯⨯-+-⨯⨯-+⨯⨯=,也就是,320a a ++=,所以,1a =-;故答案为:1-;(4)5(1)x + (1)(1)(1)(1)(1)x x x x x =+++++22(21)(21)(1)x x x x x =+++++∴一次项系数为:2112111115⨯⨯+⨯⨯+⨯⨯=;二次项系数为:1122212110++⨯+⨯+⨯=.故答案为:5,10;(5)5(21)(21)(21)(21)(21)(21)x x x x x x -=----- .22(441)(441)(21)x x x x x =-+-+-.∴一次项系数为:41(1)(4)1(1)21110-⨯⨯-+-⨯⨯-+⨯⨯=,二次项系数为:2(4)1(4)(4)(1)2⨯-⨯+-⨯--⨯40=-.故答案为:10;40-.【点睛】本题考查多项式乘以多项式,理解多项式乘以多项式所得的多项式每一项的系数是解决问题的关键.一.选择题(共10小题)1.(2023春•锡山区期中)若2(2)()2x x n x mx +-=++,则m n -的值是()A .6B .4C .2D .6-【分析】将所给等式的左边展开,然后与等式右边比较,可得含有m 和n 的等式,求出m 、n 的值即可得答案.【解答】解:2(2)()2x x n x mx +-=++ ,22(2)22x n x n x mx ∴+--=++,2n m ∴-=,22n -=3m ∴=,1n =-,314m n ∴-=+=.故选:B .【点评】本题考查了多项式乘以多项式,明确多项式乘以多项式的运算法则是解题的关键.2.(2023春•淮安区期末)小羽制作了如图所示的卡片A 类,B 类,C 类各50张,其中A ,B 两类卡片都是正方形,C 类卡片是长方形,现要拼一个长为(57)a b +,宽为(7)a b +的大长方形,那么所准备的C 类卡片的张数()A .够用,剩余4张B .够用,剩余5张C .不够用,还缺4张D .不够用,还缺5张【分析】根据大长方形的面积公式求出拼成大长方形的面积,再对比卡片的面积,即可求解.【解答】解:大长方形的面积为22(57)(7)35547a b a b a ab b ++=++,C 类卡片的面积是ab ,∴需要C 类卡片的张数是54,∴不够用,还缺4张,故选:C .【点评】本题主要考查多项式与多项式的乘法与图形的面积,掌握多项式乘以多项式的计算方法是解题的关键.3.(2023春•丹徒区期末)已知240a a +-=,代数式2(3)(2)a a -+的值是()A .2B .4-C .4D .2-【分析】根据多项式乘多项式法则即可求出答案.【解答】解:240a a +-= ,231a a ∴-=-+.∴原式(1)(2)a a =-++22a a =--24=-2=-,故选:D .【点评】本题考查多项式乘多项式法则,解题的关键是熟练运用多项式乘多项式法则,本题属于基础题型.4.(2023春•姜堰区期中)若(2)(3)M x x =--,(1)(4)N x x =--,则M 与N 的大小关系是()A .由x 的取值而定B .M N =C .M N<D .M N>【分析】先将M 和N 别去括号计算,再根据2M N -=即可得到答案.【解答】解:2(2)(3)56M x x x x =--=-+ ,2(1)(4)54N x x x x =--=-+,2M N ∴-=,M N ∴>,故选:D .【点评】本题考查整式乘法运算,解题的关键是掌握整式乘法运算法则.5.(2023春•工业园区期中)若关于x 的多项式2(2)(24)x ax x ++-展开合并后不含2x 项,则a 的值是()A .0B .12C .2D .2-【分析】根据多项式乘多项式的乘法即可求出答案.【解答】解:原式322242448x x ax ax x =-+-+-322(24)(44)8x a x a x =+-+--,由题意可知:240a -=,2a ∴=,故选:C .【点评】本题考查多项式乘多项式,解题的关键是令含2x 的系数为零,本题属于基础题型.6.(2023春•吴江区期中)已知2(3)()24x x m x nx ++=+-,则m ,n 的值分别是()A .8-,5-B .8,11C .8,15D .8-,11【分析】利用多项式乘多项式的法则进行运算,再进行解答即可.【解答】解:2(3)()24x x m x nx ++=+- ,22(3)324x m x m x nx ∴+++=+-,3m n ∴+=,324m =-,解得:8m =-,5n =-.故选:A .【点评】本题主要考查多项式乘多项式,解答的关键是对相应的运算法则的掌握.7.(2023春•东台市期中)若2(3)(2)215x x m x nx -+=+-,则()A .5m =-,1n =B .5m =,1n =-C .5m =-,1n =-D .5m =,1n =【分析】先根据多项式乘以多项式法则展开,即可得出方程组,求出方程组的解即可.【解答】解:22(3)(2)2632(6)3x x m x mx x m x m x m -+=+--=+--,2(3)(2)215x x m x nx -+=+- ,6m n ∴-=,315m -=-,解得:5m =,1n =-,故选:B .【点评】本题考查了多项式乘以多项式和解二元一次方程组,能正确运用多项式乘以多项式法则展开是解此题的关键.8.(2023春•邗江区期中)如果(2)x m +与(3)x +的乘积中不含x 的一次项,那么m 的值为()A .6-B .3-C .0D .1【分析】先根据多项式乘多项式进行计算,再合并同类项,根据乘积不含x 的一次项得出60m +=,再求出m 即可.【解答】解:(2)(3)x m x ++2263x x mx m=+++22(6)3x m x m =+++,(2)x m + 与(3)x +的乘积中不含x 的一次项,60m ∴+=,解得:6m =-,故选:A .【点评】本题考查了多项式乘多项式,能正确根据多项式乘多项式法则进行计算是解此题的关键.9.(2023春•吴江区校级期中)若2(3)(2)215x x m x nx +-=+-,则()A .5m =-,1n =B .5m =-,1n =-C .5m =,1n =D .5m =,1n =-【分析】先根据多项式乘以多项式法则展开,即可得出方程组,求出方程组的解即可.【解答】解:22(3)(2)2632(6)3x x m x mx x m x m x m +-=-+-=+-+-,2(3)(2)215x x m x nx +-=+- ,6m n ∴-+=,315m -=-,解得:5m =,1n =,故选:C .【点评】本题考查了多项式乘以多项式和解二元一次方程组,能正确运用多项式乘以多项式法则展开是解此题的关键.10.(2023春•东海县月考)计算(1)(2)x x ++的结果为()A .22x +B .232x x ++C .233x x ++D .222x x ++【分析】原式利用多项式乘以多项式法则计算即可得到结果.【解答】解:原式222232x x x x x =+++=++,故选:B .【点评】此题考查了多项式乘多项式,熟练掌握运算法则是解本题的关键.二.填空题(共8小题)11.(2023春•镇江期中)已知230x x --=,则(3)(2)x x -+的值等于3-.【分析】先将230x x -+=变形为23x x -=,再根据多项式乘以多项式法则将(3)(2)x x -+进行运算并代入求值即可.【解答】解:230x x --= ,23x x ∴-=,2(3)(2)6363x x x x ∴-+=--=-=-.故答案为:3-.【点评】本题主要考查了整式运算及代数式求值,熟练掌握多项式乘以多项式运算法则是解题关键.12.(2023春•淮安区校级期末)若3x y +=且1xy =,则代数式(2)(2)x y --=1-.【分析】将(2)(2)x y --计算后代入已知数据计算即可.【解答】解:3x y += ,1xy =,(2)(2)x y ∴--224xy x y =--+2()4xy x y =-++1234=-⨯+164=-+1=-,故答案为:1-.【点评】本题主要考查多项式乘多项式,熟练掌握相关运算法则是解题的关键.13.(2023春•淮安期中)对于实数a ,b ,c ,d ,规定一种运算a b ad bc c d=-,如101(2)0222(2)=⨯--⨯=--,那么当(1)(2)27(3)(1)x x x x ++=--时,则x =22.【分析】由题中的新定义可知,此种运算为对角线乘积相减的运算,化简所求的式子得到关于x 的方程,利用多项式乘多项式的运算法则及平方差公式化简合并即可求出x 的值.【解答】解:(1)(2)27(3)(1)x x x x ++=--,(1)(1)(2)(3)27x x x x ∴+--+-=,221(6)27x x x ∴----=,221627x x x ∴--++=,22x ∴=;故答案为:22.【点评】此题考查学生理解新定义及灵活运用新定义的能力,同时也考查了学生会进行整式的混合运算及会利用平方差公式来化简运算,是一道中档题.14.(2023春•东海县月考)2(2)(35)310x x x bx +-=--,则b =1-.【分析】根据多项式乘以多项式法则展开后,根据对应项的系数相等即可得出b 的值.【解答】解:2(2)(35)310x x x x +-=+-,2(2)(35)310x x x bx +-=-- ,1b ∴-=1b ∴=-,故答案为:1-.【点评】本题考查了多项式乘以多项式的法则的应用,主要考查学生的化简能力.15.(2023春•宝应县期中)已知多项式x a -与2221x x -+的乘积的结果中不含2x 项,则常数a 的值是1-.【分析】利用多项式乘多项式的法则进行运算,再根据结果不含2x 项,使其系数为0,从而可求解.【解答】解:2()(221)x a x x --+3222222x x x ax ax a=-+-+-322(22)2x a x x ax a=-+++- 结果不含2x 项,220a ∴+=,解得:1a =-.故答案为:1-.【点评】本题主要考查多项式乘多项式,解答的关键是明确不含2x 项,则其系数为0.16.(2023春•洪泽区期中)已知2()(31)a p a a +-+的计算结果中不含2a 项,则p 的值为3.【分析】利用多项式乘多项式的法则进行运算,再结合条件求解即可.【解答】解:2()(31)a p a a +-+32233a a a pa pa p =-++-+32(3)(13)a p a p a p =+-++-+,结果中不含2a 项,30p ∴-+=,解得:3p =.故答案为:3.【点评】本题主要考查多项式乘多项式,解答的关键是对相应的运算法则的掌握.17.(2023春•泰兴市期末)图中三角形的面积为24m -.【分析】根据三角形的面积公式求解即可.【解答】解:由题意知,三角形的面积为21(24)(2)42m m m +-=-,故答案为:24m -.【点评】本题主要考查了三角形的面积,列代数式.解题的关键在于熟练掌握三角形的面积为:12⨯⨯底高.18.(2023春•广陵区校级期中)如图,现有正方形卡片A 类,B 类和长方形卡片C 类若干张,如果要拼一个长为(4)a b +,宽为()a b +的大长方形,则需要C 类卡片5张.【分析】通过计算(4)()a b a b ++的结果可得此题结果.【解答】解:(4)()a b a b ++ 2244a ab ab b =+++2254a ab b =++,∴需要C 类卡片5张,故答案为:5.【点评】此题考查了整式乘法几何背景问题的解决能力,关键是能将代数算式与几何图形面积相结合应用.三.解答题(共10小题)19.(2023春•未央区校级月考)计算:(2)(5)x x -+.【分析】按多项式乘以多项式的乘法法则进行计算即可.【解答】解:(2)(5)x x -+25210x x x =+--2310x x =+-.【点评】本题考查多项式乘多项式,熟记“多项式乘以多项式的运算法则”是解答本题的关键.20.(2022秋•岳麓区校级期末)计算:(1)(21)(5)(2)x x x x -+--+.【分析】先根据多项式与多项式的乘法法则计算,再去括号合并同类项即可.【解答】解:原式22221(310)x x x x x =+-----22221310x x x x x =+---++229x x =++.【点评】本题考查了整式的混合运算,熟练掌握运算顺序是解答本题的关键.混合运算的顺序是先算乘方,再算乘除,最后算加减;同级运算,按从左到右的顺序计算;如果有括号,先算括号里面的,并按小括号、中括号、大括号的顺序进行;有时也可以根据运算定律改变运算的顺序.21.(2023春•工业园区校级月考)如图所示,有一块长宽为(3)a b +米和(2)a b +米的长方形土地,现准备在这块土地上修建一个长为(2)a b +米,宽为()a b +米的游泳池,剩余部分修建成休息区域.(1)请用含a 和b 的代数式表示休息区域的面积;(结果要化简)(2)若5a =,10b =,求休息区域的面积.【分析】(1)利用长方形土地的面积减去游泳池的面积,化简后即可得出结论;(2)将a ,b 的值代入(1)中的结论计算即可.【解答】解:(1)休息区域的面积(3)(2)(2)()a b a b a b a b =++-++2222(362)(22)a ab ab b a ab ab b =+++-+++222236222a ab ab b a ab ab b =+++----224a ab b =++;∴休息区域的面积为:224a ab b ++;(2)当5a =,10b =时,224a ab b ++225451010=+⨯⨯+25200100=++325=.【点评】本题主要考查了多项式乘多项式,长方形的面积,列代数式,求代数式的值,依据题意列出代数式是解题的关键.22.(2023春•吴江区期中)在1ax +与1bx +的乘积中,2x 的系数为3-,x 的系数为6-,求22a b +的值.【分析】原式利用多项式乘以多项式法则计算,合并后根据题意得出3ab =-,6a b +=-,再根据222()2a b a b ab +=+-,然后代值计算即可.【解答】解:根据题意得:2(1)(1)()1ax bx abx a b x ++=+++, 乘积中含2x 的项的系数为3,含x 项的系数为6,3ab ∴=-,6a b +=-,2222()2(6)2(3)36642a b a b ab +=+-=--⨯-=+= .【点评】此题考查了多项式乘以多项式,熟练掌握运算法则是解本题的关键.23.(2023秋•铁西区期中)回答下列问题:(1)计算:①(2)(3)x x ++=256x x ++;②(2)(3)x x +-=.③(2)(3)x x -+=;④(2)(3)x x --=.(2)总结公式2()()x a x b x ++=+x ab+(3)已知a ,b ,m 均为整数,且2()()5x a x b x mx ++=++.求m 的所有可能值.【分析】(1)根据多项式乘多项式的法则计算①②③④这四个式子即可;(2)根据(1)中的结果总结公式即可;(3)运用(2)中的结论计算等式的左边,然后根据左右两边相等得到a b m +=,5ab =,再根据a ,b ,m 均为整数,得出1a =,5b =或1a =-,5b =-或5a =,1b =或5a =-,1b =-,最后计算即可得出m 的所有可能值.【解答】解:(1)①(2)(3)x x ++2326x x x =+++256x x =++;②(2)(3)x x +-2326x x x =-+-26x x =--;③(2)(3)x x -+2326x x x =+--26x x =+-;④(2)(3)x x --2326x x x =--+256x x =-+;故答案为:256x x ++;26x x --;26x x +-;256x x -+;(2)2()()()x a x b x a b x ab ++=+++,故答案为:()a b +;(3)2()()5x a x b x mx ++=++,22()5x a b x ab x mx ∴+++=++,a b m ∴+=,5ab =,a ,b ,m 均为整数,1a ∴=,5b =或1a =-,5b =-或5a =,1b =或5a =-,1b =-,当1a =,5b =时,156m a b =+=+=;当1a =-,5b =-时,156m a b =+=--=-;当5a =,1b =时,516m a b =+=+=;当5a =-,1b =-时,516m a b =+=--=-;综上,m 的所有可能值为6或6-.【点评】本题主要考查多项式乘多项式,注意不要漏项,漏字母,有同类项的要合并同类项.24.(2023春•昭平县期末)已知2(3)(2)x mx x n +-+的展开式中不含2x 项,常数项是6-.(1)求m ,n 的值.(2)求22()()m n m mn n +-+的值.【分析】(1)直接利用多项式乘多项式将原式变形,进而得出m ,n 的值;(2)利用多项式乘多项式运算法则计算得出答案.【解答】解:(1)原式3222263x mx x nx mnx n =+-++-3222263x mx nx mnx x n=+++--322(2)(6)3x m n x mn x n =+++--,由于展开式中不含2x 项,常数项是6-,则20m n +=且36n -=-,解得:1m =-,2n =;(2)由(1)可知:1m =-,2n =,∴原式3333(1)2m n =+=-+,18=-+7=.【点评】此题主要考查了多项式乘多项式,正确掌握相关运算法则是解题关键.25.(2022秋•凤台县期末)在计算()()x a x b ++时,甲把b 错看成了6,得到结果是:2812x x ++;乙错把a 看成了a -,得到结果:26x x +-.(1)求出a ,b 的值;(2)在(1)的条件下,计算()()x a x b ++的结果.【分析】(1)根据题意得出22()(6)(6)6812x a x x a x a x x ++=+++=++,22()()()6x a x b x a b x ab x x -+=+-+-=+-,得出68a +=,1a b -+=,求出a 、b 即可;(2)把a 、b 的值代入,再根据多项式乘以多项式法则求出即可.【解答】解:(1)根据题意得:22()(6)(6)6812x a x x a x a x x ++=+++=++,22()()()6x a x b x a b x ab x x -+=+-+-=+-,所以68a +=,1a b -+=,解得:2a =,3b =;(2)当2a =,3b =时,2()()(2)(3)56x a x b x x x x ++=++=++.【点评】本题考查了多项式乘以多项式法则和解方程,能正确运用多项式乘以多项式法则进行计算是解此题的关键.26.(2023春•虎丘区校级期中)甲、乙两个长方形的边长如图所示(m 为正整数),其面积分别为1S ,2S .(1)填空:12S S -=21m -(用含m 的代数式表示);(2)若一个正方形的周长等于甲、乙两个长方形的周长之和,设该正方形的面积为3S ,试探究:3S 与122()S S +的差是否是常数?若是常数,求出这个常数,若不是常数,请说明理由.(3)若另一个正方形的边长为正整数n ,并且满足条件121n S S <- 的n 有且只有1个,求m 的值.【分析】(1)根据矩形的面积公式计算即可;(2)根据正方形的面积计算即可;(3)根据不等式组的整数解即可得结论.【解答】解:(1)12(7)(1)(4)(2)S S m m m m -=++-++21m =-.故答案为:21m -;(2)3S 与122()S S +的差是常数,21221415S S m m +=++ ,223122()(27)2(21415)S S S m m m -+=+-++224284942830m m m m =++---19=.答:3S 与122()S S +的差是常数:19;(3)121n m <-,由题意,得1212m <-,解得312m < .m 是整数,m ∴无解.答:m 无解.【点评】本题考查了多项式乘多项式、整式的加减、不等式组的整数解,解决本题的关键是求不等式组的整数解.27.(2023春•秦都区期中)有些大数值问题可以通过用字母代替数转化成整式问题来解决,请先阅读下面的解题过程,再解答下面的问题.例若67896786x =⨯,67886787y =⨯,试比较x 、y 的大小.解:设6788a =,那么2(1)(2)2x a a a a =+-=--,2(1)y a a a a =-=-.因为22(2)()2x y a a a a -=----=-,所以x y <.看完后,你学到了这种方法吗?利用上面的方法解答下列问题:若2007201120082010x =⨯-⨯,2008201220092011y =⨯-⨯,试比较x 、y 的大小.【分析】设2007a =,利用题干中的方法将x ,y 用含a 的代数式表示,再利用多项式乘多项式和单项式乘多项式的法则化简后即可得出结论.【解答】解:设2007a =,则(4)(1)(3)x a a a a =+-++224(33)a a a a a =+-+++22433a a a a a =+----3=-,(1)(5)(2)(4)y a a a a =++-++22(55)(428)a a a a a a =+++-+++2255428a a a a a a =+++----3=-,所以x y =.【点评】本题主要考查了多项式乘多项式,本题是阅读型题目,理解题干中的方法并熟练应用是解题的关键.28.(2023春•淮安期末)当我们利用两种不同的方法计算同一图形的面积时,可以得到一个等式,由图1,可得等式:22(2)()32a b a b a ab b ++=++.(1)由图2可得等式:2222()222a b c a b c ab ac bc ++=+++++.(2)利用(1)中所得到的结论,解决下面的问题:已知11a b c ++=,38ab bc ac ++=,求222a b c ++的值;(3)利用图3中的纸片(足够多),画出一种拼图,使该拼图可用来验证等式:22252(2)(2)a ab b a b a b ++=++.【分析】(1)根据图2,利用直接求与间接法分别表示出正方形面积,即可确定出所求等式;(2)根据(1)中结果,求出所求式子的值即可;(3)根据已知等式,做出相应图形,如图所示.【解答】解:(1)2222()222a b c a b c ab ac bc ++=+++++;(2)11a b c ++= ,38ab bc ac ++=,2222()2()1217645a b c a b c ab ac bc ∴++=++-++=-=;(3)如图所示:故答案为22252(2)(2)a ab b a b a b ++=++.【点评】此题考查了多项式乘以多项式,熟练掌握运算法则是解本题的关键.。
多项式乘以多项式及乘法公式习题

多项式乘以多项式及乘法公式副标题题号一二三总分得分一、选择题(本大题共12小题,共36.0分)1.若(x-1)(x+3)=x2+mx+n,则m+n=()A.-1B.-2C.-3D.22.若,则p、q的值为()A.p=-3,q=-10B.p=-3,q=10C.p=7,q=-10D.p=7,q=103.若代数式的结果中不含字母x的一次项,那么a的值是A.0B.2C. D.-4.(x-2)(x+3)的运算的结果是()A.x2-6B.x2+6C.x2-5x-6D.x2+x-65. 如果(x+1)(x2-5ax+a)的乘积中不含x2项,则a为()A. B. -C. -5D. 56.若代数式x2+kxy+9y2是完全平方式,则k的值是()A.3B.±3C.6D.±67.9x2-mxy+16y2是一个完全平方式,那么m的值是()A.12B.-12C.±12D.±248.下列多项式乘法,能用平方差公式计算的是()A.(-3x-2)(3x+2)B.(-a-b)(-b+a)C.(-3x+2)(2-3x)D.(3x+2)(2x-3)9.若x2-nx+16是一个完全平方式,则n等于( )A.4B.±4C.8D.±810. 若 -ax+x2是一个完全平方式,则常数a的值为()A. B.C. 1D. ±111. 已知,,则的值为()A.7B.5C.3D.112. 下列各式能用平方差公式计算的是()①②③④A.①②B.②③C.①③D.③④二、填空题(本大题共7小题,共21.0分)13.若(x-5)(x+20)=x2+mx+n,则m= ______ ,n= ______ .14.已知(x-1)(x+3)=ax2+bx+c,则代数式9a-3b+c的值为 ______ .15.在x+p与x2﹣2x+1的积中不含x,则p的值为.16.多项式x2-6x+9因式分解的结果为________.17.(2a-b)(-2a-b)= ______ ;(3x+5y)( ______ )=25y2-9x2.18.已知,那么.19.若是一个完全平方式,则▲ .三、计算题(本大题共7小题,共42.0分)20.若(x2+mx-8)(x2-3x+n)的展开式中不含x2和x3项,求m和n的值.21.22.已知(x+y)2=18,(x-y)2=4,求下列各式的值:(1)x2+y2;(2)xy.23.已知:x+y=6,xy=4,求下列各式的值(1)x2+y2(2)(x-y)2.24.已知a+b=5,ab=2,求下列各式的值:(1)(a+b)2;(2)a2+b2.25.1999×2001.26.已知a-b=3,ab=2,求:(1)(a+b)2(2)a2-6ab+b2的值.。
多项式的乘法算式练习题

多项式的乘法算式练习题1. 练习题一已知多项式A(x) = 2x^3 + 5x^2 - 3x + 1,B(x) = x^2 - 4x + 2,求解以下问题:a) 求A(x)与B(x)的乘积。
解答:将A(x)与B(x)依次相乘并合并同类项得到:A(x) * B(x) = (2x^3 + 5x^2 - 3x + 1) * (x^2 - 4x + 2)= 2x^5 - 3x^4 + x^3 - 9x^2 + 13x - 2b) 求A(2) * B(-1)的值。
解答:将A(x)与B(x)分别带入x=2和x=-1,得到:A(2) = 2(2)^3 + 5(2)^2 - 3(2) + 1 = 23B(-1) = (-1)^2 - 4(-1) + 2 = 7A(2) * B(-1) = 23 * 7 = 1612. 练习题二已知多项式C(x) = 3x^4 + 2x^3 - x^2 + 4x - 2,D(x) = 4x^3 - 5x^2 + 2,求解以下问题:a) 求C(x)与D(x)的乘积。
解答:将C(x)与D(x)依次相乘并合并同类项得到:C(x) * D(x) = (3x^4 + 2x^3 - x^2 + 4x - 2) * (4x^3 - 5x^2 + 2)= 12x^7 - 7x^6 - 23x^5 + 26x^4 - 39x^3 + 29x^2 - 8x + 4b) 求C(1) * D(3)的值。
解答:将C(x)与D(x)分别带入x=1和x=3,得到:C(1) = 3(1)^4 + 2(1)^3 - (1)^2 + 4(1) - 2 = 8D(3) = 4(3)^3 - 5(3)^2 + 2 = 86C(1) * D(3) = 8 * 86 = 6883. 练习题三已知多项式E(x) = x^5 - 2x^4 + 3x^3 - 4x^2 + 5x - 1,F(x) = 2x^2 - x + 3,求解以下问题:a) 求E(x)与F(x)的乘积。
多项式乘以多项式练习题

3.多项式与多项式相乘一、选择题1.计算(2a-3b)(2a+3b)的正确结果是( )A.4a2+9b2B.4a2-9b2C.4a2+12ab+9b2 D.4a2-12ab+9b22.若(x+a)(x+b)=x2-kx+ab,则k的值为( )A.a+b B.-a-b C.a-b D.b-a3.计算(2x-3y)(4x2+6xy+9y2)的正确结果是( )A.(2x-3y)2B.(2x+3y)2C.8x3-27y3D.8x3+27y3 4.(x2-px+3)(x-q)的乘积中不含x2项,则( )A.p=q B.p=±q C.p=-q D.无法确定5.若0<x<1,那么代数式(1-x)(2+x)的值是( )A.一定为正B.一定为负C.一定为非负数D.不能确定6.计算(a2+2)(a4-2a2+4)+(a2-2)(a4+2a2+4)的正确结果是( )A.2(a2+2) B.2(a2-2) C.2a3D.2a67.方程(x+4)(x-5)=x2-20的解是( )A.x=0 B.x=-4 C.x=5 D.x=408.若2x2+5x+1=a(x+1)2+b(x+1)+c,那么a,b,c应为( )A.a=2,b=-2,c=-1 B.a=2,b=2,c=-1C.a=2,b=1,c=-2 D.a=2,b=-1,c=29.若6x2-19x+15=(ax+b)(cx+d),则ac+bd等于( )A.36 B.15 C.19 D.2110.(x+1)(x-1)与(x4+x2+1)的积是( )A.x6+1 B.x6+2x3+1 C.x6-1 D.x6-2x3+1二、填空题1.(3x-1)(4x+5)=_________.2.(-4x-y)(-5x+2y)=__________.3.(x+3)(x+4)-(x-1)(x-2)=__________.4.(y-1)(y-2)(y-3)=__________.5.(x3+3x2+4x-1)(x2-2x+3)的展开式中,x4的系数是__________.6. 若(x +a )(x +2)=x 2-5x +b ,则a =__________,b =__________.7. 若a 2+a +1=2,则(5-a )(6+a )=__________.8. 当k =__________时,多项式x -1与2-kx 的乘积不含一次项.9. 若(x 2+ax +8)(x 2-3x +b )的乘积中不含x 2和x 3项,则a =_______,b =_______.10. 如果三角形的底边为(3a +2b ),高为(9a 2-6ab +4b 2),则面积=__________.三、解答题1、计算下列各式(1)(2x +3y )(3x -2y ) (2)(x +2)(x +3)-(x +6)(x -1)(3)(3x 2+2x +1)(2x 2+3x -1) (4)(3x +2y )(2x +3y )-(x -3y )(3x +4y )2、求(a +b )2-(a -b )2-4ab 的值,其中a =2009,b =2010.3、求值:2(2x -1)(2x +1)-5x (-x +3y )+4x (-4x 2-52y ),其中x =-1,y =2. 4、解方程组⎩⎪⎨⎪⎧(x -1)(2y +1)=2(x +1)(y -1)x (2+y )-6=y (x -4)四、探究创新乐园1、若(x 2+ax -b )(2x 2-3x +1)的积中,x 3的系数为5,x 2的系数为-6,求a ,b .2、根据(x +a )(x +b )=x 2+(a +b )x +ab ,直接计算下列题(1)(x -4)(x -9) (2)(xy -8a )(xy +2a ).五、数学生活实践一块长ac m ,宽bc m 的玻璃,长、宽各裁掉1 c m 后恰好能铺盖一张办公桌台面(玻璃与台面一样大小),问台面面积是多少?六、思考题:请你来计算:若1+x +x 2+x 3=0,求x +x 2+x 3+…+x2012的值.参考答案:一.1~10 BBCCA DACDC .二.填空题: 1. 12x 2+11x -5;2 20x 2-3xy -2 y 2+10.4. y 3-6y 2+11y -6..;-147.29.8.-29.3;1.10. 331(278)2a b +. 三、解答题1..12.(3).6x 4 +13x 3+5x 2+x -1(4).3x 2+18xy +18 y 2 ..4. 11x y =⎧⎨=⎩ 四、探究创新乐园1.54,2a b ==- 2. (1)x 2-13x+36. (2)x 2 y 2-6a xy -16a 2五、数学生活实践21()ab a b cm --+.六、思考题:0。
多项式乘以多项式及乘法公式习题完整版

多项式乘以多项式及乘法公式习题完整版多项式乘以多项式及乘法公式习题Document serial number【NL89WT-NY98YT-NC8CB-NNUUT-NUT108】多项式乘以多项式及乘法公式副标题题号一二三总分得分1.若(x-1)(x+3)=x2+mx+n,则m+n=()A.-1B.-2C.-3D.22.若,则p、q的值为()A.p=-3,q=-10B.p=-3,q=10C.p=7,q=-10D.p=7,q=103.若代数式的结果中不含字母x的一次项,那么a的值是A.0B.2C. D.-4.(x-2)(x+3)的运算的结果是()A.x2-6?B.x2+6?C.x2-5x-6?D.x2+x-65.如果(x+1)(x2-5ax+a)的乘积中不含x2项,则a为()A.B.-C.-5D.56.若代数式x2+kxy+9y2是完全平方式,则k的值是()A.3B.±3C.6D.±67.9x2-mxy+16y2是一个完全平方式,那么m的值是()A.12B.-12C.±12D.±248.下列多项式乘法,能用平方差公式计算的是()A.(-3x-2)(3x+2)B.(-a-b)(-b+a)C.(-3x+2)(2-3x)D.(3x+2)(2x-3)9.若x2-nx+16是一个完全平方式,则n等于()A.4B.±4C.8D.±810.若-ax+x2是一个完全平方式,则常数a的值为()A.B. C.1D.±111.已知,,则的值为()A.7B.5C.3D.112.下列各式能用平方差公式计算的是()①②③④ A.①②B.②③C.①③D.③④二、填空题(本大题共7小题,共21.0分)13.若(x-5)(x+20)=x2+mx+n,则m=______,n=______.14.已知(x-1)(x+3)=ax2+bx+c,则代数式9a-3b+c的值为______.15.在x+p与x2﹣2x+1的积中不含x,则p的值为.16.多项式x2-6x+9因式分解的结果为________.17.(2a-b)(-2a-b)=______;(3x+5y)(______)=25y2-9x2.18.已知,那么.19.若是一个完全平方式,则▲.三、计算题(本大题共7小题,共42.0分)20.若(x2+mx-8)(x2-3x+n)的展开式中不含x2和x3项,求m和n的值.21.22.已知(x+y)2=18,(x-y)2=4,求下列各式的值:(1)x2+y2;(2)xy.23.已知:x+y=6,xy=4,求下列各式的值(1)x2+y2(2)(x-y)2.24.已知a+b=5,ab=2,求下列各式的值:(1)(a+b)2;(2)a2+b2.25.1999×2001.26.已知a-b=3,ab=2,求:(1)(a+b)2(2)a2-6ab+b2的值.。
(637)多项式乘多项式专项练习30题选择解答(有答案有过程)ok

多项式乘多项式专项练习30题(有答案)1.若(X- 1)(x+3)=x2+mx+ n,那么m, n 的值分别是()A m=1 , n=3B m=4, n=5C m=2 , n= - 3D m= - 2, n=32.下列各式中,计算结果是2x +7x - 18 的是( )A (x - 1)B (x+2)(x+9)C (x-3)D (x - 2). (x+18)..(x+6).(x+9)3 .若(x - a) (x+2)的展开项中不含x的一次项,则a的值为()A a= —2B a=2C a= ±D 无法确定4.如果(x- 3) ( 2x+4) =2x2- mx+ n ,那么m、n的值分别是()A 2, 12B -2, 12C 2,- 12D -2, - 125.已知m+n=2, mn= -2,则(1 - m)(1-i n)的值为()A - 3B -1C 1D 52 2 2 26. 先化简,再求值:5 (3x y- xy )-4(- xy +3x y),其中x= - 2, y=3 .7. 计算:(1)30-2-3+ (- 3) 2-(丄)-1(2) (-2a2b3) 4+ (- a) 8? (2b4) 34(3) x (2x+1) (1 - 2x)- 4x (x - 1) (1 - x)(4) (2a- b+3) (2a+b - 3)(5) ( x- 1) ( x2+x+1 )&计算:(1) (- 7x2- 8y2) ? (- x2+3y2)2(3x - 2y) (y-3x)-( 2x- y) (3x+y) = ________9. 计算:a (a+2) (a- 3)2 210. 计算:(a+b) (a3- ab+b2)11. 计算:(2x- 3y) (x+4y)12. 计算:(1)(-泞y) 2 (2/-4曲,)(2) (- 4x- 3y2) ( 3y2- 4x)13 .计算:(2x+5y) (3x - 2y)- 2x (x - 3y)214. 5X2-( x- 2) ( 3x+1) - 2 (x+1 ) ( x- 5)2 215 .已知6x - 7xy - 3y +14x+y+a= (2x - 3y+b ) (3x+y+c ),试确定a、b、c 的值.16. 已知多项式(x2+mx+ n ) ( x2- 3x+4)展开后不含x4和x2项,试求m, n的值.17 .计算(x+2 ) (x2- 2x+4) = _____________218. 一个二次三项式x +2x+3,将它与一个二次项ax+b相乘,积中不出现一次项,且求次项系数为1, a, b的值?319 .计算:(1)- 2a (2a +3a+1) ; ( 2) (x+2y) (3x- 4y)220. (m - 2m+3) (5m - 1)21. 计算:(-3x - 2y) (4x+2y)22 •先阅读,再填空解题:2(x+5) (x+6) =x +11x+30;(x - 5) ( x- 6) =x2- 11x+30 ;2(x- 5) ( x+6) =x +x- 30;(x+5) (x - 6) =x2- x - 30.(1)观察积中的一次项系数、常数项与两因式中的常数项有何关系?答:(2)根据以上的规律,用公式表示出来:.(3) ___________________________________________________________;(y- 80) (y - 81) = ___________ 根据规律,直接写出下列各式的结果:(a+99)(a- 100) = ___________________23. 填空(x - y) (x2+xy+y 2) =; ( x- y) (x3+x2y+xy 2+y3) =根据以上等式进行猜想,当n是偶数时,可得:(x- y) (x n+x°1y+y n 2y2+ --+x2y n 2+xy n1+y n) =224 .如果(x - 3) (x+5) =x +Ax+B,求3A - B 的值.25 .计算:(1)-( 2a- b) +[a -( 3a+4b)](2) (a+b) (a2- ab+b2)26. (a - b+c - d) (c - a- d - b)27. (x - 1) (x - 2) = (x+3) (x - 4) +20.29 •小明在计算一个多项式乘以x+y - 4的题目时,误以为是加法运算,结果得到2x+2y •你能计算出这个多项式乘以x+y - 4的正确结果吗?30 .化简:(x+y ) (x4- xy+y2)多项式乘多项式30题参考答案:2 21. ■/ ( x- 1) ( x+3) =x +2x —3=x +mx+ n ,m=2 , n= —3.故选C.2 2 2 22. A、原式=x +17x —18; B、原式=x +11X+18 ; C、原式=x +3x —18; D、原式=x +7x —18.故选D23. ■/ (x —a) (x+2) =x + (2 —a) —2a.又•结果中不含x 的项,/• 2 —a=0,解得a=2.故选B4. 原方程可化为:2x2—2x —12=2x2—mx+ n , —2= —m, n= - 12,解得m=2 , n= —12•故选C5. ■/ m+n=2 , mn= —2, /• (1 —m) (1 —n) =1 —( m+n) +mn=1 —2 —2= —3.故选A十「、 2 2 2“2 2 26. 原式=15x y —5xy +4xy —12x y=3x y —xy ,当x= —2, y=3 时,原式=3X(—2) 2X3—(—2) X32=36+18=547. (1)原式=1 - 一+9 —4=—3 88 12 8 12 8 12(2)原式=16a b +8a b =24a b(3)x —4x5+4x3—8x2+4x= —8x2+5x(4)原式=(2a) 2—( b —3) 2=4a2—( b2—6b+9) =4a2—b2+6b —9(5)原式=x (x +x+1) — ( x +x+1) =x — 1& (1) (—7x2—8y2) ? (—x2+3y2) =7x6—21x2y2+8x2y2—24y4=7x4—13x2y2—24y4;(2)( 3x —2y) ( y—3x) — ( 2x —y) (3x+y ) =3xy —9x2—2y2+6xy —( 6x2+2xy —3xy —y2)2 2 2 2 2 2 .=—9x —2y +9xy —6x +xy+y = —15x —y +10xy .9. 原式=(a2+2a) ( a—3) =a3—3a2+2a2—6a=a3—a2—6a10. 原式=a3+a2b —a2b—ab2+ab2+b3=a3+b3.2 2 2 211. (2x —3y) (x+4y ) =2x —3xy+8xy —12y =2x +5xy —12y .12. (1)原式= (2x2—4xy+7y2)=二(2)原式=(-4x —3y2) (—4x+3y2) = (—4x) 2—( 3y2) 2=16x2—9y42 2 2 2 213 .原式=6x +11xy —10y —2x +6xy=4x +17xy —10y .2 2 2 2 2 214. 原式=5x —( 3x —5x —2)—2 (x —4x —5) =5x —3x +5x+2 —2x +8x+10=13x+122 215. ■/ (2x—3y+b ) (3x+y+c ) =6x —7xy —3y + (2c+3b) x+ (b —3c) y+bc2 2 2 26x —7xy —3y + (2c+3b) x+ ( b —3c) y+bc=6x —7xy —3y +14x+y+a••• 2c+3b=14 , b —3c=1 , a=bc联立以上三式可得:a=4, b=4, c=1故a=4, b=4, c=14 3 2 3 2 2 4 3 216 .原式=x —3x +4x +mx —3mx +4mx+nx —3nx+4n=x + (m —3) x + (4 —3m+n) x + (4m —3n) x+4n .4 ( x+2y) (3x—4y) =3x2—4xy+6xy —8y2=3x2+2xy —8y22 32 23 220. (m —2m+3) (5m —1) =5m —m —10m +2m+15m —3=5m —11m +17m —32 2 2 221 .原式=—3x?4x —3x?2y —2y?4x —2y?2y= —12x —6xy —8xy —4y = —12x —14xy —4y22. (1 )观察积中的一次项系数、常数项与两因式中的常数项有何关系是:一次项系数是两因式中的常数项的和,常数项是两因式中的常数项的积;2(2)根据以上的规律,用公式表示出来:(a+b) (a+c) =a + ( b+c) a+bc;o o5 根据(2)中得出的公式得:(a+99) (a—100) =a —a—9900; ( y —80) (y —81) =y —161y+6480 .故填:一次项系数是两因式中的常数项的和,常数项是两因式中的常数项的积;(a+b) (a+c) =a + (b+c) a+bc; a —a—9900, y —161y+6480由题意得m- 3=0, 4—3m+n=0 ,解得m=3, n=517. (x+2 ) (x2—2x+4) =x3—2x2+4x+2x2—4x+8=x 3+8.故答案为:x3+8.2 32 23 2 218. (x2+2x+3) X (ax+b) =ax3+bx2+2ax2+2xb+3ax+3b=ax 3+ (bx2+2ax2) + (2xb+3ax) +3b,•••积中不出现一次项,且二次项系数为1, • 2a+b=1 , 2b+3a=0 , • b= —3, a=22 3 219. (1)—2a (2a +3a+1) = —4a —6a —2a;23 .原式=x3+x2y+xy 2-x2y - xy2- y3=x3- y3;故答案为:x3- y3;原式=x4+x3y+x2y2+xy3- x3y - x2y2- xy3- y4=x4- y4;故答案为:x4- y4;n+1 n n -2 2 n-1 n n n-1 2 n-1 2 2 n-1 n n+1 n+1 n+1x n+1-原式=x +x y+xy +x y +xy - x y-x y - y y - — x y - xy - y =x - y ,故答案为:n+1y2224. •/(x- 3) (x+5) =x2+5x- 3x - 15=x2+2x - 15, /•A=2 , B= - 15, /•3A - B=21 .故3A - B 的值为21 25.( 1 )原式=- 2a+b+[a- 3a- 4b]=- 2a+b+a- 3a- 4b=- 4a- 3b;3 2 2 2 2 3 3 3( 2)原式=a - a b+ab +a b- ab +b =a +b2 226. 原式=[ ( c- b- d) +a][ ( c - b- d)- a]= ( c- b- d) 2- a22 2 2 2 2 2 2= (c-b) -2(c-b) d+d-a=c-2cb+b- 2cd+2bd+d-a27. 原方程变形为:x2- 3x+2=x2- x- 12+20 整理得:-2x- 6=0,解得:x= - 33228. 原式=- 6x3+13x2- 429. 根据题意列得:[ ( 2x+2y)-( x+y- 4) ] ( x+y- 4) =( 2x+2y- x- y+4)( x+y- 4)2 2 2= (x+y+4)(x+y- 4) =(x+y) - 16=x +2xy+y - 1630. (x+y) (x2- xy+y2) =x3- x2y+xy2+x2y- xy2+y3=x3+y3.故答案为:x3+y3.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
多项式乘以多项式及乘
法公式习题
文稿归稿存档编号:[KKUY-KKIO69-OTM243-OLUI129-G00I-FDQS58-
多项式乘以多项式及乘法公式
副标题
题号一二三总分
得分
一、选择题(本大题共12小题,共36.0分)
1.若(x-1)(x+3)=x2+mx+n,则m+n=()A.-1B.-2C.-3D.2
2.若,则p、q的值为()A.p=-3,
q=-10B.p=-3,q=10C.p=7,q=-10D.p=7,q=10
3.若代数式的结果中不含字母x的一次项,那么a的值是
A.0B.2
C. D.-
4.(x-2)(x+3)的运算的结果是()
A.x2-6?
B.x2+6?
C.x2-5x-6?
D.x2+x-6
5.如果(x+1)(x2-5ax+a)的乘积中不含x2项,则a为()
A.
B.-
C.-5
D.5
6.若代数式x2+kxy+9y2是完全平方式,则k的值是()
A.3
B.±3
C.6
D.±6
7.9x2-mxy+16y2是一个完全平方式,那么m的值是()A.12B.-12C.±12D.±24
8.下列多项式乘法,能用平方差公式计算的是()A.(-3x-2)(3x+2)B.(-a-b)(-b+a)C.(-3x+2)(2-3x)D.(3x+2)(2x-3)
9.若x2-nx+16是一个完全平方式,则n等于()A.4B.±4C.8D.±8
10.若-ax+x2是一个完全平方式,则常数a的值为()
A.
B. C.1D.±1
11.已知,,则的值为()
A.7
B.5
C.3
D.1
12.下列各式能用平方差公式计算的是()
①②
③④ A.①②B.②③C.①③D.③④
二、填空题(本大题共7小题,共21.0分)
13.若(x-5)(x+20)=x2+mx+n,则m=______,n=______.
14.已知(x-1)(x+3)=ax2+bx+c,则代数式9a-3b+c的值为
______.
15.在x+p与x2﹣2x+1的积中不含x,则p的值为.
16.多项式x2-6x+9因式分解的结果为________.
17.(2a-b)(-2a-b)=______;(3x+5y)(______)=25y2-9x2.
18.已知,那么.
19.若是一个完全平方式,则▲.
三、计算题(本大题共7小题,共42.0分)
20.若(x2+mx-8)(x2-3x+n)的展开式中不含x2和x3项,求m和n的值.
21.
22.已知(x+y)2=18,(x-y)2=4,求下列各式的值:(1)x2+y2;(2)xy.
23.已知:x+y=6,xy=4,求下列各式的值
(1)x2+y2
(2)(x-y)2.
24.已知a+b=5,ab=2,求下列各式的值:(1)(a+b)2;
(2)a2+b2.
25.1999×2001.
26.已知a-b=3,ab=2,求:
(1)(a+b)2
(2)a2-6ab+b2的值.。
