材料力学第十三章习题
第十三章北航 材料力学 全部课件 习题答案
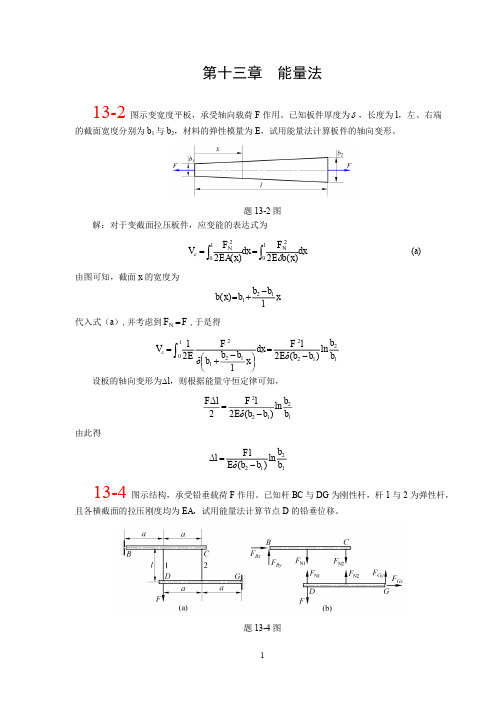
M ( x2 ) Fx2 M C ,
图 13-9 根据卡氏定理,得
C
1 [ EI
a 0
( Fx1 )(
x1 )dx1 a
a 0
( Fx2 )(1)dx2 ]
5Fa 2 () 6EI
A A
13-10 图示各梁,弯曲刚度 EI 均为常数,试用卡氏定理计算横截面 A 的挠度 与转角 。
3 3
3 3
–F
F 2
3 Fa 3 3 Fa 12
3 Fa 12
3
a
3 6
9
故有
ΔB
求 AB 的运算过程列表如下: i 1 2 3
i 1
3
F Ni FNi li 3Fa (←) EA 12EA
li
a a a
F Ni
2 3a 1
FNi
F
F Ni FNi l i
2 3 F 3
3a 1
–F
3 F 3
3 F 6
3a
F 2
故有
5 3 F 6
AB
F Ni FNi li 5 3F () EA 6 EA i1
3
(b) 解:求Δ B 和 AB 的单位状态分别示如图 13-17b(1)和 b(2) 。
图 13-17b 求 Δ B 的运算过程列表如下:
i 1 2 3 4
转角。
图示刚架,承受载荷 F 作用。设弯曲刚度 EI 为常数,试用卡氏定理计算截面 C 的
题 13-9 图 解:在截面 C 处假想附加一矩为 M C 的力偶(见图 13-9) ,由图可得
M x1 ( F
材料力学课后习题答案13章

= 7.44 × 10− 2 m = 74.4mm
而
2 × 0.050 Fd = (300 N ) 1 1 + + 2.22 × 10 − 2
= 1.004 × 10 3 N
M max = 1.004 ×10 3 N (1.00m ) = 1.004 ×10 3 N ⋅ m
设压杆微弯平衡时的挠曲轴方程为
πx w = f sin l
式中,f 为压杆中点的挠度即最大挠度。
题 13-8 图 解:由题设可知,
w = f sin
πx , l
6
w′ =
πf πx cos l l
据此可得
λ (x ) =
q cr 所作之功为
1 x 2 * 1 ( w′) dx = 2 0 2
∫
∫
x 0
(也可通过左侧题号书签直接查找题目与解)
13-2
比为 8:3。
图示圆截面简支梁,直径为 d,承受均布载荷 q 作用,弹性模量 E 与切变模量 G 之
(1)若同时考虑弯矩与剪力的作用,试计算梁的最大挠度与最大转角; (2)当 l/d =10 与 l/d =5 时,试计算剪切变形在总变形(最大挠度与最大转角)中所占百分比。
(2)被冲击面(弹簧顶面)的静位移为
∆st =
最大冲击载荷为
Pl P 500 + = 1.516 × 10 − 5 m + m = 2.52 × 10 − 3 m 3 EI k 200 × 10
2h + + Fd = P 1 1 ∆ st
于是,杆内横截面上最大的正应力为
Fl 3 ∆= 48EI
得刚度系数
0.030 4 48 × 200 × 10 × F 48 EI 12 N = 6.48 × 10 5 N k= = 3 = 3 ∆ m m l 1.00
材料力学(刘鸿文_第5版)

第十四章 习题
2012年11月5日星期一
常州大学机械学院力学教研室
第五章 习题
第六章 弯曲变形
§6-1、工程中的弯曲变形问题 §6-2、挠曲线的微分方程 §6-3、用积分法求弯曲变形 6.1和连续性条件 6.3(a) Page 196 §6-4、用叠加法求弯曲变形 6.9(a) 6.10(b) Page 200 §6-5、简单超静定梁 Page 208 6.36 §6-6、提高弯曲刚度的一些措施
第十三章 习题
§13-1、概述 §13-2、杆件应变能的计算104 Page §13-3、应变能的普遍表达式 §13-4、互等定理 Page 106 §13-5、卡氏定理 Page 107 §13-6、虚功原理 §13-7、单位载荷法 Page 109 莫尔积分 §13-8、计算莫尔积分的图乘法 Page 109
第一章 绪论
§1-1、材料力学的任务 §1-2、变形固体的基本假设 §1-3、外力及其分类 §1-4、内力、截面法和应力的概念 §1-5、变形与应变 §1-6、杆件变形的基本形式
第一章 绪论习题
Page 11 1.2 Page 11 1.4 1.6
第二章 拉伸、压缩与剪切 第二章 习题
§2-1、轴向拉伸与压缩的概念和实例 §2-2、轴向拉伸与压缩时横截面上的内力和应力 2.2 Page 53 2.1(a)(c) §2-3、直杆轴向拉伸或压缩时斜截面上的应力 Page 54 2.6 §2-4、材料拉伸时的力学性能 §2-5、材料压缩时的力学性能 §2-7、失效、安全因数与强度计算54 2.7 Page 54 2.12 Page §2-8、轴向拉伸或压缩时的变形 58 2.19 Page 61 2.30 Page
附录 I 平面图形的几何性质
材料力学(金忠谋)第六版答案第14章

材料力学(金忠谋)第六版答案第14章第十三章 动载荷13-1 铸铁杆AB 长m l 8.1=,以等角速度绕垂直轴O -O 旋转如图示。
已知铸铁的比重3/74m kN =γ,许用拉应力[]MPa 40=σ,材料的弹性模量E =160 Gpa 。
试求此杆的极限转速,并计算此杆在转速m r n /100=时的绝对伸长。
解: (1) 极限转速m rn s s l g l g A A Ndl gA dr r qd r Nd x r gAdr ma r qd x r a jx dl n n 1092260137.114175.130799.010*******.92)2(][2][)2(21][)2(21)()()()()(235222222222====⨯⨯⨯⨯⨯=≤≤≤======⎰πωωγσωσωγσσωγωγω(2) 当n =1000m rcm m Eg l r EA r Nd l s n l 0252.01052.28.91016039.072.104107423)2(2)(2172.1046010002602492233220=⨯=⨯⨯⨯⨯⨯⨯⨯===∆=⨯==-⎰ωππω(2)吊索: MPa A P d d 55.2105276.14max=⨯==-σ13-3 轴上装一钢质圆盘,盘上有一圆孔。
若轴与盘以s140=ω的匀角速度旋转,论求轴内由这一圆孔引起的最大正应力。
解:23max max 22225.1212.021*********.01060041411060064003.03.047800640404.0mMN W M mN L P N Na gA ma P s m r a z d d d d n n d n =⨯⨯==⋅=⨯⋅===⨯⨯⨯⨯=⋅⋅⋅===⨯==πσπδγω13-4 飞轮轮缘的平均直径D =1.2m ,材料比重3/72m kN =γ,弹性模量GPa E 200=,轮缘与轮幅装配时的过盈量mmD2.0=∆,若不计轮相的影响,求飞轮允许的最大转速。
《材料力学》第五版_刘鸿文第13章习题答案

13.17 桁架各杆材料和截面面积相等。在载荷P作用下, 求节点B与D间的相对位移。
求出在P力和单位力1单独作用下各杆的轴力。 δ BD = 1 2 l = 2.71Pl − 2 P ⋅1 ⋅ 2l + (− P ) 2 EA EA
0
l
+ ∫ 1× (2 Pl + 2 Px )dx
= 0.0117rad
HAII M =
=
1 1 ∑ ωM C = (ω1 M 1 + ω 2 M 2 + ω 3 M 3 ) EI EI
1 EI
1 Pl 2 l 1 Pl 2 l Pl l 1 l − × × + × × l × × + × × × 2 4 8 2 4 3 4 4 4 2 4 3 5 Pl = 384 EI
xA =
1 EI
∑ ωM C" = -
HAII MAXUN
Plh 2 2 EI
附加习题13-2:节点C受力P和力Q,AC杆长为L,求桁架 的应变能。 N1 = P + Qctgα 解:
N 2 = −Q / sin α
U =∑
N1 N2
N i2 Li 2 EAi
L Q2 2 U= (P + 2 2 EA tg α Q2 2 PQ + + ) 2 sin α cosα + tgα
θ=0
HAII MAXUN
13.15 刚架两部分的I=3×103cm4,E=200GPa。求截面D的 水平位移和转角。P=10kN,l=1m。 解: DC段
M 1 (x ) = Px
M 1 (x ) = x
材料力学-第十三章能量方法

fc
U P
M (x) M (x) dx
l EI P
1
EI
l 2 0
[(
P 2
Me l
) x1
M
e
]
x1 2
dx1
1 EI
l 2
(
P
02
Me l
) x2
x2 2
dx2
M el 2 Pl3 16EI 48EI
(
)
31
• 例13-6 求刚架B的水平位移和C点的转角。
解:
AB段: M (x1) (Pa Pf x1)
P
2
29
A截面的转角:
A
U M e
M (x) M (x) dx l EI M e
1
EI
l
2 [(
0
P 2
Me l
) x1
M e ](1
x1 l
)dx1
1
EI
l 2 0
(P 2
Me l
) x2
x2 l
dx2
M el 3EI
Pl 2 16EI
(
)
30
Me
p
A
C
X1
L/2 L/2
B
X2
C截面的挠度为:
A ②将内力对MA求偏导后,令M A=0
L xO
③求变形( 注意:M A=0)
M (x)
1
M A M 0
A
A
L
M (x) M (x) dx EI M A
L Px dx 0 EI
PL2
2 EI
A
PL2 ( 2 EI
)
“负号”说明 A与所加广义力MA反向。
吉林大学材料力学第13章 交 变 应 力

弯扭组合疲劳强度条件为 nσ nτ nστ = ≥n nσ + nτ
2 2
σ −1 ε σβ σ −1 κσ
σ
对非对称循环( 对非对称循环(r>0)时 时 还需计算屈服强度计算 即
σ n = ≥n σ
' s
στ
r
相当应力
§13、9 提高构件疲劳强度的主要措施 、 要从影响构件疲劳强度的因素入手。 要从影响构件疲劳强度的因素入手。 表面质量 疲劳裂纹的形成 构件外形引起的应力集中
按静强度建立屈服强度条件
' nσ
σs = ≥ ns σ max
一般规定的疲劳、 一般规定的疲劳、屈服安全系数 不同,故当r>0时需两个方面都算。 时需两个方面都算。 不同,故当 时需两个方面都算
M φ40
A A
M
φ2 截面A 截面
例13-3已知 已知
.m Mmax=5Mmin=502N
σb=950MPa, σs=540MPa σ-1=430MPa,ψσ=0.2, n=2,ns=1.5
C
σ ra = σ −1 − ψ σ σ rm
(σb, 0) B
σm
§13.7 非对称循环下构件的疲劳强度计算 一、构件的持久极限简化折线 材料的持久极限 构件的持久极限 屈服点控制线 σs L A E K
σa
C F B
σJ σm s 注意:影响构件持久 EK___疲劳限 极限的主要因素,其只 KJ___屈服限 影响动的部分(应力幅) EKJ内___不疲劳、 内 不疲劳、 不屈服
对称循环
σ t
σmin r= = −1 σmax
σmax = −σmin σm = 0
σa= σmax
材料力学课件第十三章弯曲的几个补充问题

(2) 绘制弯矩图 绘出 Mz (x)图 绘出 My(x) 图
A截面为梁的危险截面
y
F1=1kN
0.5m 0.5m
A z
B
C
x
F2=2kN
x
Mz = 1 kN·m
1kN·m
My= 1 kN·m
1kN·m
Mz使A截面上部受拉,下部受压
My使A截面前部受拉,后部受压
Mz(x)图
x My(x)图
(3) 应力分析
1.分解(Resolution) 将外载沿横截面的两个形心主轴分解,于是得到两个正交的
平面弯曲 2.叠加(Superposition)
对两个平面弯曲进行研究,然后将计算结果叠加起来
Fz
z
j
Fy F
y
A
z y
Bx
Fz
Fy
F
垂直纵向对称面
梁在垂直纵向对 称面 xy 面内发 生平面弯曲 。 z轴为中性轴
' My z
Iy
2.与 Mz 相应的正应力为(The bending normal stress corresponding to Mz)
'' M z y
Iz
C 点处的正应力(The normal stress at point C)
' '' M y z Mz y
Iy
Iz
m
z C ( y,z )
Fy 与均布荷载 q使梁在 xy平面内产生弯曲(z为中性轴)
Fz 使梁在 xz平面内产生弯曲(y为中性轴)
q
F 40° Fy
z
A
C
Fz B
a
a
y
(1) 画弯矩图
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
材料力学第十三章习题13-2图示压杆的截面为矩
形,h=60mm,b=40mm,杆长l=2.0m,材料为Q235
钢,E=2.1×105MPa。
两端约束示意图为:在正视图(a)的平面内相当于铰支;在俯视图(b)的平面内为弹性固定,采用μ=0.8。
试求此杆的临界力F cr。
13-4图示结构中,两根杆的横截面均为50×50mm2正方形,材料的弹性模量E=70×103MPa,试用欧拉公式确定结构失稳时的荷载F值。
13-6图示5根圆杆组成的正方形结构。
a=1m,各结点均为铰接,杆的直径均为d=35mm,截面类型为a类。
材料均为Q235钢,[σ]=170MPa,试求此时的容许荷载F。
又若力F的方向改为向外,容许荷载F又应为多少?
13-9图示结构中,1、2两杆为材料相同的圆杆,1杆直径d1=16mm,2杆直径d2=32mm,已知材料的弹性模量E=200GPa,比例极限s p=
200MPa,屈服极限s s=235MPa,结构的强度安全因素n=1.5,稳定安全因素n st=2.0。
试求该结构的容许荷载。
13-12一支柱系由4根75×75×6(见图)的角钢所组成。
截面类型为b 类。
支柱的两端为铰支,柱长,a=210mm,压力为450kN。
若材料为Q235钢,容许应力[σ]=170MPa。
试校核支柱的稳定性。
13-14图示梁杆结构,材料均为Q235钢。
AB梁为16号工字钢,BC杆为的圆杆。
已知弹性模量E=200GPa,比例极限s p=200MPa,屈服极限s s =235MPa,强度安全因数n=1.4,稳定安全因数n st=3,求容许荷载。
