大学物理-电势
合集下载
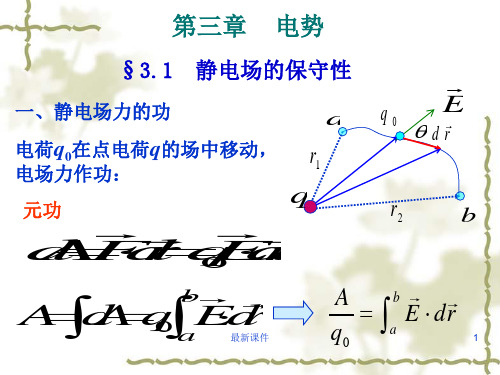
大学物理第三章电势

2 π AR + 3 λ e E3 = 6 πε 0 r
方向沿径向向外
18
(2)选距离轴线的距离为 l ( l > R ) 处为电势 零点,计算圆柱体内、 零点,计算圆柱体内、外各点的电势分 布。 注意: 求各点电势(电势分布) 注意: 求各点电势(电势分布)时,要分 区域讨论,分区方式与场强相同。 区域讨论,分区方式与场强相同。 电势零点位置选择: 电势零点位置选择: “无限长”柱状带电 无限长” 对 体产生的电场, 体产生的电场,绝对不 能选无穷远处为电势零 点,只能选其它任一点 为电势零点。 为电势零点。
qo =∫ ⋅
5
静电场的保守性(静电场环路定理) 二、 静电场的保守性(静电场环路定理)
L2
∫
L
E ⋅ dl = 0
a
.
qo
L1
b
.
在静电场中,场强沿任意闭合路径的线积 在静电场中, 分等于零。 对任何静电场, 分等于零。即:对任何静电场,电场强度的 线积分都只取决于起点和终点的位置, 线积分都只取决于起点和终点的位置,而与连 接起点和终点间的路径无关。 接起点和终点间的路径无关。
15
例2(1197)一半径为R的“无限长”圆柱形带 1197)一半径为 的 无限长” 电体, 电体,其电荷体密度为 ρ = A r ( r ≤ R ) 式中A为常数 为常数。 式中 为常数。在此圆柱体外再罩一半 径为R 无限长” 径为 1 、线电荷密度为 λ e 的“无限长”圆 试求: 筒,试求: 圆柱体内、 (1)圆柱体内、外各点的电场强度分布 (2)选距离轴线的距离为 l ( l > R ) 处为电势零点,计算圆柱体内、 处为电势零点,计算圆柱体内、 外各点的电势分布。 外各点的电势分布。 (3)柱表面与柱壳之间的电势差。 柱表面与柱壳之间的电势差。
大学物理电势ppt课件

电势定义
$V = frac{kQ}{r}$,其中$k$为静电力常量,$Q$为场源电荷量,$r$为到场源电荷的距离。
点电荷电势公式
点电荷电势计算
对于多个点电荷或连续分布电荷产生的电势,可应用叠加原理进行求解。
叠加原理
对于连续分布电荷,需采用积分方法计算电势,如线积分、面积分或体积分。
积分方法
均匀带电直线、均匀带电平面、均匀带电球体等。
大学物理电势ppt课件
目录
电势基本概念与性质 点电荷与连续分布电荷电势 导体与绝缘体在电场中电势特性 电势能、电势差及等势面 电场力做功与路径无关性讨论 总结回顾与拓展延伸
01
CHAPTER
电势基本概念与性质
电势定义及物理意义
电势定义
描述电场中某点电势能的性质,反映单位正电荷在该点所具有的电势能。
实际应用举例
04
CHAPTER
电势能、电势差及等势面
电荷在电场中具有的势能,与电荷量及所在位置有关。
电势能定义
通过电场力做功来计算,公式为W=qU,其中W为电势能,q为电荷量,U为电势差。
电势能计算
电势能具有相对性,与零电势点的选择有关。
电势能性质
电势能概念及计算
电场中两点间电势的差值,等于单位正电荷从一点移动到另一点时电场力所做的功。
常见连续分布电荷
连续分布电荷电势求解方法
均匀带电直线电势
通过高斯定理和积分方法求解,结果与观察点到直线的垂直距离和线电荷密度有关。
均匀带电平面电势
利用高斯定理和叠加原理,可求得电势与观察点到平面的距离和平面电荷密度之间的关系。
均匀带电球体电势
采用高斯定理和积分方法,可得到球体内外任意一点的电势表达式。
$V = frac{kQ}{r}$,其中$k$为静电力常量,$Q$为场源电荷量,$r$为到场源电荷的距离。
点电荷电势公式
点电荷电势计算
对于多个点电荷或连续分布电荷产生的电势,可应用叠加原理进行求解。
叠加原理
对于连续分布电荷,需采用积分方法计算电势,如线积分、面积分或体积分。
积分方法
均匀带电直线、均匀带电平面、均匀带电球体等。
大学物理电势ppt课件
目录
电势基本概念与性质 点电荷与连续分布电荷电势 导体与绝缘体在电场中电势特性 电势能、电势差及等势面 电场力做功与路径无关性讨论 总结回顾与拓展延伸
01
CHAPTER
电势基本概念与性质
电势定义及物理意义
电势定义
描述电场中某点电势能的性质,反映单位正电荷在该点所具有的电势能。
实际应用举例
04
CHAPTER
电势能、电势差及等势面
电荷在电场中具有的势能,与电荷量及所在位置有关。
电势能定义
通过电场力做功来计算,公式为W=qU,其中W为电势能,q为电荷量,U为电势差。
电势能计算
电势能具有相对性,与零电势点的选择有关。
电势能性质
电势能概念及计算
电场中两点间电势的差值,等于单位正电荷从一点移动到另一点时电场力所做的功。
常见连续分布电荷
连续分布电荷电势求解方法
均匀带电直线电势
通过高斯定理和积分方法求解,结果与观察点到直线的垂直距离和线电荷密度有关。
均匀带电平面电势
利用高斯定理和叠加原理,可求得电势与观察点到平面的距离和平面电荷密度之间的关系。
均匀带电球体电势
采用高斯定理和积分方法,可得到球体内外任意一点的电势表达式。
大学物理静电场3(电势)ppt课件
最新课件
9
单个点电荷的场的电势 U q
2)电势叠加原理(标量叠加)
q
Up Edl
Eidl
1
4
0r r1 r2
p
p
P Ei dl
qi
q2
4 0ri
或对连续分布带电体
U p
dq
4 0r
q
最新课件
dq
r
p
r3
ri
q3
qi
p
Up=?
10
Ua
i
qi
40ri
一个点电荷系的电场中,任一点的电势等于每一个点电 荷单独存在时在该点所产生电势的代数和。——电势 叠加原理
电势叠加原理 习题最指新课导件 P65 16
34
形状如图所示的绝缘细线,其上均匀分布着
正电荷。已知电荷线密度为λ,两段直线长 均为a,半圆环的半径为a。求环心O点的电 势?
电势叠加原理
求电势能和电力
习题指导P65 17
最新课件
35
3.有一边长为a的正方形平面,在其中垂线上距 中心O点a/2处,有一电量为q的正点电荷,如图所 示,则通过该平面的电场强度通量为:
b
W a W bA a bq 0 aE d r
二、电势差:
移动单位正电荷从电场中a 点到b点,静电力所做 的功,为静电场中两点的电势差:
U abU aU ba bEdr最 新W 课q 件aW qb 描只述与电电场场的有性关质6
➢某点 (a点) 的电势:
首先设定电势0点(b点):
Ua
b
Edr
积分与路径无关
最新课件
4
对任何静电场,电场强度的线积分都只取决于起 点和终点的位置而与积分路径无关--静电场的
大学物理电势

Q
+ r+ rA
r
rB
Q
4π 0
rB rA
dr r2
er
er
Q (1 1)
4π 0 rA rB
8 –7 电势
第八章静电场
(2) r R
VA VB
rB rA
E1
dr
0
(3) r R
令 rB , V 0
r +
+ +
R
o
+
+
Q
++
+ e+
+ r+ rA
A
r
dr
rB
B
由
VA
VB
A
iA
VA
VAi
i
i
qi
4π 0ri
电荷连续分布
VP
dq
4π 0r
第八章静电场
q1 q2
r1 r2
q3
r3
E3
E2
A
E1
dqqdrqP
dV
dE
8 –7 电势
第八章静电场
讨论
求电势 的方法
➢ 利用
VP
dq
4π 0r
(利用了点电荷电势 V q / 4π 0r,
这一结果已选无限远处为电势零点,即使
E dl
AB
8 –7 电势
电势差
第八章静电场
U AB VA VB
E dl
AB
(将单位正电荷从 A移到 B电场力作的功.)
注意 电势差是绝对的,与电势零点的选择无关; 电势大小是相对的,与电势零点的选择有关.
静电场力的功 WAB q0VA q0VB q0U BA
+ r+ rA
r
rB
Q
4π 0
rB rA
dr r2
er
er
Q (1 1)
4π 0 rA rB
8 –7 电势
第八章静电场
(2) r R
VA VB
rB rA
E1
dr
0
(3) r R
令 rB , V 0
r +
+ +
R
o
+
+
Q
++
+ e+
+ r+ rA
A
r
dr
rB
B
由
VA
VB
A
iA
VA
VAi
i
i
qi
4π 0ri
电荷连续分布
VP
dq
4π 0r
第八章静电场
q1 q2
r1 r2
q3
r3
E3
E2
A
E1
dqqdrqP
dV
dE
8 –7 电势
第八章静电场
讨论
求电势 的方法
➢ 利用
VP
dq
4π 0r
(利用了点电荷电势 V q / 4π 0r,
这一结果已选无限远处为电势零点,即使
E dl
AB
8 –7 电势
电势差
第八章静电场
U AB VA VB
E dl
AB
(将单位正电荷从 A移到 B电场力作的功.)
注意 电势差是绝对的,与电势零点的选择无关; 电势大小是相对的,与电势零点的选择有关.
静电场力的功 WAB q0VA q0VB q0U BA
大学物理课件电势梯度

大学物理课件-电势梯度
contents
目录
• 电势梯度的定义 • 电势梯度的性质 • 电势梯度在物理中的应用 • 电势梯度的计算实例 • 电势梯度与物理学其他概念的关系
01 电势梯度的定义
定义与公式
定义
电势梯度是描述电场中电势随位置变 化的物理量,表示为▽Φ。
公式
▽Φ = -E,其中E是电场强度矢量,Φ 是电势。
物理意义
电势梯度的方向表示电场强度矢量场的方向,即电场线方向。
计算方法
在标量场中,梯度的方向可以通过求导数的方法得到,即▽ = grad 。
电势梯度的计算方法
计算公式
电势梯度的计算公式为▽·E = ρ/ε0, 其中▽表示哈密顿算子,E表示电场强 度矢量,ρ表示电荷密度,ε0表示真 空电容率。
计算步骤
时,需要考虑这些元件的影响。
复杂电场的电势梯度计算
总结词:非线性关系 总结词:方向判断
详细描述:在复杂电场中,电势梯度与电场强度 之间的关系可能变得非线性。例如,在点电荷产 生的电场中,电势梯度随距离的增加而减小,但 仍然与电场强度成正比。
详细描述:在复杂电场中,判断电势梯度的方向 需要考虑电场线的分布和方向。通常,电势梯度 的方向与电场线增加的方向一致。
02 电势梯度的性质
电势梯度的标量性质
标量性质
电势梯度是一个标量,表示电势在空间中的变化率,没有方向。
计算公式
电势梯度等于电场强度在三维空间中的散度,计算公式为▽·E = ρ/ε0。
物理意义
电势梯度表示单位距离内的电势变化量,可用于描述电场中电势的 变化趋势。
电势梯度的方向
方向判定
电势梯度的方向由负梯度的方向确定,即电势降低的方向。
contents
目录
• 电势梯度的定义 • 电势梯度的性质 • 电势梯度在物理中的应用 • 电势梯度的计算实例 • 电势梯度与物理学其他概念的关系
01 电势梯度的定义
定义与公式
定义
电势梯度是描述电场中电势随位置变 化的物理量,表示为▽Φ。
公式
▽Φ = -E,其中E是电场强度矢量,Φ 是电势。
物理意义
电势梯度的方向表示电场强度矢量场的方向,即电场线方向。
计算方法
在标量场中,梯度的方向可以通过求导数的方法得到,即▽ = grad 。
电势梯度的计算方法
计算公式
电势梯度的计算公式为▽·E = ρ/ε0, 其中▽表示哈密顿算子,E表示电场强 度矢量,ρ表示电荷密度,ε0表示真 空电容率。
计算步骤
时,需要考虑这些元件的影响。
复杂电场的电势梯度计算
总结词:非线性关系 总结词:方向判断
详细描述:在复杂电场中,电势梯度与电场强度 之间的关系可能变得非线性。例如,在点电荷产 生的电场中,电势梯度随距离的增加而减小,但 仍然与电场强度成正比。
详细描述:在复杂电场中,判断电势梯度的方向 需要考虑电场线的分布和方向。通常,电势梯度 的方向与电场线增加的方向一致。
02 电势梯度的性质
电势梯度的标量性质
标量性质
电势梯度是一个标量,表示电势在空间中的变化率,没有方向。
计算公式
电势梯度等于电场强度在三维空间中的散度,计算公式为▽·E = ρ/ε0。
物理意义
电势梯度表示单位距离内的电势变化量,可用于描述电场中电势的 变化趋势。
电势梯度的方向
方向判定
电势梯度的方向由负梯度的方向确定,即电势降低的方向。
大学物理第2章 电势能 电势

4
Wa b
q0 q 4 0
b
a
q0 q r dr 3 r 4 0
b
a
1 d(r r ) 2 r3
q0 q 4 0
b
a
q0 q 1 dr 2 3 2 r 4 0
b
a
q0 q 1 2rdr 3 2 r 4 0
b
b
a
dr r2
q0 q 4 0
rR 0 Er Q 4 r 2 r R 0
球面内部任意一点的电势为
V (r )
r
r R
R E dl E dl E dl
r R
沿电场线积分
dr
Q 4 0 R
15
E dl Er dr
求电场的空间分布,并求在点(2,3,3)处的电 场强度。解:根据公式得
E V (2x+3y)i (3x z) j yk
代入x,y,z坐标便得到在处的电场强度为 r r r r E 2 , 3 , 3 13i 6 j 3k SI
27
沿电场线积分
(r Ra17 )
V (r )
Rb
Ra
E dl
Rb
Ra
1 1 Er dr ( ) 4 0 Ra Rb
Q
(2)两球面之间一点b的电势为
V (r )
V (r ) E dl
r Rb
Rb
r
Rb
E dl E dl
21
2.3.2 电势梯度
Va Vb E dl
《大学物理》第三章电势S

i
" p"
或: d
40 ri dq d 40 r
z • 你能否迅速算出“非均匀带电球面(只知道总电量)”
在球心处的电势? • 如果用“路径积分法”,本题应如何解?
例计算均匀带电q 的园环轴线上任一点的电势。 解: 用“电势叠加法” y (以无穷远处 先考虑点电荷dq对电势的贡献 dq 的电势为0) dq d 4 0 r r q dq q R d 0 4 r 40 r 0 x o x Q 2 2 4 0 x 2 R 2 r x R
球面A 产生的电势分布
球面B 产生的电势分布
qA r R A A 4 0 RA q r RA A A 4 0 r
r RB r RB
qB B 4 0 RB qB B 4 0 r
A B
qB
qA R A
r RA
qA qB 4 0 RA 4 0 RB
E
●
●
dr
P2
2
空间变化率:
d E cos dr d E ( d dr dr ) Max
当
0
时
E
●
有最大值
沿电场方向电势随空间的变化率最大,就把这一最大值称为
1
P 1
dr
●
P2
2
该点的电势梯度 d ( ) Max 定义电势梯度--- grad
则:E dl a b
dl
a
E
E dl
0
dl
b
——场强与等势面正交。
若再取小位移 dl 与电场同向(由点 a到点b′) 则:E dl a b 0 , a b
" p"
或: d
40 ri dq d 40 r
z • 你能否迅速算出“非均匀带电球面(只知道总电量)”
在球心处的电势? • 如果用“路径积分法”,本题应如何解?
例计算均匀带电q 的园环轴线上任一点的电势。 解: 用“电势叠加法” y (以无穷远处 先考虑点电荷dq对电势的贡献 dq 的电势为0) dq d 4 0 r r q dq q R d 0 4 r 40 r 0 x o x Q 2 2 4 0 x 2 R 2 r x R
球面A 产生的电势分布
球面B 产生的电势分布
qA r R A A 4 0 RA q r RA A A 4 0 r
r RB r RB
qB B 4 0 RB qB B 4 0 r
A B
qB
qA R A
r RA
qA qB 4 0 RA 4 0 RB
E
●
●
dr
P2
2
空间变化率:
d E cos dr d E ( d dr dr ) Max
当
0
时
E
●
有最大值
沿电场方向电势随空间的变化率最大,就把这一最大值称为
1
P 1
dr
●
P2
2
该点的电势梯度 d ( ) Max 定义电势梯度--- grad
则:E dl a b
dl
a
E
E dl
0
dl
b
——场强与等势面正交。
若再取小位移 dl 与电场同向(由点 a到点b′) 则:E dl a b 0 , a b
大学物理静电场2电势

各电势的零点应是同一点)
用“点电荷电势叠加的方法”:
对点电荷系:
对有限的 连续电荷分布:
qi
4 π ori
(选
0)
d q
q 4πor
(选 0)
例. 求半径为 R、带电量为 q 的细圆环 轴线上任意点的电势。
【解】 这是连续带电体, 任取一电荷元dq,
用“点电荷电势叠加法”
dq
R 0
r R2 x2 取轴线上任一点 P,电势:
x
x
P
d q
(q)4 π0r
所以
4π 0
q R2 x2
1/ 2
1
dq
4 π0r (q)
思考: 环上电荷均匀或不均匀结果一样吗?
等势面:
电场中电势相等的点组成的面称为等势面。 等势面是形象描述电场的一种表示方法。 画法:相邻等势面的电势差为常数。
例1. 正点电荷电场的等势面。
等势面有如下特点:
2π0 r
r > r0 的点,电势为负,
r = r0 的点,电势为零,
r < r0 的点,电势为正。
r
可以看到,若选无限远为 电势零点,
会使积分发散。
8.4.5 电势叠加原理
由
po
E
d
l
及
E
p
Ei
得 ( po p
Ei ) d l
po p
i Ei
d
l
i
i
i
i
(注意:用电势叠加原理时,
静电势能是属于电荷 q0 和场源所共有的 (正如重力势能是属于物体和地球),
也叫电荷之间的相互作用能。
例 1. 氢原子中的电子在原子核电场中的 静电势能为
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Va E dl a E dl
讨论
a
a
1)电势零点的选择(参考点)
任意 视分析问题方便而定
参考点不同电势不同
10
通常:
理论计算有限带电体电势时选无限远为参考点
实际应用中或研究电路问题时取大地、仪器外 壳等
2)电势的量纲
SI制:单位 V (伏特)
量纲
V
W q
L2 MT
3I
1
3)电势是一个长程物理量
b b
a
f dl q E dl Wa Wb
a
a
b E dl
Wa
Wb
a
q
q 与试验电荷无关
根据静电场 Wa Wb 的环路定理 q q
E dl Va Vb
a
称 a b两点电势差
若选b点的势能为参考零点 则
a点的电势:
势能零点
势能零点
VA VB
11
rB rA
E
dr
Q 4πε0
rB dr rA r 2
()
4πε0 rA rB
(2)r R
VA VB
rB rA
E
dr
0
o A B A dr B
R
drrA r
r
rB
20
(3)r R 令 rB V 0
Q 1 1
VA VB
(4)r R
()
4πε0
rA R
q
x2 R2
x
R,VP
q 4πε0 x
V
dl
q
q
4πε0 R
4πε0 x2 R2
R
r
xo x
Px
o
x
17
通过一均匀带电圆平面中心且垂直平面 的轴线上任意点的电势. dq 2πrdr
V 1 R 2πrdr ( x2 R2 x)
4πε0 0 x2 r 2 2ε0
x R
x2 R2 x R2 2x
A q0
E dl
l
i
q0 l Ei dl
结论:静电场力做功,与路径无关.
4
二 静电场的环路定理
q0 E dl q0 E dl
ABC
ADC
q0( E dl E dl ) 0
B
C
DE
ABC CDA
A
l E dl 0
结论:沿闭合路径一 周,电场力作功为零.
静电场是保守场
电场力做正功,电势能减少.
7
AB q0E dl WpA WpB (WpB WpA )
令 EpB 0
WpA AB q0E dl
A EpA
B
EpB E
试验电荷q0在电场中某点的电势能,在 数值上等于把它从该点移到零势能处静电场 力所作的功.
8
2.电势 如图示
b
E
点电荷在场中受力 f qE q
解: 平行板电容器内部的场强为 E
0
两板间的电势差
ΔV E dl Edl E dl
E ,dl
均匀场
方向一致
E
dl
d
Δ Ed
24
[例三]无限大均匀带电平面 场中电势分布.
电场分布
a o a x
E 0
0
(a x a) (x a , x a)
电荷无限分布,在有限远处选零势点.令Uo 0 , 沿 x 轴方向积分。
r
er
q
rA
q0 A
2
dA qq0 dr 4πε0r 2
A qq0 rB dr 4πε0 r rA 2 qq0 ( 1 1 ) 4πε0 rA rB
结论: A仅与q0的始末位 置有关,与路径无关.
B
rB
dr
dl
E
r
er
q
rA
q0 A
3
任意带电体的电场(点电荷的组合)
E Ei
i
rB
V (r) E dr
V (r) Q
4πε0r
E
dr
Q
r
R
4πε0 R
V
Q 4π 0 R
Q 4π0r
o
AB
R
rA
r
oR
r
rB
21
例3 “无限长”带电直导线的电势.
解 令 VB 0
VP
rB
E
dr
r
rB dr r 2 π ε0r
ln rB
2 π ε0 r
讨论:能否选 V 0?
x
11
三、电势的计算
1.点电荷场电势公式
VP E dl
Q
rP
Edl
P
E dl
dl
r
dr
r
4π
Q
0
r
2
rˆ
dr
V Q
r
Q
4 0r
2 dr
球对称
标量
4π 0 r
正负
12
电势的叠加原理
点电荷系
E Ei
i
VA
E dl
A n
A Ei dl
i 1
n
Vi
i 1
VA
(2)利用点电荷电势的叠加原理
V
1 4πε0
dq r
15
例1 正电荷q均匀分布在半径为R的细圆
环上. 求环轴线上距环心为x处的点P的电势.
解
dVP
1 4πε0
dq r
1
VP 4πε0r dq
dq
q
r
R
4πε0r q
xo x
Px
4πε0 x2 R2
16
讨论
VP 4πε0
x
0,V0
q 4πε0 R
oBP
rB
r
r
22
例2 计算电量为 Q 的带电球面球心的电势
解:
在球面上任取一电荷元 dq
则电荷元在球心的电势为 dV
dq
dq
Q oR
由电势叠加原理
4π 0 R
球面上电荷在球心的总电势
V
dV
Q
dq
Q 4π0R
Q
4π 0 R
思考:
•电量分布 均匀?
•圆环?
•圆弧?23
例3 平行板电容器两板间的电势差
n i 1
qi 4 π ε0ri
q1
r1
q2 q3
r2
r3
•
A
E3 E2
E1
13
电荷连续分布时
dq dV
dq dV
4πε0r
VA
1 4πε0
dq r
dq
r
A
14
计算电势的方法
(1)利用
VA
E dl
AB
VB
势能零点
Va E dl a
已知在积分路径上 E的函数表达式
有限大带电体,选无限远处电势为零.
5
讨论
E dl 0
L
1)静电场的基本方程之一
静电场是保守场
2) 微分形式
E 0
3)表征静电场的性质有两个方程
qi
E dl 0
L
E dS i
S
0
6
三 电势能
静电场是保守场,
静电场力是保守力. 静电场力所做的功就 等于电荷电势能增量 的负值.
A EpA
B
EpB E
AAB WpA WpB (WpB WpA )
V Q 4πε0 x
dr x2 r2
r
R ox
Px
18
例2 真空中有一电荷为Q,半径为R的
均匀带电球面. 试求
(1)球面外两点间的电势差;
(2)球面内两点间的电势差;
(3)球面外任意点
的电势;
(4)球面内任意点 的电势.
o
A
R
rA
B
r
rB
19
0 r R
解
E
Q
4ε0r 2
rR
(1)r R
Q
§4 静电场的环路定理 电势 一、静电场力的功 电势能 二、静电场的环路定理 电势 三、电势的计算 四、等势面 电势梯度
1
一 静电场力所做的功
点电荷的电场
dA
q0E dl
qq0 4πε0r 2
er
dl
er dl dl cosθ dr
dA
qq0 4πε0r 2
dr
B
rB
dr
dl
E
