最新平行线与三角形内角和的综合应用每日一题目及答案

合集下载

平行线与三角形内角和计算(人教版)(含答案)

学生做题前请先回答以下问题问题1：由角的关系得平行，可以考虑哪些定理？问题2：由平行得角的关系，可以考虑哪些定理？问题3：三角形的内角和等于_______．问题4：直角三角形两锐角_______．以下是问题及答案，请对比参考:问题1：由角的关系得平行，可以考虑哪些定理？答：同位角相等，两直线平行；内错角相等，两直线平行；同旁内角互补，两直线平行．问题2：由平行得角的关系，可以考虑哪些定理？答：两直线平行，同位角相等；两直线平行，内错角相等；两直线平行，同旁内角互补．问题3：三角形的内角和等于．答：180°．问题4：直角三角形两锐角．答：互余．平行线与三角形内角和计算（人教版）一、单选题(共10道，每道10分)1.如图，在△ABC中，AD平分∠BAC，且与BC相交于点D，∠B=40°，∠BAD=30°，则∠C 的度数为( )A.80°B.90°C.100°D.110°答案：A解题思路：试题难度：三颗星知识点：三角形内角和定理2.已知在△ABC中，∠B是∠A的2倍，∠C比∠A大20°，则∠A的度数为( )A.30°B.40°C.60°D.80°答案：B解题思路：试题难度：三颗星知识点：三角形内角和定理3.如图，在△ABC中，∠B=∠C，FD⊥BC，DE⊥AB，垂足分别为D，E．若∠AFD=158°，则∠EDF=( )A.42°B.44°C.68°D.79°答案：C解题思路：试题难度：三颗星知识点：互余4.如图，在△ABC中，AE平分∠BAC，AD⊥BC，垂足为D，若∠BAC=128°，∠C=36°，则∠DAE的度数为( )A.10°B.12°C.15°D.18°答案：A解题思路：试题难度：三颗星知识点：互余5.如图，在△ABC中，∠BAC=4∠1=4∠C，BD⊥CA于点D，则∠DBA=( )A.20°B.60°C.45°D.30°答案：D解题思路：试题难度：三颗星知识点：互余6.如图，在四边形ABCD中，点E在BC上，AB∥DE，∠B=78°，∠C=60°，则∠EDC的度数为( )A.42°B.60°C.78°D.80°答案：A解题思路：试题难度：三颗星知识点：三角形内角和定理7.如图，直线BD∥EF，AE与BD交于点C，若∠B=30°，∠A=75°，则∠CEF的度数为( )A.60°B.75°C.90°D.105°答案：D解题思路：试题难度：三颗星知识点：三角形内角和定理8.如图，直线AB∥CD，∠EFA=28°，∠EHC=50°，则∠E=( )A.28°B.22°C.32°D.38°答案：B解题思路：试题难度：三颗星知识点：三角形内角和定理9.如图，AB∥CD，AE平分∠CAB，CE平分∠ACD，则∠E=( )A.60°B.75°C.90°D.105°答案：C解题思路：试题难度：三颗星知识点：三角形内角和定理10.将一副直角三角板如图放置，已知AE∥BC，则∠AFE的度数为( )A.95°B.100°C.110°D.105°答案：D解题思路：试题难度：三颗星知识点：三角形内角和定理。

八年级数学上册平行线与三角形内角和的综合应用(习题及答案)(人教版)

）
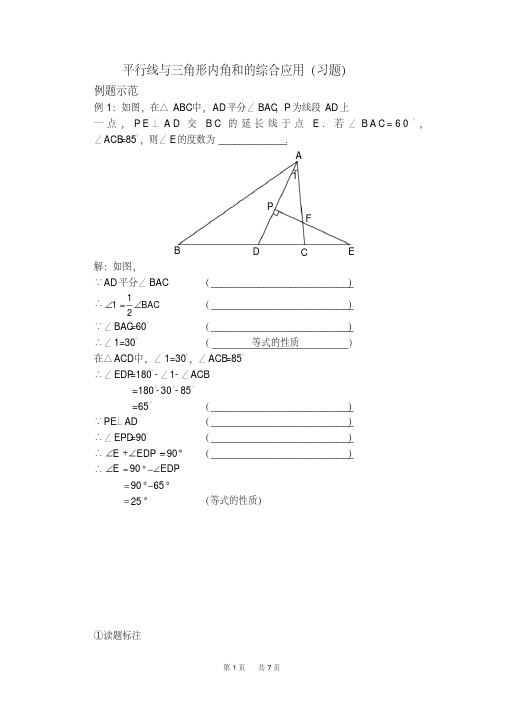
在△ ACD中，∠ 1=30°，∠ ACB=85°
∴∠ EDP=180°- ∠1- ∠ACB
=180°- 30°- 85°
=65°
（ __________________________）_
∵PE⊥ AD
（ __________________________）_
∴∠ EPD=90°
（ __________________________）_
证自明的“基本事实” ，可以当做已知的大前提来进行使用．而其中的三条，
是我们在几何证明中不经意间多次用到的，下面对它们来进行简单的解释．
当我们证明时，会遇到如下的推理：
∵a=b，b=c
∴a=c
在这个推理过程中，我们很容易就理解它的正确性，但往往不知道它的依据
是什么．其实，它的依据就是欧几里得公理体系中 5 条公理中的第一条：“（1）
∴∠ A+∠ C=90°（等量代换）
这里推理的依据就是第一条公理，我们把它简记为 “等量代换”．“等量代换”
第5页共7页
A
D
B
C
第3页共7页
6. 已知：如图， AB∥CD，∠ BAE=∠DCE=45°．求证：∠ E=90°．
A
B
1 E
Байду номын сангаас
2
C
D
7. 已知：如图， EF⊥BC， DE⊥AB，∠ B=∠ADE．求证： AD∥EF． A
E
B
F
D
C
第4页共7页
思考小结
1. 在证明过程中：（1）由平行可以想 ________相等、 __________相等、 ________互补；
=180°- 30°- 85°

平行线与三角形内角和的综合应用每日一题及答案

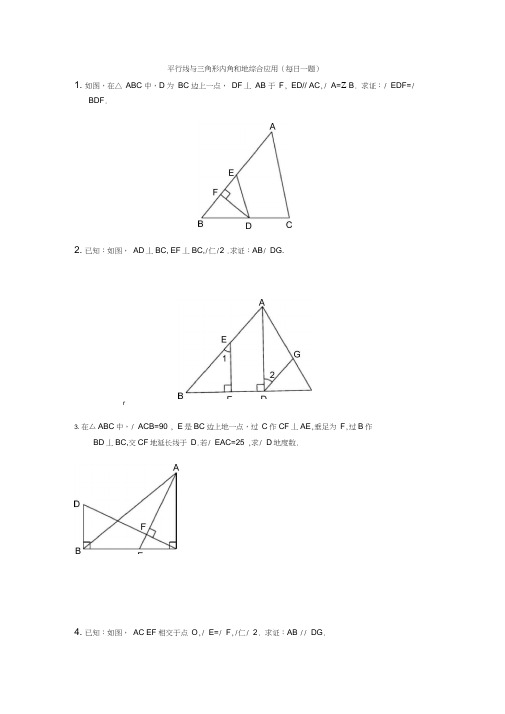
平行线与三角形内角和地综合应用（每日一题）1. 如图，在△ ABC 中，D 为BC 边上一点，DF丄AB 于F, ED// AC,/ A=Z B. 求证：/ EDF=/BDF.2. 已知：如图，AD丄BC, EF丄BC,/仁/2 .求证：AB/ DG.r3. 在厶ABC中，/ ACB=90 , E是BC边上地一点，过C作CF丄AE,垂足为F,过B作BD丄BC,交CF地延长线于D.若/ EAC=25°,求/ D地度数.4. 已知：如图，AC EF相交于点O,/ E=/ F,/仁/ 2. 求证：AB // DG.5. 已知：如图，AD// EF, BF// DG,/ A=Z B=Z G=35° 求/ EFG地度数.【参考答案】1•证明：如图,已知 )Z FED +Z EDF =Z B+Z BDF=90°( 直角三角形两锐角互余 )等角地余角相等•Z ACB=90°Z D=90°- Z DCB =90 - 25°等式性质4.证明：如图， •Z E=Z FDE// AC • / A =Z FED• / B =Z FED已知 ) 两直线平行，同位角相等 ) 已知 ) 等量代换即：Z CAB=Z DCA 等式性质 )• AB / DG( 内错角相等，两直线平行 ) 5.证明：如图，• Z A=Z B=35°( 已知 ) •Z ACB=18°0-Z A-Z B=180°-35 °-35°=110° 三角形地三个内角地和等于 180°)•Z DCF=Z ACB (对顶角相等 ) 已知( •Z 1+Z CAE =Z 2+Z FCA • DF 丄 AB • / EDF=Z BDF 2.证明：如图，•/ EF ± BC •••/ B+Z 1=90 •/ AD 丄 BC •Z 2+ Z CDG=9°0已知 ) 直角三角形两锐角互余已知 )垂直地性质•Z B=Z CDG• AB / DG 3.解：如图，•/ CF 丄 AE 已知 ) 等角地余角相等 ( 同位角相等，两直线平行已知 •Z EAC +Z ACD=9°0 )直角三角形两锐角互余即 Z DCB+Z ACD=90已知 Z DCB=Z EACZ EAC=25°等角地余角相等已知 Z DCB = 25°BD 丄 BC Z D+Z DCB=9°0) 等量代换已知 ) 直角三角形两锐角互余 = 65已知 • AE / FC内错角相等，两直线平行 •Z CAE =Z FCA两直线平行，内错角相等•Z 1=Z 2/ DCF=11O( 等量代换)BF// DG( 已知)/ D+Z DCF=180( 两直线平行，同旁内角互补 ) / D=70( 等式性质)AD/ EF( 已知)Z D=Z FEG( 两直线平行，同位角相等 )Z FEG=70°( 等量代换)Z G=35°( 已知)Z EFG=180-Z FEG-Z G=180 -70 °-3°5 °=75°(三角形地三个内角地和等于180 °)。

平行线与三角形内角和的综合应用(讲义)

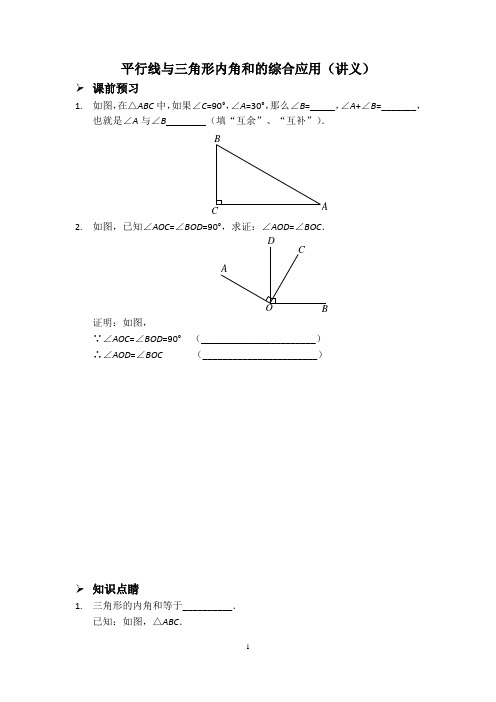
平行线与三角形内角和的综合应用（讲义）➢ 课前预习1. 如图，在△ABC 中，如果∠C =90°，∠A =30°，那么∠B =_____，∠A +∠B =_______，也就是∠A 与∠B ________（填“互余”、“互补”）．ABC2. 如图，已知∠AOC =∠BOD =90°，求证：∠AOD =∠BOC ．DCB OA证明：如图，∵∠AOC =∠BOD =90° （_______________________） ∴∠AOD =∠BOC （_______________________）➢ 知识点睛1. 三角形的内角和等于__________．已知：如图，△ABC ．求证：∠BAC +∠B +∠C =180°．A MBC12N证明：_______，___________________________． ∵MN ∥BC （已作） ∴∠B =∠1，∠C =∠2（_______________________）∵∠BAC+∠1+∠2=180°（_______________________） ∴∠BAC +∠B +∠C =180°（_______________________）2. 直角三角形两锐角___________．➢ 精讲精练1. 如图，在△ABC 中，∠A =50°，∠C =72°，BD 是△ABC 的一条角平分线，则∠ABD=__________．DAC FED C BA第1题图第2题图2. 如图，在△ABC 中，∠B =∠C ，E 是AC 上一点，ED ⊥BC ，DF ⊥AB ，垂足分别为D ，F ．若∠AED =140°，则∠C =_____，∠BDF =______，∠A =______．3. 如图，AE ∥BD ，∠1=110°，∠2=30°，则∠C =______．21EDCB A FDAEB第3题图第4题图4. 如图，AD ∥BC ，AB ∥CD ，E 在CB 的延长线上，EF 经过点A ，∠C =50°，∠FAD =60°，则∠EAB =_______．5. 如图，在△ABC 中，CD 平分∠ACB 交AB 于点D ，过点D 作DE ∥BC 交AC 于点E ．若∠A =75°，∠ADE =35°，则 ∠EDC =_________．6. 如图，在△ABC 中，∠B =40°，∠BAC =68°，AD ⊥BC 于点D ，求∠DAC 的度数．解：如图，在△ABC 中，∠B =40°，∠BAC =68°（已知） ∴∠C =180°-______-______ =180°-_____-_____=______（_______________________） ∵AD ⊥BC （已知）∴∠ADC =90°（垂直的定义） ∴∠C +_____=90°（直角三角形两锐角互余）∴∠DAC =90°-______=90°-______=______（_______________________）7. 如图，在Rt △ABC 中，∠ACB =90°，CD ⊥AB ，垂足为D ．求证：∠A =∠BCD ．证明：如图， ∵∠ACB =90°（已知）∴∠A +_____=90°（直角三角形两锐角互余） ∵CD ⊥AB （已知）ABDABCDEDCBA∴∠CDB =90°（垂直的定义）∴_____+∠B =90°（______________________） ∴∠A =∠BCD （______________________）8. 如图，在△ABC 中，∠C =90°，点D 是边AC 上一点，DE ∥BC ，∠1=60°，求∠A 的度数．ADE1BC9. 如图，BD ∥AE 交△ABC 的边AC 于点F ，∠CAE =95°，∠CBD =30°，求∠C 的度数．AB CDEF10.如图，在Rt△ABC中，∠ACB=90°，CD⊥AB于点D，AF平分∠CAB交CD于点E，交BC于点F．求证：∠1=∠2．【参考答案】➢课前预习1.60°，90°，互余2.已知，同角的余角相等➢知识点睛1.180°如图，过点A作MN∥BC两直线平行，内错角相等平角的定义等量代换2.互余➢精讲精练1.29°21FEDCB A2.50°，40°，80°3.40°4.70°5.35°6.解：如图，在△ABC中，∠B=40°，∠BAC=68°（已知）∴∠C=180°-∠B-∠BAC=180°-40°-68°=72°（三角形的内角和等于180°）∵AD⊥BC（已知）∴∠ADC=90°（垂直的定义）∴∠C+∠DAC=90°（直角三角形两锐角互余）∴∠DAC=90°-∠C=90°-72°=18°（等式的性质）7.证明：如图，∵∠ACB=90°（已知）∴∠A+∠B=90°（直角三角形两锐角互余）∵CD⊥AB（已知）∴∠CDB=90°（垂直的定义）∴∠BCD+∠B=90°（直角三角形两锐角互余）∴∠A=∠BCD（同角的余角相等）8.解：如图，∵DE∥BC（已知）∴∠1=∠B（两直线平行，同位角相等）∵∠1=60°（已知）∴∠B=60°（等量代换）∵∠C=90°（已知）∴∠A+∠B=90°（直角三角形两锐角互余）∴∠A=90°-∠B=90°-60°=30°（等式的性质）9.解：如图，∵BD∥AE（已知）∴∠CFD=∠CAE（两直线平行，同位角相等）∵∠CAE=95°（已知）∴∠CFD=95°（等量代换）∴∠CFB =180°-∠CFD=180°-95°=85°（平角的定义）在△CBF 中，∠CBD =30°，∠CFB =85°（已知） ∴∠C =180°-∠CBD -∠CFB =180°-30°-85°=65°（三角形的内角和等于180°） 10. 证明：如图，∵∠ACB =90°（已知）∴∠CAF +∠2=90°（直角三角形两锐角互余） ∵CD ⊥AB （已知）∴∠EDA =90°（垂直的定义）∴∠DAE +∠AED =90°（直角三角形两锐角互余） ∵AF 平分∠CAB （已知）∴∠CAF =∠DAE （角平分线的定义） ∴∠2=∠AED （等角的余角相等） ∵∠1=∠AED （对顶角相等） ∴∠1=∠2（等量代换）平行线与三角形内角和的综合应用（随堂测试）1. 已知：如图，AB ∥CD ，∠ABF =120°，CE ⊥BF ，垂足为E ，则∠ECF =___________．ABC D EF2. 已知：如图，在△ABC 中，∠B =40°，AD 平分∠BAC 交BC 于点D ，DE ∥BA 交AC 于点E ，∠ADE =40°，求∠C 的度数．EDC BA【参考答案】1.30°2.解：如图，∵DE∥BA（已知）∴∠BAD=∠ADE（两直线平行，内错角相等）∵∠ADE=40°（已知）∴∠BAD=40°（等量代换）∵AD平分∠BAC（已知）∴∠BAC=2∠BAD=2×40°=80°（角平分线的定义）在△ABC中，∠B=40°，∠BAC=80°（已知）∴∠C=180°-∠B-∠BAC=180°-40°-80°=60°（三角形的内角和等于180°）。

平行线与三角形内角和的综合应用作业及答案

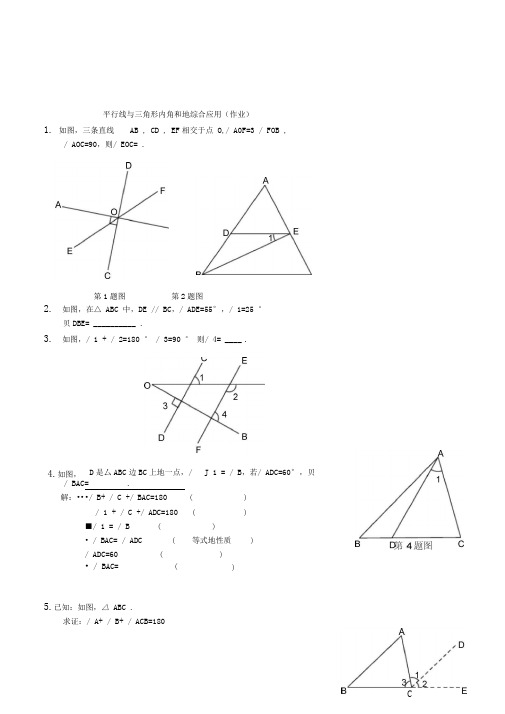
平行线与三角形内角和地综合应用（作业）1. 如图，三条直线 AB , CD , EF 相交于点 O ,/ A0F=3 / FOB ,/ AOC=90，则/ EOC= .2. 如图，在△ ABC 中，DE // BC ，/ ADE=55°，/ 1=25 °贝DBE= __________ .3. 如图，/ 1 + / 2=180 ° / 3=90 ° 则/ 4= ____ .5.已知：如图，△ ABC .求证：/ A+ / B+ / ACB=180C 第2题图4.如图， D 是厶ABC 边BC 上地一点，/ J 1 = / B ，若/ ADC=60°，贝U / BAC= .解：•• •/ B+ / C +/ BAC=180 ()/ 1 + / C +/ ADC=180 ()■/ 1 = / B ( )• / BAC= / ADC ( 等式地性质 )/ ADC=60 ( )• / BAC= ( )第1题图证明：作 BC 地延长线 CE ,过点C 作CD // AB ,•/ CD // AB•••/ A= / 1 / B= / 2 •••/ 1 + Z 2+ / 3=180° •••/ A+ / B+ / ACB=180 ( ( )(( ))) 第5题6.已知如图， AB // CD ，/ BAE= / DCE=45° ./ E=90° . •/ AB // CD ( )+ =180 ( )•••/ BAE= 7 D C E=45 ( )• 7 1+45°+ 7 2+45° =即7 1 + 7 2= ( )•••/ E=180° - (/ 1+ / 2)=180 °-90 °=90 ° ( )7.已知：如图，/ 1 = / ACB ，/ 2=7 3.求证：CD // HF.证明：•••7 1= 7 ACB ( )• // ( )• 7 2=• 7 2=7 3 ( )'• 7 3= ( )•• // ( )【参考答案】1. 45°2. 30°3. 90°4. 60 °三角形三个内角地和是 180。

平行线性质余角补角三角形内角和综合练习题(附答案)

平行线性质余角补角三角形内角和综合练习题一、单选题1.如图，若1∠=2∠，3∠=4∠，下列结论中错误的是( )A.BD 是ABC △的角平分线B. CE 是BCD △的角平分线C. 3∠=12ACB ∠ D. CE 是ABC △的角平分线 2.如图,,1110,80BCDE AED ∠︒∠︒＝＝,则A ∠的大小为( )A.20︒B.25︒C.30︒D.40︒ 3.在ABC 中，5AB =，8AC =，则第三边BC 的长可能是( ) A.2 B.3 C.6 D.134.如图，,,CD CE CF 分别是ABC 的高、角平分线、中线，则下列各式错误的是( )A.2AB BF =B.12ACE ACB ∠=∠C. AE BE =D.CD BE ⊥5.若线段,AP AQ 分别是ABC 的高和中线，则( ) A.AP AQ > B.AP AQ C.AP AQ < D.AP AQ6.如图,工人师傅砌门时,常用木条EF 固定长方形门框,使其不变形,这样做的根据是( )A.三角形的稳定性B.两点确定一条直线C.两点之间,线段最短D.长方形的四个角都是直角 7.如图,直线//AB CD ,70,40A C ∠=︒∠=︒ ,则E ∠等于( )A.30︒B.40︒C.60︒D.70︒8.小明把一副三角尺按如图所示方式摆放,其中90,45,30C F A D ∠=∠=︒∠=︒∠=︒,则αβ∠+∠等于( )A.180°B.210°C.360°D.270° 9.若n 边形恰好有n 条对角线，则n 为( )A.4B.5C.6D.710.如图，正五边形, ABCDE BG 平分,ABC DG ∠平分正五边形的外角EDF ∠，则G ∠=( )A.36°B.54°C.60°D.72°11.如图，五边形ABCDE 中，//AB CD ，123∠∠∠，，分别是该五边形的外角，则123∠+∠+∠等于_________度.二、填空题12.一个等腰三角形的两边长分别为4cm 和9cm ，则它的周长为__cm .13.已知,,a b c 是ABC 的三边长，,a b 满足2|7|(1)0,a b c -+-=为奇数，则c = . 14.如图，在ABC 中.BD DE EC ==.则线段AE 是的中线.15.直角三角形ABC 中有一个角比另一角的2倍小60︒,则该直角三角形中最小的角的度数为 .16.若ABC 的三边长分别是,,a b c ，且()20a b b c -+-=，则ABC 的形状是___________.参考答案1.答案：D解析：1∠=2∠, 3∠=4∠，根据角平分线的性质，可知:BD 是ABC △的角平分线,A 正确;CE 是BCD △的角平分线，B 正确;3∠=12ACB ∠,C 正确;CE 是BCD △的角平分线是错误的，三角形的角平分线是三角形的内角平分线与对边相交，角的顶点与对边交点之间的线段，D 错误.2.答案：C解析：BC DE ,80C AED ∴∠=∠=︒,1A C ∴∠=∠+∠,1108030A ∴∠=︒-︒=︒.故选C.3.答案：C解析：∵5,8,8585AB AC BC ==-<<+，即313BC <<.观察选项，只有选项C 符合题意.故选C.4.答案：C解析：∵,,CD CE CF 分别是ABC 的高、角平分线、中线，∴CD BE ⊥，1,22ACE ACB AB BF ∠=∠=，∴A ，B ，D 正确.故选C. 5.答案：D解析：6.答案：A解析：7.答案：A解析：如图,∵//AB CD ,70A ∠=︒ ,∴170A ∠=∠=︒,∵1,40C E C ∠=∠+∠∠=︒,∴1704030E E ∠=∠-∠=︒-︒=︒.故选A.8.答案：B解析：如图,30,90D DGA CGH F FHB CHG αβ∠=∠+∠=︒+∠∠=∠+∠=︒+∠,()309012012090210CGH CHG CGH CHG αβ∴∠+∠=︒+∠+︒+∠=︒+∠+∠=︒+︒=︒.故选B.9.答案：B 解析：由题意，得1(3)2n n n -=.因为0n ≠，所以可在方程两边同时除以n ，得1(3)12n -=，解得5n =.故选B.10.答案：B解析：如图，∵五边形ABCDE 是正五边形，∴108ABC C CDE ∠=∠=∠=︒.∵BG 平分ABC ∠，∴1542CBG ABC ∠=∠=︒，∴3605410810890DPB ∠=︒-︒-︒-︒=︒，∴90G EDG ∠+∠=︒.∵360725EDF ︒∠==︒，DG 平分EDF ∠，∴1362EDG EDF ∠=∠=︒，∴9054G EDG ∠=︒-∠=︒.故选B.11.答案：180解析：∵//AB CD ，∴180B C ∠+∠=︒，∴与B C ∠∠，两角相邻的外角的和是180°，∵五边形的外角和是360°，∴123360180180∠+∠+∠=︒-︒=︒.12.答案：22解析：①当腰是4cm ，底边是9cm 时：不满足三角形的三边关系，因此舍去．②当底边是4cm ，腰长是9cm 时，能构成三角形，则其周长49922cm =++=．故填22．13.答案：7解析： ,a b 满足()21|70|a b -+-=， 7010a b ∴-=-=，，解得71a b ==，，716718-=+=，，68c ∴<<，又c 为奇数，7c ∴=.14.答案：ADC解析：因为BD DE EC ==，所以E 是CD 的中点，所以AE 是ADC 的中线.15.答案：40︒或15︒ 解析：①当这两个角是锐角时,设直角三角形中一个锐角为x ,另一个锐角为260x -︒,根据两个锐角之和为90︒,可得26090x x +-︒=︒,解得50x =︒,较小角905040︒-︒=︒;②设当一个角是锐角,另一个角是直角时,一个锐角为则有26090y -︒=︒,解得75y =︒.另一个锐角为15︒,较小的角为15︒.16.答案：等边三角形解析：因为2()||0a b b c -+-=，所以0,0a b b c -=-=，所以,a b b c ==，所以a b c ==，所以ABC 是等边三角形.。

平行线与三角形内角和计算(北师版)(含答案)

学生做题前请先回答以下问题问题1：我们学过的，和余角、补角相关的定理分别是什么？自己尝试推理证明．问题2：由角的关系得平行，可以考虑哪些定理？问题3：由平行得角的关系，可以考虑哪些定理？平行线与三角形内角和计算（北师版）一、单选题(共10道，每道10分)1.如图，在△ABC中，AD平分∠BAC，且与BC相交于点D，∠B=40°，∠BAD=30°，则∠C 的度数为( )A.80°B.90°C.100°D.110°答案：A解题思路：如图，由于AD平分∠BAC，∠BAD=30°，则∠BAC=2∠BAD=2×30°=60°，在△ABC中，∠B=40°，由三角形的内角和等于180°，可得∠C=180°-∠B-∠BAC=180°-40°-60°=80°．故选A．试题难度：三颗星知识点：三角形内角和定理2.已知在△ABC中，∠B是∠A的2倍，∠C比∠A大20°，则∠A的度数为( )A.30°B.40°C.60°D.80°答案：B解题思路：由题意可知∠B和∠C都与∠A有关，因此可设∠A=α，则∠B=2α，∠C=α+20°，由三角形的内角和等于180°，可得α+2α+(α+20°)=180°，解得，α=40°，即∠A=40°．故选B．试题难度：三颗星知识点：三角形内角和定理3.如图，在△ABC中，∠B=∠C，FD⊥BC，DE⊥AB，垂足分别为D，E．若∠AFD=158°，则∠EDF=( )A.42°B.44°C.68°D.79°答案：C解题思路：如图，由FD⊥BC，DE⊥AB可知，∠FDC=∠DEB=90°，因为∠AFD=158°，由平角的定义，可得∠2=180°-158°=22°，再由直角三角形两锐角互余，可得∠C=68°．观察图形，并结合已知条件∠B=∠C，首先可得∠B=68°；由直角三角形两锐角互余，可得∠1+∠B=90°；又因为FD⊥BC，所以∠1+∠EDF=90°，由等角的余角相等，可得∠EDF=∠B=68°．故选C．试题难度：三颗星知识点：互余4.如图，在△ABC中，AE平分∠BAC，AD⊥BC，垂足为D，若∠BAC=128°，∠C=36°，则∠DAE 的度数为( )A.10°B.12°C.15°D.18°答案：A解题思路：如图，因为AE平分∠BAC，且∠BAC=128°，所以，由于AD⊥BC于点D，∠C=36°，根据直角三角形两锐角互余，可得∠DAC=90°-∠C=90°-36°=54°，因此∠DAE=∠CAE-∠DAC=64°-54°=10°．故选A．试题难度：三颗星知识点：三角形内角和定理5.如图，在△ABC中，∠BAC=4∠1=4∠C，BD⊥CA于点D，则∠DBA=( )A.20°B.60°C.45°D.30°答案：D解题思路：在△ABC中，由三角形的内角和等于180°，可得∠BAC+∠1+∠C=180°，由∠BAC=4∠1=4∠C，可得∠C=∠1，则4∠1+∠1+∠1=180°，解得∠1=30°，所以∠C=30°，∠BAC=120°．由平角的定义，可得∠BAD=180°-∠BAC=180°-120°=60°．因为BD⊥CA于点D，则∠D=90°，在Rt△ABD中，根据直角三角形两锐角互余，可得∠DBA=90°-∠BAD=90°-60°=30°．故选D．试题难度：三颗星知识点：三角形内角和定理6.如图，直线BD∥EF，AE与BD交于点C，若∠B=30°，∠A=75°，则∠CEF的度数为( )A.60°B.75°C.90°D.105°答案：D解题思路：如图，在△ABC中，∠B=30°，∠A=75°，由三角形的内角和等于180°，可得∠ACB=180°-∠B-∠A=180°-30°-75°=75°．根据对顶角相等，可得∠DCE=∠ACB=75°．已知BD∥EF，根据两直线平行，同旁内角互补，可得∠CEF=180°-∠DCE=180°-75°=105°．故选D．试题难度：三颗星知识点：三角形内角和定理7.如图，在四边形ABCD中，点E在BC上，AB∥DE，∠B=78°，∠C=60°，则∠EDC的度数为( )A.42°B.60°C.78°D.80°答案：A解题思路：如图，因为AB∥DE，根据两直线平行，同位角相等，可得∠DEC=∠B．已知∠B=78°，因此∠DEC=78°．在△DEC中，∠C=60°，∠DEC=78°，由三角形的内角和等于180°，可得∠EDC=180°-∠C-∠DEC=180°-60°-78°=42°．故选A．试题难度：三颗星知识点：三角形内角和定理8.如图，直线AB∥CD，∠EFA=28°，∠EHC=50°，则∠E=( )A.28°B.22°C.32°D.38°答案：B解题思路：如图，因为AB∥CD，∠EHC=50°，根据两直线平行，同旁内角互补，可得∠AGH=180°-∠EHC=180°-50°=130°，根据对顶角相等，可得∠EGF=∠AGH=130°，在△EGF中，∠EFA=28°，∠EGF=130°，由三角形的内角和等于180°，可得∠E=180°-∠EFA-∠EGF=180°-28°-130°=22°．故选B．试题难度：三颗星知识点：三角形内角和定理9.如图，AB∥CD，AE平分∠CAB，CE平分∠ACD，则∠E=( )A.60°B.75°C.90°D.105°答案：C解题思路：如图，因为AB∥CD，根据两直线平行，同旁内角互补，可得∠CAB+∠ACD=180°，因为AE平分∠CAB，CE平分∠ACD，所以∠1=∠CAB，∠2=∠ACD，∠1+∠2=(∠CAB+∠ACD)=×180°=90°．在△ACE中，由三角形的内角和等于180°，可得∠E=180°-(∠1+∠2)=180°-90°=90°．故选C．试题难度：三颗星知识点：三角形内角和定理10.将一副直角三角板如图放置，已知AE∥BC，则∠AFE的度数为( )A.95°B.100°C.110°D.105°答案：D解题思路：如图，由题意可知，∠C=30°，∠E=45°，因为AE∥BC，根据两直线平行，内错角相等，可得∠1=∠C=30°．在△AEF中，∠1=30°，∠E=45°，由三角形的内角和等于180°，可得∠AFE=180°-∠1-∠E=180°-30°-45°=105°．故选D．想一想：1．我们学过的和余角、补角相关的定理分别是什么？自己尝试推理证明．2．由角的关系得平行，可以考虑哪些定理？3．由平行得角的关系，可以考虑哪些定理？参考答案：1．同角或等角的余角相等；同角或等角的补角相等．已知∠1与∠2互余，∠1与∠3互余，由互余可得∠1+∠2=90°，∠1+∠3=90°，所以∠2=∠3，同角的余角相等；已知∠1与∠2互余，∠3与∠4互余，∠2=∠3，由互余可得∠1+∠2=90°，∠3+∠4=90°，又因为∠2=∠3，所以∠1=∠4，等角的余角相等．综上，同角或等角的余角相等．可用类似的方法推理证明，同角或等角的补角相等．2．同位角相等，两直线平行；内错角相等，两直线平行；同旁内角互补，两直线平行．3．两直线平行，同位角相等；两直线平行，内错角相等；两直线平行，同旁内角互补．试题难度：三颗星知识点：三角形内角和定理。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

平行线与三角形内角和的综合应用每日一题目及答案
平行线与三角形内角和的综合应用（每日一题）
1．如图，在△ABC 中，D 为BC 边上一点， DF ⊥AB 于F ，ED ∥AC ，∠A =
∠B ．
求证：∠EDF =∠BDF ．
F E D
C
A
2．已知：如图，AD ⊥BC ，EF ⊥BC ，∠1=∠2．求证：AB ∥DG ．
2
1
G
F E D
C
B
A
3．在△ABC 中，∠ACB =90°， E 是BC 边上的一点，过C 作CF ⊥AE ，垂足为
F ，过B 作BD ⊥BC ，交CF 的延长线于D ．若∠EAC =25°，求∠D 的度数．
F
E
D
C
B
A
4．已知：如图，AC 、EF 相交于点O ，∠E =∠F ，∠1=∠2．
求证：AB ∥DG ．
O
2
1
C
G
D
F
E
B
A
5．已知：如图，AD ∥EF ，BF ∥DG ，∠A =∠B =∠G =35°．
求∠EFG 的度数．
G
F
D
C
B
A
【参考答案】
1.证明：如图，
∵DE ∥AC （已知）
∴∠A ＝∠FED （两直线平行，同位角相等） ∵∠A =∠B （已知）
∴∠B ＝∠FED
（等量代换） ∵DF ⊥AB （已知）
∴∠FED +∠EDF =∠B +∠BDF =90°（直角三角形两锐角互余） ∴∠EDF =∠BDF （等角的余角相等） 2.证明：如图，
∵EF ⊥BC （已知）
∴∠B +∠1=90° （直角三角形两锐角互余） ∵AD ⊥BC （已知） ∴∠2+∠CDG =90° （垂直的性质） ∵∠1=∠2 （已知） ∴∠B =∠CDG （等角的余角相等） ∴AB ∥DG （同位角相等，两直线平行）
3.解：如图，
∵CF⊥AE（已知）
∴∠EAC +∠ACD=90°（直角三角形两锐角互余）
∵∠ACB=90°
即∠DCB+∠ACD=90°（已知）
∴∠DCB=∠EAC（等角的余角相等）
∵∠EAC=25°（已知）
∴∠DCB = 25°（等量代换）
∵BD⊥BC（已知）
∴∠D+∠DCB=90°（直角三角形两锐角互余）
∴∠D=90°-∠DCB
=90°-25°
= 65°（等式性质）
4.证明：如图，
∵∠E=∠F （已知）
∴AE∥FC （内错角相等，两直线平行）
∴∠CAE =∠FCA （两直线平行，内错角相等）
∵∠1=∠2 （已知）
∴∠1+∠CAE =∠2+∠FCA
即：∠CAB=∠DCA（等式性质）
∴AB∥DG （内错角相等，两直线平行）
5.证明：如图，
∵∠A=∠B=35°（已知）
∴∠ACB=180°-∠A-∠B
=180°-35°-35°
=110°（三角形的三个内角的和等于180°）∵∠DCF=∠ACB （对顶角相等）
∴∠DCF=110°（等量代换）
∵BF∥DG（已知）
∴∠D+∠DCF=180°（两直线平行，同旁内角互补）∴∠D=70°（等式性质）
∵AD∥EF （已知）
∴∠D=∠FEG （两直线平行，同位角相等）
∴∠FEG=70°（等量代换）
∵∠G=35°（已知）
∴∠EFG=180°-∠FEG-∠G
=180°-70°-35°
=75°（三角形的三个内角的和等于180°）。