高考文科数学立体几何三视图问题分类解答
高三数学空间几何体的三视图与直观图试题答案及解析
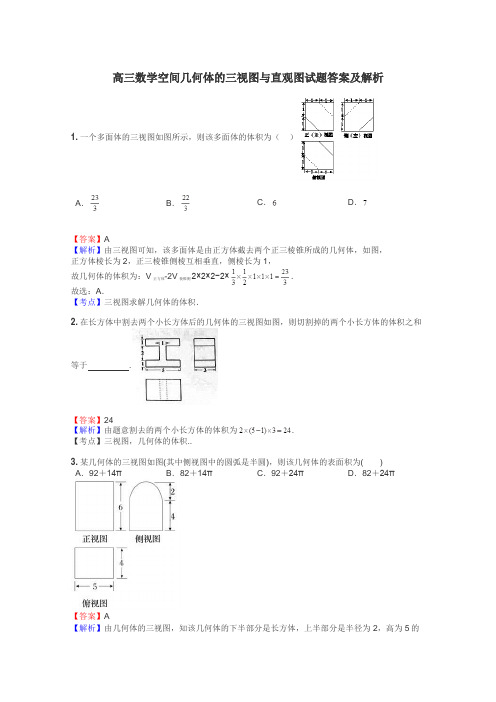
高三数学空间几何体的三视图与直观图试题答案及解析1.一个多面体的三视图如图所示，则该多面体的体积为（）A．B．C．D．【答案】A【解析】由三视图可知，该多面体是由正方体截去两个正三棱锥所成的几何体，如图，正方体棱长为2，正三棱锥侧棱互相垂直，侧棱长为1，故几何体的体积为：V正方体-2V棱锥侧2×2×2−2×．故选：A．【考点】三视图求解几何体的体积．2.在长方体中割去两个小长方体后的几何体的三视图如图，则切割掉的两个小长方体的体积之和等于.【答案】24【解析】由题意割去的两个小长方体的体积为.【考点】三视图，几何体的体积..3.某几何体的三视图如图(其中侧视图中的圆弧是半圆)，则该几何体的表面积为()A．92＋14πB．82＋14πC．92＋24πD．82＋24π【答案】A【解析】由几何体的三视图，知该几何体的下半部分是长方体，上半部分是半径为2，高为5的圆柱的一半．长方体中EH＝4，HG＝4，GK＝5，所以长方体的表面积为(去掉一个上底面)2(4×4＋4×5)＋4×5＝92．半圆柱的两个底面积为π×22＝4π，半圆柱的侧面积为π×2×5＝10π，所以整个组合体的表面积为92＋4π＋10π＝92＋14π，选A．4.在一个几何体的三视图中，正视图和俯视图如图所示，则相应的侧视图可以为()【答案】D【解析】由题目所给的几何体的正视图和俯视图，可知该几何体为半圆锥和三棱锥的组合体，如图所示，可知左视图为等腰三角形，且轮廓线为实线，故选D．5.一个正方体截去两个角后所得几何体的正视图、侧视图如图所示，则其俯视图为()【答案】C【解析】依题意可知该几何体的直观图如图所示，故其俯视图应为C．6.某几何体的三视图如图所示，则该几何体的体积为A．12B．18C．24D．30【答案】C【解析】由三视图可知该几何体是一个底面为直角三角形的直三棱柱的一部分，其直观图如上图所示，其中,侧面是矩形，其余两个侧面是直角梯形，由于,平面平面,所以平面,所以几何体的体积为：故选C.【考点】1、空间几何体的三视图；2、空间几何体的体积.7.一块石材表示的几何体的三视图如图2所示，将石材切削、打磨、加工成球，则能得到的最大球的半径等于（）A．1B．2C．3D．4【答案】B【解析】由图可得该几何体为三棱柱,因为正视图,侧视图,俯视图的内切圆半径最小的是正视图(直角三角形)所对应的内切圆,所以最大球的半径为正视图直角三角形内切圆的半径,则,故选B.【考点】三视图内切圆球三棱柱8. [2013·四川高考]一个几何体的三视图如图所示，则该几何体可以是()A．棱柱B．棱台C．圆柱D．圆台【答案】D【解析】由正视图和侧视图可知，该几何体不可能是圆柱，排除选项C；又由俯视图可知，该几何体不可能是棱柱或棱台，排除选项A、B.故选D.9.[2013·宁波质检]如图，水平放置的三棱柱的侧棱长和底边长均为2，且侧棱AA1⊥平面A1B1C1，正视图是正方形，俯视图是正三角形，该三棱柱的侧视图面积为()A．2B．C．2D．4【答案】A【解析】由题意可知，该三棱柱的侧视图应为矩形，如图所示．在该矩形中，MM1＝CC1＝2，CM＝C1M1＝·AB＝.所以侧视图的面积为S＝2.10.某几何体的三视图如图所示,则该几何体的体积的最大值为 .【答案】【解析】该几何体是类似墙角的三棱锥，假设一条直角的棱长为x，则三条直角棱长分别为.所以体积为.当且仅当时取等号.【考点】1.三视图.2.函数最值问题.3.空间想象能力.11.（2012•广东）某几何体的三视图如图所示，它的体积为（）A．12πB．45πC．57πD．81π【答案】C【解析】由三视图可知，此组合体上部是一个母线长为5，底面圆半径是3的圆锥，下部是一个高为5，底面半径是3的圆柱故它的体积是5×π×32+π×32×=57π故选C12. (2014·咸宁模拟)某几何体的三视图如图所示(其中侧视图中的圆弧是半圆),则该几何体的表面积为( )A．92+14πB．82+14πC．92+24πD．82+24π【答案】A【解析】由几何体的三视图知该几何体的下半部分是长方体,上半部分是半径为2,高为5的圆柱的一半.所以长方体的表面积为(去掉一个上底面)2(4×4+4×5)+4×5=92.半圆柱的两个底面积为π×22=4π,半圆柱的侧面积为π×2×5=10π,所以整个组合体的表面积为92+4π+10π=92+14π. 13.在一个几何体的三视图中，正视图和俯视图如图所示，则相应的侧视图可以为【答案】D【解析】条件对应的几何体是由底面棱长为r的正四棱锥沿底面对角线截出的部分与底面为半径为r的圆锥沿对称轴截出的部分构成的。
高中数学立体几何之空间几何体的三视图,含答案
空间几何体的三视图（讲义）知识点睛一、三视图主要类型分为：棱锥类、残缺类、组合类．1.棱锥类特征：俯视图多边形内部或边上有一点呈发散状，并与其他顶点相连，正、侧视图有尖顶．处理步骤：①观察俯视图，结合正、侧视图，判断顶点的位置；②确定线、面位置关系；③根据结构，找数据的对应关系；④计算．2.残缺类特征：有斜线、缺口等．处理步骤：①观察俯视图，结合正、侧视图，判断几何体的类型；②根据图形尝试切割；③根据结构，找数据的对应关系；④计算．3.组合类特征：中间有横线，曲线与直线结合等．处理步骤：①观察特征，从有曲面的图形入手，分离出几何体类型；若没有，根据分割线判断每部分几何体的类型；②确定几何体的位置关系；③根据结构，找数据的对应关系；④计算．二、球经过球面上两点和球心作截面，得到球的一个大圆，大圆上两点之间劣弧的长叫做这两点的球面距离．2．球与多面体的位置关系（1）外接球：多面体的各个顶点都在球面上；（2）内切球：多面体的各个面都与球相切．精讲精练1．某几何体的三视图如图所示，则这个几何体的体积为（）2222俯视图正视图 侧视图A．4 B．203C．263D．82．某几何体的三视图如图（单位为m），则该几何体的体积为_____________．俯视图正视图 侧视图1332223．某三棱锥的三视图如图所示，则该三棱锥的表面积是（）4俯视图正视图 侧视图A．28+65B．30+65C．56+ 125D．60+1254．如图，网格纸上小正方形的边长为1，粗实线画的是某多面体的三视图，则该多面体的各条棱中，最长的棱的长度为（）A．B．6 C．D．45．一个棱锥的三视图如图，则该棱锥的表面积为（）俯视图正视图 侧视图A．B．C．D．6．如图是一个几何体的三视图，则这个几何体的体积是（）33俯视图正视图 侧视图A．26 B．27 C．572D．287．若某多面体的三视图如图所示，则此多面体的体积是（）俯视图正视图 侧视图12--211112-2112--21A ．12B ．23C ．56D ．788．某个长方体被一个平面所截，得到的几何体的三视图如图所示，则这个几何体的体积为（ ）俯视图正视图 侧视图A ．4B ．C ．D ．89．若某几何体的三视图如图所示，则该几何体的体积为（ ）正视图 侧视图俯视图2422A ．8π3B ．3πC ．10π3D ．6π10．某几何体的三视图如图所示，则该几何体的体积为（ ）俯视图正视图 侧视图4442222A ．16+8πB ．8+8πC ．16+16πD ．8+16π11．已知某几何体的三视图如图，则该几何体的体积为（ ）俯视图正视图 侧视图211222322A ．5π42+B ．3π42+C ．π42+ D ．4π+12．如图是某简单组合体的三视图，则该组合体的体积为（ ）正视图 侧视图俯视图1212121212 A．π+ B．π2)+C．D．2)+13．若某几何体的三视图（单位：cm ）如图所示，则该几何体的体积等于___________cm 3．俯视图正视图 侧视图335414．如图，O 是半径为1的球心，点A ，B ，C 在球面上，OA ，OB ，OC 两两垂直，E ，F 分别是大圆弧AB ，AC 的中点，则点E ，F 的球面距离是（ ）432415．如图，在半径为3的球面上有A ，B ，C 三点，∠ABC =90°，BA =BC ，球心O 到平面ABC 的距离是2，则B ，C 两点的球面距离是（ ）A ．π3B ．πC ．4π3D ．2π16．设三棱柱的侧棱垂直于底面，所有棱长都为a ，顶点都在一个球面上，则该球的表面积为（ ）A ．πa 2B ．73πa 2C ．113πa 2D ．5πa 2回顾与思考________________________________________________________ ________________________________________________________ ________________________________________________________ 【参考答案】1．A2．4 m33．B4．B5．A 6．C7．D8．D9．B10．A 11．A12．B13．5014．B15．B 16．B空间几何体的三视图（随堂测试）1.已知某几何体的三视图如图所示，则该几何体的体积为（）2221 11正视图 侧视图俯视图A．233B．223C．203D．1432.已知底面边长为1的正四棱柱的各顶点均在同一个球面上，则该球的体积为（）A．2π3B．4πC．2πD．4π3【参考答案】1．A 2．D空间几何体的三视图（作业）例1：已知几何体的三视图如图所示，可得这个几何体的体积为______________．123某几何体的三视图（单位：cm ）如图所示，则此几何体的表面积是（ ）A ．90 cm 2B ．129 cm 2C ．132 cm 2D ．138 cm 2正视图 侧视图俯视图443333364343⑤ 计算1433335243482S =⨯+⨯+⨯+⨯⨯⨯=左，2(464363)108S =⨯⨯+⨯+⨯=右，2248108233138 (cm )S S S S =+-=+-⨯⨯=左右重表． 故选D ．例2： 如图，正四棱锥P -ABCD 的顶点都在同一球面上，若该棱锥的高PO 为4，底面边长为2，则该球的表面积为（ ）A ．81πB ．16πC1122俯视图正视图 侧视图17．如图是一个空间几何体的三视图，如果直角三角形的直角边长均为1，那么这个几何体的表面积为（ ）A ．13 B．2 C ．16D．2+正视图 侧视图俯视图第1题图 第2题图18．某三棱锥的侧视图、俯视图如图所示，则该三棱锥的体积为（ ）A ．3B ．2CD ．119．已知四棱锥P -ABCD 的三视图如图所示，则四棱锥P -ABCD的四个侧面中的最大面积是_________________．2222433俯视图正视图 侧视图第3题图 第4题图20．某三棱锥的三视图如图所示，则该三棱锥最长棱的棱长为___________．11112222侧视图俯视图21．一几何体的三视图如图所示，该几何体的体积为_________．第5题图 第6题图22．一个几何体的三视图如图所示，且其侧视图是一个等边三角形，则这个几何体的体积为（ ） AB．(4π+ CD23．一几何体的三视图如图所示，则该几何体的体积为（ ）A ．200+9πB ．200+18πC ．196+15πD ．140+18π俯视图正视图 侧视图21152632第7题图 第8题图24．一个几何体的三视图如图所示，则该几何体的体积为（ ）ABCD122俯视图正视图 侧视图5566俯视图正视图 侧视图6俯视图正视图 侧视图3111125．如图，网格纸上正方形小格的边长为1(表示1 cm)，图中粗线画出的是某零件的三视图，该零件由一个底面半径为3 cm ，高为6 cm 的圆柱体毛坯切削得到，则切削掉部分的体积与原来毛坯体积的比值为（ ）A ．1727B ．59C ．1027D ．13第9题图 第10题图26．某几何体三视图如图所示，则该几何体的体积为（ ）A ．82π-B ．8π-C ．π82-D ．π84-27．已知某几何体的三视图如图所示，则该几何体的体积是__________．俯视图正视图 侧视图第11题图 第12题图28．一个几何体的三视图如图所示，则该几何体的体积为_________．12211俯视图正视图 侧视图俯视图正视图 侧视图111121129．已知三棱柱ABC-A1B1C1的六个顶点都在球O的球面上，若AB=3，AC=4，AB⊥AC，AA1=12，则球O的半径为（）A．2B．C．132D．30．已知三棱锥S-ABC的所有顶点都在球O的球面上，△ABC是边长为1的正三角形，SC为球O的直径，且SC=2，则此棱锥的体积为（）A．6B．6C．3D．1231．如图，已知三点A，B，C在球心为O，半径为3的球面上，且几何体OABC 为正四面体，那么A，B两点的球面距离为_________，点O到平面ABC的距离为____________．【参考答案】1．B2．D3．64．5．2454π6．D7．A8．A9．C10．B11．8π12．22 313．C14．A15．π。
高三数学空间几何体的三视图与直观图试题答案及解析
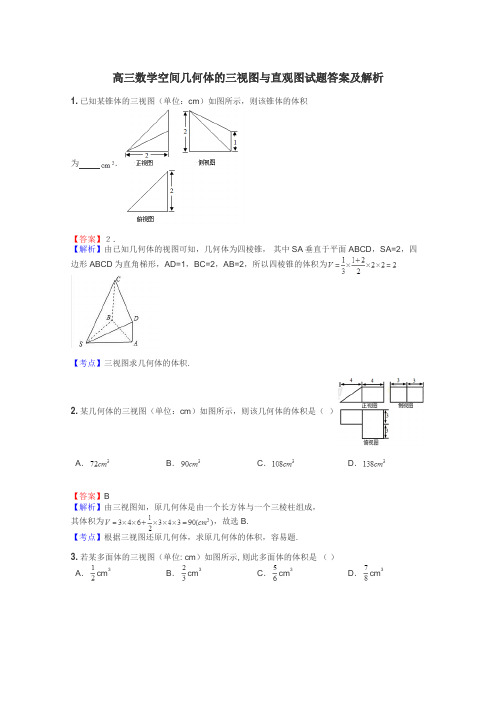
高三数学空间几何体的三视图与直观图试题答案及解析1.已知某锥体的三视图（单位：cm）如图所示，则该锥体的体积为．【答案】２．【解析】由已知几何体的视图可知，几何体为四棱锥，其中SA垂直于平面ABCD，SA=2，四边形ABCD为直角梯形，AD=1，BC=2，AB=2，所以四棱锥的体积为【考点】三视图求几何体的体积.2.某几何体的三视图（单位：cm）如图所示，则该几何体的体积是（）A．B．C．D．【答案】B【解析】由三视图知，原几何体是由一个长方体与一个三棱柱组成，其体积为，故选B.【考点】根据三视图还原几何体，求原几何体的体积，容易题.3.若某多面体的三视图（单位: cm）如图所示, 则此多面体的体积是（）A．cm3B．cm3C．cm3D．cm3【答案】C【解析】由三视图可得，该几何体相当于一个正方体切去一个三个侧棱长为1的三棱锥.所以该几何体的体积为.故选C.【考点】1.三视图.2.空间想象力.3.几何体的体积.4. (2014·孝感模拟)一个几何体的三视图如图所示,其中俯视图与侧视图均为半径是2的圆,则这个几何体的表面积是( )A．16πB．14πC．12πD．8π【答案】A【解析】由三视图可知,该几何体是球挖去半球.其中两个半圆的面积为π×22=4π.个球的表面积为×4π×22=12π,所以这个几何体的表面积是12π+4π=16π.5.如图，某几何体的三视图都是等腰直角三角形，则几何体的体积是（）A．8B．7C．9D．6【答案】C【解析】由三视图可知,几何体是底面为等腰直角三角形,有一侧棱与底面垂直(垂足在非直角处)的三棱锥,其底面面积为×6×3=9,三棱锥的高为3,所以三棱锥的体积=×9×3=9．6.已知某几何体的三视图(如图),正视图和侧视图均为两个相等的等边三角形,府视图为正方形,则几何体的体积为（）A．B．4C．9D．9【答案】C【解析】由三视图可知,几何体由两个同底之正四棱锥组成所以其体积为V=2××32×3×=9 7.一空间几何体的三视图如图所示，该几何体的体积为12π＋，则正视图中x的值为( )A．5B．4C．3D．2【答案】C【解析】三视图，由正四棱锥和圆柱组成，故选C．8.如图，一个四棱锥的底面为正方形，其三视图如图所示，则这个四棱锥的体积为（）A．1B．2C．3D．4【答案】B【解析】由题意，棱锥的高为，底面面积为，∴.【考点】三视图，体积．9.某几何体的三视图如题（6）所示，其侧视图是一个边长为1的等边三角形，俯视图是两个正三角形拼成的菱形，则这个几何体的体积为（）A．1B．C．D．【答案】C【解析】这是由两个三棱锥拼成的几何体，其体积为.选C.【考点】三视图及几何体的体积.10.―个几何体的三视图如图所示(单位：)，则该几何体的体积为．【答案】18+9【解析】由三视图可知，此几何体为两个相切的球上方放了一个长方体组成的组合体，所以其体积为：V=3×6×1+2××=18+911.一个空间几何体的三视图如图所示，该几何体的表面积为__________.【答案】152【解析】几何体为一个三棱柱，底面为一个等腰三角形，底边长为6，底边上高为4，腰长为５.棱柱的高为8.因此表面积为【考点】三视图12.某三棱锥的三视图如图所示，则这个三棱锥的体积为；表面积为．【答案】；．【解析】由三视图知几何体如下图，为一个三棱锥，且三棱锥的一个侧面与底面垂直，底面三角形的一条边长为，该边上的高为，∴几何体的体积．它的表面积为．【考点】由三视图求面积、体积．13.已知某个几何体的三视图如下，根据图中标出的尺寸（单位：cm），可得这个几何体的体积是_______.【答案】【解析】由题意可得该几何体是一个三棱锥，体积.【考点】1.三视图的知识.2.立几中的线面关系.3.三棱锥的体积公式.14.一个空间几何体的三视图如图所示，其正视图、侧视图、俯视图均为等腰直角三角形，且直角边长都为1，则这个几何体的体积是【答案】【解析】由三视图，可知该几何体是三棱锥，并且侧棱，，，则该三棱锥的高是，底面三角形是直角三角形，所以这个几何体的体积＝＝．【考点】由三视图求几何体的体积．15.一个几何体的三视图如图所示,则该机合体的体积为( )A．B．C．D．【答案】B【解析】分析可得该几何体是底面为菱形的四棱锥,则高底面面积,所以.故选B【考点】三视图四棱锥体积16.一个几何体的三视图如图所示，则该几何体的体积是【答案】【解析】通过三视图的观察可得，该几何体是一个四棱柱，底面是一个直角梯形，其上下底分别为2,3，梯形的高为2.四棱柱的高为2.所以几何体的体积为.【考点】1.三视图的知识.2.几何体的体积.3.空间想象力.17.某长方体被一个平面所截，得到的几何体的三视图如图所示，则这个几何体的体积为()A．4B．4C．6D．8【答案】D【解析】割补可得其体积为2×2×2＝8.18.某几何体的三视图如图所示，则该几何体的体积是________．【答案】16π－16【解析】由三视图知，该几何体是由一个底面半径为2，高为4的圆柱内挖去一个底面边长为2，高为4的正四棱柱后剩下的部分，∴V＝(π×22－22)×4＝16π－16.19.已知正方体ABCD-A1B1C1D1，M为棱A1B1的中点，N为棱A1D1的中点．如图是该正方体被M，N，A所确定的平面和N，D，C1所确定的平面截去两个角后所得的几何体，则这个几何体的正视图为()．【答案】B【解析】对于选项A，由于只是截去了两个角，此切割不可能使得正视图成为梯形．故A不对；对于B，正视图是正方形符合题意，线段AM的影子是一个实线段，相对面上的线段DC1的投影是正方形的对角线，由于从正面看不到，故应作成虚线，故选项B正确；对于C，正视图是正方形，符合题意，有两条实线存在于正面不符合实物图的结构，故不对；对于D，正视图是正方形，符合题意，其中的两条实线符合俯视图的特征，故D不对．20.若一个底面为正三角形、侧棱与底面垂直的棱柱的三视图如图所示，则该棱柱的体积为（）A．B．C．D．6【答案】B【解析】由三视图知该直三棱柱高为4，底面正三角形的高为3，所以正三角形边长为6，所以V＝×36×4＝36.故选B.【考点】1.三视图；2.柱体体积计算.21.某由圆柱切割获得的几何体的三视图如图所示,其中俯视图是中心角为的扇形,则该几何体的体积为（）A．B．C．D．【答案】D【解析】由题意知道，该几何体体积是圆柱体积的，即.【考点】1、三视图；2、几何体体积.22.右图是一个几何体的三视图，其中正视图和侧视图都是一个两底长分别为2和4，腰长为4的等腰梯形，则该几何体的侧面积是( )A．B．C．D．【答案】B【解析】由三视图可得该几何体是一个圆台，其两底直径分别为2和4，母线长为4，所以该几何体的侧面积是，选B..【考点】三视图，圆台的侧面积.23.如图是一个组合几何体的三视图，则该几何体的体积是 .A．B．C．D．【答案】A【解析】由三视图还原可知该几何体是一个组合体，下面是一个半径为4，高为8的圆柱，，上面是一个三棱柱，故所求体积为.【考点】三视图，圆柱、三棱柱的体积公式.24.已知一个几何体的三视图如图所示，则该几何体的体积为___________【答案】【解析】该几何体为圆柱中挖去半个球而得的组合体，其体积为.【考点】三视图.25.一个几何体的三视图如图所示（单位长度：），俯视图中圆与四边形相切，且该几何体的体积为，则该几何体的高为 .【答案】【解析】由如图所示的几何体的三视图知：这个几何体是一个半径为的球和一个直四棱柱的结合体，且这个直四棱柱的底面是对角线分别为和的棱形，这个直四棱柱的高为，∴这个几何体的体积：V=，解得h=.【考点】1.三视图；2.几何体的面积和体积26.一个几何体的三视图如图所示，则该几何体的直观图可以是（）【答案】D【解析】通过三视图的俯视图可知，该几何体是由两个旋转体组成，故选D.【考点】1.三视图的应用.27.如图为一个几何体的三视图正视图和侧视图均为矩形，俯视图中曲线部分为半圆，尺寸如图所示，则该几何体的表面积为（）A．B．C．D．【答案】D【解析】由三视图可知，这是一个由半个圆柱和一个三棱柱构成的组合体，这个组合体仍为一个柱体。
高中数学高考复习《空间几何体的三视图》经典例题解析附习题答案
3 32正视图侧视图俯视图图1空间几何体的三视图1..一个空间几何体得三视图如图所示，则该几何体的表面积为（A ）48 (B)32+8(C) 48+8(D) 80【答案】 C【命题意图】本题考查三视图的识别以及空间多面体表面积的求法.【解析】由三视图可知几何体是底面是等腰梯形的直棱柱.底面等腰梯形的上底为2，下底为4，高为4，。
故S 表【解题指导】：三视图还原很关键，每一个数据都要标注准确。
2.设图1是某几何体的三视图，则该几何体的体积为A.1229 B.1829 C. 429 D. 1836答案：B解析：由三视图可以还原为一个底面为边长是3的正方形，高为2的长方体以及一个直径为3的球组成的简单几何体，其体积等于233)23(3431829。
故选 B评析：本小题主要考查球与长方体组成的简单几何体的三视图以及几何体的体积计算.3.如图l —3．某几何体的正视图(主视图)是平行四边形，侧视图(左视图)和俯视图都是矩形，则该几何体的体积为（）b5E2RGbCAPA.63 B.93 C.123 D.183【解析】 B.由题得三视图对应的直观图是如图所示的直四棱柱，.ABCD EA 平面3931232hS VABCD平行四边形。
所以选 B4.某几何体的三视图如图所示，则它的体积是（A ）283（B ）83（C ）82（D ）23【答案】A【解析】：由三视图可知该几何体为立方体与圆锥，立方体棱长为2，圆锥底面半径为1、高为2，所以体积为3212123283故选A5．某四面体的三视图如图所示，该四面体四个面的面积中，最大的是HGFEDCBA 3123A ．8B ．62C ．10 D ．82【答案】 C6.一个正三棱柱的侧棱长和底面边长相等，体积为32，它的三视图中的俯视图如右图所示，左视图是一个矩形，则这个矩形的面积是____________.p1EanqFDPw答案：2323234aa ，解得解析：设正三棱柱的侧棱长和底面边长为a ，则由a=2，正三棱柱的左视图与底面一边垂直的截面大小相同，故该矩形的面积是322232.DXDiTa9E3d7.一个几何体的三视图如图所示（单位：m ），则这个几何体的体积为__________ 3m 【答案】6【解析】由题意知,该几何体为一个组合体,其下面是一个长方体(长为3m,宽为2m,高为1m),上面有一个圆锥(底面半径为1,高为3),所以其体积为1321363V V 长方体圆锥.8. 下图是长和宽分别相等的两个矩形．给定下列三个命题：①存在三棱柱，其正(主)视图、俯视图如下图；②存在四棱柱，其正(主)视图、俯视图如下图；③存在圆柱，其正(主)视图、俯视图如下图．其中真命题的个数是(A)3 (B)2 (C)1 (D)0 【答案】 A【解析】对于①,可以是放倒的三棱柱；容易判断②③可以.9.若某几何体的三视图如图所示，则这个几何体的直观图可以是第一节10.若一个底面是正三角形的三棱柱的正视图如图所示，则其侧面积．．．等于（）A.3 B.2 C.23 D.6【命题立意】本题考查三棱柱的三视图与直观图、表面积。
【备战高考文科数学】题型全突破：热点题型一 空间几何题的三视图与体积和表面积(解析版)
热点题型一空间几何题的三视图与体积和表面积（解析版）空间几何体的三视图及体积与表面积问题是高考的必考点，常在选择题中出现。
题目难度中等，只要考生对三视图的概念清楚，并加以练习即可掌握。
常见问题归纳如下；类型一三视图的辨识类型二三视图与几何体的体积和表面积【基础知识整合】1．空间几何体的结构特征（1）几何体的三视图包括正(主)视图、侧(左)视图、俯视图，分别是从几何体的正前方、正左方、正上方观察几何体画出的轮廓线．(2) 三视图的画法①基本要求：长对正，高平齐，宽相等．②画法规则：正(主)侧(左)一样高，正(主)俯一样长，侧(左)俯一样宽；看不到的线画虚线．3.柱、锥、台和球的表面积和体积类型一三视图的辨识【典例1】【2013年高考新课标2文（9）】一个四面体的顶点在空间直角坐标系O xyz 中的坐标分别是(1,0,1)，(1,1,0)，(0,1,1)，(0,0,0)，画该四面体三视图中的正视图时，以zOx平面为投影面，则得到正视图可以为（）A B C D【答案】A【典例2】【2016高考天津文数（3）】将一个长方形沿相邻三个面的对角线截去一个棱锥，得到的几何体的正视图与俯视图如图所示，则该几何体的侧（左）视图为（）【答案】B【变式训练】1.【2014湖北高考】在如图所示的空间直角坐标系错误！未找到引用源。
中，一个四面体的顶点坐标分别是（0,0,2），（2,2,0），（1,2，1），（2,2,2），给出编号①、②、③、④的四个图，则该四面体的正视图和俯视图分别为（）A.①和②B.③和①C. ④和③D.④和②【答案】D【解析】设错误！未找到引用源。
，在坐标系中标出已知的四个点，根据三视图的画图规则判断三棱锥的正视图为④与俯视图为②，故选D.考点：空间由已知条件，在空间坐标系中作出几何体的形状，正视图与俯视图的面积，容易题.【思路点拨】将空间几何体的三视图与空间直角坐标系融合在一起，凸显了数学学科内知识间的内在联系，充分体现了数学学科特点和知识间的内在联系，能较好的考查学生的综合知识运用能力.其解题突破口是正确地在空间直角坐标系中画出该几何体的原始图像.2. 【2014全国1文8】如图，网格纸的各小格都是正方形，粗实线画出的事一个几何体的三个几何体是（ ）A.三棱锥B.三棱柱C.四棱锥D.四棱柱【答案】B类型二 三视图与几何体的体积和表面积【典例1】【2016年高考新课标1文（7）】（7）如图,某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径.若该几何体的体积是28π3,则它的表面积是（ ）（A ）17π （B ）18π （C ）20π （D ）28π【典例2】【2016年高考新课标3文（7）】如图是由圆柱与圆锥组合而成的几何体的三视图，则该几何体的表面积为（）（A）20π（B）24π（C）28π（D）32π【答案】C考点：三视图，空间几何体的体积.【思路点拨】以三视图为载体考查几何体的体积，解题的关键是根据三视图想象原几何体的形状构成，并从三视图中发现几何体中各元素间的位置关系及数量关系，然后在直观图中求解．【变式训练】1. 【2016高考山东文数】一个由半球和四棱锥组成的几何体，其三视图如图所示.则该几何体的体积为（）（A）错误！未找到引用源。
高三数学空间几何体的三视图与直观图试题答案及解析
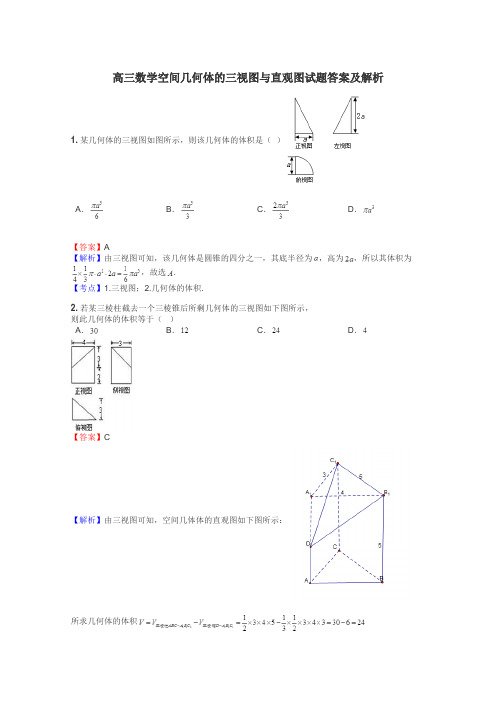
高三数学空间几何体的三视图与直观图试题答案及解析1.某几何体的三视图如图所示，则该几何体的体积是（）A．B．C．D．【答案】A【解析】由三视图可知，该几何体是圆锥的四分之一，其底半径为，高为，所以其体积为，故选.【考点】1.三视图；2.几何体的体积.2.若某三棱柱截去一个三棱锥后所剩几何体的三视图如下图所示，则此几何体的体积等于（）A．B．C．D．【答案】C【解析】由三视图可知，空间几体体的直观图如下图所示：所求几何体的体积故选C.【考点】1、三视图；2、空间几何体的体积.3.如图，一个几何体的三视图（正视图、侧视图和俯视图）为两个等腰直角三角形和一个边长为1的正方形，则其外接球的表面积为A．πB．2πC．3πD．4π【答案】C【解析】原几何体为有一条侧棱垂直于底面的四棱锥，且底面是边长为1的正方形，垂直于底面的侧棱长也为1，因此，该几何体可以补形为一个棱长为1的正方体，其外接球就是这个正方体的外接球，直径为正方体的对角线长，即2R＝，故R＝故外接球表面积为：4πR2＝3π.【考点】三视图，几何体的外接球及其表面积4.如图所示，一个三棱锥的三视图是三个直角三角形(单位： cm)，则该三棱锥的外接球的表面积为________cm2．【答案】29π【解析】从三棱锥的三视图可知，三棱锥有两侧面与底面垂直，把三棱锥补成长，宽，高分别为4,2,3的长方体，设外接球的半径为R，由42＋22＋32＝4R2得，S＝4πR2＝29π(cm2)．球5.某个长方体被一个平面所截，得到的几何体的三视图如图所示，则这个几何体的体积为()A．4B．2C．D．8【答案】D【解析】由三视图可知，该几何体如图所示，其底面为正方形，正方形的边长为2．HD＝3，BF ＝1，将相同的两个几何体放在一起，构成一个高为4的长方体，所以该几何体的体积为×2×2×4＝8．6.在一个几何体的三视图中，正视图和俯视图如图所示，则相应的侧视图可以为()【答案】D【解析】由题目所给的几何体的正视图和俯视图，可知该几何体为半圆锥和三棱锥的组合体，如图所示，可知左视图为等腰三角形，且轮廓线为实线，故选D．7.一个几何体的三视图如图所示，已知这个几何体的体积为，= .【答案】【解析】由三视图知，原几何体是一个四棱锥，底面是面积为的矩形，高为，所以，解得.【考点】三视图，空间几何体的体积.8.如图，水平放置的正三棱柱的主视图是一边长为2的正方形，则该三棱柱的左视图的面积为．【答案】【解析】左视图为一个矩形，长宽分别为，因此面积为.【考点】三视图9.若一个正三棱柱的正视图如图所示，其顶点都在一个球面上，则该球的表面积为() A．B．C．D．【答案】B【解析】依题意得，该正三棱柱的底面正三角形的边长为2，侧棱长为1．设该正三棱柱的外接球半径为R，易知该正三棱柱的底面正三角形的外接圆半径是2sin 60°×＝，所以R2＝＋＝，则该球的表面积为4πR2＝．10.图中的网格是边长为1的小正方形，在其上用粗线画出了某多面体的三视图，则该多面体的体积为________．【答案】16【解析】从三视图可知，这是一个四棱锥，.【考点】三视图.11.如图所示，一个空间几何体的正视图和左视图都是边长为的正方形，俯视图是一个直径为的圆，那么这个几何体的体积为 ( )A．B．C．D．【答案】B【解析】几何体是圆柱，.【考点】三视图，圆柱的体积.12.一个几何体的三视图如图所示，其中正视图是一个正三角形，则该几何体的体积为( )A．1B．C．D．【答案】B【解析】由三视图可知，此几何体为三棱锥，如图，其中正视图为，是边长为2的正三角形，，且，底面为等腰直角三角形，，所以体积为，故选B.13.已知棱长为1的正方体的俯视图是一个面积为1的正方形，则该正方体的正视图的面积不可能等于（）A．1B．C．D．【答案】C【解析】由题意知，正视图的最大面积为对角面的面积，最小面积为，而，故选C．【考点】三视图.14.已知某几何体的三视图如右图所示，其中俯视图是圆，且该几何体的体积为；直径为2的球的体积为．则()A．B．C．D．【答案】C【解析】由题意，该几何体是一个圆柱挖去一个圆锥得到的几何体，，，∴.选B.【考点】三视图，体积.15.三棱锥S-ABC及其三视图中的正视图和侧视图如图所示，则棱SB的长为（）A．B．C．D．【答案】B【解析】过B作BD⊥AC于点D，则BD=2，CD=2，所以BC=,因为SC⊥平面ABC，所以SC⊥BC，所以SB=,故选B.【考点】三视图、直线与平面垂直的性质.16.一个几何体的三视图如图，则该几何体的体积为（）A．B．C．D．【答案】A【解析】由三视图可知，该几何体是由一个半圆柱和一个三棱锥拼接而成，且半圆柱的底面是半径为的半圆，高为，其底面积为，故其体积为，三棱锥的底面是一个直角三角形，三棱锥的高也为，其底面积为，故其体积为，所以该几何体的体积为，故选A.【考点】1.三视图；2.组合体的体积17.右图为某几何体的三视图，则该几何体的体积为 .【答案】【解析】所求几何体为一个底面半径为1，高为1的圆柱与半径为1的四分之一的球的组合体，所以体积为【考点】三视图18.一个空间几何体的三视图如图所示，该几何体的体积为______.【答案】96【解析】几何体为一个三棱柱，底面为一个等腰三角形，底边长为6，底边上高为4，棱柱的高为8.因此所求体积为【考点】三视图19.把边长为1的正方形ABCD沿对角线BD折起，形成三棱锥C－ABD，它的主视图与俯视图如右上图所示，则二面角 C－AB－D的正切值为．【答案】【解析】如图所示,做BD,AB的中点分别为点E,F.则有CE面ABD,由于EF为等腰直角三角形ABD的中位线,故EF AB,则为二面角 C－AB－D的代表角,所以,故填.【考点】二面角三视图20.已知水平放置的△ABC的直观图△A′B′C′(斜二测画法)是边长为a的正三角形，则原△ABC 的面积为()A．a2B．a2C．a2D．a2【答案】D【解析】斜二测画法中原图面积与直观图面积之比为1∶，则易知S＝ ( a)2，∴S＝a2.21.一个空间几何体的三视图如图所示,则该几何体的体积为()A．πcm3B．3πcm3C．πcm3D．πcm3【答案】D【解析】由三视图可知,此几何体为底面半径为1cm、高为3cm的圆柱上部去掉一个半径为1cm的半球,所以其体积为V=3π-π=π(cm 3).22. 右图为一简单组合体，其底面ABCD 为正方形，PD ⊥平面ABCD ，EC ∥PD ，且PD ＝AD ＝2EC ＝2.(1)请画出该几何体的三视图； (2)求四棱锥B-CEPD 的体积．【答案】(1)见解析 (2)2【解析】解：(1)该组合体的三视图如图所示．(2)∵PD ⊥平面ABCD ， PD ⊂平面PDCE ，∴平面PDCE ⊥平面ABCD. ∵四边形ABCD 为正方形，∴BC ⊥CD ，且BC ＝DC ＝AD ＝2. 又∵平面PDCE∩平面ABCD ＝CD ， BC ⊂平面ABCD. ∴BC ⊥平面PDCE.∵PD ⊥平面ABCD ，DC ⊂平面ABCD ， ∴PD ⊥DC.又∵EC ∥PD ，PD ＝2，EC ＝1，∴四边形PDCE 为一个直角梯形，其面积： S 梯形PDCE ＝ (PD ＋EC)·DC ＝×3×2＝3， ∴四棱锥B-CEPD 的体积V B-CEPD ＝S 梯形PDCE ·BC ＝×3×2＝2.23. 某几何体的三视图如图所示，则该几何体的体积为( )．A ．16＋8πB ．8＋8πC ．16＋16πD ．8＋16π【答案】A【解析】将三视图还原成直观图为：上面是一个正四棱柱，下面是半个圆柱体．所以V＝2×2×4＋×22×π×4＝16＋8π.24.某几何体的三视图如图所示，则其体积为________．【答案】【解析】由三视图还原几何体为半个圆锥，高为2，底面半圆的半径r＝1.∴体积V＝×(π×12×2)＝.25.如图所示为一个几何体的直观图、三视图(其中正视图为直角梯形，俯视图为正方形，侧视图为直角三角形)．(1)求四棱锥P-ABCD的体积；(2)若G为BC上的动点，求证：AE⊥PG.【答案】（1）（2）见解析【解析】(1)由几何体的三视图可知，底面ABCD是边长为4的正方形，PA⊥平面ABCD，PA∥EB，且PA＝4 ，BE＝2 ，AB＝4.∴VP-ABCD ＝PA·S四边形ABCD＝×4 ×4×4＝.(2)∵＝，∠EBA＝∠BAP＝90°，∴△EBA∽△BAP，∴∠BEA＝∠PBA.∴∠BEA＋∠BAE＝∠PBA＋∠BAE＝90°，∴PB⊥AE又∵BC⊥平面APEB，∴BC⊥AE.∵BC∩PB＝B，∴AE⊥平面PBC.∵PG⊂平面PBC，∴AE⊥PG.26.如图所示，网格上小正方形的边长为1，粗线画出的是某几何体的三视图，则此几何体的体积为________．【答案】9【解析】由题意知，此几何体是三棱锥，其高h＝3，相应底面面积为S＝×6×3＝9，∴V＝Sh＝×9×3＝9.27.某几何体的三视图如图所示，主视图和侧视图为全等的直角梯形，俯视图为直角三角形.则该几何体的表面积为( )A. B. C. D【答案】B【解析】此几何体直观图如图所示。
立体几何三视图问题分类
立体几何三视图问题分类一、由空间图形画三视图1、一几何体的直观图如图，下列给出的四个俯视图中正确( )解析由直观图可知，该几何体由一个长方体和一个截角三棱柱组成．从上往下看，外层轮廓线是一个矩形，矩形内部有一条线段连接的两个三角形．答案 B2、在一个几何体的三视图中，正视图和俯视图如图所示，则相应的侧视图可以为( )【解析】由正视图和俯视图知几何体的直观图是由一个半圆锥和一个三棱锥组合而成的，故侧视图选D.3、如图，△ ABC为三角形，AA'//BB'//CC',CC'CC'⊥平面ABC 且3AA'=32BB'=CC' =AB,则多面体△ABC -A B C'''CC'的正视图（也称主视图）是（）【答案】D4.一个长方体去掉一个小长方体，所得几何体的正（主）视图与侧（左）视图分别如右图所示，则该集合体的俯视图为：答案：C二、正方体5.如图所示，E，F分别为正方体ABCD－A1B1C1D1的面ADD1A1、面BCC1B1的中心，则四边形BFD1E在该正方体的面上的正投影可能是________(填序号)．解析由正投影的定义，四边形BFD1E在面AA1D1D与面BB1C1C上的正投影是图③；其在面ABB1A1与面DCC1D1上的正投影是图②；其在面ABCD与面A1B1C1D1上的正投影也是②，故①④错误．答案②③6.已知某几何体的三视图(单位:cm)如图所示,则该几何体的体积是( )A.108cm3B.100cm3C.92cm3D.84cm3【解题指南】根据几何体的三视图,还原成几何体,再求体积.【解析】选B.由三视图可知原几何体如图所示,所以111111ABCD A B C D M A D N V V V --=-1166334410032=⨯⨯-⨯⨯⨯⨯=. 第8题图7.已知正方体的棱长为1，其俯视图是一个面积为1的正方形，侧视图是一个面积为2的矩形，则该正方体的正视图的面积等于（ ） A ．32B.1C.212+D.2【解题指南】根据面积关系得出，侧视图就是正方体的一个对角面，则正视图也是一个对角面 【解析】选D ，根据条件得知正视图和侧视图一样，是正方体的一个对角面，故面积相等8、如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的各条棱中，最长的棱的长度为( ) A ．6 2 B ．4 2 C ．6D ．4解析 如图，设辅助正方体的棱长为4，三视图对应的多面体为三棱锥A －BCD ，最长的棱为AD ＝（42）2＋22＝6，选C.9、一个四面体的顶点在空间直角坐标系O-xyz 中的坐标分别是(1,0,1),(1,1,0),(0,1,1),(0,0,0),画该四面体三视图中的正视图时,以zOx 平面为投影面,则得到正视图可以为 ( )【解析】选A.由题意可知,该四面体为正四面体,其中一个顶点在坐标原点,另外三个顶点分别在三个坐标平面内,所以以zOx 平面为投影面,则得到的正视图可以为选项A 中的图.10、一个多面体的三视图如图所示，则该多面体的表面积为( ) A ．21＋ 3 B ．18＋ 3 C ．21 D ．18解析 (1)由三视图可知该几何体是棱长为2的正方体从后面右上角和前面左下角分别截去一个小三棱锥后剩余的部分(如图所示)，其表面积为S ＝6×4－12×6＋2×34×(2)2＝21＋ 3.11、一个空间几何体的三视图如图所示，则该几何体的表面积为( )A ．48B ．32＋817C ．48＋817D ．80解析：由三视图可知本题所给的是一个底面为等腰梯形的放倒的直四棱柱，所以该直四棱柱的表面积为S ＝2×12×(2＋4)×4＋4×4＋2×4＋2×1＋16×4＝48＋817. 答案：C12、某几何体三视图如图所示，则该几何体的体积为( ) A ．8－2π B ．8－π C ．8－π2 D ．8－π4解析：直观图为棱长为2的正方体割去两个底面半径为1的14圆柱，所以该几何体的体积为23－2×π×12×2×14＝8－π. 三、三棱柱13、若一个底面是正三角形的三棱柱的正视图如图所示,则其侧面积．．．等于 ( ) A ．3 B ．2C ．23D ．6【答案】D【解析】由正视图知：三棱柱是以底面边长为2，高为1的正三棱柱，所以底面积为324234⨯⨯=，侧面积为3216⨯⨯=，选D ．14、 一个正三棱柱的侧棱长和底面边长相等，体积为23，它的三视图中的俯视图如图所示，左视图是一个矩形，则这个矩形的面积是________．【解析】由俯视图知该正三棱柱的直观图为图1－6，其中M ，N 是中点，矩形MNC 1C 为左视图．由于体积为23，所以设棱长为a ，则12×a 2×sin60°×a ＝23，解得a ＝2.所以CM ＝3，故矩形MNC 1C 面积为2 3.15、若某空间几何体的三视图如图所示，则该几何体的体积是[B]（A ）2 （B ）1（C ）23（D ）13【答案】 B解析：本题考查立体图形三视图及体积公式 如图，该立体图形为直三棱柱所以其体积为122121=⨯⨯⨯四、四棱柱16、一个几何体的三视图如图所示，则这个几何体的体积为 。
高考有方法——三视图解题超级策略
高考有方法——三视图解题超级策略一、三视图问题的常见类型及解题策略(1)由几何体的直观图求三视图．留意正视图、侧视图和俯视图的视察方向，留意看到的部分用实线表示，不能看到的部分用虚线表示．(2)由几何体的部分视图画出剩余的部分视图．先依据已知的一部分三视图，还原、推想直观图的可能形式，然后再找其剩下部分三视图的可能形式．当然作为选择题，也可将选项逐项代入，再看看给出的部分三视图是否符合．(3)由几何体的三视图还原几何体的形态．要熟识柱、锥、台、球的三视图，明确三视图的形成原理，结合空间想象将三视图还原为实物图．二、还原三视图的常用方法1、方体升点法；2、方体去点法（方体切割法）；3、三线交汇得顶点法方法一方体升点法例1：(2015·北京)某四棱锥的三视图如图所示，该四棱锥最长棱的棱长为()A．1 B. 2 C. 3 D．2答案 C解析依据三视图，可知该几何体的直观图为如图所示的四棱锥V－ABCD，其中VB⊥平面ABCD，且底面ABCD 是边长为1的正方形，VB＝1.所以四棱锥中最长棱为VD.连接BD，易知BD＝2，在Rt△VBD中，VD＝VB2＋BD2＝ 3.跟踪训练1.如图所示为三棱锥的三视图，求三棱锥的表面积或体积.跟踪训练2.如图所示为三棱锥的三视图，求三棱锥的表面积或体积.跟踪训练3.如图所示为三棱锥的三视图，求三棱锥的表面积或体积.方法二方体去点法例2：如图所示为三棱锥的三视图，主视图、俯视图是直角边长为2 的等腰直角三角形，求三棱锥的表面积或体积.跟踪训练4.如图所示为三棱锥的三视图，主视图、侧视图是直角边长为4，宽为3 的直角三角形，求三棱锥的表面积或体积.跟踪训练5.如图所示为三棱锥的三视图，三视图是直角边长为4 等腰直角三角形，虚线为中线，求三棱锥的表面积或体积.方法三三线交汇得顶点法例3：如图，网格纸上小正方形的边长为4，粗实线画出的是某多面体的三视图，则该多面体的各条棱中，最长的棱的长度是（）A．62B．6 C．42D．4正确答案是B．解：由三视图可知，原几何体的长、宽、高均为4，所以我们可用一个正方体作为载体对三视图进行还原．先画出一个正方体，如图（1）：第一步，依据正视图，在正方体中画出正视图上的四个顶点的原象所在的线段，这里我们用红线表示．如图（2），即正视图的四个顶点必定是由图中红线上的点投影而成的．其次步，侧视图有三个顶点，画出它们的原象所在的线段，用蓝线表示，如图（3）．第三步，俯视图有三个顶点，画出它们的原象所在的线段，用绿线表示，如图（4）．最终一步，三种颜色线的公共点（只有两种颜色线的交点不行）即为原几何体的顶点，连接各顶点即为原几何体，如图（5）．至此，易知哪条棱是最长棱，求出即可跟踪训练6.首先在正方体框架中描出主视图，并将轮廓的边界点平行延长，如图．类似地，将俯视图和侧视图也如法炮制．这样就可以找到三个方向的交叉点．由这些交叉点，不难得到直观图．练习1、练习2、练习1答案：练习2答案：跟踪训练7.如图所示为四棱锥的三视图，主视图是直角边长为4 等腰直角三角形，侧视图是边长为4 的正方形，求四棱锥的表面积或体积.跟踪训练8. 如图所示为四棱锥的三视图，主视图是边长为4 的正方形，侧视图是直角边长为4 等腰直角三角形，求四棱锥的表面积或体积.跟踪训练9.如图所示为四棱锥的三视图，主视图是长为4，高为5 的长方形，侧视图的长为3 的长方形，俯视图为直角三角形，求四棱锥的表面积或体积.三视图练习1、若某几何体的三视图如图所示，则此几何体的表面积是_____________.4042+2、某几何体的三视图如图所示，则该几何体的体积为_____________.3、如图，网格纸上小正方形的边长为1，粗实线及粗虚线画出的是某多面体的三视图，则该多面体外接球的表面积为（ ）DA 、8πB 、252π C 、12π D 、414π4、如图是一个四面体的三视图，这三个视图均是腰长为2的等腰直角三角形，正视图和俯视图中的虚线是三角形的中线，则四面体的体积为（ ）A A 、23 B 、43 C 、83D 、24244131211侧视图俯视图正视图侧视图正视图CDBP A5325、一个正方体被一个平面截去一部分后，剩余部分的三视图如右图，则截去部分体积与剩余部分体积的比值为（ ）D （A ）81 （B ）71 （C ）61 （D ）516、如图，网格纸上正方形小格的边长为1（表示1cm ）,图中粗线画出的是某零件的三视图，该零件由一个底面半径为3cm ，高为6cm 的圆柱体毛坯切削得到，则切削掉部分的体积与原来毛坯体积的比值为（ ） C A. 1727 B. 59C. 1027D. 137、一个四面体的顶点在空间直角坐标系O xyz -中的坐标分别是(1,0,1),(1,1,0),(0,1,1),(0,0,0)，画该四面体三视图中的正视图时，以zOx 平面为投影面，则得到正视图可以为（ ）A(A) (B) (C)8、如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则此几何体的体积为（B ） ()A 6 ()B 9 ()C 12 ()D 18O yxz (0,1,1)(0,0,0)(1,0,1)(1,1,0)DD 1C 1B 119、在一个几何体的三视图中，正视图和俯视图如左图所示，则相应的侧视图可以为（ ）D10、某几何体的三视图如图所示，则该几何体的体积为_____________.11、已知某几何体的三视图如图所示，则其体积为_____________.20或1612、若某几何体的三视图如图所示，则这个几何体中最长的棱长等于_____________.13、某几何体的三视图如图所示，则该几何体的体积为_____________.14、某几何体的三视图如图所示，则该几何体的体积为_____________.11142122222224442PBAC338332315、圆柱被一个平面截去一部分后与半球（半径为r ）组成一个几何体，该几何体的三视图中的正视图和俯视图如图所示，若该几何体的表面积为1620π+，则r =( B ) （A ）1 （B ）2 （C ）4 （D ）816、如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的各条棱中，最长的棱的长度为( C )A .62B .42C .6D .417.某几何体的三视图如图所示，则该几何体的体积为( A ) A ．168π+ B ．88π+ C ．1616π+ D ．816π+俯视图正视图r2r2rrCAP。
立体几何高考考点梳理及真题分类解析
第九章立体几何（2021年文科数学高考备考版）第一节空间几何体的三视图和直观图一、高考考点梳理（一）、空间几何体的结构特征1．多面体①棱柱：两个面互相平行，其余各面都是四边形，并且每相邻两个四边形的公共边都互相平行，这些面围成（一）、简单几何体的结构特征的几何体叫作棱柱．②棱锥：有一个面是多边形，其余各面是有一个公共顶点的三角形，这些面围成的几何体叫作棱锥．③棱台：用一个平行于棱锥底面的平面去截棱锥，底面与截面之间的部分叫作棱台．2．旋转体①圆锥可以由直角三角形绕其任一直角边旋转得到．②圆台可以由直角梯形绕直角腰或等腰梯形绕上下底中点连线旋转得到，也可由平行于圆锥底面的平面截圆锥得到．③球可以由半圆或圆绕直径旋转得到．（二）、三视图1．三视图的名称：几何体的三视图包括主视图、左视图、俯视图．2．三视图的画法①画三视图时，重叠的线只画一条，挡住的线要画成虚线．②三视图的主视图、左视图、俯视图分别是从几何体的正前方、正左方、正上方观察几何体得到的正投影图．③观察简单组合体是由哪几个简单几何体组成的，并注意它们的组成方式，特别是它们的交线位置．（三）、直观图简单几何体的直观图常用斜二测画法来画，其规则是：1．在已知图形中建立直角坐标系xOy.画直观图时，它们分别对应x′轴和y′轴，两轴交于点O′，使∠x′O′y′＝45°，它们确定的平面表示水平平面；2．已知图形中平行于x轴或y轴的线段，在直观图中分别画成平行于x′轴和y′轴的线段；3．已知图形中平行于x轴的线段，在直观图中保持原长度不变；平行于y轴的线段，长度为原来的1 2.二、历年高考真题题型分类突破题型一空间几何体的三视图【例1】（2020全国Ⅲ卷）右图为某几何体的三视图，则该几何体的表面积是（）A.B.C.D. D.解析：由三视图可知几何体的直观图如图：几何体是正方体的一个角，，、、两两垂直，故，几何体的表面积为：，故选：C．【例2】（2018全国Ⅰ卷）某圆柱的高为2，底面周长为16，其三视图如图．圆柱表面上的点M在正视图上的对应点为A，圆柱表面上的点N在左视图上的对应点为B，则在此圆柱侧面上，从M到N的路径中，最短路径的长度为（）A．217 B．2 5C．3 D．2解析：所求最短路径MN为四份之一圆柱侧面展开图对角线的长.故选B.【例3】（2017全国Ⅱ卷）如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分后所得,则该几何体的体积为( )A .90πB .63πC .42πD .36π解析：由题意,该几何体是一个组合体,下半部分是一个底面半径为3,高为4的圆柱,其体积V 1＝π×32×4＝36π,上半部分是一个底面半径为3,高为6的圆柱的一半,其体积V 2＝12×(π×32×6)＝27π,∴该组合体的体积V ＝V 1＋V 2＝63π.故选B .题型二 与球有关的几何体【例4】（2020全国Ⅰ卷）已知A ,B ,C 为球O 的球面上的三个点，⊙O 1为∆ABC 的外接圆，若⊙O 1的面积为4π，AB=BC=AC=OO 1，则球O 的表面积为( ) A ．64πB ．48πC ．36πD ．32π解析：设球O 半径为R ，⊙O 1的半径为r ，依题πr 2=4π，∴r =2。
高三数学空间几何体的三视图与直观图试题答案及解析
高三数学空间几何体的三视图与直观图试题答案及解析1.已知某锥体的三视图（单位：cm）如图所示，则该锥体的体积为．【答案】２．【解析】由已知几何体的视图可知，几何体为四棱锥，其中SA垂直于平面ABCD，SA=2，四边形ABCD为直角梯形，AD=1，BC=2，AB=2，所以四棱锥的体积为【考点】三视图求几何体的体积.2.右图为某几何体的三视图，则该几何体的体积为【答案】【解析】由三视图知，该几何体是底面半径为1，高为1的圆柱与半径为1的球体组成的组合体，其体积为=．【考点】简单几何体的三视图，圆柱的体积公式，球的体积公式3.一个几何体的三视图及尺寸如图所示，则该几何体的外接球半径为（）A．B．C．D．【答案】C【解析】由三视图可知：该几何体是一个如图所示的三棱锥P-ABC，它是一个正四棱锥P-ABCD 的一半，其中底面是一个两直角边都为6的直角三角形，高PE=4．设其外接球的球心为O，O点必在高线PE上，外接球半径为R，则在直角三角形BOE中，BO2=OE2+BE2=（PE-EO）2+BE2，即R2=（4-R）2+（3）2，解得：R=，故选C.【考点】三视图，球与多面体的切接问题，空间想象能力4.如图是一个几何体的三视图，则该几何体的表面积是____________【答案】28＋12【解析】这是一个侧放的直三棱柱，底面是等腰直角三角形，侧棱长为6故表面积为2×(×2×2)＋(2＋2＋2)×6＝28＋12.【考点】三视图，几何体的表面积.5.在长方体中割去两个小长方体后的几何体的三视图如图，则切割掉的两个小长方体的体积之和等于.【答案】24【解析】由题意割去的两个小长方体的体积为.【考点】三视图，几何体的体积..6.某空间几何体的正视图是三角形，则该几何体不可能是（）圆柱圆锥四面体三棱柱【答案】A【解析】由于圆柱的三视图不可能是三角形所以选A.【考点】三视图.7.某几何体的三视图如图所示，其中正视图是腰长为2的等腰三角形，侧视图是半径为1的半圆，则该几何体的表面积是________．【答案】2(π＋)【解析】由三视图可知此几何体的表面积分为两部分：底面积即俯视图的面积为2；侧面积为一个完整的圆锥的侧面积，且圆锥的母线长为2，底面半径为1，所以侧面积为2π．两部分加起来即为几何体的表面积，为2(π＋)．8.一个锥体的主(正)视图和左(侧)视图如图所示，下面选项中，不可能是该锥体的俯视图的是()【答案】C【解析】俯视图是选项C的锥体的正视图不可能是直角三角形．另外直观图如图1的三棱锥(OP⊥面OEF，OE⊥EF，OP＝OE＝EF＝1)的俯视图是选项A，直观图如图2的三棱锥(其中OP，OE，OF两两垂直，且长度都是1)的俯视图是选项B，直观图如图3的四棱锥(其中OP⊥平面OEGF，底面是边长为1的正方形，OP＝1)的俯视图是选项D．9.如图所示，正方形O′A′B′C′的边长为1，它是水平放置的一个平面图形的直观图，则原图形的周长是()A．6B．8C．2＋3D．2＋2【答案】B【解析】如图，OB＝2，OA＝1，则AB＝3．∴周长为8．10.某几何体的三视图如图所示，且该几何体的体积是2，则正(主)视图的面积等于()A．2B．C．D．3【答案】A【解析】由三视图可知该几何体是一个四棱锥，其底面积就是俯视图的面积S＝(1＋2)×2＝3，其高就是正(主)视图以及侧(左)视图的高x，因此有×3×x＝2，解得x＝2，于是正(主)视图的面积S＝×2×2＝2．11.如图，三棱柱的侧棱长和底边长均为2，且侧棱AA1⊥底面A1B1C1，正视图是边长为2的正方形，俯视图为一个等边三角形，则该三棱柱的侧视图的面积为( )A. C.4 D.【答案】A【解析】侧视图也为矩形，底宽为原底等边三角形的高，侧视图的高为侧棱长，所以侧视图的面积为,故选B.【考点】三视图12.一个几何体的三视图如图所示，则该几何体内切球的体积为 .【答案】【解析】依题意可得该几何体是一个正三棱柱，底面边长为2，高为.由球的对称性可得内切球的半径为.由已知计算得底面内切圆的半径也为.所以内切球的体积为.【考点】1.三视图.2.几何体内切球的对称性.3.球的体积公式.4.空间想象力.13.已知一个正三棱柱的所有棱长均等于2，它的俯视图是一个边长为2的正三角形，那么它的左视图面积的最小值是________．【答案】【解析】如图，正三棱柱中，分别是的中点，则当面与侧面平行时，左视图面积最小，且面积为.【考点】三视图.14.某几何体的三视图如图3所示，则其体积为________．【答案】【解析】原几何体可视为圆锥的一半，其底面半径为1，高为2，∴其体积为×π×12×2×＝.15.已知正△ABC的边长为2，那么用斜二测画法得到的△ABC的直观图△A′B′C′的面积为（）A．B．C．D．【答案】D【解析】∵正△ABC的边长为2，故正△ABC的面积S==设△ABC的直观图△A′B′C′的面积为S′则S′=S=•=故选D16.一个体积为12的正三棱柱的三视图如图所示，则这个三棱柱的侧视图的面积为（）A．B．C．D．【答案】A【解析】依题意可得三棱柱的底面是边长为4正三角形.又由体积为.所以可得三棱柱的高为3.所以侧面积为.故选A.【考点】1.三视图的知识.2.棱柱的体积公式.3.空间想象力.17.某几何体的三视图如题（6）所示，其侧视图是一个边长为1的等边三角形，俯视图是两个正三角形拼成的菱形，则这个几何体的体积为（）A．1B．C．D．【答案】C【解析】这是由两个三棱锥拼成的几何体，其体积为.选C.【考点】三视图及几何体的体积.18.一个四面体的顶点在空间直角坐系O－xyz中的坐标分别是（1，0，1），（1，1，0），（0，1，1），（0，0，0），画该四面体三视图中的正视图时，以zOx平面为投影面，则得到的正视图可以为（）A．B．C．D．【答案】A【解析】设O(0，0，0)，A(1，0，1)，B(1，1，0)，C(0，1，1)，将以O，A，B，C为顶点的四面体补成一正方体后，因为OA⊥BC，所以补成的几何体以zOx平面为投影面的正视图为A．19.如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则此几体的体积为（）A．6B．9C．12D．18【答案】B【解析】由三视图可知，此几何体为如图所示的三棱锥，其底面△ABC为等腰三角形且AB=BC，AC=6，AC边上的高为3，SB⊥底面ABC，且SB=3，因此此几体的体积为V=××6×3×3=920.如图所示，一个空间几何体的正视图和侧视图都是边长为1的正方形，俯视图是一个直径为1的圆，那么这个几何体的表面积为 .【答案】【解析】由三视图知，该几何体是一个圆柱，其表面积为.【考点】三视图及几何体的表面积.21.在三棱锥中，，平面ABC,.若其主视图，俯视图如图所示，则其左视图的面积为【答案】【解析】左视图是一个直角三角形，其直角边分别是2与.所以面积为.【考点】1.三视图知识.2.三角形面积的计算.22.一个几何体的三视图如图所示,则这个几何体的体积是_________.【答案】【解析】由三视图还原几何体，该几何体为底面半径为，高为的圆柱，去掉底面半径为，高为的圆锥的剩余部分，则其体积为．【考点】1、三视图；2、几何体的体积.23.棱长为2的正方体被一平面截成两个几何体，其中一个几何体的三视图如图所示，那么该几何体的体积是( ).A．B．4C．D．3【答案】B【解析】如图，红色虚线表示截面，可见这个截面将正方体分为完全相同的两个几何体，则所求几何体的体积即是原正方体的体积的一半，.【考点】1.三视图；2.正方体的体积24.如图，一个四棱锥的底面为正方形，其三视图如图所示，则这个四棱锥的体积为（）A．1B．2C．3D．4【答案】Ｂ【解析】由题设及图知，此几何体为一个四棱锥，其底面为一个对角线长为的正方形，故其底面积为，由三视图知其中一个侧棱为棱锥的高，其相对的侧棱与高及底面正方形的对角线组成一个直角三角形，由于此侧棱长为，对角线长为，故棱锥的高为，此棱锥的体积为，故选B．【考点】由三视图求面积、体积．25.已知某几何体的三视图如右图所示，其中，正视图，侧视图均是由三角形与半圆构成，俯视图由圆与内接三角形构成，根据图中的数据可得此几何体的体积为（）A．B．C．D．【答案】C【解析】由已知的三视图可知原几何体是上方是三棱锥,下方是半球,∴，故选C.【考点】1.三视图；2.几何体的体积.26.如图是一个组合几何体的三视图,则该几何体的体积是.【答案】36+128π【解析】由三视图还原可知该几何体是一个组合体,下面是一个圆柱,上面是一个三棱柱,故所求体积为V=×3×4×6+16π×8=36+128π.27.某几何体的三视图如图所示，其中俯视图为扇形，则该几何体的体积为（）A．B．C．D．【答案】D【解析】由三视图可知，该几何体是三分之一个圆锥，其体积为.【考点】三视图及几何体的体积.28.某几何体的三视图(图中单位：cm)如图所示，则此几何体的体积是()A．36 cm3B．48 cm3C．60 cm3D．72 cm3【答案】B【解析】由三视图可知几何体上方是一长方体，下方是一放倒的直四棱柱，且四棱柱底面是等腰梯形，上底长为2 cm，下底长为6 cm，高为2 cm，故几何体的体积是2×2×4＋×(2＋6)×2×4＝48(cm3)，故选B.29.如图是某三棱柱被削去一个底面后的直观图、侧(左)视图与俯视图．已知CF＝2AD，侧视图是边长为2的等边三角形，俯视图是直角梯形，有关数据如图所示．求该几何体的体积．【答案】3【解析】解：取CF中点P，过P作PQ∥CB交BE于Q，连接PD，QD，则AD∥CP，且AD＝CP.所以四边形ACPD为平行四边形，所以AC∥PD.所以平面PDQ∥平面ABC.该几何体可分割成三棱柱PDQ－CAB和四棱锥D－PQEF，所以V＝V－CAB＋V D－PQEFPDQ＝×22sin 60°×2＋××＝3.30.一个几何体的三视图如图所示，则该几何体的表面积是()A．6＋8B．12＋7C．12＋8D．18＋2【答案】C【解析】该空间几何体是一个三棱柱．底面为等腰三角形且底面三角形的高是1，底边长是2 ，两个底面三角形的面积之和是2，侧面积是(2＋2＋2)×3＝12＋6，故其表面积是12＋8.31. 已知四棱锥P-ABCD 的三视图如右图所示，则四棱锥P-ABCD 的四个侧面中的最大面积是( )．A ．6B ．8C ．2D ．3【答案】A【解析】四棱锥如图所示：PM ＝3，S △PDC ＝×4×＝2，S △PBC ＝S △PAD ＝×2×3＝3，S △PAB ＝×4×3＝6，所以四棱锥P-ABCD 的四个侧面中的最大面积是6.32. 若某几何体的三视图如图所示，则这个几何体的直观图可以是( )．【答案】B【解析】分别从三视图中去验证、排除．由正视图可知，A 不正确；由俯视图可知，C ，D 不正确，所以选B.33. 一个几何体的三视图如图所示，已知这个几何体的体积为，则h________.【答案】【解析】依题意可得四棱锥的体积为.所以可得.解得.故填.本小题的是常见的立几中的三视图的题型，这类题型关键是要能还原几何体的直观图形.所以培养空间的思想很重要.【考点】1.三视图的识别.2.空间几何体的直观图.34.图中的网格纸是边长为的小正方形，在其上用粗线画出了一四棱锥的三视图，则该四棱锥的体积为（）A．B．C．D．【答案】C【解析】由三视图知，该几何体是一个四棱锥，且其底面为一个矩形，底面积，高为，故该几何体的体积，故选C.【考点】1.三视图；2.锥体的体积35.已知某几何体的三视图如图，其中主视图中半圆直径为2，则该几何体的体积____________【答案】24-【解析】由三视图可知，该几何体是有长方体里面挖了一个半圆柱体，可知，长方体的长为4，宽为3，高为2，那么圆柱体的高位3，底面的半径为1，则可知该几何体的体积为，故答案为．【考点】由三视图求面积、体积．36.把边长为的正方形沿对角线折起，连结，得到三棱锥，其正视图、俯视图均为全等的等腰直角三角形（如图所示），则其侧视图的面积为（）A．B．C．D．【答案】B【解析】在三棱锥中，在平面上的射影为的中点，∵正方形边长为，∴，∴侧视图的面积为.【考点】1.三视图；2.三角形的面积.37.一个几何体的三视图如图所示，其中正视图是一个正三角形，则这个几何体的（）A．外接球的半径为B．体积为C．表面积为D．外接球的表面积为【答案】D．【解析】由题意设外接球半径为，则，A错误；外接球的表面积为，D正确；此几何体的体积为，故B错误；此几何体的表面积为，C错误．【考点】三视图及球的表面积公式.38.一个几何体的三视图如图所示，则该几何体的体积为( )A．4B．8C．D．【答案】B【解析】有三视图可以看出，该几何体是一个三棱锥，它的体积为．【考点】三视图，几何体的体积．39.如图，直三棱柱的侧棱长和底面边长均为2，正视图和俯视图如图所示，则其侧视图的面积为（）A．B．C．4D．2【答案】A【解析】由题意易知，直三棱柱的底面是边长为2的正三角形.其侧视图为矩形，矩形的高为2，宽为底面正三角形的高.易知边长为2的正三角形的高为.所以面积为.【考点】三视图40.如果一个几何体的三视图如图所示(单位长度:cm),则此几何体的表面积是( )A．B．21C．D．24【答案】A【解析】还原几何体，得棱长为2的正方体和高为1的正四棱锥构成的简单组合体，如图所示，=，选A.【考点】1、几何体的表面积；2、三视图.41.某几何体的三视图如图所示，则它的表面积为（）A．B．C．D．【答案】A【解析】易知该三视图的直观图是倒立的半个三棱锥，其表面积由底面半圆，侧面三角形和侧面扇形，所以，故选A.【考点】1.立体几何三视图；2.表面积和体积的求法.42.一几何体的三视图如图所示，则该几何体的体积为（）A．200＋9πB．200＋18πC．140＋9πD．140＋18π【答案】A【解析】通过观察三视图，易知该几何体是由半个圆柱和长方体组成的，则半个圆柱体积；长方体的体积为,所以该几何体的最终体积，故选A.【考点】1.三视图的应用；2.简单几何体体积的求解.43.一个几何体的三视图如图所示，其中主视图和左视图是腰长为1的两个全等的等腰直角三角形，则该几何体的外接球的表面积为( )A．B．C．D．【解析】把原来的几何体补成以为长、宽、高的长方体，原几何体四棱锥与长方体是同一个外接球，，，.【考点】1.补体法；2.几何体与外接球之间的元素换算.44.一个几何体的三视图如图所示，其中府视图为正三角形，则侧视图的面积为（）A．8B．C．D．4【答案】B【解析】由三视图可知：该几何体是一个正三棱柱，高为4，底面是一个边长为2的正三角形．因此，侧视图是一个长为４，宽为的矩形，．【考点】三视图与几何体的关系、几何体的侧面积的求法能力．45.某几何体的三视图如图所示，则它的侧面积为（）A．B．C．24D．【答案】A【解析】由三视图得,这是一个正四棱台,由条件，侧面积.【考点】1.三视图；2.正棱台侧面积的求法.46.一个几何体的三视图如图所示，其中正视图与侧视图都是底边长为6、腰长为5的等腰三角形，则这个几何体的全面积为（）A．B．C．D．【解析】由三视图知，该几何体是一个圆锥，且圆锥的底面直径为，母线长为，用表示圆锥的底面半径，表示圆锥的母线长，则，，故该圆锥的全面积为.【考点】三视图、圆锥的表面积47.一个空间几何体的三视图如右图所示，其中主视图和侧视图都是半径为的圆，且这个几何体是球体的一部分，则这个几何体的表面积为( )A．3πB．4πC．6πD．8π【答案】B【解析】此空间几何体是球体切去四分之一的体积，表面积是四分之三的球表面积加上切面面积，切面面积是两个半圆面面积.故这个几何体的表面积是.【考点】1、几何体的三视图; 2、球的表面积公式.48.右图是一个几何体的三视图，其中正视图和侧视图都是一个两底长分别为和，腰长为的等腰梯形，则该几何体的表面积是．【答案】【解析】从三视图可以看出：几何体是一个圆台，上底面是一个直径为4的圆，下底面是一个直径为2的圆，侧棱长为4．上底面积，下底面积，侧面是一个扇环形，面积为，所以表面积为．【考点】空间几何体的三视图、表面积的计算．49.某零件的正（主）视图与侧（左）视图均是如图所示的图形（实线组成半径为的半圆，虚线是等腰三角形的两腰），俯视图是一个半径为的圆（包括圆心），则该零件的体积是 ( )A．B．C．D．【解析】由题意易知该几何体为一半球内部挖去一圆锥所成，故体积为.故选C.【考点】1.体积； 2.三视图.50.某四棱台的三视图如图所示,则该四棱台的体积是 ( )A．B．C．D．【答案】B【解析】由三视图可知,该四棱台的上下底面边长分别为和的正方形,高为,故,故选B．【考点】三视图与四棱台的体积51.若一个底面是正三角形的三棱柱的正视图如图所示，其顶点都在一个球面上，则该球的表面积为（）A．B．C．D．【答案】B【解析】由已知底面是正三角形的三棱柱的正视图,我们可得该三棱柱的底面棱长为2，高为1,则底面外接圆半径，球心到底面的球心距,则球半径,则该球的表面积，故选B.【考点】由三视图求面积、体积．点评：本题考查的知识点是由三视图求表面积，其中根据截面圆半径、球心距、球半径满足勾股定理计算球的半径，是解答本题的关键．52.如图所示是某一容器的三视图，现向容器中匀速注水，容器中水面的高度随时间变化的可能图像是（）A． B． C． D．【答案】B【解析】由三视图可知该几何体是圆锥，顶点在下，底面圆在上，在匀速注水过程中水面高度随着时间的增大而增大，且刚开始时截面积较小，所以高度变化较快，随着水面的升高，截面圆面积增大，高度变化速度减缓，因此函数的瞬时变化率逐渐减小，导数减小，图像为B项【考点】函数导数的定义点评：本题通过高度的瞬时变化率的变化情况得到函数的导数的大小，从而通过做出的切线斜率的变化得出正确图像53.已知一个三棱锥的主视图与俯视图如图所示，则该三棱锥的侧视图面积为（）A．B．C．D．【答案】B【解析】根据题意，由于三棱锥的俯视图为直角三角形，正视图为直角三角形，且斜边长为2，直角边长为，那么结合图像可知其侧视图为底面边长为1，高为的三角形，因此其面积为，故选B.【考点】三棱锥点评：解决的关键是根据三棱锥的三视图来得到底面积和高进而求解侧视图，属于基础题。
高考数学：立体几何——三视图——命题类型规律和解题技巧
高考数学：立体几何——三视图——命题类型规律和解题技巧三视图问题是高考中的重要题型。
此类问题要求学生有较强的空间想象能力，因此成为很多考生做题的难点。
下面将三视图考题的出题规律和解题技巧，归结如下。
根据高考所考查几何体的结构特征，其出题类型分为三种：单体型、组合型和切削型，现逐一分析。
一、单体型所谓单体型，即根据三视图还原后的几何体是一个我们常见的基本几何体，如长方体、三棱锥、圆锥、三棱柱、球等。
一般情况下，我们可以根据下列结论来判断所求几何体的结构特征：(1)三视图为三个三角形，对应三棱锥；(2)三视图为两个三角形和一个四边形，对应四棱锥；(3)三视图为两个三角形和一个圆，对应圆锥；(4)三视图为一个三角形和两个四边形，对应三棱柱；(5)三视图为两个四边形和一个圆，对应圆柱。
二、组合型所谓组合型,即根据三视图还原后的几何体是两个或两个以上的几何单体组合而成的，此时我们只需根据三视图看懂相应部分对应的每个单体的结构特征即可。
三、切削型所谓切削型．即根据三视图还原后的几何体可以看成是从某一熟悉的几何单体(我们可以将其看成所求几何体的载体)中截去一部分后得到的。
对于此类问题，我们的解决方案是：先画出所求几何体的载体，再根据题意截去其中一部分，最后根据题目中的位置关系和数量关系进行推理和计算。
例1：[2018全国卷Ⅲ,3,5分]中国古建筑借助榫卯将木构件连接起来，构件的凸出部分叫棒头，凹进部分叫卯眼，图中木构件右边的小长方体是棒头．若如图摆放的木构件与某一带卯眼的木构件咬合成长方体，则咬合时带卯眼的木构件的俯视图可以是（）思路分析：根据题意画出带卯眼的木构件的直观图，借助直观图判断俯视图。
解析：由题意带卯眼的木构件的直观图如下图所示，由直观图知其俯视图应选A。
答案：A注意：不要忽视木构件俯视图中的虚线。
例2：[2018北京卷,5,5分]某四棱锥的三视图如图所示，在此三棱锥的侧面中，直角三角形的个数为（）A．1 B．2 C．3 D．4思路分析：根据还原出来几何体的形状，判断直角三角形的个数。
三视图高考题解题技巧
三视图高考题解题技巧
三视图高考题解题技巧
1、主视图和左视图如果都是三角形的必然是椎体，要么是棱锥要么是圆锥。
还有两种特殊的情况：
1、是棱锥和半圆锥的组合体。
2、就是半圆锥。
到底如何如确定就是通过俯视图观察。
(1) 若俯视图是三角形时，就是三棱锥。
(2) 若俯视图是多边形时，就是多棱锥。
(3) 若俯视图是半圆和三角形时，就是是棱锥和半圆锥的组合体。
(4) 若俯视图是半圆时，就是半圆锥。
(5) 注意虚线和实线的意义，虚线代表的是看不到的线，实线代表的是能看的见得都是一种平行投影所创造出来的。
2、三视图求体积时候，先观察主视图和侧视图，注意主视图和侧视图的高一定都是一样的，并且肯定是立体图形的高，先通过观察判定图形到底是什么立体图形，看看到底是棱锥，棱柱，还是组合体，通常的组合体都是较为简单的.组合体，无需过多考虑。
(1) 如果是棱锥的话，就看俯视图是什么图形，判定后算出俯视图的面积即可，应用体积公式。
(2) 如果是棱柱的话，同样看俯视图的图形，求出面积，应用公式即可。
(3) 如果是组合体，要分辨出是哪两种规则图形的组合，分别算出体积相加即可。
专题34：几何体三视图的解题策略(解析版)
专题34：几何体三视图的解题策略（解析版）一.空间几何体的三视图正视图：光线从几何体的前面向后面正投影得到的投影图；反映了物体的高度和长度 侧视图：光线从几何体的左面向右面正投影得到的投影图；反映了物体的高度和宽度 俯视图：光线从几何体的上面向下面正投影得到的投影图。
反映了物体的长度和宽度 三视图中反应的长、宽、高的特点：“长对正”，“高平齐”，“宽相等”二.空间几何体的直观图斜二测画法的基本步骤：①建立适当直角坐标系xOy （尽可能使更多的点在坐标轴上） ②建立斜坐标系'''x O y ∠，使'''x O y ∠=450（或1350） ③画对应图形在已知图形平行于X 轴的线段，在直观图中画成平行于X ‘轴，且长度保持不变；在已知图形平行于Y 轴的线段，在直观图中画成平行于Y ‘轴，且长度变为原来的一半； 直观图与原图形的面积关系：42S ⋅=原图形直观图S一，切割法例1．某几何体的三视图如图所示，则该几何体的体积是（ ）A．20B．24C．18D．16【答案】A【分析】由三视图还原出该几何体的直观图，如图所示，该几何体是一个直三棱柱去掉一个三棱锥得到的，然后计算体积即可【详解】解：由几何体的三视图还原出该几何体的直观图，如图所示．该几何体是一个直三棱柱去掉一个三棱锥得到的．由题中数据可得三棱柱的体积为1344=242⨯⨯⨯，截去的三棱锥的体积为4，故该几何体的体积是20．故选：A【点睛】此题考查由三视图求几何体的体积，需熟记锥体的体积公式，属于基础题.切割法规律总结：1、还原到常见几何体中2、实线当面切，虚线背后切3、切完后对照三视图进行检验二，三点交汇法例2某三棱锥的三视图如图所示，如果网格纸上小正方形的边长为1，则该三棱锥的体积为( )A．4B．8C．12D．24【答案】A【分析】由三视图还原几体何体，可知该几何体是从长为4，宽为4，高为3的长方体中截得（如图），直接由三棱锥的体积公式可得答案.【详解】由三视图还原几体何体如图，三棱锥D ABC-是从长为4，宽为4，高为3的长方体中截得，所以11423432D ABCV-=⨯⨯⨯⨯=故选：A【点睛】此题考查由三视图求多面体的体积，关键是由三视图还原几何体，属于中档题. 三点交汇法规律：三线交汇得顶点，各顶必在其中选多顶可能用不完，个中取舍是关键:三、拔高法例3：3某几何体的三视图如图所示，则该几何体的表面积是（ ）A ．424+B ．228+C ．428+D ．12【答案】B【分析】 由三视图可得此几何体为如图所示的四棱锥，然后求出各个面的面积即可【详解】解：由三视图可得此几何体为如图所示的四棱锥E ABCD -，由题可得，2AB BC CD AD CE =====,22DE BE ==，所以该几何体的表面积为112222222282222⨯+⨯⨯⨯+⨯⨯⨯=+， 故选：B拔高法规律总结：1.标出俯视图所有结点，画出俯视图对应的直观图2.由主、侧视图的左中右找出被拔高的点.四、去点法例4：某四棱锥的三视图如图所示，则该四棱锥的体积是（）A．6B．12C．24D．36【答案】B【分析】由三视图可得原图，结合原图，利用四棱锥的体积公式即可得解.【详解】原图如图所示，可得1334=123V=⨯⨯⨯，故选：B.【点睛】本题考查了三视图，考查了利用三视图画直观图，同时考查了锥体的体积公式，属于基础题.去点法规律：画立方体删多余点连剩余点六字真言：先去除、再确定走进高考1．2014年全国普通高等学校招生统一考试理科数学（全国Ⅱ卷）如图，网格纸上正方形小格的边长为1（表示1cm）,图中粗线画出的是某零件的三视图，该零件由一个底面半径为3cm，高为6cm的圆柱体毛坯切削得到，则切削掉部分的体积与原来毛坯体积的比值为（）A．1727B．59C．1027D．13【答案】A 【详解】因为加工前的零件半径为3，高为6，所以体积154Vπ=，又因为加工后的零件，左半部为小圆柱，半径为2，高4，右半部为大圆柱，半径为3，高为2，所以体积2161834Vπππ=+=，所以削掉部分的体积与原体积之比为5434105427πππ-=，故选A.考点：本小题主要考查立体几何中的三视图，考查同学们的空间想象能力.2．2018年全国卷Ⅲ文数高考试题中国古建筑借助榫卯将木构件连接起来，构件的凸出部分叫榫头，凹进部分叫卯眼，图中木构件右边的小长方体是榫头．若如图摆放的木构件与某一带卯眼的木构件咬合成长方体，则咬合时带卯眼的木构件的俯视图可以是A．B．C．D．【答案】A【详解】详解：由题意知，题干中所给的是榫头，是凸出的几何体，求得是卯眼的俯视图，卯眼是凹进去的，即俯视图中应有一不可见的长方形，且俯视图应为对称图形故俯视图为故选A.点睛：本题主要考查空间几何体的三视图，考查学生的空间想象能力，属于基础题．3．2017年全国普通高等学校招生统一考试文科数学（新课标1卷）如图，在下列四个正方体中，A，B为正方体的两个顶点，M，N，Q为所在棱的中点，则在这四个正方体中，直接AB与平面MNQ不平行的是A．B．C．D．【答案】A【解析】对于B，易知AB∥MQ，则直线AB∥平面MNQ；对于C，易知AB∥MQ，则直线AB∥平面MNQ；对于D，易知AB∥NQ，则直线AB∥平面MNQ．故排除B，C，D，选A．点睛:本题主要考查线面平行的判定定理以及空间想象能力，属容易题．证明线面平行的常用方法：①利用线面平行的判定定理，使用这个定理的关键是设法在平面内找到一条与已知直线平行的直线，可利用几何体的特征，合理利用中位线定理、线面平行的性质或者构造平行四边形、寻找比例式证明两直线平行．②利用面面平行的性质，即两平面平行，在其中一平面内的直线平行于另一平面．4．2017年全国普通高等学校招生统一考试文科数学（新课标2卷）如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，该几何体由一平面将一圆柱截去一部分后所得，则该几何体的体积为A ．90πB ．63πC ．42πD ．36π【答案】B【解析】 由题意，该几何体是由高为6的圆柱截取一半后的图形加上高为4的圆柱，故其体积为2213634632V πππ=⋅⋅⋅+⋅⋅=，故选B. 点睛:（1）解答此类题目的关键是由多面体的三视图想象出空间几何体的形状并画出其直观图．（2）三视图中“正侧一样高、正俯一样长、俯侧一样宽”，因此，可以根据三视图的形状及相关数据推断出原几何图形中的点、线、面之间的位置关系及相关数据．5．2014年全国普通高等学校招生统一考试理科数学如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的各条棱中，最长的棱的长度为（ ）A ．63B ．6C ．62D ．4【答案】B【详解】由正视图、侧视图、俯视图形状，可判断该几何体为四面体，且四面体的长、宽、高均为4个单位，故可考虑置于棱长为4个单位的正方体中研究，如图所示，该四面体为D ABC -，且4AB BC ==, 42AC =,25DB DC ==,2(42)46DA =+=，故最长的棱长为6，选B ．6．2016年全国普通高等学校招生统一考试理科数学（全国2卷）如图是由圆柱与圆锥组合而成的几何体的三视图，则该几何体的表面积为（ ）A ．20πB ．24πC ．28πD ．32π【答案】C【解析】 试题分析：由三视图分析可知，该几何体的表面积为圆锥的表面积与圆柱的侧面积之和．，，所以几何体的表面积为．考点：三视图与表面积．7．2016年全国普通高等学校招生统一考试文科数学（新课标3卷）如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的表面积为（）A．B．C．90D．81【答案】B【解析】【详解】试题分析：解：由已知中的三视图可得：该几何体是一个以俯视图为底面的斜四棱柱，其底面面积为：3×6=18，前后侧面的面积为：3×6×2=36，左右侧面的面积为：，故棱柱的表面积为：．故选：B．点睛：本题考查的知识点是由三视图，求体积和表面积，根据已知的三视图，判断几何体的形状是解答的关键，由三视图判断空间几何体（包括多面体、旋转体和组合体）的结构特征是高考中的热点问题.8．2015年全国普通高等学校招生统一考试文科数学（新课标Ⅰ）圆柱被一个平面截去一部分后与半球（半径为r）组成一个几何体，该几何体的三视图中的正视图和俯视图如图所示，若该几何体的表面积为1620π+，则r = ( )A ．1B ．2C ．4D ．8【答案】B【解析】试题分析：由正视图和俯视图知，该几何体是半球与半个圆柱的组合体，圆柱的半径与球的半径都为r ，圆柱的高为2r ，其表面积为22142222r r r r r r πππ⨯+⨯++⨯=2254r r π+="16" + 20π，解得r=2，故选B. 考点：简单几何体的三视图；球的表面积公式；圆柱的测面积公式9．2015年全国普通高等学校招生统一考试文科数学（新课标Ⅱ）一个正方体被一个平面截去一部分后,剩余部分的三视图如下图,则截去部分体积与剩余部分体积的比值为（ ）A ．18B ．17C ．16D ．15【答案】D【详解】试题分析：如图所示，截去部分是正方体的一个角,其体积是正方体体积的16,剩余部分体积是正方体体积的56,所以截去部分体积与剩余部分体积的比值为,故选D.考点：本题主要考查三视图及几何体体积的计算.10．2014年全国普通高等学校招生统一考试文科数学（新课标Ⅰ）如图，网格纸的各小格都是正方形，粗实线画出的事一个几何体的三视图，则这个几何体是（）A．三棱锥B．三棱柱C．四棱锥D．四棱柱【答案】B【解析】试题分析：由三视图中的正视图可知，由一个面为直角三角形，左视图和俯视图可知其它的面为长方形．综合可判断为三棱柱．考点：由三视图还原几何体.11．2014年全国普通高等学校招生统一考试文科数学（全国Ⅱ卷）如图，网格纸上正方形小格的边长为1（表示1cm），图中粗线画出的是某零件的三视图，该零件由一个底面半径为3cm ，高为6cm 的圆柱体毛坯切削得到，则切削的部分的体积与原来毛坯体积的比值为（ ）A ．2717B ．95C ．2710D ．31【答案】C【解析】试题分析：由三视图还原几何体为一个小圆柱和大圆柱组成的简单组合体．其中小圆柱底面半径为2、高为4，大圆柱底面半径为3、高为2，则其体积和为22243234πππ⨯⨯+⨯⨯=，而圆柱形毛坯体积为23654ππ⨯⨯=，故切削部分体积为20π，从而切削的部分的体积与原来毛坯体积的比值为20105427ππ=． 考点：三视图． 12．2020年全国统一高考数学试卷（理科）（新课标Ⅱ）如图是一个多面体的三视图，这个多面体某条棱的一个端点在正视图中对应的点为M ，在俯视图中对应的点为N ，则该端点在侧视图中对应的点为（ ）A ．EB ．FC ．GD ．H【答案】A【分析】根据三视图，画出多面体立体图形，即可求得M 点在侧视图中对应的点.【详解】根据三视图，画出多面体立体图形，14D D 上的点在正视图中都对应点M ,直线34B C 上的点在俯视图中对应的点为N, ∴在正视图中对应M ,在俯视图中对应N 的点是4D ,线段34D D ,上的所有点在侧试图中都对应E ,∴点4D 在侧视图中对应的点为E .故选：A【点睛】本题主要考查了根据三视图判断点的位置，解题关键是掌握三视图的基础知识和根据三视图能还原立体图形的方法，考查了分析能力和空间想象，属于基础题.13．2020年全国统一高考数学试卷（理科）（新课标Ⅲ）下图为某几何体的三视图，则该几何体的表面积是（ ）A ．6+42B ．4+42C ．6+23D ．4+23【答案】C【分析】 根据三视图特征，在正方体中截取出符合题意的立体图形，求出每个面的面积，即可求得其表面积.【详解】根据三视图特征，在正方体中截取出符合题意的立体图形根据立体图形可得：12222ABC ADC CDB S S S ===⨯⨯=△△△ 根据勾股定理可得：22AB AD DB ===∴ADB △是边长为22根据三角形面积公式可得：2113sin 60(22)23222ADB S AB AD =⋅⋅︒==△∴该几何体的表面积是：2362332=⨯++故选：C.【点睛】本题主要考查了根据三视图求立体图形的表面积问题，解题关键是掌握根据三视图画出立体图形，考查了分析能力和空间想象能力，属于基础题.14．2017年全国普通高等学校招生统一考试理科数学（新课标1卷）某多面体的三视图如图所示，其中正视图和左视图都由正方形和等腰直角三角形组成，正方形的边长为2，俯视图为等腰直角三角形.该多面体的各个面中有若干个是梯形，这些梯形的面积之和为A．10B．12C．14D．16【答案】B【解析】由题意该几何体的直观图是由一个三棱锥和三棱柱构成，如下图，则该几何体各面内只有两个相同的梯形，则这些梯形的面积之和为12(24)2122⨯+⨯⨯=，故选B.点睛:三视图往往与几何体的体积、表面积以及空间线面关系、角、距离等问题相结合，解决此类问题的关键是由三视图准确确定空间几何体的形状及其结构特征并且熟悉常见几何体的三视图.15．2015年全国普通高等学校招生统一考试理科数学（新课标Ⅱ）一个正方体被一个平面截去一部分后，剩余部分的三视图如右图，则截去部分体积与剩余部分体积的比值为（）A ．B ．C ．D ．【答案】D【解析】试题分析：设正方体的棱长为1，由三视图判断，正方体被切掉的部分为三棱锥，∴正方体切掉部分的体积为111111326⨯⨯⨯⨯=，∴剩余部分体积为15166-=，∴截去部分体积与剩余部分体积的比值为15． 故选D ．考点：由三视图求体积16．2016年全国普通高等学校招生统一考试理科数学（新课标1卷）如图，某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径.若该几何体的体积是，则它的表面积是A ．17πB ．18πC ．20πD ．28π【答案】A试题分析：由三视图知，该几何体的直观图如图所示：是一个球被切掉左上角的,即该几何体是个球，设球的半径为，则，解得，所以它的表面积是的球面面积和三个扇形面积之和,即，故选A．【考点】三视图及球的表面积与体积【名师点睛】由于三视图能有效地考查学生的空间想象能力,所以以三视图为载体的立体几何题基本上是高考每年必考内容,高考试题中三视图一般与几何体的表面积与体积相结合.由三视图还原出原几何体是解决此类问题的关键.17．2016年全国普通高等学校招生统一考试理科数学（新课标2卷）如图是由圆柱与圆锥组合而成的几何体的三视图，则该几何体的表面积为（）A．B．C．D．【答案】C试题分析：由三视图分析可知，该几何体的表面积为圆锥的表面积与圆柱的侧面积之和。
高考文科数学_立体几何三视图问题分类解答
高考文科数学：三视图问题分类解答例1、概念问题1、下列几何体各自的三视图中，有且仅有两个视图相同的是．（填序号）①正方体④正四棱锥③三棱台②圆锥2、如图，折线ABC表示嵌在玻璃正方体内的一根铁丝，请把它的三视图补充完整．俯视图左视图正视图CBA3 、已知某个几何体的三视图如下图所示，试根据图中所标出的尺寸（单位：㎝），可得这个几何体的体积是．101020202020正视图左视图俯视图4、已知某个几何体的三视图如下图所示，试根据图中所标出的尺寸（单位：㎝），可得这个几何体的面积是．222233俯视图正视图左视图例2、图形判定问题1、一个几何体的三视图形状都相同，大小均相等，那么这个几何体不可以是（ D ）A．球 B．三棱锥 C．正方体 D．圆柱2、某几何体的正视图和侧视图均如图1所示，则该几何体的俯视图不可能是（ D ）4、某几何体的正视图如左图所示，则该几何体的俯视图不可能的是( C )6、一个简单几何体的正视图、侧视图如图所示，则其俯视图不可能为B第5题图①长方形；②正方形；③圆；④椭圆. 其中正确的是（A）①②（B）②③（C）③④（D）①④例3、三视图和几何体的体积相结合的问题1、下图是一个几何体的三视图，其中正视图是边长为2的等边三角形，侧视图是直角边长分别为1与3的直角三角形，俯视图是半径为1的半圆，则该几何体的体积等于（A ）π63 （B ）π33 （C ）π334 （D ）π21答案：A2、一个四棱锥的三视图如图所示，其左视图是等边三角形，该四棱锥的体积等于 A A ．3B ．23C ．33D ．633、设图１是某几何体的三视图，则该几何体的体积为 A ．942π+ Ｂ．3618π+ Ｃ．9122π+ Ｄ．9182π+其体积3439+332=18322V ππ=⨯⨯+（）。
答案：D4、如图是一个几何体的三视图，其中正视图是腰长为2的等腰三角形，俯视图是半径为1的半圆，则该几何体的体积是( B )43π63π C.12π 3π例4、三视图和几何体的表面积相结合1、一个几何体的三视图如图所示，则该几何体的表面积为_____38___。
高考数学专题—立体几何(三视图还原求几何体表面积与体积)
高考数学专题—立体几何（三视图还原求表面积、体积）基础知识点：一、面积公式：圆柱（底面半径为r，母线长为l）圆锥（底面半径为r，母线长为l）圆台（上、下底面半径分别为r′，r，母线长为l）侧面展开图底面面积2π底S r=2π底S r=22,ππ上底下底S r S r='=侧面面积2π侧S rl=π侧S rl=()π侧S l r r='+表面积()2π表S r r l=+()π表S r r l=+()22π表S r r r l rl='++'+二、体积公式几何体体积柱体柱体V Sh=(S为底面面积，h为高)2π圆柱V r h=(r为底面半径，h为高) 锥体13锥体V Sh=(S为底面面积，h为高)213π圆锥V r h=(r为底面半径，h为高)基本方法：一、构造长方体或正方体—将还原后的几何体放在长方体或正方体中，一方面有利于计算，另一方面可检查还原是否正确例1、如图，网格纸上小正方形的边长为1，粗线画的是某几何体的三视图，则该几何体的体积为（）A．B．C．D．4【答案】A【解析】由三视图可得，该几何体是如图所示的三棱柱挖去一个三棱锥，故所求几何体的体积为，故选A．236727611ABB DCC-E FCG-()111232221112326⎛⎫⨯⨯⨯-⨯⨯⨯⨯=⎪⎝⎭例2、若某三棱柱截去一个三棱锥后所剩几何体的三视图如图所示，则所截去的三棱锥．．．．．．的外接球的表面积等于（ ）A ．B ．C ．D ．【答案】A【解析】由三视图知几何体是底面为边长为3，4，5的三角形， 高为5的三棱柱被平面截得的，如图所示，截去的是一个三棱锥，底面是边长为3，4，5的直角三角形，高为3的棱锥， 如图蓝色线条的图像是该棱锥，三棱锥上底面外接圆半径圆心设为半径为， 球心到底面距离为，设球心为， 由勾股定理得到，，故选A ．例3、如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的外接球的表面积为（ ）34π32π17π172π52M r 32O 2222253342224h R r ⎛⎫⎛⎫⎛⎫=+=+= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭2434S R =π=πA ．B ．C ．D ．【答案】C【解析】还原几何体如图所示三棱锥由（如下左图），将此三棱锥补形为直三棱柱（如上右图），在直三棱柱中取的中点，取中点， ，，故答案为C ．例4、一个四棱锥的三视图如图所示，则该几何体的表面积为（ ）A ．B ．C ．D ．【答案】B【解析】根据三视图，画出原空间结构图如下图所示：∴表面积为，∴故选B ． 例5、已知一个三棱锥的三视图如图所示，其中三视图的长、宽、高分别为2，，，且32π16π36π72π1B BCD -111B C D BCD -111BC D BCD -1BC BC 、12O O、12O O O 3R ==2244336S R =π=⨯=π表6+8+6+8+111111111111DA D DA B DB C DC D A B C D S S S S S S =++++11112222222282222=⨯⨯+⨯⨯⨯⨯⨯⨯+⨯=+a b，则此三棱锥外接球表面积的最小值为（ ）A ．B ．C ．D ．【答案】B【解析】由已知条件及三视图得，此三棱锥的四个顶点位于长方体的四个顶点，即为三棱锥，且长方体的长、宽、高分别为2，，，∴此三棱锥的外接球即为长方体的外接球， 且球半径为，∴三棱锥外接球表面积为， ∴当且仅当，时，三棱锥外接球的表面积取得最小值为．故选B ． 二、三线交轨法—三视图即由三种视觉方向形成，故可以在平面图形的端点处形成一条线，然后在线上取合适的点例6、如图为某几何体的三视图，则该几何体的表面积是A ．B ．C ．D ．()520,02a b a b +=>>174π214π4π5π1111ABCD A B C D -11A CB D -1111ABCD A B C D -ab 1111ABCD A B C D-R ==()()22222144514a b a ππ=π++=π-+⎝⎭1a =12b =214π【答案】C【解析】根据三视图特征，在正方体中截取出符合题意的立体图形根据立体图形可得：12222ABC ADC CDB S S S ===⨯⨯=△△△根据勾股定理可得：AB AD DB ===∴ADB △是边长为根据三角形面积公式可得：211sin 6022ADB S AB AD =⋅⋅︒==△∴该几何体的表面积是：632=⨯++【点睛】本题主要考查了根据三视图求立体图形的表面积问题，解题关键是掌握根据三视图画出立体图形，考查了分析能力和空间想象能力，属于基础题.例7、某多面体的三视图如图所示，其中正视图和左视图都由正方形和等腰直角三角形组成，正方形的边长为2，俯视图为等腰直角三角形.该多面体的各个面中有若干个是梯形，这些梯形的面积之和为（ ）A．10 B．12 C．14 D．16【答案】B例8、如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体最长的棱长等于（）A. B. C. D.【答案】B【解析】由三视图可知，该几何体的直观图如图所示，由直观图可知，最长的棱为.例9、祖暅是我国南北朝时代的伟大科学家,他提出的“幂势既同,则积不容异”称为祖暅原理,利用该原理可以得到柱体的体积公式V 柱体=Sh,其中S 是柱体的底面积,h 是柱体的高.若某柱体的三视图如图所示(单位:cm),则该柱体的体积(单位:cm 3)是( )A.158B.162C.182D.324【答案】B【解析】由三视图得该棱柱的高为6,底面五边形可以看作是由两个直角梯形组合而成,其中一个上底为4,下底为6,高为3,另一个的上底为2,下底为6,高为3,则该棱柱的体积为2+62×3+4+62×3×6=162.例10、某四棱锥的三视图如图所示,在此四棱锥的侧面中,直角三角形的个数为 ( )A.1B.2C.3D.4【答案】C【解析】由该四棱锥的三视图,得其直观图如图.由正视图和侧视图都是等腰直角三角形,知PD ⊥平面ABCD,所以侧面PAD 和PDC 都是直角三角形.由俯视图为直角梯形,易知DC ⊥平面PAD.又AB ∥DC,所以AB ⊥平面PAD,所以AB ⊥PA,所以侧面PAB 也是直角三角形. 易知PC=2√2,BC=√5,PB=3,从而△PBC 不是直角三角形.故选C.例11、一个正方体被一个平面截去一部分后,剩余部分的三视图如下图,则截去部分体积与剩余部分体积的比值为( )A.18 B.17C.16D.15【答案】D【解析】由题意知该正方体截去了一个三棱锥,如图所示,设正方体棱长为a,则V 正方体=a 3,V 截去部分=16a 3,故截去部分体积与剩余部分体积的比值为16a 3∶56a 3=1∶5.例12、某几何体的三视图如图所示(单位:cm),则该几何体的体积是( )A.8 cm 3B.12 cm 3C.323cm 3D.403cm 3【答案】C【解析】由题中三视图知该几何体是一个正方体与正四棱锥的组合体,其中正方体与正四棱锥的底面边长为2 cm,正四棱锥的高为2 cm,则该几何体的体积V=2×2×2+13×2×2×2=323(cm 3),故选C.例13、如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各条棱中,最长的棱的长度为( )A.6√2B.6C.4√2D.4【答案】B【解析】如图所示的正方体ABCD-A 1B 1C 1D 1的棱长为4.取B 1B 的中点G,即三棱锥G-CC 1D 1为满足要求的几何体,其中最长棱为D 1G,D 1G=√(4√2)2+22=6.例14、如图,网格纸的各小格都是正方形,粗实线画出的是一个几何体的三视图,则这个几何体是( ) A.三棱锥B.三棱柱C.四棱锥D.四棱柱【答案】B【解析】由所给三视图可知该几何体是一个三棱柱(如图).例16、已知某几何体的三视图(单位:cm)如图所示,则该几何体的体积是( )A.108 cm3B.100 cm3C.92 cm3D.84 cm3【答案】B【解析】由三视图可知,该几何体是如图所示长方体去掉一个三棱锥,故几何体的体积是6×3×6-13×12×3×42=100(cm3).故选B.。
文科数学高考真题分类汇编 空间几何体的三视图、表面积和体积答案
故 7 4 r3 = 28 ，所以 r = 2，表面积S = 7 4r 2 + 3 r 2 =17 ，选 A．
83
3
8
4
14．C【解析】该几何体是圆锥与圆柱的组合体，设圆柱底面圆半径为r ，周长为 c ，圆锥
母线长为l ，圆柱高为h ．
( ) 由图得r = 2 ，c = 2πr = 4π ，由勾股定理得：l =
所以，四棱锥 E
−
BB1C1C
的体积V
=
1 3 6 3 = 18 3
.
F
3.解析 该模型为长方体 ABCD − A1B1C1D1 ，挖去四棱锥 O − EFGH 后所得的几何体，其 中 O 为长方体的中心， E ， F ， G ， H ，分别为所在棱的中点， AB = BC = 6cm ， AA1 = 4cm ，所以该模型体积为：
S 即 五边形ABCDE
=
1 2
(4 +
6)
3+
1 2
(2 +
6)
3=
27 ，高为6，
则该柱体的体积是 V = 276 =162 ．
故选B．
2010-2018 年
1．B【解析】∵过直线 O1O2 的平面截该圆柱所得的截面是面积为 8 的正方形，所以圆柱的 高为 2 2 ，底面圆的直径为 2 2 ，所以该圆柱的表面积为
32
10．A【解析】该几何体是由一个高为 3 的圆锥的一半，和高为 3 的三棱锥组成（如图），
其体积为： 1 (1 12 3) +1 (1 2 13) = +1．选 A．
32
32
2
11．B【解析】由题意，该几何体是由高为 6 的圆柱截取一半后的图形加上高为 4 的圆柱，
高考热点：三视图原还方法归类与题型总结，最全类型都在此了
高考热点：三视图原还方法归类与题型总结，最全类型都在此了三视图几乎可以说是高考的必考题，一般在选择题中，此类题看上去简单，实际上有些题型很容易失分，很难搞定，今天我们从基础题型出发，重点分析切割类型的三视图还原问题。
1三视图还原基础题同学们要做到对一些常规立体图形非常熟悉，柱、锥、台、球体，它们规律如下：1.三视图中如果有两个识图是矩形，那么该几何体为柱体。
若第三个视图是圆形，则为圆柱，否则就是棱柱；2.三视图中如果有两个视图是三角形，那么该几何体为锥体。
若第三个视图是圆形，则为圆锥，否则为棱锥；3.三视图中如果有两个视图是梯形，那么该几何体为台体，若第三个视图是圆形，则为圆台，否则为棱台，球体的三视图都是圆形，最容易识别；根据此三点可以快速还原几何体。
题型1.直接还原此题明显是直接还原的题型，还原并不难大多数同学是可以搞定的此题还原也并不困难，锥体顶点的位置要结合三个视图进行，P点在底面上的投影在BC中点上。
题型2直接切割型一般是由一个几何体切割一部分而形成的立体图形“实线表示当面切割，虚线表示背后切割”例1直接在三棱柱中进行切割，由于是实线切割，难度不大。
例2此题可以直观得出是一个三棱锥，但是直接去还原时，很多同学还原不出来。
此时可以借助长方体或者正方体进行切割，如下图所示：例3大家可以先思考此题，此题是一个正方切被一个平面截去一部分得到的三视图，答案看结尾处题型3背面切割一般三视图中有虚线部分，也即从某一方向上看不到的切割，此类还原有时有一定的难度此题依旧可以借助长方体来进行切割，但是俯视图中的实线与虚线怎么还原是难点，虚线是背面切割，实线是正面切割。
还原图如下所示。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
高考文科数学：三视图问题分类解答
例1、概念问题
1、下列几何体各自的三视图中，有且仅有两个视图相同的是．（填序号）
①正方体④正四棱锥
③三棱台
②圆锥
2、如图，折线ABC表示嵌在玻璃正方体内的一根铁丝，请把它的三视图补充完整．
俯视图
左视图
正视图
C
B
A
3 、已知某个几何体的三视图如下图所示，试根据图中所标出的尺寸（单位：㎝），可得这个几何体的体积是．
10
10
20
20
20
20
正视图左视图俯视图
4、已知某个几何体的三视图如下图所示，试根据图中所标出的尺寸（单位：㎝），可得这个几何体的面积是．
2
2
2
2
33
俯视图
正视图左视图
例2、图形判定问题
1、一个几何体的三视图形状都相同，大小均相等，那么这个几何体不可以是（ D ）
A ．球
B ．三棱锥
C ．正方体
D ．圆柱
2、某几何体的正视图和侧视图均如图1所示，则该几何体的俯视图不可能是（ D ）
4、某几何体的正视图如左图所示，则该几何体的俯视图不可能的是(
C )
5、在一个几何体的三视图中，正视图和俯视图如左图，则相应的侧视图可以为（ D ）
6、一个简单几何体的正视图、侧
视图如图所示，则其俯视图不可能为
B
①长方形；②正方形；③圆；④椭圆. 其中正确的是
（A ）①② （B ） ②③ （C ）③④ （D ） ①④ 例3、三视图和几何体的体积相结合的问题
1、下图是一个几何体的三视图，其中正视图是边长为2的等边三角形，侧视图是直角边长分别为1与
3的直角三角形，俯视图是半径为1的半圆，则该几何体的体积等于
A
B
C
D
第5题图
（A ）π63 （B ）π33 （C ）π
33
4 （D ）π21
答案：A
2、一个四棱锥的三视图如图所示，其左视图是等边三角形，该四棱锥的体积等于 A
A ．3
B ．23
C ．33
D ．63
3、设图１是某几何体的三视图，则该几何体的体积为
A ．942π+ Ｂ．36
18π+ Ｃ．9
122
π+ Ｄ．9
182
π+
其体积3439
+332=18322
V ππ=⨯⨯+（）。
答案：D
4、如图是一个几何体的三视图，其中正视图是腰长为2的等腰三角形，俯视图是半径为1的半圆，则该几何体的体积是( B )
A.43
3
π
B.63
6
π
C.12
π D.33
π
例4、三视图和几何体的表面积相结合
1、一个几何体的三视图如图所示，则该几何体的表面积为_____38___。
2、一个多面体的三视图如图所示，其中正视图是正方形，侧视图是等腰三角形. 则该几何体的表面积为( A ) A ．88 B ．98 C ．108 D ．158
3、一个空间几何体得三视图如图所示，则该几何体的表面积为（ C ）
（A ） 48 (B)32+817 (C) 48+817 (D) 80
【解析】由三视图可知几何体是底面是等腰梯形的直棱柱.底面等腰梯形的上底为2，
下底为4，高为4，两底面积和为()1
2244242⨯+⨯=，四个侧面的面积为
()
44221724817++=+，所以几何体的表面积为48817+.故选C.
5、若一个底面是正三角形的三棱柱的正视图如图所示,则其侧面积．．．
等于 ( D )
A.3
B.2
C.23
D.6
6、如图，一个空间几何体的主视图、左视图都是边长为1且一个内角为60°的菱形，俯视图是圆，那么这个几何体的表面积为 （ A ）
A ．π
B ．π2
C ．π3
D ．π4 答案：A
例5、综合问题
1.如图是某直三棱柱（侧棱与底面垂直）被削去上底后的 直观图与三视图的侧视图、俯视图，在直观图中，M 是
BD 的中点，侧视图是直角梯形，俯视图是等腰直角三
角形，有关数据如图所示.
(Ⅰ)求出该几何体的体积。
(Ⅱ)若N 是BC 的中点，求证：//AN 平面CME ； (Ⅲ)求证：平面BDE ⊥平面BCD .
解：(Ⅰ)由题意可知：四棱锥ACDE B -中， 平面ABC ⊥平面ACDE ，AC AB ⊥
所以，⊥AB 平面ACDE 又4,2====CD AE AB AC ，
则四棱锥ACDE B -的体积为：422
2
)24(3131=⨯⨯+⨯
=⋅=AB S V ACDE
4
2
2 2
侧视图
俯视图
直观图
M
D
E
B
A C
N
(Ⅱ)连接MN ，则,//,//CD AE CD MN
又CD AE MN 2
1
==，所以四边形ANME 为平行四边形，EM AN //∴⊄AN 平面CME ,⊂EM 平面
CME ,
所以，//AN 平面CME ；
(Ⅲ)AB AC = ,N 是BC 的中点,BC AN ⊥ 又平面⊥ABC 平面BCD ⊥∴AN 平面BCD 由(Ⅱ)知：EM AN // ⊥∴EM 平面BCD 又⊂EM 平面BDE
所以，平面BDE ⊥平面BCD .
2.已知四棱锥P ABCD -的三视图如右图所示，其中主视图、侧视图是直角三角形，俯视图是有一条对角线的正方形.E 是侧棱PC 上的动点．（Ⅰ）求证：BD AE ⊥（Ⅱ）若E 为PC 的中点，求直线BE 与平面PBD 所成角的正弦值；
(1)证明
：由已知
,PC BC PC DC PC ABCD ⊥⊥⇒⊥面
BD ABCD BD PC ⊂⇒⊥ 面,又因为BD AC ⊥
,,.BD PAC AE PAC BD AE ∴⊥⊂∴⊥ 面又面
(2)连AC 交BD 于点O ，连PO ，由(1)知BD PAC ⊥面，BED PAC ⇒⊥面面，
E EH PO H ⊥过点作于，则EH PBD ⊥面，EBH ∴∠为BE 与平面PBD 所成的角1
3
EH =
,2,BE =则1
2
3sin .62
EBH ∠==
3.已知某几何体的俯视图是如图5所示的矩形，正视图(或称主视图)是一个底边长为8、高为4的等
腰三角形，侧视图(或称左视图)是一个底边长为6、高为4的等腰三角形． (1)求该几何体的体积V ； (2)求该几何体的侧面积S
解: 由已知可得该几何体是一个底面为矩形,高为4,顶点在底面 的射影是矩形中心的四棱锥V-ABCD 。
(1) ()1
864643
V =⨯⨯⨯=
(2) 该四棱锥有两个侧面VAD. VBC 是全等的等腰三角形,
A
且BC 边上的高为
2
2
184422h ⎛⎫
=+= ⎪⎝⎭
, 另两个侧面V AB. VCD 也是全等的等腰三角形,
AB 边上的高为2
226452h ⎛⎫
=+= ⎪⎝⎭
∴112(64285)4024222S =⨯⨯+⨯⨯=+。