第三章 平面机构的运动分析 习题与答案
机械原理习题及答案
第1章平面机构的结构分析1.1解释下列概念1.运动副;2.机构自由度;3.机构运动简图;4.机构结构分析;5.高副低代。
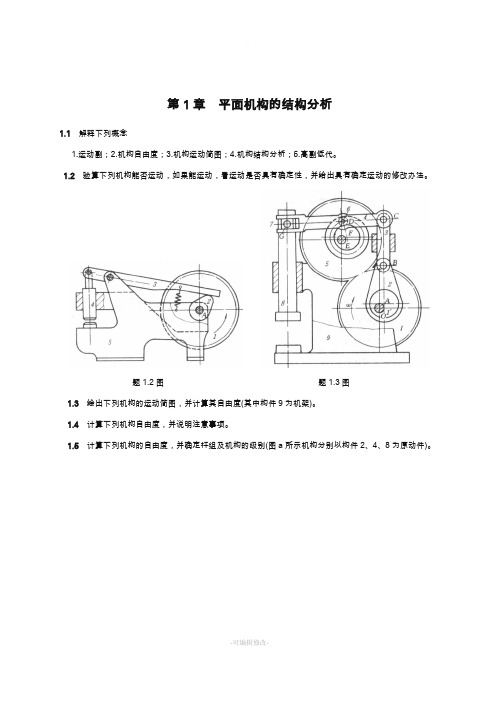
1.2验算下列机构能否运动,如果能运动,看运动是否具有确定性,并给出具有确定运动的修改办法。
题1.2图题1.3图1.3 绘出下列机构的运动简图,并计算其自由度(其中构件9为机架)。
1.4 计算下列机构自由度,并说明注意事项。
1.5计算下列机构的自由度,并确定杆组及机构的级别(图a所示机构分别以构件2、4、8为原动件)。
题1.4图题1.5图第2章平面机构的运动分析2.1试求图示各机构在图示位置时全部瞬心。
题2.1图2.2在图示机构中,已知各构件尺寸为l AB=180mm , l BC=280mm , l BD=450mm ,l CD=250mm ,l AE =120mm ,φ=30º, 构件AB上点E的速度为v E=150 mm /s ,试求该位置时C、D两点的速度及连杆2的角速度ω2。
2.3 在图示的摆动导杆机构中,已知l AB=30mm , l AC=100mm , l BD=50mm ,l DE=40mm ,φ1=45º,曲柄1以等角速度ω1=10 rad/s沿逆时针方向回转。
求D点和E点的速度和加速度及构件3的角速度和角加速度(用相对运动图解法)。
题2.2图题2.3图2.4 在图示机构中,已知l AB =50mm , l BC =200mm , x D =120mm , 原动件的位置φ1=30º, 角速度ω1=10 rad/s ,角加速度α1=0,试求机构在该位置时构件5的速度和加速度,以及构件2的角速度和角加速度。
题2.4图2.5 图示为机构的运动简图及相应的速度图和加速度图。
(1)在图示的速度、加速度多边形中注明各矢量所表示的相应的速度、加速度矢量。
(2)以给出的速度和加速度矢量为已知条件,用相对运动矢量法写出求构件上D 点的速度和加速度矢量方程。
平面机构运动分析思考题与习题

平面机构运动分析一、基本概念1、速度瞬心和机构中速度瞬心的数目1) 瞬心的定义瞬心:相对作平面运动的两构件上瞬时相对速度为零的点(即等速重合点)称为速度瞬心,简称瞬心。
瞬时等速重合点。
绝对速度瞬心:如果两构件之一是静止的,即绝对速度为零的瞬心称为绝对速度瞬心。
相对速度瞬心:如果两个构件都是运动的,即绝对速度不为零的瞬心称为相对速度瞬心。
2) 瞬心数目因为发生相对运动的任意两构件间都有一个瞬心,如果一个机构由m个构件组成,则瞬心数K为:2. 瞬心位置的确定(1)当两构件直接以运动副链接时,按定义确定:1) 当两构件组成转动副时,转动副的转动中心是它们的瞬心;2) 当两构件组成移动副时,瞬心位于导路垂线无穷远处;3) 当两构件组成纯滚动的高副时,接触点就是其速度瞬心;4) 当两构件组成滑动兼滚动的高副时,瞬心位于接触点的公法线上,具体还需据其它条件确定;(2) 对于不直接接触的构件,其瞬心可用三心定理来确定。
三心定理:作相对运动的三个构件共有三个瞬心,这三个瞬心位于一条直线上。
3、矢量图解法原理:1)用一条“有向线段”对应“一个矢量”2)作图遵循“同侧首末相连,两侧起点相同”的原则4、速度、加速度影响定理1)使用场合:统一构件,知2求3。
2)ΔBCD(机构位置图)∽Δbcd(速度多边形)∽Δb’c’d’(加速度多边形)。
3)字母排列顺序一致。
二、思考题1、机构运动分析的目的和任务是什么?图解法和解析法各有何优缺点?2、什么是速度瞬心?绝对瞬心和相对瞬心有何异同点?3.什么是“三心定理”?在确定不直接相联的两构件瞬心位置时,可能会出现什么情况(指不便于作图的情况)?三、练习题1、在图1示曲柄滑块机构中,原动件曲柄以等角速度ω1=5rad/s 逆时针转动。
已知机构尺寸:a=0.30m,b=0.6m。
1)试用瞬心法确定机构在ϕ1=60º位置时滑块3的速度2)用矢量图解法求滑块3的速度,构件2的角速度ω23)求BC上中点D的速度图1 图22、图2所示正弦机构中,已知:曲柄AB以等角速度转动,ω1=5rad/s,l AB=0.1m。
第3章 平面机构的自由度和运动分析

第3章 平面机构的自由度和运动分析
【例3 - 1】 试绘制如图3 - 13(a)所示偏心油泵机构 的运动简图。 解 (1) 分析机构的运动, 判别构件的类型和数目。 图示偏心油泵机构是由偏心轮1、 外环2、 圆柱3和机 架4组成的, 共4个构件。 其中, 偏心轮1为主动件, 它绕着固定轴心A转动。 圆柱3绕轴心C转动, 而外环 2上的叶片a可在圆柱3中移动。 当偏心轮1按图示方向 连续转动时, 偏心油泵可将右侧进油口输入的油液从 其左侧的出油口输出, 从而起到泵油的作用。
第3章 平面机构的自由度和运动分析
【例3 - 2】 计算图3 - 13所示偏心油泵机构的自由度。 解 在偏心油泵机构中, 有三个活动构件, n=3 ; 包含 四个转动副, PL=4; 没有高副, PH=0。 所以由式 (3 - 1)可得机构自由度为 F=3n-2PL-PH=3×3-2×4=1
第3章 平面机构的自由度和运动分析
3.3.2 机构具有确定运动的条件 运动链和机构都是由构件和运动副组成的系统。 机构要实现预期的运动传递或改变, 就必须具有可动 性和运动的确定性。 将运动链中的一个构件作为机架, 当运动链中的一个或几个主动件的运动确定时, 其余 从动件的运动也随之确定, 则称机构具有确定的相对 运动。 运动链可动性的判别可利用式(3 - 1)表示的机构自 由度的计算公式来进行, 见表 3 – 1(略)。
第3章 平面机构的自由度和运动分析
1 3 2 (a) 2
1
3 (b)
图3 - 16 复合铰链
第3章 平面机构的自由度和运动分析
【例3 - 3】 在图3 - 17所示的压缩机机构中,试判 断铰链C和铰链E是否是复合铰链。 解 从图3 - 17中可知, 铰链 C和E 处均有两个以上的 构件, 而且相互汇交在一起。 其中, 铰链C处有5个 构件, 即构件2、 3、 4、 5和8; 而铰链E处有4个构 件, 即构件5、6、 7和8。 (1) 分析。 分析过程见表3 - 2。
平面机构的运动分析习题和答案Word版
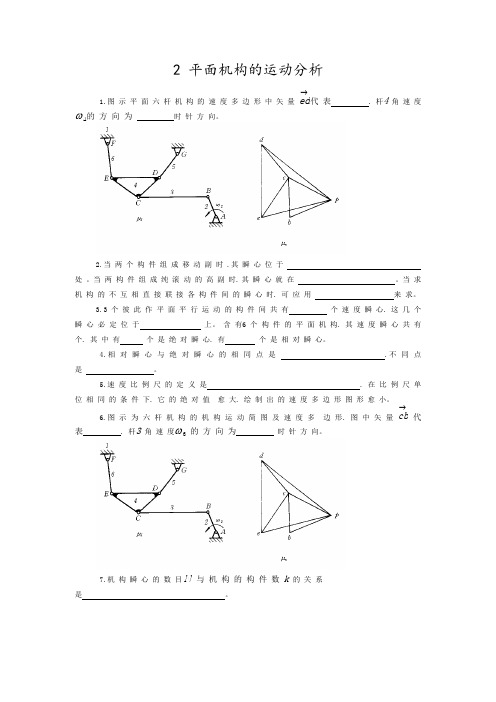
24.在同一构件上.任意两点的绝对加速度间的关系式中不包含哥氏加速度。- - - - ( )
25.当牵连运动为转动.相对运动是移动时.一定会产生哥氏加速度。- - - - - - - - ( )
26.在平面机构中.不与机架直接相连的构件上任一点的绝对速度均不为零。- - - ( )
27.两构件组成一般情况的高副即非纯滚动高副时.其瞬心就在高副接触点处。- - ( )
28.给定导杆机构在图示位置的速度多边形。该瞬时 和 的正确组合应是图。
29.给定图示六杆机构的加速度多边形.可得出
(A)矢量 代表 . 是顺时针方向;
(B)矢量 代表 . 是逆时针方向;
(C)矢量 代表 . 是顺时针方向;
(A)绝对速度等于零的重合点;
(B)绝对速度和相对速度都等于零的重合点;
(C)绝对速度不一定等于零但绝对速度相等或相对速度等于零的重合点。
40.下图是四种机构在某一瞬时的位置图。在图示位置哥氏加速度不为零的机构为。
41.利用相对运动图解法求图示机构中滑块2上 点的速度 的解题过程的恰当步骤和利用的矢量方程为:
9.当两构件组成转动副时.其速度瞬心在处;组成移动副时.其速度瞬心在处;组成兼有相对滚动和滑动的平面高副时.其速度瞬心在上。
10..速度瞬心是两刚体上为零的重合点。
11.铰链四杆机构共有个速度瞬心.其中个是绝对瞬心.个是相对瞬心。
12.速度影像的相似原理只能应用于的各点.而不能应用于机构的的各点。
13.作相对运动的3个构件的3个瞬心必。
14.当两构件组成转动副时.其瞬心就是。
15.在摆动导杆机构中.当导杆和滑块的相对运动为动.牵连运动为动时.两构件的重合点之间将有哥氏加速度。哥氏加速度的大小为;方向与的方向一致。
3平面机构的运动分析习题

cb→第三章平面机构的运动分析学号姓名一、填空题1.当两个构件组成移动副时,其瞬心位于垂直于移动方向的处。
当两构件组成纯滚动的高副时,其瞬心就在点。
当求机构中不互相直接连接各构件间的瞬心时,可应用来求。
2.3个彼此作平面平行运动的构件间共有个速度瞬心,这几个瞬心必定位于条直线上。
含有6个构件的平面机构,其速度瞬心共有个,其中个是绝对瞬心,有个是相对瞬心。
3.图示为六杆机构的机构运动简图及速度多边形,图中矢量代表,杆3角速度ω3的方向为时针方向。
4.速度影像的相似原理只能应用于________________的各点,而不能应用于机构的____________的各点。
5.一个运动矢量方程只能求解________个未知量。
6.当两构件的相对运动为动,牵连运动为动时,两构件的重合点之间将有哥氏加速度。
哥氏加速度的大小为,方向与的方向一致。
二、选择题1.下列说法中正确的是。
A、在机构中,若某一瞬时,两构件上的重合点的速度大小相等,则该点为两构件的瞬心;B、在机构中,若某一瞬时,一可动构件上某点的速度为零,则该点为可动构件与机架的瞬心;C、在机构中,若某一瞬时,两可动构件上重合点的速度相同,则该点称为它们的绝对瞬心;D、两构件构成高副,则它们的瞬心一定在接触点上。
2.下列机构中k C Ca 32 不为零的机构是。
A 、(a)与(b);B 、(b)与(c);C 、(a)与(c);D 、(b)。
3.下列机构中k C Ca 32 为零的机构是。
A 、(a);B 、(b);C 、(c);D 、(b)与(c)。
4.两个运动构件间相对瞬心的绝对速度。
A 、均为零;B 、不相等;C 、不为零且相等5.图示连杆机构中滑块2上E 点的轨迹应是。
A 、直线;B 、圆弧;C 、椭圆;D 、复杂平面曲线。
三、画出图示机构在图示位置时的全部速度瞬心的位置四、在图示机构中,设已知L AB=0.3m,L BC=0.5m,ω1=1rad/S以顺时针转动,当曲柄AB在图示位置时,试用矢量方程图解法求解:1)滑块3的速度υC和连杆2的角速度ω2。
第七版《机械原理》-西北工业大学孙恒-配套习题册答案详解

题 2-8 图示为一刹车机构。刹车时,操作杆 1 向右拉,通过构件 2、3、4、5、6 使两闸瓦刹住车轮。试计 算机构的自由度,并就刹车过程说明此机构自由度的变化情况。(注:车轮不属于刹车机构中的构件。)
解:1)未刹车时,刹车机构的自由度
n 6 pl 8 ph 0
F 3n 2 pl ph 3 6 28 0 2
2) n 5 pl 7 ph 0
F 3n 2 pl ph 35 2 7 0 1
所设计的一种假肢膝关节机构,该机构能 为机架,
自由度,并作出大腿弯曲 90 度时的机构
简图。大腿弯曲 90 度时的机构运动简图
题 2-6 试计算如图所示各机构的自由度。图
a、d 为齿轮-连杆组合机构;图 b 为凸轮-连
销子与件 5 上的连杆曲线槽组成的销槽联接使活动台板实现收
放动作。在图示位置时,虽在活动台板上放有较重的重物,活
动台板也不会自动收起,必须沿箭头方向推动件 2,使铰链 B、D 重合时,活动台板才可收起(如图中双
点划线所示)。现已知机构尺寸 lAB=lAD=90mm,lBC=lCD=25mm,试绘制机构的运动简图,并计算其自由度。
p 2 pl ph 3n 2 17 3 310 3 4 局部自由度 F 4
F 3n (2 pl ph p) F 313 (217 4 4) 4 1
解法二:如图 2-7(b)
局部自由度 F 1 F 3n (2 pl ph p) F 3 3 (2 3 1 0) 1 1
压运动。试绘制其机构运动简图,并计算自由度。
解:分析机构的组成: 此机构由偏心轮 1’(与齿轮 1 固结)、连杆 2、滑杆 3、摆杆 4、齿轮 5、滚子 6、滑块 7、冲头 8 和机 架 9 组成。偏心轮 1’与机架 9、连杆 2 与滑杆 3、滑杆 3 与摆杆 4、摆杆 4 与滚子 6、齿轮 5 与机架 9、滑 块 7 与冲头 8 均组成转动副,滑杆 3 与机架 9、摆杆 4 与滑块 7、冲头 8 与机架 9 均组成移动副,齿轮 1
西北工业大学机械原理习题答案

p'=1F'=1
2×14+1-1)-1=1
机构原动件数目=1
机构有无确定运动?有确定运动
计算下列机构的自由度,并判断机构级别。
1—10 1)按传动顺序用数字1、2、3…在图示机构上给构件编号。
2)计算自由度,并判断有无确定运动:
方向:⊥CD ⊥AB ⊥BC 方向:C→D ⊥CD B→A C→B ⊥CB
大小: ? ω1lAB? 大小:ωCD2lCD? ω12lABωCB2lCB?
有:vC=0,ω3=0,ω2=0.5ω1aC=aCt=1.5aB=1.5ω12lAB
方向: ? ⊥AB ⊥BC∥BC
大小: ? ω1lAB? 0 ?
在图中指明复合铰链、局部自由度和虚约束
n=9pl=13ph=0
p'=0F'=0
F=3n-(2pl+ph-p′)-F′
=3×9-(2×13+0-0)-0=1
机构原动件数目=1
机构有无确定运动?有确定运动
3)杆组拆分,并判断机构级别:
(从远离原动件的方向开始拆分)可见,该机构为II级机构。
1—111)按传动顺序用数字1、2、3…在图示机构上给构件编号。
解:自由度计算:画出机构示意图:
n=3
pL=4pH=0
p'=0F'=0
F=3n-(2pl+ph-p′)-F′
=3×3-(2×4+0-0)-0
=1
图b)缝纫机针杆机构原动件1绕铰链A作整周转动,使得滑块2沿滑槽滑动,同时针杆作上下移动,完成缝线动作。
解:自由度计算:画出机构示意图:
n=3
pL=4pH=0
2)计算自由度,并判断有无确定运动:
第三章 平面机构的运动分析

解:解:
a) b)
解:解:
c)d)
想一想:在图c及图d所示的机构中,两高副元素间是否为纯滚动?它们的瞬心应位于何处?
3-3在图示的齿轮连杆组合机构中,试用瞬心法求齿轮1与齿轮3的传动比1/3。
解:1)计算此机构所有瞬心的数目
3-5在图示的摇杆机构中,已知lAB=30mm,lAC=100mm,lBD=50mm,lDE=40mm,,曲柄以等角速度=10rad/s回转,试用图解法求机构在º位置时,点D和点E的速度和加速度,以及构件2的角速度和角加速度。
解:(1)选取比例尺(l=0.002m/mm)做机构运动简图
(2)速度分析(v=0.005(m/s)/mm)
第三章
3-1填空题
(1)当构件组成转动副时,其瞬心在处;当组成移动副时,其瞬心在处;当组成兼有滑动和滚动的高副时,其瞬心在处。
(2)哥氏加速度的大小为________;方向为。
(3)在由N个构件组成的机构中,共有个瞬心,其中个绝对瞬心。
(4)速度影像的相似原理只能应用于的各点,而不能应用于机构中不同构件上的各点。
K=
2)为了求传动比1/3需求出如下瞬心(填出下角标)
PPPPP
3)传动比1/3的计算公式是
想一想:齿轮1与齿轮3的转向是相同还是相反?
3-4判断图中哥氏加速度的方向是否正确(正确的在括号里打“√”,错误的在括号里打“×”,)。
解:
图a ( )图b ( )图c ( )
想一想:在什么条件下存在哥氏加速度?在判断哥氏加速度时需要注意哪些事项?
(2)构件2上速度为零的点I的位置,并求出该点的加速度aI;
(3)构件2上加速度为零的点Q的位置,并求出该点的速度vQ。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三章平面机构的运动分析1 机构运动分析包括哪些内容2 对机构进行运动分析的目的是什么3 什么叫速度瞬心4 相对速度瞬心和绝对速度瞬心有什么区别5 在进行机构运动分析时,速度瞬心法的优点及局限是什么6 什么叫三心定理7 怎样确定组成转动副、移动副、高副的两构件的瞬心怎样确定机构中不组成运动副的两构件的瞬心8 在同一构件上两点的速度和加速度之间有什么关系9组成移动副两平面运动构件在瞬时重合点上的速度和加速度之间有什么关系·10 平面机构的速度和加速度多边形有何特性11 什么叫“速度影像”和“加速度影像”,它在速度和加速度分析中有何用处12 机构运动时在什么情况下有哥氏加速度出现它的大小及方向如何决定13 如何根据速度和加速度多边形确定构件的角速度和角加速度的大小和方向14 如何确定构件上某点法向加速度的大小和方向15 当某一机构改换原动件时,其速度多边形是否改变其加速度多边形是否改变16 什么叫运动线图它在机构运动分析时有什么优点17 当两构件组成转动副时,其相对速度瞬心在处;组成移动副时,其瞬心在处;组成滑动兼滚动的高副时,其瞬心在处.18相对瞬心与绝对瞬心相同点是,而不同点是.19速度影像的相似原理只能用于两点,而不能用于机构的各点.…20速度瞬心可以定义为互相作平面相对运动的两构件上的点.21 3个彼此作平面平行运动的构件共有个速度瞬心,这几个瞬心必位于.含有6个构件的平面机构,其速度瞬心共有个,其中个是绝对瞬心,有个相对瞬心.22 在图示机构中,已知原动件1以匀角速度沿逆时针方向转动,试确定:(1)机构的全部瞬心;(2)构件3的速度v3(需写出表达式)。
23如图所示齿轮连杆机构中,已知齿轮2和5的齿数相等,即25z z =,齿轮2以2100ω=rad/s 顺时针方向转动,试用瞬心法求构件3的角速度ω3的大小和方向。
(取0.001l μ=m/mm 。
)24 图示为按比例尺绘制的牛头刨床机构运动简图和速度矢量多边形。
试由图中的比例尺计算导杆3的角速度ω3和滑块2的角速度ω2,并指出其方向。
(提示:S 3为构件3上特殊点,据3S B CD ⊥、3D S D v ⊥求得,作题时不必去研究v S 3如何求得。
)(取0.005l μ=m/mm ,0.003v μ=(m/s)/mm 。
)25在图示机构中,已知机构位置图和各杆尺寸,ω1=常数,BDBE l l =,13EF BC BE l l l ==,试用相对运动图解法求v F 、a F 、v C 、a C 及ω2、。
\26 在图示机构中,已知:各杆长度,ω1为常数。
试求v5及a5。
27 在图示机构中,已知AB BE EC EF CD====12,AB BC⊥,BC EF⊥,BC CD⊥,ω1=常数,求构件5的角速度和角加速度大小和方向。
28图示为十字滑块联轴器的运动简图。
若ω115=rad/s,试用相对运动图解法求:(1)ω3、;(2)杆2相对杆1和杆3的滑动速度;(3)杆2上C点的加速度a C。
(μl=0002.m/mm。
)。
29已知机构位置如图,各杆长度已知,活塞杆以v 匀速运动。
求:(1)3v 、3a 、2ω; (2)5v 、5a 、2α。
(用相对运动图解法,并列出必要的解算式。
)30在图示机构中,已知各构件尺寸1AB l l =,2AC l l =,3CD l l =,4DE l l =,原动件1以等角速度ω1沿逆时针方向转动。
用解析法求滑块2对于杆3的相对滑动速度r r v s =和加速度r r a s =,杆3、4的加速度3ω、ω4和角加速度α3、α4,以及滑块5的速度v E 和加速度a E 。
;第三章 平面机构的运动分析17.当两构件组成转动副时,其相对速度瞬心在 转动副的圆心 处;组成移动副时,其瞬心在 垂直于移动导路的无穷远 处;组成滑动兼滚动的高副时,其瞬心在接触点两轮廓线的公法线上. 18.相对瞬心与绝对瞬心相同点是 都是两构件上相对速度为零,绝对速度相等的点 ,而不同点是 相对瞬心的绝对速度不为零,而绝对瞬心的绝对速度为零 .19.速度影像的相似原理只能用于 同一构件上的 两点,而不能用于机构 不同构件上 的各点. 20.速度瞬心可以定义为互相作平面相对运动的两构件上,相对速度为零,绝对速度相等 的点. 21. 3个彼此作平面平行运动的构件共有 3 个速度瞬心,这几个瞬心必位于 同一条直线上 .含有6个构件的平面机构,其速度瞬心共有 15 个,其中 5 个是绝对瞬心,有 9 个相对瞬心. 22(1)求出瞬心数(1)43622k k N -⨯>=== 瞬心如图。
(2)31314131P v v PP ω==⋅ 方向向上'23(1)求出13P(2)求3ω23P 点速度1323AB BP v l l ωω=⋅=⋅10AB l l AB μ=⋅=mm 131325BP l l BP μ=⋅=mm1332101004025AB BP l l ωω==⨯=rad/s ,逆时针方向2433333/( )/()DC DC v l v l d c DC ωμμ==⋅⋅(640.003)/(640.005)0.6=⨯⨯=rad/s ,顺时针方向。
23ωω=25 (1)速度分析)112B AB B v l v ω==3232B B B B v v v =+,取μv 作速度多边形,影像法得e 和f 点。
F v v pf μ=,2333//B BD v BD v l pb l ωωμ===,顺时针方向22C B CB v v v =+,2C v v pc μ=。
(或另法2323C C C C v v v =+)(2)n 21112B B AB B a a l a ω===,n t k r3323232B B B B B B B a a a a a +=++,取μa 作图,影像法得e '和f '点。
F a a f πμ'=,n t222C B CB CB a a a a =++ 其中t233/B BD a l αα==,顺时针方向,2C a a c πμ'=26(1)C B CB v v v =+,取μv 作图求出v C 、v CB 。
利用影像法求v D 2(扩大杆2)。
4242D D D D v v v =+%求得544v v pd ==,指向如图。
(2)n tC B CB CBa a a a =++,取a μ作图。
k r424242D D D D D D a a a a =++求得n544 D a a a d πμ==。
27 (1)求5ωr vB //rv C ,∴构件2瞬时平动,ω20=41E B AB v v l ω==,4545E E E E v v v =+,v E 4//v E 5⊥v E E 45 450E E v =,4515E E AB EF v v l l ωω=== AB EF l l =,51ωω=,逆时针方向[(2)求α524E E a a =n t 444E B E B E B a a a a =++,平动n40E B a =n t k r4554545E E E E E E E a a a a a =+++ 450E E v =,k4554520E E E E a v ω==t n t r25545B E B E E E E a a a a a +=++将该式向BC 方向投影有t 50E a =,即50α=28(1)32115 ωωω===rad/s ,3210ααα===(2)2222C A CA B CB v v v v v =+=+,2121A A A A v v v =+》2323B B B B v v v =+,220.72CA CA v l ω==m/s ,22 1.29CB CB v l ω==m/s由速度多边形量得:2122= 1.33A A A v v v p a μ==m/s ,2322= 0.74 B B B v v v p b μ==m/s(3)n t n t222222 CA CA CAB CB CB a a a a a a a =++=++ k r 212121A A A A A A a a a a =++,k r232323B B B B B B a a a a =++整理得:k r n k r n2121223232C A A A A CA B B B B CB a a a a a a a =++=++ k2139.9 A A a =m/s 2,n 210.8 CA a =m/s 2 k 2322.2 B B a =m/s 2,n 219.8 CB a =m/s 2由图:n460 C a a c πμ==m/s 2 (比例尺0.02 v μ=(m/s)/mm , 1 a μ=(m/s 2)/mm)\29(1)B A BA v v v =+,选比例尺μv 作速度多边形3 B v v v p b μ==用影像法求得22 C v v p c μ=4242C C C C v v v =+544 C v v v p c μ==2/ /BA AB v AB v l b a l ωμ==,顺时针方向4224C C v v c c μ=(2)n t B A BA BA a a a a =++,选比例尺μa 作加速度多边形。
由影像法求得22 C a a c πμ'=、k r424242C C C C C C a a a a =++3 B a a a b πμ'== 544C a a a c πμ'== t242//BA BA a BA a l n b l ααμ''===,逆时针方向。
30 (1) (机构位置) 封闭矢量方程∆ABC :12r 0l l s +-=∆CDE :340E l l x +-=位置矢量在x 、y 轴上的投影:s L r cos cos θθ311=,s L L r sin sin θθ3112=+ L L x E 33440cos cos θθ+-=,L L 33440sin sin θθ+=(2)速度矩阵方程位置方程微分 ~v s L r r cos sin sin θωθωθ333111-=-,v s L r r sin cos cos θωθωθ333111+=---=L L v E 3334440ωθωθsin sin ,L L 3334440ωθωθcos cos +=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----00cos sin 0cos cos 01sin sin 000cos sin 00sin cos 11111143r 443344333r 33r 3θωθωωωθθθθθθθθL L v v L L L L s s E(3)加速度矩阵方程速度方程微分a v v s L r r r r cos sin sin (cos sin )cos θωθωθωθαθωθ33333323331121---+=- a v v s L r r r r sin cos cos (sin cos )sin θωθωθωθαθωθ33333323331121+++-+=------=L L L L a E 332333344244440ωθαθωθαθcos sin cossin -+-+=L L L L 332333344244440ωθαθωθαθsin cos sin cos。
