(完整版)初三解直角三角形练习题基础
中考《解直角三角形》复习练习题及答案
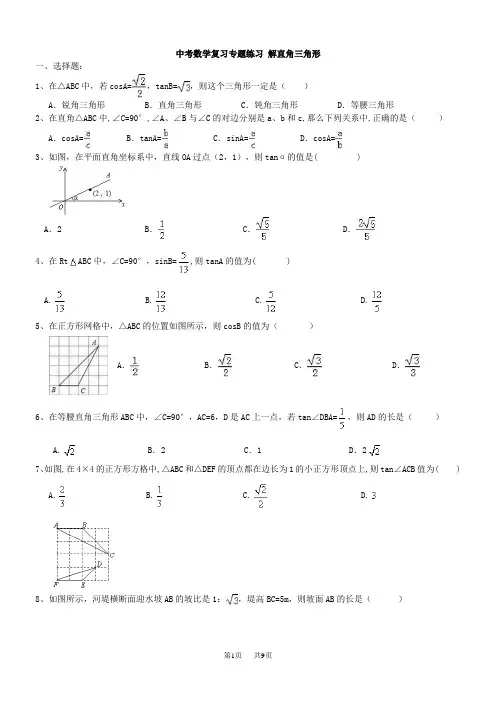
中考数学复习专题练习解直角三角形一、选择题：1、在△ABC中，若cosA=，tanB=，则这个三角形一定是（）A．锐角三角形 B．直角三角形 C．钝角三角形 D．等腰三角形2、在直角△ABC中,∠C=90°,∠A、∠B与∠C的对边分别是a、b和c,那么下列关系中,正确的是（）A．cosA= B．tanA= C．sinA= D．cosA=3、如图，在平面直角坐标系中，直线OA过点（2，1），则tanα的值是( )A．2 B． C． D．4、在Rt ABC中，∠C=90°，sinB=,则tanA的值为( )A. B. C. D.5、在正方形网格中，△ABC的位置如图所示，则cosB的值为（）A． B． C． D．6、在等腰直角三角形ABC中，∠C=90°，AC=6，D是AC上一点，若tan∠DBA=，则AD的长是（）A. B．2 C．1 D．27、如图,在4×4的正方形方格中,△ABC和△DEF的顶点都在边长为1的小正方形顶点上,则tan∠ACB值为( )A. B. C. D.8、如图所示，河堤横断面迎水坡AB的坡比是1：，堤高BC=5m，则坡面AB的长是（）A.10mB.mC.15m D．m9、如图是拦水坝的横断面，斜坡AB的水平宽度为12米，斜面坡度为1：2，则斜坡AB的长为( )A.4米B.6米C.12米D.24米10、如图,在△ABC中，∠BAC=90°，AB=AC，点D为边AC的中点，DE⊥BC于点E，连接BD，则tan∠DBC的值为( )A. B.－1 C．2－ D.11、如图,已知的三个顶点都在方格图的格点上，则的值为( )A. B. C. D.12、如图，在四边形ABCD中，E、F分別是AB、AD的中点，若EF=2，BC=5，CD=3，则tanC等于（）A． B． C． D．二、填空题:13、在△ABC中，∠A，∠B都是锐角，若sinA=，cosB=，则∠C=________．14、已知在Rt△ABC中，∠C=90°，AB=15，cosB=，则BC= ．15、如图，先锋村准备在坡角为α=30°山坡上栽树，要求相邻两树之间的水平距离为5米，那么这两树在坡面上的距离AB为______米．16、如图，菱形ABCD的边长为15，sin∠BAC=，则对角线AC的长为______．17、如图,正方形ABCD的边长为4,点M在边DC上,M、N两点关于对角线AC对称,若DM=1,则tan∠ADN= ．18、如图，△ABC的三个顶点分别在边长为1的正方形网格的格点上，则tan(+) tan+tan.（填“＞”“＝”“＜”）19、如图在四边形ABCD中，∠ACB=∠BAD=105°，∠B=∠D=45°若 AD=,则AB=__________20、如图所示的半圆中，是直径，且，，则的值是．21、如图，在菱形ABCD中，DE⊥AB，，BE=2，则________.22、如图,在中,是边边上的中线,如果,tanB值是________23、如图，小明在一块平地上测山高，先在B处测得山顶A的仰角为30°，然后向山脚直行100米到达C处，再测得山顶A的仰角为45°，那么山高AD为米.24、如图，在顶角为30°的等腰三角形ABC中，AB=AC，若过点C作CD⊥AB于点D，则∠BCD=15°．根据图形计算tan15°= ．三、简答题:25、在△ABC中，a，b，c分别是∠A，∠B，∠C的对边，且c=,若关于x的方程(＋b)x2＋2ax＋(-b)=0有两个相等的实数根，方程2x2-(10sin A)x＋5sin A=0的两个实数根的平方和为6，求△ABC的面积．26、已知：如图，正方形ABCD中，点E为AD边的中点，联结CE. 求cos∠ACE和tan∠ACE的值.27、如图，一艘海轮在A点时测得灯塔C在它的北偏东42°方向上，它沿正东方向航行80海里后到达B处，此时灯塔C在它的北偏西55°方向上．（1）求海轮在航行过程中与灯塔C的最短距离（结果精确到0.1）；（2）求海轮在B处时与灯塔C的距离（结果保留整数）．（参考数据：sin55°≈0.819，cos55°≈0.574，tan55°≈1.428，tan42°≈0.900，tan35°≈0.700，tan48°≈1.111）28、如图，河流两岸a，b互相平行，C，D是河岸a上间隔50m的两个电线杆．某人在河岸b上的A处测得∠DAB=30°，然后沿河岸走了100m到达B处，测得∠CBF=60°，求河流的宽度CF的值．（结果精确到个位）29、张老师利用休息时间组织学生测量山坡上一棵大树CD的高度，如图，山坡与水平面成30°角（即∠MAN=30°），在山坡底部A处测得大树顶端点C的仰角为45°，沿坡面前进20米，到达B处，又测得树顶端点C的仰角为60°（图中各点均在同一平面内），求这棵大树CD的高度（结果精确到0.1米，参考数据：≈1.732）30、如图，在正方形ABCD中，点E、F分别是BC、CD的中点，DE交AF于点M，点N为DE的中点．（1）若AB=4，求△DNF的周长及sin∠DAF的值；（2）求证：2AD•NF=DE•DM．31、中考英语听力测试期间T需要杜绝考点周围的噪音．如图，点A是某市一中考考点，在位于考点南偏西15°方向距离500米的C点处有一消防队．在听力考试期间，消防队突然接到报警电话，消防车需沿北偏东75°方向的公路CF前往救援．已知消防车的警报声传播半径为400米，若消防车的警报声对听力测试造成影响，则消防车必须改道行驶．试问：消防车是否需要改道行驶？说明理由．（≈1.732）参考答案1、A．2、C．3、B．4、D.5、B．6、B.7、B.8、A．9、B.10、A.11、D.12、B．13、答案为：60°14、答案为：9．15、答案为：（米）．16、答案为24．17、答案为：4．3 18、答案为：>. 19、答案为：.20、答案为： ;21、答案为：2 ;22、答案为：23、答案为：137．24、答案为：2﹣．25、解：∵方程(5＋b)x2＋2ax＋(5－b)=0有两个相等的实数根，且c=5，∴△=(2a)2－4(c＋b)(c-b)=0，∴a2＋b2=c2,则△ABC为直角三角形，且∠C=90°．设x1，x2是方程2x2－(10sin A)x＋5sin A=0的两个根，则根据根与系数的关系有x1＋x2=5sin A，x1·x2=sin A．∴x12＋x22=(x1＋x2)2－2x l·x2=(5sin A)2－2×sin A=6，解得sinA=或sinA=－(舍去)，∴a=csin A=3，b==4，S△ABC=ab==18．26、解：过点作于点，∵四边形是正方形，∴平分，．∴，．∵是中点，∴．设，则，，．在Rt△AEF中，，．∴．∴，．27、【解答】解：（1）过C作AB的垂线，设垂足为D，根据题意可得：∠1=∠2=42°，∠3=∠4=55°，设CD的长为x海里，在Rt△ACD中，tan42°=，则AD=x•tan42°，在Rt△BCD中，tan55°=，则BD=x•tan55°，∵AB=80，∴AD+BD=80，∴x•tan42°+x•tan55°=80，解得：x≈34.4，答：海轮在航行过程中与灯塔C的最短距离是34.4海里；（2）在Rt△BCD中，cos55°=，∴BC=≈60海里，答：海轮在B处时与灯塔C的距离约为60海里．28、【解答】解：过点C作CE∥AD，交AB于E∵CD∥AE，CE∥AD∴四边形AECD是平行四边形∴AE=CD=50m，EB=AB﹣AE=50m，∠CEB=∠DAB=30°又∠CBF=60°，故∠ECB=30°∴CB=EB=50m∴在Rt△CFB中，CF=CB•sin∠CBF=50•sin60°≈43m答：河流的宽度CF的值为43m．29、解：如图，过B作BE⊥CD交CD延长线于E，∵∠CAN=45°，∠MAN=30°，∴∠CAB=15°∵∠CBD=60°，∠DBE=30°，∴∠CBD=30°，∵∠CBE=∠CAB+∠ACB，∴∠CAB=∠ACB=15°，∴AB=BC=20，在Rt△BCE中，∠CBE=60°，BC=20，∴CE=BCsin∠CBE=20×BE=BCcos∠CBE=20×0.5=10，在Rt△DBE中，∠DBE=30°，BE=10，∴DE=BEtan∠DBE=10×，∴CD=CE﹣DE=≈11.5，答：这棵大树CD的高度大约为11.5米．30、：（1）解：∵点E、F分别是BC、CD的中点，∴EC=DF=×4=2，由勾股定理得，DE==2，∵点F是CD的中点，点N为DE的中点，∴DN=DE=×2=，NF=EC=×2=1，∴△DNF的周长=1++2=3+；在Rt△ADF中，由勾股定理得，AF===2，所以，sin∠DAF===；（2）证明：在△ADF和△DCE中，，∴△ADF≌△DCE（SAS），∴AF=DE，∠DAF=∠CDE，∵∠DAF+∠AFD=90°，∴∠CDE+∠AFD=90°，∴AF⊥DE，∵点E、F分别是BC、CD的中点，∴NF是△CDE的中位线，∴DF=EC=2NF，∵cos∠DAF==，cos∠CDE==，∴=，∴2AD•NF=DE•DM．31、【解答】解：过A作AD⊥CF于D，由题意得∠CAG=15°，∴∠ACE=15°，∵∠ECF=75°，∴∠ACD=60°，在Rt△ACD中，sin∠ACD=，则AD=AC•sin∠ACD=250≈433米，433米＞400米，∴不需要改道．答：消防车不需要改道行驶．。
解直角三角形基础训练题
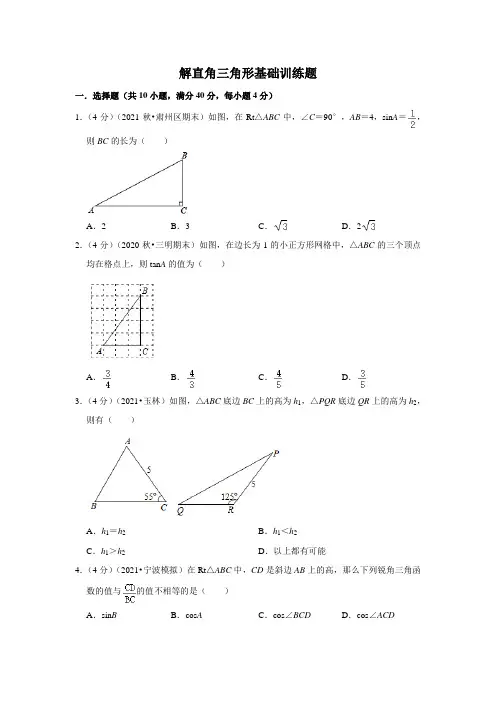
解直角三角形基础训练题一．选择题（共10小题，满分40分，每小题4分）1．（4分）（2021秋•肃州区期末）如图，在Rt△ABC中，∠C＝90°，AB＝4，sin A＝，则BC的长为（）A．2B．3C．D．22．（4分）（2020秋•三明期末）如图，在边长为1的小正方形网格中，△ABC的三个顶点均在格点上，则tan A的值为（）A．B．C．D．3．（4分）（2021•玉林）如图，△ABC底边BC上的高为h1，△PQR底边QR上的高为h2，则有（）A．h1＝h2B．h1＜h2C．h1＞h2D．以上都有可能4．（4分）（2021•宁波模拟）在Rt△ABC中，CD是斜边AB上的高，那么下列锐角三角函数的值与的值不相等的是（）A．sin B B．cos A C．cos∠BCD D．cos∠ACD5．（4分）（2021秋•钢城区期末）在Rt△ABC中，∠C＝90°，cos A＝，AB＝10，则AC 的长为（）A．3B．4C．6D．86．（4分）（2021秋•岱岳区期末）如图，在Rt△ABC中，∠ACB＝90°，CD⊥AB，D为垂足．若AC＝8，BC＝6，则sin∠ACD的值为（）A．B．C．D．7．（4分）（2021秋•万州区期末）在△ABC中，∠A、∠B为锐角，cos A＝，tan B＝，则△ABC的形状为（）A．等腰三角形B．等边三角形C．直角三角形D．锐角三角形8．（4分）（2022•锦江区校级开学）在Rt△ABC中，∠ACB＝90°，BC＝12，tan B＝，则AB的长为（）A．8B．12C．13D．189．（4分）（2021秋•启东市期末）如图，在平面直角坐标系xOy中，AB＝2，连结AB 并延长至C，连结OC，若满足OC2＝BC•AC，tanα＝3，则点C的坐标为（）A．（﹣2，6）B．（﹣3，9）C．（﹣，）D．（﹣，）10．（4分）（2022•绿园区校级一模）如图，电线杆AB的中点C处有一标志物，在地面D 点处测得标志物的仰角为32°，若点D到电线杆底部点B的距离为a米，则电线杆AB的长可表示为（）A．米B．米C．2a•cos32°米D．2a•tan32°米二．填空题（共6小题，满分30分，每小题5分）11．（5分）（2021秋•长春期末）如图，在△ABC中，CD⊥AB，垂足为D．若AB＝12，CD ＝6，tan A＝，则sin B的值为．12．（5分）（2021秋•船营区校级期末）如图，在Rt△ABC中，∠C＝90°，点D在AC上，∠DBC＝∠A，若AC＝4，cos A＝，则BD的长度为．13．（5分）（2021秋•温江区校级月考）在Rt△ABC中，∠ACB＝90°，∠A＝30°，则AC：BC＝．14．（5分）（2021秋•巴中期末）定义：等腰三角形中底边与腰的比叫做顶角正对（sad），即在△ABC中，AB＝AC，顶角A的正对记作sadA，这时sadA＝．如图，若在△ABC中，AB＝AC，sin B＝，则sadA的值是．15．（5分）（2021秋•城关区期末）如图，在Rt△ABD中，AB＝6，tan∠ADB＝，点C 为斜边BD的中点，P为AD上任一点，过点P作PE⊥AC于点E，PF⊥BD于点F，则PE+PF＝．16．（5分）（2020秋•德江县期末）如图，在Rt△ABC中，∠ACB＝90°，CD⊥AB，垂足为D，AF平分∠CAB，交CD于点E，交CB于点F，若AC＝6，tan B＝，则CE＝．三．解答题（共5小题，满分50分，每小题10分）17．（10分）（2021秋•五华区校级期末）在Rt△ABC中，∠C＝90°，∠B＝25°，b＝10，解这个直角三角形（结果保留小数点后一位）．（参考数据：sin25°≈0.42，cos25°≈0.91，tan25°≈0.47）18．（10分）（2021秋•长丰县期末）如图，在△ABC中，AB＝5，AC＝8，∠A＝60°．（1）求BC的长．（2）求sin B．19．（10分）（2021春•徐汇区校级月考）如图，在△ABC中，∠ACB＝90°，∠CAB＞∠B，CD是斜边AB上的中线，过点A作∠CAE＝∠B，交BC于点E，交CD于点H，且AH ＝2CH．（1）求sin B的值；（2）当CD＝时，求BE的长．20．（10分）（2020秋•宁德期末）如图，在四边形ABCD中，∠ABC＝90°，AD＝BD，BC ＝CD．（1）若BD＝13，AB＝10，求cos∠CBD的值；（2）设△ABD的面积为S1，△BCD的面积为S2，求证：＝4cos2∠CBD．21．（10分）（2021•苏州二模）如图，∠ABC＝45°，其中P、Q分别是射线BA、BC上的点，BP＝3．（1）给出条件①PQ＝4；②∠BPQ＝105°；③PQ＝6．能使BQ的长唯一确定的条件是；（2）在题（1）中选一个使BQ的长唯一确定的条件，求出此时BQ的长度．。
九年级解直角三角形经典习题附答案
解直角三角形班级： 姓名 成绩解直角三角形1、已知：如图，在ΔABC 中，∠ACB ＝90°，CD ⊥AB ，垂足为D ，若∠B ＝30°，CD ＝6，求AB 的长．2、我国为了维护队钓鱼岛P 的主权，决定对钓鱼岛进行常态化的立体巡航．在一次巡航中，轮船和飞机的航向相同（AP ∥BD ），当轮船航行到距钓鱼岛20km 的A 处时，飞机在B 处测得轮船的俯角是45°；当轮船航行到C 处时，飞机在轮船正上方的E 处，此时EC =5km ．轮船到达钓鱼岛P 时，测得D 处的飞机的仰角为30°．试求飞机的飞行距离BD （结果保留根号）．3、如图，某公路路基横断面为等腰梯形.按工程设计要求路面宽度为10米，坡角为︒55，路基高度为5.8米，求路基下底宽（精确到0.1米）.C AD B︒ 55 5.8m 10mA BC D 姓名： 得分：M E NCA4、为申办2010年冬奥会，须改变哈尔滨市的交通状况。
在大直街拓宽工程中，要伐掉一棵树AB ，在地面上事先划定以B 为圆心，半径与AB 等长的圆形危险区，现在某工人站在离B 点3米远的D 处，从C 点测得树的顶端A 点的仰角为60°，树的底部B 点的俯角为30°. 问：距离B 点8米远的保护物是否在危险区内？5、如图，某一水库大坝的横断面是梯形ABCD ，坝顶宽CD ＝5米，斜坡AD ＝16 米，坝高 6米，斜坡BC 的坡度3:1=i .求斜坡AD 的坡角∠A （精确到1分）和坝底宽AB ．（精确到0.1米）6. 在一次实践活动中，某课题学习小组用测倾器、皮尺测量旗杆的高度，他们设计了如下的方案（如图1所示）：（1） 在测点A 处安置测倾器，测得旗杆顶部M 的仰角∠MCE ＝α ； （2） 量出测点A 到旗杆底部N 的水平距离AN ＝m; （3） 量出测倾器的高度AC ＝h 。
根据上述测量数据，即可求出旗杆的高度MN 。
解直角三角形精选题
解直角三角形精选题42道一．选择题（共17小题）1．如图，在△ABC中，AB＝AC，BC＝12，E为AC边的中点，线段BE的垂直平分线交边BC于点D．设BD＝x，tan∠ACB＝y，则（）A．x﹣y2＝3B．2x﹣y2＝9C．3x﹣y2＝15D．4x﹣y2＝212．如图，Rt△ABC中，∠C＝90°，点D在AC上，∠DBC＝∠A．若AC＝4，cos A＝，则BD的长度为（）A．B．C．D．43．如图，点A，B，C在正方形网格的格点上，则sin∠BAC＝（）A．B．C．D．4．如图，在△ABC中，∠C＝90°，AC＝8cm，AB的垂直平分线MN交AC于D，连接BD，若cos∠BDC＝，则BC的长是（）A．4cm B．6cm C．8cm D．10cm5．如图，在四边形ABCD中，∠B＝∠D＝90°，AB＝3，BC＝2，tan A＝，则CD的值为（）A．B．C．D．26．如图，在△ABC中，sin B＝，tan C＝2，AB＝3，则AC的长为（）A．B．C．D．27．如图，在4×5的正方形网格中，每个小正方形的边长都是1，△ABC的顶点都在这些小正方形的顶点上，那么sin∠ACB的值为（）A．B．C．D．8．如图，在△ABC中，点O是角平分线AD、BE的交点，若AB＝AC＝10，BC＝12，则tan ∠OBD的值是（）A．B．2C．D．9．在Rt△ABC中，∠C＝90°，sin A＝，AC＝6cm，则BC的长度为（）A．6cm B．7cm C．8cm D．9cm10．如图，Rt△ABC中，∠BAC＝90°，cos B＝，点D是边BC的中点，以AD为底边在其右侧作等腰三角形ADE，使∠ADE＝∠B，连结CE，则的值为（）A．B．C．D．211．在如图所示8×8的网格中，小正方形的边长为1，点A、B、C、D都在格点上，AB与CD相交于点E，则∠AED的正切值是（）A．2B．C．D．12．如图，在△ABC中，∠ACB＝90°，点D在AB的延长线上，连接CD，若AB＝2BD，tan∠BCD＝，则的值为（）A．1B．2C．D．13．如图，⊙O的直径AB＝4，BC切⊙O于点B，OC平行于弦AD，OC＝5，则AD的长为（）A．B．C．D．14．如图，在正方形网格中，△ABC的位置如图，其中点A、B、C分别在格点上，则sin A 的值是（）A．B．C．D．15．如图，△ABC的顶点是正方形网格的格点，则cos∠ABC的值为（）A．B．C．D．16．如图，在直角△BAD中，延长斜边BD到点C，使DC＝BD，连接AC，若tan B＝，则tan∠CAD的值（）A．B．C．D．17．如图，在边长为1的正方形网格中，连接格点D、N和E、C，DN和EC相交于点P，tan∠CPN为（）A．1B．2C．D．二．填空题（共17小题）18．如图，在Rt△ABC中，∠ACB＝90°，AC＝8，BC＝6，CD⊥AB，垂足为D，则tan∠BCD的值是．19．已知在△ABC中，AB＝AC＝8，∠BAC＝30°，将△ABC绕点A旋转，使点B落在原△ABC的点C处，此时点C落在点D处，延长线段AD，交原△ABC的边BC的延长线于点E，那么线段DE的长等于．20．已知△ABC中，AB＝10，AC＝2，∠B＝30°，则△ABC的面积等于．21．如图所示，四边形ABCD中，∠B＝90°，AB＝2，CD＝8，AC⊥CD，若sin∠ACB＝，则cos∠ADC＝．22．如图所示，∠AOB是放置在正方形网格中的一个角，则sin∠AOB的值是．23．如图，在△ABC中，AB＝4，BC＝7，∠B＝60°，点D在边BC上，CD＝3，连接AD．如果将△ACD沿直线AD翻折后，点C的对应点为点E，那么点E到直线BD的距离为．24．如图，在由10个完全相同的正三角形构成的网格图中，∠α、∠β如图所示，则cos（α+β）＝．25．如图，在△ABC中，∠ACB＝90°，点D为AB边的中点，连接CD，若BC＝4，CD＝3，则cos∠DCB的值为．26．△ABC中，AB＝12，AC＝，∠B＝30°，则△ABC的面积是．27．在菱形ABCD中，DE⊥AB，，BE＝2，则tan∠DBE的值是．28．如图，△ABC的顶点B、C的坐标分别是（1，0）、（0，），且∠ABC＝90°，∠A＝30°，则顶点A的坐标是．29．将一副三角尺如图所示叠放在一起，若AB＝4cm，则阴影部分的面积是cm2．30．如图，在等腰Rt△ABC中，∠C＝90°，AC＝6，D是AC上一点，若tan∠DBA＝，则AD的长为．31．如图，在Rt△ABC中，∠ACB＝90°，sin A＝，点C关于直线AB的对称点为D，点E为边AC上不与点A，C重合的动点，过点D作BE的垂线交BC于点F，则的值为．32．如图，点D为△ABC的AB边上的中点，点E为AD的中点，△ADC为正三角形，给出下列结论，①CB＝2CE，②tan∠B＝，③∠ECD＝∠DCB，④若AC＝2，点P是AB 上一动点，点P到AC、BC边的距离分别为d1，d2，则d12+d22的最小值是3．其中正确的结论是（填写正确结论的序号）．33．已知，在△ABC中，∠A＝45°，AB＝4，BC＝5，则△ABC的面积为．34．新定义：有一组对角互余的凸四边形称为对余四边形，如图，已知在对余四边形ABCD 中，AB＝10，BC＝12，CD＝5，tan B＝，那么边AD的长为．三．解答题（共8小题）35．如图，已知△ABD中，AC⊥BD，BC＝8，CD＝4，cos∠ABC＝，BF为AD边上的中线．（1）求AC的长；（2）求tan∠FBD的值．36．已知：如图，在△ABC中，AD⊥BC于点D，E是AD的中点，连接CE并延长交边AB于点F，AC＝13，BC＝8，cos∠ACB＝．（1）求tan∠DCE的值；（2）求的值．37．在△ABC中，AD是BC边上的高，∠C＝45°，sin B＝，AD＝1．求BC的长．38．如图，在△ABC中，AD⊥BC于点D，若AD＝6．tan C＝，BC＝12，求cos B的值．39．如图，在△ABC中，∠A＝30°，∠B＝45°，AC＝，求AB的长．40．如图，在△ABC中，CD是边AB上的中线，∠B是锐角，sin B＝，tan A＝，AC＝，（1）求∠B的度数和AB的长．（2）求tan∠CDB的值．41．一副直角三角板如图放置，点C在FD的延长线上，AB∥CF，∠F＝∠ACB＝90°，∠E＝45°，∠A＝60°，AC＝10，试求CD的长．42．如图，在△ABC中，∠C＝90°，点D，E分别在AC，AB上，BD平分∠ABC，DE⊥AB于点E，AE＝6，cos A＝．（1）求CD的长；（2）求tan∠DBC的值．解直角三角形精选题42道参考答案与试题解析一．选择题（共17小题）1．如图，在△ABC中，AB＝AC，BC＝12，E为AC边的中点，线段BE的垂直平分线交边BC于点D．设BD＝x，tan∠ACB＝y，则（）A．x﹣y2＝3B．2x﹣y2＝9C．3x﹣y2＝15D．4x﹣y2＝21【解答】解：过A作AQ⊥BC于Q，过E作EM⊥BC于M，连接DE，∵BE的垂直平分线交BC于D，BD＝x，∴BD＝DE＝x，∵AB＝AC，BC＝12，tan∠ACB＝y，∴＝＝y，BQ＝CQ＝6，∴AQ＝6y，∵AQ⊥BC，EM⊥BC，∴AQ∥EM，∵E为AC中点，∴CM＝QM＝CQ＝3，∴EM＝3y，∴DM＝12﹣3﹣x＝9﹣x，在Rt△EDM中，由勾股定理得：x2＝（3y）2+（9﹣x）2，即2x﹣y2＝9，故选：B．2．如图，Rt△ABC中，∠C＝90°，点D在AC上，∠DBC＝∠A．若AC＝4，cos A＝，则BD的长度为（）A．B．C．D．4【解答】解：∵∠C＝90°，AC＝4，cos A＝，∴AB＝，∴，∵∠DBC＝∠A．∴cos∠DBC＝cos∠A＝，∴，故选：C．3．如图，点A，B，C在正方形网格的格点上，则sin∠BAC＝（）A．B．C．D．【解答】解：如图，过点B作BD⊥AC于D，由勾股定理得，AB＝＝，AC＝＝3，∵S△ABC＝AC•BD＝×3•BD＝×1×3，∴BD＝，∴sin∠BAC＝＝＝．故选：B．4．如图，在△ABC中，∠C＝90°，AC＝8cm，AB的垂直平分线MN交AC于D，连接BD，若cos∠BDC＝，则BC的长是（）A．4cm B．6cm C．8cm D．10cm【解答】解：∵∠C＝90°，AC＝8cm，AB的垂直平分线MN交AC于D，∴BD＝AD，∴CD+BD＝8，∵cos∠BDC＝＝，∴＝，解得：CD＝3，BD＝5，∴BC＝4．故选：A．5．如图，在四边形ABCD中，∠B＝∠D＝90°，AB＝3，BC＝2，tan A＝，则CD的值为（）A．B．C．D．2【解答】解：延长AD、BC，两线交于O，∵在Rt△ABO中，∠B＝90°，tan A＝＝，AB＝3，∴OB＝4，∵BC＝2，∴OC＝OB﹣BC＝4﹣2＝2，在Rt△ABO中，∠B＝90°，AB＝3，OB＝4，由勾股定理得：AO＝5，∵∠ADC＝90°，∴∠ODC＝90°＝∠B，∵∠O＝∠O，∴△ODC∽△OBA，∴＝，∴＝，解得：DC＝，故选：C．6．如图，在△ABC中，sin B＝，tan C＝2，AB＝3，则AC的长为（）A．B．C．D．2【解答】解：过A作AD⊥BC于D，则∠ADC＝∠ADB＝90°，∵tan C＝2＝，sin B＝＝，∴AD＝2DC，AB＝3AD，∵AB＝3，∴AD＝1，DC＝，在Rt△ADC中，由勾股定理得：AC＝＝＝，故选：B．7．如图，在4×5的正方形网格中，每个小正方形的边长都是1，△ABC的顶点都在这些小正方形的顶点上，那么sin∠ACB的值为（）A．B．C．D．【解答】解：如图，过点A作AH⊥BC于H．在Rt△ACH中，∵AH＝4，CH＝3，∴AC＝＝＝5，∴sin∠ACH＝＝，故选：D．8．如图，在△ABC中，点O是角平分线AD、BE的交点，若AB＝AC＝10，BC＝12，则tan ∠OBD的值是（）A．B．2C．D．【解答】解：如图：作OF⊥AB于F，∵AB＝AC，AD平分∠BAC．∴∠ODB＝90°．BD＝CD＝6．∴根据勾股定理得：AD＝＝8．∵BE平分∠ABC．∴OF＝OD，BF＝BD＝6，AF＝10﹣6＝4．设OD＝OF＝x，则AO＝8﹣x，在Rt△AOF中，根据勾股定理得：（8﹣x）2＝x2+42．∴x＝3．∴OD＝3．在Rt△OBD中，tan∠OBD＝＝＝．法二：在求出AF＝4后∵tan∠BAD＝＝．∴＝．∴OF＝3．∴OD＝OF＝3．∴tan∠OBD＝＝．故选：A．9．在Rt△ABC中，∠C＝90°，sin A＝，AC＝6cm，则BC的长度为（）A．6cm B．7cm C．8cm D．9cm【解答】解：∵sin A＝＝，∴设BC＝4x，AB＝5x，又∵AC2+BC2＝AB2，∴62+（4x）2＝（5x）2，解得：x＝2或x＝﹣2（舍），则BC＝4x＝8cm，故选：C．10．如图，Rt△ABC中，∠BAC＝90°，cos B＝，点D是边BC的中点，以AD为底边在其右侧作等腰三角形ADE，使∠ADE＝∠B，连结CE，则的值为（）A．B．C．D．2【解答】解：设DE交AC于T,过点E作EH⊥CD于H．∵∠BAC＝90°,BD＝DC,∴AD＝DB＝DC,∴∠B＝∠DAB,∵∠B＝∠ADE,∴∠DAB＝∠ADE,∴AB∥DE,∴∠DTC＝∠BAC＝90°,∵DT∥AB,BD＝DC,∴AT＝TC,∴EA＝EC＝ED,∴∠EDC＝∠ECD,∵EH⊥CD,∴CH＝DH,∵DE∥AB,∴∠EDC＝∠B,∴∠ECD＝∠B,∴cos∠ECH＝cos B＝,∴＝,∴＝＝2,故选：D．11．在如图所示8×8的网格中，小正方形的边长为1，点A、B、C、D都在格点上，AB与CD相交于点E，则∠AED的正切值是（）A．2B．C．D．【解答】解：如图，取格点K，连接AK，BK．观察图形可知AK⊥BK，BK＝2AK，BK∥CD，∴∠AED＝∠ABK，∴tan∠AED＝tan∠ABK＝＝，故选：B．12．如图，在△ABC中，∠ACB＝90°，点D在AB的延长线上，连接CD，若AB＝2BD，tan∠BCD＝，则的值为（）A．1B．2C．D．【解答】解：过点D作DM⊥BC，交CB的延长线于点M，∵∠ACB＝∠DMB＝90°，∠ABC＝∠DBM，∴△ABC∽△DBM，∴＝＝，∵AB＝2BD，∴＝＝＝，在Rt△CDM中，由于tan∠MCD＝＝，设DM＝2k，则CM＝3k，又∵＝＝，∴BC＝2k，AC＝4k，∴＝＝2，故选：B．13．如图，⊙O的直径AB＝4，BC切⊙O于点B，OC平行于弦AD，OC＝5，则AD的长为（）A．B．C．D．【解答】解：连接BD．∵AB是直径，∴∠ADB＝90°．∵OC∥AD，∴∠A＝∠BOC，∴cos∠A＝cos∠BOC．∵BC切⊙O于点B，∴OB⊥BC，∴cos∠BOC＝＝，∴cos∠A＝cos∠BOC＝．又∵cos∠A＝，AB＝4，∴AD＝．故选：B．14．如图，在正方形网格中，△ABC的位置如图，其中点A、B、C分别在格点上，则sin A 的值是（）A．B．C．D．【解答】解：过点C作CD⊥AB于点D，∵BC＝2，∴S△ABC＝BC×4＝4，∵AB＝＝4，∴CD＝＝，∵AC＝＝2，∴sin A＝＝＝，故选：A．15．如图，△ABC的顶点是正方形网格的格点，则cos∠ABC的值为（）A．B．C．D．【解答】解：法一、如图，在Rt△ABD中，∠ADB＝90°，AD＝BD＝3，∴AB＝＝＝3，∴cos∠ABC＝＝＝．故选：B．法二、在Rt△ABD中，∠ADB＝90°，AD＝BD＝3，∴∠ABD＝∠BAD＝45°，∴cos∠ABC＝cos45°＝．故选：B．16．如图，在直角△BAD中，延长斜边BD到点C，使DC＝BD，连接AC，若tan B＝，则tan∠CAD的值（）A．B．C．D．【解答】解：如图，延长AD，过点C作CE⊥AD，垂足为E，∵tan B＝，即＝，∴设AD＝5x，则AB＝3x，∵∠CDE＝∠BDA，∠CED＝∠BAD，∴△CDE∽△BDA，∴，∴CE＝x，DE＝，∴AE＝，∴tan∠CAD＝＝．故选：D．17．如图，在边长为1的正方形网格中，连接格点D、N和E、C，DN和EC相交于点P，tan∠CPN为（）A．1B．2C．D．【解答】解：连接格点MN、DM，如图所示：则四边形MNCE是平行四边形，△DAM和△MBN都是等腰直角三角形，∴EC∥MN，∠DMA＝∠NMB＝45°，DM＝AD＝2，MN＝BM＝，∴∠CPN＝∠DNM，∴tan∠CPN＝tan∠DNM，∵∠DMN＝180°﹣∠DMA﹣∠NMB＝180°﹣45°﹣45°＝90°，∴tan∠CPN＝tan∠DNM＝＝＝2，故选：B．二．填空题（共17小题）18．如图，在Rt△ABC中，∠ACB＝90°，AC＝8，BC＝6，CD⊥AB，垂足为D，则tan∠BCD的值是．【解答】解：在Rt△ABC与Rt△BCD中，∠A+∠B＝90°，∠BCD+∠B＝90°．∴∠A＝∠BCD．∴tan∠BCD＝tan∠A＝＝＝．故答案为．19．已知在△ABC中，AB＝AC＝8，∠BAC＝30°，将△ABC绕点A旋转，使点B落在原△ABC的点C处，此时点C落在点D处，延长线段AD，交原△ABC的边BC的延长线于点E，那么线段DE的长等于4﹣4．【解答】解：作CH⊥AE于H，如图，∵AB＝AC＝8，∴∠B＝∠ACB＝（180°﹣∠BAC）＝（180°﹣30°）＝75°，∵△ABC绕点A旋转，使点B落在原△ABC的点C处，此时点C落在点D处，∴AD＝AB＝8，∠CAD＝∠BAC＝30°，∵∠ACB＝∠CAD+∠E，∴∠E＝75°﹣30°＝45°，在Rt△ACH中，∵∠CAH＝30°，∴CH＝AC＝4，AH＝CH＝4，∴DH＝AD﹣AH＝8﹣4，在Rt△CEH中，∵∠E＝45°，∴EH＝CH＝4，∴DE＝EH﹣DH＝4﹣（8﹣4）＝4﹣4．故答案为4﹣4．20．已知△ABC中，AB＝10，AC＝2，∠B＝30°，则△ABC的面积等于15或10．【解答】解：作AD⊥BC交BC（或BC延长线）于点D，①如图1，当AB、AC位于AD异侧时，在Rt△ABD中，∵∠B＝30°，AB＝10，∴AD＝AB sin B＝5，BD＝AB cos B＝5，在Rt△ACD中，∵AC＝2，∴CD＝＝＝，则BC＝BD+CD＝6，∴S△ABC＝•BC•AD＝×6×5＝15；②如图2，当AB、AC在AD的同侧时，由①知，BD＝5，CD＝，则BC＝BD﹣CD＝4，∴S△ABC＝•BC•AD＝×4×5＝10．综上，△ABC的面积是15或10，故答案为15或10．21．如图所示，四边形ABCD中，∠B＝90°，AB＝2，CD＝8，AC⊥CD，若sin∠ACB＝，则cos∠ADC＝．【解答】解：∵∠B＝90°，sin∠ACB＝，∴＝，∵AB＝2，∴AC＝6，∵AC⊥CD，∴∠ACD＝90°，∴AD＝＝＝10，∴cos∠ADC＝＝．故答案为：．22．如图所示，∠AOB是放置在正方形网格中的一个角，则sin∠AOB的值是．【解答】解：如图，连接AB．∵OA＝AB＝，OB＝2，∴OB2＝OA2+AB2，∴∠OAB＝90°，∴△AOB是等腰直角三角形，∴∠AOB＝45°，∴sin∠AOB＝，故答案为：．23．如图，在△ABC中，AB＝4，BC＝7，∠B＝60°，点D在边BC上，CD＝3，连接AD．如果将△ACD沿直线AD翻折后，点C的对应点为点E，那么点E到直线BD的距离为．【解答】解：如图，过点E作EH⊥BC于H．∵BC＝7，CD＝3，∴BD＝BC﹣CD＝4，∵AB＝4＝BD，∠B＝60°，∴△ABD是等边三角形，∴∠ADB＝60°，∴∠ADC＝∠ADE＝120°，∴∠EDH＝60°，∵EH⊥BC，∴∠EHD＝90°，∵DE＝DC＝3，∴EH＝DE•sin60°＝，∴E到直线BD的距离为，故答案为．24．如图，在由10个完全相同的正三角形构成的网格图中，∠α、∠β如图所示，则cos（α+β）＝．【解答】解：给图中相关点标上字母，连接DE，如图所示．在△ABC中，∠ABC＝120°，BA＝BC，∴∠α＝30°．同理，可得出：∠CDE＝∠CED＝30°＝∠α．又∵∠AEC＝60°，∴∠AED＝∠AEC+∠CED＝90°．设等边三角形的边长为a，则AE＝2a，DE＝2×sin60°•a＝a，∴AD＝＝a，∴cos（α+β）＝＝．故答案为：．25．如图，在△ABC中，∠ACB＝90°，点D为AB边的中点，连接CD，若BC＝4，CD＝3，则cos∠DCB的值为．【解答】解：∵在△ABC中，∠ACB＝90°，点D为AB边的中点，∴AD＝BD＝CD＝AB，又∵CD＝3，∴AB＝6，∴cos∠DCB＝cos∠B＝＝＝，故答案为：．26．△ABC中，AB＝12，AC＝，∠B＝30°，则△ABC的面积是21或15．【解答】解：①如图1，作AD⊥BC，垂足为点D，在Rt△ABD中，∵AB＝12、∠B＝30°，∴AD＝AB＝6，BD＝AB cos B＝12×＝6，在Rt△ACD中，CD＝＝＝，∴BC＝BD+CD＝6+＝7，则S△ABC＝×BC×AD＝×7×6＝21；②如图2，作AD⊥BC，交BC延长线于点D，由①知，AD＝6、BD＝6、CD＝，则BC＝BD﹣CD＝5，∴S△ABC＝×BC×AD＝×5×6＝15，故答案为：21或15．27．在菱形ABCD中，DE⊥AB，，BE＝2，则tan∠DBE的值是2．【解答】解：设菱形ABCD边长为t，∵BE＝2，∴AE＝t﹣2，∵cos A＝，∴，∴＝，∴t＝5，∴AE＝5﹣2＝3，∴DE＝＝4，∴tan∠DBE＝＝＝2．故答案为：2．28．如图，△ABC的顶点B、C的坐标分别是（1，0）、（0，），且∠ABC＝90°，∠A＝30°，则顶点A的坐标是（4，）．【解答】解：过点A作AG⊥x轴，交x轴于点G．∵B、C的坐标分别是（1，0）、（0，），∴OC＝，OB＝1，∴BC＝＝2．∵∠ABC＝90°，∠BAC＝30°，∴AB＝＝＝＝2．∵∠ABG+∠CBO＝90°，∠BCO+∠CBO＝90°，∴∠ABG＝∠BCO．∴sin∠ABG＝＝＝，cos∠ABG＝＝＝，∴AG＝，BG＝3．∴OG＝1+3＝4，∴顶点A的坐标是（4，）．故答案为：（4，）．29．将一副三角尺如图所示叠放在一起，若AB＝4cm，则阴影部分的面积是2cm2．【解答】解：∵∠B＝30°，∠ACB＝90°，AB＝4cm，∴AC＝2cm．由题意可知BC∥ED，∴∠AFC＝∠ADE＝45°，∴AC＝CF＝2cm．故S△ACF＝×2×2＝2（cm2）．故答案为：2．30．如图，在等腰Rt△ABC中，∠C＝90°，AC＝6，D是AC上一点，若tan∠DBA＝，则AD的长为2．【解答】解：作DE⊥AB于E，如图，∵∠C＝90°，AC＝BC＝6，∴△ACB为等腰直角三角形，AB＝AC＝6，∴∠A＝45°，在Rt△ADE中，设AE＝x，则DE＝x，AD＝x，在Rt△BED中，tan∠DBE＝＝，∴BE＝5x，∴x+5x＝6，解得x＝，∴AD＝×＝2．故答案为：2．31．如图，在Rt△ABC中，∠ACB＝90°，sin A＝，点C关于直线AB的对称点为D，点E为边AC上不与点A，C重合的动点，过点D作BE的垂线交BC于点F，则的值为．【解答】解：如图，设DF交AB于M，CD交AB于N，BE交DF于J．∵∠ACB＝90°，∴sin A＝＝，∴可以假设BC＝4k，AB＝5k，则AC＝3k，∵C，D关于AB对称，∴CD⊥AB，CN＝DN，∵S△ABC＝×BC×AC＝×AB×CN，∴CN＝DN＝k，∴CD＝k，∵∠FCD+∠DCA＝90°，∠DCA+∠A＝90°，∴∠DCF＝∠A，∵DF⊥BE，CD⊥AB，∴∠BJM＝∠DNM＝90°，∵∠BMJ＝∠DMN，∴∠D＝∠ABE，∴△DCF∽△BAE，∴＝＝＝．32．如图，点D为△ABC的AB边上的中点，点E为AD的中点，△ADC为正三角形，给出下列结论，①CB＝2CE，②tan∠B＝，③∠ECD＝∠DCB，④若AC＝2，点P是AB 上一动点，点P到AC、BC边的距离分别为d1，d2，则d12+d22的最小值是3．其中正确的结论是①③④（填写正确结论的序号）．【解答】解：∵D是AB中点∴AD＝BD∵△ACD是等边三角形，E是AD中点∴AD＝CD，∠ADC＝60°＝∠ACD，CE⊥AB，∠DCE＝30°∴CD＝BD∴∠B＝∠DCB＝30°，且∠DCE＝30°，CE⊥AB∴∠ECD＝∠DCB，BC＝2CE，tan∠B＝故①③正确，②错误∵∠DCB＝30°，∠ACD＝60°∴∠ACB＝90°若AC＝2，点P是AB上一动点，点P到AC、BC边的距离分别为d1，d2，∴四边形PMCN是矩形∴MN＝CP∵d12+d22＝MN2＝CP2∴当CP为最小值，d12+d22的值最小∴根据垂线段最短，则当CP⊥AB时，d12+d22的值最小此时：∠CAB＝60°，AC＝2，CP⊥AB∴CP＝∴d12+d22＝MN2＝CP2＝3即d12+d22的最小值为3故④正确故答案为①③④33．已知，在△ABC中，∠A＝45°，AB＝4，BC＝5，则△ABC的面积为2或14．【解答】解：过点B作AC边的高BD，Rt△ABD中，∠A＝45°，AB＝4，∴BD＝AD＝4，在Rt△BDC中，BC＝5，∴CD＝＝3，①△ABC是钝角三角形时，AC＝AD﹣CD＝1，∴S△ABC＝AC•BD＝＝2；②△ABC是锐角三角形时，AC＝AD+CD＝7，∴S△ABC＝AC•BD＝×7×4＝14，故答案为：2或14．34．新定义：有一组对角互余的凸四边形称为对余四边形，如图，已知在对余四边形ABCD 中，AB＝10，BC＝12，CD＝5，tan B＝，那么边AD的长为9．【解答】解：如图，过点A作AH⊥BC于H，过点C作CE⊥AD于E，连接AC．在Rt△ABH中，tan B＝＝，∴可以假设AH＝3k，BH＝4k，则AB＝5k＝10，∴k＝2，∴AH＝6，BH＝8，∵BC＝12，∴CH＝BC﹣BH＝12﹣8＝4，∴AC＝＝＝2，∵∠B+∠D＝90°，∠D+∠ECD＝90°，∴∠ECD＝∠B，在Rt△CED中，tan∠ECD＝＝，∵CD＝5，∴DE＝3，CE＝4，∴AE＝＝＝6，∴AD＝AE+DE＝9．故答案为：9．三．解答题（共8小题）35．如图，已知△ABD中，AC⊥BD，BC＝8，CD＝4，cos∠ABC＝，BF为AD边上的中线．（1）求AC的长；（2）求tan∠FBD的值．【解答】解：（1）∵AC⊥BD，cos∠ABC＝＝，BC＝8，∴AB＝10，在Rt△ACB中，由勾股定理得，AC＝＝＝6，即AC的长为6；（2）如图，连接CF，过F点作BD的垂线，垂足E，∵BF为AD边上的中线，即F为AD的中点，∴CF＝AD＝FD，在Rt△ACD中，由勾股定理得，AD＝＝＝2，∵三角形CFD为等腰三角形，FE⊥CD，∴CE＝CD＝2，在Rt△EFC中，EF＝＝＝3，∴tan∠FBD＝＝＝．解法二：∵BF为AD边上的中线，∴F是AD中点，∵FE⊥BD，AC⊥BD，∴FE∥AC，∴FE是△ACD的中位线，∴FE＝AC＝3，CE＝CD＝2，∴在Rt△BFE中，tan∠FBD＝＝＝．36．已知：如图，在△ABC中，AD⊥BC于点D，E是AD的中点，连接CE并延长交边AB 于点F，AC＝13，BC＝8，cos∠ACB＝．（1）求tan∠DCE的值；（2）求的值．【解答】解：（1）∵AD⊥BC，∴∠ADC＝90°，在Rt△ADC中，AC＝13，cos∠ACB＝＝，∴CD＝5，由勾股定理得：AD＝＝12，∵E是AD的中点，∴ED＝AD＝6，∴tan∠DCE＝＝；（2）过D作DG∥CF交AB于点G，如图所示：∵BC＝8，CD＝5，∴BD＝BC﹣CD＝3，∵DG∥CF，∴＝＝，＝＝1，∴AF＝FG，设BG＝3x，则AF＝FG＝5x，BF＝FG+BG＝8x∴＝．37．在△ABC中，AD是BC边上的高，∠C＝45°，sin B＝，AD＝1．求BC的长．【解答】解：在Rt△ABD中，∵，又∵AD＝1，∴AB＝3，∵BD2＝AB2﹣AD2，∴．在Rt△ADC中，∵∠C＝45°，∴CD＝AD＝1．∴BC＝BD+DC＝+1．38．如图，在△ABC中，AD⊥BC于点D，若AD＝6．tan C＝，BC＝12，求cos B的值．【解答】解：∵tan C＝＝＝，∴CD＝4．∴BD＝12﹣4＝8．在Rt△ABD中，AB＝＝10．∴cos B＝＝．39．如图，在△ABC中，∠A＝30°，∠B＝45°，AC＝，求AB的长．【解答】解：过C作CD⊥AB于D，∴∠ADC＝∠BDC＝90°，∵∠B＝45°，∴∠BCD＝∠B＝45°，∴CD＝BD，∵∠A＝30°，AC＝2，∴CD＝，∴BD＝CD＝，由勾股定理得：AD＝＝3，∴AB＝AD+BD＝3+，答：AB的长是3+．40．如图，在△ABC中，CD是边AB上的中线，∠B是锐角，sin B＝，tan A＝，AC＝，（1）求∠B的度数和AB的长．（2）求tan∠CDB的值．【解答】解：（1）作CE⊥AB于E，设CE＝x，在Rt△ACE中，∵tan A＝＝，∴AE＝2x，∴AC＝＝x，∴x＝，解得x＝1，∴CE＝1，AE＝2，在Rt△BCE中，∵sin B＝，∴∠B＝45°，∴△BCE为等腰直角三角形，∴BE＝CE＝1，∴AB＝AE+BE＝3，答：∠B的度数为45°，AB的值为3；（2）∵CD为中线，∴BD＝AB＝1.5，∴DE＝BD﹣BE＝1.5﹣1＝0.5，∴tan∠CDE＝＝＝2，即tan∠CDB的值为2．41．一副直角三角板如图放置，点C在FD的延长线上，AB∥CF，∠F＝∠ACB＝90°，∠E＝45°，∠A＝60°，AC＝10，试求CD的长．【解答】解：过点B作BM⊥FD于点M，在△ACB中，∠ACB＝90°，∠A＝60°，AC＝10，∴∠ABC＝30°，BC＝AC×tan60°＝10，∵AB∥CF，∴BM＝BC×sin30°＝10×＝5，CM＝BC×cos30°＝15，在△EFD中，∠F＝90°，∠E＝45°，∴∠EDF＝45°，∴MD＝BM＝5，∴CD＝CM﹣MD＝15﹣5．42．如图，在△ABC中，∠C＝90°，点D，E分别在AC，AB上，BD平分∠ABC，DE⊥AB于点E，AE＝6，cos A＝．（1）求CD的长；（2）求tan∠DBC的值．【解答】解：（1）在Rt△ADE中，∠AED＝90°，AE＝6，cos A＝，∴AD＝＝10，∴＝＝8．∵BD平分∠ABC，DE⊥AB，DC⊥BC，∴CD＝DE＝8；（2）由（1）AD＝10，DC＝8，∴AC＝AD+DC＝18，在△ADE与△ABC中，∵∠A＝∠A，∠AED＝∠ACB，∴△ADE∽△ABC，∴，即＝，∴BC＝24，∴．。
中考数学解直角三角形练习
中考数学解直角三角形练习第一课时(锐角三角函数)课标要求1、 通过实例认识直角三角形的边角关系：即锐角三角函数（sinA 、cosA 、tanA 、cotA ）2、 熟知300、450、600角的三角函数值3、 会用计算器求锐角的三角函数值：以及由已知的三角函数值求相应的锐角。
4、 通过特殊角三角函数值：知道互余两角的三角函数的关系。
5、 了解同角三角函数的平方关系。
sin 2α+cos 2α=1：倒数关系tan α·cot α=1.6、 熟知直角三角形中：300角的性质。
中招考点1、 锐角三角函数的概念：锐角三角函数的性质。
2、 300、450、600角的三角函数值及计算代数式的值。
3、 运用计算器求的三角函数值或由锐角三角函数值求角度。
典型例题[例题1] 选择题（四选一）1、如图19-1：在Rt △ABC 中：CD 是斜边AB 上的高：则下列线段比中不等于sinA 的是（ ）A. AC CDB. CB BDC.AB CBD.CBCD分析：sinA=AC CD ； sinA=sin ∠BCD=BC BD ;sinA= ABBC；从而判断D 不正确。
故应选D.。
2、在Rt △ABC 中：∠C ＝900：∠A ＝∠B ：则cosA 的值是（ ） A.21B. 22 C.23 D.1分析：先求出∠A 的度数：因为∠C ＝900：∠A ＝∠B ：故∠A ＝∠B ＝450：再由特殊角的三角函数值可得：cosA=cos450=22故选B.。
3、在△ABC 中：∠C ＝900：sinA=23 ；则cosB 的值为（ ）A. 21B. 22C.23D.33分析：方法一：因为sinA=23；故锐角A ＝600。
因为∠C ＝900：所以∠B ＝300.cosB=23.故选C.方法二：因为 ∠C ＝900：故 ∠A 与 ∠B 互余.所以cosB=sin A ＝23.故选C..4、如图19-2：在△ABC 中：∠C ＝900：sinA=53.则BC ：AC 等于（ ）A C图19-1A. 3：4B. 4：3C.3：5D.4：5 分析： 因为∠C ＝900：sinA ＝53 ；又sinA=AB BC .所以AB BC ＝53； 不妨设BC ＝3k ；AB=5k ；由勾股定理可得AC ＝22BC AB -＝4k ；所以BC ：AC ＝3k:4k=3:4故选A.。
九年级中考数学复习解直角三角形专项练习(含答案)
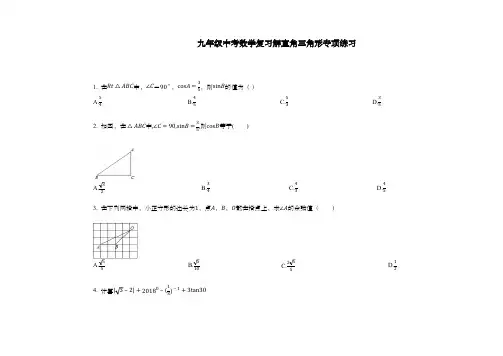
1. 在������������ △ ������������������中，∠������＝90 ∘ ，cos������ = 35，则sin������的值为（ ）
5
4
5
3
A.4
B.5
C.3
D.5
2. 如图，在 △ ������������������中,∠������ = 90,sin������ = 35,则cos������等于( )
31. 如图，港口������在观测站������的正西方向，������������ = 4������������，某船从港口������出发，沿北偏西15 ∘ 方向航行一段距离后到达������处，此时从观测站������ 处测得该船位于北偏西60 ∘ 的方向，则该船航行的距离（即������������的长）为多少？（结果保留根号）
14.
计算：������������������60 ⋅ ������������������30 ‒ ������������������45 = ________. 15. 若 2cos������ ‒ 1 = 0,则������ = ________.
16. 计算：| 2 ‒ 2| + ( 2 ‒ 1)0 + 2sin45 ∘ ．
28. 如图，两座建筑物的水平距离������������为60������，从������点测得������点的仰角������为53 ∘ ，从������点测得������点的俯角������为37 ∘ ，求两座建筑物的高度（参 考数据：sin37 ∘ ≈ 35，cos37 ∘ ≈ 45，tan37 ∘ ≈ 34，sin53 ∘ ≈ 45，cos53 ∘ ≈ 35，tan53 ∘ ≈ 43）．
解直角三角形测试题与答案
解直角三角形测试题与答案一、选择题（每小题 5 分，共 25 分）1、在直角三角形中，若一个锐角为 30°，斜边与较小直角边的和为 12，则斜边的长为（）A 4B 6C 8D 10答案：C解析：设较小直角边为 x，则斜边为 2x，由题意得 2x ＋ x ＝ 12，解得 x ＝ 4，所以斜边为 8。
2、在 Rt△ABC 中，∠C ＝ 90°，sinA ＝，则 tanB 的值为（）A B C D答案：D解析：因为 sinA ＝，设 BC ＝ 4x，AB ＝ 5x，则 AC ＝ 3x，所以tanB ＝。
3、如图，在△ABC 中，∠C ＝ 90°，AC ＝ 8，∠A 的平分线 AD ＝，则 BC 的长为（）A 12B 10C 8D 6答案：B解析：因为 AD 是∠A 的平分线，所以∠CAD ＝∠BAC。
在Rt△ACD 中，cos∠CAD ＝，即，解得 CD ＝ 6。
在 Rt△ABC 中，BC ＝。
4、已知在 Rt△ABC 中，∠C ＝ 90°，tanA ＝，则 sinA 的值为（）A B C D答案：B解析：设 BC ＝ 3x，AC ＝ 4x，则 AB ＝ 5x，所以 sinA ＝。
5、如图，在菱形 ABCD 中，DE⊥AB，cosA ＝，BE ＝ 2，则tan∠DBE 的值是（）A B 2C D答案：C解析：因为 cosA ＝，设 AD ＝ 5x，AE ＝ 3x，则 DE ＝ 4x。
因为BE ＝ 2，所以 5x 3x ＝ 2，解得 x ＝ 1，所以 DE ＝ 4。
在 Rt△BDE 中，tan∠DBE ＝。
二、填空题（每小题 5 分，共 25 分）1、在 Rt△ABC 中，∠C ＝ 90°，若 sinA ＝，AB ＝ 10，则 BC＝＿_______。
答案：6解析：因为 sinA ＝，所以，设 BC ＝ 3x，AB ＝ 5x，因为 AB ＝10，所以 5x ＝ 10，解得 x ＝ 2，所以 BC ＝ 6。
初三数学解直角三角形试题
初三数学解直角三角形试题1.一公路大桥引桥长100米，已知引桥的坡度i=1：3，那么引桥的铅直高度为米（结果保留根号）．【答案】10.【解析】根据坡度的定义：坡度是坡面的铅直高度h和水平宽度l的比，又叫做坡比，求解即可．试题解析：如图：由题意得，桥长AB=10米，∵BC：AC=1：3，∴设BC=x，AC=3x，则AB=解得：x=10【考点】解直角三角形的应用-坡度坡角问题．2.如图，若△ABC和△DEF的面积分别为、，则A．B．C．D．【答案】D．【解析】在两个图形中分别作BC、EF边上的高，求出、，比较即可．如图，过点A、D分别作AG⊥BC，DH⊥EF，垂足分别为G、H，在Rt△ABG中，AG="ABsinB=5×sin" 40°="5sin" 40°，在Rt△DHE中，∠DEH=180°﹣130°=50°，DH=DEsin∠DEH="5sin" 40°，∴AG=DH．∵BC=8，EF=5，∴．故选D．【考点】解直角三角形．3.在直角三角形ABC中，已知∠C=90°，∠A=40°，BC=3，则AC=（）A．B．C．D．【答案】D.【解析】∵∠C=90°，∠A=40°，∴∠B=50°.∵BC=3，，∴.故选D.【考点】1.直角三角形两锐角的关系；2.锐角三角函数定义.4.如图，从热气球P上测得两建筑物A、B的底部的俯角分别为45°和30°，如果A、B两建筑物的距离为60米，P点在地面上的正投影恰好落在线段AB上，求热气球P的高度．（结果保留根号）【答案】（30-30）米．【解析】过P作AB的垂线，设垂足为G．分别在Rt△APG和Rt△BPG中，用PG表示出AG、BG的长，进而由AB=AG+BG=90求得PC的长，即热气球P的高度．试题解析：过点P作PG⊥AB与点G，设PG=x，则AG=PG=x，BG=x，∴x+x=60，∴x=30-30．答：热气球P的高度是（30-30）米．考点: 解直角三角形的应用----仰角俯角问题．5.如图，在夕阳西下的傍晚，某人看见高压电线的铁塔在阳光的照射下，铁塔的影子的一部分落在小山的斜坡上，为了测得铁塔的高度，他测得铁塔底部B到小山坡脚D的距离为2米，铁塔在小山斜坡上的影长DC为3.4米，斜坡的坡度，同时他测得自己的影长NH﹦336cm，而他的身长MN为168cm，求铁塔的高度．【答案】AB=4.1米 .【解析】作AC的延长线交BD的延长线于E，作CF⊥DE，垂足为F．利用勾股定理和相似三角形的性质求出DF，FE，从而得到BE的长，再用相似三角形的性质求出AB即可．试题解析：过点C作CE⊥BD于点E，延长AC交BD延长线于点F在Rt△CDE中，∴设CE="8x" ,DE="15x" ，则CD=17x∵DC=3.4米∴CE=1.6米，DE=3米在Rt△MNH中，tan∠MHN∴在Rt△ABF中，tan∠F tan∠MHN∴EF=3.2米即BF=2+3+3.2=8.2米∴在Rt△CEF中，tan∠F∴AB=4.1米答：铁塔的高度是4.1米．【考点】1.解直角三角形的应用-坡度坡角问题；2.相似三角形的应用．6. tan60°的值等于A．1B．C．D．2【答案】C.【解析】试题解析：根据tan60°=即可得出答案．故选C.考点: 特殊角的三角函数值．7.如图，在△ABC中，AB=BC，∠B=120°，AB的垂直平分线交AC于点D．若AC=6cm，则AD= cm．【答案】2.【解析】如图，过点B作BE⊥AC，垂足为点E，AB的垂直平分线交AB于点F.∵在△ABC中，AB＝BC，∠B＝1200，AC＝6cm，∴∠A＝300，AE＝3cm。
解直角三角形测试题与答案
解直角三角形测试题与答案一、选择题（每小题 3 分，共 30 分）1、在直角三角形中，若一个锐角为 30°，斜边与较小直角边的和为 12，则斜边的长为（）A 4B 6C 8D 10答案：C解析：在直角三角形中，30°角所对的直角边等于斜边的一半。
设较小直角边为 x，则斜边为 2x，由题意得 2x ＋ x ＝ 12，解得 x ＝ 4，所以斜边为 8。
2、已知在 Rt△ABC 中，∠C ＝ 90°，sinA ＝，则 tanB 的值为（）A B C D答案：A解析：因为 sinA ＝，所以设 BC ＝ 3x，AB ＝ 5x，则 AC ＝ 4x。
所以 tanB ＝。
3、在△ABC 中，∠C ＝ 90°，AB ＝ 15，sinA ＝，则 BC 等于（）A 9B 12C 10D 6答案：B解析：因为 sinA ＝，所以 BC ＝ AB×sinA ＝ 15×＝ 9。
4、如图，在 Rt△ABC 中，∠C ＝ 90°，AC ＝ 4，AB ＝ 5，则cosB 的值是（）A B C D答案：A解析：因为在 Rt△ABC 中，∠C ＝ 90°，AC ＝ 4，AB ＝ 5，所以BC ＝ 3。
所以 cosB ＝。
5、一个直角三角形的两条直角边分别为 6 和 8，则其斜边上的高为（）A 48B 5C 3D 10答案：A解析：根据勾股定理可得斜边为 10，设斜边上的高为 h，根据面积相等可得 ×6×8 ＝ ×10×h，解得 h ＝ 48。
6、在 Rt△ABC 中，∠C ＝ 90°，若 sinA ＝，则 cosA 的值为（）A B C D答案：B解析：因为 sin²A ＋ cos²A ＝ 1，sinA ＝，所以 cosA ＝。
7、如图，在 Rt△ABC 中，∠ACB ＝ 90°，CD⊥AB 于点 D，若AC ＝，BC ＝ 2，则 sin∠ACD 的值为（）A B C D答案：A解析：因为∠ACB ＝ 90°，AC ＝，BC ＝ 2，所以 AB ＝ 3。
解直角三角形练习题
解直角三角形练习题解直角三角形练习题一、基础知识练习题：1. 在一个直角三角形ABC中，∠A = 90°， AB = 6cm， AC = 8cm，求BC的长度。
2. 若一个直角三角形的另外两个角的度数分别是30°和60°，求斜边的长。
3. 已知一个直角三角形的斜边长是10cm，一个锐角的度数是45°，求直角边的长度。
4. 在一个直角三角形PQR中，∠P = 90°， PQ = 5cm， QR = 13cm，求PR的长度。
5. 若一个直角三角形的直角边长分别是3cm和4cm，求斜边的长。
二、综合运用练习题：1. 一个直角三角形ABC，∠A = 90°， AB = x cm， AC = 8cm，BC = 10cm。
求x的值。
2. 已知一个直角三角形的斜边长是8cm，一个锐角的度数是30°，求直角边的长度。
3. 在一个直角三角形MNP中，∠N = 90°， MN = x cm， NP = 12cm， MP = 20cm。
求x的值。
4. 若一个直角三角形的直角边长分别是2x cm和3x cm，求斜边的长。
5. 已知一个直角三角形的斜边长是15cm，一个锐角的度数是60°，求直角边的长度。
三、挑战练习题：1. 在一个直角三角形DEF中，∠D = 90°， DE = 12cm， DF = x cm， EF = x + 2cm。
求x的值。
2. 若一个直角三角形的直角边长是4x cm和5x cm，求斜边的长。
3. 在一个直角三角形XYZ中，∠Z = 90°， XY = 10cm， XZ = 3x cm， YZ = 4x cm。
求x的值。
4. 已知一个直角三角形的斜边长是20cm，一个锐角的度数是45°，求直角边的长度。
5. 在一个直角三角形GHI中，∠G = 90°， GH = x cm， GI = 15cm， HI = 3x cm。
初三中考复习 解直角三角形 专题复习训练题 含答案
初三中考复习解直角三角形专题复习训练题含答案2019 初三中考复习解直角三角形专题复习训练题1. 如图，在以BC为底边的等腰△ABC中，∠A＝30°，AC＝8，则AC边上的高BD的长是( )A．4 B．8 C．2 3 D．4 32. 如图，在△ABC中，∠ACB＝90°，CD⊥AB，垂足为D，点E是AB的中点，CD＝DE＝a，则AB的长为( )A．2a B．22a C.3a D．43 3a3. 如图，△ABC的顶点是正方形网格的格点，则sin A的值为( )A.12B．55C.1010D．2554．直线y＝3x－3与x轴所成的锐角为x，则tan x＝______. 5．计算：cos230°－2sin60°－tan30°＋tan245°＝_______.6．如图，在△ABC中，D是AB的中点，DC⊥AC，且tan∠BCD＝13，求sin A、cos A、tan A的值．7. 如图，在△ABC中，∠C＝90°，sinA＝23，AB＝6，求BC的长．8. 如图，为了测量某条河的宽度，现在河边的一岸边任意取一点A，又在河的另一岸边取两点B、C测得∠α＝30°，∠β＝45°，量得BC长为100米．求河的宽度．(结果保留根号)9. 如图，在△ABC中，AD⊥BC，BE⊥AC，垂足分别为D、E，AD与BE相交于点F.(1)求证：△ACD∽△BFD;(2)当tan∠ABD＝1，AC＝3时，求BF的长．10. 如图在△ABC中，AB＝1，AC＝2，sinB＝24，求BC的长．5. 346. 解：过点D 作DE ⊥CD 交BC 于点E ，在Rt △CDE 中，∵tan ∠BCD ＝13＝DECD ，设DE ＝x ，则CD ＝3x.又∵DE ⊥AC ，∴DE ∥AC ，∵AD ＝BD ＝12AB ，∴DE ＝12AC ，∴AC ＝2DE ＝2x.在Rt △ACD 中，AC ＝2x ，CD ＝3x ，∴AD ＝13x ，∴sinA ＝31313，cosA ＝21313，tanA ＝32.7. 解：在Rt △ABC 中，∠C ＝90°sinA＝BC AB ＝23，∵AB ＝6，∴BC ＝4. 8. 解：过点A 作AD ⊥BC 于点D ，∵∠β＝45°，∠ADC ＝90°，∴AD ＝DC ，设AD ＝DC ＝xm ，则tan30°＝x x ＋100＝33，解得：x ＝50(3＋1)，答：河的宽度为50(3＋1)m.9. (1)证明：∵AD ⊥BC ，BE ⊥AC, ∴∠BDF ＝∠ADC ＝∠BEC ＝90°， ∴∠C ＋∠DBF ＝90°，∠C ＋∠DAC ＝90°， ∴∠DBF ＝∠DAC, ∴△ACD ∽△BFD ； (2)∵tan ∠ABD ＝1，∠ADB ＝90° ∴ADBD ＝1, ∴AD ＝BD, ∵△ACD ∽△BFD, ∴AC BF ＝ADBD＝1, ∴BF ＝AC ＝3. 10. 解：过点A 作AD ⊥BC 于点D ，Rt △ABD 中，sinB ＝AD AB ＝24，∴AD ＝24，BD ＝AB 2－AD 2＝1－18＝144.在Rt △ACD 中，CD ＝AC 2－AD 2＝2－18＝304.∴BC ＝BD ＋CD ＝13＋304.11. 解：∵在Rt △DBC 中，∠DBC ＝45°，且CD ＝2.3米，∴BC ＝2.3m ，∵在Rt △ABC 中，∠ABC ＝70.5°，∴tan70.5°＝AC BC ＝AD ＋2.32.3≈2.824，解得：AD≈4.2，答：像体AD 的高度约为4.2m.12. 解：∵BN ∥ED ，∴∠NBD ＝∠BDE ＝37°，∵AE ⊥DE ，∴∠E ＝90°，∴BE ＝DE·tan∠BDE≈18.75(cm)，如图，过C 作AE 的垂线，垂足为F ，∵∠FCA ＝∠CAM ＝45°，∴AF ＝FC ＝25cm ，∵CD ∥AE ，∴四边形CDEF 为矩形，∴CD ＝EF ，∵AE ＝AB ＋EB ＝35.75(cm)，∴CD ＝EF ＝AE －AF≈10.8(cm)，答：线段BE 的长约等于18.8cm ，线段CD 的长约等于10.8cm.13. 解：根据题意，得△ABE 和△BDC 是直角三角形，∴∠3＝∠4＝90°，∵∠A ＋∠2＝90°，∠1＋∠2＝90°.∴tan ∠1＝tanA ＝13.在Rt △BCD 中，tan ∠1＝CD BD ，设CD ＝x ，则BD ＝3x ，∴x 2＋(3x)2＝(5)2，∴x ＝22，BD ＝3x ＝322.答：BD 的长为322米．14. 解：(a)由入射角等于反射角，得△AOB ∽△COD ，∴AB CD ＝OB OD ，即AB 1.7＝63.4，∴AB ＝3(m)； (b)由同一时刻物高与影长成正比，得AB BE ＝CD DF ，即AB 1.8＝10.6，∴AB ＝3(m)； (c)由光的直线传播，得△CEF ∽△CAB ，△CFG ∽△CBD ，∴EF AB ＝CFCB ＝FG BD ，∴0.2AB ＝0.69，∴AB ＝3(m)． 15. 解：(1)如图，过点D 作DE ⊥AB ，过点B 作BF ⊥CD ，∵∠A ＝∠C ＝45°，∠ADB ＝∠ABC ＝105°，∴△ADE 与△BCF 为等腰直角三角形，∴∠CBF ＝45°，在四边形ABCD中，∠ADC＝360°－∠A－∠C－∠ABC＝360°－45°－45°－105°＝165°，∴∠BDF＝∠ADC－∠ADB＝165°－105°＝60°，∴∠DBF＝30°，∵AD＝2，∴由勾股定理得AE＝DE＝ 2.∵∠ABC＝105°，∴∠ABD＝105°－45°－30°＝30°，∴在Rt△BDE中，BD＝2DE＝2 2.由勾股定理得BE＝ 6.∴AB＝2＋6；(2)设DE＝x，则AE＝x，BD＝2x，∴DF＝12BD＝x，由勾股定理得BE＝3x，BF＝BD2－DF2＝2x2－x2＝3x，∴CF＝3x，∵AB＝AE＋BE＝x＋3x，CD ＝DF＋CF＝x＋3x，AB＋CD＝(2＋23)x＝23＋2，∴x＝1，∴AB＝(3＋1)x ＝3＋1.。
九年级数学(下)《解直角三角形》练习题含答案
九年级数学（下）《解直角三角形》练习题1、测得某坡面垂直高度为2m,水平宽度为4m,则坡度为 [ ]2、在Rt △ABC 中，∠C=90°，∠A=30°，b=310，则a= ，c= ；3、已知在直角梯形ABCD 中，上底CD=4，下底AB=10，非直角腰BC=34，则底角∠B= ；4．如图：铁路的路基的横截面是等腰梯形，斜坡AB 的坡度为1∶3，BE 为33米，基面AD 宽2米，求路基的高AE ，基底的宽BEC 及坡角B 的度数.（答案可带根号）5．水坝横断面为等腰梯形，尺寸如图，（单位：米）坡度I=DEAE =1，求坡面倾斜角（坡角），并计算修建长1000米的水坝约需要多少土方？ 6．如图，上午9时，一条船从A 处出发，以20节的速度向正北航行，11时到达B 处，从A ，B 望灯塔C ，测得∠NAC ＝36°，∠NBC ＝72°，那么从B 处到灯塔C 的距离是多少海里？7．如图，王聪同学拿一把∠ACB ＝30°的小型直角三角尺ABC 目测河流在市区河段的宽度．他先在岸边的点A 顺着30°角的邻边AC 的方向确定河对岸岸边的一棵树M ．然后，沿30°角的对边AB 的方向前进到点B ′，顺着斜边C B ''的方向看见M ，并测得B A '＝100 m ，那么他目测的宽大约为多少？(结果精确到 1m)8．海中有一个小岛A，它的周围8海里内有暗礁，渔船跟踪鱼群由西向东航行，在B点测得小岛A在北偏东60°，航行12海里到达D点，这时测得小岛A在北偏东30°．如果渔船不改变航向，继续向东捕捞，有没有触礁的危险？思考·探索·交流1．如图，MN表示某引水工程的一段设计路线，从M到N的走向为南偏东30°，在M的南偏东60°的方向上有一点A，以A为圆心、500 m为半径的圆形区域为居民区．取MN上另一点B，测得BA的方向为南偏东 75°．已知MB＝400 m，通过计算回答，如果不改变方向，输水路线是否会穿过居民区？答案：1、D 2、10，20 3、30°4．解：∵3133 AE∴AE=3（米）BC=（2+63）（米）∠B=30°5. 45°,444000土方6．40 海里．7．河宽约 173 m ．8．渔船没有触礁的危险．思考·探索·交流答案：1．输水路线不会穿过居民区．提示：过点A 作MN 的垂线，垂足为C ，求AC。
初三解直角三角形的练习题
初三解直角三角形的练习题直角三角形是初中数学中的重要概念，解直角三角形的练习题有助于学生巩固对直角三角形的认识和运算能力。
本文将为大家提供一些初三解直角三角形的练习题，以帮助大家在学习中更好地理解和应用直角三角形的知识。
一、计算临边和斜边长度题目1：已知直角三角形的一条直角边长为5cm，另一条直角边长为12cm，求斜边的长度。
解题思路：根据勾股定理，斜边的长度等于两条直角边长度的平方和的平方根。
解题步骤：1. 根据勾股定理计算斜边的长度：斜边长度= √(5^2 + 12^2) = √(25+ 144) = √169 = 13cm。
题目2：已知直角三角形的斜边长为17cm，其中一直角边长为8cm，求另一直角边的长度。
解题思路：根据勾股定理，已知斜边和一条直角边，可以求得另一条直角边的长度。
解题步骤：1. 根据勾股定理计算另一直角边的长度：另一直角边的长度 =√(17^2 - 8^2) = √(289 - 64) = √225 = 15cm。
二、计算三角形的角度题目1：已知直角三角形的两条直角边长度分别为3cm和4cm，求直角三角形的两个锐角的正弦值、余弦值和正切值。
解题思路：根据正弦、余弦和正切的定义公式，可以计算出直角三角形两个锐角的三角函数值。
解题步骤：1. 计算第一个锐角的正弦值：sin(θ) = 对边长度 / 斜边长度 = 3 / 5 = 0.6；计算第一个锐角的余弦值：cos(θ) = 临边长度 / 斜边长度 = 4 / 5 = 0.8；计算第一个锐角的正切值：tan(θ) = 对边长度 / 临边长度 = 3 / 4 = 0.75。
2. 计算第二个锐角的正弦值：sin(90° - θ) = cos(θ) = 0.8；计算第二个锐角的余弦值：cos(90° - θ) = sin(θ) = 0.6；计算第二个锐角的正切值：tan(90° - θ) = 1 / tan(θ) = 1 / 0.75 =1.333。
新人教版初三解直角三角形练习题基础1
初三解直角三角形练习题一、 真空题：1、在Rt △ABC 中，∠B ＝900，AB ＝3，BC ＝4，则sinA= 2、 在Rt △ABC 中，∠C ＝900，AB ＝,35cm BC cm =则SinA= cosA=3、 Rt △ABC 中，∠C ＝900，SinA=54,AB=10,则BC ＝ 4、α是锐角，若sin α=cos150,则α＝ 若sin53018\=0.8018，则cos36042\=5、 ∠B 为锐角，且2cosB －1＝0则∠B ＝6、在△ABC 中，∠C ＝900，∠A ，∠B ，∠C 所对的边分别为a ，b ，c ，a ＝9，b ＝12，则sinA= sinB=7、 Rt △ABC 中，∠C ＝900，tanA=0.5,则cotA=8、 在Rt △ABC 中，∠C ＝900，若b a 32=则tanA=9．等腰三角形中，腰长为5cm ，底边长8cm ，则它的底角的正切值是10、若∠A 为锐角，且tan 2A+2tanA －3＝0则∠A ＝11、Rt △ABC 中，∠A ＝600，c=8，则a ＝ ，b ＝12、在△ABC 中，若32=c ,b ＝3，则tanB= ,面积S ＝13、在△ABC 中，AC ：BC ＝1：3，AB ＝6，∠B ＝ ，AC ＝BC ＝ 14、在△ABC 中，∠B ＝900，AC 边上的中线BD ＝5，AB ＝8，则tanACB=二、选择题1、在Rt △ABC 中，各边的长度都扩大2倍，那么锐角A 的正弦、余弦值 （ ）A 、都扩大2倍B 、都扩大4倍C 、没有变化D 、都缩小一半2、若∠A 为锐角，且cotA ＜3，则∠A （ ）A 、小于300B 、大于300C 、大于450且小于600D 、大于6003、在Rt △ABC 中，已知a 边及∠A ，则斜边应为 （ ）A 、asinAB 、 A asin C 、acosA D 、A acos4、等腰三角形底边与底边上的高的比是2：3，则顶角为（ ）A 、600B 、900C 、1200D 、15005、在△ABC 中，A ，B 为锐角，且有sinA ＝cosB ，则这个三角形是（）A 、等腰三角形 B 、直角三角形 C 、钝角三角形 D 、锐角三角形6、有一个角是300的直角三角形，斜边为1cm ，则斜边上的高为（）A 、41cmB 、21cmC 、43cmD 、23cm三、求下列各式的值1、sin 2600+cos 26002、sin600－2sin300cos3003. sin300－cos 24504. 2cos450+|32-|5. 0045cos 360sin 2+6. 130sin 560cos 300-7. 2sin 2300·tan300+cos600·cot300 8. sin 2450-tan 2300四、解答下列各题1、在Rt △ABC 中，∠C ＝900，，AB ＝13，BC ＝5，求sinA, cosA, tanA, cotA2. 在Rt △ABC 中，∠C ＝900，若1312sin =A 求cosA, sinB, cosB3. 在Rt △ABC 中，∠C ＝900，b=17, ∠B=450,求a, c 与∠A四、根据下列条件解直角三角形。
九年级数学解直角三角形同步练习题(含答案)
九年级数学解直角三角形同步练习题（含答案）一、选择题（本大题共15小题，共45.0分）1.若角α的余角是30∘，则cosα的值是()A. 12B. √32C. √22D. √332.在Rt▵ABC中，∠C=90∘，sinA=35，则cosB的值是()A. 45B. 35C. 34D. 433.如图，Rt△ABC中，∠C=90°，点D在AC上，∠DBC=∠A.若AC=4，cosA=45，则BD的长度为()A. 94B. 125C. 154D. 44.已知a，b，c是△ABC的∠A，∠B，∠C的对边，且a：b：c=1：√2：√3，则cos B的值为()A. √63B. √33C. √22D. √245.如图，Rt△ABC中，∠C=90°，AB=5，cosA=45，以点B为圆心，r为半径作⊙B，当r=3时，⊙B与AC的位置关系是()A. 相离B. 相切C. 相交D. 无法确定6.如图，数学活动小组利用测角仪和皮尺测量学校旗杆的高度，在点D处测得旗杆顶端A的仰角∠ADE为55°，测角仪CD的高度为1米，其底端C与旗杆底端B之间的距离为6米，设旗杆AB的高度为x米，则下列关系式正确的是()A. tan55°=B. tan55°=C. sin55°=D. cos55°=7.如图，已知点A、点B是同一幢楼上的两个不同位置，从A点观测标志物C的俯角是65°，从B点观测标志物C的俯角是35°，则∠ACB的度数为()A. 25°B. 30°C. 35°D. 65°8.在Rt△ABC中，已知∠C=90∘.若AC=2BC，则sin∠A的值是()A. 12B. 2 C. √55D. √529.△ABC中，∠C=90°，若∠A=2∠B，则cosB等于()A. √3B. √33C. √32D. 1210.如图，△ABC中，AD⊥BC于点D，AD=2√3，∠B=30°，S△ABC=10√3，则tanC的值为()A. 13B. 12C. √33D. √3211.在Rt△ABC中，∠C=90，AC=12，cosA=1213，则tanA等于()A. 513B. 1312C. 125D. 51212.如图，点A、B、C均在小正方形的顶点上，且每个小正方形的边长均为1，则cos∠BAC的值为()A. 12B. √22C. 1D. √213.从一艘船上测得海岸上高为42米的灯塔顶部的仰角为30°时，船离灯塔的水平距离是()A. 42√3米B. 14√3米C. 21米D. 42米14.如图，在8×4的正方形网格中，若△ABC的三个顶点在图中相应的格点上，则tan∠ACB的值为()A. 13B. √1010C. 12D. √2215.把Rt△ABC三边的长度都扩大为原来的3倍，则锐角A的余弦值()A. 不变B. 缩小为原来的13C. 扩大为原来的3倍D. 扩大为原来的9倍二、填空题（本大题共1小题，共3.0分）16.计算：√27+(13)−2−3tan60°+(π−√2)0=______．三、计算题（本大题共1小题，共6.0分）17.如图，在A的正东方向有一港口B.某巡逻艇从A沿着北偏东55°方向巡逻，到达C时接到命令，立刻从C沿南偏东60°方向以20海里/小时的速度航行，从C到B航行了3小时．求A，B间的距离(结果保留整数).(参考数据：sin55°≈0.82，cos55°≈0.57，tan55°≈1.43，√3≈1.73)四、解答题（本大题共5小题，共40.0分）18.如图，A，B两点被池塘隔开，在AB外选一点C，连接AC，BC.测得BC=221m，∠ACB=45°，∠ABC=58°.根据测得的数据，求AB的长(结果取整数)．参考数据：sin58°≈0.85，cos58°≈0.53，tan58°≈1.60．19.如图，在平面直角坐标系内，O为原点，点A的坐标为(10,0)，点B在第一象限内，BO=5，sin∠BOA=．(1)求点B的坐标；(2)求tan∠BAO的值．)−1+√18−6sin45°．20.计算：(1221.如图，平台AB高为12m，在B处测得楼房CD顶部点D的仰角为45°，底部点C的俯角为30°，求楼房CD的高度(√3取1.7)．22.如图，在△ABC中，∠C=90°，点D，E分别在AC，AB上，BD平分∠ABC，DE⊥AB于点E，AE=6，cosA=3．5(1)求CD的长；(2)求tan∠DBC的值．1.【答案】A【解析】【分析】本题考查了特殊角的三角函数值，属于基础题．先根据题意求得α的值，再求它的余弦值．【解答】解：因为角α的余角是30∘，所以α=90°−30°=60°，则．故选A．2.【答案】B【解析】解：在Rt△ABC中，∠C=90°，∴∠A+∠B=90°，∴cosB=sinA=，故选：B．3.【答案】C【解析】解：∵∠C=90°，AC=4，cosA=45，∴AB=ACcosA=5，∴BC=√AB2−AC2=3，∵∠DBC=∠A．∴cos∠DBC=cosA=BCBD =45，∴BD=3×54=154，故选：C．在△ABC中，由三角函数求得AB，再由勾股定理求得BC，最后在△BCD中由三角函数求得BD．本题主要考查了勾股定理，解直角三角形的应用，关键是解直角三角形．4.【答案】B【解析】解：∵，∴△ABC为直角三角形．cosB==．故选：B．5.【答案】B【解析】【分析】本题考查了直线与圆的位置关系的应用，注意：直线和圆有三种位置关系：相切、相交、相离．根据三角函数的定义得到AC，根据勾股定理求得BC，和⊙B的半径比较即可．【解答】解：∵Rt△ABC中，∠C=90°，AB=5，cosA=45，∴ACAB =AC5=45，∴AC=4，∴BC=√AB2−AC2=3，∵r=3，∴⊙B与AC的位置关系是相切，故选：B．6.【答案】B【解析】【解析】解：∵在Rt△ADE中，DE=6，AE=AB−BE=AB−CD=x−1，∠ADE=55°，∴sin55°=，cos55°=，tan55°=，故选：B．7.【答案】B【解析】【解析】解：根据题意可知：∠ACD=65°，∠BCD=35°，∴∠ACB=∠ACD−∠BCD=30°．故选：B．8.【答案】C【解析】【分析】本题主要考查了锐角三角函数的求法，属于基础题．可先求出斜边AB，然后根据正弦的定义求出角A的正弦即可．【答案】解：∵AC=2BC，由勾股定理可得：AB=√AC2+BC2=√(2BC)2+BC2=√5BC，∴sin∠A=BCAB =√5=√55，故选C．9.【答案】C【解析】解：∵∠C=90°，∴∠A+∠B=90°，∵∠A=2∠B，∴∠B=30°，∴cosB=cos30°=√32，故选：C．根据直角三角形的性质求出∠B，根据30°的余弦值是√32解答．本题考查的是特殊角的三角函数值、直角三角形的性质，熟记特殊角的三角函数值是解题的关键．10.【答案】D【解析】解：∵在△ABD中，∠ADB=90°，AD=2√3，∠B=30°，∴BD=ADtanB =√3√33=6．∵S△ABC=12BC⋅AD=10√3，∴12BC⋅2√3=10√3，∴BC=10，∴CD=BC−BD=10−6=4，∴tanC=ADCD =2√34=√32．故选：D．首先解直角△ABD，求得BD，再根据S△ABC=10√3，求出BC，那么CD=BC−BD，然后在直角△ACD中利用正切函数定义即可求得tanC的值．本题考查了解直角三角形，三角形的面积，锐角三角函数定义，解题的关键是求出CD的长．【解析】解：∵cosA=ACAB =1213，AC=12，∴AB=13，BC=√AB2−AC2=5，∴tanA=BCAC =512．故选：D．根据cosA=1213求出第三边长的表达式，求出tanA即可．本题利用了勾股定理和锐角三角函数的定义．12.【答案】B【解析】解：连接BC，∵每个小正方形的边长均为1，∴AB=√5，BC=√5，AC=√10，∵(√5)2+(√5)2=(√10)2，∴△ABC是直角三角形，∴cos∠BAC=ABAC =√5√10=√22，故选：B．根据题目中的数据和勾股定理，可以求得AB、BC、AC的长，然后根据勾股定理逆定理可以判断△ABC的形状，从而可以求得cos∠BAC的值．本题考查解直角三角形、勾股定理与逆定理，解答本题的关键是明确题意，判断出△ABC 的形状，利用锐角三角函数解答．13.【答案】A【解析】解：根据题意可得：船离海岸线的距离为42÷tan30°=42√3(米)故选：A．在直角三角形中，已知角的对边求邻边，可以用正切函数来解决．本题考查解直角三角形的应用−仰角的定义，要求学生能借助仰角构造直角三角形并解直角三角形．【解析】【分析】本题主要考查正切值的求法，解题的关键是构造直角三角形．作AH⊥CB，交CB延长线于H点，∠ACB的正切值是AH与CH的比值．【解答】解：如图，作AH⊥CB，交CB延长线于H点，则tan∠ACB=AHHC =26=13．故选A．15.【答案】A【解析】【分析】本题考查的是相似三角形的判定和性质、锐角三角函数的定义，掌握相似三角形的对应角相等是解题的关键．根据相似三角形的性质解答．【解答】解：三边的长度都扩大为原来的3倍，则所得的三角形与原三角形相似，∴锐角A的大小不变，∴锐角A的余弦值不变，故选：A．16.【答案】10【解析】解：原式=3√3+9−3√3+1=10．故答案为：10．直接利用零指数幂的性质以及特殊角的三角函数值、负整数指数幂的性质分别化简得出答案．此题主要考查了实数运算，正确化简各数是解题关键．17.【答案】解：如图，过点C作CD⊥AB于点D，由题意可知：∠ACD=55°，∠BCD=60°，BC=20×3=60(海里)，BC=30(海里)，BD=30√3(海里)，在Rt△BCD中，CD=12在Rt△ADC中，AD=CD⋅tan55°=30×1.43≈42.90(海里)，∴AB=AD+BD=42.90+30√3≈95(海里)．答：A，B间的距离为95海里．【解析】过点C作CD⊥AB于点D，根据三角函数分别求出CD、BD、AD的长，进而可求出A、B间的距离．本题考查了解直角三角形的应用−方向角问题，解决本题的关键是掌握方向角的定义．18.【答案】解：如图，过点A作AD⊥BC，垂足为D，∵∠ACB=45°，∴AD=CD，设AB=x，在Rt△ADB中，AD=AB⋅sin58°≈0.85x，BD=AB⋅cos58°≈0.53x，又∵BC=221，即CD+BD=221，∴0.85x+0.53x=221，解得，x≈160，答：AB的长约为160m．【解析】通过作高，构造直角三角形，利用直角三角形的边角关系，列方程求解即可．本题考查直角三角形的边角关系，掌握直角三角形的边角关系，即锐角三角函数，是正确解答的前提，通过作辅助线构造直角三角形是常用的方法．19.【答案】解：(1)如图，过点B作BH⊥OA于点H，∵OB=5，sin∠BOA=，∴BH=3，OH=4，∴点B的坐标为(4,3)，(2)∵OA=10，∴AH=OA−OH=10−4=6，∴在Rt△AHB中，tan∠BAO===．【解析】解答案20.【答案】解：(12)−1+√18−6sin45°=2+3√2−6×√2 2=2+3√2−3√2=2．【解析】首先计算负整数指数幂、开方和特殊角的三角函数值，然后计算乘法，最后从左向右依次计算，求出算式的值即可．此题主要考查了实数的运算，解答此题的关键是要明确：在进行实数运算时，和有理数运算一样，要从高级到低级，即先算乘方、开方，再算乘除，最后算加减，有括号的要先算括号里面的，同级运算要按照从左到右的顺序进行．另外，有理数的运算律在实数范围内仍然适用．21.【答案】解：如图，过点B作BE⊥CD于点E，根据题意，∠DBE=45°，∠CBE=30°．∵AB⊥AC，CD⊥AC，∴四边形ABEC为矩形．∴CE=AB=12m．在Rt△CBE中，cot∠CBE=BE，CE∴BE=CE⋅cot30°=12×√3=12√3．在Rt△BDE中，由∠DBE=45°，得DE=BE=12√3．∴CD=CE+DE=12(√3+1)≈32.4．答：楼房CD的高度约为32.4m．【解析】首先分析图形，根据题意构造直角三角形．本题涉及多个直角三角形，应利用其公共边构造关系式求解．考查了解直角三角形的应用−仰角俯角问题，本题要求学生借助俯角构造直角三角形，并结合图形利用三角函数解直角三角形．22.【答案】解：(1)在Rt△ADE中，∠AED=90°，AE=6，cosA=3，5∴AD=AE=10，cosA∴DE=√AD2−AE2=√102−62=8．∵BD平分∠ABC，DE⊥AB，DC⊥BC，∴CD=DE=8；(2)由(1)AD=10，DC=8，∴AC=AD+DC=18，在△ADE与△ABC中，∵∠A=∠A，∠AED=∠ACB，∴△ADE∽△ABC，∴DEBC =AEAC，即8BC=618,BC=24，∴tan∠DBC=CDBC =824=13．【解析】(1)在Rt△ADE中，根据余弦函数的定义求出AD，利用勾股定理求出DE，再由角平分线的性质可得DC=DE=8；(2)由AD=10，DC=8，得AC=AD+DC=18.由∠A=∠A，∠AED=∠ACB，可知△ADE∽△ABC，由相似三角形对应边成比例可求出BC的长，根据三角函数的定义可求出tan∠DBC=13．本题考查了解直角三角形，角平分线的性质、相似三角形的判定与性质，三角函数的定义，求出DE是解第(1)小题的关键；求出BC是解第(2)小题的关键．。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
初三解直角三角形练习题一、 真空题： 1、 在Rt △ABC 中，∠B ＝900，AB ＝3，BC ＝4，则sinA= 2、在Rt △ABC 中，∠C ＝900，AB ＝,35cm BC cm=则SinA= cosA= 3、Rt △ABC 中，∠C ＝900，SinA=54,AB=10,则BC ＝4、α是锐角，若sin α=cos150,则α＝ 若sin53018\=0.8018，则cos36042\=5、 ∠B 为锐角，且2cosB －1＝0则∠B ＝6、在△ABC 中，∠C ＝900，∠A ，∠B ，∠C 所对的边分别为a ，b ，c ，a ＝9，b ＝12，则sinA= sinB=7、 Rt △ABC 中，∠C ＝900，tanA=0.5,则cotA= 8、 在Rt △ABC 中，∠C ＝900，若b a 32=则tanA= 9．等腰三角形中，腰长为5cm ，底边长8cm ，则它的底角的正切值是10、若∠A 为锐角，且tan 2A+2tanA －3＝0则∠A ＝ 11、Rt △ABC 中，∠A ＝600，c=8，则a ＝ ，b ＝ 12、在△ABC 中，若32=c ,b ＝3，则tanB= ,面积S ＝ 13、在△ABC 中，AC ：BC ＝1：3，AB ＝6，∠B ＝ ，AC ＝ BC ＝ 14、在△ABC 中，∠B ＝900，AC 边上的中线BD ＝5，AB ＝8，则tanACB= 二、选择题1、在Rt △ABC 中，各边的长度都扩大2倍，那么锐角A 的正弦、余弦值 （ ） A 、都扩大2倍 B 、都扩大4倍 C 、没有变化 D 、都缩小一半2、若∠A 为锐角，且cotA ＜3，则∠A （ ）A 、小于300B 、大于300C 、大于450且小于600D 、大于600 3、在Rt △ABC 中，已知a 边及∠A ，则斜边应为 （ ） A 、asinA B 、A a sin C 、acosA D 、Aa cos 4、等腰三角形底边与底边上的高的比是2：3，则顶角为（ ） A 、600 B 、900 C 、1200 D 、15005、在△ABC 中，A ，B 为锐角，且有sinA ＝cosB ，则这个三角形是（ ）A 、等腰三角形 B 、直角三角形 C 、钝角三角形 D 、锐角三角形6、有一个角是300的直角三角形，斜边为1cm ，则斜边上的高为（ ）A 、41cmB 、21cmC 、43cmD 、23cm三、求下列各式的值1、sin 2600+cos 26002、sin600－2sin300cos3003. sin300－cos 24504. 2cos450+|32 |5. 0045cos 360sin 2+ 6. 130sin 560cos 300-7. 2sin 2300·tan300+cos600·cot300 8. sin 2450-tan 2300四、解答下列各题1、在Rt △ABC 中，∠C ＝900，，AB ＝13，BC ＝5， 求sinA, cosA, tanA, cotA2. 在Rt △ABC 中，∠C ＝900，若1312sin =A 求cosA, sinB, cosB3. 在Rt △ABC 中，∠C ＝900，b=17, ∠B=450,求a, c 与∠A四、根据下列条件解直角三角形。
在Rt △ABC 中。
1、c=20 ∠A=450 2. a=36 ∠B=3003.a=19 c=2194. a=66,26 b五、等腰梯形的一个底角的余弦值是232，腰长是6，上底是22求下底及面积解直角三角形练习题A 组1、 锐角A 满足2 sin(A-150)=3,则∠A= .2、已知：CD ⊥AB,CD=33m ，∠CAD=∠DBC=600, 则拉线AC 的长是 m 。
3、如图，为了测量河两岸A 、B 两点的距离，在与AB 垂直的方向上取点C ，测得AC ＝a ，∠ACB ＝α，那么AB 等于____________4、如图，在矩形ABCD 中，DE ⊥AC于E ，设∠ADE=α，且53cos =α，AB = 4, 则AD 的长为_______________5、在山坡上种树，要求株距为5.5米，测得斜坡的倾斜角为300，则斜坡上的相邻两株间的坡面距离是 米。
6、如图所示，某建筑物BC 直立于水平地面，AC=9米，要建造阶梯AB ，使倾斜角为300，且每阶高不超过20厘米，则阶梯至少要建 阶。
一阶计算；3取1.732）（最后一阶的高不足20厘米时，按B 组1、 △ABC 中，∠A=600,∠B=450,AB=8.求△ABC 的面积（结果可保留根号）。
DCBAAB CDEa BA C CBA2、 如图：四边形 ABCD 中， ∠B=∠D=900，∠BAD=600，且BC=11，CD=2，求AC 的长。
3、甲、乙两楼相距100米，从乙楼底望甲楼顶仰角为60°，从甲楼顶望乙楼顶俯角为30°，要求画出正确图形并求两楼的高度。
4、如图，在两面墙之间有一个底端在A 点的梯子，当它靠在一侧墙上时，梯子的顶端在B 点;当它靠在另一侧墙上时，梯子的顶端在D 点。
已知∠BAC=600,∠DAE=450,点D 到地面的垂直距离DE=32m 。
求点B 到地面的垂直距离BC. C 组1.如图，Rt △ABC 中，∠ACB=900，D 是AB 的中点， sin α=32,AC=54,求ABC S 。
D EB CAαC2、某居民小区有一朝向为正南方向的居民楼（如图8），该居民楼的一楼是高6米的小区超市，超市以上是居民住房.在该楼的前面15米处要盖一栋高20米的新楼.当冬季正午的阳光与水平线的夹角为32°时.（1）问超市以上的居民住房采光是否有影响，为什么？ （2）若要使超市采光不受影响，两楼应相距多少米？ （结果保留整数）图88532tan ,12510632cos ,1005332sin 000≈≈=初中数学解直角三角形总复习题一、填空题：（2`×21=42`）1、解直角三角形是指在一个直角三角形中，除 外共 个个元素，已知个元素（其中至少有一个是 ），求出其余 个元素的过程。
2、在Rt △ABC 中，∠C = 90°，三条边a 、b 、c 这间的关系式是 ，两锐角∠A 、∠B 之间的关系式是 ，边角a 、b 、c 、∠A 、∠B 之间的关系是 ， ， ， ； ， ， ， 。
3、在Rt △ABC 中，∠C = 90°，∠B= 30°，c = 3，则①∠A = ，②a = ，③b = 。
4、在Rt △ABC 中，∠C = 90°，∠B= 45°，c = 3，则①∠A = ，②a = ，③b = 。
5、在Rt △ABC 中，∠C = 90°，a = 1. 5，c = 3，则①∠A = ，② ∠B = ，③b = 。
6、在Rt △ABC 中，∠C = 90°，a = 2，sinA = 31，则①∠A = ，② ∠B= ，③b= ④c = 。
（保留根号）7、在Rt △ABC 中，∠C = 90°，a = 2，tanB = 31，则①∠A = ，② ∠B= ，③b= ④c = 。
（保留根号）8、在Rt △ABC 中，∠C = 90°，a = 2，cotB = 31，则①∠A = ，② ∠B= ，③b= ④c = 。
（保留根号）9、在Rt △ABC 中，∠C = 90°，a = 2，3a = 2b ，则①∠A = ，② ∠B = ，③b= ④c = 。
（保留根号）10、在Rt △ABC 中，∠C = 90°，a = 2，5a = 3c ，则①∠A = ，② ∠B = ，③b= ④c = 。
（保留根号） 11、在Rt △ABC 中，∠C = 90°，a = 10，S △ABC =3350，则①∠A = ， ② ∠B = ，③b= ④c = 。
（保留根号） 12、在△ABC 中，∠A= 75°，∠B= 45°，c = 26，则①a = ，②b = 。
13、在△ABC 中，c = b =3 ，a= 2，则sinA = 。
14、在Rt △ABC 中，∠C = 90°，∠A = 60°，斜边上的高CD =3， 则 ①∠B = ，② a = ，③b= ④c = 。
（保留根号）15、在Rt △ABC 中，∠C = 90°，∠A = 60°，a ＋b =14， 则①∠B = ，② a = ，③b= ④c = 。
（保留根号） 16、在Rt △ABC 中，∠C = 90°，斜边上的高CD =12，AD = 16， 则①∠B = ，② ∠B = ，③a = ，④b= ⑤c = 。
（保留根号）17、在Rt △ABC 中，∠C = 90°，若sinA = cosA ，则tanB = 。
18、cos43°= 0. 7314，sinx = 0.7314 ，则x = 。
19、在Rt △ABC 中，∠C = 90°，∠B= 30°，则tanA ＋sinB= 。
20、tanA ·tan15°= 1，则锐角∠A = 。
21、某人上坡走了10米，实际升高了6 ，则这斜坡的坡度i= 二、填空题：（3`×8=24`）1、在Rt △ABC 中，∠C = 90°，a 、b 、c 分别是三角形的三边，则下列正确的是（ ）A 、a = c sinB B 、a = b cotBC 、b = c sinBD 、c = atanB 2、关于锐角α、β，下列说法正确的是（ ） A 、若α＋β=90°则sin α＝sin β B 、sin （α＋β）=sin α＋sin β C 、若α＜β,则cot β－cot α＞0 D 、sin α＋sin β＞1 3、已知0°＜x ＜90°，且sinx = cos60°，则cot 2x =（ ） A 、30°B 、60°C 、3D 、33 4、当x 为锐角时，下面的命题中正确的是（ ） A 、sinx ＜tanx B 、cosx ＞cotx C 、sinx ＜ cosxD 、tanx ＞cotx5、已知sinx = 31，则锐角x 满足（ ）A 、0°＜x ＜30°B 、30°＜x ＜45°C 、45°＜x ＜60°D 、60°＜x ＜90° 6、当锐角A ＞30°时，cosA 的值（ ） A 、小于22 B 、大于22 C 、小于23 D 、大于23 7、在Rt △ABC 中，∠C = 90°，则正确的是（ ） A 、sinA = cos （90°－B ） B 、tanA = cot （90°－B ） C 、sin 2A ＋sin 2B = 1 D 、cosA = sinA8、令a = sin60°，b = cos45°，c = tan30°，则它们的大小关系是（ ） A 、c ＜b ＜a B 、b ＜a ＜c C 、a ＜c ＜b D 、b ＜c ＜a三、解答题:1、（10`）如图：已知楼房AB 高40米，铁塔CD 塔基中心C 到AB 楼房房基间水平距离B 为40米，从A 望D 的仰角30°求塔CD 的高.2、（11`）数学实验课上，同学们调查知道：本乡位于距离学校不远处最高的山顶上的电信发射台铁塔高30米，为了测量此小山相对学校的高度，在学校里操场上用自制的测仰角的仪器做测试实验，如图：在一个地方测的仰角为α=45°，仰角β高。