(完整word版)频率分布与直方图练习题.doc
概率频率分布直方图练习题【范本模板】
（1）估计这60名乘客中候车时间少于10分钟的人数；
组别
候车时间
人数
一
2
二
6
三
4
四
2
五
1
（2）若从上表第三、四组的6人中随机抽取2人作进一步的问卷调查，求抽到的两人恰好来自不同组的概率．
记从“一等品中随机抽取2件,2件等级系数都是8"为事件 ，
则 包含的基本事件有 共3种， ………11分
故所求的概率 . ……………………12分
4、解:（1）共有1400名学生，高二级抽取的人数为 （人)…………3分
（2)“服务满意度为3”时的5个数据的平均数为 ，……………4分
所以方差 ………………7分
组别
达标
不达标
总计
甲班
8
乙班
54
合计
120
7、（本小题满分12分）
对某校高一年级学生参加社区服务次数统计，随机抽去了 名学生作为样本,得到这 名学生参加社区服务的次数，根据此数据作出了频数与频率的统计表如下：
（1）求出表中 的值；
（2)在所取样本中,从参加社区服务的次数不少于 次的学生中任选 人,求至少一人参加社区服务次数在区间 内的概率．
三等品的频率为 ，故估计该厂产品的三等品率为 ．………………………6分
（2）样本中一等品有6件，其中等级系数为7的有3件，等级系数为8的有3件,…7分
记等级系数为7的3件产品分别为 、 、 ，等级系数为8的3件产品分别为 、 、 ,则从样本的一等品中随机抽取2件的所有可能为: ， , ， ， , ， , , ， ， , ， ， 共15种， …………10分
频率分布与直方图练习题
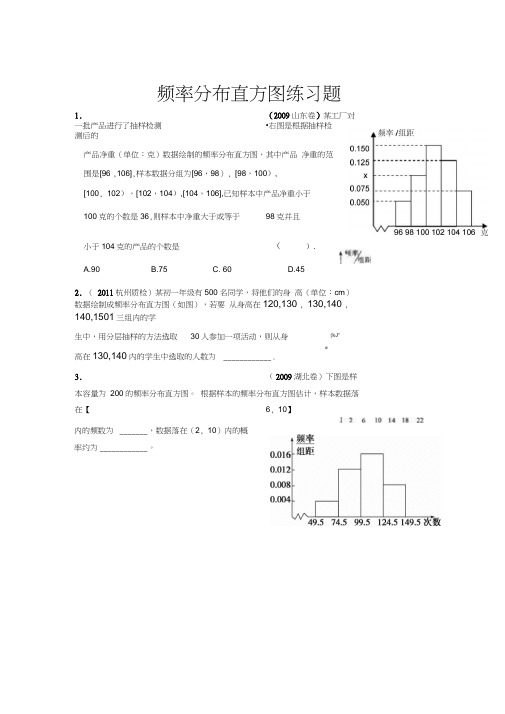
频率分布直方图练习题1.（2009山东卷）某工厂对一批产品进行了抽样检测 •右图是根据抽样检测后的产品净重（单位：克）数据绘制的频率分布直方图，其中产品 净重的范围是[96 ,106],样本数据分组为[96，98）, [98，100）,[100, 102），[102，104）,[104，106],已知样本中产品净重小于 100克的个数是36,则样本中净重大于或等于98克并且小于104克的产品的个数是 （）. A.90B.75C. 60D.452. （ 2011杭州质检）某初一年级有500名同学，将他们的身 高（单位：cm ）数据绘制成频率分布直方图（如图），若要 从身高在120,130 , 130,140 ,140,1501三组内的学生中，用分层抽样的方法选取30人参加一项活动，则从身高在130,140内的学生中选取的人数为 ____________ . 3.（ 2009湖北卷）下图是样本容量为 200的频率分布直方图。
根据样本的频率分布直方图估计，样本数据落在【 6, 10】内的频数为 _______ ，数据落在（2, 10）内的概 率约为 ____________ 。
(kJ* ■4.（2011华附月考）为了了解小学生的体能情况，抽取了某小学同年级部分学生进行跳绳测试，将所得数据整理后，画出频率分布直方图如图所示，已知图中从左到右前三个小组的频率分别是0.1, 0.3, 0.4,第一小组的频数为 5.（1）求第四小组的频率；（2）参加这次测试的学生人数是多少？（3）估计在这次测试中，学生跳绳次数的中位数、众数、平均数及方差。
5. （2011惠州调研）右图是2010年在惠州市举行的全省运动会上，七位评委为某跳水比赛项 目打出的分数的茎叶统计图，去掉一个最高分和一个最低分后，所剩 数据的平均数和方差分别为()A . 84, 4.84B . 84, 1.6C . 85, 1.6D . 85, 46. （2011佛山一检）某班同学利用国庆节进行社会实践，对进行了一次生活习惯是否符合低碳观念的调查，若生活习惯符合低碳观念的称为 低碳族”,否则称为 非低碳族”，得到如下统计表和各年龄段人数频率分布直方图:7. 下图甲是某市对当地干部的月收入情况调查后画出的样本频率分布直方图,图乙已知图甲中从左向右第一组的频数为 4000.在样本中记月收入在[1000,1500）, [1500,2000）, [2000, 2500） , [2500 , 3000） , [3000, 3500） , [3500 , 4000]的人数依次为 A 「A ?、…、人6・图 乙是统计图甲中月工资收入在一定范围内的人数的算法流程图，则样本的容量n=_;图乙输出的 S= __.（用数字作答） 8•为了了解某地区高三学生的身体发育情况，抽查了该地区(MOD MOOt AA 十~Aj” ............./辅出百/[25,55]岁的人群随机抽取 n 人低碳娱的人数占本组的频率策1组120 0.6第二组1勺5P第三组琢）1000 5[40.45)|：30 4300.3 第六组邓习15D-3图甲（I ）补全频率分布直方图并求 n 、a 、 p 的值；（n ）略100名年龄为17.5岁〜18岁的男生体重（kg）,得到频率分布直方图如下：根据上图可得这100名学生中体重在[56.5 , 64.5）的学生人数是 ___________________________9. 某班50名学生在一次百米测试中，成绩全部介于13秒与19秒之间，将测试结果按如下方式分成六组：第一组，成绩大于等于13秒且小于14秒；第二组，成绩大于等于14秒且小于15秒；…… 第六组，成绩大于等于18秒且小于等于19秒.右图是按上述分组方法得到的频率分布直方图•设成绩小于17秒的学生人数占全班总人数的百分比为X,成绩大于等于15秒且小于17秒的学生人数为y,则从频率分布直方图中可分析出x和y分别为_______________ .10. 在学校开展的综合实践活动中，某班进行了小制作评比，作品上交时间为5月1日至30 日,评委会把同学们上交作品的件数按5天一组分组统计，绘制了频率分布直方图(如图所示)，已知从左到右各长方形高的比为2 :3 :4 : 6：4：1 ,第三组的频数为12,请解答下列问题：(1 )本次活动共有多少件作品参加评比？(2)哪组上交的作品数量最多？有多少件？(3)经过评比，第四组和第六组分别有10件、2件作品获奖，问这两组哪组获奖率高?11. 为了了解高一学生的体能情况，某校抽取部分学生进行一分钟跳绳次数测试，将所得数据整理后，画出频率分布直方图(如图所示)，图中从左到右各小长方形面积之比为2 : 4 : 17 ：15 ：9 : 3，第二小组频数为12.(1)第二小组的频率是多少？样本容量是多少？(2 )若次数在110以上(含110次)为达标，试估计该学校全体高一学生的达标率是多少？但具体落到实处应该是一种尊重，一种接人待物的方式方法。
《频数分布表和频数分布直方图》课后练习
《频数分布表和频数分布直方图》课后练习一、选择题:1. 一个容量为80的样本最大值为141,最小值为50,取组距为10, 则可以分成( ).A. 10 组B. 9 组C. 8 组D. 7 组2. 已知在一个样本中,50 个数据分别落在5 个组内, 第一、二、三、五组数据频数分别为2、8、15、5，则第四组数据的频数和频率分别为( )A.25 ．50%B. 20 。
50%C. 20.40%D.25.40%3. 下列说法正确的是( )A. 样本的数据个数等于频数之和B. 扇形统计图可以告诉我们各部分的数量分别是多少C. 如果一组数据可以用扇形统计图表示，那么它一定可以用频数分布直方图表示•D. 将频数分布直方图中小长方形上面一边的一个端点顺次连结起来, 就可以得到频数折线图.4. 在1000个数据中，用适当的方法抽取50 个作为样本进行统计，频数分布表中54.5~57.5 这一组的频率为0.12，那么估计总体数据落在54.5~57.5 之间的约有( )A. 120 个B. 60 个C. 12 个D. 6 个5. 在样本的频数分布直方图中，有11个小长方形，若中间一个长方形的面积等于其他10个小长方形面积的和的四分之一，且样本数据有160个，则中间一组的频数为( )A. 0.2B. 32C. 0.25D. 40二、填空题：6. 对某班同学的身高进行统计( 单位:厘米)，频数分布表中165.5~170.5 这一组学生人数是12，频率为0.25，则该班共有_____ 名同学.7. 为了帮助班上的两名贫困学生解决经济困难，班上的20 名学生捐出了息的零化钱，他们捐款数如下:( 单位:元) 19，20，25，30，24，23，25， 29，27，27，28，28，26，27，21，30，20，19，22，20. 班主任老师准备将这组数据制成频数分布直方图，以表彰他们的爱心. 制图时先计算最大值与最小值的差是___，若取组距为2，则应分成_______ 组; 若第一组的起点定为18.5. 则在26.5~28.5 范围内的频数为三.解答题：8.2003年中考结束后，某市从参加中考的12000名学生中抽取200名学生的数学成绩(考生得分均为整数，满分120分)进行统计，评估数学考试情况，经过整理得到如下频数分布直方图，请回答下列问题：(1)此次抽样调查的样本容量是____ ；(2)补全频数分布直方图⑶若成绩在72分以上(含72分) 为及格，请你评估该市考生数学成绩的及格率与数学考试及格人数。
频率分布直方图 小练 (含答案)
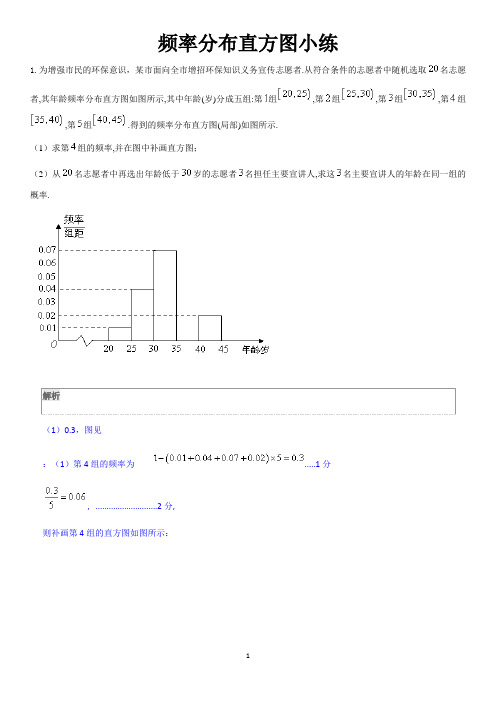
频率分布直方图小练1.为增强市民的环保意识，某市面向全市增招环保知识义务宣传志愿者.从符合条件的志愿者中随机选取名志愿者,其年龄频率分布直方图如图所示,其中年龄(岁)分成五组:第组,第组,第组,第组,第组.得到的频率分布直方图(局部)如图所示.（1）求第组的频率,并在图中补画直方图；（2）从名志愿者中再选出年龄低于岁的志愿者名担任主要宣讲人,求这名主要宣讲人的年龄在同一组的概率.解析（1）0.3，图见：（1）第4组的频率为.....1分, ............................2分,则补画第4组的直方图如图所示：.............................................4分（２）设“从20名志愿者中再选出年龄低于30岁的志愿者3名担任主要宣讲人, 其年龄均在同一组”为事件A...............................................5分第一组的人数为人第二组的人数为人......................6分设第一组的志愿者为m，第二组的4名志愿者分别为a,b,c,d.......................7分从m, a,b,c,d中选出3名志愿者共有10种选取方法。
.........10分其中都在第二组的共有4种选取方法..........11分所以，所求事件的概率为........................12分2.某校为了解高一期末数学考试的情况，从高一的所有学生数学试卷中随机抽取份，试卷进行成绩分析，得到数学成绩频率分布直方图（如图所示），其中成绩在的学生人数为6.（Ⅰ）估计所抽取的数学成绩的众数；（Ⅱ）用分层抽样的方法在成绩为和这两组中共抽取5个学生，并从这5个学生中任取2人进行点评，求分数在恰有1人的概率.考点6.统计图表解析解：（Ⅰ）由频率分布直方图可知：样本的众数为75．…………3分（Ⅱ）由频率分布直方图可得：第三组的频率：，所以，…………………………………………4分第四组的频数：；第五组的频数：；用分层抽样的方法抽取5份得：第四组抽取：；第五组抽取：．……7分记抽到第四组的三位同学为，抽到第五组的两位同学为则从5个同学中任取2人的基本事件有：，，共10种．其中分数在恰有1人有：，共6种．所求概率：．……………………………12分3.某校研究性学习小组从汽车市场上随机抽取20辆纯电动汽车调查其续驶里程（单次充电后能行驶的最大里程），被调查汽车的续驶里程全部介于公里和公里之间，将统计结果分成组：，，，，，绘制成如图所示的频率分布直方图．（Ⅰ）求直方图中的值；（Ⅱ）求续驶里程在的车辆数；（Ⅲ）若从续驶里程在的车辆中随机抽取2辆车，求其中恰有一辆车的续驶里程为的概率.考点6.统计图表解析解:（Ⅰ）由直方图可得：∴.------------------3分（Ⅱ）由题意可知，续驶里程在的车辆数为：------------------5分（Ⅲ）由（Ⅱ）及题意可知，续驶里程在的车辆数为，分别记为，续驶里程在的车辆数为，分别记为，设事件“其中恰有一辆汽车的续驶里程为”----------------------7分从该辆汽车中随机抽取辆，所有的可能如下：共种情况，----------------10分事件包含的可能有共种情况，则.------------------12分4.某中学高三(1)班共有50名学生，他们每天自主学习的时间在180到330分钟之间，将全班学生的自主学习时间作分组统计，得其频率分布如下表所示：组序分组频数频率第一组[180，210)50.1第二组[210，240)100.2第三组[240，270)120.24第四组[270，300)a b第五组[300，330)6c(1)求表中a、b、c的值；(2)某课题小组为了研究自主学习时间与成绩的相关性，需用分层抽样的方法从这50名学生中随机抽取20名作统计分析，则在第二组学生中应抽取多少人？(3)已知第一组学生中有3名男生和2名女生，从这5名学生中随机抽取2人，求恰好抽到1名男生和1名女生的概率．某单位N名员工参加“社区低碳你我他”活动，他们的年龄在25岁至50岁之间。
高二数学频率分布直方图练习题
高二数学频率分布直方图练习题在高二数学学习中，频率分布直方图是一个重要的概念和工具。
它能够帮助我们直观地了解数据的分布情况，并能够进行一些有关数据分析的操作。
下面是一些高二数学频率分布直方图练习题，希望能对同学们的学习有所帮助。
1. 一家超市通过调查了解到顾客每天购买的饮料数量，数据如下：2, 3, 2, 4, 1, 2, 4, 2, 3, 2, 1, 3, 2, 1, 2, 4, 2, 3, 2, 1根据以上数据绘制频率分布直方图，并确定众数、中位数、均值。
2. 某班级同学们的体重数据如下：52, 55, 53, 57, 54, 56, 55, 51, 58, 60, 59, 62, 63, 64, 61, 56, 55, 54, 57, 59根据以上数据绘制频率分布直方图，并确定众数、中位数、均值。
3. 某城市某月份的降水量数据如下：20, 15, 18, 22, 17, 19, 23, 16, 21, 20, 15, 20, 19, 23, 20, 18, 16, 22, 19, 17根据以上数据绘制频率分布直方图，并确定众数、中位数、均值。
4. 下面是一组学生在一次月考中的数学成绩数据：90, 85, 78, 92, 88, 79, 81, 85, 86, 90, 84, 88, 92, 89, 77, 82, 84, 87, 91, 83根据以上数据绘制频率分布直方图，并确定众数、中位数、均值。
5. 某工厂生产了一批产品，产品的重量数据如下：2.5, 2.7, 2.8, 2.6, 2.9, 2.7, 2.6, 2.8, 2.7, 2.6, 2.8, 2.7, 2.5, 2.8, 2.6, 2.9根据以上数据绘制频率分布直方图，并确定众数、中位数、均值。
以上是几道关于频率分布直方图的练习题。
通过解决这些题目，我们可以巩固对频率分布直方图的理解和应用，提高数据分析的能力。
在实际问题中，频率分布直方图也可以用来对比不同数据集的分布情况，帮助我们做出更好的决策。
七年级数学频数分布表和频数分布直方图练习题
图3数学： 12.3频数分布表和频数分布直方图一、选择题1、( 0 7 湖州)如图1是某班全体学生外出时乘车、步行、骑车的人数分布直方图和扇形分布图（两图都不完整），则下列结论中错误的是( ) A.该班总人数为50人 B.步行人数为30人C.骑车人数占总人数的20％D.乘车人数是骑车人数的2.5倍2、(08温州)体育老师对九年级（1）班学生“你最喜欢的体育项目是什么？（只写一项）”的问题进行了调查，把所得数据绘制成频数分布直方图（如图2）．由图可知，最喜欢篮球的频率是（ ）A ．二、解答题3、 (07义乌) 每年的6月6日是全国的爱眼日，让我们行动起来，爱护我们的眼睛！某校为了做好全校2000名学生的眼睛保健工作，对学生的视力情况进行一次抽样调查，下图3是利用所得数据绘制的频数分布直方图（视力精确到0.1）.请你根据此图提供的信息，回答下列问题： （1）本次调查共抽测了 名学生；（2）视力在4.9及4.9以上的同学约占全校学生比例为多少？步行 30％乘车50%骑车 图1图2（3）如果视力在第1，2，3组范围内(视力在4.9以下)均属视力不良，应给予治疗、矫正.请计算该校视力不良学生约有多少名？4、(08宁德)“五一”期间，新华商场贴出促销海报，内容如图4．在商场活动期间，统计了200人次的摸奖情况，绘制成如图5（1）补齐频数分布直方图；（2）求所调查的200人次摸奖的获奖率；（3）若商场每天约有2000人次摸奖，请估算商场一天送出的购物券总金额是多少元？图4 购物券人次图55、(08湛江)为了了解某校2000名学生参加环保知识竞赛的成绩，从中抽取了部分学生的竞赛成绩（均为整数），整理后绘制成如下的频数分布直方图(如图8)，请结合图形解答下列问题．(1) 指出这个问题中的总体．(2) 求竞赛成绩在79.5～89.5这一小组的频率．(3) 如果竞赛成绩在90分以上（含90分）的同学可获得奖励，请估计全校约有多少人获得奖励．6、（08西宁）中考体育测试中，1分钟跳绳为自选项目．某中学九年级共有50名女同学选考1分钟跳绳，根据测试评分标准，将她们的成绩进行统计后分为A B C D ，，，四等，并绘制成下面的频数分布表（注：6~7的意义为大于等于6分且小于7分，其余类似）和扇形统计图（如图9）．频数分布表等级 分值 跳绳（次/1分钟） 频数A9~10 150~170 48~9 140~150 12 B 7~8 130~140 176~7 120~130 mC 5~6 110~120 04~5 90~110 nD3~4 70~90 1 0~3 0~70 0（1）求m n ，的值；（2）在抽取的这个样本中，请说明哪个分数段的学生最多？请你帮助老师计算这次1分钟跳绳测试的及格率（6分以上含6分为及格）．7、(08湘潭市)某县七年级有15000名学生参加安全应急预案知识竞赛活动，为了了解6图8图9本次知识竞赛的成绩分布情况，从中抽取了400名学生的得分（得分取正整数，满分100分）进行统计：请你根据不完整的频率分布表. 解答下列问题： （1）补全频率分布表； （2）补全频数分布直方图；（3）若将得分转化为等级，规定得分低于59.5分评为“D ”，59.5~69.5分评为“C ”，69.5~89.5分评为“B ”，89.5~100.5分评为“A ”，这次15000名学生中约有多少人评为“D ”？如果随机抽取一名参赛学生的成绩等级，则这名学生的成绩评为“A ”、“B ”、“C ”、“D ”哪一个等级的可能性大？请说明理由.8、(08常州)为了解九年级女生的身高(单位:cm)情况,某中学对部分九年级女生身高进行,并画了部分频数分布直方图(图、表如下):cm)成绩（分） 图10图11根据以上图表,回答下列问题:(1)M=_______,m=_______,N=_______,n=__________; (2)补全频数分布直方图.9、（08泰州）为了增强环境保护意识，6月5日“世界环境日”当天，在环保局工作人员指导下，若干名“环保小卫士”组成的“控制噪声污染”课题学习研究小组，抽样调查了全市40个噪声测量点在某时刻的噪声声级（单位：dB ），将调查的数据进行处理（设所根据表中提供的信息解答下列问题：（1）频数分布表中的a =________，b =________，c =_________； （2）补充完整频数分布直方图；（3）如果全市共有200个测量点，那么在这一时刻噪声声级小于75dB 的测量点约有多少个？10、(08台州)八年级（1）班开展了为期一周的“孝敬父母，帮做家务”社会活动，并根据学生帮家长做家务的时间来评价学生在活动中的表现，把结果划分成A B C D E，，，，五个等级．老师通过家长调查了全班50名学生在这次活动中帮父母做家图12务的时间，制作成如下的频数分布表和扇形统计图．（1）求的值；（2）根据频数分布表估计该班学生在这次社会活动中帮父母做家务的平均时间；（3）该班的小明同学这一周帮父母做家务2小时，他认为自己帮父母做家务的时间比班级里一半以上的同学多，你认为小明的判断符合实际吗？请用适当的统计量说明理由．B AE DC 40% （第22题）学生帮父母做家务活动评价等级分布扇形统计图参考答案1、B ；2、D ；3、解：（1）由条形统计图可得，本次调查共抽测学生人数为：10+20+30+40+60=160 （2）视力在4.9及4.9以上的人数为40+20=60(人)，所占的比例为：6031608= (3)视力在第1，2，3组的人数在样本中所占的比例为10051608=． ∴该校视力不良学生约有5200012508⨯=（人)．4、解：⑴获得20元购物劵的人次：200-（122+37+11）=30（人次）. 补齐频数分布直方图，如图所示：⑵摸奖的获奖率：%39%1002078=⨯.⑶675.6200501120305370122=⨯+⨯+⨯+⨯=x .6.675×2000＝13350（元）估计商场一天送出的购物券总金额是13350元.5、 解： (1) 总体是某校2000名学生参加环保知识竞赛的成绩．（2）15150.256912151860==++++答：竞赛成绩在79.5～89.5这一小组的频率为0.25．（3）9200030069121518⨯=++++ 答：估计全校约有300人获得奖励．6、解：（1）根据题意，得50(412171)16m n +=-+++=；171006450m+⨯=％％． 则161732m n m +=⎧⎨+=⎩①②购物券人次30解之，得151m n =⎧⎨=⎩（2）7~8分数段的学生最多及格人数412171548=+++=（人），及格率481009650=⨯=％％ 答：这次1分钟跳绳测试的及格率为96％． 7． 解：（1）略； （2）略 ；（3）150000.05750⨯=（人） B 的频率为0.20.310.51+=，大于A 、C 、D 的频率，故这名学生评为B 等的可能性最大．8、略9、(1)a=8，b=12，c=0.3.（每对一个给1分） (2)略（3）算出样本中噪声声级小于75dB 的测量点的频率是0.3 0.3×200＝60∴在这一时噪声声级小于75dB 的测量点约有60个. 10、略。
八年级数学-频数分布表与直方图练习题(含解析)
八年级数学-频数分布表与直方图练习题（含解析）1．考察50名学生的年龄,列频数分布表时,这些学生的年龄落在了5个小组中,第一、二、三、五组的数据个数分别是2,8,15,5,则第四组的频数是( A )A．20 B．10 C．15 D．30解析：∵第一、二、三、五组的数据个数分别是2,8,15,5,∴第四组的频数是50－(2＋8＋15＋5)＝20.故选A.2．为了绘制频数分布直方图,先要对数据分组,若一个样本的容量为80,最大值为141,最小值为50,取组距为10,则可以分成( A )A．10组 B．9组 C．8组 D．7组解析：141－50＝9191÷10＝9.1,9.1＞9,∴分成10组．故选A.3．在频数分布直方图中,小长方形的高( C )A．与频数成正比B．是该组的频率C．是该组对应的频数D．是该组的组距解析：由作图可知．故选C.4．赵老师想了解本校“生活中的数学”知识大赛的成绩分布情况,随机抽取了100份试卷的成绩(满分为120分,成绩为整数),绘制成如图所示的统计图．由图可知,成绩不低于90分的共有27人．100份“生活中的数学”知识大赛试卷的成绩频数分布直方图解析：由题可知,成绩在89.5～109.5分数段的学生有24人,成绩在109.5～129.5分数段的学生有3人,所以成绩不低于90分的学生共有24＋3＝27(人)．5．将50个数据分成五组,列出频数分布表,其中第一小组的频数为6,第二小组与第五小组的频数之和为20,那么第三小组和第四小组的频数之和为24.解析：50－6－20＝24.6．为了提高学生书写汉字的能力,增强保护汉字的意识,某校举办了首届“汉字听写大赛”．学生经选拔后进入决赛,测试同时听写100个汉字,每正确听写出一个汉字得1分．本次决赛,学生成绩为x(分),且50≤x<100,将其按分数分为五组,绘制出以下不完整表格：组别成绩x/分频数频率一50≤x<6020.04二60≤x<70100.2三70≤x<8014b四80≤x<90 a 0.32五90≤x<10080.16(1)本次决赛共有50名学生参加；(2)直接写出表中a＝16,b＝0.28；(3)请补全如图所示的频数分布直方图；解：补全的频数分布直方图如图所示．(4)若决赛成绩不低于80分为优秀,则本次大赛的优秀率为48%.7．为了了解某校九年级学生的跳高水平,随机抽取该年级50名学生进行跳高测试,并把测试成绩绘制成如图所示的频数表和未完成的频数直方图(每组含前一个边界值,不含后一个边界值)．某校九年级50名学生跳高测试成绩的频数表组别/m频数1.09～1.1981.19～1.29121.29～1.39a1.39～1.4910(1)求a的值,(2)该年级共有500名学生,估计该年级学生跳高成绩在1.29 m(含1.29 m)以上的人数．解：(1)a＝50－8－12－10＝20,某校九年级50名学生跳高测试成绩的频数直方图20＋10 50＝300(人)．(2)该年级学生跳高成绩在1.29 m(含1.29 m)以上的人数是500×。
2024学年八年级数学经典好题专项(频数分布表和频数分布直方图)练习(附答案)
2024学年八年级数学经典好题专项（频数分布表和频数分布直方图）练习一、选择题1、一组数据的最大值与最小值之差为80，若取组距为9，则分成的组数应是（ ） A. 7 B. 8 C. 9 D. 102、一个容量为80的样本，最大值是141，最小值是50，取组距为10，则可以分 （ ）A．10组 B．9组 C．8组 D．7组3、现有一组数据，最大值为93，最小值为22，现要把它分成6组，则下列组距中，合适的为 （ ） A. 9 B. 12 C. 15 D. 184、某棉纺厂为了了解一批棉花的质量，从中随机抽取了20根棉花纤维进行测量，其长度x (单位：mm)的数据分布如下表，则棉花纤维长度的数据在8≤x ＜32这个范围的频率为( )棉花纤维长度x频数 0≤x ＜8 1 8≤x ＜16 2 16≤x ＜24 8 24≤x ＜32 6 32≤x ＜403A.0.8 B ．0.7 C ．0.4 D ．0.25、小杰调查了本班同学的体重情况，画出频数直方图如图所示，下列结论中，错误的是( )A. 全班总人数为45人B. 体重在50～55 kg 的人数最多C. “45～50 kg ”这一组的频率比“60～65 kg ”这一组的大0.1D. 体重在60～65 kg 的人数占全班总人数的196、某一组数据中，已知最大值是84，最小值是52，若分成6组，且组距为整数，某组组中值为72.5，则这组数据可能是（ ）A. 51.5~57.5B. 69.5~75.5C. 68.5~76.5D. 70.5~74.57、为了了解本校八年级学生的体能情况，随机抽查了其中30名学生，测试了1分钟仰卧起坐的次数，并绘制成如图所示的频数分布直方图. 若25次为及格，则及格人数占总人数的（ ）A. 56.7%B. 90%C. 16.7%D. 33.3%8、为了解某校学生今年五一期间参加社团活动时间的情况，随机抽查了其中100名学生进行统计，并绘制成如图所示的频数直方图，已知该校共有1000名学生，据此估计，该校五一期间参加社团活动时间在8～10小时之间的学生数大约是（ ）A．280 B．240 C．300 D．260二、填空题9、一个样本有20个数据：35，31，33，35，37，39，35，38，40，39，36，34，35，37，36，32，34，35，36，34．在列频数分布表时，如果取组距为3，那么应分成 组10、有30个数据，其中最大值为40，最小值为15，若取组距为4，则应该分成 组11、有一个含有50个数据的数据组，已知最小数据是15，最大数据是45，且各数据都是整数，则这50个数据分为8组时，组距是________；若第1组的下限为14.5，则其上限为________，最末一组的上限为________.12、阅读对学生的成长有着深远的影响，某中学为了解学生每周课余阅读的时间，在本校随机抽取若干名学生进行调查，并依据调査结果绘制了如下不完整的统计表．则表中的a＝____.组别时间/时频数(人)频率A 0≤t≤0.560.15B 0.5≤t≤1 a 0.313、某中学抽取部分学生对“你最喜欢的球类运动”调查问卷，收集整理数据后列频数分布表（部分）如下：项目 乒乓球 羽毛球 篮球 足球频数 80 50百分比 40% 25% m则表格中m的值为14、某校在践行“社会主义核心价值观”演讲比赛中，对名列前20名的选手的综合分数m进行分组统计，结果如表所示，则a= ．组号 分组 频数一 6≤m＜7 2二 7≤m＜8 7三 8≤m＜9 a四 9≤m≤10 215、一个容量为60的样本，样本中最大值是172，最小值是150，取组距为3，则该样本可以分为 组16、小丽抽样调查了学校40名同学的体重（均精确到1kg），绘制了如图频数分布直方图，那么在该样本中体重不小于55kg的频率是 ．17、某地区中考现场考试内容有两项，50米跑为必考项目，另在立定跳远、坐位体前屈、实心球和一分钟跳绳中选一项测试．王老师对参加体育中考的九（1）班40名学生的一项选测科目作了统计，列出如图所示的统计表，则本班参加坐位体前屈的人数是 人．组别 立定跳远 坐位体前屈 实心球 一分钟跳绳频率 0.4 0.35 0.1 0.1518、空气质量指数，简称AQI，如果AQI在0～50空气质量类别为优，在51～100空气质量类别为良，在101～150空气质量类别为轻度污染，按照某市最近一段时间的AQI画出的频数分布直方图如图所示．已知每天的AQI都是整数，那么空气质量类别为优和良的天数占总天数的百分比为 %．19、将100个数据分成①～⑧组，如表所示：编号 ① ② ③ ④ ⑤ ⑥ ⑦ ⑧频数 4 8 12 24 18 7 3那么第④组的频数为 ．20、若小明统计了他家12月份打电话的通话时长，并列出频数分布表，则通话时长不超过10min的频率是 ．通话时长 x/min 0＜x≤5 5＜x≤10 10＜x≤15 x＞15频数（通话次数）20 16 20 4三、解答题21、体育委员统计了全班同学60s跳绳的次数，并列出频数表如下：次数 60≤x<80 80≤x<100 100≤x<120 120≤x<140 140≤x<160 160≤x<180频数 2 4 21 13 8 4 （1）全班共有多少名学生？（2）组距是多少？组数是多少？（3）跳绳次数在120≤x＜160范围内的学生有多少？22、每年的6月6日是全国爱眼日．某校为了做好全校2000名学生的眼睛保健工作，对学生的视力情况进行一次抽样调查．如图所示为利用所得的数据绘制的频数直方图(长方形的高表示该组人数)．请你根据图中提供的信息，回答下列问题：(1)本次调查共抽测了____名学生．(2)在这个问题中，样本是指_____________________．(3)视力在4.85～5.15这一组内的频数是_______．(4)如果视力小于4.85均属视力不良，那么该校约有_________名学生的视力不良，应给予治疗、矫正．23、为了了解某地九年级学生参加消防知识竞赛成绩（均为整数），从中抽取了1%的同学的竞赛成绩，整理后绘制了如下的频数直方图，请结合图形解答下列问题：（1）这个问题中的总体是 ；（2）竞赛成绩在84.5～89.5分这一小组的频率是 ；（3）若竞赛成绩在90分以上（含90分）的同学可以获得奖励，则估计该地获得奖励的九年级学生约有________人．24、在学校开展的综合实践活动中，某班进行了小制作评比，作品上交时间为5月1日至30日，评委会把同学们上交作品的件数按5天一组分组统计，绘制了频数直方图如下图所示，已知从左至右各长方形的高的比为2∶3∶4∶6∶4∶1，第三组的频数为12.请解答下列问题：(1)本次活动共有多少件作品参加评比？(2)哪组上交的作品数量最多？有多少件？(3)经过评比，第四组和第六组分别有10件，2件作品获奖，问：这两组哪一组获奖率较高？25、在开展“经典阅读”活动中，某校为了解全校学生利用课外时间阅读的情况，学校团委随机抽取若干名学生，调查他们一周的课外阅读时间，并根据调查结果绘制了如下尚不完整的统计图表．根据图表信息回答下列问题：(1)填空：a＝____，b＝____，m＝____，n＝____．(2)将频数直方图补充完整．(3)若该校有3000名学生，请根据上述调查结果，估计该校学生一周的课外阅读时间不足3 h的人数．26、为了让地震受灾的儿童得到救助，某社区组织“献爱心手拉手”捐款活动，对社区部分捐款户数进行调查和分组统计后，将数据整理成如图所示的统计表和统计图（图中信息不完整）．已知A、B两组捐款户数的比为1：5．请结合以上信息解答下列问题．（1）a= ，本次调查样本的容量是 ；（2）补全“捐款户数分组统计表和捐款户数统计图1”；（3）若该社区共有1000户住户参与捐款，请根据以上信息估计，全社区捐款不少于300元的户数是 户．27、为了了解某次“小学生书法比赛”的成绩情况，随机抽取了30名学生的成绩进行统计，并将统计情况绘制成如图所示的频数直方图，已知成绩x(单位：分)均满足“50≤x＜100”．根据图中信息回答下列问题：(1)图中a的值为____．(2)绘制扇形统计图时，成绩x在“70≤x＜80”范围内所对应扇形的圆心角的度数为____．(3)此次比赛共有300名学生参加，若将“x≥80”的成绩记为“优秀”，则获得“优秀”的学生大约有____人．28、为庆祝中华人民共和国成立70周年，郑州市某校组织八年级学生进行“方阵表演”．为了整齐划一，需了解学生的身高，现随机抽取该校八年级学生进行抽样调查，根据所得数据绘制出如下统计图表根据图表提供的信息，回答下列问题：（1）这次抽样调查，一共抽取学生 人；（2）扇形统计图中，扇形E的圆心角度数是 ；（3）请补全频数分布直方图；（4）已知该校八年级共有学生400人，请估计身高在160≤x＜170的学生约有多少人？参考答案一、选择题1、一组数据的最大值与最小值之差为80，若取组距为9，则分成的组数应是（ C ）A. 7B. 8C. 9D. 102、一个容量为80的样本，最大值是141，最小值是50，取组距为10，则可以分 （ A ）A．10组 B．9组 C．8组 D．7组3、现有一组数据，最大值为93，最小值为22，现要把它分成6组，则下列组距中，合适的为 （ B ）A. 9B. 12C. 15D. 184、某棉纺厂为了了解一批棉花的质量，从中随机抽取了20根棉花纤维进行测量，其长度x(单位：mm)的数据分布如下表，则棉花纤维长度的数据在8≤x＜32这个范围的频率为(A)棉花纤维长度x 频数0≤x＜8 18≤x＜16 216≤x＜24824≤x＜32 632≤x＜40 3A.0.8 B．0.7 C．0.4 D．0.25、小杰调查了本班同学的体重情况，画出频数直方图如图所示，下列结论中，错误的是(C )A. 全班总人数为45人B. 体重在50～55 kg 的人数最多C. “45～50 kg ”这一组的频率比“60～65 kg ”这一组的大0.1D. 体重在60～65 kg 的人数占全班总人数的19 【解】 8＋10＋14＋8＋5＝45(人)，故A 选项正确． 体重在50～55 kg 的人数有14人，最多，故B 选项正确． “45～50 kg ”这一组的频率是10÷45＝29， “60～65 kg ”这一组的频率是5÷45＝19， 29－19＝19≠0.1，故C 选项错误．5÷45＝19，故D 选项正确． 故选C.6、某一组数据中，已知最大值是84，最小值是52，若分成6组，且组距为整数，某组组中值为72.5，则这组数据可能是（ B ） A. 51.5~57.5 B. 69.5~75.5 C. 68.5~76.5 D. 70.5~74.57、为了了解本校八年级学生的体能情况，随机抽查了其中30名学生，测试了1分钟仰卧起坐的次数，并绘制成如图所示的频数分布直方图. 若25次为及格，则及格人数占总人数的（ A ）A. 56.7%B. 90%C. 16.7%D. 33.3%8、为了解某校学生今年五一期间参加社团活动时间的情况，随机抽查了其中100名学生进行统计，并绘制成如图所示的频数直方图，已知该校共有1000名学生，据此估计，该校五一期间参加社团活动时间在8～10小时之间的学生数大约是（ ）A．280 B．240 C．300 D．260【解答】解：由题可得，抽查的学生中参加社团活动时间在8～10小时之间的学生数为100﹣30﹣24﹣10﹣8＝28（人），∴1000280（人），即该校五一期间参加社团活动时间在8～10小时之间的学生数大约是280人．故选：A．二、填空题9、一个样本有20个数据：35，31，33，35，37，39，35，38，40，39，36，34，35，37，36，32，34，35，36，34．在列频数分布表时，如果取组距为3，那么应分成 4 组10、有30个数据，其中最大值为40，最小值为15，若取组距为4，则应该分成 7 组11、有一个含有50个数据的数据组，已知最小数据是15，最大数据是45，且各数据都是整数，则这50个数据分为8组时，组距是________；若第1组的下限为14.5，则其上限为________，最末一组的上限为________.[解析] 45－15＝30，3＜30÷8＜4，∴组距应为4.若第1组的下限为14.5，则其上限为14.5＋4＝18.5；最末一组的上限为14.5＋4×8＝14.5＋32＝46.5.[答案] 418.546.512、阅读对学生的成长有着深远的影响，某中学为了解学生每周课余阅读的时间，在本校随机抽取若干名学生进行调查，并依据调査结果绘制了如下不完整的统计表．则表中的a＝____.组别时间/时频数(人)频率A 0≤t≤0.560.15B 0.5≤t≤1 a 0.3【解析】∵被调查的总人数为6÷0.15＝40(人)，∴B组的人数为40×0.3＝12(人)，即a＝12.13、某中学抽取部分学生对“你最喜欢的球类运动”调查问卷，收集整理数据后列频数分布表（部分）如下：项目 乒乓球 羽毛球 篮球 足球频数 80 50百分比 40% 25% m则表格中m的值为 10%14、某校在践行“社会主义核心价值观”演讲比赛中，对名列前20名的选手的综合分数m进行分组统计，结果如表所示，则a= 9 ．组号 分组 频数一 6≤m＜7 2二 7≤m＜8 7三 8≤m＜9 a四 9≤m≤10 215、一个容量为60的样本，样本中最大值是172，最小值是150，取组距为3，则该样本可以分为 8 组16、小丽抽样调查了学校40名同学的体重（均精确到1kg），绘制了如图频数分布直方图，那么在该样本中体重不小于55kg的频率是 ．【解答】解：观察直方图可知：因为该样本中体重不小于55kg的频数为：9+5+2＝16，所以该样本中体重不小于55kg的频率是0.4．故答案为：0.4．17、某地区中考现场考试内容有两项，50米跑为必考项目，另在立定跳远、坐位体前屈、实心球和一分钟跳绳中选一项测试．王老师对参加体育中考的九（1）班40名学生的一项选测科目作了统计，列出如图所示的统计表，则本班参加坐位体前屈的人数是 人．组别 立定跳远 坐位体前屈 实心球 一分钟跳绳频率 0.4 0.35 0.1 0.15【解答】解：∵频率，∴频数＝频率×总数＝0.35×40＝14人．故答案为14．18、空气质量指数，简称AQI，如果AQI在0～50空气质量类别为优，在51～100空气质量类别为良，在101～150空气质量类别为轻度污染，按照某市最近一段时间的AQI画出的频数分布直方图如图所示．已知每天的AQI都是整数，那么空气质量类别为优和良的天数占总天数的百分比为 %．【解答】解：空气质量类别为优和良的天数占总天数的百分比为100%＝80%， 故答案为：80．19、将100个数据分成①～⑧组，如表所示：编号 ① ② ③ ④ ⑤ ⑥ ⑦ ⑧频数 4 8 12 24 18 7 3那么第④组的频数为 24．【解答】解：由题意可得，第④组的频数为：100﹣4﹣8﹣12﹣24﹣18﹣7﹣3＝24，故答案为：24．20、若小明统计了他家12月份打电话的通话时长，并列出频数分布表，则通话时长不超过10min的频率是 0.6 ．通话时长 x/min 0＜x≤5 5＜x≤10 10＜x≤15 x＞15频数（通话次数）20 16 20 4三、解答题21、体育委员统计了全班同学60s跳绳的次数，并列出频数表如下：次数 60≤x<80 80≤x<100 100≤x<120 120≤x<140 140≤x<160 160≤x<180频数 2 4 21 13 8 4 （1）全班共有多少名学生？（2）组距是多少？组数是多少？（3）跳绳次数在120≤x＜160范围内的学生有多少？解：（1）全班共有2＋4＋21＋13＋8＋4＝52（名）学生．（2）组距是80－60＝20次，组数是6.（3）跳绳次数在120≤x＜160范围内的学生有13＋8＝21（人）．22、每年的6月6日是全国爱眼日．某校为了做好全校2000名学生的眼睛保健工作，对学生的视力情况进行一次抽样调查．如图所示为利用所得的数据绘制的频数直方图(长方形的高表示该组人数)．请你根据图中提供的信息，回答下列问题：(1)本次调查共抽测了__160__名学生．(2)在这个问题中，样本是指__160名学生的视力情况__．(3)视力在4.85～5.15这一组内的频数是__40__．(4)如果视力小于4.85均属视力不良，那么该校约有__1250__名学生的视力不良，应给予治疗、矫正．23、为了了解某地九年级学生参加消防知识竞赛成绩（均为整数），从中抽取了1%的同学的竞赛成绩，整理后绘制了如下的频数直方图，请结合图形解答下列问题：（1）这个问题中的总体是 ；（2）竞赛成绩在84.5～89.5分这一小组的频率是 ；（3）若竞赛成绩在90分以上（含90分）的同学可以获得奖励，则估计该地获得奖励的九年级学生约有________人．解（1）某地九年级学生参加消防知识竞赛的成绩（2）＝0.32.（3）该地九年级获得奖励的人数约是（13＋7）÷1%＝2000（人）24、在学校开展的综合实践活动中，某班进行了小制作评比，作品上交时间为5月1日至30日，评委会把同学们上交作品的件数按5天一组分组统计，绘制了频数直方图如下图所示，已知从左至右各长方形的高的比为2∶3∶4∶6∶4∶1，第三组的频数为12.请解答下列问题： (1)本次活动共有多少件作品参加评比？ (2)哪组上交的作品数量最多？有多少件？(3)经过评比，第四组和第六组分别有10件，2件作品获奖，问：这两组哪一组获奖率较高？【解】 (1)12÷42＋3＋4＋6＋4＋1＝60(件)．(2)第四组上交的作品数量最多，有12×64＝18(件)．(3)第四组的获奖率为1018＝59，第六组的获奖率为2÷⎝⎛⎭⎫12×14＝23＝69. ∵59<69，∴第六组获奖率较高．25、在开展“经典阅读”活动中，某校为了解全校学生利用课外时间阅读的情况，学校团委随机抽取若干名学生，调查他们一周的课外阅读时间，并根据调查结果绘制了如下尚不完整的统计图表．根据图表信息回答下列问题：(1)填空：a ＝____，b ＝____，m ＝____，n ＝____． (2)将频数直方图补充完整．(3)若该校有3000名学生，请根据上述调查结果，估计该校学生一周的课外阅读时间不足3 h 的人数．【解】 (1)∵b ＝18÷0.12＝150，∴n ＝36÷150＝0.24，∴m ＝1－0.12－0.3－0.24－0.14＝0.2，∴a＝0.2×150＝30.(2)补全频数直方图如解图中斜纹所示．(3)3000×(0.12＋0.2)＝960.答：估计该校学生一周的课外阅读时间不足3 h的人数为960.26、为了让地震受灾的儿童得到救助，某社区组织“献爱心手拉手”捐款活动，对社区部分捐款户数进行调查和分组统计后，将数据整理成如图所示的统计表和统计图（图中信息不完整）．已知A、B两组捐款户数的比为1：5．请结合以上信息解答下列问题．（1）a= ，本次调查样本的容量是 ；（2）补全“捐款户数分组统计表和捐款户数统计图1”；（3）若该社区共有1000户住户参与捐款，请根据以上信息估计，全社区捐款不少于300元的户数是 户．解：（1）B组捐款户数是10，则A组捐款户数为10×=2，样本容量为（2+10）÷（1﹣8%﹣40%﹣28%）=50.（2）统计表C、D、E 组的户数分别为20，14，4．组别 捐款额（x）元 户数A 1≤x＜50 aB 100≤x＜200 10C 200≤x＜300 20D 300≤x＜400 14E x≥400 4（3）估计全社区捐款不少于300元的户数是1000×（28%+8%）=360（户）.27、为了了解某次“小学生书法比赛”的成绩情况，随机抽取了30名学生的成绩进行统计，并将统计情况绘制成如图所示的频数直方图，已知成绩x(单位：分)均满足“50≤x ＜100”．根据图中信息回答下列问题： (1)图中a 的值为____．(2)绘制扇形统计图时，成绩x 在“70≤x ＜80”范围内所对应扇形的圆心角的度数为____． (3)此次比赛共有300名学生参加，若将“x ≥80”的成绩记为“优秀”，则获得“优秀”的学生大约有____人．【解】 (1)a ＝30－(2＋12＋8＋2)＝6，故a ＝6.(2)成绩x 在“70≤x ＜80”范围内所对应扇形的圆心角的度数为360°×1230＝144°. (3)获得“优秀”的学生大约有300×8＋230＝100(人)．28、为庆祝中华人民共和国成立70周年，郑州市某校组织八年级学生进行“方阵表演”．为了整齐划一，需了解学生的身高，现随机抽取该校八年级学生进行抽样调查，根据所得数据绘制出如下统计图表根据图表提供的信息，回答下列问题： （1）这次抽样调查，一共抽取学生 人； （2）扇形统计图中，扇形E 的圆心角度数是 ；（3）请补全频数分布直方图；（4）已知该校八年级共有学生400人，请估计身高在160≤x＜170的学生约有多少人？【解答】解：（1）这次抽样调查，一共抽取学生4÷10%＝40（人）；（2）扇形统计图中，扇形E的圆心角度数是36054°，故答案为：40；54°；（3）身高在160≤x＜170的人数为：40×20%＝8人，补全频数分布直方图如图所示；（4）400×45%＝180（人），答：估计身高在160≤x＜170的学生约有180人．。
概率频率分布直方图练习题
概率频率分布直方图练习题Prepared on 22 November 20201．(本题满分１２分)某学校随机抽取部分新生调查其上学路上所需时间（单位：分钟），并将所得数据绘制成频率分布直方图（如图），其中，上学路上所需时间的范围是[0,100]，样本数据分组为[0,20)，[20,40)，[40,60)，[60,80)，[80,100].（１）求直方图中x 的值；（２）如果上学路上所需时间不少于40分钟的学生可申请在学校住宿，请估计学校1000名新生中有多少名学生可以申请住宿.2、(本题满分12分)为调查民营企业的经营状况，某统计机构用分层抽样的方法从A 、B 、C 三个城市中，抽取若干个民营企业组成样本进行深入研究，有关数据见下表：（单位：个）（1）求x 、y 的值；（2）若从城市A 与B 抽取的民营企业中再随机选2个进行跟踪式调研，求这2个都来自城市A 的概率.3、某产品按行业生产标准分成8个等级，等级系数ξ依次为1,2,,8…，产品的等级系数越大表明产品的质量越好.现从该厂生产的产品中随机抽取30件，相应的等级系数组成一个样本，数据如下：34 53 67该行业规定产品的等级系数7ξ≥的为一等品，等级系数57ξ≤<的为二等品，等级系数35ξ≤<的为三等品，3ξ<为不合格品．（1）试分别估计该厂生产的产品的一等品率、二等品率和三等品率； （2）从样本的一等品中随机抽取2件，求所抽得2件产品等级系数都是8的概率．4、某中学在校就餐的高一年级学生有440名，高二年级学生有460名，高三年级学生有500名；为了解学校食堂的服务质量情况，用分层抽样的方法从中抽取70名学生进行抽样调查，把学生对食堂的“服务满意度”与“价格满意度”都分为五个等级：1级（很不满意）；2级（不满意）；3级（一般）；4级（满意）；5级（很满意），其统计结果如下表（服务满意度为x ，价格满意度为y ）.（1）求高二年级共抽取学生人数；（2）求“服务满意度”为3时的5个“价格满意度”数据的方差；（3）为提高食堂服务质量，现从3x <且24y ≤<的所有学生中随机抽取两人征求意见，求至少有一人的“服务满意度”为1的概率.5、（本小题满分12分）为调查乘客的候车情况，公交公司在某站台的60名候车乘客中随机抽取15人，将他们的候车时间（单位：分钟）作为样本分成5组，如下表所示：（1）估计这60名乘客中候车时间少于10分钟的人数； （2）若从上表第三、四组的6人中随机抽取2人作进一步的问卷调查，求抽到的两人恰好来自不同组的概率．6、（本小题满分12分）某学校甲、乙两个班参加体育达标测试，统计 测试成绩达标人数情况得到如图所示的列联表，已知在全部学生中随机抽取1人为不达标的概率为110. （1）请完成上面的列联表；（2）若用分层抽样的方法在所有测试不达标的学生中随机抽取6人，问其中从甲、乙两个班分别抽取多少人（3）从（2）中的6人中随机抽取2人，求抽到的两人恰好都来自甲班的概率．7、（本小题满分12分）对某校高一年级学生参加社区服务次数统计，随机抽去了M 名学生作为样本，得到这M 名学生参加社区服务的次数，根据此数据作出了频数与频率的统计表如下：（1）求出表中,,,M r m n 的值； （2）在所取样本中，从参加社区服务的次数不少于20次的学生中任选2人，求组别 候车时间 人数 一 2 二 6 三 4 四 2 五1组别 达标不达标 总计甲班8乙班 54合计120图3a0.06b 至少一人参加社区服务次数在区间[)25,30内的概率． 8、（本小题满分12分）某地区有小学21所，中学14所，大学7所，现采取分层抽样的方法从这些学校中抽取6所学校对学生进行视力调查。
频率分布直方图练习题
频率分布直方图练习题1、根据《中华人民共和国道路交通安全法》，酒后驾车的血液酒精浓度在20~80mg/100mL（不含80）组距之间，而醉酒驾车的血液酒精浓度在80mg/100mL（含0.080）以上。
在某地区一周内，共查处500名酒后驾车和醉酒驾车的司机。
通过对这些司机血液中酒精含量的检测，得到了频率分布直方图。
根据直方图，可估算醉酒驾车的司机人数约为70人。
2、对100名学生进行随机抽样，测得他们的身高（单位cm）。
将身高分为区间[155,160)，[160,165)，[165,170)，[170,175)，[175,180)，[180,185)，并得到样本身高的频率分布直方图。
根据直方图，可以得到身高在170cm以上的学生人数为30人。
将身高在[170,175)，[175,180)，[180,185)三个区间内的学生分别记为A、B、C三组，从这三组中分层抽样选取6人，则从A、B、C三组中分别抽取的人数为2、2、2人。
3、某部门为了确定对某路段进行限速60km/h是否合理，对通过该路段的500辆汽车的车速进行检测，并将所得数据按照组距[40,50)，[50,60)，[60,70)，[70,80]分组，得到频率分布直方图。
根据直方图，可以得出这500辆汽车中车速低于限速的汽车有90辆。
4、某校从参加高三年级期末考试的学生中抽出60名学生，并统计了他们的历史成绩（成绩均为整数且满分为100分）。
将不低于50分的成绩分为五段，得到部分频率分布直方图。
根据直方图，历史成绩在[70,80)的学生人数为16人。
5、给定XXX青年歌手大奖赛上某位选手得分的茎叶图，去掉一个最高分和一个最低分后，所剩数据的方差为25.4.6、从某小学随机抽取100名同学，将他们的身高（单位：厘米）数据绘制成频率分布直方图。
根据直方图，可得到a=141.若要从身高在[120,130)，[130,140)，[140,150)三组内的学生中，用分层抽样的方法选取18人参加活动，则应从每组中分别选取6人。
频率分布直方图考试卷试题.doc
频率分布直方图北鲲五班练习题1. 用本估体，下列法正确的是（）A．本的果就是体的果B．本容量越大，估就越精确C．本的准差可以近似地反映体的平均状 D ．数据的方差越大，明数据越定2．一支田径有男56 人，女 42 人，用分抽的方法从全体运中抽出一个容量 28 的本，抽取男的人数（）A．12B．14C．16D．183. 某学校有教工共160 人，其中有教104 人，管理人32 人，后勤服人24 人，要从中抽取一个容量20 的本，用分抽的方法抽取本，在20 人的本中抽取后勤人的人数()A. 3B. 4C. 5D. 64.某位有工 750 人，其中青年工 350 人，中年工 250 人，老年工 150 人 . 了了解位工的健康情况，决定采用分抽的方法，从中抽取容量15 的本 . 从上述各中依次抽取的人数分是（）A. 8 ， 4， 3B. 6，5，4C. 7，5，3D. 8，5，25.某会有 200 名会，要从中抽取 40 名会作本，采用系抽法等距抽取本，将全体会随机按1~200 号，并按号序平均分40 （ 1－5 号，6－10 号，⋯，196－ 200 号） . 若第 5 抽出的号22，第 1 至第 3 抽出的号依次是（）A. 3 ， 8， 13B. 2，7，12C. 3，9，15D. 2，6，126. 一个容量 n 的本 , 分成若干 , 已知某的数和率分是40,0.125,n 的A. 640B.320C.240D. 1607. 个容量 32 的本 , 已知某本的率0.125, 本的数.A. 2B. 4C. 6D. 8()8.我校高中生共有 2700 人 , 其中高一年 900 人, 高二年 1200 人 , 高三年 600 人, 采取分抽法抽取容量 135 的本 , 那么高一、高二、高三各年抽取的人数分 ( )A.45,75,15B. 45,45,45C.30,90,15D. 45,60,309.某位有老年人 28 人 , 中年人 54 人 , 青年人 81 人 , 了他的身体状况的某指 ,需从他中抽取一个容量36 的本 , 老年人、中年人、青年人分各抽取的人数是( ) A. 6,12,18 B. 7,11,19 C. 6,13,17 D. 7,12,1710.某班的 78 名同学已号 1,2,3, ⋯ ,78, 了解班同学的作情况 , 老收取了学号能被5整除的15名同学的作本,里运用的抽方法是( ).A.随机抽法B.系抽法C.分抽法D.抽法11.某工厂生 A、B、 C 三种不同型号的品 , 品数量之比依次 2 ：3 ：5. 用分抽方法抽出一个容量 n 的本 , 本中 A 种型号品有 16 件 , 那么此本的容量n12.某学校共有教 490 人 , 其中不到 40 的有 350 人 ,40 及以上的有 140 人 , 了解普通在校教中的推广普及情况, 用分抽的方法, 从全体教中抽取一个容量70 人的本行普通水平, 其中不到 40 的教中抽取的人数是___________. 13．在某次学生考的成中随机抽取若干学生的成，分与各的数如下：[40,50),4；[50,60),1；[60,70),10；[70,80),11；[80,90),18；[90,100),6，估本次考的及格率 __________ .14．把容量是 100的本分成 8 ，从第 1 到第 4 的数分是15，17，11，13，第5 到第 7 的率之和是0.32 ，那么第 8 的率是.15.《中人民共和国道路交通安全法》定：血液酒精度在 20~80 mg/100mL（不含 80）之，属于酒后血液酒精度在 80mg/100mL （含 80）以0.00.01；0.00.00 上20 30 40 50 60 70 80酒精90（mg/100mL时，属醉酒驾车。
高考数学频率分布直方图大题训练题(含答案)
频率分布直方图大题训练题一、解答题（共18题；共205分）1.（2020·龙岩模拟）某电讯企业为了了解某地区居民对电讯服务质量评价情况，随机调查100 名用户，根据这100名用户对该电讯企业的评分，绘制频率分布直方图，如图所示，其中样本数据分组为，，…… .（1）估计该地区用户对该电讯企业评分不低于70分的概率，并估计对该电讯企业评分的中位数；（2）现从评分在的调查用户中随机抽取2人，求2人评分都在的概率.2.（2020·芜湖模拟）某学校为了了解该校高三年级学生寒假在家自主学习的情况，随机对该校300名高三学生寒假的每天学习时间（单位：h）进行统计，按照，，，，的分组作出频率分布直方图如图所示．参考公式：，其中．参考附表：0.050 0.010 0.001（Ⅰ）根据频率分布直方图计算该校高三年级学生的平均每天学习时间（同一组中的数据用该组区间中点值代表）；（Ⅱ）该校规定学习时间超过4h为合格，否则不合格．已知这300名学生中男生有140人，其中合格的有70人，请补全下表，根据表中数据，能否有99.9%的把握认为该校高三年级学生的性别与学习时长合格有关？3.（2020·泰安模拟）某水果批发商经销某种水果(以下简称A水果)，购入价为300元/袋，并以360元／袋的价格售出，若前8小时内所购进的A水果没有售完，则批发商将没售完的A水果以220元／袋的价格低价处理完毕(根据经验，2小时内完全能够把A水果低价处理完，且当天不再购进)．该水果批发商根据往年的销量，统计了100天A水果在每天的前8小时内的销售量，制成如下频数分布条形图．现以记录的100天的A水果在每天的前8小时内的销售量的频率作为A水果在一天的前8小时内的销售量的概率，记X表示A水果一天前8小时内的销售量，n表示水果批发商一天批发A水果的袋数．（1）求X的分布列；（2）以日利润的期望值为决策依据，在与中选其一，应选用哪个?4.（2020·南昌模拟）某产品自生产并投入市场以来，生产企业为确保产品质量，决定邀请第三方检测机构对产品进行质量检测，并依据质量指标Z来衡量产品的质量.当时，产品为优等品；当时，产品为一等品；当时，产品为二等品.第三方检测机构在该产品中随机抽取500件，绘制了这500件产品的质量指标Z的条形图.用随机抽取的500件产品作为样本，估计该企业生产该产品的质量情况，并用频率估计概率．（1）从该企业生产的所有产品中随机抽取4件，求至少有1件优等品的概率；（2）现某人决定购买80件该产品.已知每件成本1000元，购买前，邀请第三方检测机构对要购买的80件产品进行抽样检测，买家、企业及第三方检测机构就检测方案达成以下协议：从80件产品中随机抽出4件产品进行检测，若检测出3件或4件为优等品，则按每件1600元购买，否则按每件1500元购买，每件产品的检测费用250元由企业承担．记企业的收益为X元，求X的分布列与数学期望.5.（2020·南昌模拟）在“挑战不可能”的电视节目上，甲、乙、丙三个人组成的解密团队参加一项解密挑战活动，规则是由密码专家给出题目，然后由3个人依次出场解密，每人限定时间是1分钟内，否则派下一个人.3个人中只要有一人解密正确，则认为该团队挑战成功，否则挑战失败.根据甲以往解密测试情况，抽取了甲100次的测试记录，绘制了如下的频率分布直方图.（1）若甲解密成功所需时间的中位数为47，求a、b的值，并求出甲在1分钟内解密成功的频率；（2）在“挑战不可能”节目上由于来自各方及自身的心理压力，甲，乙，丙解密成功的概率分别为，其中表示第个出场选手解密成功的概率，并且定义为甲抽样中解密成功的频率代替，各人是否解密成功相互独立.①求该团队挑战成功的概率；②该团队以从小到大的顺序按排甲、乙、丙三个人上场解密，求团队挑战成功所需派出的人员数目X 的分布列与数学期望.6.（2020·江西模拟）冠状病毒是一个大型病毒家族，可引起感冒以及中东呼吸综合征（MERS）和严重急性呼吸综合征（SARS）等较严重疾病．出现的新型冠状病毒（nCoV）是从未在人体中发现的冠状病毒新毒株．人感染了新型冠状病毒后常见体征有呼吸道症状、发热、咳嗽、气促和呼吸困难等．在较严重病例中，感染可导致肺炎、严重急性呼吸综合征、肾衰竭，甚至死亡．某医院为筛查冠状病毒，需要检测血液中的指标A．现从采集的血液样品中抽取500份检测指标A的值，由测量结果得下侧频率分布直方图：（1）求这500份血液样品指标A值的平均数和样本方差（同一组数据用该区间的中点值作代表，记作）；（2）由频率分布直方图可以认为，这项指标的值X服从正态分布，其中近似为样本平均数，近似为样本方差．在统计学中，把发生概率小于3‰的事件称为小概率事件（正常条件下小概率事件的发生是不正常的）．该医院非常关注本院医生健康状况，随机抽取20名医生，独立的检测血液中指标A的值，结果发现4名医生血液中指标A的值大于正常值20.03，试根据题中条件判断该院医生的健康率是否正常，并说明理由．附：参考数据与公式：，，；若，则① ；② ；③．，，，．7.（2020·江西模拟）年前某市质监部门根据质量管理考核指标对本地的500家食品生产企业进行考核，然后通过随机抽样抽取其中的50家，统计其考核成绩（单位：分），并制成如下频率分布直方图.（1）求这50家食品生产企业考核成绩的平均数（同一组中的数据用该组区间的中点值为代表）及中位数a（精确到0.01）（2）该市质监部门打算举办食品生产企业质量交流会，并从这50家食品生产企业中随机抽取4家考核成绩不低于88分的企业发言，记抽到的企业中考核成绩在的企业数为X，求X的分布列与数学期望（3）若该市食品生产企业的考核成绩X服从正态分布其中近似为50家食品生产企业考核成绩的平均数，近似为样本方差，经计算得，利用该正态分布，估计该市500家食品生产企业质量管理考核成绩高于90.06分的有多少家?（结果保留整数）.附参考数据与公式：则，.8.（2020·漯河模拟）十九大以来，某贫困地区扶贫办积极贯彻落实国家精准扶贫的政策要求，带领广大农村地区人民群众脱贫奔小康.经过不懈的奋力拼搏，新农村建设取得巨大进步，农民年收入也逐年增加，为了制定提升农民收入、实现2020年脱贫的工作计划，该地扶贫办统计了2019年50位农民的年收入并制成如下频率分布直方图：附参考数据：，若随机变量X服从正态分布，则，，.（1）根据频率分布直方图，估计50位农民的平均年收入（单位：千元）；（同一组数据用该组数据区间的中点值表示）；（2）由频率分布直方图，可以认为该贫困地区农民年收入X服从正态分布，其中近似为年平均收入，近似为样本方差，经计算得=6.92，利用该正态分布，求：①在扶贫攻坚工作中，若使该地区约有占总农民人数的的农民的年收入高于扶贫办制定的最低年收入标准，则最低年收入标准大约为多少千元？②为了调研“精准扶贫，不落一人”的政策要求落实情况，扶贫办随机走访了1000位农民.若每位农民的年收入互相独立，问：这1000位农民中的年收入不少于12.14千元的人数最有可能是多少？9.（2017·黑龙江模拟）某学生社团在对本校学生学习方法开展问卷调查的过程中发现，在回收上来的1000份有效问卷中，同学们背英语单词的时间安排共有两种：白天背和晚上临睡前背．为研究背单词时间安排对记忆效果的影响，该社团以5%的比例对这1000名学生按时间安排粪型进行分层抽样，并完成一项实验，实验方法是，使两组学生记忆40个无意义音节（如xIQ、GEH），均要求在刚能全部记清时就停止识记，并在8小时后进行记忆测验．不同的是，甲组同学识记结束后一直不睡觉，8小时后测验；乙组同学识记停止后立刻睡觉，8小时后叫醒测验．两组同学识记停止8小时后的准确回忆（保持）情况如图（区间含左端点而不舍右端点）（1）估计1000名被调查的学生中识记停止后8小时40个音节的保持率大于等于60%的人数；（2）从乙组准确回忆结束在|12，24）范围内的学生中随机选3人，记能准确回忆20个以上（含20）的人数为随机变量x．求X分布列及数学期望；（3）从本次实验的结果来看，上述两种时间安排方法中哪种方法背英语单词记忆效果更好？计算并说明理由．10.（2018·南宁模拟）在某单位的食堂中，食堂每天以10元/斤的价格购进米粉，然后以4.4元/碗的价格出售，每碗内含米粉0.2斤，如果当天卖不完，剩下的米粉以2元/斤的价格卖给养猪场.根据以往统计资料，得到食堂某天米粉需求量的频率分布直方图如图所示，若食堂购进了80斤米粉，以（斤）（其中）表示米粉的需求量，（元）表示利润.（1）估计该天食堂利润不少于760元的概率；（2）在直方图的需求量分组中，以区间中间值作为该区间的需求量，以需求量落入该区间的频率作为需求量在该区间的概率，求的分布列和数学期望.11.（2020·辽宁模拟）某城市100户居民的月平均用电量（单位：度），以，，，，，，分组的频率分布直方图如图．（1）求直方图中x的值；（2）求月平均用电量的众数和中位数；（3）在月平均用电量为，，，的四组用户中，用分层抽样的方法抽取户居民，则月平均用电量在的用户中应抽取多少户？12.（2020·大连模拟）某校从参加高三模拟考试的学生中随机抽取名学生，将其数学成绩（均为整数）分成六段后得到如下部分频率分布直方图．观察图形的信息，回答下列问题：（1）求分数在内的频率，并补全这个频率分布直方图；（2）统计方法中，同一组数据常用该组区间的中点值作为代表，据此估计本次考试的平均分；（3）用分层抽样的方法在分数段为的学生中抽取一个容量为的样本，将该样本看成一个总体，从中任取个，求至多有人在分数段内的概率．13.（2020·莆田模拟）为了解某地网民浏览购物网站的情况，从该地随机抽取100名网民进行调查，其中男性、女性人数分别为45和55.下面是根据调查结果绘制的网民日均浏览购物网站时间的频率分布直方图，将日均浏览购物网站时间不低于40分钟的网民称为“网购达人”，已知“网购达人”中女性有10人.参考公式：，其中.参考数据：0.102.7063.841 5.024 6.635 7.879 10.828（1）根据已知条件完成下面的列联表，并判断是否有90%的把握认为是否为“网购达人”与性别有关；（2）将上述调査所得到的频率视为概率，现在从该地的网民中随机抽取3名，记被抽取的3名网民中的“网购达人”的人数为X，求X的分布列、数学期望和方差.14.（2020·长春模拟）笔、墨、纸、砚是中国独有的文书工具，即“文房四宝”.笔、墨、纸、砚之名，起源于南北朝时期，其中的“纸”指的是宣纸，宣纸“始于唐代，产于泾县”，而唐代泾县隶属于宣州府管辖，故因地而得名“宣纸”，宣纸按质量等级，可分为正牌和副牌（优等品和合格品），某公司年产宣纸10000刀（每刀100张），公司按照某种质量标准值给宣纸确定质量等级，如下表所示：公式在所生产的宣纸中随机抽取了一刀（100张）进行检验，得到频率分布直方图如图所示，已知每张正牌纸的利润是10元，副牌纸的利润是5元，废品亏损10元.（1）估计该公式生产宣纸的年利润（单位：万元）；（2）该公司预备购买一种售价为100万元的机器改进生产工艺，这种机器的使用寿命是一年，只能提高宣纸的质量，不影响产量，这种机器生产的宣纸的质量标准值的频率，如下表所示：其中为改进工艺前质量标准值的平均值，改进工艺后，每张正牌和副牌宣纸的利润都下降2元，请判断该公司是否应该购买这种机器，并说明理由.15.（2020·蚌埠模拟）随着网购人数的日益增多，网上的支付方式也呈现一种多样化的状态，越来越多的便捷移动支付方式受到了人们的青睐，更被网友们评为“新四大发明”之一.随着人们消费观念的进步，许多人喜欢用信用卡购物，考虑到这一点，一种“网上的信用卡”横空出世——蚂蚁花呗.这是一款支付宝和蚂蚁金融合作开发的新支付方式，简单便捷，同时也满足了部分网上消费群体在支付宝余额不足时的“赊购”消费需求.为了调查使用蚂蚁花呗“赊购”消费与消费者年龄段的关系，某网站对其注册用户开展抽样调查，在每个年龄段的注册用户中各随机抽取100人，得到各年龄段使用蚂蚁花呗“赊购”的人数百分比如图所示.参考答案：，.（1）由大数据可知，在18到44岁之间使用花呗“赊购”的人数百分比y与年龄x成线性相关关系，利用统计图表中的数据，以各年龄段的区间中点代表该年龄段的年龄，求所调查群体各年龄段“赊购”人数百分比y与年龄x的线性回归方程（回归直线方程的斜率和截距保留两位有效数字）；（2）该网站年龄为20岁的注册用户共有2000人，试估算该网站20岁的注册用户中使用花呗“赊购”的人数；（3）已知该网店中年龄段在18-26岁和27-35岁的注册用户人数相同，现从18到35岁之间使用花呗“赊购”的人群中按分层抽样的方法随机抽取8人，再从这8人中简单随机抽取2人调查他们每个月使用花呗消费的额度，求抽取的两人年龄都在18到26岁的概率.16.（2020·辽宁模拟）港珠澳大桥是一座具有划时代意义的大桥.它连通了珠海香港澳门三地，大大缩短了三地的时空距离，盘活了珠江三角洲的经济，被誉为新的世界七大奇迹.截至2019年10月23日8点，珠海公路口岸共验放出入境旅客超过1400万人次，日均客流量已经达到4万人次，验放出入境车辆超过70万辆次，2019年春节期间，客流再次大幅增长，日均客流达8万人次，单日客流量更是创下11.3万人次的最高纪录.2019年从五月一日开始的连续100天客流量频率分布直方图如下（1）①同一组数据用该区间的中点值代替，根据频率分布直方图.估计客流量的平均数.②求客流量的中位数.（2）设这100天中客流量超过5万人次的有天，从这天中任取两天，设为这两天中客流量超过7万人的天数.求的分布列和期望．17.（2020·江门模拟）2019年7月1日到3日，世界新能源汽车大会在海南博鳌召开，大会着眼于全球汽车产业的转型升级和生态环境的持续改善．某汽车公司顺应时代潮流，最新研发了一款新能源汽车，并在出厂前对100辆汽车进行了单次最大续航里程（理论上是指新能源汽车所装载的燃料或电池所能够提供给车行驶的最远里程）的测试．现对测试数据进行分析，得到如图的频率分布直方图．（1）估计这100辆汽车的单次最大续航里程的平均值（同一组中的数据用该组区间的中点值代表）；（2）根据大量的汽车测试数据，可以认为这款汽车的单次最大续航量程X近似地服从正态分布，经计算第（1）问中样本标准差s的近似值为50．用样本平均数作为的近似值，用样本标准差s作为的估计值，现任取一辆汽车，求它的单次最大续航里程恰在250千米到400千米之间的概率；（3）某汽车销售公司为推广此款新能源汽车，现面向意向客户推出“玩游戏，送大奖”活动，客户可根据抛掷硬币的结果，操控微型遥控车在方格图上行进，若遥控车最终停在“胜利大本营”，则可获得购车优惠券．已知硬币出现正，反面的概率都是，方格图上标有第0格、第1格、第2格……第50格．遥控车开始在第0格，客户每掷一次硬币，遥控车向前移动一次，若掷出正面，遥控车向前移动一格（从k到），若掷出反面，遥控车向前移动两格（从k到），直到遥控车移到第49格（胜利大本营）或第50格（失败大本营）时，游戏结束．设遥控车移到第n格的概率为，试证明是等比数列，并解释此方案能否成功吸引顾客购买该款新能源汽车．参考数据：若随机变量服从正态分布，则，，．18.（2020·肇庆模拟）某公司新上一条生产线，为保证新的生产线正常工作，需对该生产线进行检测，现从该生产线上随机抽取100件产品，测量产品数据，用统计方法得到样本的平均数，标准差，绘制如图所示的频率分布直方图，以频率值作为概率估值．（1）从该生产线加工的产品中任意抽取一件，记其数据为，依据以下不等式评判（表示对应事件的概率）①②③评判规则为：若至少满足以上两个不等式，则生产状况为优，无需检修；否则需检修生产线，试判断该生产线是否需要检修；（2）将数据不在内的产品视为次品，从该生产线加工的产品中任意抽取2件，次品数记为，求的分布列与数学期望．答案解析部分一、解答题1.【答案】（1）解：由题意，该地区用户对该电讯企业评分的频率分布如下表：因此可估计评分不低于70分的概率为；对该电讯企业评分的中位数设为x，可得，则，解得，所以可估计对该电讯企业评分的中位数为；（2）解：受调查用户评分在的有人，若编号依次为1，2，3，4，从中选2人的事件有、、、、、，共有个基本事件；受调查用户评分在的有人，若编号依次为1，2，3，..9，10，从中选2人，可得共有个基本事件；因此2人评分都在的概率.【解析】【分析】（1）由题意列出频率分布表，求和即可估计该地区用户对该电讯企业评分不低于70分的概率；利用中位数两侧的概率和相等列方程即可估计对该电讯企业评分的中位数；（2）由题意计算出受调查用户评分在、的人数，求出总的基本事件个数及满足要求的基本事件的个数，由古典概型概率公式即可得解.2.【答案】解：(Ⅰ)高三年级学生平均每天的学习时间为:(h);(Ⅱ)300名学生中合格的人数为(人),故补全表格如下:所以所以有99.9%的把握认为该校高三年级学生的性别与学习时长合格有关.【解析】【分析】(Ⅰ)根据频率分布直方图直接计算平均值即可;(Ⅱ)先求出300名学生中合格的人数,再补全表格,然后根据表格数据和公式计算,最后将与进行比较,进而得出结论.3.【答案】（1）解：由题意知，根据条形图，可得A水果在每天的前8小时内的销售量分别为14，15，16，17的频率分别是0.2，0.3，0.4和0.1 ，所以X的分布列为140.2（2）解：当时，设Y为水果批发商的日利润，则Y的可能取值为760，900，可得，所以期望，当时，设Z为水果批发商的日利润，则Z的可能取值为680，820，960，可得，所以期望.因为，综上可知，当时的日利润期望值大于时的日利润期望值，故答案为：.【解析】【分析】（1）由题意知，根据条形图，得到销售量分别为14，15，16，17的频率，进而得到随机变量X的分布列；（2）分别求得当和时，利润的数学期望，比较即可得到结论.4.【答案】（1）解：由题意知，500件产品中共有优等品件，则从样本中随机取一件为优等品的概率为，所以从该企业生产的所有产品中随机抽取4件，没有一件是优等品的概率为，则随机抽取4件，至少有1件优等品的概率为.（2）解：检测出3件或4件为优等品时，检测出的优等品低于3件时，，由题意知，，故X的分布列为所以数学期望.【解析】【分析】（1）先求出从样本中随机取一件为优等品的概率，再求从该企业生产的所有产品中随机抽取4件，没有一件是优等品的概率，从而可求出至少有一件是优等品的概率.（2）由题意求出检测出3件或4件为优等品时及检测出的优等品低于3件时的X的值，结合第一问求出，，从而可得X的分布列，即可计算其数学期望5.【答案】（1）解：甲解密成功所需时间的中位数为47，，解得，，解得，由频率分布直方图知，甲在分钟内解密成功的频率是；（2）解：①由题意及（1）可知第一个出场选手解密成功的概率为，第二个出场选手解密成功的概率为，第三个出场选手解密成功的概率为，所以该团队挑战成功的概率为；②由①可知按从小到大的顺序的概率分别、、，根据题意知的取值为、、，则，，，所以所需派出的人员数目的分布列为：因此，.【解析】【分析】（1）根据中位数左右两边的矩形面积之和均为0.5可求得a、b的值，并根据频率分布直方图求得甲在1分钟内解密成功的频率；（2）①由（1）得出，求出、的值，由此得出该团队挑战成功的概率为；②由题意可得出随机变量X的可能取值有1、2、3，利用独立事件的概率乘法公式计算出随机变量X在不同取值下的概率，据此可得出随机变量X的分布列，结合期望公式可计算出X的数学期望值.6.【答案】（1）解：根据题意，由频率分布直方图可知，500份血液样品指标A值的平均数为：，500份血液样品指标A值的样本方差为：．（2）解：由题意知：指标的值服从正态分布，，，则，所以，．随机抽取20名医生独立检测血液中指标的值，就相当于进行了20次独立重复试验，记“20名医生中出现4名医生血液中指标的值大于正常值20,03”为事件，则，所以从血液中指标的值的角度来看：该院医生的健康率是正常的．【解析】【分析】（1）由频率分布直方图，直接利用平均数和方差公式，求出500份血液样品指标值的平均数和样本方差；（2）由（1）得出指标的值服从正态分布，从而可求出，在根据独立重复试验中的概率求法，求出20名医生中出现4名医生血液中指标的值大于正常值20.03的概率，即可判断该院医生的健康率是否正常7.【答案】（1）解：由题意，这50家食品生产企业考核成绩的平均数为：（分）,由频率分布图可知内，所以，解得分.（2）解：根据题意，这50家食品生产企业中考核成绩不低于88分的企业有:（家），其中考核成绩在内的企业有（家），所以X可能取值有0，1，2，3，4则，，，，，所以X的分布列为所以.（3）解：由题意得，所以，所以，所以（家），所以500家食品生产企业质量管理考核成绩高于90.06分的有79家.【解析】【分析】（1）利用频率分布直方图的性质能求出这50家食品生产企业考核成绩的平均数和中位数；（2）由已知得到考核成绩在内的企业有5家，得出随机变量的可能取值，分别求出相应的概率和分布列，求得数学期望；（3）根据题意得，由此估计该市500家食品生产企业质量管理考核成绩高于90.06分的企业个数.8.【答案】（1）解：千元.故估计50位农民的年平均收入为17.40千元.（2）解：由题意知，① ，所以时，满足题意，即最低年收入大约为14.77千元.②由，每个农民的年收入不少于12.14千元的事件的概率为0.9773，记1000个农民的年收入不少于12.14千元的人数为则，其中于是恰好有k个农民的年收入不少于12.14千元的事件概率为，。
课下能力提升：(十一) 频率分布表 频率分布直方图与折线图 Word版含答案
课下能力提升(十一) 频率分布表频率分布直方图与折线图一、填空题1．如图是容量为100的样本的频率分布直方图，试根据图形中的数据填空．(1)样本数据在范围[6,10)内的频率为________；(2)样本数据落在范围[10,14)内的频数为________．2．为了调查某厂工人生产某种产品的能力，随机抽查了20名工人某天生产该产品的数量，产品数量的分组区间为[45,55)，[55,65)，[65,75)，[75,85)，[85,95]，由此得到频率分布直方图如下图，则这20名工人中一天生产该产品数量在[55,75)的人数是________．3．将容量为100的样本数据，按从小到大的顺序分成8个组，如下表：4．为提高公众对健康的自我管理能力和科学认识，某调查机构共调查了200人在一天中的睡眠时间．现将数据整理分组，如下表所示．由于操作不慎，表中A，B，C，D四处数据污损，统计员只记得A处的数据比C处的数据大4，由此可知B处的数据为________.5.(如图)，但是年龄组为[25,30)的数据不慎丢失，则依据此图可得：(1)[25,30)年龄组对应小矩形的高度为________；(2)据此估计该市“四城同创”活动中志愿者年龄在[25,35)的人数为________． 二、解答题6.某工厂对一批产品进行了抽样检测，右图是根据抽样检测后的产品净重(单位：克)数据绘制的频率分布直方图，其中产品净重的范围是[96,106]，样本数据分组为[96,98)，[98,100)，[100,102)，[102,104)，[104,106)．已知样本中产品净重小于100克的个数是36，则样本中净重大于或等于98克并且小于104克的产品的个数是多少？7.根据空气质量指数API(为整数)的不同，可将空气质量分级如下表：对某城市一年(365天)的空气质量进行监测，获得的API 数据按照区间[0,50]，(50,100]，(100,150]，(150,200]，(200,250]，(250,300]进行分组，得到频率分布直方图如图．(1)求频率分布直方图中x 的值；(2)计算一年中空气质量为良和轻微污染的总天数．(提示：结果用分数表示．已知57＝78 125,27＝128，31 825＋2365＋71 825＋31 825＋89 125＝1239 125，365＝73×5)8．为了了解一个小水库中养殖的鱼的有关情况，从这个水库中多个不同位置捕捞出100条鱼，称得每条鱼的质量(单位：千克)，并将所得数据分组，画出频率分布直方图(如图所示)．(1)求出各组相应的频率；(2)估计数据落在[1.15，1.30]中的概率为多少；(3)将上面捕捞的100条鱼分别作一记号后再放回水库，几天后再从水库的多处不同位置捕捞出120条鱼，其中还有记号的鱼有6条，请根据这一情况来估计该水库中鱼的总条数．答案1．解析：(1)样本数据在[6,10)内频率为0.08×4＝0.32.(2)在[10,14)内的频数为0.09×4×100＝36.答案：(1)0.32 (2)362．解析：由题意得，这20名工人中一天生产该产品数量在[55,75)的人数是20×[(0.040＋0.025)×10]＝13(人)．答案：133．解析：9＋14＋14＋13＋12＋x＋13＋10＝100，x＝15.P＝15100＝0.15. 答案：0.154．解析：设A处的数据为x，则C处的数据为x－4，则x＋x－4＋8＋52＋20＋4＝200，x＝60，则B 处数据为60200＝0.3.答案：0.35．解析：设[25,30)年龄组对应小矩形的高度为h ，则5×(0.01＋h ＋0.07＋0.06＋0.02)＝1，h ＝0.04.志愿者年龄在[25,35)的频率为5×(0.04＋0.07)＝0.55，故志愿者年龄在[25,35)的人数约为0.55×800＝440.答案：0.04 4406．解：产品净重小于100克的频率为(0.050＋0.100)×2＝0.300，已知样本中产品净重小于100克的个数是36，设样本容量为n ，则36n＝0.300，所以n ＝120，净重大于或等于98克并且小于104克的产品的频率为(0.100＋0.150＋0.125)×2＝0.750，所以样本中净重大于或等于98克并且小于104克的产品的个数是120×0.750＝90.7．解：(1)由图可知50x ＝1－(31 825＋2365＋71 825＋31 825＋89 125)×50＝1－1239 125×50，解得x ＝11918 250；(2)365×(11918 250×50＋2365×50)＝219.答：一年中空气质量为良和轻微污染的总天数为219天． 8．解：(1)由频率分布直方图和频率＝组距×(频率组距)可得下表(2)0.30＋0.15＋0.02＝中的概率约为0.47.(3)由分层抽样中每个个体被抽到的概率相同知：设水库中鱼的总条数为N ，则120N ＝6100，即N ＝2 000，故水库中鱼的总条数约为2 000条．。
高考数学频率分布直方图大题训练题(含答案)
频率分布直方图大题训练题一、解答题（共18题；共205分）1.（2020·龙岩模拟）某电讯企业为了了解某地区居民对电讯服务质量评价情况，随机调查100 名用户，根据这100名用户对该电讯企业的评分，绘制频率分布直方图，如图所示，其中样本数据分组为，，…… .（1）估计该地区用户对该电讯企业评分不低于70分的概率，并估计对该电讯企业评分的中位数；（2）现从评分在的调查用户中随机抽取2人，求2人评分都在的概率.2.（2020·芜湖模拟）某学校为了了解该校高三年级学生寒假在家自主学习的情况，随机对该校300名高三学生寒假的每天学习时间（单位：h）进行统计，按照，，，，的分组作出频率分布直方图如图所示．参考公式：，其中．参考附表：0.050 0.010 0.001（Ⅰ）根据频率分布直方图计算该校高三年级学生的平均每天学习时间（同一组中的数据用该组区间中点值代表）；（Ⅱ）该校规定学习时间超过4h为合格，否则不合格．已知这300名学生中男生有140人，其中合格的有70人，请补全下表，根据表中数据，能否有99.9%的把握认为该校高三年级学生的性别与学习时长合格有关？3.（2020·泰安模拟）某水果批发商经销某种水果(以下简称A水果)，购入价为300元/袋，并以360元／袋的价格售出，若前8小时内所购进的A水果没有售完，则批发商将没售完的A水果以220元／袋的价格低价处理完毕(根据经验，2小时内完全能够把A水果低价处理完，且当天不再购进)．该水果批发商根据往年的销量，统计了100天A水果在每天的前8小时内的销售量，制成如下频数分布条形图．现以记录的100天的A水果在每天的前8小时内的销售量的频率作为A水果在一天的前8小时内的销售量的概率，记X表示A水果一天前8小时内的销售量，n表示水果批发商一天批发A水果的袋数．（1）求X的分布列；（2）以日利润的期望值为决策依据，在与中选其一，应选用哪个?4.（2020·南昌模拟）某产品自生产并投入市场以来，生产企业为确保产品质量，决定邀请第三方检测机构对产品进行质量检测，并依据质量指标Z来衡量产品的质量.当时，产品为优等品；当时，产品为一等品；当时，产品为二等品.第三方检测机构在该产品中随机抽取500件，绘制了这500件产品的质量指标Z的条形图.用随机抽取的500件产品作为样本，估计该企业生产该产品的质量情况，并用频率估计概率．（1）从该企业生产的所有产品中随机抽取4件，求至少有1件优等品的概率；（2）现某人决定购买80件该产品.已知每件成本1000元，购买前，邀请第三方检测机构对要购买的80件产品进行抽样检测，买家、企业及第三方检测机构就检测方案达成以下协议：从80件产品中随机抽出4件产品进行检测，若检测出3件或4件为优等品，则按每件1600元购买，否则按每件1500元购买，每件产品的检测费用250元由企业承担．记企业的收益为X元，求X的分布列与数学期望.5.（2020·南昌模拟）在“挑战不可能”的电视节目上，甲、乙、丙三个人组成的解密团队参加一项解密挑战活动，规则是由密码专家给出题目，然后由3个人依次出场解密，每人限定时间是1分钟内，否则派下一个人.3个人中只要有一人解密正确，则认为该团队挑战成功，否则挑战失败.根据甲以往解密测试情况，抽取了甲100次的测试记录，绘制了如下的频率分布直方图.（1）若甲解密成功所需时间的中位数为47，求a、b的值，并求出甲在1分钟内解密成功的频率；（2）在“挑战不可能”节目上由于来自各方及自身的心理压力，甲，乙，丙解密成功的概率分别为，其中表示第个出场选手解密成功的概率，并且定义为甲抽样中解密成功的频率代替，各人是否解密成功相互独立.①求该团队挑战成功的概率；②该团队以从小到大的顺序按排甲、乙、丙三个人上场解密，求团队挑战成功所需派出的人员数目X 的分布列与数学期望.6.（2020·江西模拟）冠状病毒是一个大型病毒家族，可引起感冒以及中东呼吸综合征（MERS）和严重急性呼吸综合征（SARS）等较严重疾病．出现的新型冠状病毒（nCoV）是从未在人体中发现的冠状病毒新毒株．人感染了新型冠状病毒后常见体征有呼吸道症状、发热、咳嗽、气促和呼吸困难等．在较严重病例中，感染可导致肺炎、严重急性呼吸综合征、肾衰竭，甚至死亡．某医院为筛查冠状病毒，需要检测血液中的指标A．现从采集的血液样品中抽取500份检测指标A的值，由测量结果得下侧频率分布直方图：（1）求这500份血液样品指标A值的平均数和样本方差（同一组数据用该区间的中点值作代表，记作）；（2）由频率分布直方图可以认为，这项指标的值X服从正态分布，其中近似为样本平均数，近似为样本方差．在统计学中，把发生概率小于3‰的事件称为小概率事件（正常条件下小概率事件的发生是不正常的）．该医院非常关注本院医生健康状况，随机抽取20名医生，独立的检测血液中指标A的值，结果发现4名医生血液中指标A的值大于正常值20.03，试根据题中条件判断该院医生的健康率是否正常，并说明理由．附：参考数据与公式：，，；若，则① ；② ；③．，，，．7.（2020·江西模拟）年前某市质监部门根据质量管理考核指标对本地的500家食品生产企业进行考核，然后通过随机抽样抽取其中的50家，统计其考核成绩（单位：分），并制成如下频率分布直方图.（1）求这50家食品生产企业考核成绩的平均数（同一组中的数据用该组区间的中点值为代表）及中位数a（精确到0.01）（2）该市质监部门打算举办食品生产企业质量交流会，并从这50家食品生产企业中随机抽取4家考核成绩不低于88分的企业发言，记抽到的企业中考核成绩在的企业数为X，求X的分布列与数学期望（3）若该市食品生产企业的考核成绩X服从正态分布其中近似为50家食品生产企业考核成绩的平均数，近似为样本方差，经计算得，利用该正态分布，估计该市500家食品生产企业质量管理考核成绩高于90.06分的有多少家?（结果保留整数）.附参考数据与公式：则，.8.（2020·漯河模拟）十九大以来，某贫困地区扶贫办积极贯彻落实国家精准扶贫的政策要求，带领广大农村地区人民群众脱贫奔小康.经过不懈的奋力拼搏，新农村建设取得巨大进步，农民年收入也逐年增加，为了制定提升农民收入、实现2020年脱贫的工作计划，该地扶贫办统计了2019年50位农民的年收入并制成如下频率分布直方图：附参考数据：，若随机变量X服从正态分布，则，，.（1）根据频率分布直方图，估计50位农民的平均年收入（单位：千元）；（同一组数据用该组数据区间的中点值表示）；（2）由频率分布直方图，可以认为该贫困地区农民年收入X服从正态分布，其中近似为年平均收入，近似为样本方差，经计算得=6.92，利用该正态分布，求：①在扶贫攻坚工作中，若使该地区约有占总农民人数的的农民的年收入高于扶贫办制定的最低年收入标准，则最低年收入标准大约为多少千元？②为了调研“精准扶贫，不落一人”的政策要求落实情况，扶贫办随机走访了1000位农民.若每位农民的年收入互相独立，问：这1000位农民中的年收入不少于12.14千元的人数最有可能是多少？9.（2017·黑龙江模拟）某学生社团在对本校学生学习方法开展问卷调查的过程中发现，在回收上来的1000份有效问卷中，同学们背英语单词的时间安排共有两种：白天背和晚上临睡前背．为研究背单词时间安排对记忆效果的影响，该社团以5%的比例对这1000名学生按时间安排粪型进行分层抽样，并完成一项实验，实验方法是，使两组学生记忆40个无意义音节（如xIQ、GEH），均要求在刚能全部记清时就停止识记，并在8小时后进行记忆测验．不同的是，甲组同学识记结束后一直不睡觉，8小时后测验；乙组同学识记停止后立刻睡觉，8小时后叫醒测验．两组同学识记停止8小时后的准确回忆（保持）情况如图（区间含左端点而不舍右端点）（1）估计1000名被调查的学生中识记停止后8小时40个音节的保持率大于等于60%的人数；（2）从乙组准确回忆结束在|12，24）范围内的学生中随机选3人，记能准确回忆20个以上（含20）的人数为随机变量x．求X分布列及数学期望；（3）从本次实验的结果来看，上述两种时间安排方法中哪种方法背英语单词记忆效果更好？计算并说明理由．10.（2018·南宁模拟）在某单位的食堂中，食堂每天以10元/斤的价格购进米粉，然后以4.4元/碗的价格出售，每碗内含米粉0.2斤，如果当天卖不完，剩下的米粉以2元/斤的价格卖给养猪场.根据以往统计资料，得到食堂某天米粉需求量的频率分布直方图如图所示，若食堂购进了80斤米粉，以（斤）（其中）表示米粉的需求量，（元）表示利润.（1）估计该天食堂利润不少于760元的概率；（2）在直方图的需求量分组中，以区间中间值作为该区间的需求量，以需求量落入该区间的频率作为需求量在该区间的概率，求的分布列和数学期望.11.（2020·辽宁模拟）某城市100户居民的月平均用电量（单位：度），以，，，，，，分组的频率分布直方图如图．（1）求直方图中x的值；（2）求月平均用电量的众数和中位数；（3）在月平均用电量为，，，的四组用户中，用分层抽样的方法抽取户居民，则月平均用电量在的用户中应抽取多少户？12.（2020·大连模拟）某校从参加高三模拟考试的学生中随机抽取名学生，将其数学成绩（均为整数）分成六段后得到如下部分频率分布直方图．观察图形的信息，回答下列问题：（1）求分数在内的频率，并补全这个频率分布直方图；（2）统计方法中，同一组数据常用该组区间的中点值作为代表，据此估计本次考试的平均分；（3）用分层抽样的方法在分数段为的学生中抽取一个容量为的样本，将该样本看成一个总体，从中任取个，求至多有人在分数段内的概率．13.（2020·莆田模拟）为了解某地网民浏览购物网站的情况，从该地随机抽取100名网民进行调查，其中男性、女性人数分别为45和55.下面是根据调查结果绘制的网民日均浏览购物网站时间的频率分布直方图，将日均浏览购物网站时间不低于40分钟的网民称为“网购达人”，已知“网购达人”中女性有10人.参考公式：，其中.参考数据：0.102.7063.841 5.024 6.635 7.879 10.828（1）根据已知条件完成下面的列联表，并判断是否有90%的把握认为是否为“网购达人”与性别有关；（2）将上述调査所得到的频率视为概率，现在从该地的网民中随机抽取3名，记被抽取的3名网民中的“网购达人”的人数为X，求X的分布列、数学期望和方差.14.（2020·长春模拟）笔、墨、纸、砚是中国独有的文书工具，即“文房四宝”.笔、墨、纸、砚之名，起源于南北朝时期，其中的“纸”指的是宣纸，宣纸“始于唐代，产于泾县”，而唐代泾县隶属于宣州府管辖，故因地而得名“宣纸”，宣纸按质量等级，可分为正牌和副牌（优等品和合格品），某公司年产宣纸10000刀（每刀100张），公司按照某种质量标准值给宣纸确定质量等级，如下表所示：公式在所生产的宣纸中随机抽取了一刀（100张）进行检验，得到频率分布直方图如图所示，已知每张正牌纸的利润是10元，副牌纸的利润是5元，废品亏损10元.（1）估计该公式生产宣纸的年利润（单位：万元）；（2）该公司预备购买一种售价为100万元的机器改进生产工艺，这种机器的使用寿命是一年，只能提高宣纸的质量，不影响产量，这种机器生产的宣纸的质量标准值的频率，如下表所示：其中为改进工艺前质量标准值的平均值，改进工艺后，每张正牌和副牌宣纸的利润都下降2元，请判断该公司是否应该购买这种机器，并说明理由.15.（2020·蚌埠模拟）随着网购人数的日益增多，网上的支付方式也呈现一种多样化的状态，越来越多的便捷移动支付方式受到了人们的青睐，更被网友们评为“新四大发明”之一.随着人们消费观念的进步，许多人喜欢用信用卡购物，考虑到这一点，一种“网上的信用卡”横空出世——蚂蚁花呗.这是一款支付宝和蚂蚁金融合作开发的新支付方式，简单便捷，同时也满足了部分网上消费群体在支付宝余额不足时的“赊购”消费需求.为了调查使用蚂蚁花呗“赊购”消费与消费者年龄段的关系，某网站对其注册用户开展抽样调查，在每个年龄段的注册用户中各随机抽取100人，得到各年龄段使用蚂蚁花呗“赊购”的人数百分比如图所示.参考答案：，.（1）由大数据可知，在18到44岁之间使用花呗“赊购”的人数百分比y与年龄x成线性相关关系，利用统计图表中的数据，以各年龄段的区间中点代表该年龄段的年龄，求所调查群体各年龄段“赊购”人数百分比y与年龄x的线性回归方程（回归直线方程的斜率和截距保留两位有效数字）；（2）该网站年龄为20岁的注册用户共有2000人，试估算该网站20岁的注册用户中使用花呗“赊购”的人数；（3）已知该网店中年龄段在18-26岁和27-35岁的注册用户人数相同，现从18到35岁之间使用花呗“赊购”的人群中按分层抽样的方法随机抽取8人，再从这8人中简单随机抽取2人调查他们每个月使用花呗消费的额度，求抽取的两人年龄都在18到26岁的概率.16.（2020·辽宁模拟）港珠澳大桥是一座具有划时代意义的大桥.它连通了珠海香港澳门三地，大大缩短了三地的时空距离，盘活了珠江三角洲的经济，被誉为新的世界七大奇迹.截至2019年10月23日8点，珠海公路口岸共验放出入境旅客超过1400万人次，日均客流量已经达到4万人次，验放出入境车辆超过70万辆次，2019年春节期间，客流再次大幅增长，日均客流达8万人次，单日客流量更是创下11.3万人次的最高纪录.2019年从五月一日开始的连续100天客流量频率分布直方图如下（1）①同一组数据用该区间的中点值代替，根据频率分布直方图.估计客流量的平均数.②求客流量的中位数.（2）设这100天中客流量超过5万人次的有天，从这天中任取两天，设为这两天中客流量超过7万人的天数.求的分布列和期望．17.（2020·江门模拟）2019年7月1日到3日，世界新能源汽车大会在海南博鳌召开，大会着眼于全球汽车产业的转型升级和生态环境的持续改善．某汽车公司顺应时代潮流，最新研发了一款新能源汽车，并在出厂前对100辆汽车进行了单次最大续航里程（理论上是指新能源汽车所装载的燃料或电池所能够提供给车行驶的最远里程）的测试．现对测试数据进行分析，得到如图的频率分布直方图．（1）估计这100辆汽车的单次最大续航里程的平均值（同一组中的数据用该组区间的中点值代表）；（2）根据大量的汽车测试数据，可以认为这款汽车的单次最大续航量程X近似地服从正态分布，经计算第（1）问中样本标准差s的近似值为50．用样本平均数作为的近似值，用样本标准差s作为的估计值，现任取一辆汽车，求它的单次最大续航里程恰在250千米到400千米之间的概率；（3）某汽车销售公司为推广此款新能源汽车，现面向意向客户推出“玩游戏，送大奖”活动，客户可根据抛掷硬币的结果，操控微型遥控车在方格图上行进，若遥控车最终停在“胜利大本营”，则可获得购车优惠券．已知硬币出现正，反面的概率都是，方格图上标有第0格、第1格、第2格……第50格．遥控车开始在第0格，客户每掷一次硬币，遥控车向前移动一次，若掷出正面，遥控车向前移动一格（从k到），若掷出反面，遥控车向前移动两格（从k到），直到遥控车移到第49格（胜利大本营）或第50格（失败大本营）时，游戏结束．设遥控车移到第n格的概率为，试证明是等比数列，并解释此方案能否成功吸引顾客购买该款新能源汽车．参考数据：若随机变量服从正态分布，则，，．18.（2020·肇庆模拟）某公司新上一条生产线，为保证新的生产线正常工作，需对该生产线进行检测，现从该生产线上随机抽取100件产品，测量产品数据，用统计方法得到样本的平均数，标准差，绘制如图所示的频率分布直方图，以频率值作为概率估值．（1）从该生产线加工的产品中任意抽取一件，记其数据为，依据以下不等式评判（表示对应事件的概率）①②③评判规则为：若至少满足以上两个不等式，则生产状况为优，无需检修；否则需检修生产线，试判断该生产线是否需要检修；（2）将数据不在内的产品视为次品，从该生产线加工的产品中任意抽取2件，次品数记为，求的分布列与数学期望．答案解析部分一、解答题1.【答案】（1）解：由题意，该地区用户对该电讯企业评分的频率分布如下表：因此可估计评分不低于70分的概率为；对该电讯企业评分的中位数设为x，可得，则，解得，所以可估计对该电讯企业评分的中位数为；（2）解：受调查用户评分在的有人，若编号依次为1，2，3，4，从中选2人的事件有、、、、、，共有个基本事件；受调查用户评分在的有人，若编号依次为1，2，3，..9，10，从中选2人，可得共有个基本事件；因此2人评分都在的概率.【解析】【分析】（1）由题意列出频率分布表，求和即可估计该地区用户对该电讯企业评分不低于70分的概率；利用中位数两侧的概率和相等列方程即可估计对该电讯企业评分的中位数；（2）由题意计算出受调查用户评分在、的人数，求出总的基本事件个数及满足要求的基本事件的个数，由古典概型概率公式即可得解.2.【答案】解：(Ⅰ)高三年级学生平均每天的学习时间为:(h);(Ⅱ)300名学生中合格的人数为(人),故补全表格如下:所以所以有99.9%的把握认为该校高三年级学生的性别与学习时长合格有关.【解析】【分析】(Ⅰ)根据频率分布直方图直接计算平均值即可;(Ⅱ)先求出300名学生中合格的人数,再补全表格,然后根据表格数据和公式计算,最后将与进行比较,进而得出结论.3.【答案】（1）解：由题意知，根据条形图，可得A水果在每天的前8小时内的销售量分别为14，15，16，17的频率分别是0.2，0.3，0.4和0.1 ，所以X的分布列为140.2（2）解：当时，设Y为水果批发商的日利润，则Y的可能取值为760，900，可得，所以期望，当时，设Z为水果批发商的日利润，则Z的可能取值为680，820，960，可得，所以期望.因为，综上可知，当时的日利润期望值大于时的日利润期望值，故答案为：.【解析】【分析】（1）由题意知，根据条形图，得到销售量分别为14，15，16，17的频率，进而得到随机变量X的分布列；（2）分别求得当和时，利润的数学期望，比较即可得到结论.4.【答案】（1）解：由题意知，500件产品中共有优等品件，则从样本中随机取一件为优等品的概率为，所以从该企业生产的所有产品中随机抽取4件，没有一件是优等品的概率为，则随机抽取4件，至少有1件优等品的概率为.（2）解：检测出3件或4件为优等品时，检测出的优等品低于3件时，，由题意知，，故X的分布列为所以数学期望.【解析】【分析】（1）先求出从样本中随机取一件为优等品的概率，再求从该企业生产的所有产品中随机抽取4件，没有一件是优等品的概率，从而可求出至少有一件是优等品的概率.（2）由题意求出检测出3件或4件为优等品时及检测出的优等品低于3件时的X的值，结合第一问求出，，从而可得X的分布列，即可计算其数学期望5.【答案】（1）解：甲解密成功所需时间的中位数为47，，解得，，解得，由频率分布直方图知，甲在分钟内解密成功的频率是；（2）解：①由题意及（1）可知第一个出场选手解密成功的概率为，第二个出场选手解密成功的概率为，第三个出场选手解密成功的概率为，所以该团队挑战成功的概率为；②由①可知按从小到大的顺序的概率分别、、，根据题意知的取值为、、，则，，，所以所需派出的人员数目的分布列为：因此，.【解析】【分析】（1）根据中位数左右两边的矩形面积之和均为0.5可求得a、b的值，并根据频率分布直方图求得甲在1分钟内解密成功的频率；（2）①由（1）得出，求出、的值，由此得出该团队挑战成功的概率为；②由题意可得出随机变量X的可能取值有1、2、3，利用独立事件的概率乘法公式计算出随机变量X在不同取值下的概率，据此可得出随机变量X的分布列，结合期望公式可计算出X的数学期望值.6.【答案】（1）解：根据题意，由频率分布直方图可知，500份血液样品指标A值的平均数为：，500份血液样品指标A值的样本方差为：．（2）解：由题意知：指标的值服从正态分布，，，则，所以，．随机抽取20名医生独立检测血液中指标的值，就相当于进行了20次独立重复试验，记“20名医生中出现4名医生血液中指标的值大于正常值20,03”为事件，则，所以从血液中指标的值的角度来看：该院医生的健康率是正常的．【解析】【分析】（1）由频率分布直方图，直接利用平均数和方差公式，求出500份血液样品指标值的平均数和样本方差；（2）由（1）得出指标的值服从正态分布，从而可求出，在根据独立重复试验中的概率求法，求出20名医生中出现4名医生血液中指标的值大于正常值20.03的概率，即可判断该院医生的健康率是否正常7.【答案】（1）解：由题意，这50家食品生产企业考核成绩的平均数为：（分）,由频率分布图可知内，所以，解得分.（2）解：根据题意，这50家食品生产企业中考核成绩不低于88分的企业有:（家），其中考核成绩在内的企业有（家），所以X可能取值有0，1，2，3，4则，，，，，所以X的分布列为所以.（3）解：由题意得，所以，所以，所以（家），所以500家食品生产企业质量管理考核成绩高于90.06分的有79家.【解析】【分析】（1）利用频率分布直方图的性质能求出这50家食品生产企业考核成绩的平均数和中位数；（2）由已知得到考核成绩在内的企业有5家，得出随机变量的可能取值，分别求出相应的概率和分布列，求得数学期望；（3）根据题意得，由此估计该市500家食品生产企业质量管理考核成绩高于90.06分的企业个数.8.【答案】（1）解：千元.故估计50位农民的年平均收入为17.40千元.（2）解：由题意知，① ，所以时，满足题意，即最低年收入大约为14.77千元.②由，每个农民的年收入不少于12.14千元的事件的概率为0.9773，记1000个农民的年收入不少于12.14千元的人数为则，其中于是恰好有k个农民的年收入不少于12.14千元的事件概率为，。
概率频率分布直方图练习题
1．(本题满分１２分)某学校随机抽取部分新生调查其上学路上所需时间（单位：分钟），并将所得数据绘制成频率分布直方图（如图），其中，上学路上所需时间的范围是[0,100]，样本数据分组为[0,20)，[20,40)，[40,60)，[60,80)，[80,100].（１）求直方图中x 的值； （２）如果上学路上所需时间不少于40分钟的学生可申请在学校住宿，请估计学校1000名新生中有多少名学生可以申请住宿.2、(本题满分12分)为调查民营企业的经营状况，某统计机构用分层抽样的方法从A 、B 、C 三个城市中，抽取若干个民营企业组成样本进行深入研究，有关数据见下表：（单位：个）（1）求x 、y 的值；（2）若从城市A 与B 抽取的民营企业中再随机选2个进行跟踪式调研，求这2个都来自城市A 的概率.3、某产品按行业生产标准分成8个等级，等级系数ξ依次为1,2,,8…，产品的等级系数越大表明产品的质量越好.现从该厂生产的产品中随机抽取30件，相应的等级系数组成一个样本，数据如下：3 5 3 3 8 5 5 6 34 6 3 4 75 3 4 8 5 3 8 3 4 3 4 4 7 56 7该行业规定产品的等级系数7ξ≥的为一等品，等级系数57ξ≤<的为二等品，等级系数35ξ≤<的为三等品，3ξ<为不合格品．（1）试分别估计该厂生产的产品的一等品率、二等品率和三等品率；（2）从样本的一等品中随机抽取2件，求所抽得2件产品等级系数都是8的概率． 4、某中学在校就餐的高一年级学生有440名，高二年级学生有460名，高三年级学生有500名；为了解学校食堂的服务质量情况，用分层抽样的方法从中抽取70名学生进行抽样调查，把学生对食堂的“服务满意度”与“价格满意度”都分为五个等级： 1级（很不满意）；2级（不满意）；3级（一般）；4级（满意）；5级（很满意），其统计结果如下表（服务满意度为x ，价格满意度为y ）.（1）求高二年级共抽取学生人数；（2）求“服务满意度”为3时的5个“价格满意度”数据的方差；（3）为提高食堂服务质量，现从3x <且24y ≤<的所有学生中随机抽取两人征求意见，求至少有一人的“服务满意度”为1的概率.5、（本小题满分12分）为调查乘客的候车情况，公交公司在某站台的60名候车乘客中随机抽取15人，将他们的候车时间（单位：分钟）作为样本分成5组，如下表所示： （1）估计这60名乘客中候车时间少于10分钟的人数； （2）若从上表第三、四组的6人中随机抽取2人作进一步的问卷调查，求抽到的两人恰好来自不同组的概率．6、（本小题满分12分）某学校甲、乙两个班参加体育达标测试，统计 测试成绩达标人数情况得到如图所示的列联表，已知在全部学生中随机抽取1人为不达标的概率为110. （1）请完成上面的列联表；（2）若用分层抽样的方法在所有测试不达标的学生中随机抽取6人，问其中从甲、乙两个班分别抽取多少人？（3）从（2）中的6人中随机抽取2人，求抽到的两人恰好都来自甲班的概率．7、（本小题满分12分）对某校高一年级学生参加社区服务次数统计，随机抽去了M 名学生作为样本，得到这M 名学生参加社区服务的次数，根据此数据作出了频数与频率的统计表如下： （1）求出表中,,,M r m n 的值；（2）在所取样本中，从参加社区服务的次数不少于20次的学生中任选2人，求至少一人参加社区服务次数在区间[)25,30内的概率．8、（本小题满分12分）某地区有小学21所，中学14所，大学7所，现采取分层抽样的方法从这些学校中抽取6所学校对学生进行视力调查。
概率频率分布直方图练习题
1．(本题满分１２分)某学校随机抽取部分新生调查其上学路上所需时间（单位：分钟），并将所得数据绘制成频率分布直方图（如图），其中，上学路上所需时间的范围是[0,100]，样本数据分组为[0,20)，[20,40)，[40,60)，[60,80)，[80,100]. （１）求直方图中x 的值；（２）如果上学路上所需时间不少于40分钟的学生可申请在学校住宿，请估计学校1000名新生中有多少名学生可以申请住宿.2、(本题满分12分)为调查民营企业的经营状况，某统计机构用分层抽样的方法从A 、B 、C 三个城市中，抽取若干个民营企业组成样本进行深入研究，有关数据见下表：（单位：个）（1）求x 、y 的值；（2）若从城市A 与B 抽取的民营企业中再随机选2个进行跟踪式调研，求这2个都来自城市A 的概率.3、某产品按行业生产标准分成8个等级，等级系数ξ依次为1,2,,8…，产品的等级系数越大表明产品的质量越好.现从该厂生产的产品中随机抽取30件，相应的等级系数组成一个样本，数据如下：3 5 3 3 8 5 5 6 3 46 3 47 5 3 48 5 3 8 3 4 3 4 4 7 5 6 7该行业规定产品的等级系数7ξ≥的为一等品，等级系数57ξ≤<的为二等品，等级系数35ξ≤<的为三等品，3ξ<为不合格品．（1）试分别估计该厂生产的产品的一等品率、二等品率和三等品率；（2）从样本的一等品中随机抽取2件，求所抽得2件产品等级系数都是8的概率． 4、某中学在校就餐的高一年级学生有440名，高二年级学生有460名，高三年级学生有500名；为了解学校食堂的服务质量情况，用分层抽样的方法从中抽取70名学生进行抽样调查，把学生对食堂的“服务满意度”与“价格满意度”都分为五个等级： 1级（很不满意）；2级（不满意）；3级（一般）；4级（满意）；5级（很满意），其统计结果如下表（服务满意度为x ，价格满意度为y ）.（1）求高二年级共抽取学生人数；（2）求“服务满意度”为3时的5个“价格满意度”数据的方差；（3）为提高食堂服务质量，现从3x <且24y ≤<的所有学生中随机抽取两人征求意见，求至少有一人的“服务满意度”为1的概率.5、（本小题满分12分）为调查乘客的候车情况，公交公司在某站台的60名候车乘客中随机抽取15人，将他们的候车时间（单位：分钟）作为样本分成5组，如下表所示：（1）估计这60名乘客中候车时间少于10分钟的人数；（2）若从上表第三、四组的6人中随机抽取2人作进一步Array的问卷调查，求抽到的两人恰好来自不同组的概率．6、（本小题满分12分）某学校甲、乙两个班参加体育达标测试，统计测试成绩达标人数情况得到如图所示的列联表，已知.在全部学生中随机抽取1人为不达标的概率为110（1）请完成上面的列联表；（2）若用分层抽样的方法在所有测试不达标的学生中随机抽取6人，问其中从甲、乙两个班分别抽取多少人？（3）从（2）中的6人中随机抽取2人，求抽到的两人恰好都来自甲班的概率．7、（本小题满分12分）对某校高一年级学生参加社区服务次数统计，随机抽去了M 名学生作为样本，得到这M 名学生参加社区服务的次数，根据此数据作出了频数与频率的统计表如下：（1）求出表中,,,M r m n 的值；（2）在所取样本中，从参加社区服务的次数不少于20次的学生中任选2人，求至少一人参加社区服务次数在区间[)25,30内的概率．8、（本小题满分12分）某地区有小学21所，中学14所，大学7所，现采取分层抽样的方法从这些学校中抽取6所学校对学生进行视力调查。
初二数学频数分布表和频数分布直方图作业练习题（含答案）
初二数学频数分布表和频数分布直方图作业练习题（含答案）初二数学频数分布表和频数分布直方图作业练习题一．选择题（共8小题）1．如图是某班43名同学爱心捐款额的频数分布直方图（每组含前一个边界值，不含后一个边界值），则捐款人数最少的一组是( )A ．5~10元B ．10~15元C ．15~20元D ．20~25元2．如图是某组15名学生数学测试成绩统计图，则成绩高于或等于60分的人数是( )A ．4人B ．8人C ．10人D ．12人组号① ② ③ ④ ⑤频数 12 4 16 10则第3组的频数是( )A ．8B ．0.8C ．16D ．0.16 4．九年级体育测试某班跳绳成绩的频数分布表如下：次数100120x跳绳次数x 在160180xA ．6%B ．12%C ．26%D ．52%5．调查50名学生的年龄，列频数分布表时，这些学生的年龄落在5个小组中，第一、二、三、五组数据个数分别是2，8，15，5，则第四组的频数是( )A ．20B ．30C ．0.4D ．0.66．在1000个数据中，用适当的方法抽取50个作为样本进行统计，频数分布表中54.5~57.5这一组的频数是6，那么它的频率为( )A ．0.12B ．0.60C ．6D ．127．某班级的一次数学考试成绩统计图如图，则下列说法错误的是()A．得分在70~80分的人数最多B．该班的总人数为40C．人数最少的得分段的频数为2D．得分及格(60)…的有12人8．某校组织部分学参加安全知识竞赛，并将成绩整理后绘制成直方图，图中从左至右前四组的百分比分别是4%，12%，40%，28%，第五组的频数是8．则：①参加本次竞赛的学生共有100人；②第五组的百分比为16%；③成绩在7080-分的人数最多；④80分以上的学生有14名；其中正确的个数有()A．1个B．2个C．3个D．4个二．填空题（共6小题）9．若某校有学生4000名，从中随机抽取了40名学生，调查他们每天做作业的时间，结果如下表：每大做作业时间t（时)01t<?12t<?23t<?34t<?4t>人数316984则全校学生每天做作业超过3小时的人数约有．10．某校为了解七年级同学的体能情况，随机选取部分学生测试一分钟仰卧起坐的次数，并绘制了如图所示的直方图，学校七年级共有600人，则计该校一分钟仰卧起坐的次数不少于25次的有人．11．已知数据：25，21，23，25，29，27，28，25，27，30，22，26，25，24，26，28，26，25，24，27．若取组距为2，则列频数表时，应将数据分成的组数是．12．整理某个样本，其中最大值是24，最小值是2，取组距为3，则该样本可以分为组．13．为了更好的刻画数据的总体的规律，我们还可以在得到的频数分布直方图上，，得到图．14．频数分布折线图能直观地反映数据的．三．解答题（共2小题）15．某校为了了解初三年级1000名学生的身体健康情况，从该年级随机抽取了若干名学生，将他们按体重（均为整数，单位：)kg 分成五组(:39.5~46A ；:46.5~53.5B ；:53.560.5::60.5~67.5C D ；:67.5~74.5)E ，并依据统计数据绘制了如下两幅尚不完整的统计图．解答下列问题．（1）这次一共抽取了名学生，并补全频数直方图；（2）C 组学生的人数所占的百分比为；（3）在扇形统计图中D 组的圆心角是度；（4）请你估计该校初三年级体重超过60kg 的学生大约有多少名？16．为了解七年级学生的身体素质情况，体育老师对该年级部分学生进行了一分钟跳绳次数的测试，并把测试成绩绘制成如图所示的频数表和频数直方图（每组含前一个边界值，（2）求a ，b 的值，并把频数直方图补充完整．（3）若该年级共有320名学生，估计该年级学生一分钟跳绳次数不少于120次的人数．某校七年级部分学生一分钟跳绳次数测试的频数表组别（次)频数频率 80~1005 0.125 100~1208 0.2 120~140a 0.225 40~160l12 b 160~180 6 0.15。
频率分布直方图经典练习题
频率 组距
0.036 0.024 0.01
元 20 30 40 50 60
况，将所得的数据整理后，画出了频率分布直方图 （如图），已知图中从左到右的前3个小组的频率之 比为1∶2∶3，第1小组的频数为6，则报考飞行员的
学生人数是（ ）
学校为了调查学生在课外读物方面的支出情况，抽 出了一个容量为的x样本，其频率分布直方图如图所 示，其中支出在[50,60]元的同学有39人，则x的值
大于或等于98克并且 小于104克的产品的个数是
( ).
频率/组距
0.150 0.125 x 0.075 0.050
96 98 100 102 104 106克
变式：（2009湖北卷B）下图是样本容量为200的 频率分布直方图。 根据样本的频率分布直方图估计， 样本数据落在【6，10】内的频数为 ，数据落在
频率 组距
0.04
0.03
0.02
0.01
40 50 60 70 80 时 速
4、(08年)为了调查某厂工人生产某种产品的能力， 随机抽查了20位工人某天生产该产品的数量。产品 数量的分组区间为,,，由此得到频率分布直方图如图 3，则这20名工人中一天生产该产品数量在[65,85)
的人数是
.
为了了解某校今年准备报考飞行员的学生的体重情
人数是 ；优秀率为
．
频率
0.04 组距 0.035 0.03 0.025 0.02 0.015 0.01 0005
分数
40 50 60 70 80 90 100
3.(2009惠州第三次调研文)某雷达测速区规定：凡 车速大于或等于70km/h的汽车视为“超速”，并将 受到处罚，如图是某路段的一个检测点对辆汽车的 车速进行检测所得结果的频率分布直方图，则从图 中可以看得出将被处罚的汽车大约有 ( )
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
频率分布直方图练习题
1.(2009 山东卷 )某工厂对一批产品进行了抽样检测.右图是根据抽样检测后的
产品净重（单位：克）数据绘制的频率分布直方图，其中产品频率 /组距净重的范围是[96 ， 106] ，样本数据分组为 [96 ，98）， [98，100),
0.150
0.125
[100 ， 102)， [102 ，104),[104 ， 106], 已知样本中产品净重小于x
100 克的个数是 36，则样本中净重大于或等于98 克并且0.075 0.050
小于 104 克的产品的个数是( ).
A.90
B.75
C. 60
D.45 96 98 100 102 104 106 克
2.（ 2011 杭州质检）某初一年级有500 名同学，将他们的身
高（单位： cm）数据绘制成频率分布直方图（如图），若要
从身高在 120,130 ， 130,140 ， 140,150 三组内的学
生中，用分层抽样的方法选取30 人参加一项活动，则从身
高在 130,140 内的学生中选取的人数为．
3（. 2009 湖北卷）下图是样本容量为200 的频率分布直方图。
根据样本的频率分布直方图估计，样本数据落在【6， 10】
内的频数为，数据落在（ 2，10）内的概
率约为。
4（. 2011 华附月考）为了了解小学生的体能情况，
抽取了某小学同年级部分学生进行跳绳测试，将
所得数据整理后，画出频率分布直方图如图所
示，已知图中从左到右前三个小组的频率分别是
0.1， 0.3， 0.4，第一小组的频数为 5.
（1）求第四小组的频率；
（2）参加这次测试的学生人数是多少？
（3）估计在这次测试中，学生跳绳次数的中位数、众数、平均数及方差。
5.(2011 惠·州研 )右是 2010 年在惠州市行的全省运会上，七位委某跳水比目打出的分数的茎叶，去掉一个最高分和一个最低分后，所剩
数据的平均数和方差分（）
A ． 84， 4.84 B． 84， 1.6
C． 85， 1.6 D． 85， 4 79
8 4 4 6 4 7
9 3
6. 2011
佛山一）某班同学利用国行社会践，[25,55]
的人群随机抽取 n 人
（
行了一次生活是否符合低碳念的，若生活符合低碳念的称“低碳族”，否称“非低碳族”，得到如下表和各年段人数率分布直方：
（Ⅰ）全率分布直方并求n 、 a 、p的；（Ⅱ）略
7.下甲是某市当地干部的月收入情况后画出的本率分布直方，
已知甲中从左向右第一的数4000．在本中月收入在[1000，1500），[1500 ，2000），[2000，2500），[2500，3000），[3000 ，3500），[3500，4000]的人数依次 A 1、A 2、⋯、A 6．乙是甲中月工收入在一定范内的人数的算法流程，本的容量n= _________ ；乙出的 S= _________ ．（用数字作答）
8.了了解某地区高三学生的身体育情况，抽了地区
100 名年 17.5 ～ 18 的男生体重（ kg），得到率分
布直方如下：根据上可得100 名学生中体重在［ 56.5，
64.5）的学生人数是.
9.某班 50 名学生在一次百米中，成全部介于13 秒与19 秒之，将果按如下方式分成六：第一，成
大于等于13 秒且小于14 秒；第二，成大于等于14 秒且小于 15 秒；⋯⋯第六，成大于等于18 秒且小于等于 19 秒 .右是按上述分方法得到的率分布直方.
成小于17 秒的学生人数占全班人数的百分比x, 成大于等于15 秒且小于17 秒的学生人数y，从率
分布直方中可分析出x 和 y 分.
10.在学校开展的合践活中，某班行了小制作比，作品上交 5 月 1 日至 30 日，委会把同学上交作品的件数按 5 天一分，
制了率分布直方（如所示），已知从左到右各方形高的
比
2∶ 3∶ 4∶ 6∶ 4∶ 1，第三的数12，解答下列：
（1）本次活共有多少件作品参加比？
（2）哪上交的作品数量最多？有多少件？
（3）比，第四和第六分有10 件、 2 件作品，两哪率高？
11.了了解高一学生的体能情况，某校抽取部分学生
行一分跳次数，将所得数据整理后，画出
率分布直方（如所示），中从左到右各小方形
面之比2∶ 4∶ 17∶ 15∶ 9∶ 3，第二小数12. （1）第二小的率是多少？本容量是多少？
（2）若次数在 110 以上（含 110 次）达，估学校全体高
一学生的达率是多少？。