上海徐汇2014学年第一学期初二数学期中考试试题
2022-2023学年上海市徐汇区西南模范中学初二数学第一学期期末试卷及解析
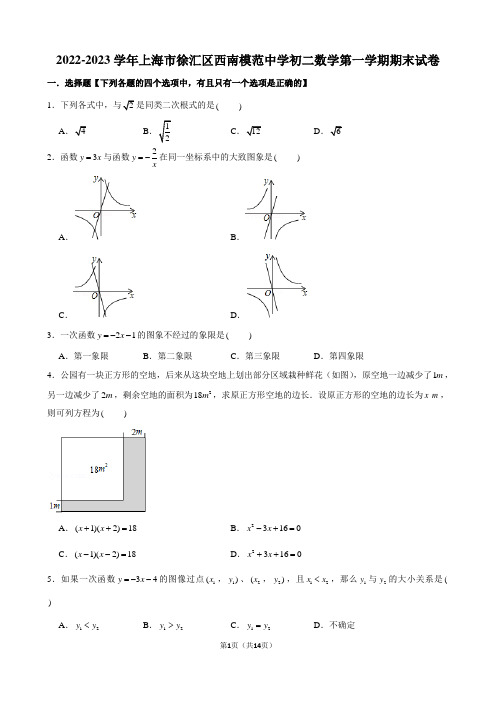
2022-2023学年上海市徐汇区西南模范中学初二数学第一学期期末试卷一．选择题【下列各题的四个选项中，有且只有一个选项是正确的】 1．下列各式中，与2是同类二次根式的是( ) A ．4B ．12C ．12D ．62．函数3y x =与函数2y x=-在同一坐标系中的大致图象是( )A ．B ．C ．D ．3．一次函数21y x =--的图象不经过的象限是( ) A ．第一象限B ．第二象限C ．第三象限D ．第四象限4．公园有一块正方形的空地，后来从这块空地上划出部分区域栽种鲜花（如图），原空地一边减少了1m ，另一边减少了2m ，剩余空地的面积为218m ，求原正方形空地的边长．设原正方形的空地的边长为x m ，则可列方程为( )A ．(1)(2)18x x ++=B ．23160x x -+=C ．(1)(2)18x x --=D ．23160x x ++=5．如果一次函数34y x =--的图像过点1(x ，1)y 、2(x ，2)y ，且12x x <，那么1y 与2y 的大小关系是()A ．12y y <B ．12y y >C ．12y y =D ．不确定6．如图，已知ABC ∆中，90ACB ∠=︒，CH ，CM 分别是斜边AB 上的高和中线，则下列结论不正确的是( )A ．AM BM =B ．90AHC ∠=︒ C ．ACH B ∠=∠D ．MC BC =二．填空题7．化简：50= ． 8．方程2x x =的根是 ．9．函数22y x =-的定义域是 ．10．在实数范围内分解因式：231x x -+= ． 11．如果函数1()2f x x=-，那么f （3）= ．12．在平面直角坐标系中，如果点(3,)A m -在一次函数483y x =+图像上，那么点A 和坐标原点的距离是 ．13．在平面内，经过点P 且半径等于1的圆的圆心的轨迹是 ．14．已知关于x 的方程20x x m +-=的一个根为2，那么它的另一个根是 ．15．某产品原价每件价格为x 元，经过两次降价，且每次降价的百分率相同，均为30%，现在每件售价为y 元，那么y 与x 之间的函数关系式为 ．16．如图，在ABC ∆中，AD 平分角BAC ，6AB =，4AC =，ABD ∆的面积为9，则ADC ∆的面积为 ．17．已知：如图，ABC ∆中，45ABC ∠=︒，H 是高AD 和BE 的交点，12AD =，17BC =，则线段BH 的长为 ．18．给出如下定义：在平面直角坐标系xOy 中，已知点1(,)P a b ，2(,)P c b ，3(,)P c d ，这三个点中任意两点间的距离的最小值称为点1P ，2P ，3P 的“最佳间距”． 例如：如图，点1(1,2)P -，2(1,2)P ，3(1,3)P 的“最佳间距”是1．已知点(0,0)O ，(3,0)A -，(3,)B t -．若点O ，A ，B 的“最佳间距”是2，则t 的值为 ．三、解答题19．计算：121275123+-． 20．解方程：21122y y -+=．21．为了解决某贫困地区两村村民子女就近入学问题，某爱心企业捐资助学，计划新建一所学校，如图AB ，AC 表示两条公路，点M ，N 表示两个村庄，学校的位置需满足三个条件：①到两条公路的距离相等；②到两个村庄的距离相等；③在BAC ∠的内部．请运用尺规作图确定学校的位置，不写作法，保留作图痕迹并写明结论．22．某新建火车站站前广场有一块长为20米，宽为8米的矩形空地，计划在其中修建两块相同的矩形绿地，它们的面积之和为56米2，两块绿地之间及周边留有宽度相等的人行通道（如图所示），问人行通道的宽度是多少米？23．一辆汽车在某次行驶过程中，油箱中的剩余油量y （升)与行驶路程x （千米）之间是一次函数关系，其部分图象如图所示．（1）求y 关于x 的函数关系式；（不需要写定义域）（2）已知当油箱中的剩余油量为8升时，该汽车会开始提示加油，在此次行驶过程中，行驶了500千米时，司机发现离前方最近的加油站有30千米的路程，在开往该加油站的途中，汽车开始提示加油，这时离加油站的路程是多少千米？24．如图，已知AB BC ⊥，DC BC ⊥，垂足分别是点B 、C ，点E 是线段BC 上一点，且AE ED ⊥，AE ED =，如果3BE =，11AB BC +=，求AE 的长．25．如图，ABC ∆中，D 为BC 边上一点，BE AD ⊥，交AD 的延长线于点E ，CF AD ⊥于F ，BE CF =． （1）求证：点D 为BC 的中点； （2）若2BC AC =，求证：AF ED =．26．如图，在平面直角坐标系xOy 中，直线135:44l y x =-+与x 轴交于点A ，直线2:2l y x b =+与x 轴交于点B ，且与直线1l 交于点(1,)C m -． （1）求m 和b 的值； （2）求ABC ∆的面积；（3）若将直线2l 向下平移(0)t t >个单位长度后，所得到的直线与直线1l 的交点在第一象限，直接写出t 的取值范围．27．已知四边形ABCD是边长为3的正方形，点E在边AD所在的直线上，联结CE，以CE为边，作正方形CEFG（点D，点F在直线CE的同侧），联结BF．（1）如图1，当点E与点A重合时，请直接写出BF的长；（2）如图2，当点E在线段AD上时，1AE=；①求点F到AD的距离；②求BF的长；（3）若65BF=，求AE的长．答案与解析一．选择题【下列各题的四个选项中，有且只有一个选项是正确的】1．2=，因此选项A 不符合题意；B 符合题意；=，因此选项C 不符合题意；不是同类二次根式，因此选项D 不符合题意；故选：B ． 2．解：2y x =，20>，∴图象经过一、三象限，函数2y x=-中系数小于0，∴图象在二、四象限．故选：B ．3．解：一次函数21y x =--中， 20-<，10-<，∴函数图象经过第二、三、四象限，不经过第一象限．故选：A ．4．解：设原正方形的边长为xm ，依题意有 (1)(2)18x x --=，故选：C ．5．解：30k =-<， y ∴随x 的增大而减小，又12x x <，12y y ∴>．故选：B ．6．解：90ACB ∠=︒，CM 是斜边AB 上的中线， 12AM BM CM AB ∴===，故A 选项正确，不符合题意；90ACH BCH ∠+∠=︒， CH 分别是斜边AB 上的高线， CH AB ∴⊥，90AHC BHC ∴∠=∠=︒，故B 选项正确，不符合题意； 90B BCH ∴∠+∠=︒，ACH B ∴∠=∠，故C 选项正确，不符合题意；只有当30A ∠=︒时，12BC AB MC ==，故D 选项错误，符合题意． 故选：D ． 二．填空题7．=故答案为 8．解：20x x -=， (1)0x x -=， 0x ∴=或10x -=， 10x ∴=，21x =．故答案为10x =，21x =． 9．解：根据题意得：220x -， 解得1x ． 故答案为：1x ．10．解：原式299(3)144x x =-++-223()2x =--(x x =．故答案为：(x x -．11．解：f （3）2=，故答案为：2．12．解：将点(3,)A m -代入一次函数483y x =+得4(3)843m =⨯-+=，∴点A 和坐标原点的距离是22345+=．故答案为：5．13．解：在平面内，经过点P 且半径等于1的圆的圆心的轨迹是以点P 为圆心，1为半径的圆． 故答案为：以点P 为圆心，1为半径的圆． 14．解：1a =，1b =，方程的一个根为2，∴方程的另一个根是12231b a --=--=-． 故答案为：3-．15．解：由题意可得：2(130%)0.49y x x =-=． 故答案为：0.49y x =．16．解：作DE AB ⊥于E ，DF AC ⊥于F ，AD 平分角BAC ，DE AB ⊥，DF AC ⊥， DE DF ∴=，ABD ∴∆的面积：ADC ∆的面积:AB AC =， ABD ∆的面积为9，ADC ∴∆的面积为6，故答案为：6．17．解：45ABC ∠=︒，AD BC ⊥，BE AC ⊥，AD BD ∴=，90ADB BEA ∠==︒．2AHE ∠=∠，1290∠+∠=︒，390AHE ∠+∠=︒，13∴∠=∠（等角的余角相等）在ADC ∆和BDH ∆中， 31AD BDADC BDH ∠=∠⎧⎪=⎨⎪∠=∠⎩， ()ADC BDH ASA ∴∆≅∆，17BC =，12AD =， 17125CD ∴=-=，在Rt ACD ∆中，2213AC AD CD =+=， 13BH AC ∴==．故答案为13．18．解：点(0,0)O ，(3,0)A -，(3,)B t -． OAB ∴∆是直角三角形，90OAB ∠=︒，当33y -时，点O ，A ，B 的“最佳间距”是||3t AB =，当3y >或3<-时，3AB >，点O ，A ，B 的“最佳间距”是3OA =，∴点O ，A ，B 的“最佳间距”为3．故答案为：3． 三、解答题19．解：121275123435343=53=20．解：方程化为一般式为2220y y --=， 1a =，2b =-，2c =-，△2(2)41(2)120=--⨯⨯-=>，2422313b b ac y -±-±===±所以113y =+213y =-21．解：点P 为线段MN 的垂直平分线与BAC ∠的平分线的交点，则点P 到点M 、N 的距离相等，到AB 、AC 的距离也相等，作图如下：22．解：设人行通道的宽度为x 米，这每块矩形绿地的长为2032x-米、宽为(82)x -米(04)x <<， 根据题意得：2032(82)562xx -⨯⨯-=， 整理得：2332520x x -+=， 解得：12x =，2263x =（不合题意，舍去）． 答：人行通道的宽为2米．23．解：（1）设该一次函数解析式为y kx b =+， 将(150,45)、(0,60)代入y kx b =+中， 1504560k b b +=⎧⎨=⎩，解得：11060k b ⎧=-⎪⎨⎪=⎩， ∴该一次函数解析式为16010y x =-+． （2）当160810y x =-+=时， 解得520x =．即行驶520千米时，油箱中的剩余油量为8升． 53052010-=千米，油箱中的剩余油量为8升时，距离加油站10千米．∴在开往该加油站的途中，汽车开始提示加油，这时离加油站的路程是10千米．24．解：AB BC ⊥，DC BC ⊥，垂足分别是点B 、C ，90B C ∴∠=∠=︒． 90A AEB ∴∠+∠=︒，AE DE ⊥，90AED ∴∠=︒，180AEB AED DEC ∠+∠+∠=︒， 90AEB DEC ∴∠+∠=︒， A DEC ∴∠=∠，在ABE ∆和ECD ∆中，A DECB CAE ED ∠=∠⎧⎪∠=∠⎨⎪=⎩， ()ABE ECD AAS ∴∆≅∆，AB CE ∴=，BC BE CE BE AB =+=+，211AB BC AB BE ∴+=+=，3BE =，4AB ∴=．25．证明：（1）BE AD ⊥的延长线于E ，CF AD ⊥于F ， 90CFD BED ∴∠=∠=︒，在BED ∆和CFD ∆中，90CFD BED CDF BDEBE CF ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩， ()CDF BDE AAS ∴∆≅∆CD BD ∴=．D ∴为BC 的中点；（2）2BC AC =，CD DB =，CA CD ∴=，CF AD ⊥，AD DF ∴=，CDF BDE ∆≅∆，DF DE ∴=，AF DE ∴=．26．解：（1）把点(1,)C m -代入54得，35(1)244m =-⨯-+=， (1,2)C ∴-， 把(1,2)C -代入2y x b =+得，22b =-+，解得4b =；（2）直线135:44l y x =-+和与x 轴交于点A ，直线2:24l y x =+与x 轴交于点B ， 5(3A ∴，0)，(2,0)B -， 113AB ∴=， 111112233ABC S ∆∴=⨯⨯=； （3）将直线2l 向下平移(0)t t >个单位长度后，所得到的直线的解析式为24y x t =+-， 直线135:44l y x =-+和与y 轴交点为5(0,)4， 把5(0,)4代入24y x t =+-得，544t -=，解得114t =， 把5(3A ，0)代入24y x t =+-得，10403t +-=，解得223t =， ∴平移后所得到的直线与直线1l 的交点在第一象限，t 的取值范围是112243t <<． 27．解：（1）作FH AB ⊥于H ，如图1所示：则90FHE ∠=︒，四边形ABCD 和四边形CEFG 是正方形，3AD CD ∴==，EF CE =，90ADC DAH BAD CEF ∠=∠=∠=∠=︒， FEH CED ∴∠=∠，在EFH ∆和ECD ∆中，90FHE EDC FEH CEDEF CE ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩，()EFH ECD AAS ∴∆≅∆，3FH CD ∴==，3AH AD ==，6BH AB AH ∴=+=，BF ∴=；（2）过F 作FH AD ⊥交AD 的延长线于点H ，作FM AB ⊥于M ，如图2所示：则FM AH =，AM FH =，①3AD =，1AE =，2DE ∴=，同（1）得：()EFH CED AAS ∆≅∆， 2FH DE ∴==，3EH CD ==，即点F 到AD 的距离为2；②325BM AB AM ∴=+=+=，4FM AE EH =+=， 22225441BF BM FM ∴=+=+=；（3）分三种情况：①当点E 在边AD 的左侧时，过F 作FH AD ⊥交AD 于点H ，交BC 于K ．如图3所示：同（1）得：EFH CED ∆≅∆，3FH DE AE ∴==+，3EH CD ==， 6FK AE ∴=+，在Rt BFK ∆中，3BK AH EH AE AE ==-=-， 由勾股定理得：222(3)(6)(65)AE AE -++=， 解得：2AE =或5AE =-（舍去），2AE ∴=；②当点E 在边AD 的右侧时，过F 作FH AD ⊥交AD 的延长线于点H ，交BC 延长线于K ，如图4所示：同（1）得：EFH CED ∆≅∆，3FH DE AE ∴==-，3EH CD ==， 33FK FH HK AE AE ∴=+=-+=， 在Rt BFK ∆中，3BK AH AE AD AE ==-=-， 由勾股定理得：222(3)(65)AE AE -+=， 解得：7AE =或4-（舍去）．③当点E 在AD 上时，可得：22(6)(3)65AE AE -++=， 解得5AE =或2-，53>不符合题意．综上所述：AE 的长为2或7．。
郑州一中教育集团2013—2014学年上学期期中考试初二数学试题(含答案)
郑州一中教育集团2013—2014学年上学期期中考试八年级数学试题说明： 1、本试卷分第Ⅰ卷（选择题、填空题）和第Ⅱ卷（解答题）满分100分，考试时间90分钟。
2、将第Ⅰ卷的答案填在答题卷的答题表中.第Ⅰ卷一、选择题：（每小题3分，共24分。
下列各小题均有四个答案，其中只有一个是正确的）1.下列说法正确的是（）家的距离y与时间x的关系的大致图象是（）A. B. C. D.8.已知一次函数y=kx﹣k，若y随x的增大而减小，则该函数的图象经过（）A．第一，二，三象限B．第一，二，四象限C．第二，三，四象限D．第一，三，四象限二．填空题（本题共8小题，每小题3分，共24分）（2013—2014学年上期期中考试答案卷八年级数学二、填空题:（本题共8小题，每题3分，共24分）9、_________ 10、_______ 11、________12、________1314、________三、解答题：（本题共6小题，17题6分，18、19、20题每题8分，21题10分，22题12分，共52分）17.计算（6分）：45)53)(51(52452-++++-+526+20.（8分）如图是一个没有上盖的圆柱形食品盒，一只蚂蚁在盒外表面的A处，它想吃到盒内表面对侧中点B处的食物，已知盒高10cm，底面圆周长为32cm，A距下底面3cm．求出蚂蚁需要爬行的最短路程的长。
21．（10分）为响应2013年的“郑州慈善日”活动，郑州一中“慈善小组”筹集到1240元善款，全部用于购买水果和蛋糕，然后到福利院送给老人，决定购买巧克力蛋糕和普通蛋糕共20盒，剩下的钱用于购买水果，要求购买水果的钱数不少于180元但不超过240元．已知巧克力蛋糕比普通蛋糕每盒贵15元，若用300元恰好可以买到2盒巧克力蛋糕和4盒普通蛋糕．（1）请求出两种口味的蛋糕每盒的价格；（2）设买巧克力蛋糕x盒，买水果共用了w元．①请求出w关于x的函数关系式；②求出购买两种蛋糕的所有可能方案，并说明哪一种方案使购买水果的钱数最多．2013—2014学年上期期中考试试题答案八年级数学答案四、填空题:（本题共8小题，每题3分，共24分）9、 36 10、6- 11、 2 12、 四 13、x x y 2y 32-=-=或14、 -1≤k ≤ 3 15、 29 16、43- 三、解答题：215515345341525)51(5353151125.172--=++--+-+-=++-++++-=解：原式 ............4分..............6分三、（1）n n -+1 ............2分（2）99-1002-31-2+++= 原式 .............4分=10-1=9 .............5分（3） ）（原式2011-20133-51-321+++= ..............7分 21201321)12013(21-=-=..............8分 19.（1）图略 . .......3分 （2） 由图可知 AB=10，AC=5，BC=55222AC AB BC +=∴ ∴A B C ∆为直角三角形 ......6分 （3） ABC ∆为直角三角形 ∴AC AB S ABC ∙=∆21=25 .......8分20.解：如图为圆柱形食品盒侧面展开图作点B 关于直线PQ 的对称点B '，AC ⊥BC 于点C ， .............3分 则B B '=10-3+5=12cm AC=3221⨯=16cm 在B AC Rt '∆中,222C B AC B A '+='∴2222201612=+='B A .............7分∴ B A '=20cm 即蚂蚁爬行最短路程20cm .............8分21.解：（1）设普通蛋糕每盒x 元，则巧克力蛋糕每盒（x+15）元 由题意知： 2（x+15）+4x=300x=45 ∴x+15=60所以巧克力蛋糕每盒60元，普通蛋糕每盒45元 .............3分 （2）①w=1240-60x-45（20-x ） 即w=340-15x ..............5分② 180≤w ≤240，∴326≤x ≤3210 由题意知x 为正整数，∴x=7,8,9,10所以买两种蛋糕的方案为：1，买7盒巧克力蛋糕，13盒普通蛋糕2，买8盒巧克力蛋糕，12盒普通蛋糕 3，买9盒巧克力蛋糕，11盒普通蛋糕4，买10盒巧克力蛋糕，10盒普通蛋糕 .............9分-15<0,x 越小，y 越大， ∴x=7时，y 最大所以方案1买7盒巧克力蛋糕，13盒普通蛋糕使购买水果钱数最多 .............10分 22.(1)解方程组{y x y x ==-263得{612==x yOA<OB ∴0A=6，0B=12 ∴A(6，0)，B(0，12)设直线AB 解析式为y=kx+b ，则有6k+b=0，b=12 ∴k=-2，b=12 ∴直线AB 解析式为y=-2x+12点C 是直线y=2x 与y=-2x+12 令-2x+12=2x ，x=3，此时y=6 ∴C(3,6）...........4分（2）设D(a ，2a) 且a>0 OD=52 ∴222)52()2(=+a a a>0 ∴a=2∴D(2，,4）设直线AD 的解析式为y=11b x k +，则有{6421111=+=+b k b k ，解得{1611-==k b∴直线AD 解析式为y=-x+6 (8)分（3）假设存在直线AD 上一点P 使∆POD 与∆AOC 面积相等 设P （m ，-m+6）易知126421,186621=⨯⨯==⨯⨯=∆∆AOD AOC S S 当-m+6>0时，301812=+=+=∆∆∆AO D PO D PO A S S S ∴21(-m+6)⨯6=30∴m=-4 ∴P（-4,10）当-m+6<0，61218=-=-=∆∆∆AO D PO D PO A S S S ，∴66621=⨯+-m ∴m=8 ∴P(8，-2) 综上，存在P （-4,10）或(8，-2) 满足条件。
2014—2015学年度第一学期期中测试初二数学试卷(1)(新人教版)
2014—2015学年度第一学期期中测试初二数学试卷（100分钟）试卷满分：第Ⅰ卷30分 第Ⅱ卷70分 共100分第Ⅰ卷（机读卷 选择题30分） 一、选择题（每题3分，共30分）1．多项式b a c ab 33812-的公因式是（ ） A ． 24ab B ．abc 4- C ．24ab - D ．ab 42．如图，将两根钢条AA′，BB′ 的中点O 钉在一起，使AA′，BB′ 能绕点O 自由转动，就做成一个测量工具，测A′B′ 的长即等于内槽宽AB ，那么判定△OAB ≌△OA′B′的理由是（ ）．A ．边角边B ．角边角C ．边边边D ．斜边直角边3．若3x =-是分式方程312axx=-的解，则a 的值为（ ） A. 95- B. 95 C. 59 D. 59-4. 如图，△ABC≌△CDA，∠BAC＝85°，∠B＝65°， 则∠CAD 度数为（ ）A. 30°B. 65°C. 40°D. 85°5．解分式方程12133x x x+-=，去分母后所得的方程是（ ） A. 13(21)3x -+= B. 13(21)3x x -+= C. 13(21)9x x -+= D. 1639x x -+= 6．下列变形正确的是（ ） A ．11a ab b+=+B ．11a ab b--=--C ．221a b a b a b-=--D ．()()221a b a b --=-+7. 如图，已知△ABC 的六个元素，则下列甲、乙、丙三个三角形中和△ABC 全等的图形是( )A ．甲B ．乙与丙C ．丙D ．乙ＤＣ Ａ ＢE DCBA 8．下列分解因式错误．．的是（ ） A ．222)(2y x y xy x -=+- B.322()x x x x x x -+=- C ．)(22y x xy xy y x -=- D.))((22y x y x y x +-=- 9．某饭馆用320元钱到商场去购买“白猫”洗洁精，经过还价， 每瓶便宜0.5元，结果比用原价买多买了20瓶，求原价每瓶 多少元？设原价每瓶x 元，则可列出方程为（ ）A. 320320200.5x x -=-B. 3203200.520x x -=- C.320320200.5x x -=- D. 3203200.520x x -=- 10. 在数学活动课上，小明提出这样一个问题：如右图, ∠B =∠C = 90︒, E 是BC 的中点, DE 平分∠ADC, ∠CED = 35︒, 则∠EAB 的度数是 ( ) A ．65︒ B ．55︒ C ．45︒ D ．35︒第Ⅱ卷 （非机读卷 共70分）二、填空题（每小题2分，8个小题，共16分）11.自从扫描隧道显微镜发明后，世界上便诞生了一门新学科，这 就是“纳米技术”，已知52个纳米的长度为0.000000052米,用科 学记数法表示这个数为__ 米 12.计算:=÷-----322324)()2(b a c b a13.能使分式122--x x x 的值为零的所有x 的值是14. 如图，已知AB ⊥BD , AB ∥ED ，AB =ED ，要 证明ΔABC ≌ΔEDC ，若以“SAS”为依据， 还要添加的条件为_________；若添加条件AC =EC ，则可以用______方法判定全等. 15.关于x 的方程211x a x +=-的解是正数，则a 的取值范围是16.根据下列已知条件，能确定△ABC 的大小和形状的是 ①AB ＝3，BC ＝4，AC ＝5 ②AB ＝4，BC ＝3，∠A ＝30º ③∠A ＝60º，∠B ＝45º，AB ＝4 ④∠C ＝90º，AB ＝6，AC =5 17. 当n=_ ___ 时，x 2＋(n+3)x ＋25是完全平方式 18．在平面直角坐标系中，已知点A （1，2），B （6，5）， C （5，2），存在点E ，使△ACE 和△ACB 全等，写出所有满足条件 的E 点的坐标E D CBA三、计算题（其中19题，每小题4分；20、21题每题5分，共18分） 19．分解因式：（1）92-x （2）y xy y x 442+-20．先化简再求值：xx x x x x x 1)121(22÷+---+，其中3x =．21．解方程： 512552x x x+=--四、列方程解应用题（本题5分）22．八年级学生去距学校10km 的博物馆参观，一部分学生骑自行车先走，过了20min 后，其余学生乘汽车出发，结果他们同时到达。
2018-2019学年上海市徐汇区实验西校八年级上学期期中数学试卷
上海市2018实验西校八年级期中试卷一、选择题1、下列二次根式中，√2的同类二次根式是 （ ）【A 】√4 【B 】√2x 【C 】√29 【D 】√12 【答案】 D2、二次根式√a 2+2ab +b 2，√26xy ，√1p−1，√25中，最简二次根式共有 （ ）【A 】1个 【B 】2个 【C 】3个 【D 】4个 【答案】 B3、下列式子一定成立的是 （ ）【A 】√2+√3=√5 【B 】√x 2−4=√x +2∙√x −2 【C 】√4a 3=2a √a 【D 】√4925=235【答案】 D4、下列命题中，真命题是（ ）【A 】有两边和一角对应相等的两个三角形一定全等【B 】有两角及其中一角的平分线对应相等的两个三角形一定全等 【C 】两个等边三角形一定全等【D 】等腰三角形的高、角平分线、中线三线合一 【答案】 B二、填空题5、√a −b 的有理化因式的是 【答案】 √a −b6、边长为(2−√3)cm 的正方形面积是 cm 2 【答案】7−4√37、如果代数式√2x+1有意义，那么x 的取值范围是【答案】x >−128、关于x 的方程(a −1)x a 2+1−3x +2=0是一元二次方程，则a 的值是【答案】-19、如果最简根式√3m 2m+n与√2m −n 是同类二次根式，那么mn 的值为 【答案】-410、在实数范围内因式分解：3y 2−y −1=【答案】)6131)(6131(3+---y y 11、如图，AC 、BD 相交于O ，AB=DC ，要使△AOB ≅△DOC ，还需添加一个条件，这个条件可以是： 【答案】∠B=∠C12、如图，在△ABC 中，△C=50°，将△ABC 绕着点A 顺时针旋转到△ADE 的位置，此时，点E 正好落在边BC 上，那么△BED= 度 【答案】80°13、不等式(√5−2)x <3的解集是 【答案】x <3√5+614、有一件商品，按原价的定价连续两次打折扣，每次折扣相同，原定价是75元，打了两次折扣后的售价是48元，则每次折扣是上次定价的 折。
上海徐汇中学2014学年第一学期初二数学期中考试试题
页眉内容试卷、教案、课件、论文、素材徐汇中学2013学年第一学期初二数学期中考试试题一、填空题：（每空2分，共36分）1、4的平方根是____________，827-的立方根是____________。
2x 的取值范围是____________。
3、若最简二次根式ba b +=____________。
4、化简：若a ＜0。
5，=____________。
6、若方程2(1)10m x mx ---=是一元二次方程，那么m 的取值范围是____________。
7、方程2(1)9x -=的解为____________，方程(1)3(1)x x x +=+的解为____________。
8、关于x 的方程220mx x m m +++=有一根是零，那么m =____________。
9、在实数范围内因式分解：2221x x --=________________，4232x x -+=________________。
页眉内容试卷、教案、课件、论文、素材12题AB CD13题ABCDE10、将命题“全等三角形的面积相等”改写为“如果……，那么……”的形式为_________________________________________。
11、某学校4月份的水电费为a元，计划5、6两个月的水电费平均比上月降低10%，那么6月份的水电费预计____________元。
12、如图，已知AC BD=，要使ABC DCB∆≅∆，只需增加一个条件是________________。
13、如图，ABC∆中，已知90C∠=︒，DE是AB的垂直平分线，若:1:2DAC DAB∠∠=，那么BAC∠=________度。
14、已知a、b、c均为实数，且4a b+=，2210c ab-=-，那么abc=__________。
二、选择题：（本大题共4题，每题3分，共12分）15、在下列各组根式中，属于同类二次根式的是…………………………………（）页眉内容试卷、教案、课件、论文、素材A、页眉内容试卷、教案、课件、论文、素材18题ABCDE16、下列方程中，无实数解的是……………………………………………………（ ）A 、213904x x -+= B 、23520x x --=C 、2290y y -+= D2)y y -=17、一元二次方程220x px q ++=的两根为1-和2，那么二次三次式22x px q ++可分解为……………………………………………………………………………………（ ）A 、(1)(2)x x +-B 、(21)(2)x x +-C 、2(1)(2)x x -+D 、2(1)(2)x x +-18、如图，ABC EDB ∠=∠，2AB DB DE ==，C 是BD 中点则下列结论：①AC BE =，②AC BE ⊥，③A EBD ∠=∠， ④BC DE =中正确的个数是……………………………（ ） A 、1个 B 、2个 C 、3个 D 、4个 三、（本大题共5题，每题5分，共25分）19+页眉内容试卷、教案、课件、论文、素材21、解方程：(31)(2)20x x -+= 22、用配方法解方程22470x x --=23、已知：5a b +=-，1ab =，求的值。
2014——2015学年度第一学期八年级数学期中考试卷(含答案)
2014——2015学年度第一学期 八年级数学期中考试卷（含答案）（考试时间：100分钟 满分：120分）一、选择题：（每小题3分，共42分）下列各题都有A 、B 、C 、D 四个答案供选择，其中只有一个答案是正确的，请把认为正确1、4的算术平方根是A ． 2B ． 2-C ． 2±D ． 2±2、与数轴上的点成一一对应关系的数是A ． 有理数B ． 无理数C ． 实数D ． 整数 3、下列从左边到右边的变形，属于因式分解的是A ． 1)1)(1(2-=-+x x x B ． 1)2(122+-=+-x x x xC ． )4)(4(422y x y x y x -+=-D ． 22)3(96-=+-x x x4、下列命题中是真命题的是A ．三角形的内角和为180°B ．同位角相等C ．三角形的外角和为180°D ．内错角相等 5、使式子32+x 有意义的实数x 的取值范围是A ．32>x B ． 23>x C ． 23-≥x D ． 32-≥x6、在实数73，1+π，4，3.14，38，8，0， 11.21211211中，无理数有A ． 2个B ． 3个C ． 4个D ． 5个7、一个正方形的边长增加了cm 2，面积相应增加了232cm ，则这个正方形的边长为 A ． 6cm B ． 5cm C ． 8cm D ． 7cm8、计算：()20132013125.08-⨯等于A ． 1-B ． 1C ． 2013D ． 2013- 9、下列条件中，不能证明△ABC ≌△'''C B A 的是 A ．''''C A AC B B A A =∠=∠∠=∠，，学校：班别： 姓名： 座号：………………………………………………………………装………………订………………线………………………………………………得分 B'C BB ．''''B A AB B B A A =∠=∠∠=∠，，C ．'''''C A AC A A B A AB =∠=∠=，，D ．'''''C B BC B A AB A A ==∠=∠，， 10、下列算式计算正确的是A ．523a a a =+B ．623a a a =⋅C ．923)(a a =D ． a a a =÷2311、估计15的大小在A ． 2和3之间B ． 3和4之间C ． 4和5之间D ． 5和6之间12、若(x+a)(x-5)展开式中不含有x 的一次项,则a 的值为A ． 5-B ． 5C ． 0D ． 5± 13、如右图，△ABC ≌△EDF ，DF ＝BC ，AB=ED ，AF ＝20，EC ＝10，则AE 等于 A ． 5 B ． 8 C ．10 D ． 15 14、如果则的值分别是A ． 2 和 3B ． 2和－3C ． 2和D ．二、填空题：（每小题4分，共16分） 15、计算:=⨯-2016201020132________。
上海市闵行区2024—-2025学年上学期八年级期中数学试题(无答案)
2024学年第一学期期中考试八年级数学试卷（考试时间：90分钟满分100分）题号一二三（19-22）四（23-24）五（25）总分分值1824321610100得分一、选择题：（本大题共6题，每题3分，满分18分）1）ABCD2的一个有理化因式是（ ）AB ．CD3．下列等式正确的是（ ）A ．BCD4．方程的根是（）A ．，B．，C ．，D ．，5．下列说法正确的是（）A ．等腰三角形两腰上的中线一定相等B ．方程一定无实数根（a 为任意实数）C ．在同一平面内垂直于同一条直线的两条直线可能有交点D ．两边及一个角对应相等的两个三角形一定全等6．在平面直角坐标系中，，，，点D 是平面直角坐标系内任意一点，若以A 、B 、D 为顶点的三角形与全等（点D 与点C 不重合），那么符合要求的点D 的个数有（ ）A ．2个B ．3个C ．4个D ．5个二、填空题：（本大题共12题，每题2分，满分24分）7有意义的实数x 的取值范围是____________．8____________．1+1-+=132=3.14π=-÷+=-(2)(3)6x x -+=12x =23x =-12x =-23x =14x =-23x =14x =23x =-2x a =-(0,4)A (3,0)B (0,2)C -ACB △)0x >=9中是最简二次根式的有____________个．10．方程的根是____________．11．已知关于x 的一元二次方程有两个相等的实数根，那么m 的值为____________．12的解集是____________．13．在实数范围内分解因式：____________．14．已知一个一元二次方程有一个根是1，且它的一次项系数是，写出一个符合要求的方程：____________．15．已知当时，二次三项式的值是5，那么当时，这个二次三项式的值是____________．16．2024年10月1日，某高速路检票口车流量约500万辆次，10月2日该高速路检票口的车流量减少．假设从3日、4日车流量有所增加且增长率相同，预计10月4日该高速路检票口车流量达到648万辆次，设10月3日、4日车流量的增长率为x ，那么可列方程为____________．17．定义一种运算，对于任意角和，，已知，的值是____________．18．如图，在四边形中，联结、．已知，，，的面积是____________．三、简答题：（本大题共4题，满分32分）19．（本题满分10分，其中每小题各5分）（1）计算：（2）计算：20．（本题满分10分，其中每小题各5分）（1）解方程：；（2）用配方法解方程：．21．（本题满分6分）212x x =-230x x m -+-=12x ->23x x --=3-2x =22x x a -+2x =-10%αβtan tan tan()1tan tan αβαβαβ++=-⋅tan 451︒=tan 60︒=tan105tan15︒⋅︒ABCD AC BD DBC DBA DAC ∠=∠=∠90BCA ∠=︒6AC =AB CB =+ADC △-+÷22(29)(6)x x -=-22410x x +-=已知：，求代数式的值．22．（本题满分6分）已知m 、n 为实数，且，求的值．四、解答题：（本大题共2题，满分16分）23．（本题共2小题，其中第（1）小题4分，第（2）小题4分，满分8分）如图，在中，点D 是边的中点，联结，且．E 是边上任意一点（不与点A 、C 重合），过点B 作，点F 落在的延长线上．（1）求证：；（2）联结，当时，求证：．24．（本题共2小题，其中第（1）小题3分，第（2）小题5分，满分8分）如图，（）是一张周长为36厘米的长方形纸片，设长方形纸片的长为x 厘米，将纸片的四个角各剪下一个边长为2厘米的正方形．（1）如果剪去四个角剩下的纸片的面积为，请用含有x 的式子表示（结果要求化简）；（2）如图，沿虚线将剪去四个角剩下的纸片折成一个无盖的长方体纸盒，如果所得的长方体纸盒的体积是48立方厘米，求的长．五、综合题；（本大题共1题，满分10分）25．（本题满分10分，第（1）小题3分，第（2）小题4分，第（3）小题3分）如图，在中，已知，，点A 在上，，，a =b =a ab b ++2222()(2)15m n m n ++-=22m n +ABC △AB CD AD CD =AC //BF AC ED AC BC ⊥CF 90CDE ∠=︒BF CF AC +=ABCD AD AB >AD 1S 1S AD ABC △90BAC ∠=︒AB AC =DE 90BDA ∠=︒90AEC ∠=︒点H 是边上的一个动点．（1）求证：；（2）如图①，当点H 是边的中点时，联结、，求的度数；（3）如图②，联结、，当，且时，设，请用含x 的代数式表示的度数．图①图②BC AD CE =BC DH HE HDE ∠AH HE AH HE ⊥CH CE =ABD x ∠=︒BAH ∠。
2022-2023学年度第一学期期中考试八年级数学试卷
2022/2023学年度第一学期期中考试八年级数学试题时间：100分钟分值：120分考试形式：闭卷命题人：审核人：一、选择题（本大题共有8小题，每小题3分，共24分．在每小题所给出的四个选项中，只有一项是符合题目要求的，请将正确选项的字母代号填写在答题卡相应位置上）1．下列四个图形中，是轴对称图形的为【▲ 】A ．B ．C ．D ．2．下列等式正确的是【▲ 】A ．±＝2B ．＝﹣2C ．＝﹣2D ．＝0.13．下列各组数中，能作为直角三角形三边长的是【▲ 】A．1，2，3 B．4，5，6 C．6，8，10 D．7，8，94．在联欢会上，有A、B、C三名选手站在一个三角形的三个顶点位置上，他们在玩“抢手绢”游戏，要求在他们中间放一个手绢，谁先抢到手绢谁获胜，为使游戏公平，则手绢应放的最适当的位置是在△ABC的【▲ 】A．三边垂直平分线的交点B．三边中线的交点C．三条角平分线的交点D．三边上高的交点5．如图，点P是∠BAC的平分线AD上一点，PE⊥AC于点E．已知PE＝10，则点P到AB的距离是【▲ 】A．15 B．12 C．5 D．10（第5题）（第6题）（第8题）（第11题）6．如图，DE是△ABC中边AC的垂直平分线，若BC＝18cm，AB＝10cm，则△ABD的周长为【▲ 】A．16cm B．28cm C．26cm D．18cm7．若等腰三角形一个外角等于100°，则它的顶角度数为【▲ 】A．20°B．80°C．20°或80°D．无法确定8．如图，在四边形ABCD中，AC平分∠BAD，BC＝CD＝10，AC＝17，AD＝9．则AB为【▲ 】A．19 B．12 C．21 D．26二、填空题（本大题共有8小题，每小题3分，共24分．不需写出解答过程，请将答案直接写在答题卡相应位置上）．9．16的算术平方根是▲ .10．已知+（n ﹣1）2＝0，则mn＝▲ .11．如图所示，是一块由花园小道围成的边长为12米的正方形绿地，在离C处5米的绿地旁边B 处有健身器材，为提醒居住在A处的居民爱护绿地，不直接穿过绿地从A到B，而是沿小道从A→C→B，请问你多走了▲ 米．12．如图，点D是BC上的一点，若△ABC≌△ADE，且∠B＝65°，则∠EAC＝▲ °．（第12题）（第14题）（第15题）（第16题）13．直角三角形的两边长为5、12，则斜边上的中线长为▲ ．14．如图，折叠长方形纸片ABCD，使点D落在边BC上的点F处，折痕为AE．已知AB＝6cm，BC＝10cm．则EC的长为▲ cm．15．如图，A、B两点在正方形网格的格点上，每个方格都是边长为1的正方形、点C也在格点上，且△ABC为等腰三角形，则符合条件的点C共有▲个．16．如图，在Rt△ABC中，∠C＝90°，点P为AC边上的一点，延长BP至点D，使得AD＝AP ＝5，当AD⊥AB时，过D作DE⊥AC于E，若DE＝4，则△BCP面积为▲ ．三、解答题（本大题共有10小题，共72分．请在答题卡指定区域内作答，解答时应写出文字说明、推理过程或演算步骤）17．（本题满分6分）求下列各式中x的值：（1）x2﹣25＝0；（2）（x﹣2）3﹣8＝0．18．（本题满分6分）已知2a﹣1的平方根为±3，3a+b﹣1的算术平方根为4．（1）求a、b的值；（2）求a+2b的算术平方根．19．（本题满分5分）如图，校园有两条路OA、OB，在交叉口附近有两块宣传牌C、D，学校准备在这里安装一盏路灯，要求灯柱的位置P离两块宣传牌一样远，并且到两条路的距离也一样远，请你用尺规作出灯柱的位置点P．（请保留作图痕迹）20．（本题满分5分）如图，B、C、D、E在同一条直线上，AB∥EF，BC＝DE，AB＝EF，求证：△ACB≌△FDE．（第19题）（第20题）21．（本题满分6分）如图，秋千OA静止的时候，踏板离地高一尺（AC＝1尺），将它往前推进两步（EB＝10尺），此时踏板升高离地五尺（BD＝5尺），求秋千绳索（OA或OB）的长度．22．（本题满分6分）如图，在长度为1个单位长度的小正方形组成的正方形中，点A、B、C在小正方形的顶点上．（1）在图中画出与△ABC关于直线l成轴对称的△AB′C′；（2）三角形ABC 的面积为▲；（3）在直线l上找一点P，使PB+PC的长最短．23．（本题满分8分）如图，已知在四边形ABCD中，点E在AD上，∠BCE＝∠ACD，∠BAC＝∠D，BC＝CE．（1）求证：AC＝CD．（2）若AC＝AE，∠ACD＝80°，求∠DEC的度数．24．（本题满分8分）如图，在△ABC中，AB、AC边的垂直平分线相交于点O，分别交BC边于点M、N，连接AM，AN．（1）若△AMN的周长为6，求BC的长；（2）若∠MON ＝30°，求∠MAN的度数；（3）若∠MON＝45°，BM＝3，BC＝12，求MN的长度．25．（本题满分10分）阅读理解：亲爱的同学们，在以后的学习中我们会学习一个定理：直角三角形斜边上的中线等于斜边的一半．即：如图1：在Rt△ABC中，∠ACB＝90°，若点D是斜边AB的中点，则CD＝AB．牛刀小试：（1）在图1中，若AC＝6，BC＝8，其他条件不变，则CD＝▲；活学活用：（2）如图2，已知∠ABC＝∠ADC＝90°，点E、F分别为AC、BD的中点，AC＝26，BD＝24．求EF的长；问题解决：（3）如图3，在Rt△ABC中，∠ACB＝90°，AB＝10，以AB为边在AB上方作等边三角形ABD，连接CD，求CD的最大值．26．（本题满分12分）阅读以下材料，完成以下两个问题．[阅读材料]已知：如图，△ABC（AB≠AC）中，D、E在BC上，且DE＝EC，过D作DF∥BA 交AE于点F，DF＝AC．求证：AE平分∠BAC．结合此题，DE＝EC，点E是DC的中点，考虑倍长，并且要考虑连接哪两点，目的是为了证明全等，从而转移边和角．有两种考虑方法：①考虑倍长FE，如图（1）所示；②考虑倍长AE，如图（2）所示以图（1）为例，证明过程如下：证明：延长FE至G，使EG＝EF，连接CG．在△DEP和△CEG中，，∴△DEF≌△CEG（SAS）．∴DF＝CG，∠DFE＝∠G．∵DF＝AC，∴CG＝AC．∴∠G＝∠CAE．∴∠DFE＝∠CAE．∵DF∥AB，∴∠DFE＝∠BAE．∴∠BAE＝∠CAE．∴AE平分∠BAC．问题1：参考上述方法，请完成图（2）的证明．问题2：根据上述材料，完成下列问题：已知，如图3，在△ABC中，AD是BC边上的中线，分别以AB，AC为直角边向外作等腰直角三角形，∠BAE＝∠CAF＝90°，AE＝AB，AC＝AF，AD＝3，求EF的长．。
上海市徐汇中学2023-2024学年高三上学期期中考试数学试题
= 2sin Asin Acos B + 2sin B sin Acos A = 2sin A(sin Acos B + sin B cos A)
= 2sin Asin ( A + B) ，
因为 0<C<
， AD = 3 ，E、F 分别为棱 PD、PA 的中点．
(1)求证： EF ∥ 平面 PBC； (2)求异面直线 PB 与 AE 所成的角．
18．已知函数
f
(x)
=
3 2
sin w x
+
3 2
cosw
x
（其中
w
>
0
）．
（1）若函数 f (x) 的最小正周期为 3p ,求w 的值，并求函数 f (x) 的单调递增区间；
π 2
，0 < C
=
π - 3A<
π 2
可得
π6π<
A<
4
，
所以
2 2
< cos A <
3 2
，1 2
< cos2
A<
3 4
，
由正弦定理得
c a
=
sin C sin A
=
sin 3A sin A
=
sin (2A +
sin A
A)
=
sin
2 Acos
A + cos sin A
2 Asin
参考答案：
【详解】 A = {1, 2, 3, 4,5}, B = {x 1 £ x £ 3} Þ A Ç B = {1, 2,3}
2022-2023学年上海市徐汇中学八年级上学期期中数学试题含答案
徐汇中学2022学年初二年级第一学期期中考试数学试卷一、选择题（本大题共6小题，每小题2分，满分12分）1.下列根式中，最简二次根式有（）个．，A.2 B.3 C.4D.52.下列各式中是--有理化因式的是（）A.+B.-C.D.3.下列二次三项式在实数范围内一定能因式分解的是（）A.223x x ++ B.222x x m -- C.22x x m-- D.22345x xy y -+4.12a =-，则a 的取值范围为（）A.12a ≥ B.102a ≤≤ C.12a ≤ D.一切实数5.已知ABC 为等腰三角形，已知它的两条边的长度分别是方程22750x x -+=的两个根，那么该三角形的周长是（）A.92或6 B.92C.5D.66.下列命题的逆命题是假命题的是（）A.直角三角形的两个锐角互余B.两直线平行，内错角相等C.三条边对应相等的两个三角形是全等三角形D .若x y =，则22x y =二、填空题（本大题共12小题，每空2分，满分24分）7.如果二次根式有意义，那么实数a 的取值范围是______．8.0)a >=__________．9.已知2a =则a 的倒数为__________．10.在实数范围内因式分解：225x x --=__________．11.52x ->的解集是___________．12.如果关于x 的一元二次方程2320x x m +-=没有实数根，那么m 的取值范围是_____．13.命题“同旁内角相等，两直线平行”是__________________（填“真”或“假”）命题﹒14.与x 的值是_____．15.如图，在ABC 中，AB AC =，CD AB ⊥，点D 为垂足，请写出A ∠与BCD ∠的数量关系__________．16.如图在△ABC 中，AB ＝AC ，BF ＝CD ，BD ＝CE ，∠FDE ＝70°，那么∠A ＝_____．17.如图，将△ABC 绕点A 顺时针旋转，使点C 落在边AB 上的点E 处，点B 落在点D 处，联结BD ，如果∠DAC ＝∠DBA ，那么∠BAC ＝___度．18.设a 的小数部分，b 为的小数部分，则21b a-值为__________．三、计算题（本大题共6小题，每小题5分，满分30分）19.计算：⎛- ⎝20.计算：÷21.解方程：2132-+=x x x 22.解方程：21(21)(12)02x x ---=23.解方程：23270x x --=24.已知x =,求代数式2623x x x -+-的值.四、解答题（本大题共4小题，25题8分，26题、27题6分，28题14分，满分34分）25.已知关于x 的方程x 2﹣（2m ﹣2）x ＋m 2＝0有两个实数根．（1）求m 的取值范围；（2）当m 取最大非零整数时，求方程的两个根．26.将进货单价为100元的商品按120元售出时，能卖出500件．已知这种商品每涨1元，其销售量就减少10件．如果希望能获得利润12000元，售价应定多少元？这时应进货多少件？27.如图，在ABC 中，CD 是C ∠的角平分线，2A B ∠=∠，求证：BC AC AD =+．28.如图，在ABC 中，点D 是射线AB 上的动点，满足CE CD ⊥且CE CD =．（1）如果CA CB =，90ACB ∠=︒，①当点D 在线段AB 上，如图1，线段BE 、AD 之间的数量关系是__________，位置关系是__________．②当点D 在线段AB 上，如图2，如果线段DE 与BC 相交于点F ，当BE BF =时，求ACD ∠的大小．③当点D 在线段AB 的延长线上，如图3，①的结论是否成立，为什么？（2）如果CA CB ≠，90ACB ∠≠︒，当点D 在线段AB 上运动时，尝试探究：当ABC ∠的度数是多少时，可得BE AD ⊥（点B 与E 重合除外）？请说明理由．徐汇中学2022学年初二年级第一学期期中考试数学试卷一、选择题（本大题共6小题，每小题2分，满分12分）【1题答案】C【2题答案】B【3题答案】B【4题答案】A【5题答案】D【6题答案】D二、填空题（本大题共12小题，每空2分，满分24分）【7题答案】1a ≥-【8题答案】5ab【9题答案】2-【10题答案】141141244x x ⎛⎫⎛⎫-- ⎪⎪ ⎪⎪⎝⎭⎝⎭【11题答案】10x <--【12题答案】98m <-【13题答案】假【14题答案】2【15题答案】2A BCD∠=∠【16题答案】40°【17题答案】36【181三、计算题（本大题共6小题，每小题5分，满分30分）【19题答案】【20【21题答案】12x =，212x =-【22题答案】112x =，214x =【23题答案】11223x +=，21223x =【24题答案】4四、解答题（本大题共4小题，25题8分，26题、27题6分，28题14分，满分34分）【25题答案】（1）m ≤12；（2）x 1＝﹣2x 2＝﹣2【26题答案】售价应定130元，这时应进货400个，或售价应定140元，这时应进货300个．【28题答案】（1）①BE AD =，BE AD ⊥；②22.5︒；③成立（2）45︒。
上海徐汇2014学年第一学期初二数学期中考试试题
112题A B C D 13题A BC DE 八年级数学期中复习题（1） 2015-10-16班级：____ 姓名：________一、填空题：（每空2分，共36分） 1、4的平方根是____________，827-的立方根是____________. 2x 的取值范围是____________.3、若最简二次根式a b +=____________. 4、化简：若a ＜056、若方程2(1)10m x mx ---=是一元二次方程，那么m 的取值范围是____________.7、方程2(1)9x -=的解为____________，方程(1)3(1)x x x +=+的解为____________.8、关于x 的方程220mx x m m +++=有一根是零，那么m =____________. 9、在实数范围内因式分解：2221x x --=________________，4232x x -+=________________. 10、将命题“全等三角形的面积相等”改写为“如果……，那么……”的形式为_________________________________________. 11、某学校4月份的水电费为a 元，计划5、6两个月的水电费 平均比上月降低10%，那么6月份的水电费预计____________元. 12、如图，已知AC BD =，要使ABC DCB ∆≅∆，只需增加 一个条件是________________. 13、如图，ABC ∆中，已知90C ∠=︒，DE 是AB 的垂直平分线，若:1:2DAC DAB ∠∠=，那么BAC ∠=________度.14、已知a 、b 、c 均为实数，且4a b +=，2210c ab -=-，那么abc =__________. 二、选择题：（本大题共4题，每题3分，共12分）15、在下列各组根式中，属于同类二次根式的是…………………………………（ ） ABCD…………………………密○………………………………………封○………………………………………○线…………………………218题ABC DE16、下列方程中，无实数解的是……………………………………………………（ ） A 、213904x x -+= B 、23520x x --= C 、2290y y -+= D2)y y -=17、一元二次方程220x px q ++=的两根为1-和2，那么二次三次式22x px q ++可分解为……………………………………………………………………………………（ ） A 、(1)(2)x x +- B 、(21)(2)x x +-C 、2(1)(2)x x -+D 、2(1)(2)x x +- 18、如图，ABC EDB ∠=∠，2AB DB DE ==，C 是BD 中 点则下列结论：①AC BE =，②AC BE ⊥，③A EBD ∠=∠， ④BC DE =中正确的个数是……………………………（ ） A 、1个 B 、2个 C 、3个 D 、4个 三、（本大题共5题，每题5分，共25分） 192021、解方程：(31)(2)20x x -+= 22、用配方法解方程22470x x --=323、已知：5a b +=-，1ab =，求.四、（本大题共5题，第24、27小题各6分，第25、26、28题各5分，满分27分） 24、已知关于x 的一元二次方程2(1)230m x mx m -+++=（1）若方程有两个相等的实数根时，求m 的值.（3分）（2）当方程没有实数根时，求出m 的最小正整数的值.（3分）25、为了把一个长100米的矩形游泳池扩建成一个周长为600米的矩形水上游乐场，把游泳池的长增加x 米，当x 为多少时，水上游乐场面积为20000平方米？（5分）26、如图，四边形ABCD 的对角线AC 与BD 相交于点O ，12∠=∠，34∠=∠.求证：（1）ABC ADC ∆≅∆（3分） （2）BO OD =（2分）4321AB CO427、RT ∆三角形ABC 中，90C ∠=度，M 是AB 的中点，点E 在BC 边上，ME AB ⊥，ME 的延长线与AC 的延长线交于点F .（1）求证A CEF ∠=∠（3分）（2）在A ∠大小改变的过程中，ECF ∆是否可能与ABC ∆全等？如果可能，请求出A ∠的度数；如果不可能，请简要说明理由.（3分）28、阅读理解：法国数学家韦达在研究一元二次方程时有一项重大发现：如果一元二次方程20(0)ax bx c a ++=≠的两个根分别是1x ，2x .那么12b x x a +=-，12c x x a=. 例如：已知方程22350x x +-=的两根分别为1x ，2x 则：1232b x x a +=-=-，125522c x x a -===- 请同学阅读后完成以下问题：（1）已知方程3x 2－4x －6=0的两根分别为12x x .求12x x +和12x x 的值.（2分）（2）已知方程2320x x +-=的两根分别为12x x ，求1211x x +的值.（1分）（3）若一元二次方程2230x mx +-=的一根大于1，另一根小于1，求m 的取值范围.（2分）…………………………密○………………………………………封○………………………………………○线…………………………M EAB CF。
2021-2022学年八年级第一学期期中考试数学试卷附答案
2021-2022学年八年级上学期期中考试数学试卷一．选择题（共12小题，满分48分，每小题4分）1．下列图形中，是轴对称图形的是（ ）A ．B ．C ．D ．2．下列判定两个三角形全等的说法中，不正确的是（ ）A ．三角对应相等的两个三角形全等B ．三边对应相等的两个三角形全等C ．有一边及其对角和另一角对应相等的两个三角形全等D ．有一组直角边和一组斜边对应相等的两个直角三角形全等3．等腰三角形的两边长分别为3cm 和7cm ，则周长为（ ）A ．13cmB ．17cmC ．13cm 或17cmD ．11cm 或17cm4．已知∠AOB ，求作射线OC ，使OC 平分∠AOB 作法的合理顺序是（ ）①作射线OC ；②在OA 和OB 上分别截取OD ，OE ，使OD ＝OE ；③分别以D ，E 为圆心，大于12DE 的长为半径作弧，在∠AOB 内，两弧交于C ． A ．①②③ B ．②①③ C ．②③① D ．③②①5．小明同学在学习了全等三角形的相关知识后发现，只用两把完全相同的长方形直尺就可以作出一个角的平分线．如图：一把直尺压住射线OB ，另一把直尺压住射线OA 并且与第一把直尺交于点P ，小明说：“射线OP 就是∠BOA 的角平分线．”他这样做的依据是（ ）A．角的内部到角的两边的距离相等的点在角的平分线上B．角平分线上的点到这个角两边的距离相等C．三角形三条角平分线的交点到三条边的距离相等D．以上均不正确6．如图，将△ABC沿过边上两点D，E的直线折叠后，使得点B与点A重合．若已知BE ＝4cm，DE＝3cm，则△ABC的周长与△ADC的周长的差为（）A．4cm B．5cm C．8cm D．10cm7．已知：如图，在△ABC中，AB＝AC，AB的垂直平分线DE，分别交AB，AC于点D，E．若AD＝3，BC＝5，则△BEC的周长为（）A．8B．10C．11D．138．如图，在△ABC中，∠C＝90°，∠B＝30°，以A为圆心，任意长为半径画弧分别交AB、AC于点M和N，再分别以M、N为圆心，大于12MN的长为半径画弧，两弧交于点P，连结AP并延长交BC于点D，若CD＝3，则BD的长是（）A．7B．6C．5D．49．如图，在△ABC中，∠B＝90°，AB＝6，BC＝8，AD为∠BAC的角平分线，则三角形ADC的面积为（）A．3B．10C．12D．15 10．如图，△ABC中，AB＝AC，D是BC中点，下列结论中不正确的是（）A．∠B＝∠C B．AD⊥BC C．AD平分∠BAC D．AB＝2BD 11．如图，已知AE∥DF，BE∥CF，AC＝BD，则下列说法错误的是（）A．△AEB≌△DFC B．△EBD≌△FCA C．ED＝AF D．EA＝EC 12．等边三角形的三条高把这个三角形分成（）个直角三角形．A．8B．10C．11D．12二．填空题（共6小题，满分24分，每小题4分）13．平面直角坐标系中的点P(2−m，12m)关于x轴的对称点在第四象限，则m的取值范围为．14．如图，已知∠1＝58°，∠B＝60°，则∠2＝°．15．如图，已知BC与DE交于点M，则∠A+∠B+∠C+∠D+∠E+∠F的度数为．16．如果一斜坡的坡度为i＝1：√3，某物体沿斜面向上推进了10米，那么物体升高了米．17．在平面直角坐标系中，点A、B、C的坐标分别为A（8，0），B（2，6），C（4，0），点P，Q是△ABO边上的两个动点（点P不与点C重合），以P，O，Q为顶点的三角形与△COQ全等，则满足条件的点P的坐标为．18．如图，在第1个△A1BC中，∠B＝20°，A1B＝CB；在边A1B上任取一点D，延长CA1到A2，使A1A2＝A1D，得到第2个△A1A2D；在边A2D上任取一点E，延长A1A2到A3，使A2A3＝A2E，得到第3个△A2A3E，…按此做法继续下去，则第5个等腰三角形的底角度数是．三．解答题（共7小题）19．如图，五边形ABCDE的内角都相等，EF平分∠AED，求证：EF⊥BC．20．画图并填空：如图，请画出自A地经过B地去河边l的最短路线．（1）确定由A地到B地最短路线的依据是．（2）确定由B地到河边l的最短路线的依据是．21．已知如图，AC交BD于点O，AB＝DC，∠A＝∠D．（1）请写出符合上述条件的五个结论（并且不再添加辅助线，对顶角除外）；（2）从你写出的5个结论中，任选一个加以证明．22．如图，△ABC中，A点坐标为（2，4），B点坐标为（﹣3，﹣2），C点坐标为（3，1）．（1）在图中画出△ABC关于y轴对称的△A′B′C′（不写画法），并写出点A′，B′，C′的坐标．（2）求△ABC的面积．23．如图，在△ABC中，∠B＝36°，∠C＝76°，AD是△ABC的角平分线，BE是△ABD 中AD边上的高，求∠ABE的度数．24．如图1，在△CAB和△CDE中，CA＝CB，CD＝CE，∠ACB＝∠DCE＝α，连接AD、BE．（1）求证：△ACD≌△BCE；（2）如图2，当α＝90°时，取AD、BE的中点P、Q，连接CP、CQ、PQ，判断△CPQ 的形状，并加以证明．25．问题发现：如图1，在△ABC中，AB＝AC，∠BAC＝60°，D为BC边上一点（不与点B，C重合），将线段AD绕点A逆时针旋转60°得到AE，连接EC，则：（1）①∠ACE的度数是；②线段AC，CD，CE之间的数量关系是．拓展探究：（2）如图2，在△ABC中，AB＝AC，∠BAC＝90°，D为BC边上一点（不与点B，C 重合），将线段AD绕点A逆时针旋转90°得到AE，连接EC，请写出∠ACE的度数及线段AD，BD，CD之间的数量关系，并说明理由；解决问题：（3）如图3，在Rt△DBC中，DB＝3，DC＝5，∠BDC＝90°，若点A满足AB＝AC，∠BAC＝90°，请直接写出线段AD的长度．2021-2022学年八年级上学期期中考试数学试卷参考答案与试题解析一．选择题（共12小题，满分48分，每小题4分）1．下列图形中，是轴对称图形的是（）A．B．C．D．解：A、不是轴对称图形，故此选项错误；B、不是轴对称图形，故此选项错误；C、是轴对称图形，故此选项正确；D、不是轴对称图形，故此选项错误；故选：C．2．下列判定两个三角形全等的说法中，不正确的是（）A．三角对应相等的两个三角形全等B．三边对应相等的两个三角形全等C．有一边及其对角和另一角对应相等的两个三角形全等D．有一组直角边和一组斜边对应相等的两个直角三角形全等解：A、三角对应相等的两个三角形不一定全等，故A选项符合题意；B、三边对应相等的两个三角形全等，故B选项不符合题意；C、有一边及其对角和另一角对应相等的两个三角形全等，故C选项不符合题意；D、有一组直角边和一组斜边对应相等的两个直角三角形全等，故D选项不符合题意；故选：A．3．等腰三角形的两边长分别为3cm和7cm，则周长为（）A．13cm B．17cm C．13cm或17cm D．11cm或17cm 解：当7为腰时，周长＝7+7+3＝17cm；当3为腰时，因为3+3＜7，所以不能构成三角形；故三角形的周长是17cm．故选：B ．4．已知∠AOB ，求作射线OC ，使OC 平分∠AOB 作法的合理顺序是（ ）①作射线OC ；②在OA 和OB 上分别截取OD ，OE ，使OD ＝OE ；③分别以D ，E 为圆心，大于12DE 的长为半径作弧，在∠AOB 内，两弧交于C ． A ．①②③ B ．②①③ C ．②③① D ．③②①解：角平分线的作法是：在OA 和OB 上分别截取OD ，OE ，使OD ＝OE ；分别以D ，E 为圆心，大于12DE 的长为半径作弧，在∠AOB 内，两弧交于C ； 作射线OC ．故其顺序为②③①．故选：C ．5．小明同学在学习了全等三角形的相关知识后发现，只用两把完全相同的长方形直尺就可以作出一个角的平分线．如图：一把直尺压住射线OB ，另一把直尺压住射线OA 并且与第一把直尺交于点P ，小明说：“射线OP 就是∠BOA 的角平分线．”他这样做的依据是（ ）A ．角的内部到角的两边的距离相等的点在角的平分线上B ．角平分线上的点到这个角两边的距离相等C ．三角形三条角平分线的交点到三条边的距离相等D ．以上均不正确解：（1）如图所示：过两把直尺的交点P 作PE ⊥AO ，PF ⊥BO ，∵两把完全相同的长方形直尺，∴PE ＝PF ，∴OP 平分∠AOB （角的内部到角的两边的距离相等的点在这个角的平分线上），故选：A ．6．如图，将△ABC沿过边上两点D，E的直线折叠后，使得点B与点A重合．若已知BE ＝4cm，DE＝3cm，则△ABC的周长与△ADC的周长的差为（）A．4cm B．5cm C．8cm D．10cm解：∵将△ABC沿直线DE折叠后，使得点B与点A重合，∴AD＝BD，BE＝AE＝4，∴AB＝BE+AE＝4+4＝8，∴△ABC的周长﹣△ADC的周长＝AB+BC+AC﹣AC﹣CD﹣AD＝AB+BD﹣AD＝AB＝8（cm），故选：C．7．已知：如图，在△ABC中，AB＝AC，AB的垂直平分线DE，分别交AB，AC于点D，E．若AD＝3，BC＝5，则△BEC的周长为（）A．8B．10C．11D．13解：∵AB的垂直平分线DE分别交AB、AC于点D、E，∴AE＝BE，∵AD＝3，∴AB＝6，∴AE+EC＝AC＝AB＝6，∵BC＝5，∴△EBC的周长＝BC+BE+CE＝BC+AE+CE＝BC+AC＝6+5＝11；故选：C．8．如图，在△ABC中，∠C＝90°，∠B＝30°，以A为圆心，任意长为半径画弧分别交AB、AC于点M和N，再分别以M、N为圆心，大于12MN的长为半径画弧，两弧交于点P，连结AP并延长交BC于点D，若CD＝3，则BD的长是（）A．7B．6C．5D．4解：如图，作DE⊥AB于点E，∵AD为∠CAB的平分线，∴DE＝CD＝3，∵∠B＝30°，则BD＝2DE＝6，故选：B．9．如图，在△ABC中，∠B＝90°，AB＝6，BC＝8，AD为∠BAC的角平分线，则三角形ADC的面积为（）A ．3B ．10C ．12D ．15解：作DH ⊥AC 于H ，如图，在Rt △ABC 中，∠B ＝90°，AB ＝6，BC ＝8，∴AC =√62+82=10，∵AD 为∠BAC 的角平分线，∴DB ＝DH ，∵12×AB ×CD =12DH ×AC ， ∴6（8﹣DH ）＝10DH ，解得DH ＝3，∴S △ADC =12×10×3＝15．故选：D ．10．如图，△ABC 中，AB ＝AC ，D 是BC 中点，下列结论中不正确的是（ ）A ．∠B ＝∠C B ．AD ⊥BC C ．AD 平分∠BAC D ．AB ＝2BD解：∵△ABC 中，AB ＝AC ，D 是BC 中点∴∠B ＝∠C ，（故A 正确）AD ⊥BC ，（故B 正确）∠BAD ＝∠CAD （故C 正确）无法得到AB ＝2BD ，（故D 不正确）．故选：D ．11．如图，已知AE ∥DF ，BE ∥CF ，AC ＝BD ，则下列说法错误的是（ ）A ．△AEB ≌△DFC B ．△EBD ≌△FCA C ．ED ＝AFD ．EA ＝EC 证明：∵AE ∥DF ，∴∠EAB ＝∠FDC ，∵BE ∥CF ，∴∠EBC ＝∠BCF ，∴∠ABE ＝∠FCD ，∵AC ＝BD ，∴AB ＝CD ，在△AEB 和△DFC 中，{∠EAB =∠FDC AB =CD ∠ABE =∠FCD，△AEB ≌△DFC （ASA ），∴BE ＝CF ，在△EBD 和△FCA 中，{BE =CF ∠EBD =∠ACF AC =BD，∴△EBD ≌△FCA （SAS ），∴ED ＝AF ．故A ，B ，C 选项正确，AE ＝CE 说法不正确，故选：D ．12．等边三角形的三条高把这个三角形分成（ ）个直角三角形．A ．8B ．10C ．11D ．12 解：如图：直角三角形有△ABE 、△ACE 、△ABF 、△BCF 、△ACD 、△BCD 、△ADO 、△AFO 、△CFO 、△CEO ，△BEO 、△BDO ，共12个．故选：D ．二．填空题（共6小题，满分24分，每小题4分）13．平面直角坐标系中的点P (2−m ，12m)关于x 轴的对称点在第四象限，则m 的取值范围为 0＜m ＜2 ．解：点P （2﹣m ，12m ）关于x 轴对称的点的坐标为P 1（2﹣m ，−12m ）， ∵P 1（2﹣m ，−12m ）在第四象限，∴{2−m ＞0−12m ＜0，解得0＜m ＜2， ∴m 的取值范围为 0＜m ＜2．故答案为0＜m ＜2．14．如图，已知∠1＝58°，∠B ＝60°，则∠2＝ 118 °．解：∵∠2＝∠B +∠1，∴∠2＝58°+60°＝118°，故答案为118．15．如图，已知BC 与DE 交于点M ，则∠A +∠B +∠C +∠D +∠E +∠F 的度数为 360° ．解：连接BE．∵△CDM和△BEM中，∠DMC＝∠BME，∴∠C+∠D＝∠MBE+∠BEM，∴∠A+∠B+∠C+∠D+∠E+∠F＝∠A+∠B+∠MBE+∠BEM+∠E+∠F＝∠A+∠F+∠ABE+∠BEF＝360°．故答案为：360°．16．如果一斜坡的坡度为i＝1：√3，某物体沿斜面向上推进了10米，那么物体升高了5米．解：∵斜坡的坡度为i＝1：√3，又∵i＝tan∠ABC=AC BC∴ACBC =√3=√33，∴∠ABC＝30°，∵某物体沿斜面向上推进了10米，即AB＝10，∴AC＝5．故答案为：5．17．在平面直角坐标系中，点A、B、C的坐标分别为A（8，0），B（2，6），C（4，0），点P ，Q 是△ABO 边上的两个动点（点P 不与点C 重合），以P ，O ，Q 为顶点的三角形与△COQ 全等，则满足条件的点P 的坐标为 （2√105，6√105）或（1，3）或P （5，3）或（8﹣2√2，2√2） ．解：以P ，O ，Q 为顶点的三角形与△COQ 全等，①如图1所示，当△POQ ≌△COQ 时，即OP ＝OC ＝4，过P 作PE ⊥OA 于E ，过B 作BF ⊥OA 于F ，则PE ∥BF ，∵B （2，6），∴OF ＝2，BF ＝6，∴OB =√22+62=2√10，∵PE ∥BF ，∴△POE ∽△BOF ，∴OP OB =PE BF =OE OF ， ∴2√10=PE 6=OE2， ∴PE =6√105，OE =2√105， ∴点P 的坐标为（2√105，6√105）；②如图2，当△POQ ≌△CQO 时，即QP ＝OC ＝4，OP ＝CQ ，∴四边形PQCO 是平行四边形，∴PQ ∥OA ，过P 作PE ⊥OA 于E ，过B 作BF ⊥OA 于F ， 则PE ∥BF ，∵B（2，6），∴OF＝2，BF＝6，∴OB=√22+62=2√10，∵PQ∥OA，∴PBOB =PQ OA，∴PB=√10，∴PE=√10，∴点P是OB的中点，∵PE∥BF，∴PE=12BF＝3，OE=12EF＝1，∴点P的坐标为（1，3），如图3，如图3，当△OQC≌△QOP时，过P作PE⊥OA于E，过B作BF⊥OA于F，则PE∥BF，∵B（2，6），∴OF＝2，BF＝6，∴AF＝6，∴△ABF和△APE是等腰直角三角形，∴PE＝AE，∵直线AB的解析式为y＝﹣x+8，∴设点P的坐标为（x，﹣x+8），连接PC∵△OQC≌△QOP，∴∠POQ＝∠CQO，PQ＝OC，CQ＝OP，∴△PQC≌△COP，∴∠OPC＝∠QCP，∴∠OQC＝∠QCP，∴PC∥OQ，∴PC=12OB=√10，∵PC2＝CE2+PE2，∴10＝（x ﹣4）2+（﹣x +8）2，解得：x ＝5，x ＝7（不合题意舍去），∴P （5，3）；如图4，当△OQC ≌△QOP 时，过P 作PE ⊥OA 于E ，连接PC ，同理PE ＝AE ，PC ∥OQ ，∵AC ＝OC ，∴AP ＝PQ ，∵△OQC ≌△QOP ，∴PQ ＝OC ＝4，∴AP ＝PQ ＝4，∴PE ＝AE ＝2√2，∴OE ＝8﹣2√2，∴P （8﹣2√2，2√2），综上所述，点P 的坐标为（2√105，6√105）或（1，3）或P （5，3）或（8﹣2√2，2√2）． 故答案为（2√105，6√105）或（1，3）或P （5，3）或（8﹣2√2，2√2）．18．如图，在第1个△A 1BC 中，∠B ＝20°，A 1B ＝CB ；在边A 1B 上任取一点D ，延长CA 1到A 2，使A 1A 2＝A 1D ，得到第2个△A 1A 2D ；在边A 2D 上任取一点E ，延长A 1A 2到A 3，使A 2A 3＝A 2E ，得到第3个△A 2A 3E ，…按此做法继续下去，则第5个等腰三角形的底角度数是 5° ．解：∵在△CBA 1中，∠B ＝20°，A 1B ＝CB ，∴∠BA 1C =180°−∠B 2=80°， ∵A 1A 2＝A 1D ，∠BA 1C 是△A 1A 2D 的外角，∴∠DA 2A 1=12∠BA 1C =12×80°； 同理可得，∠EA 3A 2＝（12）2×80°，∠F A 4A 3＝（12）3×80°， ∴第n 个等腰三角形的底角度数是（12）n ﹣1×80°． ∴第5个等腰三角形的底角度数为：(12)4×80°=5°，故答案为：5°．三．解答题（共7小题）19．如图，五边形ABCDE的内角都相等，EF平分∠AED，求证：EF⊥BC．证明：五边形内角和为：（5﹣2）×180°＝540°．∵5个内角都相等，∴∠A＝∠B＝∠AED=540°5=108°．∵EF平分∠AED，∴∠1＝∠2＝54°．∵四边形的内角和为360°，在四边形ABFE中，∠3＝360°﹣（108°+108°+54°）＝90°．∴EF⊥BC．20．画图并填空：如图，请画出自A地经过B地去河边l的最短路线．（1）确定由A地到B地最短路线的依据是两点之间线段最短．（2）确定由B地到河边l的最短路线的依据是垂线段最短．解：自A地经过B地去河边l的最短路线，如图所示．（1）确定由A地到B地最短路线的依据是两点之间线段最短．（2）确定由B地到河边l的最短路线的依据是垂线段最短．21．已知如图，AC交BD于点O，AB＝DC，∠A＝∠D．（1）请写出符合上述条件的五个结论（并且不再添加辅助线，对顶角除外）；（2）从你写出的5个结论中，任选一个加以证明．解：（1）符合上述条件的五个结论为：△AOB ≌△DOC ，OA ＝OD ，OB ＝OC ，∠ABO ＝∠DCO ，∠OBC ＝∠OCB ．（2）证明如下：∵AB ＝DC ，∠A ＝∠D ，又有∠AOB ＝∠DOC∴△AOB ≌△DOC∴OA ＝OD ，OB ＝OC ，∠ABO ＝∠DCO∵OB ＝OC∴∠OBC ＝∠OCB ．22．如图，△ABC 中，A 点坐标为（2，4），B 点坐标为（﹣3，﹣2），C 点坐标为（3，1）．（1）在图中画出△ABC 关于y 轴对称的△A ′B ′C ′（不写画法），并写出点A ′，B ′，C ′的坐标．（2）求△ABC 的面积．解：（1）如图，A ′（﹣2，4），B ′（3，﹣2），C ′（﹣3，1）；（2）S △ABC ＝6×6−12×5×6−12×6×3−12×1×3，＝36﹣15﹣9﹣112， ＝1012．23．如图，在△ABC中，∠B＝36°，∠C＝76°，AD是△ABC的角平分线，BE是△ABD 中AD边上的高，求∠ABE的度数．解：∵∠B＝36°，∠C＝76°，∴∠BAC＝180°﹣∠B﹣∠C＝180°﹣36°﹣76°＝68°，∵AD是∠BAC的平分线，∴∠BAD=12×68°＝34°，∵AE⊥BE，∴∠AEB＝90°，∴∠ABE＝180°﹣∠AEB﹣∠BAE＝180°﹣90°﹣34°＝56°．24．如图1，在△CAB和△CDE中，CA＝CB，CD＝CE，∠ACB＝∠DCE＝α，连接AD、BE．（1）求证：△ACD≌△BCE；（2）如图2，当α＝90°时，取AD、BE的中点P、Q，连接CP、CQ、PQ，判断△CPQ的形状，并加以证明．解：（1）如图1，∵∠ACB ＝∠DCE ＝α，∴∠ACD ＝∠BCE ，在△ACD 和△BCE 中，{CA =CB ∠ACD =∠BCE CD =CE，∴△ACD ≌△BCE （SAS ），∴BE ＝AD ；（2）△CPQ 为等腰直角三角形．证明：如图2，由（1）可得，BE ＝AD ，∵AD ，BE 的中点分别为点P 、Q ，∴AP ＝BQ ，∵△ACD ≌△BCE ，∴∠CAP ＝∠CBQ ，在△ACP 和△BCQ 中，{CA =CB∠CAP =∠CBQ AP =BQ，∴△ACP ≌△BCQ （SAS ），∴CP＝CQ，且∠ACP＝∠BCQ，又∵∠ACP+∠PCB＝90°，∴∠BCQ+∠PCB＝90°，∴∠PCQ＝90°，∴△CPQ为等腰直角三角形．25．问题发现：如图1，在△ABC中，AB＝AC，∠BAC＝60°，D为BC边上一点（不与点B，C重合），将线段AD绕点A逆时针旋转60°得到AE，连接EC，则：（1）①∠ACE的度数是60°；②线段AC，CD，CE之间的数量关系是AC＝DC+EC．拓展探究：（2）如图2，在△ABC中，AB＝AC，∠BAC＝90°，D为BC边上一点（不与点B，C 重合），将线段AD绕点A逆时针旋转90°得到AE，连接EC，请写出∠ACE的度数及线段AD，BD，CD之间的数量关系，并说明理由；解决问题：（3）如图3，在Rt△DBC中，DB＝3，DC＝5，∠BDC＝90°，若点A满足AB＝AC，∠BAC＝90°，请直接写出线段AD的长度．解：（1）∵在△ABC中，AB＝AC，∠BAC＝60°，∴∠BAC＝∠DAE＝60°，∴∠BAC﹣∠DAC＝∠DAE﹣∠DAC，即∠BAD＝∠CAE，在△BAD和△CAE中，{AB=AC∠BAD=∠CAE AD=AE，∴△BAD≌△CAE（SAS），∴∴∠ACE＝∠B＝60°，BD＝CE，∴BC＝BD+CD＝EC+CD，∴AC＝BC＝EC+CD；故答案为：60°，AC＝DC+EC；（2）BD2+CD2＝2AD2，理由如下：由（1）得，△BAD≌△CAE，∴BD＝CE，∠ACE＝∠B＝45°，∴∠DCE＝90°，∴CE2+CD2＝ED2，在Rt△ADE中，AD2+AE2＝ED2，又AD＝AE，∴BD2+CD2＝2AD2；（3）如图3，作AE⊥CD于E，连接AD，∵在Rt△DBC中，DB＝3，DC＝5，∠BDC＝90°，∴BC=√9+25=√34，∵∠BAC＝90°，AB＝AC，∴AB＝AC=√17，∠ABC＝∠ACB＝45°，∵∠BDC＝∠BAC＝90°，∴点B，C，A，D四点共圆，∴∠ADE＝45°，∴△ADE是等腰直角三角形，∴AE＝DE，∴CE＝5﹣DE，∵AE2+CE2＝AC2，∴AE2+（5﹣AE）2＝17，∴AE＝1，AE＝4，∴AD=√2或AD＝4√2．。
2013.11徐汇中学第一学期八年级期中试卷
徐汇中学2013学年初二年级第一学期期中考试数学试卷（本试题满分100分，时间90分钟）一、填空题（本大题共16题，每空2分，满分34分）1、8的平方根是2、化简：)0(1249>xxy=3、若244xx+－=2-x，则x的取值范围是________________4、不等式：152+>xx的解集是______________5、方程xx42=的根是6、方程2560x x--=的根是7、已知关于x的一元二次方程0142=--xkx有两个实数根，则k的取值范围是8、在实数范围内因式分解：2x2－3x－1 =9、函数xxy-=5的定义域为10、点)32(，-P在正比例函数的图像上，则它的解析式为，它的图像经过第象限11、反比例函数xky2-=的图像在每个象限内y的值随着x的逐渐增大而增大, 那么k的取值范围是12、一件衬衫的原售价为200元，连续两次降价后，现售价为128元．如果每次降价的百分率相同，这个百分率为13是同类根式，则x=______________14、在反比例函数xy=(k﹥0)的图像上有三点()11,yx、()22,yx、()33,yx，且1x＜2x＜0＜3x，则1y、2y、3y的大小关系是（用“＜”连接）15、如图，点A的坐标(1，2),将线段OA绕点A逆时针旋转090，点O的对应点C恰好落在双曲线xky=(x>0) 上，则k =考生诚信考试承诺书我郑重承诺：在本次考试中我自觉遵守了考场规则、诚信应考。
班级____________姓名________________学号____________…………………………密○………………………………………封○………………………………………○线…………………………16、如图，直线l 经过第一、二象限，且平行于x轴，点A 、B 分别是直线l 与反比例函数xy 1=和xy 2-=图像的交点，且AC ⊥x 轴， BD ⊥x 轴，垂足分别为C 、D 。
上海市徐汇区八年级上学期期末数学试题(含答案)
徐汇区学年初二年级第一学期期末考试数学试卷（考试时间90分钟，满分100分）一．选择题（本大题共6题，每题3分，满分18分）1. 下列二次根式中，是最简二次根式是（ ）A.B.C.D.2.下列方程中，没有实数根的是（） A.2310x x −−= B.230x x −= C.2210x x −+= D.2230x x −+=3.如果正比例函数图像与反比例函数图像一个交点的坐标为（3，-4），那么另一个交点的坐标为（ ）A.（-3，-4）B.（3，4）C.（−3，4）D.（-4，3）4.满足下列条件的三角形中，不是直角三角形的是（）A.三内角之比为3：4：5B.三边长的平方之比为1：2：3C.三边长之比为7：24：25D.三内角之比为1：2：35.下列命题中，其逆命题是真命题的命题个数有（） （1）全等三角形的对应边相等； （2）对顶角相等；（3）等角对等边；（4）全等三角形的面积相等．A.1个 B.2个 C.3个 D.4个6. 如图所示，在平面直角坐标系xOy 中，点A 、B 、C 为反比例函数y =k x（k ＞0）上不同的三点，连接OA 、OB 、OC ，过点A 作AD ⊥y 轴于点D ，过点B 、C 分别作BE ，CF 垂直x 轴于点E 、F ，OC 与BE 相交于点M ，记△AOD 、△BOM 、四边形CMEF 的面积分别为S 1、S 2、S 3，则（ ） 的的A. S 1=S 2+S 3B. S 2=S 3C. S 3＞S 2＞S 1D. S 1S 2＜S 32二．填空题（本大题共12题，每题2分，满分24分）7. 函数y = ___________________．8. 已知函数y ＝1x x −，当x 时，y ＝_____． 9. 已知0是关于x 的一元二次方程22(1)210m x x m −++−=的一个实数根，则m =______．10. 在实数范围内因式分解：2231x x −−=_________．11. 若1(1,)M y −、21(,)2N y −两点都在函数k y x=的图像上，且1y <2y ，则k 的取值范围是______． 12. 已知正比例函数()0y kx k =≠的图象经过第一、三象限，且经过点（k ，k +2），则k =________．13. 以线段AB 为底边的等腰三角形，它的两底角平分线交点的轨迹是_____．14. 如图，在△ABC 中，∠C =37°，边BC 的垂直平分线分别与AC 、BC 交于点D 、E ，AB =CD ，那么∠A =____°．15. 如图，∠AOE ＝∠BOE ＝15°，EF //OB ，EC ⊥OB ，若EC ＝2，则EF ＝___．16. 如图，梯形ABCD 中，AD ∥BC ，AF ⊥BC 于F ，M 是CD 中点，AM 的延长线交BC 的延长线于E ，AE ⊥AB ，∠B =60°，AF =，则梯形的面积是___．17. 如果三角形有一边上的中线长恰好等于这边的长，那么称这个三角形为“好玩三角形”，在Rt △ABC 中，∠C =90° ，AC =2，若Rt △ABC 是“好玩三角形”，则AB =_______．18. 小华用一张直角三角形纸片玩折纸游戏，如图1，在Rt ABC △中，90ACB ∠=°，30B ∠=°，1AC =．第一步，在AB 边上找一点D ，将纸片沿CD 折叠，点A 落在A ′处，如图2，第二步，将纸片沿CA ′折叠，点D 落在D ¢处，如图3．当点D ¢恰好在原直角三角形纸片的边上时，线段A D ′′的长为__________．三．简答题（第19、20、21、22、23每题6分，24、25每题8分，26题12分）19.2−． 20. 用配方法解方程：2420x x −−=．21. 关于x 的一元二次方程22(2)20x m x +−+=有两个相等的实数根，求m 的值及方程的根． 22. 某商场今年2月份的营业额为400万元，3月份的营业额比2月份增加10%，月份的营业额达到633.6万元．求3月份到5月份营业额的平均月增长率．23. 接种疫苗是预防控制传染病最有效手段．甲、乙两地分别对本地各40万人接种新冠病毒疫苗．甲地在前期完成5万人员接种后，甲、乙两地同时以相同速度接种．甲地经过a 天接种后，由于情况变化，接种速度放缓．图中的折线BCD 和线段OA 分别反映了甲、乙两地的接种人数y （万人）与接种时间x (天)之间的函数关系．根据图像所提供的信息回答下列问题的（1）乙地比甲地提前了________天完成疫苗接种工作．（2）试写出乙地接种人数2y（万人）与接种时间x(天)之间的函数解析式______．（3）当甲地放缓接种速度后，每天可接种_______万人．24. 如图，在△ABC中，∠ACB=90°，AC=4，CB=2，点D是AB的中点，点E在AC上，点E、D、F一条直线上，且ED=FD，（1）求证：FB⊥CB；（2）联结CD，若CD⊥EF，求CE的长．25. 在平面直角坐标系中，反比例函数y＝kx（x＞0，k＞0图象上的两点（n，3n）、（n+1，2n）．（1）求n的值；（2）如图，直线l为正比例函数y＝x的图象，点A在反比例函数y＝kx（x＞0，k＞0）的图象上，过点A作AB⊥l于点B，过点B作BC⊥x轴于点C，过点A作AD⊥BC于点D，记△BOC的面积为S1，△ABD的面积为S2，求S1﹣S2的值．26. 如图1所示，已知△ABC 中，∠ACB =90°，BC =2，AC=D 在射线BC 上，以点D 为圆心，BD 为半径画弧交AB 边AB 于点E ，过点E 作EF ⊥AB 交边AC 于点F ，射线ED 交射线AC 于点G ．（1）求证：EA =EG ；（2）若点G 在线段AC BD =x ，FC =y ，求y 关于x 函数解析式并写出定义域； （3）联结DF ，当△DFG 是等腰三角形时，请直接写出BD 长度．的的徐汇区学年初二年级第一学期期末考试数学试卷（考试时间90分钟，满分100分）一．选择题（本大题共6题，每题3分，满分18分）1. 下列二次根式中，是最简二次根式的是（）A.B.C.D.【答案】D【解析】【分析】根据最简二次根式的定义去判断即可．含有分母，不是最简二次根式，故A不符合题意；含有开方不尽的因数，不最简二次根式，故B不符合题意；含有开方不尽的因数，不是最简二次根式，故C不符合题意；是最简二次根式，故D符合题意；故选D．【点睛】本题考查了最简二次根式即被开方数中的每一个因数的指数都小于根指数2，正确理解最简二次根式的定义是解题的关键．2. 下列方程中，没有实数根的是（）是A. 2310x x −−=B. 230x x −=C. 2210x x −+=D. 2230x x −+=【答案】D【解析】 【分析】利用一元二次方程根的判别式，即可求解．【详解】解：A 、()()2341130∆=−−×−=> ，所以方程有两个不相等的实数根，故本选项不符合题意；B 、()234090∆=−−×=>，所以方程有两个不相等的实数根，故本选项不符合题意； C 、()22410∆=−−×=，所以方程有两个相等的实数根，故本选项不符合题意； D 、()224380∆=−−×=−<，所以方程没有的实数根，故本选项符合题意；故选：D【点睛】本题主要考查了一元二次方程根的判别式，熟练掌握二次函数()20y ax bx c a ++≠ ，当240b ac ∆=−> 时，方程有两个不相等的实数根；当240b ac ∆=−= 时，方程有两个相等的实数根；当240b ac ∆=−< 时，方程没有实数根是解题的关键．3. 如果正比例函数图像与反比例函数图像的一个交点的坐标为（3，-4），那么另一个交点的坐标为（ ）A. （-3，-4）B. （3）C. （−3，4）D. （-4，3） 【答案】C【解析】【分析】根据两交点关于原点对称求解．【详解】设正比例函数解析式为y kx =，反比例函数解析式为a y x= ∴联立得a y x y kx = = ，解得2a x k =，x y = =或x y = =− ∴正比例函数和反比例函数交点关于原点对称∴如果正比例函数图像与反比例函数图像的一个交点的坐标为（3，-4），那么另一个交点的坐标为（−3，4）故选：C【点睛】本题考查了反比例函数图象的对称性，联立两函数解析式求交点坐标是常用的方法，也是基本的方法，需熟练掌握，另外，利用对称性求解更简单，且不容易出错．4. 满足下列条件的三角形中，不是直角三角形的是（ ）A. 三内角之比为3：4：5B. 三边长的平方之比为1：2：3C. 三边长之比为7：24：25D. 三内角之比为1：2：3【答案】A【解析】【分析】根据勾股定理逆定理及三角形内角和可直接进行排除选项．【详解】解：A 、由三内角之比为3：4：5可设这个三角形的三个内角分别为3,4,5k k k ，根据三角形内角和可得345180k k k ++=°，所以15k =°，所以这个三角形的最大角为5×15°=75°，故不是直角三角形，符合题意；B 、由三边长的平方之比为1：2：3可知该三角形满足勾股定理逆定理，即1+2=3，所以是直角三角形，故不符合题意；C 、由三边长之比为7：24：25可设这个三角形的三边长分别为7,24,25k k k ，则有()()()22272425k k k +=，所以是直角三角形，故不符合题意； D 、由三内角之比为1：2：3可设这个三角形的三个内角分别为,2,3k k k ，根据三角形内角和可得23180k k k ++=°，所以30k =3×30°=90°，是直角三角形，故不符合题意；故选A ．【点睛】本题主要考查勾股定理逆定理及三角形内角和，熟练掌握勾股定理逆定理及三角形内角和是解题的关键．5. 下列命题中，其逆命题是真命题的命题个数有（ ）（1）全等三角形的对应边相等； （2）对顶角相等；（3）等角对等边； （4）全等三角形的面积相等．A. 1个B. 2个C. 3个D. 4个 【答案】B【解析】【分析】首先写出各个命题的逆命题，再进一步判断真假．【详解】（1）逆命题是：对应边相等的两个三角形全等，正确；（2）逆命题是：相等的角是对顶角，错误；（3）逆命题是：等边对等角，正确；（4）逆命题是：面积相等，两三角形全等，错误．故选：B ．【点睛】本题主要考查了逆命题的定义及真假性，学生易出现只判断原命题的真假，也就是审题不认真，难度适中．6. 如图所示，在平面直角坐标系xOy 中，点A 、B 、C 为反比例函数y =k x（k ＞0）上不同的三点，连接OA 、OB 、OC ，过点A 作AD ⊥y 轴于点D ，过点B 、C 分别作BE ，CF 垂直x 轴于点E 、F ，OC 与BE 相交于点M ，记△AOD 、△BOM 、四边形CMEF 的面积分别为S 1、S 2、S 3，则（ ）A. S 1=S 2+S 3B. S 2=S 3C. S 3＞S 2＞S 1D. S 1S 2＜S 32 【答案】B【解析】【分析】先根据反比例函数的几何意义可得,,AOD BOE COF V V V 的面积都等于2k ，再逐项分析即可得． 【详解】解：由题意得：,,AOD BOE COF V V V 的面积都等于2k ， 123,22EOM k k S S S S =−=∴=V ， A 、1S 与23S S +不一定相等，此项错误；B 、23S S =，此项正确；C 、321S S S =<，此项错误；D 、12222223S S S S S S >==，此项错误；故选：B ．【点睛】本题考查了反比例函数的几何意义，熟练掌握反比例函数的几何意义是解题关键．二．填空题（本大题共12题，每题2分，满分24分）7. 函数y = ___________________．【答案】x ≤2.【解析】【分析】y =2-x≥0，解不等式即可得到所求定义域．【详解】解：y= 可得2-x≥0，解得x≤2.故答案为x≤2.【点睛】本题考查求函数的定义域的问题，解题时应根据函数的解析式，列出使解析式有意义的不等式，从而求出定义域来．8. 已知函数y ＝1x x −，当x 时，y ＝_____．【答案】【解析】【分析】把自变量x 的值代入函数关系式进行计算即可．【详解】解：当x 时，函数y ＝1x x −，故答案为：．【点睛】本题考查了求函数值及分母有理化，理解求函数值的方法及分母有理化是解题关键．9. 已知0是关于x 的一元二次方程22(1)210m x x m −++−=的一个实数根，则m =______．【答案】-1【解析】【分析】根据一元二次方程的二次项系数不等于零可得10m −≠，由0是一元二次方程方程的解，把0x =，代入方程可得210m −=，进而即可解得m 的值．【详解】解：∵0是关于x 的一元二次方程22(1)210m x x m −++−=的一个实数根，∴210m −=，且10m −≠，∴1m =−，故应填-1．【点睛】本题主要考查了一元二次方程中的字母求值问题．10. 在实数范围内因式分解：2231x x −−=_________．【答案】2x x −−【解析】 【分析】结合题意，当231022x x −−=时，通过求解一元二次方程，得231022x x x x −−== ，结合2231231222x x x x −−=−− ，即可得到答案． 【详解】2231231222x x x x −−=−−当231022x x −−=时，得x =∴231022x x x x −−==∴23122x x x x −−=∴22312x x x x −−=故答案为：2x x−− ． 【点睛】本题考查了因式分解和一元二次方程的知识；解题的关键是熟练掌握一元二次方程的性质，从而完成求解．11. 若1(1,)M y −、21(,)2N y −两点都在函数k y x=的图像上，且1y <2y ，则k 的取值范围是______． 【答案】k <0【解析】 【分析】根据112−<−，且1y <2y ，可得y 随x 的增大而增大，即可求解 【详解】解：∵112−<− ，且1y <2y ， ∴y 随x 的增大而增大， ∴0k <故答案为：0k < 【点睛】本题主要考查了反比例函数的图象和性质，熟练掌握对于反比例函数()0k y k x=≠ ，当0k > 时，在每一象限内， y 随x 的增大而减小，当0k < 时，在每一象限内，y 随x 的增大而增大是解题的关键．12. 已知正比例函数()0y kx k =≠的图象经过第一、三象限，且经过点（k ，k +2），则k =________．【答案】2【解析】【分析】先根据正比例函数的图象可得0k >，再将点(,2)k k +代入函数的解析式可得一个关于k 的一元二次方程，解方程即可得．【详解】解：Q 正比例函数()0y kx k =≠的图象经过第一、三象限， 0k ∴>，由题意，将点(,2)k k +代入函数()0y kx k =≠得：22k k =+， 解得2k =或10k =−<（舍去）， 故答案为：2．【点睛】本题考查了正比例函数的图象、一元二次方程的应用，熟练掌握正比例函数的图象特点是解题关键．13. 以线段AB 为底边的等腰三角形，它的两底角平分线交点的轨迹是_____．【答案】线段AB 的垂直平分线（AB 中点除外）【解析】【分析】根据等边对等角，得到两个底角相等，两个底角的一半也是相等的，利用等角对等边，交点到A，B的距离相等，得到结论．【详解】如图，∵CA=CB，∴∠CAB=∠CBA，∵AD，BD分别是∠CAB，∠CBA的平分线，∴12∠CAB=12∠CBA，∴∠DAB=∠DBA，∴D在AB的垂直平分线上，故答案为：线段AB的垂直平分线（AB中点除外）．【点睛】本题考查了等腰三角形的性质，等腰三角形的判定，线段垂直平分线的逆定理，熟练等腰三角形的性质，线段垂直平分线的逆定理是解题的关键．14. 如图，在△ABC中，∠C=37°，边BC的垂直平分线分别与AC、BC交于点D、E，AB=CD，那么∠A=____°．【答案】74【解析】【分析】连接BD，由题意易得BD=CD=AB，然后可得∠DBC=∠C=37°，进而根据三角形外角的性质及等腰三角形的性质可求解．【详解】解：连接BD，如图所示：∵DE垂直平分BC，AB=CD，∴BD=CD=AB，∵∠C=37°，∴∠DBC=∠C=37°，∴∠ADB=2∠C=74°，∵AB=BD，∴∠A=∠ADB=74°，故答案为74．【点睛】本题主要考查线段垂直平分线的性质定理、三角形外角的性质及等腰三角形的性质，熟练掌握线段垂直平分线的性质定理、三角形外角的性质及等腰三角形的性质是解题的关键．15. 如图，∠AOE＝∠BOE＝15°，EF//OB，EC⊥OB，若EC＝2，则EF＝___．【答案】4【解析】【分析】作EG⊥OA于G，根据角平分线的性质得到EG的长度，再根据平行线的性质得到∠OEF＝∠COE＝15°，然后利用三角形的外角和内角的关系求出∠EFG＝30°，利用30°角所对的直角边是斜边的一半解题．【详解】解：作EG⊥OA于G，如图所示：∵EF//OB，∠AOE＝∠BOE＝15°，EC⊥OB，∴∠OEF＝∠COE＝15°，EG＝CE＝2，∵∠AOE＝15°，∴∠EFG＝15°＋15°＝30°，∴EF＝2EG＝4．故答案为：4．【点睛】本题考查了角平分线的性质、平行线的性质、含30°角的直角三角形的性质；熟练掌握角平分线的性质，证出∠EFG＝30°是解决问题的关键．16. 如图，梯形ABCD中，AD∥BC，AF⊥BC于F，M是CD中点，AM的延长线交BC的延长线于E，AE⊥AB，∠B=60°，AF=，则梯形的面积是___．【答案】【解析】【分析】根据已知条件易证△ADM≌△ECM，得S△ADM＝S△ECM，进而得到S梯形＝S△ABE，然后解直角△ABF，求出AB，进而可得AE，根据三角形面积公式求出S△ABE即可．【详解】解：∵AD∥BC，∴∠DAM ＝∠E ，∠D ＝∠ECM ，∵DM ＝CM ，∴△ADM ≌△ECM ，∴S △ADM ＝S △ECM ， ∴S 梯形＝S △ABE ，∵AF ⊥BC ，∠B ＝60°，AF ＝，∴sin60°＝AF AB ， 解得：4AB =，∵AE ⊥AB ，∴AE =∴S △ABE ＝11422AB AE ?创=，即梯形的面积是故答案为：【点睛】本题考查了平行线的性质、全等三角形的判定和性质以及解直角三角形等知识点，求出S 梯形＝S △ABE 是解题关键． 17. 如果三角形有一边上的中线长恰好等于这边的长，那么称这个三角形为“好玩三角形”，在Rt △ABC 中，∠C =90° ，AC =2，若Rt △“好玩三角形”，则AB =_______．或【解析】【分析】分AC 边上的中线BD 等于AC ，BC 边上的中线AE 等于BC 两种情况，根据勾股定理计算．【详解】解：当AC 边上的中线BD 等于AC 时，如图，∵∠C =90°，AC =2，∴CD =1,BD =2∴22222213BC BD CD =−=−=,∴AB =当BC 边上的中线AE 等于BC 时，∵AC 2=AE 2−CE 2，∴BC 2−(12BC )2=22， 解得，BC 2=163，∴AB ===,综上所述，AB AB或【点睛】本题考查的是勾股定理，如果直角三角形的两条直角边长分别是a ，b ，斜边长为c ，那么a 2+b 2=c 2. 熟练掌握勾股定理是解本题的关键.18. 小华用一张直角三角形纸片玩折纸游戏，如图1，在Rt ABC △中，90ACB ∠=°，30B ∠=°，1AC =．第一步，在AB 边上找一点D ，将纸片沿CD 折叠，点A 落在A ′处，如图2，第二步，将纸片沿CA ′折叠，点D 落在D ¢处，如图3．当点D ¢恰好在原直角三角形纸片的边上时，线段A D ′′的长为__________．【答案】12或2− 【解析】 【分析】因为点D ¢恰好在原直角三角形纸片的边上，所以分为当D ¢落在AB 边上和BC 边上两种情况分析，根据勾股定理求解即可．【详解】解：当D ¢落在AB 边上时，如图（1）：设DD ′交AB 于点E ，由折叠知：60EA D A ′∠=∠=°,ADA D A D ′′′==,DD A E ′′⊥,A C AC ′= 90ACB ∠=°Q ，30B ∠=°，1AC =2,AB BC ∴==设AD x =，则在Rt A ED ′V 中，12A E x ′=在Rt ECB V 中，12EC BC ==A C AC ′=Q112x ∴+=即2x =−．当D ¢落在BC 边上时，如图（2）因为折叠，30,ACD A CD A CD ′′′∠=∠=∠=° ∴ 11,122A D A C AB AC A B AC ′′′′′′===== 12AD A D ′′∴．故答案为：12或2 【点睛】本题考查了轴对称变换，勾股定理，直角三角形中30°的性质，正确的作出图形是解题的关键．三．简答题（第19、20、21、22、23每题6分，24、25每题8分，26题12分）19. 2−．【答案】4+−【解析】 【分析】先根据二次根式的乘法、分母有理化和完全平方公式化简，再计算加减即可．【详解】解：原式15+−+4．【点睛】本题主要考查二次根式的混合运算，解题的关键是掌握二次根式的混合运算顺序和法则． 20. 用配方法解方程：2420x x −−=．【答案】12x =+，22x =【解析】【分析】利用配方法解一元二次方程即可得．【详解】解：2420x x −−=，2x 4x 2−=，24424x x −+=+，2(26)x −=，2x −2x =±即1222x x −【点睛】本题考查了利用配方法解一元二次方程，熟练掌握配方法是解题关键．21. 关于x 的一元二次方程22(2)20x m x +−+=有两个相等的实数根，求m 的值及方程的根．【答案】当16m =时，121x x ==−；当22m =−时，121x x == 【解析】【分析】根据原方程有两个相等的实数根可以得到有关m 的方程，解得m 的值，再代入得到方程的解即可．【详解】∵方程有两个相等的实数根，∴22(2)422412m m m ∆=−−××=−−=0∴126,2m m ==−当16m =时，121x x ==−当22m =−时，121x x == 【点睛】考查了根的判别式的知识，解题的关键是根据根的情况得到方程．当Δ=0时，方程有两个相等的两个实数根；22. 某商场今年2月份的营业额为400万元，3月份的营业额比2月份增加10%，月份的营业额达到633.6万元．求3月份到5月份营业额的平均月增长率．【答案】20%【解析】【分析】主要考查增长率问题，一般用增长后的量=增长前的量×（1+增长率），设3月份到5月份营业额的平均增长率是x ，则四月份的营业额是400（1+10%）（1+x ），5月份的营业额是400（1+10%）（1+x ）2，据此即可列方程求解．要注意根据实际意义进行值的取舍．【详解】设月份至月份的营业额的平均月增长率为．依题意，得: 2400(110%)(1)633.6x ++=．整理得: 2(1) 1.44x +=．解得: 120.2, 2.2x x ==−（不合题意，舍去）． 答：月份至月份的营业额的平均月增长率为20%．【点睛】可根据题意列出方程，判断所求的解是否符合题意，舍去不合题意的解．找到关键描述语，找到等量关系准确的列出方程是解决问题的关键．23. 接种疫苗是预防控制传染病最有效的手段．甲、乙两地分别对本地各40万人接种新冠病毒疫苗．甲地在前期完成5万人员接种后，甲、乙两地同时以相同速度接种．甲地经过a 天接种后，由于情况变化，接种速度放缓．图中的折线BCD 和线段OA 分别反映了甲、乙两地的接种人数y （万人）与接种时间x (天)之间的函数关系．根据图像所提供的信息回答下列问题（1）乙地比甲地提前了________天完成疫苗接种工作．（2）试写出乙地接种人数2y （万人）与接种时间x (天)之间的函数解析式______．（3）当甲地放缓接种速度后，每天可接种_______万人．【答案】（1）20 （2）212y x =（3）0.25【解析】【分析】（1）看图像，乙地用80天完成，甲地用100天，时间差即提前天数．（2）乙地接种人数2y （万人）与接种时间x (天)成正比，且过点（80，40），用待定系数法求解即可；为（3）先根据BC 与2y 相同，求得BC 的解析式，确定a 值，再确定CD 的解析式即可．【小问1详解】看图像，乙地用80天完成，甲地用100天，∴提前100-80=20（天），故答案为：20．小问2详解】∵乙地接种人数2y （万人）与接种时间x (天)成正比，∴设2y =mx ，∵函数经过点（80，40），∴40=80m ，解得m =12， ∴2y =12x ， 故答案为：2y =12x ． 【小问3详解】∵2y =12x ， ∴BC y =12x +b ， ∵B （0，5），∴b =5，∴BC y =12x +5， ∴25=12a +5， ∴a =40，∴C （40，25），D （100，40），∴设CD y =kx +n ，∴402510040k n k n += += ， 【解得0.2515k n = =， ∴设CD y =0.25x +15，故答案为：0.25．【点睛】本题考查了正比例函数，一次函数解析式的确定，正确获取图像信息，灵活用待定系数法是解题的关键．24. 如图，在△ABC 中，∠ACB =90°，AC =4，CB =2，点D 是AB 的中点，点E 在AC 上，点E 、D 、F 一条直线上，且ED =FD ，（1）求证：FB ⊥CB ；（2）联结CD ，若CD ⊥EF ，求的长．【答案】（1）见解析 （2）52 【解析】【分析】（1）先证明△ADE ≅△BDF 可得A FBD ∠∠=，再由∠ACB =90°可得∠A +∠ABC =90°，再根据等量代换可得∠FBC =90°即可证明结论；（2）如图：联结CD 、CF ．根据题意可得CF =EF ，设CE =x ，则CF =x ，BF =AE =4-x ，然后根据勾股定理列方程求得x 即可．【小问1详解】（1）证明：∵D 是AB 中点，∴AD =BD在△ADE 与△BDF 中，AD BD ADE BDF ED FD = ∠=∠ =∴△ADE ≅△BDF∴A FBD ∠∠=，AE =BF ．∵∠ACB =90°，∴∠A +∠ABC =90°，∴FBD ∠+∠ABC =90°，即∠FBC =90°，∴FB ⊥CB ．【小问2详解】解：（2）如图：联结CD 、CF ．∵CD ⊥EF ，ED =FD ，∴CF =CE ，设CE =x ，则CF =x ，BF =AE =4-x ，Rt △FBC 中，222BF BC CF +=，∴2222(4x x +−=），∴x =52 ，即CE =52．【点睛】本题主要考查了全等三角形的判定与性质、等腰三角形的性质、勾股定理等知识点，正确运用勾股定理列方程成为解答本题的关键．25. 在平面直角坐标系中，反比例函数y ＝k x （x ＞0，k ＞0图象上的两点（n ，3n ）、（n+1，2n ）． （1）求n 的值；（2）如图，直线l为正比例函数y＝x的图象，点A在反比例函数y＝kx（x＞0，k＞0）的图象上，过点A作AB⊥l于点B，过点B作BC⊥x轴于点C，过点A作AD⊥BC于点D，记△BOC的面积为S1，△ABD的面积为S2，求S1﹣S2的值．【答案】（1）2（2）6【解析】【分析】（1）利用反比例函数图象上点的坐标特征得到n•3n＝（n+1）•2n，然后解方程可得n的值；（2）设B（m，m），利用△OBC为等腰直角三角形得到∠OBC＝45°，再证明△ABD为等腰直角三角形，则可设BD＝AD＝t，所以A（m+t，m﹣t），把A（m+t，m﹣t）代入y＝12x中得到m2﹣t2＝12，然后利用整体代入的方法计算S1﹣S2．【详解】解：（1）∵反比例函数y＝kx（x＞0，k＞0图象上的两点（n，3n）、（n+1，2n）．∴n•3n＝（n+1）•2n，解得n＝2或n＝0（舍去），∴n的值为2；（2）反比例函数解析式为y＝12x，设B（m，m），∵OC＝BC＝m，∴△OBC为等腰直角三角形，∴∠OBC＝45°，∵AB⊥OB，∴∠ABO＝90°，∴∠ABC＝45°，∴△ABD为等腰直角三角形，设BD ＝AD ＝t ，则A （m+t ，m ﹣t ），∵A （m+t ，m ﹣t ）在反比例函数解析式为y ＝12x 上， ∴（m+t ）（m ﹣t ）＝12，∴m 2﹣t 2＝12，∴S 1﹣S 2＝2211112222m t −=×＝6． 【点睛】本题考查了反比例函数系数k 的几何意义：在反比例函数y ＝k x（k ≠0）图象中任取一点，过这一个点向x 轴和y 轴分别作垂线，与坐标轴围成的矩形的面积是定值|k|．也考查了反比例函数的性质．26. 如图1所示，已知△ABC 中，∠ACB =90°，BC =2，AC =D 在射线BC 上，以点D 为圆心，BD 为半径画弧交AB 边AB 于点E ，过点E 作EF ⊥AB 交边AC 于点F ，射线ED 交射线AC 于点G ．（1）求证：EA =EG ；（2）若点G 在线段AC 延长线上时，设BD =x ，FC =y ，求y 关于x 的函数解析式并写出定义域；（3）联结DF ，当△DFG 是等腰三角形时，请直接写出BD 的长度．【答案】（1）见解析 （2）)12y x =≤<（3）85 【解析】【分析】（1）在BA 上截取BM =BC =2，在Rt △ACB 中，由勾股定理222AC BC AB +=，可得AB =4，进而可得∠A =30°，∠B =60°；由DE =DB ，可证△DEB 是等边三角形，∠BED =60°，由外角和定理得∠BED =∠A +∠G ，进而得∠G =30°，所以∠A =∠G ，即可证EA =EG ；（2）由△DEB 是等边三角形可得BE =DE ，由BD =x ，FC =y ，得BE =x ， DE =x ，AE =AB -BE =4-x ，在Rt △AEF 中，由勾股定理可表示出AF =，把相关量代入FC =AC -AF ，整理即可得y 关于x 的函数解析式；当F 点与C 点重合时，x 取得最小值1，G 在线段AC 延长线上,可知，D 点不能与C 点重合，所以x 最大值小于2，故可得1≤x <2；（3）连接DF ，根据等腰三角形判定定理，有两条边相等的三角形是等腰三角形，分三种情况①当CF CG =时，②当DG FG =时③当DF FG =时，分别计算即可得BD 的长．【小问1详解】如图，BA 上截取BM =BC =2，Rt △ACB 中，∠C =90°∵ACBC =2，∴AB4=∴AM =AB -BM =2，∴CM =BM =AM =2，∴△BCM 是等边三角形，∴∠B =60°，∴∠A =30°，∵DE =DB ，∴△DEB 是等边三角形， 的在∴∠BED=60°，∵∠BED=∠A+∠G，∴∠G=30°∴∠A=∠G，∴EA=EG．【小问2详解】∵△DEB是等边三角形，∴BE=DE设BE=x，则DE=x，AE=AB-BE=4-x ∵∠A=30°，∠AEF=90°，∴EF=12 AF，Rt△AEF中，222AE EF AF+=∴AF=∵FC=AC-AF，∴y=定义域：1≤x<2【小问3详解】连接DF，Rt △ACB 中，∠C =90°∴222AC BC AB +=∵AC BC =2，BD =x ，∴AB =4，EA =EG=4-x ，42DG x =−，2DC x =−，①当CF CG =时，在Rt △DCG 中，∴222DG DC CG =+，222(42)(2)x x =−−+， 解得：14x =（舍去），285x =； ②当DG FG =时，在Rt △DCG 中，∠G =30°，∴DG =2DC ，∴CG )2x ==−∴42)x x −=−+，解之得：x =； ③当DF FG =时，在Rt △DCF 中，22222(2)DF DC CF x =+=−+， ∴22DF FG =， 222(2)2)x x −+−+，解得：x =综上所述：BD 的长为85【点睛】本题主要考查了勾股定理，等腰三角形的判定等有关知识，正确进行分析，熟练掌握和灵活运用相关知识是解题的关键，注意分类思想的运用．。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
百度文库 - 让每个人平等地提升自我
1
12题
A B C D 13题
A B
D
E 八年级数学期中复习题（1） 2015-10-16
班级：____ 姓名：________
一、填空题：（每空2分，共36分） 1、4的平方根是____________，8
27
-
的立方根是____________. 2
x 的取值范围是____________.
3
、若最简二次根式b
a b +=____________. 4、化简：若a ＜0
5
=____________. 6、若方程2
(1)10m x mx ---=是一元二次方程，那么m 的取值范围是____________. 7、方程2
(1)9x -=的解为____________，方程(1)3(1)x x x +=+的解为____________. 8、关于x 的方程2
2
0mx x m m +++=有一根是零，那么m =____________. 9、在实数范围内因式分解：
2
221x x --=________________，4
2
32x x -+=________________.
10、将命题“全等三角形的面积相等”改写为“如果……，那么……”的形式为
_________________________________________. 11、某学校4月份的水电费为a 元，计划5、6两个月的水电费 平均比上月降低10%，那么6月份的水电费预计____________元. 12、如图，已知AC BD =，要使ABC DCB ∆≅∆，只需增加 一个条件是________________. 13、如图，ABC ∆中，已知90C ∠=︒，DE 是AB 的垂直平
分线，若:1:2DAC DAB ∠∠=，那么BAC ∠=________度.
14、已知a 、b 、
c 均为实数，且4a b +=
，2
210c ab -=-，那么abc =__________. 二、选择题：（本大题共4题，每题3分，共12分）
15、在下列各组根式中，属于同类二次根式的是…………………………………（ ）
…………………………密○………………………………………封○………………………………………○线…………………………
百度文库- 让每个人平等地提升自我
2 A
B
C
D
百度文库 - 让每个人平等地提升自我
3
18题
A
B
C D
E
16、下列方程中，无实数解的是……………………………………………………（ ） A 、
2
13904
x x -+= B 、23520x x --= C 、2
290y y -+= D
2)y y -=
17、一元二次方程220x px q ++=的两根为1-和2，那么二次三次式2
2x px q ++可分解为……………………………………………………………………………………（ ） A 、(1)(2)x x +- B 、(21)(2)x x +-
C 、2(1)(2)x x -+
D 、2(1)(2)x x +- 18、如图，ABC EDB ∠=∠，2AB DB D
E ==，C 是BD 中 点则下列结论：①AC BE =，②AC BE ⊥，③A EBD ∠=∠， ④BC DE =中正确的个数是……………………………（ ） A 、1个 B 、2个 C 、3个 D 、4个 三、（本大题共5题，每题5分，共25分） 19
20
21、解方程：(31)(2)20x x -+= 22、用配方法解方程2
2470x x --=
百度文库 - 让每个人平等地提升自我
4
23、已知：5a b +=-，1ab =
，求的值.
四、（本大题共5题，第24、27小题各6分，第25、26、28题各5分，满分27分） 24、已知关于x 的一元二次方程2
(1)230m x mx m -+++=
（1）若方程有两个相等的实数根时，求m 的值.（3分）
（2）当方程没有实数根时，求出m 的最小正整数的值.（3分）
25、为了把一个长100米的矩形游泳池扩建成一个周长为600米的矩形水上游乐场，把游泳池的长增加x 米，当x 为多少时，水上游乐场面积为20000平方米？（5分）
26、如图，四边形ABCD 的对角线AC 与BD 相交于点O ，12∠=∠，34∠=∠.
求证：（1）ABC ADC ∆≅∆（3分） （2）BO OD =（2分） 4
32
1A
B C
D
O
百度文库 - 让每个人平等地提升自我
5
27、RT ∆三角形ABC 中，90C ∠=度，M 是AB 的中点，点E 在BC 边上，ME AB ⊥，ME 的延长线与AC 的延长线交于点F . （1）求证A CEF ∠=∠（3分）
（2）在A ∠大小改变的过程中，ECF ∆是否可能与ABC ∆全
等？如果可能，请求出A ∠的度数；如果不可能，请简要说明理
由.（3分）
28、阅读理解：法国数学家韦达在研究一元二次方程时有一项重大发现：如果一元二次方程2
0(0)ax bx c a ++=≠的两个根分别是1x ，2x .那么12b x x a +=-，12c x x a
=. 例如：已知方程2
2350x x +-=的两根分别为1x ，2x 则：1232b x x a +=-
=-，1255
22
c x x a -===- 请同学阅读后完成以下问题：
（1）已知方程3x 2－4x －6=0的两根分别为12x x .求12x x +和12x x 的值.（2分）
（2）已知方程2
320x x +-=的两根分别为12x x ，求12
11
x x +的值.（1分）
（3）若一元二次方程2
230x mx +-=的一根大于1，另一根小于1，求m 的取值范围.（2
…………………………密○………………………………………封○………………………………………○线…………………………
M E
A B C
F
百度文库- 让每个人平等地提升自我分）
6。