第九章静电场中的导体和电介质
合集下载
第九章 导体和电介质的静电场-wmx剖析
空腔内部电荷及电场变化会对导体壳的外界产生影响
2. 腔内有带电体 q
▪ 腔内的电场不再为零，其分布
• 与电荷 q电量和分布有关
• 与内表面形状、腔内介质等因素有关
-q q
q
• 与导体外其它带电体的分布无关
这就是说：导体空腔外的电荷对空腔内的电场
及电荷分布没有影响 在腔内仍有： E外表面电荷 E其他带电体 0
1.导体的静电平衡状态 (electrostatice quilibrium)：
指导体内部和表面都没有电荷作宏观的定向运 静电平衡条件(electrostatic equilibrium condition) ：
导体内部电场强度处处为零 这也是静电平衡问题的出发点
油罐内油品蒸汽的击穿场强约为 4.5 102 kV / m 引燃可燃蒸汽的最小放电能量为 0.2mJ
防止静电事故的措施护
减少静电产生 注意消除静电放电
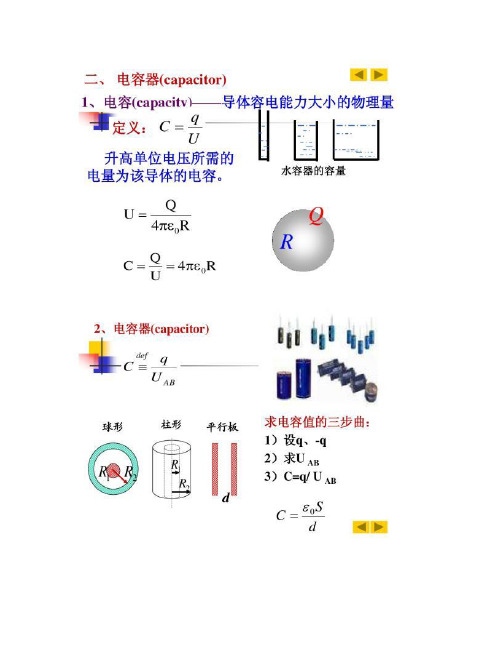
§9-3 电容器(capacitor)的电容(capacity)
• 孤立导体的电容
孤立导体的电容定义为：导体带电量与导体电势的比：
q C V
物理意义：使导体升高单位电势所需的电荷量。 1、电容是导体的客观性质，电容反映了该导体在给定电势
参考“尖端效应及其数学表示”．《大学物理》. 1993. (6).
通过实验人们得到一些定性结论：
在表面凸出的尖锐部分(曲率是正值且较大) 电荷面密度较大， 在比较平坦部分(曲率较小)电荷面密度较小， 在表面凹进部分带电面密度最小。
孤立导体
特殊情况：孤立带电导体球、长直圆柱或大的平板， 它们的面电荷分布是均匀的
S 过导体的内表面上的面元 S 作圆柱形高斯面
E dS 0 设内表面的面电荷密度为
0ch9-静电场中的导体与电介质
电磁能量.
第一讲：第1-2节 第三讲：第5-6节
第二讲：第3-4节 第四讲：习题课 1
College Physics
第一讲
§9-1 静电场中的导体 掌握导体静电平衡条件, 能用该条件分 析带电导体在静电场中的电荷分布； 求解有导体存在时场强与电势分布；
§9-2 电容 电容器 理解电容的定义 掌握计算电容的方法
思考题：
1. 希望制备一个电容为C的充满油的平行板电 容器，在等于或低于某一最大电位差Vm的情 况下, 它不致发生电弧而能安全地工作. 可是, 因为设计师设计得不够好, 电容器偶尔要发生 电弧. 试问使用同样的电介质并在C与Vm保持 不变的情况下, 你将如何重新设计这个电容器?
2. 如果电容器的电位差保持不变, 这个电容器 在有电介质时所储存的电荷是大于还是小于 没有电介质(即真空)时所储存的电荷?试以微 观来说明这种情况.
由电荷守恒
QB内 q QB外 Q q
q A
Q B
11
College Physics
2) A的电势UA
方法一：场强 积分
U A
E dl
A R2
E
dl
R3
E
dl
E dl
R1
R2
R3
R2 qdr
R1 4 0r 2
24
College Physics
结论: 电容器大小只决定于电容器极板的形状, 大
小, 相对位置以及板间电介质的性质, 而与电 容器所带电量和两板间电压无关.
计算电容的一般步骤: 1) 设电容器两个极板带有等量异号电荷; 2) 求出极板间的电场强度分布; 3) 计算两板间的电势差; 4) 由电容器电容的定义式求电容.
第一讲：第1-2节 第三讲：第5-6节
第二讲：第3-4节 第四讲：习题课 1
College Physics
第一讲
§9-1 静电场中的导体 掌握导体静电平衡条件, 能用该条件分 析带电导体在静电场中的电荷分布； 求解有导体存在时场强与电势分布；
§9-2 电容 电容器 理解电容的定义 掌握计算电容的方法
思考题：
1. 希望制备一个电容为C的充满油的平行板电 容器，在等于或低于某一最大电位差Vm的情 况下, 它不致发生电弧而能安全地工作. 可是, 因为设计师设计得不够好, 电容器偶尔要发生 电弧. 试问使用同样的电介质并在C与Vm保持 不变的情况下, 你将如何重新设计这个电容器?
2. 如果电容器的电位差保持不变, 这个电容器 在有电介质时所储存的电荷是大于还是小于 没有电介质(即真空)时所储存的电荷?试以微 观来说明这种情况.
由电荷守恒
QB内 q QB外 Q q
q A
Q B
11
College Physics
2) A的电势UA
方法一：场强 积分
U A
E dl
A R2
E
dl
R3
E
dl
E dl
R1
R2
R3
R2 qdr
R1 4 0r 2
24
College Physics
结论: 电容器大小只决定于电容器极板的形状, 大
小, 相对位置以及板间电介质的性质, 而与电 容器所带电量和两板间电压无关.
计算电容的一般步骤: 1) 设电容器两个极板带有等量异号电荷; 2) 求出极板间的电场强度分布; 3) 计算两板间的电势差; 4) 由电容器电容的定义式求电容.
第九章 导体和电介质的静电场-wmx剖析
针尖与荧光膜之间加高压，
样品附近极强的电场使吸附在表面的 H e
原 子 电离，氦离子沿电力线运动， 撞击荧光膜引起发光，
从而获得样品表面的图象。
接真空泵或 充氦气设备
荧光质 导电膜
接地
+ 高压
§9-2 空腔导体内外的静电场 何谓空腔导体 空腔导体（导体壳）的几何结构
腔外 腔内
腔内、腔外 内表面、外表面
S
S1 +q
+q
+
S2
1) 实心
2) 空腔
3) 空腔含电荷
静电平衡中的导体
由
S
E
dS
1
0
ρ dV
V
0
得 ρ ＝０
2. 导体表面电荷的面密度与曲率有关。
3. 导体表面电荷的面密度与表面附近场强有关。
E
σ
0
【证明】： 设导体表面电荷面密度σ ，如图所示。
取一足够小闭合正柱面，两端面面积ΔS，并紧贴导体表面 内外两侧，且与导体表面平行，参见图 。
设其电势为V
在腔内紧邻内表面作另一等势面 S，对应电势为V’
证明：通过闭合面S 的电通量
V
由高斯定理
E腔内
B
A
无加外外电电场场
Hale Waihona Puke E0电子在和电晶场格力点作阵用作下随作机 宏的观微定观向热运动
导体的静电感应过程
E0
外感场应EEEE00''
导体的静电感应过程
E0
E'
E
E E0 E' 0
静电平衡状态
一、静电感应现象：
在导体内部存在电场时，自由电子受电场力 作用作定向运动，从而引起导体内部正负电荷的 的重新分布，结果使导体一端带正电荷，一端带 负电荷。这就是静电感应，分布在导体上的电荷 便是感应电荷。
9-(1-2)静电场中的导体
r
q
4 0 R1
q 4 0 r
(
1 R3
)
q
( R1 r R2 )
V2
1
4 0 R3
( ) 4 0 r R2 R3
q
1
q3
q2
q
R3
R2
第六章热力学基础 ( R2 r R3 )
V3 q 4 0 r
q 4 0 R3
R1 r
q 4 0 r
'
0
R1 R2 R2 R3 R1 R3
'
q2
'
R1 R3 R2 R3 R1 R2
q3 q q2
'
( R2 R3 R1 R3 )q R1 R3 R2 R3 R1 R2
q3 '
q2 '
q'
R1 r
第六章热力学基础 球壳内表面的电势：
V3
q1 4 0 r
第六章热力学基础 电压：在AB之间 1. 4产生的场强抵消，
2 . 3产生的场强相加，
(若 2 >0,电力线如图) 2 d 故：U AB Ed 0
a
d
a
X
若QA=-QB0
1 4
QA QB
QA QB 2S
0
2S
2 3
这时电场只集中在两板之间。
+++ ++
+
+
+++
< 避雷针 >
尖端放电现象的利用
2、空腔导体 1）腔内无带电体
第九章-2静电场中的导体与电介质
εr1q σ1 = εr1S1 + εr2S2 εr2q σ2 = εr1S1 + εr2S2
S2 σ2 S σ1 S1 +q ﹢﹢﹢﹢﹢ ﹢ ﹢ ﹢ ﹢
εr1
−σ1
εr2
−σ2
d
−q - - - - - - - - V =Ed 1 ± qd = ε0(εr1S1 + εr2S2 ) q C= V ±
=
4 0εr R πε
Q
例2、求电荷分布、场 求电荷分布、 电位移及电容。 强、电位移及电容。 解 关键是把自由电荷 确定下来。 的分布 确定下来。
+q
S1
S
S2
εr1
εr2
d
−q
S2 σ2 S σ1 S1 +q ﹢﹢﹢﹢﹢ ﹢ ﹢ ﹢ ﹢
在介质1内 在介质 内：
σ1 E σ1 10 E = ;E = = 10 1 ε0 εr1 ε0εr1
r r 表示： S 电位移通量用 ΦD 表示： ΦD = ∫ D⋅ d =
S
∑q
in side
0i
电位移的计算 r r r r 再利用公式： 先求得场强 E ，再利用公式： D = ε 0 ε r E 求出电位移 D .
例1、 已知 导体球 R Q 、 已知:导体球 介质
εr
εr
R
r 求:1 球外任一点的 E 1
r D a
r D b
电位移线
b
r D
r D
方向:切线 方向 切线
在介质中 产生电场
a
大小: 位 线 数 大小 电 移 条
S⊥
有介质时的高斯定理: 有介质时的高斯定理
r r ∫εrε0E•dS =∑qi
第九章 静电场中的导体和电介质3_百度文库讲解
S d/2 金属板—— 金属板d/2 ε1 r ε2 r d d U = E1 + E 2 2 2 σ0 d σ0 d = + ε0ε r1 2= =U U 2ε 0 ε r1ε r 2S ⇒C = (ε r1 + ε r 2 d击穿(breakdown 当外场很大时， 击穿(breakdown ——当外场很大时，电介 当外场很大时 质的绝缘性能遭到破坏。
质的绝缘性能遭到破坏。
所能承受的不被击穿的最大场强叫做击穿 所能承受的不被击穿的最大场强叫做击穿 场强(breakdown field strength 场强 击穿场强所对应的电压值叫做耐压值 击穿场强所对应的电压值叫做耐压值 击穿场强所对应的电荷值叫做最大储电量 击穿场强所对应的电荷值叫做最大储电量 最大 空气 1.00059 3 (kV/mm 12 (kV/mm 160 (kV/mm 变压器油2.2~2.5 云母 5.4例3、一圆柱形电容器，外柱的直径为 、一圆柱形电容器，外柱的直径为4cm ，内柱的直 ， 径可以适当选择。
若其间充满各向同性的均匀介质， 径可以适当选择。
若其间充满各向同性的均匀介质， 该介质的击穿场强是200V/cm ，试求该电容器可能承 该介质的击穿场强是 ， 受的最高电压。
（自然对数的底e=2.7183） 。
（自然对数的底 受的最高电压。
（自然对数的底 ） 设内外圆柱单位长度带电λ 解: 设内外圆柱单位长度带电λe 、 -λe λ R1 R2 ∫∫ D ⋅ dS = 2πrLD = λeL L λe ⇒D= 2πr λe D E= = ε 0ε r 2πε0ε r rE 击 λe = = 200 V / cm 2 πε 0 ε r R 1 E 击R1 λe ⇒E= = 2πε0εr r r U R1R2 = E 击 R1 ∫ R2 R1 dr R2 = E 击 R 1 ln r R1 dR1 R1 R2 dUR1R2 R2 = 0 ⇒ R1 = e L U R1R2 max = 147 kV。
普通物理学第五版第9章导体和电介质中的静电场章答案
解： (1)由于静电感应，外球内表面电量为 -q，外表面电量为+q q 外球的电势为： U2 = 4pe0 r2 (2)外球内表面电量仍为-q,外表面电量为零 外球的电势为： ´ U2 = 0
(3)设内球电量为q1,内球电势为零 q1 q r1 U1 = q1 = r q 4pe0 r1 + 4pe0 r2 =0 2 q1 q U外 = 4pe0 r2
q1 q2 U1 = 4pe0 R1 + R2 q2 q1 = R1 4pe0 U1 R2
1
2700 -2 = 5.0×10 9.0×109 = 1.0×10-8(C) 8.0×10-9 8.0×10-2
结束 目录
两球接触后，内球电荷q1全部移至外球 壳，两球为等势体。
q1 + q2 U= = 2.03×103(V) 4pe0R2 ΔU内 = 2.7×103 2.03×103 = 6.7×102(V)
d +q
结束 目录
9-6 半径为r1 、 r2 (r1 < r2 )的两个同心导 体球壳互相绝缘，现把+q 的电荷量给予内 球，求： （1）外球的电荷量及电势； （2）把外球接地后再重新绝缘，外球的 电荷量及电势； （3）然后把内球接地，内球的电荷量及 外球的电势的改变(设内球离地球很远)。
结束 目录
结束 目录
9-11 三平行金属板A、B 、C面积均为 200cm2，A、B 间相距4.0mm， A、C 间 相距2.0mm，B 和C 两板都接地。如果使A 板带正电3.0×10-7C ，求： （1）B 、C 板上感应电荷； （2）A 板的电势。 2mm 4mm C A B
目录
解：设A板带电为q =q1+q2，B、C两板的感 应电荷分别为- q1及- q2 。 EAB dAB = EAC dAC UA UB = UA UC q2 q1 EAC = EAB = e0S 2mm 4mm e0 S q1 EAB dAC 1 C A B = E =d = 2 q2 AC AB q1 q2 q1= 1.0×10-7(C) -q1 -q2 q2= 2.0×10-7(C) qB= -q1= -1.0×10-7(C) qC= -q2= -2.0×10-7(C)
静电场中的导体和电介质
3、对 D 的讨论
(1)
形式上的简单而引入的,没有确切的物 理意义;描述电场性质的物理量仍然是
D 是辅助量,是为了计算方便、定理
(2) 对各向同性介质,某点 E 确定, D也
确定.两者关系：
E 和 V。
D 0 r E E
（3）电位移通量是和自由电荷联系在 起的。
S
Q0 1 SE dS 0 0
P dS
S
令
D 0E P
则：
S
D dS Q0
2、电介质中的高斯定理
叙述:任何电场中，通过任意闭合曲面的 电位移通量等于该面所包围的自 由电荷的代数和。 数学表达：
n D dS (Q0 ) i S i 1
( R1 r R2 )
E1 (r R1 ) 2π 0 r R1 E2 (r R2 ) 2π 0 r R2
所以，电介质两表面极化电荷面密度的值分别为
1 ( r 1) 0 E1 ( r 1) 2π r R1 ( r 1) 0 E2 ( r 1) 2 2π r R2
2 D dS D 4r q0 q0 D 所以 2 4r q0 写成矢量式为 D r 3 4r 因 D E , 所以离球心r 处P点的场强为 D q0 q0 E E r r 3 3 4r 4 0 r r r
解 （1）由于电荷分布是均匀对称的，所以电介 质中的电场也是柱对称的，电场强度的方向沿柱 面的径矢方向。 作一与圆柱导体同轴的柱形高 斯面，其半径为 r ( R1 r R2 ) 、长为 l 。 因为电介质中的电位移 D 与柱形高斯面的两底面 的法线垂直，所以通过这两底面的电位移通量为 零。 根据电介质中的高斯定理，有
第九章静电场中的导体和介质部分习题分析与解答
Q d d 1 2 U BA 0S d d 1 2 Q d d2 1 U AC 0S d 1 d 2
9-6 在真空中，将半径为R的金属球接地，与球心 O相距为r(r>R)处放置一点电荷q，不计接地导线上 电荷的影响。求金属球表面上的感应电荷总量。 解：金属球为等势体，金属 q’ 球上任一点的电势V等于点电 R q 荷q和金属球表面感应电荷q’ O 在球心处激发的电势之和。 r 而金属球接地，总电势为零。 所以球心处的电势为
解： （1）由于静电平衡时电荷只分布于导体的表面上， 故：球A在外表面带电QA=3.0 10-8 C，球壳B内表面 带电-QA= -3.0 10-8 C，球壳B外表面带电QA + QB = 5.0 10-8 C。 由电势的叠加，知球A和球壳B的电势分别为： Q Q Q 3 A A Q A B V 5 . 6 10 V A 4 R R R 0 1 4 0 2 4 0 3
QA qA VB 40R 3
R R Q 8 1 2 A 解得： q 2 . 12 10 C A R R R R R R 1 2 2 3 1 3
Q q 2 A A 得： V 7 . 92 10 V B 4 R 0 3
即，球A的外表面、球壳B的内、外表面所带的电荷 分别为：2.1210-8 C、 -2.1210-8 C、 -0.910-8 C.
( 1 ) Q r P ( 1 ) E ； n r 0 n 2 4 ( R d ) r ( 1 ) Q 8 2 r P 1 . 6 10 C m ； n 2 4 ( R d ) r
在介质内表面：
( 1 ) Q r P ( 1 ) E ； n r 0 n 2 4 rR ( 1 ) Q 8 2 r P 6 . 4 10 C m ； n 2 4 R r
普通物理学第五版第9章导体和电介质中的静电场章答案
σ
-q dm
结束 目录
解：
F =qE =ma
σ 2e
0
q
=ma
a
=
σq 2e 0m
v=
2ad
=
σ qd 2e 0m
t
=
v a
=
σ qd 2e 0m
.
2e σ
0m q
=
4e 0md σq
结束 目录
9-2 有一块很大的带电金属板及一小球，
已知小球的质量为m =1.0×10-3g，带有电
荷量q =2.0×10-8C，小球悬挂在一丝线的
结束 目录
解：(1)
UR2=
q
4pe0 R2
=
9.0×109×
4.0×10-10 3.0×10-2
=120(V)
(2)由静电感应和电势叠加原理
Ur
=
1
4pe0
q r
qq R1 + R2
1
=9.0×109×4×10-10× 1×10-2
1 2×10-2
+
1 3×10-2
=300(V)
(3)因不影响导体壳外表面电荷，所以电势
与(1)相同。
结束 目录
9-8 有直径为16cm及10cm的非常薄的两 个铜制球壳，同心放置时，内球的电势为 2700V，外球带有电荷量为8.0×10-9C，现 把内球和外球接触，两球的电势各变化多少？
结束 目录
解：设内球电势为U1 ，电量为q1，外球 电势为U2 ，电量为q2
U1
=
1
4pe0
q1 R1
1 2 34
结束 目录
解：设两个板四个面的电荷面密度分别为
s1, s2, s3, s4,
-q dm
结束 目录
解：
F =qE =ma
σ 2e
0
q
=ma
a
=
σq 2e 0m
v=
2ad
=
σ qd 2e 0m
t
=
v a
=
σ qd 2e 0m
.
2e σ
0m q
=
4e 0md σq
结束 目录
9-2 有一块很大的带电金属板及一小球，
已知小球的质量为m =1.0×10-3g，带有电
荷量q =2.0×10-8C，小球悬挂在一丝线的
结束 目录
解：(1)
UR2=
q
4pe0 R2
=
9.0×109×
4.0×10-10 3.0×10-2
=120(V)
(2)由静电感应和电势叠加原理
Ur
=
1
4pe0
q r
qq R1 + R2
1
=9.0×109×4×10-10× 1×10-2
1 2×10-2
+
1 3×10-2
=300(V)
(3)因不影响导体壳外表面电荷，所以电势
与(1)相同。
结束 目录
9-8 有直径为16cm及10cm的非常薄的两 个铜制球壳，同心放置时，内球的电势为 2700V，外球带有电荷量为8.0×10-9C，现 把内球和外球接触，两球的电势各变化多少？
结束 目录
解：设内球电势为U1 ，电量为q1，外球 电势为U2 ，电量为q2
U1
=
1
4pe0
q1 R1
1 2 34
结束 目录
解：设两个板四个面的电荷面密度分别为
s1, s2, s3, s4,