框架内力组合
框架设计内力计算与组合

C
四 框架内力组合 3 梁柱内力调整
强剪弱弯
强剪弱弯、强柱弱梁、强结点弱构件
组合后的调整(有地震组合) 梁剪力调整(有地震组合)
l (M b M br ) V RE b VGb ln
强剪弱弯 强柱弱梁
柱弯矩调整(有地震组合) 柱剪力调整
M
C
C M b
t b V C ( M C MC ) / Hn
强剪弱弯——梁剪力调整
受弯 0.75
受剪 0.85
l (M b M br ) V RE b VGb l n
262 .76 350 .347 0.75
29.703kN/m
292 .59 390 .12 0.75
262 .76 350 .347 0.75
B 5.4m
29.703kN/m
195 .56 260 .747 0.75
A
1.2 260 .747
A B 5.4m
29.703kN/m
1.2 350 .347
左震
135 .799
135 .799
A
B 5.4m
80 .198
80 .198
梁柱
1.2SGk 0.91.4SQK 1.4SWK 1.35SGk 1.4 0.7SQK
1.2SGk 1.4SQk
四 框架内力组合
2 梁柱内力组合
有地震作用效应的组合 rRES≤R
受弯:0.75
受剪: 0.85
SGK
SQK
SEK
屋面荷载取雪荷载 对多层结构,风荷载不参与组合
A
B
M
C
C M b
内力组合(框架柱内力组合表)

-52.00
-12.39
-4.9 7.6
底 N 464.97 117.62(100.31) -4.9
柱 M 52.00
12.39
-15.2
4
顶 柱
N M
649.09 176.61(159.30)
-52.00
-12.39
-5.2 12.4
底 N 734.74 176.61(159.30) -5.2
柱 M 52.00
17.80
33.6 21.2
底 N ####### 283.26(283.24) 33.6
柱 M -77.48
-19.54
-34.5
1
顶 柱
N ####### 340.15(340.13)
M 38.74
9.77
47.7 67.0
底 N ####### 340.15(340.13) 47.7
表6-5(a
柱 M -81.40
-21.53
-21.4
3
顶 柱
N M
879.34 80.91
226.62(226.6) 21.04
21.7 17.5
底 N 993.54 226.62(226.6) 21.7
柱 M -76.72
-20.00
-25.9
2
顶 柱
N ####### 283.26(283.24)
M 71.36
28.42 -28.42 -69.03 -71.55
###### 12.01 160.21 161.27
###### 95.63 67.10 77.25
###### 40.24 382.59 387.00
63.75 -63.75 -67.84 -74.62
内力组合及内力调整

7 内力组合及内力调整7.1内力组合各种荷载情况下的框架内力求得后,根据最不利又是可能的原则进行内力组合。
当考虑结构塑性内力重分布的有利影响时,应在内力组合之前对竖向荷载作用下的内力进行增幅。
分别考虑恒荷载和活荷载由可变荷载效应控制的组合和由永久荷载效应控制的组合,并比较两种组合的内力,取最不利者。
由于构件控制截面的内力值应取自支座边缘处,为此,进行组合前,应先计算各控制截面处的(支座边缘处的)内力值。
1)、在恒载和活载作用下,跨间max M 可以近似取跨中的M 代替,在重力荷载代表值和水平地震作用下,跨内最大弯矩max M 采用解析法计算:先确定跨内最大弯矩max M 的位置,再计算该位置处的max M 。
当传到梁上的荷载为均布线荷载或可近似等效为均布线荷载时,按公式7-1计算。
计算方式见图7-1、7-2括号内数值,字母C 、D 仅代表公式推导,不代表本设计实际节点标号字母。
2max182M M M ql +≈-右左 且满足2max 116M ql = (7-1) 式中:q ——作用在梁上的恒荷载或活荷载的均布线荷载标准值;M 左、M 右——恒载和活载作用下梁左、右端弯矩标准值;l ——梁的计算跨度。
2)、在重力荷载代表值和地震作用组合时,左震时取梁的隔离体受力图,见图7-1所示, 调幅前后剪力值变化,见图7-2。
图7-1 框架梁内力组合图图7-2 调幅前后剪力值变化图中:GC M 、GD M ——重力荷载作用下梁端的弯矩; EC M 、CD M ——水平地震作用下梁端的弯矩C R 、D R ——竖向荷载与地震荷载共同作用下梁端支座反力。
左端梁支座反力:()C 1=2GD GC EC ED ql R M M M M l--++;由0M ddx=,可求得跨间max M 的位置为:1C /X R q = ; 将1X 代入任一截面x 处的弯矩表达式,可得跨间最大弯矩为: 弯矩最大点位置距左端的距离为1X ,1=/E X R q ;()101X ≤≤; 最大组合弯矩值:2max 1/2GE EF M qX M M =-+;当10X <或11X >时,表示最大弯矩发生在支座处,取1=0X 或1=X l ,最大弯矩组合设计值的计算式为:2max C 11/2GE EF M R X qX M M =--+; 右震作用时,上式中的GE M 、EF M 应该反号。
框架柱内力的基本组合值
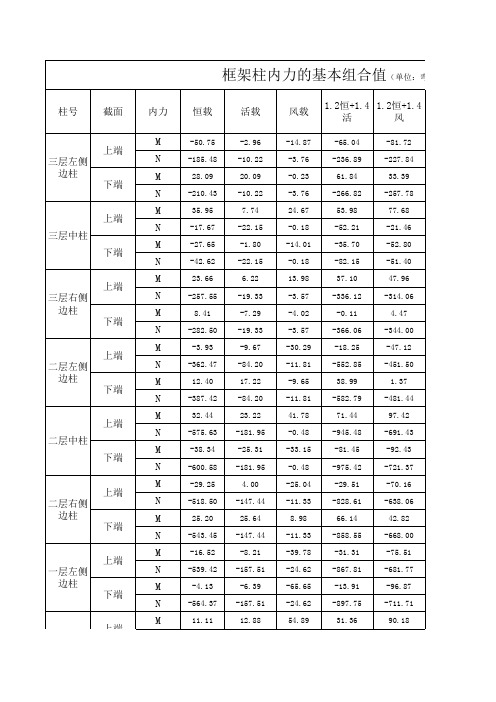
选取内力
Mmax=-83.36; 相应N=240.19 Nmax=270.13; 相应M=61.84 Nmin=-217.32; 相应M=-40.08 Mmax=83.97; 相应N=-52.21 Nmax=-82.15; 相应M=-53.1 Nmin=-20.95; 相应M=8.61 Mmax=53.84; 相应N=-37.91 Nmax=-367.86; 相应M=-4.61 Nmin=-304.05; 相应M=8.81 Mmax=-55.06; 相应N=-555.94 Nmax=-585.88; 相应M=38.99 Nmin=-418.43 相应M=37.69 Mmax=-119.69; 相应N=-975.42 Nmax=-975.42; 相应M=-119.69 Nmin=-690.08; 相应M=-19.56 Mmax=73.87; 相应N=-858.55 Nmax=-858.55; 相应M=73.87 Nmin=-606.34; 相应M=0.04 Mmax=-96.87; 相应N=-906.72 Nmax=-906.72; 相应M=-96.87 Nmin=-612.83; 相应M=35.86 Mmax=-135.11; 相应N=-1488.63 Nmax=-1488.63; 相应M=-135.11 Nmin=-968.37; 相应M=-63.53
-987.88 -124.03 -1017.81 -79.48 -966.64 -95.43 -996.58
值(单位:弯矩kN·m,剪力kN,轴力kN)
1.2恒+1.26× (活+风)
-83.36 -240.19 58.73 -270.13 83.97 -49.34 -53.10 -79.28 53.84 -337.91 -4.16 -367.86 -55.06 -555.94 24.42 -585.88 120.83 -920.61 -119.69 -950.55 -61.62 -822.24 73.87 -852.18 -80.28 -876.78 -95.73 -906.72 98.72
第七章-内力组合

第7章 框架结构的内力组合§7.1框架结构梁内力组合§7.1.1. 框架结构梁的内力组合在竖向荷载作用下,可以考虑梁端塑性变形内力重分布而对梁端负弯距进行调幅,调幅系数为现浇框架:0.8-0.9,本设计取0.85。
计算结果见表7-1 横梁弯矩调幅。
由于风荷载作用下的组合与考虑地震组合相比,一般较小,对于结构设计不起控制作用,故不考虑。
只考虑以下三种组合形式: 一.由可变荷载效应控制的组合:1.2 1.4QK QKS S S =+(71)-二.由永久荷载效应控制的组合:1.35 1.40.7QK QK S S S =+⨯⨯ (72)-三.竖向荷载与水平地震作用下的组合:1.2(0.5) 1.3QK QK EK S r S S =+⨯+ (73)-具体组合过程见表7.2,其中弯矩KN.m ,剪力KN ,弯矩的上部受拉为负,剪力的产生顺时针为正。
表7-1 横梁弯矩调幅§7.1.2 梁端弯矩控制值梁的支座截面考虑了柱支撑宽度的影响,按支座边缘截面的弯矩计算,即:`/2=-⨯(7-4),M M V b式中:M为梁内力组合表中支座轴线的弯矩值;V为相应的支座剪力;b为相应的柱的宽度;计算结果见表7-3表7-3 梁端弯矩控制值§7.1.3梁端截面组合的剪力设计值调整为防止梁在弯曲屈服前发生剪切破坏,即保证“强剪弱弯”截面设计须对有地震作用的组合剪力设计值按(7-5)进行调整。
()/lr vb b b n GB V M M l V η=-+ (7-5)式中:n l 为梁的净跨;GB V :为梁的重力荷载代表值,按简支梁分析的梁端截面剪力设计值;,l r b b M M :分别为梁左右净截面,逆时针或顺时针方向的弯矩设计值;vb η:为梁端剪力增大系数,对于二级框架取1.2 计算结果见表7-4§7.2框架结构柱的内力组合§7.2.1框架结构柱的内力组合柱上端控制值截面在梁底,下端在梁顶,应按轴线计算简图所得的柱端内力值换成控制截面的相应值,此计算为简化起见,采用轴线处内力值。
六层框架楼内力组合形式

内力组合各种荷载情况下的框架内力求得后,根据最不利又是可能的原则进行内力组合。
当考虑结构塑性内力重分布的有利影响时,应在内力组合之前对竖向荷载作用下的内力进行调幅。
其中在恒载作用下,对梁端负弯矩进行调幅,调幅系数为0.8,而且当梁端负弯矩减小后,应按平衡条件计算调幅后的跨中弯矩,调整后梁跨中正弯矩至少应取按简支梁计算的跨中弯矩的一半,即20161gl M ≥中。
在活载作用下,采用满跨布置荷载的方法,对梁端负弯矩进行调幅,调幅系数也为0.8,而且当梁端负弯矩减小后,应按平衡条件计算调幅后的跨中弯矩。
但在满跨布置荷载时,求得的梁的跨中弯矩比最不利荷载位置法的计算结果要小,因此对跨中弯矩应乘以1.2的系数予以增大。
调整后梁跨中正弯矩至少应取按简支梁计算的跨中弯矩的一半,即20161ql M ≥中。
分别考虑恒荷载和活荷载有可变荷载效应控制的组合和由永久荷载效应控制的组合,并比较两种组合的内力,取最不利者。
由于构件控制截面的内力值应取自支座边缘处,为此,进行组合前,应先计算各控制截面处的(支座边缘处的)内力值。
梁支座边缘处的内力值:2-2b -b q V V V M M ⋅=⋅=边边式中 边M -支座边缘截面的弯矩标准值; 边V -支座边缘截面的剪力标准值; M -梁柱中线交点处的弯矩标准值;V - 与M 相应的梁柱中线交点处的剪力标准值; q -梁单位长度的均布荷载标准值; b -梁端支座宽度(即柱截面高度)。
柱上端控制截面在上层的梁底,柱下端控制截面在下层梁顶。
按轴线计算简图算得的柱端内力值,宜换算到控制截面处的值。
23表 3 梁控制截面弯矩和剪力值表 4框架梁的内力组合表78910表 5 框架柱的内力组合表表 6 梁端剪力设计值调整。
框架结构的内力组合及截面设计
框架梁的控制截面最不利内力组合有以下几种: 1) 梁端支座截面 M 、 max M max 和 Vmax 。 2) 梁跨中截面 M 、 max M max 。
(2)框架柱 柱的内力包括弯矩、剪力和轴力。框架柱的控制截面一般在柱
的两端,柱的两端为弯矩最大值,剪力和轴力在同一层中无变化或 变化很小。
由于框架柱一般采用对称配筋,组合时要选择绝对值 最大的弯矩,柱最不利内力可归纳成以下四种:
① Mmax 及相应的 N 、V 。 ② N max 及相应的 M 、V 。 ③ Nmin 及相应的 M 、V 。 ④ M 比较大(不是绝对最大),但N比较小或比较大(不是绝 对最小或最大)。绝对最大或最小的内力不一定就是最不利 的,对大偏心受压构件,若 M 不是最大,而N较小,则 e0 M / N 最大,截面配筋可能最多;对小偏心受压构件, e0 越小截面配筋越多。
对于现浇框架,支座弯矩的调幅系数采用 0.8~0.9;对于装配整体式框架,由于钢筋焊接 及接缝不密实等原因,后浇节点连接刚度较差, 受力后可能产生节点变形,造梁端弯矩降低, 调幅系数取0.7~0.8。
支座弯矩降低会引起跨中弯矩增加,但荷 载组合求出的跨中最大正弯矩和支座最大负弯 矩不是在同一荷载作用下出现的,支座弯矩调 幅后,若调幅后的跨中弯矩不超过跨中最不利 正弯矩,跨中配筋不必增大。
以上组合中前三组用来计算柱正截面受压 承载力,以确定纵向受力钢筋数量;第四组用以 计算斜截面受剪承载力,以确定箍筋数量。
进行内力分析时是以柱轴线处考虑的,实际 梁支座截面的最不利位
第七章-内力组合
-98.5282
-95.3882
-102.29
-64.4735
M
68.24
27.54
12.603
-18.2556
-14.5966
-23.351
37.679
-69.779
C4D4
M
-68.58
-22.51
6.719
-6.719
77.76
-77.76
-113.81
-115.093
-72.8894
-91.7026
-102.193
-119.125
5.286
-196.89
V
-67.62
-24.59
-1.671
-7.929
-67.131
V
-12.96
-0.88
-1.333
1.333
-16.87
16.87
-16.784
-18.376
-17.4182
-13.6858
-18.3404
-14.9812
-38.011
5.851
跨中
M
-32.24
-1.43
0
0
0
0
-40.69
-44.954
-38.688
-38.688
-69.261
-100.696
-98.9193
-93.808
-74.8405
M
69.53
24.59
5.039
-5.039
63.17
-63.17
117.862
118.4555
90.4906
76.3814
120.7685
内力组合表 (2)
附录2 内力组合表附录2.1 框架梁的内力组合表层次截面内力S GK S QKS EK S EK组合一组合二组合三组合四组合五组合六组合七组合八组合九组合十组合十一组合十二组合十三剪力调整左风右风左震右震一层AM -92.23-24.57(-24.74)43.80 -27.30 160.80 -171.40 -145.06 -49.35 -148.89 -86.43 -176.02 -111.79 -171.51 -30.91 -130.45 62.65 -261.25 78.34 -245.56144.04 V94.1024.4(24.4)-10.40 6.50 -38.30 40.90 147.08 98.36 122.02 130.56 151.85 142.21 156.41 79.54 103.20 66.10 153.62 48.03 135.55跨中M120.4835.52(35.64)2.65 -1.65 9.50 -10.10 194.30 148.29 142.27 192.67 187.25 199.68 196.07 124.19 118.17 133.73 114.62 112.99 93.88B左M-110.84-31.03(-30.77)-38.50 24.00 -141.80 151.20 -176.44 -186.91 -99.41 -220.61 -141.86 -212.38 -159.88 -164.74 -77.24 -251.86 33.82 -232.92 52.75 V99.6026.3(26.2)-10.40 6.50 -38.30 40.90 156.34 104.96 128.62 139.55 160.85 151.50 165.69 85.04 108.70 72.63 160.15 53.47 140.99B右M-20.91-5.78(-5.36)21.10 -13.20 77.50 -82.90 -33.18 4.45 -43.57 -5.79 -49.01 -16.17 -44.98 8.63 -39.39 54.33 -102.06 57.87 -98.52121.80 V23.905.8(4.7)-18.90 11.50 -69.40 74.30 36.80 2.22 44.78 12.17 50.48 22.07 47.61 -2.56 40.00 -49.91 108.88 -54.37 104.41跨中M 1.20-0.36(-1.08)-2.60 1.65 -9.45 10.15 0.94 -2.20 3.75 -2.29 3.07 -0.92 2.65 -2.44 3.51 -8.62 10.49 -8.72 10.39CM-0.17-0.255(-0.77)-26.30 16.50 -96.40 103.20 -0.56 -37.02 22.90 -33.66 20.26 -22.57 13.38 -36.99 22.93 -93.80 100.81 -93.83 100.78 V 3.700.1(1.1)-18.90 11.50 -69.40 74.30 4.58 -22.02 20.54 -19.25 19.06 -10.78 14.75 -22.76 19.80 -72.35 86.44 -73.07 85.71二层AM-89.17-24.31(-24.99)31.50 -19.70 137.20 -142.80 -141.03 -62.90 -134.58 -97.94 -162.45 -117.74 -160.74 -45.07 -116.75 42.28 -230.72 57.53 -215.48110.30 V93.8024.4(24.4)-7.60 4.70 -32.90 34.30 146.72 101.92 119.14 133.73 149.23 144.16 154.49 83.16 100.38 71.77 146.02 53.75 128.00跨中M123.6036(35.28)1.55 -1.00 7.10 -7.35 198.72 150.49 146.92 195.63 192.42 203.44 201.30 125.77 122.20 134.04 119.95 112.85 98.76B左M-109.57-30.77(-31.03)-28.40 17.70 -123.00 128.10 -174.56 -171.24 -106.70 -206.03 -147.95 -201.92 -163.20 -149.33 -84.79 -232.49 12.33 -213.73 31.09 V99.9026.3(26.2)-7.60 4.70 -32.90 34.30 156.70 109.24 126.46 143.44 158.94 154.26 164.59 89.26 106.48 78.91 153.16 59.70 133.95B右M-22.95-6.035(-5.19)15.20 -9.50 66.10 -68.90 -35.99 -6.26 -40.84 -15.99 -47.11 -24.13 -44.88 -1.67 -36.25 41.46 -90.17 45.29 -86.33101.40 V25.60 6(4.6) -13.40 8.30 -58.40 60.90 39.12 11.96 42.34 21.40 48.74 29.18 47.41 6.84 37.22 -5.95 95.75 -40.82 91.01跨中M 2.28-0.48(-0.96)-1.60 1.00 -7.05 7.35 2.06 0.50 4.14 0.12 3.39 1.26 3.45 0.04 3.68 -5.25 8.79 -5.52 8.52CM-1.190.34(0.68)-18.40 11.50 -80.20 83.60 -0.95 -27.19 14.67 -24.18 13.49 -16.73 8.39 -26.95 14.91 -78.96 80.75 -78.83 80.87 V 2.00 0.3 (1) -13.40 8.30 -58.40 60.90 2.82 -16.36 14.02 -14.11 13.24 -8.26 9.97 -16.76 13.62 -61.98 69.84 -62.41 69.42注:表中组合一到组合十三的荷载组合式子以及剪力的调整见计算书的4.6.2节()中的数值为雪荷载作用下的内力;弯矩M的单位为kN·m,剪力V的单位为kN。
毕业设计-框架内力组合(柱)
根据实验数据,分析框架内力组合(柱)在不同工况 下的受力性能,探究其受力规律和破坏机理。
结论总结
总结实验结果,得出框架内力组合(柱)的受力性能 和适用范围,为工程实践提供理论依据。
04
框架内力组合(柱)的数值模
拟研究
数值模拟方法介绍
有限元法
01
将结构离散化为有限个小的单元,通过求解这些单元的力学平
01
02
03
试件制作
根据实验要求,制作不同 尺寸和材料的框架内力组 合(柱)试件。
加载装置
设计合理的加载装置,模 拟实际工程中的受力情况, 对试件进行加载。
数据采集
在实验过程中,使用测量 仪器实时采集试件的应变、 位移等数据,记录实验过 程中的重要信息。
实验结果分析
数据处理
对采集的数据进行整理、分析和处理,提取有用 的信息。
工程特点
建筑高度高,抗震设防烈度高,对结构安全 性要求高
框架内力组合(柱)在工程中的应用分析
内力组合柱的设计
根据建筑需求和结构要求,进行内力 组合柱的截面尺寸、配筋等设计。
内力组合柱的承载能力分析
通过有限元分析等方法,对内力组合 柱的承载能力进行计算和评估。
内力组合柱的稳定性分析
考虑轴压比、长细比等因素,对内力 组合柱的稳定性进行分析。
内力组合柱的优化设计
根据分析结果,对内力组合柱的设计 进行优化,以提高结构的安全性和经 济性。
框架内力组合(柱)在工程中的优化建议
合理选择材料
优化截面尺寸
选用高强度钢材或混凝土,以提高内力组 合柱的承载能力和抗震性能。
根据计算和分析结果,合理调整内力组合 柱的截面尺寸,以实现经济、合理的结构 设计。
