直线方程题型分类总结
直线方程公式大全
直线方程公式大全一、一般式方程直线的一般式方程表示为 Ax + By + C = 0，其中 A、B、C 为常数。
直线方程大全中的其他形式可以通过一般式方程推导得出。
二、斜截式方程斜截式方程是直线方程的另一种常见形式。
它表示为 y = mx + c，其中 m 为斜率，c 为截距。
三、截距式方程截距式方程也是直线方程的一种常见形式，表示为 x/a + y/b = 1，其中 a、b 分别为 x 轴和 y 轴的截距。
四、两点式方程两点式方程通过直线上的两个点来表示直线方程。
设直线上的两个点为 (x1, y1) 和 (x2, y2)，则两点式方程表示为 (y - y1) = ((y2 - y1)/(x2 - x1))(x - x1)。
五、点斜式方程点斜式方程利用直线上的一个已知点的坐标和该直线的斜率来表示方程。
设已知点为 (x1, y1)，斜率为 m，则点斜式方程表示为 y - y1 = m(x - x1)。
六、垂直线方程垂直线的特点是斜率不存在，所以其方程可以表示为 x = a，其中 a 为与 y 轴垂直的线在 x 轴上的截距。
七、水平线方程水平线的特点是斜率为零，所以其方程可以表示为 y = a，其中 a 为与 x 轴平行的线在 y 轴上的截距。
八、点式方程点式方程是直线方程中最简单的形式，利用直线上的一个已知点的坐标来表示直线方程。
设已知点为 (x1, y1)，则点式方程表示为 (y - y1) = m(x - x1)，其中 m 为直线的斜率。
九、角平分线方程角平分线是将一个角平分成两个相等的角的线段。
设角的两边斜率分别为 m1 和 m2，角平分线的斜率可表示为 m = (m1 + m2)/2，将平分线上的一个点坐标 (x1, y1) 代入点斜式方程可得到角平分线方程。
十、法线方程直线的法线是与该直线垂直的直线。
设直线的斜率为 m，法线的斜率可表示为-1/m，再通过已知点 (x1, y1) 可以得到法线方程。
直线的方程知识点及题型归纳总结
直线的方程知识点及题型归纳总结知识点精讲一、基本概念 斜率与倾斜角我们把直线y kx b =+中k 的系数k （k R ∈）叫做这条直线的斜率，垂直于x 轴的直线，其斜率不存在。
x 轴正方向与直线向上的方向所成的角叫这条直线的倾斜角。
倾斜角[)0,απ∈，规定与x 轴平行或重合的直线的倾斜角为0，倾斜角不是2π的直线的倾斜角的正切值叫该直线的斜率，常用k 表示，即tan k α=。
当0k =时，直线平行于轴或与轴重合；当0k >时，直线的倾斜角为锐角，倾斜角随k 的增大而增大； 当0k <时，直线的倾斜角为钝角，倾斜角k 随的增大而减小； 二、基本公式1. 111222(,),(,)P x y P x y 两点间的距离公式12||PP =2. 111222(,),(,)P x y P x y 的直线斜率公式121212tan (,)2y y k x x x x παα-==≠≠-3.直线方程的几种形式（1）点斜式：直线的斜率k 存在且过00(,)x y ，00()y y k x x -=- 注：①当0k =时，0y y =；②当k 不存在时，0x x = （2）斜截式：直线的斜率k 存在且过(0,)b ，y kx b =+（3）两点式：112121y y x x y y x x --=--，不能表示垂直于坐标轴的直线。
注：211121()()()()x x y y x x y y --=--可表示经过两点1122(,),(,)P x y Q x y 的所有直线 （4）截距式：1x ya b+=不能表示垂直于坐标轴及过原点的直线。
（5）一般式：220(0)Ax By C A B ++=+≠，能表示平面上任何一条直线（其中，向量(,)n A B =是这条直线的一个法向量）题型归纳及思路提示题型1 倾斜角与斜率的计算 思路提示正确理解倾斜角的定义，明确倾斜角的取值范围，熟记斜率公式1212y y k x x -=-，根据该公式求出经过两点的直线斜率，当1212,x x y y =≠时，直线的斜率不存在，倾斜角为90求斜率可用tan (90)k αα=≠，其中α为倾斜角，由此可见倾斜角与斜率相互关联，不可分割。
专题2.2 直线的方程(一)：直线方程的几种形式【八大题型】(举一反三)(人教A版2019选择性必修
专题2.2 直线的方程（一）：直线方程的几种形式【八大题型】【人教A版（2019）】【题型1 直线的点斜式方程及辨析】 (2)【题型2 直线的斜截式方程及辨析】 (2)【题型3 直线的两点式方程及辨析】 (3)【题型4 直线的截距式方程及辨析】 (4)【题型5 直线的一般式方程及辨析】 (5)【题型6 直线一般式方程与其他形式之间的互化】 (6)【题型7 求直线的方向向量】 (7)【题型8 根据直线的方向向量求直线方程】 (7)【知识点1 直线的点斜式、斜截式方程】1．直线的点斜式方程(1)直线的点斜式方程的定义：设直线l经过一点，斜率为k l的点斜式方程.(2)点斜式方程的使用方法：①已知直线的斜率并且经过一个点时，可以直接使用该公式求直线方程.②当已知直线的倾斜角时，若直线的倾斜角，则直线的斜率不存在，其方程不能用点斜式表示，但因为l上每一个点的横坐标都等于x1，所以直线方程为x=x1；若直线的倾斜角，则直线的斜率，直线的方程为.2．直线的斜截式方程(1)直线的斜截式方程的定义：设直线l的斜率为k，在y轴上的截距为b，则直线方程为y=kx+b，这个方程叫作直线l的斜截式方程.(2)斜截式方程的使用方法：已知直线的斜率以及直线在y轴上的截距时，可以直接使用该公式求直线方程.【题型1 直线的点斜式方程及辨析】【例1】（2023春·江西九江·高二校考期中）过两点(0,3),(2,1)的直线方程为()A．x−y−3=0B．x+y−3=0C．x+y+3=0D．x−y+3=0【变式1-1】（2023·上海·高二专题练习）过点P(−5,7)，倾斜角为135°的直线方程为（）A．x−y+12=0B．x+y−2=0C．x+y−12=0D．x−y+2=0【变式1-2】（2023秋·广东广州·高二校考期末）经过点(1,2)，且斜率为2的直线方程是（）A．2x−y=0B．2x+y=0C．x−2y+1=0D．x+2y−3=0【变式1-3】（2023·全国·高二专题练习）方程y=k(x−2)表示（）A．通过点(2,0)的所有直线B．通过点(2,0)且不垂直于y轴的所有直线C．通过点(2,0)且不垂直于x轴的所有直线D．通过点(2,0)且除去x轴的所有直线【题型2 直线的斜截式方程及辨析】【例2】（2022·全国·高二专题练习）直线2x+y−3=0用斜截式表示，下列表达式中，最合理的是（）【变式2-1】（2022秋·高二校考课时练习）与直线y=−x+2垂直，且在x轴上的截距为2的直线的斜截式方程为（）.A．y=x+2B．y=x−2C．y=−x+2D．y=−x+4A．y=x+1B．y=x−1C．y=−x−1D．y=−x+1【变式2-3】（2023秋·江西吉安·高二校考期中）与直线2x−y−1=0垂直，且在y轴上的截距为4的直线的斜截式方程是（）(1)直线的两点式方程的定义：设直线l经过两点()，则方程l的两点式方程.(2)两点式方程的使用方法：①已知直线上的两个点，且时，可以直接使用该公式求直线方程.②当().③当(2．直线的截距式方程(1)直线的截距式方程的定义：设直线l在x轴上的截距为a，在y轴上的截距为b，且a≠0，b≠0，则方程l的截距式方程.(2)直线的截距式方程的适用范围：选用截距式方程的条件是a≠0，b≠0，即直线l在两条坐标轴上的截距非零，所以截距式方程不能表示过原点的直线，也不能表示与坐标轴平行(或重合)的直线.(3)截距式方程的使用方法：①已知直线在x轴上的截距、y轴上的截距，且都不为0时，可以直接使用该公式求直线方程.②已知直线在x轴上的截距、y轴上的截距，且都为0时，可设直线方程为y=kx，利用直线经过的点的坐标求解k，得到直线方程.【题型3 直线的两点式方程及辨析】【例3】（2023·全国·高三专题练习）已知直线l过点G(1,−3)，H(−2,1)，则直线l的方程为（）A．4x+y+7=0B．2x−3y−11=0C．4x+3y+5=0D．4x+3y−13=0【变式3-1】（2023秋·浙江温州·高二统考期末）过两点A(3,−5)，B(−5,5)的直线在y轴上的截距为（）【变式3-2】（2022秋·浙江杭州·高二校联考期中）已知直线l过点G(1，−3)，H(2，1)，则直线l的方程为（）A．4x+y+7=0B．4x−y−7=0C．2x−3y−11=0D．4x−y+7=0【变式3-3】（2022·高二课时练习）已知直线l经过(−2,−2)、(2,4)两点，点(1348,m)在直线l上，则m的值为（）A．2021B．2022C．2023D．2024【题型4 直线的截距式方程及辨析】【例4】（2023春·上海闵行·高二校考阶段练习）经过点A(5,2)，并且在两坐标轴上的截距相等的直线l有（）条A．0B．1C．2D．3【变式4-1】（2023秋·吉林·高二校联考期末）过点(3,−6)且在两坐标轴上截距相等的直线的方程是（）A．2x+y=0B．x+y+3=0C．x−y+3=0D．x+y+3=0或2x+y=0【变式4-2】（2023·全国·高二专题练习）若直线l过点A(−2,0),B(0,3)，则直线l的方程为（）A．3x−2y+6=0B．2x−3y+6=0C．3x−2y−6=0D．3x+2y−6=0【变式4-3】（2023秋·安徽六安·高二校考期末）已知直线l过A(−2,1)，且在两坐标轴上的截距为相反数，那么直线l的方程是（）．A．x+2y=0或x−y+3=0B．x−y−1=0或x−y+3=0C．x−y−1=0或x+y−3=0D．x+2y=0或x+y−3=0【知识点3 直线的一般式方程】1．直线的一般式方程(1)直线的一般式方程的定义：在平面直角坐标系中，任何一个关于x，y的二元一次方程都表示一条直线.我们把关于x，y的二元一次方程Ax+By+C=0(其中A,B不同时为0)叫作直线的一般式方程.对于方程Ax+By+C=0(A,B不全为0)：当B≠0时，方程Ax+By+C=0可以写成y=它表示斜率为在y轴上的截距为线.特别地，当A=0时，它表示垂直于y轴的直线.当B=0时，A≠0，方程Ax+By+C=0可以写成x=，它表示垂直于x轴的直线.(2)一般式方程的使用方法：直线的一般式方程是直线方程中最为一般的表达式，它适用于任何一条直线.2．辨析直线方程的五种形式【题型5 直线的一般式方程及辨析】【例5】（2023秋·高二课时练习）经过点(0,−1)，且倾斜角为60°的直线的一般式方程为（）1=0【变式5-1】（2023·全国·高二专题练习）在直角坐标系中，直线x−2y+3=0经过（）A．一、二、三象限B．一、二、四象限C．一、三、四象限D．二、三、四象限【变式5-2】（2023秋·北京西城·高二校考期末）已知直线l过点A(−3,1)，且与直线x−2y+3=0垂直，则直线l的一般式方程为（）A．2x+y+3=0B．2x+y+5=0C．2x+y−1=0D．2x+y−2=0【变式5-3】（2023秋·广东江门·高二统考期末）直线Ax+By+C=0（A,B不同时为0），则下列选项正确的是（）A．无论A,B取任何值，直线都存在斜率B．当A=0，且B≠0时，直线只与x轴相交C．当A≠0，或B≠0时，直线与两条坐标轴都相交D．当A≠0，且B=0，且C=0时，直线是y轴所在直线【题型6 直线一般式方程与其他形式之间的互化】A．2x+3y+3=0B．2x+3y−3=0C．2x+3y+2=0D．3x−2y−2=0【变式6-1】（2023秋·江苏盐城·高二校考期末）如果AB<0，BC<0，那么直线Ax+By+C=0不经过（）A．第一象限B．第二象限C．第三象限D．第四象限A．1B．−1C．2D．−2【变式6-3】（2023秋·甘肃兰州·高二校考期末）已知直线l过点(2,4)，且在x轴上的截距是在y轴上的截距的2倍，则直线l的方程为（）A．x+2y−10=0B．x+2y+10=0C．2x−y=0或x+2y−4=0D．2x−y=0或x+2y−10=0【知识点4 方向向量与直线的参数方程】1．方向向量与直线的参数方程除了直线的点斜式、斜截式、两点式、截距式、一般式方程外，还有一种形式的直线方程与向量有紧密的联系，它由一个定点和这条直线的方向向量唯一确定，与直线的点斜式方程本质上是一致的.如图1，设直线l经过点，=(m,n)是它的一个方向向量，P(x,y)是直线l上的任意一点，则向量与共线.根据向量共线的充要条件，存在唯一的实数t，使=t，即)=t(m,n)，所以①.在①中，实数t是对应点P的参变数，简称参数.由上可知，对于直线l上的任意一点P(x,y)，存在唯一实数t使①成立；反之，对于参数t的每一个确定的值，由①可以确定直线l上的一个点P(x,y).我们把①称为直线的参数方程.【题型7 求直线的方向向量】【例7】（2023·上海·高二专题练习）直线x−2y+1=0的一个方向向量是（）A．(2,1)B．(1,2)C．(2,−1)D．(1,−2)【变式7-1】（2023秋·广东肇庆·高二统考期末）直线2mx+my−3=0的一个方向向量是（）A．(1,2)B．(2,−1)C．(2,1)D．(1,−2)【变式7-2】（2023秋·北京丰台·高二统考期末）已知经过A(0,2)，B(1,0)两点的直线的一个方向向量为(1,k)，那么k=（）【变式7-3】（2022秋·高二课时练习）已知直线l:mx+2y+6=0，且向量(1−m,1)是直线l的一个方向向量，则实数m的值为（）A．−1B．1C．2D．−1或2【题型8 根据直线的方向向量求直线方程】【例8】（2023春·河南开封·高二统考期末）已知直线l的一个方向向量为(2,−1)，且经过点A(1,0)，则直线l的方程为（）A．x−y−1=0B．x+y−1=0C．x−2y−1=0D．x+2y−1=0【变式8-1】（2022秋·广东广州·高二校联考期中）直线l的方向向量为(2,3)，直线m过点(1,1)且与l垂直，则直线m的方程为（）A．2x+3y−5=0B．2x−3y+1=0C．3x+2y−5=0D．3x−2y−1=0【变式8-2】（2022秋·北京·高二校考期末）已知直线l：(2m+1)x+(m+1)y+m=0经过定点P，直线l′经过点P，且l′的方向向量a⃗=(3,2)，则直线l′的方程为（）A．2x−3y+5=0B．2x−3y−5=0C．3x−2y+5=0D．3x−2y−5=0【变式8-3】（2023秋·重庆渝中·高二校考期中）已知直线l1的方向向量为a⃑＝(1，3)，直线l2的方向向量为b⃑⃑＝(－1，k)，若直线l2过点(0，5)，且l1①l2，则直线l2的方程是（）A．x＋3y－5＝0B．x＋3y－15＝0C．x－3y＋5＝0D．x－3y＋15＝0。
直线方程题型及解题方法
直线方程题型及解题方法直线方程是数学中的常见题型，往往需要用到代数、几何和图像的知识进行解答。
本文将介绍几个常见的直线方程题型，并提供相应的解题方法。
一、点斜式方程点斜式方程是直线方程中最常见的一种形式。
它可以通过给定直线上的一点和直线的斜率来确定直线的方程。
具体的表示形式为：y - y₁ = m(x - x₁)其中(x₁, y₁)是直线上的一点坐标，m是直线的斜率。
以下是使用点斜式方程解题的步骤：步骤 1：根据题目给出的信息，确定直线上的一点(x₁, y₁)和直线的斜率m。
步骤 2：代入点斜式方程，计算直线的方程。
例题 1：已知直线上的一点为 P(2, 4)，斜率为 3，求直线的方程。
解题步骤：步骤 1：将 P 的坐标代入点斜式方程，得到y - 4 = 3(x - 2)。
步骤 2：展开并化简方程，得到y - 4 = 3x - 6。
最终答案为y = 3x - 2。
二、截距式方程截距式方程是直线方程的另一种常见形式。
它可以通过给定直线在 x 轴和 y 轴上的截距来确定直线的方程。
具体的表示形式为：y = yy + y其中m是直线的斜率，b是直线在 y 轴上的截距。
以下是使用截距式方程解题的步骤：步骤 1：根据题目给出的信息，确定直线在 x 轴和 y 轴上的截距，即(0, b)和(a, 0)。
步骤 2：利用截距式方程，代入相应的截距和斜率，计算直线的方程。
例题 2：已知直线在 x 轴和 y 轴上的截距分别为 2 和 -3，求直线的方程。
解题步骤：步骤 1：将 x 轴上的截距代入截距式方程，得到y = mx + 2。
步骤 2：将 y 轴上的截距代入方程，得到-3 = m * 0 + 2。
解方程得到m = -3/2。
最终答案为y = -3/2x + 2。
三、两点式方程两点式方程是直线方程的一种形式，用于通过直线上的两点来确定直线的方程。
具体的表示形式为：(y - y₁) / (x - x₁) = (y - y₂) / (x - x₂)其中(x₁, y₁)和(x₂, y₂)是直线上的两个点。
第12讲直线的一般式方程(7种题型)(原卷版)-2024年新高二数学核心知识点与常见题型通关讲解练(
第12讲直线的一般式方程（7种题型）【知识梳理】一．直线的一般式方程与直线的性质【直线的一般式方程】直线方程表示的是只有一个自变量，自变量的次数为一次，且因变量随着自变量的变化而变化．直线的一般方程的表达式是ay+bx+c＝0．1、两条直线平行与垂直的判定对于两条不重合的直线l1、l2，其斜率分别为k1、k2，有：（1）l1∥l2⇔k1＝k2；（2）l1⊥l2⇔k1•k2＝﹣1．2、直线的一般式方程：（1）一般式：Ax+By+C＝0，注意A、B不同时为0．直线一般式方程Ax+By+C＝0（B≠0）化为斜截式方程y＝﹣x﹣，表示斜率为﹣，y轴上截距为﹣的直线．（2）与直线l：Ax+By+C＝0平行的直线，可设所求方程为Ax+By+C1＝0；与直线Ax+By+C＝0垂直的直线，可设所求方程为Bx﹣Ay+C1＝0．（3）已知直线l1，l2的方程分别是：l1：A1x+B1y+C1＝0（A1，B1不同时为0），l2：A2x+B2y+C2＝0（A2，B2不同时为0），则两条直线的位置关系可以如下判别：①l1⊥l2⇔A1A2+B1B2＝0；②l1∥l2⇔A1B2﹣A2B1＝0，A1C2﹣A2B1≠0；③l1与l2重合⇔A1B2﹣A2B1＝0，A1C2﹣A2B1＝0；④l1与l2相交⇔A1B2﹣A2B1≠0．如果A2B2C2≠0时，则l1∥l2⇔；l1与l2重合⇔；l1与l2相交⇔．二．直线的一般式方程与直线的平行关系1、两条直线平行与垂直的判定对于两条不重合的直线l1、l2，其斜率分别为k1、k2，有：（1）l1∥l2⇔k1＝k2；（2）l1⊥l2⇔k1•k2＝﹣1．2、直线的一般式方程：（1）一般式：Ax+By+C＝0，注意A、B不同时为0．直线一般式方程Ax+By+C＝0（B≠0）化为斜截式方程y＝﹣x﹣，表示斜率为﹣，y轴上截距为﹣的直线．（2）与直线l：Ax+By+C＝0平行的直线，可设所求方程为Ax+By+C1＝0；与直线Ax+By+C＝0垂直的直线，可设所求方程为Bx﹣Ay+C1＝0．（3）已知直线l1，l2的方程分别是：l1：A1x+B1y+C1＝0（A1，B1不同时为0），l2：A2x+B2y+C2＝0（A2，B2不同时为0），则两条直线的位置关系可以如下判别：①l1⊥l2⇔A1A2+B1B2＝0；②l1∥l2⇔A1B2﹣A2B1＝0，A1C2﹣A2B1≠0；③l1与l2重合⇔A1B2﹣A2B1＝0，A1C2﹣A2B1＝0；④l1与l2相交⇔A1B2﹣A2B1≠0．如果A2B2C2≠0时，则l1∥l2⇔；l1与l2重合⇔；l1与l2相交⇔．三．直线的一般式方程与直线的垂直关系1、两条直线平行与垂直的判定对于两条不重合的直线l1、l2，其斜率分别为k1、k2，有：（1）l1∥l2⇔k1＝k2；（2）l1∥l2⇔k1•k2＝﹣1．2、直线的一般式方程：（1）一般式：Ax+By+C＝0，注意A、B不同时为0．直线一般式方程Ax+By+C＝0（B≠0）化为斜截式方程y＝﹣x﹣，表示斜率为﹣，y轴上截距为﹣的直线．（2）与直线l：Ax+By+C＝0平行的直线，可设所求方程为Ax+By+C1＝0；与直线Ax+By+C＝0垂直的直线，可设所求方程为Bx﹣Ay+C1＝0．（3）已知直线l1，l2的方程分别是：l1：A1x+B1y+C1＝0（A1，B1不同时为0），l2：A2x+B2y+C2＝0（A2，B2不同时为0），则两条直线的位置关系可以如下判别：①l1⊥l2⇔A1A2+B1B2＝0；②l1∥l2⇔A1B2﹣A2B1＝0，A1C2﹣A2B1≠0；③l1与l2重合⇔A1B2﹣A2B1＝0，A1C2﹣A2B1＝0；④l1与l2相交⇔A1B2﹣A2B1≠0．如果A2B2C2≠0时，则l1∥l2⇔；l1与l2重合⇔；l1与l2相交⇔．四．待定系数法求直线方程求直线方程的一般方法：（1）直接法：根据已知条件，选择适当的直线方程形式，直接求出直线方程．应明确直线方程的几种形式及各自的特点，合理选择解决方法．一般地，已知一点通常选择点斜式；已知斜率选择斜截式或点斜式；已知在两坐标轴上的截距用截距式；已知两点用两点式，这时应特别注意斜率不存在的情况．（2）待定系数法：先设出直线的方程，再根据已知条件求出假设系数，最后代入直线方程，待定系数法常适用于斜截式，已知两点坐标等．利用待定系数法求直线方程的步骤：①设方程；②求系数；③代入方程得直线方程，如果已知直线过一个定A（x0，y0），可以利用直线的点斜式y﹣y0＝k（x﹣x0）求方程，也可以利用斜截式、截距式等形式求解．五．两条直线的交点坐标两条直线的交点坐标：（1）一般地，将两条直线的方程联立，得到二元一次方程组．若方程组有惟一解，则两条直线相交，此解就是交点的坐标；若方程组无解，则两条直线无公共点，此时两条直线平行；若方程组有无数解，则两条直线有无数个公共点，此时两条直线重合．（2）方程λ（A1x+B1y+C1）+（A2x+B2y+C2）＝0为直线系，所有的直线恒过一个定点，其定点就是A1x+B1y+C1＝0与A2x+B2y+C2＝0的交点．六．方程组解的个数与两直线的位置关系两条直线的交点坐标：（1）一般地，将两条直线的方程联立，得到二元一次方程组．若方程组有惟一解，则两条直线相交，此解就是交点的坐标；若方程组无解，则两条直线无公共点，此时两条直线平行；若方程组有无数解，则两条直线有无数个公共点，此时两条直线重合．（2）方程λ（A1x+B1y+C1）+（A2x+B2y+C2）＝0为直线系，所有的直线恒过一个定点，其定点就是A1x+B1y+C1＝0与A2x+B2y+C2＝0的交点．七．与直线有关的动点轨迹方程1、求曲线的轨迹方程常采用的方法有直接法、定义法、代入法、参数法．（1）直接法：直接法是将动点满足的几何条件或者等量关系，直接坐标化，列出等式化简即得动点轨迹方程．（2）定义法：若动点轨迹的条件符合某一基本轨迹的定义（如椭圆、双曲线、抛物线、圆等），可用定义直接探求．（3）相关点法：根据相关点所满足的方程，通过转换而求动点的轨迹方程．（4）参数法：若动点的坐标（x，y）中的x，y分别随另一变量的变化而变化，我们可以以这个变量为参数，建立轨迹的参数方程．求轨迹方程，一定要注意轨迹的纯粹性和完备性．要注意区别“轨迹”与“轨迹方程”是两个不同的概念．2、求轨迹方程的一般步骤：（1）建立适当的直角坐标系（如果已给出，本步骤省略）；（2）设曲线上任意一点的坐标为（x，y）；（3）根据曲线上点所适合的条件，写出等式；（4）用坐标（x，y）表示这个等式，并化简；（5）证明已化简后的方程的解为坐标的点都是曲线上的点．上述五个步骤可简记为：建系；设点；写出集合；列方程、化简；证明．【考点剖析】一．直线的一般式方程与直线的性质（共13小题）1．（2022秋•永昌县校级期末）已知直线l1：x﹣2y﹣2＝0的倾斜角为θ，直线l2的倾斜角为2θ，且直线l2在y轴上的截距为3，则直线l2的一般式方程为（）A．x+y﹣3＝0B．4x﹣3y+9＝0C．3x﹣4y+3＝0D．2x+y﹣3＝02．（2022秋•西湖区校级期末）以A（1，3），B（﹣5，1）为端点的线段的垂直平分线方程是．3．（2022秋•项城市校级期末）过点A（3，2）且垂直于直线4x+5y﹣8＝0的直线方程为．4．（2022秋•福州期末）已知平行四边形ABCD的三个顶点坐标为A（﹣2，﹣1），B（4，1），C（2，3）．（1）求AD所在的直线方程；（2）求平行四边形ABCD的面积．5．（2022秋•苏州期末）如图，在平面直角坐标系xOy中，已知四边形OABC满足|OA|＝|AB|＝4，∠OAB＝120°，BC⊥OB，OC∥AB．（1）求直线AB的方程；（2）求点C的坐标．6．（2022秋•玉林期末）在△ABC中，A（1，1），B（3，﹣2），C（2，0）．（1）求△ABC的中线AD所在直线的方程；（2）求△ABC的面积．7．（2022秋•衡南县期末）已知O为坐标原点，倾斜角为的直线l与x，y轴的正半轴分别相交于点A，B，△AOB的面积为．（1）求直线l的方程；（2）直线，点P在l'上，求|P A|+|PB|的最小值．8．（2022秋•房山区期末）已知△ABC的边AC，AB上的高所在直线方程分别为2x﹣3y+1＝0，x+y＝0，顶点A（1，2）．（1）求顶点C的坐标；（2）求BC边所在的直线方程．9．（2022秋•聊城期末）已知△ABC的边AB，AC所在直线的方程分别为y＝﹣1，2x﹣y+7＝0，点P（1，2）在边BC上．（1）若△ABC为直角三角形，求边BC所在直线的方程；（2）若P为BC的中点，求边BC所在直线的方程．10．（2022秋•雅安期末）在△ABC中，已知点A（8，4），B（4，﹣1），C（﹣6，3）．（1）求BC边上中线的方程．（2）若某一直线过B点，且x轴上截距是y轴上截距的2倍，求该直线的一般式方程．11．（2022秋•崇川区期末）已知△ABC的一条内角平分线CD的方程为x+y＝0，一个顶点为A（2，1），AC 边上的中线BE所在直线的方程为5x﹣2y+10＝0．（1）求顶点C的坐标；（2）求△ABC的面积．12．（2022秋•定州市期末）已知△ABC的顶点B（3，2），AB边上的高所在的直线方程为x﹣2y﹣5＝0．（1）求直线AB的方程；（2）在两个条件中任选一个，补充在下面问题中．①角A的平分线所在直线方程为x+2y﹣13＝0②BC边上的中线所在的直线方程为2x﹣y﹣12＝0 _____，求直线AC的方程．13．（2022秋•佛山期末）△ABC的三个顶点分别为A（1，2），B（3，0），C（4，5），M是AB的中点．（1）求边AB上的中线CM所在直线的方程；（2）求△BCM的面积．二．直线的一般式方程与直线的平行关系（共11小题）14．（2022秋•宁河区校级期末）设a∈R，则“a＝﹣2”是“直线l1：ax+2y﹣1＝0与直线l2：x+（a+1）y+2＝0平行”的（）A．充分不必要条件B．必要不充分条件C．充分必要条件D．既不充分也不必要条件15．（2022秋•滕州市期末）过点A（2，3）且与直线l：2x﹣4y+7＝0平行的直线方程是（）A．x﹣2y+4＝0B．2x+y﹣7＝0C．2x﹣y﹣1＝0D．x+2y﹣8＝016．（2022秋•河南期末）若直线mx﹣4y+1＝0与直线x+2y﹣3＝0平行，则实数m＝（）A．2B．﹣2C．D．17．（2023春•虹口区期末）已知平面直角坐标系中的三点A（﹣2，﹣1）、B（2，2）、C（0，3），若直线l 过点C且与直线AB平行，则l的方程为．18．（2022秋•红山区期末）求解下列问题：（1）求过直线x﹣y﹣5＝0与直线x+y﹣3＝0的交点，且与直线3x﹣4y+6＝0平行的直线方程；（2）已知A（1，﹣2），B（﹣1，4），求以线段AB为直径的圆的方程．19．（2022秋•钦州期末）已知点P（2，4）和直线l：2x+y+1＝0．（1）求经过点P且与l平行的直线方程；（2）求经过点P且在两坐标轴上截距相等的直线方程．20．（2022秋•沙市区校级期末）已知直线l1：mx+（1﹣2m）y+2﹣m＝0，．（1）当直线l1在x轴上的截距是它在y上的截距2倍时，求实数m的值；（2）若l1∥l2，实数m的值．21．（2022秋•米东区校级期末）已知直线l1：（m+2）x+（m2﹣3m）y+4＝0和直线l2：2mx+2（m﹣3）y+m+2＝0（m∈R）．（1）当m为何值时，直线l1和l2平行？（2）当m为何值时，直线l1和l2重合？22．（2022秋•凌河区校级期末）已知直线3x+4y﹣2＝0与直线2x+y+2＝0交于点P．（1）直线l1经过点P，且平行于直线3x﹣4y+5＝0，求直线l1的方程；（2）直线l2经过点P，且与两坐标轴围成一个等腰直角三角形，求直线l2的方程．（注：结果都写成直线方程的一般式）23．（2022秋•金华期末）已知平面直角坐标系xOy中，△ABC的三个顶点的坐标分别为A（3，2），B（5，﹣2），C（﹣1，﹣1）．（1）若直线l过点C且与直线AB平行，求直线l的方程；（2）求线段BC的垂直平分线方程．24．（2022秋•新化县期末）已知直线l的方程为ax+y﹣2a﹣2＝0（a∈R）．（1）若l与直线x+2y＝0平行，求a的值；（2）若l在x轴，y轴上的截距相等，求l的方程．三．直线的一般式方程与直线的垂直关系（共11小题）25．（2023春•奎屯市校级期中）过点P（﹣1，3）且垂直于直线x+2y﹣3＝0的直线方程为（）A．x+2y+5＝0B．2x﹣y+5＝0C．x+2y﹣5＝0D．2x﹣y﹣5＝026．（2022秋•郴州期末）直线ax﹣4y＝0与直线4x+2y﹣1＝0垂直，则a等于（）A．2B．C．1D．﹣127．（2023•忻州开学）已知倾斜角为θ的直线l与直线x+2y+1＝0垂直，则＝．28．（2023春•虹口区期末）若直线l1：ax+2y+3a＝0与直线l2：2x+（a﹣1）y+4＝0互相垂直，则实数a的值为．29．（2022秋•长春期末）求解下列问题：（1）求过点P（4，2）且平行于直线l：3x﹣y+1＝0的直线的方程；（2）求过点P（﹣2，3）且垂直于直线m：x﹣3y﹣4＝0的直线的方程．30．（2022秋•龙华区期末）已知A（2，0），B（1，3）．（1）求线段AB的垂直平分线l所在直线的方程；（2）若一圆的圆心在直线x+2y﹣2＝0上，且经过点A，B，求该圆的方程．31．（2022秋•广安期末）已知△ABC的三个顶点分别是A（4，0），B（6，6），C（0，2）．（1）求BC边上的高所在直线的方程；（2）求AB边的垂直平分线所在直线的方程．32．（2022秋•益阳期末）已知点P（2，﹣1）和直线l：x+2y﹣5＝0．（1）若直线l1经过点P，且l1⊥l，求直线l1的方程；（2）若直线l2过原点，且点P到直线l2，l的距离相等，求直线l2的方程．33．（2022秋•香坊区校级期末）（1）求与直线3x+4y+1＝0平行且过点（1，2）的直线l的方程；（2）当m为何值时，直线（2m2+m﹣3）x+（m2﹣m）y＝4m﹣1与直线2x﹣3y＝5垂直．34．（2022秋•广安期末）已知△ABC的三个顶点分别是A（4，0），B（6，6），C（0，2）．（1）求AB边上的高所在直线的方程；（2）求AC边的垂直平分线所在直线的方程．35．（2022秋•涪城区期末）已知△ABC的三个顶点的坐标分别是A（5，1），B（7，﹣3），C（2，﹣8）．（1）求边AB的中线所在直线的方程；（2）若AD⊥BC，垂足为D，求点D的坐标．四．待定系数法求直线方程（共6小题）36．（2022秋•龙川县校级期末）过点P（﹣1，1）引直线，使A（2，3），B（4，﹣5），两点到直线的距离相等，则直线方程是（）A．2x+y+1＝0B．x+2y﹣1＝0C．2x+y+1＝0或4x+y+3＝0D．x+2y﹣1＝0或4x+y+3＝037．（2022秋•钦州期末）若直线过点（，﹣3）和点（0，﹣4），则该直线的方程为（）A．y＝x﹣4B．y＝x+4C．y＝x﹣6D．y＝x+238．（2022秋•宿迁期末）过点（3，2）的直线l，被直线l1：2x﹣5y+9＝0，l2：2x﹣5y﹣7＝0所截得的线段AB的中点恰好在直线x﹣4y﹣1＝0上，则直线l的方程为．39．（2022秋•大丰区期末）已知△ABC的一条内角平分线CD的方程2x+y﹣1＝0，两个顶点为A（1，2），B（﹣1，﹣1），则顶点C的坐标为．40．（2022秋•奉化区期末）已知△ABC的顶点A（5，1），AB边上的中线CM所在直线方程为2x﹣y﹣5＝0，AC边上的高BH所在的直线方程为x﹣2y﹣5＝0，则顶点C的坐标为．41．（2022秋•渝北区校级期末）已知直线l1：ax+2y﹣12＝0，直线l2过点A（﹣4，1），____．在①直线l2的斜率是直线y＝﹣x的斜率的2倍，②直线l2不过原点且在x轴上的截距等于在y轴上的截距的2倍这两个条件中任选一个，补充在上面的横线中，并解答下列问题．（1）求l2的方程；（2）若l1与l2在x轴上的截距相等，求l1在y轴上的截距．五．方程组解的个数与两直线的位置关系（共3小题）42．（2022秋•崇州市校级月考）点A（﹣3，2），B（3，2），直线ax﹣y﹣1＝0与线段AB相交，则实数a 的取值范围是（）A．B．a≥1或a≤﹣1C．﹣1≤a≤1D．或43．（2022秋•东安区校级月考）已知直线l：ax﹣y+1＝0，点A（1，﹣3），B（2，3），若直线l与线段AB 有公共点，则实数a的取值范围是（）A．[﹣4，1]B．[﹣，1]C．（﹣∞，﹣]∪[1，+∞）D．（﹣∞，﹣4]∪[1，+∞）44．（2022秋•武昌区校级期中）写出使得关于x，y的方程组无解的一个a的值为.（写出一个即可）六．与直线关于点、直线对称的直线方程（共6小题）45．（2022秋•泸州期末）点（0，0）与点（﹣2，2）关于直线l对称，则l的方程是（）A．x+y+2＝0B．x﹣y+2＝0C．x+y﹣2＝0D．x﹣y﹣2＝046．（2023春•仙桃校级月考）已知点A（5，2），B（7，﹣7），点P是直线y＝x上动点，则|P A|+|PB|的最小值是．47．（2022秋•新余期末）一束光线从点A（2，3）射出，经x轴上一点C反射后到达圆（x+3）2+（y﹣2）2＝2上一点B，则|AC|+|BC|的最大值为（）A．B．C．D．48．（2022秋•怀仁市校级期末）点（﹣1，3）关于直线x+y+2＝0的对称点的坐标为．49．（2022秋•淄博期末）直线ax+y+3a﹣1＝0恒过定点M，则点M关于直线2x+3y﹣6＝0对称的点N坐标为．50．（2022秋•海淀区校级期末）已知直线l1：y＝1与直线l2：y＝kx﹣2交于点A，点A关于坐标原点的对称点为C，点B在直线l1上，点D在直线l2上．（Ⅰ）当k＝1时，求C点的坐标；（Ⅱ）当四边形ABCD为菱形时，求k的值．七．与直线有关的动点轨迹方程（共3小题）51．（2022秋•浦东新区校级月考）已知t∈R，且t∈（0，10），由t确定两个任意点P（t，t），Q（10﹣t，0）．（Ⅰ）直线PQ是否经过点M（6，1）？（Ⅱ）在△OPQ内作内接正方形ABCD，顶点A，B在边OQ上，顶点D在边OP上．①求证：顶点C一定在直线上；②求图中阴影部分面积的最大值，并求这时顶点A，B，C，D的坐标．52．（2022秋•洛阳月考）已知直线l：3x+y+2＝0与x，y轴的交点分别为A，B，且直线l1：mx﹣y﹣3m+1＝0与直线l2：x+my﹣3m﹣1＝0相交于点P，则△P AB面积的最大值是．53．（2022•栖霞区校级开学）如图，在直角坐标系中，射线OA：x﹣y＝0（x≥0），OB：x+3y＝0（x≥0），过点P （1，0）作直线分别交射线OA 、OB 于A 、B 点．①当AB 的中点为P 时，求直线AB 的方程；②当AB 的中点在直线y ＝x 上时，求直线AB 的方程．【过关检测】一、单选题 1．（2023·全国·高二专题练习）直线13kx y k -+=，当k 变动时，所有直线恒过定点坐标为（ ） A ．()0,0 B ．()0,1 C ．()3,1 D ．()2,12．（2023·江苏·高二假期作业）直线0cx dy a ++=与0dx cy b -+= (,c d 不同时为0)的位置关系是（ ） A ．平行B ．垂直C ．斜交D ．与a b c d ,,,的值有关3．（2023春·广西南宁·高二校联考开学考试）直线l 过点1,2且与直线2340x y -+=垂直，则l 的方程是（ ）A ．2350x y -+=B ．3270x y ++=)(,1)-∞- 2,1](2,3) 2][1,)+∞高二课时练习）已知直线Ax +在x 轴的截距大于在轴的截距，则0C B > 0 二、多选题B ．直线()12y k x -=-恒过定点()2,1C ．直线30x y +-=的倾斜角为135°D ．过点()2,1，且在两坐标轴上截距相等的直线仅有一条12．（2023·江苏·高二假期作业）过点(2,1)，且斜率2k =-的直线方程为（ ）A ．()122x y -=--B ．210x y +-=C ．()122y x -=--D ．250x y +-=三、填空题13．（2023春·上海金山·高二华东师范大学第三附属中学校考期末）已知直线:21l x y =+，则直线l 的斜率k =______． 14．（2023秋·重庆长寿·高二统考期末）经过点(1,2)且与直线210x y -+=垂直的直线方程是________．（用一般式表示）15．（2023·江苏·高二假期作业）直线l 在x 轴上的截距比在y 轴上的截距小1，且过定点(3,8)A -，则直线l 的方程为________________.16．（2023春·上海黄浦·高二统考期末）两直线10ax y +-=与420x ay +-=平行，则a 的值是______；四、解答题 17．（2023·江苏·高二假期作业）已知ABC 在第一象限，若(1,1)A ，(5,1)B ，60A ∠=︒，45B ∠=︒，求：(1)AB 边所在直线的方程；(2)AC 边所在直线的点斜式方程.18．（2023春·江苏扬州·高二统考开学考试）已知直线:3450l x y ++=，求：(1)过点()1,1A 且与直线l 平行的直线的方程；(2)过点()1,1A 且与直线l 垂直的直线的方程．19．（2023·江苏·高二假期作业）如图，射线OA 、OB 分别与x 轴成45°角和30°角，过点(1,0)P 作直线AB 分别与OA ，OB 交于点A 、B ，当AB 的中点为P 时，求直线AB 的方程.20．（2023·江苏·高二假期作业）对于问题“求经过点(21)(3,4)M N --,,的直线l 的方程”，某同学采取的方法如下：首先设直线:0l Ax By C ++=，然后由直线l 经过M ，N 两点得到20340A B C A B C -+=⎧⎨-++=⎩,做到这里，该同学认为题目条件不够，无法求解直线l 的方程，你同意该同学的观点吗？说明自己的观点及依据.21．（2023秋·安徽蚌埠·高二统考期末）已知直线1:0l x ay a +-=和直线()2:2320l ax a y a --+-=.(1)若12l l ⊥，求实数a 的值；(2)若12l l ∥，求实数a 的值.22．（2023春·新疆塔城·高二统考开学考试）已知ABC 的顶点分别为(2,4),(0,2),(2,3)A B C --，求：(1)直线AB 的方程;(2)AB 边上的高所在直线的方程;。
史上最全直线与直线方程题型归纳
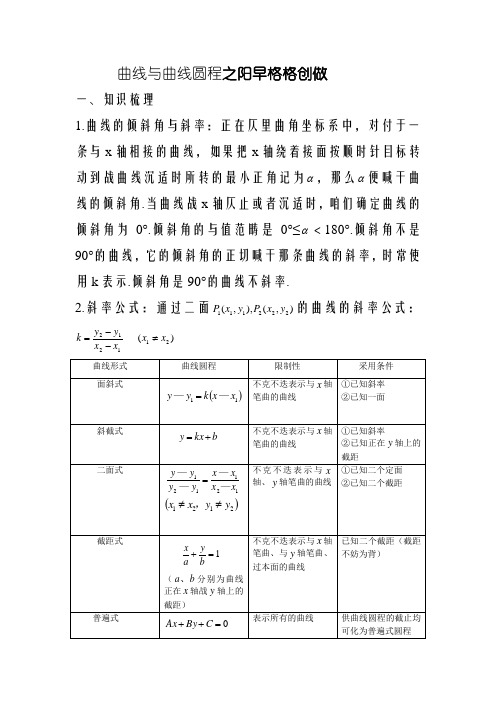
曲线与曲线圆程之阳早格格创做一、知识梳理1.曲线的倾斜角与斜率：正在仄里曲角坐标系中，对付于一条与x 轴相接的曲线，如果把x 轴绕着接面按顺时针目标转动到战曲线沉适时所转的最小正角记为α，那么α便喊干曲线的倾斜角.当曲线战x 轴仄止或者沉适时，咱们确定曲线的倾斜角为0°.倾斜角的与值范畴是0°≤α＜180°.倾斜角不是90°的曲线，它的倾斜角的正切喊干那条曲线的斜率，时常使用k 表示.倾斜角是90°的曲线不斜率.2.斜率公式：通过二面),(),,(222111y x P y x P 的曲线的斜率公式：)(211212x x x x y y k ≠--=()0不全为、B A7．斜率存留时二曲线的仄止：21//l l ⇔1k =2k 且21b b ≠. 8．斜率存留时二曲线的笔曲：⇔⊥21l l 121-=k k ．9．特殊情况下的二曲线仄止与笔曲:当二条曲线中有一条曲线不斜率时：(1)当另一条曲线的斜率也不存留时，二曲线的倾斜角皆为90°，互相仄止；(2)当另一条曲线的斜率为0时，一条曲线的倾斜角为90°，另一条曲线的倾斜角为0°，二曲线互相笔曲．二、典例粗析题型一：倾斜角与斜率【例1】下列道法粗确的个数是（ ） ①所有一条曲线皆有唯一的倾斜角； ②倾斜角为030的曲线有且仅有一条； ③若曲线的斜率为θtan ，则倾斜角为θ； ④如果二曲线仄止，则它们的斜率相等A. 0个B.1个C.2个D.3个 【训练】如果0<AC 且0<BC ，那么曲线0=++C By Ax 短亨过（ ）【例2】如图，曲线l 通过二、三、四象限，l 的倾斜角为α，斜率为k ，则( )A ．ksinα>0B ．kcosα>0C ．ksinα≤0D ．kcosα≤0【训练】图中的曲线l1，l2，l3的斜率分别为k1，k2，k3，则()．A ．k1＜k2＜k3B ．k3＜k1＜k2C ．k3＜k2＜k1D ．k1＜k3＜k2【例3】通过面()2,1P 做曲线l ，若曲线l 与对接()10—，A ，()1,4B 的线段总有大众面，供曲线l 的倾斜角α与斜率k 的与值范畴. 【训练】已知二面()4,3-A ，()2,3B ，过面()1-2，P 的曲线l 与线段AB 有大众面，供曲线l 的斜率k 的与值范畴.【例4】若曲线l 的圆程为2tan +=αx y ，则（ ）A.α一定是曲线l 的倾斜角 B.α一定不是曲线l 的倾斜角C.α—π一定是曲线l 的倾斜角D.α纷歧定是曲线l 的倾斜角【训练】设曲线0=++c by ax 的倾斜角为α，且0cos sin =+αα，则b a 、谦脚（ ）A.1=+b aB.1=b a —C.0=+b aD.0=b a —题型二：斜率的应用 【例5】若面()()()4,0,0,2,2C a B A ，共线则a的值为_________________.【训练】若三面()()()b C a B A ,0,0,2,2，()0≠ab 共线，则ba11+的值为_____________.【例6】已知真数y x 、谦脚82=+y x ，当32≤≤x 时，供xy 的最大值为_______，最小值为_________________ 【训练】1、若45ln ,23ln ,12ln ===c b a ，则（ ）A.c b a <<B.a b c <<C.b a c <<D.c a b <<2、供函数1212+=x x y —的值域.题型三：二曲线位子闭系的推断已知，二曲线21,l l 斜率存留且分别为21,k k ，若二曲线仄止或者沉合则有21__________k k ，若二曲线笔曲则有21__________k k . 【例7】已知曲线1l 的倾斜角为 60，曲线2l 通过面()3,1，A ，()322—，—B ，推断曲线1l 与2l 的位子闭系.【训练】1、已知面()3,2P ，()5,4Q ,()a A ，—1，()2,2a B 当a 为何值时，曲线PQ 与曲线AB 相互笔曲？2、已知曲线1m 通过面()()3,23—，，a B a A ，曲线2m 通过面()()5,6,3N a M ，，若21m m ⊥，供a 的值.【例8】正在仄里曲角坐标系中，对付Ra ∈，曲线012:012:21=+=+—和—y ax l ay x l （ ）.A 互相仄止 .B 互相笔曲.C 闭于本面对付称 .D 闭于曲线x y —=对付称【训练】曲线()()()()07425084123=++=+++——与—y a x a y a x a 笔曲，供a 的值.题型四：供曲线圆程（一）面斜式【例9】根据条件写出下列曲线的圆程：（1）通过面A(1,2),斜率为2；（2）通过面B （—1,4），倾斜角为 135； （3）通过面C （4,2），倾斜角为 90；（4）通过面D （—3，—2），且与x 轴仄止.已知曲线过一面，可设面斜式【训练】已知ABCAD⊥于D,∆中，()()()0,2，CA，BCB—，46,2，1—供AD的曲线圆程.（二）斜截式【例10】根据条件写出下列曲线的圆程：（1）斜率为2，正在y轴上的截距是5；150，正在y轴的截距为—2；（2）倾斜角为（3）倾斜角为 45，正在y轴上的截距为0.已知斜率时，可设斜截式：3，且与坐标轴围成的三角形周少是12的【训练】供斜率为4曲线l的圆程.（三）截距式【例12】根据条件写出下列曲线的圆程：（1)正在x轴上的截距为—3，正在y轴上的截距为2；（2)正在x轴上的截距为1，正在y轴上的截距为—4；与截距相闭的问题，可设截距式【训练】曲线l过面()3,4P，且正在轴x上的截距之比为1:2，轴、y供曲线l的圆程.（四）二面式【例11】供通过下列二面的曲线圆程：（1)A(2,5),B(4,3) (2)A(2,5),B(4,5) (3)A(2,5),B(2,7) 适时应用“二面决定一条曲线”【训练】过面()1,0M 做曲线l ，使他被二条已知曲线04:103:21=+++y x l y x l 和—所截得的线段AB被面M l 的圆程.【例12】1、已知面A （3,3）战曲线l ：2543—x y =.供：（1）通过面A 且与曲线l 仄止的曲线圆程； （2）通过面A 且与曲线l 笔曲的曲线圆程.2、已知三角形三个顶面的坐标分别为A （—1,0），B （2,0），C （2,3），试供AB 边上的下的曲线圆程.(思索：如果供AB 边上的中线、角仄分线呢？）【例13】已知曲线l 的斜率为2，且l 战二坐标轴围成里积为4的三角形，则曲线l 的圆程为________________．【训练】已知，曲线l 通过面（—5，—4），且与二坐标轴所围成的三角形里积为5，则曲线l 的圆程为________________ 【例14】曲线l 不通过第三象限，其斜率为k ，正在y 轴上的截距为b （0≠b ），则（ ）A.00>≤b k 且 B.0<≥b k 且 C.00><b k 且D.00>>b k 且【训练】二条曲线y=ax+b 与y=bx+a 正在共背来角坐标系中的图象位子大概是（ ） A ． B ． C ． D ．三、课后训练<一>采用题：1、若曲线l ：y=kx-3与曲线2x+3y-6=0的接面位于第一象限，则曲线l 的倾斜角的与值范畴（ ）A ．[6π，3π) B ．(6π，2π) C ．(3π，2π) D ．[6π，2π]2、已知曲线l1：（k-3）x+（5-k ）y+1=0与l2：2（k-3）x-2y+3=0笔曲，则K 的值是（ ）A ．1或者3B ．1或者5C ．1或者4D ．1或者23、曲线y=3x 绕本面顺时针转动90°，再背左仄移1个单位，所得到的曲线为（ ）A ．3131+=x y — B ．131+=x y — C ．33—x y = D ．13+=x y<二>挖空题：1、正在仄里曲角坐标系中，如果x 与y 皆是整数，便称面（x ，y ）为整面，下列命题中粗确的是 _________________（写出所有粗确命题的编号）．①存留那样的曲线，既不与坐标轴仄止又不通过所有整面 ②如果k 与b 皆是无理数，则曲线y=kx+b 不通过所有整面 ③曲线l 通过无贫多个整面，当且仅当l 通过二个分歧的整面④曲线y=kx+b 通过无贫多个整面的充分需要条件是：k 与b 皆是有理数⑤存留恰通过一个整面的曲线．2、若面()21—，P 正在曲线l 上的射影为()1,1—Q ，则曲线l 的圆程为__________________.3、正在仄里曲角坐标系xOy 中，过坐标本面的一条曲线与函数f(x)=x2的图象接于P 、Q 二面，则线段PQ 少的最小值是________________. <三>解问题：1、设曲线1l ：11+=x k y ，2l ：12—x k y =，其中真数21,k k 谦脚0221=+•k k ，道明1l 与2l 相接.2、已知曲线圆程为b kx y +=，当[][]13,8,4,3—时—∈∈y x ，供此曲线的圆程.3、当20<<a 时，曲线1l ：422:422222+=+=a y a x l a y ax 与——战二坐标轴围成一个四边形，问a 与何值时，那个四边形的里积最小?并供出最小里积.。
高中数学必修二直线与直线方程题型归纳总结
高中数学必修二直线与直线方程题型归纳总结知识点归纳概括：1.直线的倾斜角为0°≤α<180°，斜率为k=tanα（α≠90°）。
2.已知两点求斜率公式为k=(y2-y1)/(x2-x1)（x2≠x1）。
3.两直线平行时，它们的斜率相等；垂直时，它们的斜率之积为-1.4.直线的五种方程：点斜式、斜截式、两点式、截距式、一般式。
5.两直线的交点坐标可通过联立两直线方程求得，两点间距离可用距离公式计算。
题型归纳分析：1.直线的倾斜角与斜率的计算。
2.平行和垂直直线的判断及斜率之间的关系。
3.直线的方程及其应用。
4.两直线交点坐标和两点间距离的计算。
例1：过点M(-2,a)和N(a,4)的直线的斜率等于1，则a的值为（）。
A。
1B。
4C。
1或3D。
1或4解析：由题意可得，直线MN的斜率为1，即(k=(4-a)/(a+2)=1)，解得a=2，故选B。
变式1：已知点A(1,3)、B(-1,3)，则直线AB的倾斜角是（）。
A。
60°B。
30°C。
120°D。
150°解析：由斜率公式可得，k=(3-3)/(-1-1)=0，因为斜率为0，所以直线与x轴平行，倾斜角为0°，故选A。
变式2：已知两点A(3,2)、B(-4,1)，求过点C(-1.)的直线l与线段AB有公共点，求直线l的斜率k的取值范围。
解析：首先求出AB的斜率k1=(1-2)/(-4-3)=-1/7，然后求出点C到直线AB的距离d，d=|(-1-3)×(-1)+(?-2)×(-4+3)|/√((-4+3)²+(1-2)²)=|4-2×(?-1)|/√5，因为直线l与AB有公共点，所以点C到直线l的距离也为d，根据距离公式可得，|k1×(-1)+1×(?-1)-d|/√(k1²+1²)=d，化简得，|k1×(-1)+1×(?-1)|=2d√(k1²+1²)，即|k1+?(?-1)|=2d√(k1²+1²)，因为直线l过点C，所以直线l的斜率为k2=(?-1)/(-1-3)，代入得，|k1+k2|=2d√(k1²+1²)，整理得，|?-1+7k2|=2d√(50)，因为|?-1+7k2|≥0，所以d≥0，又因为√(50)>7，所以|?-1+7k2|≤2d×7，即|?-1+7k2|≤14d，代入得|?-1+7(?-1)/(-1-3)|≤14d，即|-2?-6/(-4)|≤14d，解得-1/2≤d≤1/2，因为d≥0，所以1/2≥d≥0，代入得-1/2≤?-1+7k2≤1/2，解得-3/14≤k2≤1/14，故k2的取值范围为[-3/14,1/14]。
直线与方程题型总结答案
题型一：重点考查直线的倾斜角)2cos10,2sin10，)2cos130,2sin130，则直线．160【详解】方法一：由斜率和倾斜角关系，利用两点连线斜率公式可得tan 方法二：根据三角函数定义可知,P Q 在圆160QOM +，由此可得倾斜角.的倾斜角为)0180θ≤<，()()33cos10sin10sin 12010sin102sin1302sin10222cos1302cos10cos 12010cos1033cos10sin1022−+−−==−+−−−()()3sin10cos103sin 1030sin 20sin 202tan 20sin 70cos 2033sin 1060sin10cos102−−==−=−=−++tan160.PQ 的倾斜角为160；方法二：由三角函数的定义可知：点,P Q 在圆24x y +=上，如图所示，为直线PQ 与轴的交点，则10，130QOM ∠，120=，又OQ =，30OQM ∴∠，160QOM +∠，∴直线PQ 的倾斜角为160. 160.2023春·安徽合肥·高二统考开学考试）直线y ++ 34π⎤⎡⋃⎥⎢⎦⎣精练核心考点3,24ππ⎤⎡⎫⎪⎥⎢⎦⎣⎭3,24ππ⎤⎡⎫⎪⎥⎢⎦⎣⎭3,4ππ⎤⎡⎫⎪⎥⎢⎦⎣⎭【详解】解：直线l 的斜率为3≤，α∈3,4⎤⎡⎫⎪⎥⎢⎦⎣⎭ππ. ．（2023·全国·高二专题练习）直线,135︒︒⎤⎦【详解】解：直线x y −，则3x =，直线的斜率不存在，倾斜角为90；1≤，可得为不等于90的倾斜角），90135θ︒<≤综合，倾斜角的取值范围是45︒≤．题型二：重点考查直线的斜率19,6⎤⎡⎫+∞⎪⎥⎢⎦⎣⎭）因为点M 在函数)在线段AB ()19,6⎤⎡⎫+∞⎪⎥⎢⎦⎣⎭，记点16,2P ⎛− ⎝16,2P ⎛⎫− ⎪⎝⎭，所以21y +精练核心考点30，则实数D ．323303=两点的直线的方向向量为题型三：重点考查斜率与倾斜角的变化关系第一象限，则直线l 的倾斜角的取值范围是（)30,60)30,90 )60,9060,90⎤⎦B【详解】因为直线:l ，直线23x y +()0,2B ;30； 90；)30,90.·全国·高二专题练习）经过点P10PA k −=且直线l 与连接点如下图所示，则tan PA k ≤α∴∈π[0,4故选：B例题3．（精练核心考点2．（2023·全国·高二专题练习）已知坐标平面内三点ABC 的边A ．0,⎡⎢⎣C ．3⎡⎢⎣【答案】D【详解】如图所示，1为ABC 的边BD 斜率k ．（2023·全国·高二专题练习）若实数的取值范围为5,73⎡⎤⎢⎥⎣⎦题型四：重点考查斜率公式的应用精练核心考点题型五：重点考查由直线与线段相交求直线斜率（倾斜角）范围3,7⎤⎡⎫+∞⎪⎥⎢⎦⎣⎭【详解】解：设过点P 且垂直于当直线l 由位置PA 绕点P 此时，11354725PA k k +≥==+当直线l 由位置PC 绕点P 此时，1254PB k k +≤==精练核心考点1,2⎤⎡⎫+∞⎪⎥⎢⎦⎣⎭1,2⎤⎡⎫+∞⎪⎥⎢⎦⎣⎭题型六：重点考查两直线的平行或垂直关系；方法二：直线1l 的方向向量()6,3AB =−的方向向量(3,6CD =因为0AB CD ⋅=，所以AB CD ⊥，所以5．（2023·全国·高二专题练习）已知两条直线60my +=2)30m x y −+=，当m 为何值时，相交； 平行； 垂直．【答案】(1)m ≠−3；题型七：重点考查直线的方程．（2023·全国·高二专题练习）在ABC中，已知点轴上截距是y轴上截距的3⎫，即(−⎪⎭；题型八：重点考查两直线的交点坐标【详解】三条直线不能构成三角形三条直线相交于同一点S的最小值AOBS最小值为AOB题型九：重点考查两点间的距离公式故选：B.xA B'=所以函数的最小值为故答案为：42精练核心考点1．（2023·全国·高二专题练习）已知故选：B2．（2023·全国·高二课堂例题）【答案】32【详解】()2221x x x ++=+()(224824x x x −+=−+=如图，设点(),0A x ，()1,1B −，值．由于AB AC BC +≥，当A ，B 故答案为： 32.3．（2023·全国·高二专题练习）函数为 ．【答案】41【详解】()()219f x x =−+1故答案为：41题型十：重点考查点到直线的距离公式例题2．（2023秋·高二课时练习）求垂直于直线3105的直线l 的方程． 【答案】390x y −+=或3x −【详解】设与直线35x y +−则由点到直线的距离公式知()()2310310⨯−−+−===mm d350y+=.春·上海·高二期中）已知ABC的三个顶点y+=，且60)2,3，所以因此有+24=723+6=0m n m n −−⎧⎨⎩或+24=723+6=0m n m n −−−⎧⎨⎩，解得：=3=4m n ⎧⎨⎩或=3=0m n −⎧⎨⎩， 所以点A 的坐标为：()3,4或()3,0−．题型十一：重点考查两条平行线间的距离公式精练核心考点。
直线方程经典题型总结
直线与直线方程经典题型题型一：倾斜角与斜率【例1】下列说法正确的个数是( )①任何一条直线都有唯一的倾斜角；②倾斜角为300的直线有且仅有一条；③若直线的斜率为tan「则倾斜角为二④如果两直线平行，则它们的斜率相等'」A. 0 个B.1 个C.2 个D.3 个h\/ 2【练习】如果AC <0且BC <0，那么直线Ax+By+C=0不通过( 、；'、、、A.第一象限 B. 第二象限C.第三象限 D.第四象卩―方/\ ；【例2】如图，直线I经过二、三、四象限，I的倾斜角为a,斜率为％,则() A. ksin a >0 B . kcos a >0 C . ksin a< 0 D. kcos a< 0【练习】图中的直线I1 , I2 , I3的斜率分别为k1, k2, k3，则()A. k1 v k2 v k3B. k3 v k1 v k2C. k3 v k2 v k1D. k1 v k3 v k2【例3】经过点P1,2作直线I，若直线I与连接A0,—1 , B4,1的线段总有公共点，求直线I的倾斜角:与斜率k的取值范围。
【练习】已知两点A-3,4 , B 3,2 ,过点P2,-1的直线I与线段AB有公共点，求直线I的斜率k的取值范围。
【例4】若直线I的方程为y二xtan：・2，则( )A.—定是直线I的倾斜角B. :- 一定不是直线I的倾斜角C.n—一定是直线I的倾斜角D.:不一定是直线I的倾斜角【练习】设直线ax by c 0的倾斜角为「，且A.a b=1B. a —b=1C. a b=0D. a —b=0题型二：斜率的应用【例5】若点A(2,2 ) B(a,0)C(0,4 )共线则a的值为 ___________________【练习】若三点A(2,2 ) B(a,0)C(0,b) (ab#0 共线，则丄+丄的值为 a b【例6】已知实数x、y满足2x + y=8，当2兰x兰3时，求*的最大值为 ______ ，最小x值为___________________【练习】1、若a二哑小二也，•心，则( )1 2 4A. a : b cB. c : b aC. c : a bD. b a c2、求函数y二三二1的值域.2 +1题型三：两直线位置关系的判断已知，两直线l i,l2斜率存在且分别为k i,k2 ,若两直线平行或重合则有k i ___________________________ k2 , 若两直线垂直则有k i ___________________ k2.【例7】已知直线l i的倾斜角为60，直线12经过点A1，,3，B —2,—2 3，判断直线h与12的位置关系.【练习】1、已知点P 2,3，Q 4,5 , A —1，a，B 2a,2当a为何值时，直线PQ与直线AB 相互垂直？2、已知直线g经过点A 3，a，B a —2,3，直线经过点M3, a , N 6,5，若m2，求a的值.【例8】在平面直角坐标系中，对R，直线1i：x —2ay i=0和12 : 2ax y —^0 （）A.互相平行B.互相垂直C.关于原点对称D.关于直线y=—x对称【练习】直线3a 2 x 1 —4ay 8=0与5a —2x a 4 y —7=0垂直，求a的值.题型四：求直线方程（一）点斜式【例9】根据条件写出下列直线的方程：（1）经过点A（1,2）,斜率为2；（2）经过点B （—1,4 ），倾斜角为135 ；（3）经过点C（4,2 ），倾斜角为90 ；（4）经过点D （—3，—2），且与x轴平行.已知直线过一点，可设点斜式【练习】已知ABC中，A1,—4，B 2,6，C —2,0，AD _ BC于D,求AD的直线方程.（二）斜截式【例10】根据条件写出下列直线的方程:（1）斜率为2,在y轴上的截距是5；（2）倾斜角为150 •，在y轴的截距为一2;（3）倾斜角为45 ,在y轴上的截距为0.已知斜率时，可设斜截式：【练习】求斜率为？，且与坐标轴围成的三角形周长是12的直线I的方程.4（三）截距式【例12】根据条件写出下列直线的方程：在x轴上的截距为一3,在y轴上的截距为2；（1）⑵在x轴上的截距为1，在y轴上的截距为一4；与截距相关的问题，可设截距式【练习】直线I过点P 4,3，且在x轴、y轴上的截距之比为1:2，求直线I的方程.（四）两点式【例11】求经过下列两点的直线方程：（1）A（2,5）,B（4,3）（2）A（2,5）,B（4,5）（3）A（2,5）,B （2,7）适时应用“两点确定一条直线”【练习】过点M 0,1作直线I，使他被两条已知直线l1：x —3y 10和l2：x y ^0所截得的线段AB被点M平分.求直线I的方程.【例12】1、已知点A（3,3 ）和直线I : y=3x —仝求：4 2（1）经过点A且与直线I平行的直线方程；（2）经过点A且与直线I垂直的直线方程.2、已知三角形三个顶点的坐标分别为 A （—1,0），B（2,0），C（2,3 ），试求AB边上的高的直线方程.（思考：如果求AB边上的中线、角平分线呢？）【例13】已知直线I的斜率为2，且I和两坐标轴围成面积为4的三角形，则直线l 的方程为 _________________ .【练习】已知，直线I 经过点（一5,— 4）,且与两坐标轴所围成的三角形面积为 5,则直线I 的方程为 ___________________【例14】直线I 不经过第三象限，其斜率为k ，在y 轴上的截距为b （骨0），则 k_0且b ：：0 C. k - 0且b 0 D. k • 0且b . 0y=ax+b 与y=bx+a 在同一直角坐标系中的图象位置可能是五、直线的交点坐标与距离公式1、求两条直线的交点（联立方程组）1 例（1）若三条直线： 2x+3y+8=0,x-y-1=0 和 x+ky+k+ 2 =0 相交于 点，贝U k=（2）已知直线I1 : x+y+2=0, I2 : 2x-3y-3=0,求经过的交点且与已知直线3x+y-仁0平行的直线I 的方程2、两点间的距离公式丨P1P2| =（区-为亍+⑴-力）2例（1）已知点A （a,-5 ）与B （0,10 ）间的距离是17,求a 的值。
高考直线方程题型归纳(最新整理)
高考直线方程题型归纳知识点梳理1．点斜式方程设直线l 过点P 0(x 0，y 0)，且斜率为k ，则直线的方程为y －y 0=k (x －x 0)，由于此方程是由直线上一点P 0(x 0，y 0)和斜率k 所确定的直线方程，我们把这个方程叫做直线的点斜式方程.注意：利用点斜式求直线方程时，需要先判断斜率存在与否.（1）当直线l 的倾斜角α=90°时，斜率k 不存在，不能用点斜式方程表示，但这时直线l 恰与y 轴平行或重合，这时直线l 上每个点的横坐标都等于x 0，所以此时的方程为x =x 0.（2）当直线l 的倾斜角α=0°时，k =0，此时直线l 的方程为y =y 0，即y－y 0=0.（3）当直线l 的倾斜角不为0°或90°时，可以直接代入方程求解.2．斜截式方程：如果一条直线通过点(0，b )且斜率为k ，则直线的点斜式方程为y =kx + b 其中k 为斜率，b 叫做直线y =kx +b 在y 轴上的截距，简称直线的截距. 注意：利用斜截式求直线方程时，需要先判断斜率存在与否.（1）并非所有直线在y 轴上都有截距，当直线的斜率不存在时，如直线x =2在y 轴上就没有截距，即只有不与y 轴平行的直线在y 轴上有截距，从而得斜截式方程不能表示与x 轴垂直的直线的方程.（2）直线的斜截式方程y =kx +b 是y 关于x 的函数，当k =0时，该函数为常量函数.x =b ；当k ≠0时，该函数为一次函数，且当k >0时，函数单调递增，当k <0时，函数单调递减.（3）直线的斜截式方程是直线的点斜式方程的特例。
要注意它们之间的区别和联系及其相互转化.3．直线的两点式方程若直线l 经过两点A (x 1，y 1)，B (x 2，y 2)，(x 1≠x 2)，则直线l 的方程为，这112121y y x x y y x x --=--种形式的方程叫做直线的两点式方程.注意（1）当直线没有斜率(x 1=x 2)或斜率为零(y 1=y 2)时，不能用两点式表示112121y y x x y y x x --=--它的方程；（2）可以把两点式的方程化为整式(x 2－x 1)(y －y 1)= (y 2－y 1)(x －x 1)，就可以用它来求过平面上任意两点的直线方程； 如过两点A (1，2)，B (1，3)的直线方程可以求得x =1，过两点A (1，3)，B (－2，3)的直线方程可以求得y =3.（3）需要特别注意整式(x 2－x 1)(y －y 1)= (y 2－y 1)(x －x 1)与两点式方程的112121y y x x y y x x --=--区别，前者对于任意的两点都适用，而后者则有条件的限制，两者并不相同，前者是后者的拓展。
直线方程常见题型归纳
直线方程常见题型归纳一定点问题1.若kÎR时，直线y-2=k(x-1)总通过一个定点，这个定点是（）A（1，-2）B（-1,2）C（-2,1）D（1,2）2.方程y=k（x-2），xÎR表示（）A通过点（-2,0）的一切直线B通过点（2,0）的一切直线C通过点（2,0）且不垂直x轴的一切直线D通过点（2,0）且除去x轴的一切直线3.已知直线l的方程为：（2m-3）x+y-m+6=0，则对于任意的mÎR，直线l恒过定点_____ 二截距问题1.直线mx+ny=1(mn≠0)与两坐标轴围成的面积是（）A 12mn B 1||2mn C 12mnD 12||mn2.过点P（2,3）并且在两坐标轴上截距相等的直线方程是：________ 3.过点（5,2）且在x轴上截距是y轴上截距两倍的直线方程是：__________ 4.过点（5,2），且在坐标轴上截距互为相反数的直线方程为（）A x-y-3=0 B x-y+3=0或2x-5y=0 C x-y+3=0 D x-y-3=0或2x-5y=0 5.已知直线L与两坐标轴围成一个等腰直角三角形，且此三角形的面积为18，求直线L的方程。
三最值问题1.过点P(2,1)作直线l分别交x轴、y轴的正半轴于点A、B.求AOBD的面积最小时直线l的方程; 2. 若直线l过点（1,1），且与两坐标轴所围成的三角形的面积为2，则这样的直线l有（）条A 1 B 2 C 3 D 4 （变式题：若面积为5呢，面积为1呢？）3.过点P(2,1) 作直线l分别交x轴、y轴于点A、B，求|PA|·|PB|取最小值时直线l的方程. 4．已知点M(1,3),N(5,-2),在x轴上取一点P，使得||PM|-|PN||最大，则P点坐标是（）A （5,0）B （13,0）C （0,13）D （3.4,0）变式：若使||PM|+|PN||最小呢？四、对称问题1.点A （4,5）关于直线l 的对称点为B （-2,7），则l 的方程为____________2.点A （1,2）关于直线x-2y-2=0的对称点B 的坐标是_________3.已知M （a ，b ）与N 关于x 轴对称，点P 与点N 关于y 轴对称，点Q 与点P 关于直线x+y=0对称，则点Q 的坐标为（ ）A （a ，b ）B （b ，a ）C （-a ，-b ）D （-b ，-a ）4. 直线042=--y x 上有一点P ，它与两定点)4,3()1,4(B A 、-的距离之差最大，则P 点的坐标是___.五、易错题1.已知直线L 的横截距为a ，纵截距为b ，斜率为k ，则下列命题正确的是（ ）A 直线与坐标轴围成的面积是12ab B 直线的方程是：1x y a b += C 斜率k=b a - D 以上都不对 2.若直线L 过点（1,2）且两截距相等，则直线L 的斜率k 是（ ）A k=-1或k=2B k=±1或k=2C k=-1D k=1或k=23. 下列四个命题中属于真命题的是 （ ）A 、经过定点的直线都可以用方程00()y y k x x -=-B 、经过任意两个不同点111222(,),(,)P x y P x y 的直线都可以用121121()()()()y y x x x x y y --=--表示C 、不经过原点的直线都可以用1x y a b+=表示； D 、经过点(0,)A b 的直线都可以用方程y kx b =+表示4.直线tan +y-1=07x π的倾斜角是（ ） A -7π B 7πC 75πD 76π5.若111:0L A x B y C ++=与222:0L A x B y C ++=只有一个公共点则（ ）A 1122AB -A B =0 B 1221A B +A B =0C 1212A A B B ¹D 1122A B A B ¹ 6.当q 是第四象限角时，直线sin 1cos -a=0x y q q ++和直线1cos +b=0x y q +-的位置关系是（ ）A 平行B 相交但不垂直C 垂直D 与q 角有关 7.若直线L 1：x+ay+6=0与直线L 2：（a-2）x+3y+2a=0互相平行，则a 的值为（ ）A -1或3B 1或3C -1D 以上都不对8.过（x 1，y 1）和（x 2，y 2）两点的直线方程是（ ）A 112121y y x x y y x x --=--B 122112y y x x y y x x --=-- C 211211()()()()0y y x x x x y y -----= D 211211()()()()0x x x x y y y y -----=9.下列命题：○1若有斜率的两条直线斜率不相等，则这两条直线不平行 ○2若两条直线平行，则这两条直线的斜率相等 ○3若两条直线都有斜率，且斜率相等，则这两条直线必定平行 其中不正确的命题是_______10.已知两点A （-1,2），B （m ，3）（1）求直线AB 的斜率k（2）求直线AB 的方程（3）已知实数m 3[1,31]3m Î---，求直线Ab 的倾斜角a 的取值范围11.求过点P （-5，-4）且分别满足下列条件的直线方程（1）倾斜角的正弦值是45； （2）倾斜角是直线l ：314y x =+的倾斜角的一半（3）与x 轴和y 轴分别交于A 、B 两点，且||3||5AP BP =。
史上最全直线与直线方程题型归纳
精心整理直线与直线方程一、知识梳理1.直线的倾斜角与斜率：在平面直角坐标系中，对于一条与x 轴相交的直线，如果把x 轴绕着交点按逆时针方向旋转到和直线重合时所转的最小正角记为α，那么α就叫做直线的倾斜角.当直线和x 轴平行或重合时，我们规定直线的倾斜角为0°.倾斜角的取值范围是0°≤α＜180°.倾斜角不是90°的直线，它的倾斜角的正切叫做这条直线的斜率，常用k 表示.倾斜角是90°的直线没有斜率.2.斜率公式：经过两点),(),,(222111y x P y x P 的直线的斜率公式：)(211212x x x x y y k ≠--=3.直线方程的五种形式直线形式 直线方程局限性选择条件 点斜式不能表示与x 轴垂直的直线①已知斜率 ②已知一点 斜截式不能表示与x 轴垂直的直线①已知斜率②已知在y 轴上的截距两点式不能表示与x 轴、y 轴垂直的直线①已知两个定点 ②已知两个截距 截距式（b a 、分别为直线在x 轴和y 轴上的截距）不能表示与x 轴垂直、与y 轴垂直、过原点的直线 已知两个截距（截距可以为负）一般式表示所有的直线求直线方程的结果均可化为一般式方程 7．斜率存在时两直线的平行：21//l l ⇔1k =2k 且21b b ≠. 8．斜率存在时两直线的垂直：⇔⊥21l l 121-=k k ．9．特殊情况下的两直线平行与垂直:当两条直线中有一条直线没有斜率时：(1)当另一条直线的斜率也不存在时，两直线的倾斜角都为90°，互相平行；(2)当另一条直线的斜率为0时，一条直线的倾斜角为90°，另一条直线的倾斜角为0°，两直线互相垂直． 二、典例精析题型一：倾斜角与斜率【例1】下列说法正确的个数是（） ①任何一条直线都有唯一的倾斜角；②倾斜角为030的直线有且仅有一条； ③若直线的斜率为θtan ，则倾斜角为θ； ④如果两直线平行，则它们的斜率相等 A.0个B.1个C.2个D.3个【练习】如果0<AC 且0<BC ，那么直线0=++C By Ax 不通过（） A.第一象限B.第二象限C.第三象限D.第四象限【例2】如图，直线l 经过二、三、四象限，l 的倾斜角为α，斜率为k ，则( ) A ．k sin α>0 B ．k cos α>0C ．k sin α≤0 D ．k cos α≤0【练习】图中的直线l 1，l 2，l 3的斜率分别为k 1，k 2，k 3，则()．A ．k 1＜k 2＜k 3B ．k 3＜k 1＜k 2C ．k 3＜k 2＜k 1D ．k 1＜k 3＜k 2【例3】经过点()2,1P 作直线l ，若直线l 与连接()10—，A ，()1,4B 的线段总有公共点，求直线l 的倾斜角α与斜率k 的取值范围。
直线方程重点题型
直线方程重难点题型1、斜率问题1. 若三点)2,2(A ，)0,(a B ，),0(b C )0(≠ab 共线，则=+ba 11 。
2. 若直线先向做平移一个单位，再向上平移两个单位，所得直线与原直线重合，则该直线的斜率为 。
3. 直线01=++y ax 与连接)3,2(A ，)2,3(-B 的线段相交，则a 的取值范围是（ ）A . ]2,1[-B . ),2[)1,(+∞⋃--∞C . ]1,2[-D . ),1[)2,(+∞⋃--∞4. 已知实数y x ,满足222+-=x x y )11(≤≤-x ，试求23++x y 的最大值与最小值。
拓展：著名数学家华罗庚曾说过：“数形结合百般好，割裂分家万事休。
”事实上，很多代数问题可以转化为几何问题加以解决。
如：22)()(b y a x -+-可以转化为平面上的点),(y x M 与点),(b a N 的距离。
结合上述观点，可得102204)(22+++++=x x x x x f 的最小值为 。
2、求直线方程 5. 已知两直线07:111=++y b x a l ，07:222=++y b x a l 都经过点)5,3(，则经过点),(11b a ，),(22b a )(21a a ≠的直线方程 。
3、中点问题6. 一条直线l 被两条直线064:1=++y x l 和0653:2=--y x l 截得的线段中点M 恰好是坐标原点，求直线l 的方程。
7. 过点)1,0(M 作直线，使得它被两条直线0103:1=+-y x l 和082:2=-+y x l 所截得的线段恰好被点M 平分，求此直线的方程。
4、距离问题8. 到直线012:=++y x l 的距离为55的点的轨迹方程为（ ） A . 直线022=-+y x B . 直线02=+y xC . 直线02=+y x 或直线022=-+y xD . 直线02=+y x 或直线022=++y x9.已知正方形的中心为直线2x－y＋2=0和x＋y＋1=0的交点，正方形一边所在直线的方程为x＋3y－5=0，求其他三边所在直线的方程．5、对称问题及应用（1）点关于直线对称10.已知P(2,3)和直线l:x＋y＋1=0．求(1)点P关于直线l的对称点；(2)若一束光线由P点射到l上，反射后经过点Q(1,1)，求入射光线及反射光线的方程．11.如图，已知)0,4(A，)4,0(B，从点)0,2(P射出的光线经直线AB反射后再射到OB上，最后经直线OB反射后又回到点P，则光线所经过的路程是。
直线方程基础知识小结
直线方程基础知识小结一 .网络结构图：平面直角坐标系中的直线：⎪⎪⎩⎪⎪⎨⎧简单的线性规划直线的位置关系直线方程的五种形式直线的倾斜角和斜率二．直线的倾斜角和斜率：1.直线方程的概念：（1，这条直线叫做这个方程的直线.2.直线的倾斜角：在平面直角坐标系中，对于一条与x 时针方向旋转到和直线重合时所转的最小正角记为αx 轴平行重合时， 规定直线的倾斜角为0°.3.直线的斜率：倾斜角不是90°的直线，k 表示.倾斜角是︒90的直线没有斜率4. 三个题型： （1）已知倾斜角求斜率：⎪⎭⎫ ⎝⎛≠<≤=2,0tan παπααK （2）已知斜率求倾斜角：即由K =αtan 求αα＝（3）已知倾斜角的范围求斜率的范围：已知斜率的范围求倾斜角的范围：方法：应用如上正切曲线，数形结合解决问题5.斜率公式：经过两点),(),,(222111y x P y x P )2x ≠（当2121,y y x x ≠=（即直线和x6.直线的方向向量：直线上的向量→21P P 及与它平行的所有非零向量λ→21P P （）且0≠∈λλR 都是该直线的方向向量 常用的直线的方向向量有：（1） （2） （3） （4）7.证明三点共线的方法：（1）函数法；（2）定比分点公式（3）共线向量（4）斜率相等（5）线段和五．点到直线的距离公式：（1）P ()00,y x 到直线0:=++C By Ax l 的距离公式：（2）0:;0:2211=++=++C By Ax l C By Ax l 的距离公式：（3）P ()00,y x 到直线a x l =:的距离公式：P ()00,y x 到直线b y l =:的距离公式： 六．直线的对称问题：1．点关于点的对称点问题：()()())2,2(),(,,00y b x a y x y x ba ----任意点，坐标原点关于方法依据：中点坐标公式 2. 点关于直线的对称点问题：()()()()()()()()()(),,0,,,,2,,2,,=++=+-=++-=====-=+----------C By Ax c y x c y x xy xy by ax y y x x c x c y c x c y x y x y y b x y x a y x y x 直线直线直线直线直线直线直线直线直线关于说明：01（1）到（4）方法依据是中点坐标公式02（5）到（9）方法依据是：点关于直线对称点的基本解法3点关于直线对称的基本解法：直接法：设所求的对称点坐标是（),00y x 则由题意有：⎪⎪⎩⎪⎪⎨⎧-=-⨯--=++++1)(0220000B A x x y y C y y B xx A ⎩⎨⎧==∴00y x间接法 ：3.三个典型题：（1）距离和的最小值问题：在定直线l 上取点P ，求P 到两定点A,B 距离和PB PA +的最小值当两定点A,B 在直线l 的两侧时：PB PA +AB ≥，最小值是,AB 此时点P 坐标由方程组⎩⎨⎧=++:0:AB l C By Ax l 决定 当两定点A,B 在直线l 的同侧时：先求点B 关于定直线l 的对称点 /B ，则PB PA +＝//AB PB PA ≥+，最小值是/AB此时点P 坐标由方程组 ⎩⎨⎧=++:0:/AB l C By Ax l 决定 （2）距离差的最大值问题：在定直线l 上取点P ，求P 到两定点A,B 距离差PB PA -的最大值当两定点A,B 在直线l 的同侧时：PB PA -AB ≥，最大值是,AB 此时点P 坐标由方程组⎩⎨⎧=++:0:AB l C By Ax l 决定 当两定点A,B 在直线l 的两侧时：先求点B 关于定直线l 的对称点 /B ，PB PA -＝//AB PB PA ≤- ，最大值是,AB 此时点P 坐标由方程组⎩⎨⎧=++:0:/AB l C By Ax l 决定（3）入射光线和反射光线问题：入射光线上的点关于界面的对称点在反射光线上；反射光线上的点关于界面的对称点在入射光线上； 入射光线与界面的交点在反射光线上； 反射光线与界面的交点在入射光线上；界面是x 轴（y 轴）时，考虑入射光线与反射光线的斜率互为相反数； 界面是直线y=x(y=-x)时，考虑入射光线与反射光线上点的对称 例5光线由点)4,1(-A 射出，遇到直线l ：0632=-+y x 后被反射，已知其)1362,3(B ， 求反射光线所在直线的方程.七.几组特殊的直线系方程：1.直线系方程的定义：具有某种共同性质(过某点、共斜率等)的所有直线的集合叫做直线系。
史上最全直线与直线方程题型归纳
史上最全直线与直线方程题型归纳．直线与直线方程一、知识梳理1.直线的倾斜角与斜率：在平面直角坐标系中，xx轴绕着交对于一条与如果把轴相交的直线，点按逆时针方向旋转到和直线重合时所转的最小正角记为，那么就叫做直线的倾斜角.当直??x轴平行或重合时，我们规定直线的倾斜角线和为0°.倾斜角的取值范围是0°≤＜180°.倾?斜角不是90°的直线，它的倾斜角的正切叫做k表示.倾斜角是90这条直线的斜率，常用°的直线没有斜率.2.斜率公式：经过两点的直线的斜率),y),P(x(Px,y111222y?y公式：12)k?xx(?21xx?12直线方程的五种形式3.- 2 -.且7．斜率存在时两直线的平行：=?kkb?bll//212211．．斜率存在时两直线的垂直：81kk???l?l2112当两条直线:．9特殊情况下的两直线平行与垂直- 3 -中有一条直线没有斜率时：(1)当另一条直线的斜率也不存在时，两直线的倾斜角都为90°，互相平行；(2)当另一条直线的斜率为0时，一条直线的倾斜角为90°，另一条直线的倾斜角为0°，两直线互相垂直．二、典例精析题型一：倾斜角与斜率【例1】下列说法正确的个数是（）①任何一条直线都有唯一的倾斜角；②倾斜角为的直线有且仅有一条；030；③若直线的斜率为，则倾斜角为??tan④如果两直线平行，则它们的斜率相等C.2 B.1个 A. 0个D.3个个，那么直线【练习】如果且0BCAC?0?）不通过（0?C?ByAx? C.第三象限 A.第一象限 B.第二象限第四象限D.的l】如图，直线l经过二、三、四象限，例2【)(倾斜角为α，斜率为k，则0αkC >0 cos．>0sin．AkαBkα．sin≤- 4 -D．kcosα≤0【练习】图中的直线l，l，l的斜率分别为k，1213k，k，则()．32A．k＜k＜kB．k＜k＜k 2113 32C．k＜k＜k D．k＜k＜k2 23131【例3】经过点作直线，若直线与连接??ll21,P 的倾斜的线段总有公共点，求直线，????l14,BA0，—1角与斜率的取值范围。
直线与方程知识点总结(实用4篇)
直线与方程知识点总结第1篇空间两条直线只有三种位置关系。
1、按是否共面可分为两类：（1）共面：平行、相交（2）异面：异面直线的定义：不同在任何一个平面内的两条直线或既不平行也不相交。
异面直线判定定理：用平面内一点与平面外一点的直线，与平面内不经过该点的直线是异面直线。
两异面直线xxx的角：范围为（0，90）esp。
空间向量法两异面直线间距离：公垂线段（有且只有一条）esp。
空间向量法2、若从有无公共点的角度看可分为两类：（1）有且仅有一个公共点相交直线；（2）没有公共点平行或异面直线与方程知识点总结第2篇常见的三角函数包括正弦函数、余弦函数和正切函数。
有些学生仍然在遇到三角函数题目的时候画直角三角形协助理解，这是十分危险的，也是我们所不提倡的。
三角函数的定义在引入了实数角和弧度制之后，已经发生了革命性的变化，sinA中的A不一定是一个锐角，也不一定是一个钝角，而是一个实数弧度制的角。
有了这样一个思维上的飞跃，三角函数就不再是三角形的一个附属产品（初中三角函数很多时候依附于相似三角形），而是一个具有独立意义的函数表现形式。
既然三角函数作为一种函数意义的理解，那么，它的知识结构就可以完全和函数一章联系起来，函数的精髓，就在于图象，有了图象，就有了所有的性质。
对于三角函数，除了图象，单位圆作为辅助手段，也是非常有效就好像配方在二次函数中应用广泛是一个道理。
三角恒等变形部分，并无太多诀窍，从教学中可以看出，学生听懂公式都不难，应用起来比较熟练的都是那些做题比较多的同学。
题目做到一定程度，其实很容易发现，高一考察的三角恒等只有不多的几种题型，在课程与复习中，我们也会注重给学生总结三角恒等变形的统一论，把握住降次，辅助角和万能公式这些关键方法，一般的三角恒等迎刃而解。
关键是，一定要多做题。
直线与方程知识点总结第3篇①定义:倾斜角不是90°的直线,它的倾斜角的正切叫做这条直线的斜率。
直线的斜率xxx 表示。
直线与双曲线题型总结
直线与双曲线题型总结直线题型1. 直线方程直线的一般方程为 $Ax + By + C = 0$，其中 $A$、$B$、$C$ 为常数。
已知点 $P_1(x_1, y_1)$ 和点 $P_2(x_2, y_2)$，可以通过以下公式之一求得直线的方程：- 斜率截距形式：$y = mx + c$，其中 $m$ 为直线的斜率，$c$ 为直线在 $y$ 轴上的截距。
- 两点形式：$y = \frac{{y_2 - y_1}}{{x_2 - x_1}}(x - x_1) +y_1$。
2. 直线与直线的位置关系判断两条直线的位置关系可以通过判断它们的斜率和截距是否相等。
- 平行线：两条直线的斜率相等但截距不相等。
- 垂直线：两条直线的斜率乘积为 $-1$。
3. 点到直线的距离已知点 $P(x_0, y_0)$ 到直线 $Ax + By + C = 0$ 的距离可以通过以下公式计算：$$d = \frac{{|Ax_0 + By_0 + C|}}{{\sqrt{A^2 + B^2}}}$$双曲线题型1. 双曲线方程双曲线的一般方程为 $\frac{{x^2}}{{a^2}} -\frac{{y^2}}{{b^2}} = 1$，其中 $a$、$b$ 为正常数。
已知中心点$O(h, k)$，可以通过以下公式之一求得双曲线的方程：- 极坐标形式：$\frac{{x - h}}{{a^2}} - \frac{{y - k}}{{b^2}} = 1$。
- 对称轴形式：$\frac{{x - h}}{{a^2}} + \frac{{y - k}}{{b^2}} = 1$。
2. 双曲线的焦点和短轴双曲线的焦点到中心的距离称为焦距，记为 $c$。
焦点所在的直线称为焦点直线。
双曲线的短轴长度为 $2b$。
3. 双曲线的渐近线双曲线的渐近线是与双曲线趋于无限远处的直线接近的直线。
以上为直线与双曲线题型的总结。
在解题过程中，注意运用相关的公式和性质，如斜率、截距、距离公式等，以提高解题效率。
高考直线方程题型归纳
高考直线方程题型归纳知识点梳理 1．点斜式方程设直线l 过点P 0x 0,y 0,且斜率为k ,则直线的方程为y －y 0=kx －x 0,由于此方程是由直线上一点P 0x 0,y 0和斜率k 所确定的直线方程,我们把这个方程叫做直线的点斜式方程.注意：利用点斜式求直线方程时,需要先判断斜率存在与否. 1当直线l 的倾斜角α=90°时,斜率k 不存在,不能用点斜式方程表示,但这时直线l 恰与y 轴平行或重合,这时直线l 上每个点的横坐标都等于x 0,所以此时的方程为x =x 0.2当直线l 的倾斜角α=0°时,k =0,此时直线l 的方程为y =y 0,即y －y 0=0.3当直线l 的倾斜角不为0°或90°时,可以直接代入方程求解. 2．斜截式方程：如果一条直线通过点0,b 且斜率为k ,则直线的点斜式方程为y =kx + b 其中k 为斜率,b 叫做直线y =kx +b 在y 轴上的截距,简称直线的截距. 注意：利用斜截式求直线方程时,需要先判断斜率存在与否.1并非所有直线在y 轴上都有截距,当直线的斜率不存在时,如直线x =2在y 轴上就没有截距,即只有不与y 轴平行的直线在y 轴上有截距,从而得斜截式方程不能表示与x 轴垂直的直线的方程.2直线的斜截式方程y =kx +b 是y 关于x 的函数,当k =0时,该函数为常量函数.x =b ；当k ≠0时,该函数为一次函数,且当k >0时,函数单调递增,当k <0时,函数单调递减.3直线的斜截式方程是直线的点斜式方程的特例;要注意它们之间的区别和联系及其相互转化.3．直线的两点式方程若直线l 经过两点Ax 1,y 1,Bx 2,y 2,x 1≠x 2,则直线l 的方程为112121y y x x y y x x --=--,这种形式的方程叫做直线的两点式方程. 注意1当直线没有斜率x 1=x 2或斜率为零y 1=y 2时,不能用两点式112121y y x x y y x x --=--表示它的方程；2可以把两点式的方程化为整式x 2－x 1y －y 1= y 2－y 1x －x 1,就可以用它来求过平面上任意两点的直线方程； 如过两点A 1,2,B 1,3的直线方程可以求得x =1,过两点A 1,3,B －2,3的直线方程可以求得y =3.3需要特别注意整式x 2－x 1y －y 1= y 2－y 1x －x 1与两点式方程112121y y x x y y x x --=--的区别,前者对于任意的两点都适用,而后者则有条件的限制,两者并不相同,前者是后者的拓展; 4．直线的截距式方程若直线l 在x 轴上的截距是a ,在y 轴上的截距是b ,且a ≠0,b ≠0,则直线l 的方程为1x ya b+=,这种形式的方程叫做直线的截距式方程; 注意：1方程的条件限制为a ≠0,b ≠0,即两个截距均不能为零,因此截距式方程不能表示过原点的直线以及与坐标轴平行的直线；2用截距式方程最便于作图,要注意截距是坐标而不是长度；3要注意“截距相等”与“截距绝对值相等”是两个不同的概念,截距式中的截距可正、可负,但不可为零; 截距式方程的应用1与坐标轴围成的三角形的周长为：|a |+|b；2直线与坐标轴围成的三角形面积为：S =1||2ab ；3直线在两坐标轴上的截距相等,则k =－1或直线过原点,常设此方程为x +y =a 或y =kx . 5．直线方程的一般形式方程Ax +By +C =0A 、B 不全为零叫做直线的一般式方程. 注意1．两个独立的条件可求直线方程：求直线方程,表面上需求A 、B 、C 三个系数,由于A 、B 不同时为零,若A ≠0,则方程化为0B Cx y A A++=,只需确定,B C A A 的值；若B ≠0,同理只需确定两个数值即可；因此,只要给出两个条件,就可以求出直线方程； 2．直线方程的其他形式都可以化成一般式,解题时,如果没有特殊说明应把最后结果化为一般式,一般式也可以化为其他形式; 3．在一般式Ax +By +C =0A 、B 不全为零中,若A =0,则y =CB -,它表示一条与y 轴垂直的直线；若B =0,则Cx A=-,它表示一条与x 轴垂直的直线.6.直线方程的选择1待定系数法是求直线方程的最基本、最常用的方法,但要注意选择形式,一般地已知一点,可以待定斜率k ,但要注意讨论斜率k 不存在的情形,如果已知斜率可以选择斜截式待定截距等；2直线方程的几种特殊形式都有其使用的局限性,解题过程中要能够根据不同的题设条件,截距式方程 一般式能表示所有的直线求直线方程的最后结果均可以化为一般式方程典型例题剖析题型1．直线的点斜式方程例1．一条直线经过点M －2,－3,倾斜角α=135°,求这条直线的方程;例2．求斜率为33,且分别满足下列条件的直线方程： 1经过点M 3,－1；2在x 轴上的截距是－5. 题型2．直线的斜截式方程例3．若直线Ax +By +C =0通过第二、三、四象限,则系数A 、B 、C 需满足条件AA 、B 、C 同号 BAC <0,BC <0 CC =0,AB <0 DA =0,BC <0例4．直线y =ax +b a +b =0的图象是例5．写出过下列两点的直线方程,再化成斜截式方程. 1P 12,1,P 20,－3；2P 12,0,P 20,3;例6． 三角形的顶点是A －5,0、B 3,－3、C 0,2,求这个三角形三边所在的直线方程. 题型4．直线的截距式方程例7．已知直线的斜率为61,且和坐标轴围成面积为3的三角形,求该直线的方程;例8．过点A 1,4且纵截距与横截距的绝对值相等的直线共有的条数为 A 1 B 2 C 3 D 4 题型5．直线的一般式方程例9．已知直线经过点A 6,－4,斜率为－34,求直线的点斜式和一般式方程.例10．把直线l 的方程x －2y +6=0化成斜截式,求出直线l 的斜率和它在x 轴与y 轴上的截距,并画图. 题型6.定点问题 例11、已知直线所过定点的横、纵坐标分别是等差数列{}的第一项与第二项,若,数列的前n 项和为T n ,则T 10=A. B. C. D.题型7.对称问题例12、已知直线l 1：y ＝2x ＋3,直线l 2与l 1关于直线y ＝－x 对称,则直线l 2的斜率为A. B ．－ C ．2 D ．－2例13、直线关于直线对称的直线方程是A． B．C． D．例14、直线2x－y－4=0上有一点P,它与两定点A4,－1,B3,4的距离之差最大,则P点坐标是_________例15.1求点A3,2关于点B－3,4的对称点C的坐标；2求直线3x－y－4＝0关于点P2,－1对称的直线l的方程；3求点A2,2关于直线2x－4y＋9＝0的对称点的坐标．题型8.最值问题例16、若点m,n在直线4x＋3y－10＝0上,则m2＋n2的最小值是A．2 B．2 C．4 D．2例17、直线与直线互相垂直,则的最小值为A．1 B．2 C．4 D．5例18.过点P1,2作直线l,交x,y轴的正半轴于A、B两点,求使△OAB面积取得最小值时直线l 的方程.题型9．创新问题例19．已知两直线a1x+b1y+1=0和a2x+b2y+1=0的交点为P2,3,求过两点Q1a1,b1,Q2a2,b2的直线方程.例20、已知点A－1,0,B1,0,C0,1,直线y＝ax＋ba>0将△ABC分割为面积相等的两部分,则b的取值范围是A．0,1 B. C. D.例21、在平面直角坐标系中,定义dP,Q=|x1﹣x2|+|y1﹣y2|为两点Px1,y1,Qx2,y2之间的“折线距离”,在这个定义下,给出下列命题：①到原点的“折线距离”等于1的点的集合是一个圆；②到原点的“折线距离”小于等于2的点构成的区域面积为8；③到M0,﹣2,N0,2两点的“折线距离”相等的点的轨迹方程是y=0；④直线y=x+1上的点到N0,2的“折线距离”的最小值为1．其中真命题有A．1个B．2个C．3个D．4个例22、已知两定点M-2,0,N2,0,若直线上存在点P,使得,则该称直线为“A 型直线”.给出下列直线： ①, ②, ③, ④,其中是“A 型直线”的序号是 .例23、已知直线l ：A ,B 不全为0,两点,,若,且,则A ．直线l 与直线P 1P 2不相交B ．直线l 与线段P 2 P 1的延长线相交C ．直线l 与线段P 1 P 2的延长线相交D ．直线l 与线段P 1P 2相交例24. 已知实数x,y 满足y ＝x 2－2x ＋2－1≤x≤1．试求错误!的最大值与最小值．强化训练1．下列说法中不正确的是A 点斜式y －y 0=kx －x 0适用于不垂直于x 轴的任何直线B 斜截式y =kx +b 适用于不垂直x 轴的任何直线C 两点式112121y y x x y y x x --=--适用于不垂直于坐标轴的任何直线 D 截距式1x ya b+=适用于不过原点的任何直线2．直线3x －2y =4的截距式方程为A 3142x y -=B 11132x y -=C 3142x y -=-D 1423x y +=-3．过点3,－4且平行于x 轴的直线方程是 ；过点5,－2且平行于y 轴的直线方程是 ;4．过点P 1,3的直线分别与两坐标轴交于A 、B 两点,若P 为AB 的中点,求直线的方程. 5．已知△ABC 中,A 1,－4,B 6,6,C －2,0,求：1△ABC 的平行于BC 边的中位线的一般式方程和截距式方程； 2BC 边的中线的一般式方程,并化为截距式方程. 6．如果AC <0,BC <0,那么直线Ax +By +C =0不通过A 第一象限B 第二象限C 第三象限D 第四象限7．直线l 过点P 1,3,且与x ,y 轴正半轴所围成的三角形的面积等于6,则l 的方程是 A 3x +y －6=0 Bx +3y －10=0 C 3x －y =0 Dx －3y +8=08．若直线2m 2+m －3x +m 2－my =4m －1在x 轴上的截距为1,则实数m 是A 1B 2C －21D 2或－219．已知直线l ：Ax +By +C =0A 2+B 2≠0,点Px 0,y 0在l 上,则l 的方程可化为AAx +x 0+By +y 0+C =0 BAx +x 0+By +y 0=0 CAx －x 0+By －y 0+C =0 DAx －x 0+By －y 0=010．经过点－3,－2,在两坐标轴上截距相等的直线方程为 11．若点a ,12在过点1,3及点5,7的直线上,则a = .12．、在平面直角坐标系中,是坐标原点,设函数的图象为直线,且与轴、轴分别交于、两点,给出下列四个命题：①存在正实数,使△的面积为的直线仅有一条；②存在正实数,使△的面积为的直线仅有两条；③存在正实数,使△的面积为的直线仅有三条；④存在正实数,使△的面积为的直线仅有四条.其中所有真命题的序号是 .13、在平面直角坐标系xOy中,设点、,定义：．已知点,点M为直线上的动点,则使取最小值时点M的坐标是．141已知直线l：2m2+m－3x+m2－my－4m+1=0,求m的取值范围2如果ab>0,bc<0,那么直线ax－by－c必经过第几象限。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
直线方程常见题型分类总结
直线的点斜式与斜截式不能表示斜率不存在（垂直于x 轴）的直线；两点式不能表示平行或重合两坐标轴的直线；截距式不能表示平行或重合两坐标轴的直线及过原点的直线。
题型一：两直线的位置关系
判断直线平行：已知直线12l l ，的方程为1111:0l A x B y C ++=，2222:0l A x B y C ++=，若12//l l ，则有12210A B A B -=，且1221B C B C ≠或1221A C B C ≠
判断直线相交:1111:0l A x B y C ++=，2222:0l A x B y C ++=，若两直线相交，则有
12210AB A B -≠
判断直线垂直:已知直线12l l ，的方程为1111:0l A x B y C ++=，2222:0l A x B y C ++=，若
12l l ⊥，则有12120A A B B +=，反之亦然。
两点间的距离，点到直线的距离，两条平行线间的距离 1.两点间距离公式：
设平面内两点111(,)P x y ，222(,)P x y ，则两点间的距离为：12||PP .
特别地，当12,P P 所在直线与x 轴平行时，1212||||PP x x =-；当12,P
P 所在直线与y 轴平行时，
1212||||PP y y =-；
2.点到直线距离公式：点()00,y x P 到直线0:1=++C By Ax l 的距离2
200B A C By Ax d +++=
3.两平行直线距离公式：
两条平行直线
11:0l Ax By C ++=，22:0l Ax By C ++=之间的距离公式d =
，
1.若直线210ax y ++=与直线20x y +-=互相垂直，那么a 的值等于 A ．1 B ．13-
C ．2
3
- D ．2- 2.若直线1:(3)4350l m x y m +++-=与2:2(5)80l x m y ++-=平行，则m 的值为 A ．7- B ．1-或7- C ．6- D ．13
3
- 题型二：定点问题
1. 直线130kx y k -+-=，当k 变化时，所有直线恒过定点. A ．(0,0) B ．（3，1）C ．(1,3) D ．(1,3)--
2.若不论m 取何实数，直线:120l mx y m +-+=恒过一定点，则该定点的坐标为 A ．(2,1)- B ． (2,1)- C ．(2,1)-- D ．(2,1)
3.不论m 为何实数，直线(m －1)x －y ＋2m ＋1＝0 恒过定点 A.(1, －
2
1
) B.(－2, 0) C.(2, 3) D.(－2, 3) 题型三：对称问题
1.已知点(5,8),(4,1)A B ，则点A 关于点B 的对称点C 的坐标 .
2.求点（1,2）关于直线20x y --=的对称点。
3.与直线2360x y +-=关于点(1,1)-对称的直线方程是
A ．3220x y -+=
B ．2370x y ++=
C ．32120x y --=
D ．2380x y ++= 4.光线由点P (2,3)射到x 轴后，经过反射过点Q (1,1),则反射光线方程是
A ．450x y +-=
B ．430x y --=
C ．3210x y --=
D ．2310x y -+= 题型四：截距相等问题
1.若直线过)1,2(P 点且在两坐标轴上的截距相等，则这样的直线有几条 A. 1条 条 条 D.以上都有可能
2.过点（1，2）且在两坐标轴上的截距相等的直线的方程 .
3.直线l 在两坐标轴上的截距相等，且(43)P ，到直线l 的距离为32，求直线l 的方程． 题型五：最值问题
、Q 分别为01043=-+y x 与0586=++y x 上任意一点，则PQ 的最小值为 （A ）
95 （B ）6 （C ） 3 （D ）2
5
2.已知点A(1,3)、B(5,2)，点P 在x 轴上，使|AP |–|BP |取得最大值时P 的坐标 A. （4,0） B. (13,0)
C. (5,0)
D. (1,0)
3.已知点)10,2(),5,1(-B A ，直线1:+=x y l ，在直线l 上找一点P 使得PB PA +最小，则这个最小值为
（A ）34 （B ）8 （C ）9 （D ）10 4.过点(1,2)且与原点距离最大的直线方程是
A.250x y +-=
B.240x y +-=
C.370x y +-=
D.350x y +-= 5.点P(-1,3)到直线l:y=k(x-2)的距离的最大值等于( ) (A)2 (B)3 (C)3
(D)2
题型六：与线段相交的斜率问题
1.已知点(2,3),(3,2)A B --，若直线l 过点(1,1)P 与线段AB 相交，则直线l 的斜率k 的取值范围是（ ） A ．324
k
k ≥≤或 B ．3
24k ≤≤
C ．3
4
k ≥
D ．2k ≤ 2.已知直线l 过点P （1,2）且与以A(-2,-3)、B （3,0）为端点的线段相交，求直线l 的斜率的取值范围.
题型七:待定系数法求直线方程
1.与直线:51260l x y -+=平行且到l 的距离为2的直线方程.
2.求过点(2,1)A ，且与直线0102=-+y x 垂直的直线l 的方程.
3.过点M (0，1)作直线，使它被两已知直线l 1: x －3y +10=0和l 2:2x +y －8=0所截得的线段恰好
被M 所平分，求此直线方程. 题型八：三角形面积问题
1. 直线l 过点M （2,1），且分别与x,y 轴的正半轴交于A ，B 两点，O 为坐标原点，当AOB ∆的面积最小时，求直线l 的方程 习题：
1..若点P 在直线x +3y =0上，且它到原点的距离与到直线x +3y –2=0的距离相等，则点P 的坐标是 .
2..直线l 过点A (0, 1)，且点B (2, –1)到l 的距离是点C (1, 2)到l 的距离的2倍，则直线l 的方程是 .
3.设点P 在直线30x y +=上，且P 到原点的距离与P 到直线320x y +-=的距离相等，则点P 坐标是 ．
4.若两平行直线3x –2y –1=0和6x +ay +c =0之间的距离是
213
13
，则2c a +的值为
5.直线l 与两直线1y =和70x y --=分别交于,A B 两点，若线段AB 的中点为
(1,1)M -，则直线l 的斜率为 A ．23 B ．32 C ．32- D ． 23-。