《工程力学(工程静力学与材料力学)(第3版)》习题解答：第6章 杆件的内力分析
工程力学课后习题答案（静力学和材料力学）
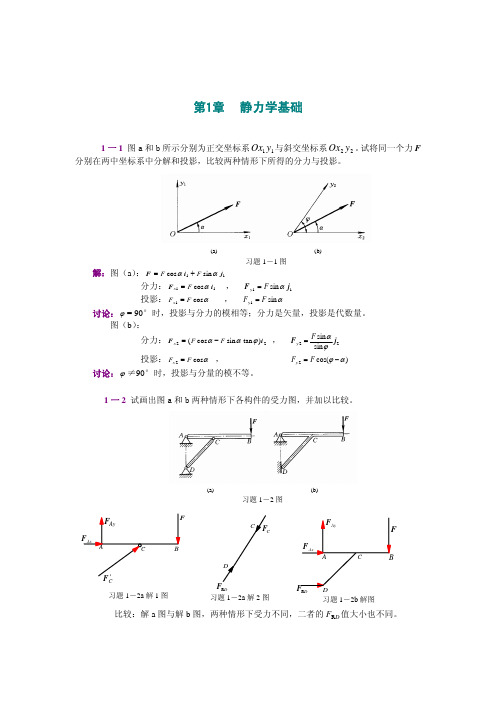
解：图（a）：θ = arcsin 4 ,
5
∑ Fx = 0 ,
F sin(60° − θ ) − W sinθ = 0 , F = 1672 N
图（b）：θ = 53.13° ,
∑ Fx = 0 , F cos(θ − 30°) − W sinθ = 0 , F = 217N
Fy
x
30D B
Wθ
y
可推出图（b）中 FAB = 10FDB = 100F = 80 kN。
FED αD
FDB FD′ B
FCB
α
B
F 习题 1－12 解 1 图
F AB 习题 1－12 解 2 图
1—13 杆 AB 及其两端滚子的整体重心在 G 点，滚子搁置在倾斜的光滑刚性平面上，如
图所示。对于给定的θ 角，试求平衡时的 β 角。
=
25 kN 6
即
FR
= ( 5 , 10 )kN 23
作用线方程： y = 4 x + 4 3
讨论：本题由于已知数值的特殊性，实际 G 点与 E 点重合。
2－3三个小拖船拖着一条大船，如图所示。每根拖缆的拉力为5kN。试求：(1)作用于大 船上的合力的大小和方向。(2)当A船与大船轴线x的夹角θ为何值时，合力沿大船轴线方向。
投影： Fx1 = F cosα ， Fy1 = F sinα
讨论： ϕ = 90°时，投影与分力的模相等；分力是矢量，投影是代数量。
图（b）：
分力： Fx2 = (F cosα − F sin α tan ϕ )i2 ，
Fy2
=
F sinα sinϕ
j2
投影： Fx2 = F cosα ，
Fy2 = F cos(ϕ − α )
《工程力学(静力学与材料力学)》第6章 静力学专题
谢传锋:工程力学(静力学)
6
静力学
木桁架节点
§1 桁架
榫接
谢传锋:工程力学(静力学)
7
静力学
钢桁架节点
§1 桁架
铆接
谢传锋:工程力学(静力学)
焊接
8
静力学
钢筋混凝土桁架节点
§1 桁架
刚接
谢传锋:工程力学(静力学) 9
静力学
桁架模型简化的基本假设
§1 桁架
假设1：各杆件都用光滑铰链相连接
谢传锋:工程力学(静力学) 10
40
解：取梯子为研究对象,
P
C D
W
F
B
Fs
FB
谢传锋:工程力学(静力学)
静力学
FA
A
§2 摩擦
W a a W Fs tan F (1 ), FB W , FA F tan 2 L L 2
W
C D
F
B
维持平衡的条件: FA 0 FS f FB
Fs
FS f FB
x
FN1 = 0 FN 2= 0
谢传锋:工程力学(静力学)
16
静力学
§1 桁架
例题： 试确定图示桁架中的零力杆 FP
C A G
E
H
I
D
B
FP
谢传锋:工程力学(静力学)
17
静力学
§1 桁架
节点法的特点:1、研究对象为节点（汇交力系）
2、每个节点可以建立两个独立的平衡方程
1
问题1: 在图示桁架中, 哪些杆件为零力杆? 问题2: 在图示桁架中, 杆1的内力如何求?
F
W
F F M
x
建筑力学李前程教材第六章习题解
Q图(kN)
N图(kN)
取节点B验算：∑mi=20kN.m-20kN.m=0 ∑Yi=45kN-45kN=0 ∑Xi=20kN-20kN=0 节点平衡， ∴ 计算正确
(f)先求支座反力，由∑Xi=0 得 XA=P=5kN 由∑mA=0 得 YB=(3q ×1.5+P ×2)/3=55/3kN 由∑Yi=0 得 YA=3q-55/3=35/3kN，做内力图。
YA
YB
【6-5】作下列各梁的剪力图和弯矩图。 M =8kN.m 【解】(a)先求支座反力， A 由∑mB=0 得 YA×l+M1-M2=0 Y YA=(M1-M2)/4=1kN 1kN 由∑Yi=0 得 YA+YB=0 , YB=-1kN (↓) 于是，QA=1kN，QB=1kN ， 8 kN.m MA=8kN.m , MB=12kN.m 分别连直线，的Q图和M图，见右上图。
q=4kN/m A 3m YA 16 Q图(kN) 4
P=8kN B 3m YB
C
4
16
Pl/4=12 ql2/8 =18 M图(kN.m) 30
(e)先求支座反力， 由∑mD=0 得 YA×4-P×3-2q×1=0 YA=(3P+2q)/4=3.5kN 由∑Yi=0 得 YA+YD-P-2q=0 YD=P+2q-YA=6.5kN QA=YA=3.5kN , QB左=YA=3.5kN , QB右=YA-P=1.5kN ,QC= YA-P=1.5kN , QD=-YD=-6.5kN, MA=MD=0 , MB=YA×1=3.5kN.m , MC=YA ×2-P ×1=5kN.m
C D qb2/6 qb/2
取节点C验算： ∑mi=40+40-80 =0 ∑Yi=80-40-40 =0
《工程力学(工程静力学与材料力学)(第3版)》习题解答：第3章 力系的平衡
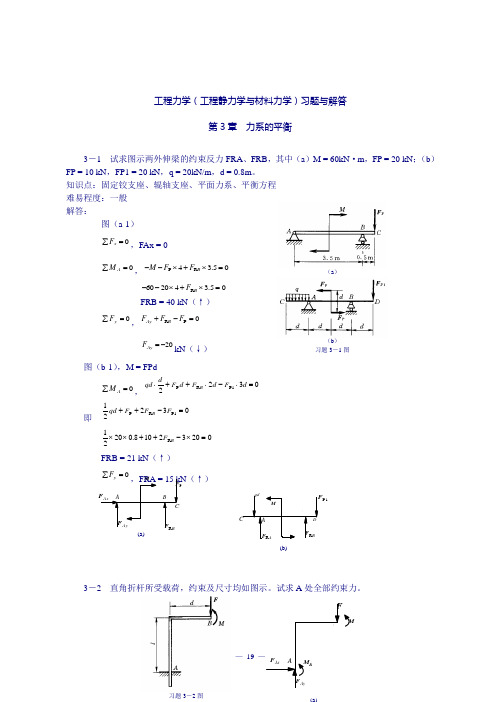
工程力学（工程静力学与材料力学）习题与解答第3章 力系的平衡3－1 试求图示两外伸梁的约束反力FRA 、FRB ，其中（a ）M = 60kN ·m ，FP = 20 kN ；（b ）FP = 10 kN ，FP1 = 20 kN ，q = 20kN/m ，d = 0.8m 。
知识点：固定铰支座、辊轴支座、平面力系、平衡方程 难易程度：一般 解答：图（a-1） 0=∑x F ，FAx = 00=∑A M ，05.34R P =⨯+⨯--B F F M 05.342060R =⨯+⨯--B F FRB = 40 kN （↑）=∑y F ，0P R =-+F F F B Ay20-=Ay F kN （↓）图（b-1），M = FPd 0=∑A M ，03221P R P =⋅-⋅++⋅d F d F d F dqd B即 032211P R P =-++F F F qd B 02032108.02021R =⨯-++⨯⨯B FFRB = 21 kN （↑）=∑y F ，FRA = 15 kN （↑）3－2 直角折杆所受载荷，约束及尺寸均如图示。
试求A 处全部约束力。
A MB Ay F B R F CAx F PF(a) M A B B R F A R F P 1F C qdBD(b)（a ）（b ） 习题3－1图FMB习题3－3图sF W A F ABF BF AN F(a)知识点：固定端约束、平面力系、平衡方程 难易程度：一般 解答： 图（a ）： 0=∑x F ，0=Ax F=∑y F ，=Ay F （↑）0=∑A M ，0=-+Fd M M AM Fd M A -=3－3 图示拖车重W = 20kN ，汽车对它的牵引力FS = 10 kN 。
试求拖车匀速直线行驶时，车轮A 、B 对地面的正压力。
知识点：固定端约束、平面力系、平衡方程 难易程度：一般解答： 图（a ）：0)(=∑F A M 08.214.1NB S =⨯+⨯-⨯-F F W6.13NB =F kN=∑y F ，4.6NA =F kN3－4 图示起重机ABC 具有铅垂转动轴AB ，起重机重W = 3.5kN ，重心在D 。
《工程力学》课后习题答案全集
工程力学习题答案第一章 静力学基础知识思考题：1. ×;2. √;3. √;4. √;5. ×;6. ×;7. √;8. √习题一1．根据三力汇交定理，画出下面各图中A 点的约束反力方向。
解：（a ）杆AB 在A 、B 、C 三处受力作用。
由于力和的作用线交于点O 。
如图（a ）所示，根据三力平衡汇交定理， 可以判断支座A 点的约束反力必沿 通过A 、O 两点的连线。
（b ）同上。
由于力和的作用线 交于O 点，根据三力平衡汇交定理， 可判断A 点的约束反力方向如 下图（b ）所示。
2．不计杆重，画出下列各图中AB 杆的受力图。
解：（a ）取杆AB 为研究对象，杆除受力外，在B 处受绳索作用的拉力，在A 和E 两处还受光滑接触面约束。
约束力和的方向分别沿其接触表面的公法线，并指向杆。
其中力与杆垂直，力通过半圆槽的圆心O 。
AB 杆受力图见下图（a ）。
(b)由于不计杆重，曲杆BC 只在两端受铰销B 和C 对它作用的约束力和，故曲杆BC 是二力构件或二力体，此两力的作用线必须通过B 、C 两点的连线，且=。
研究杆AB ，杆在A 、B 两点受到约束反力和，以及力偶m 的作用而平衡。
根据力偶的性质，和必组成一力偶。
(d)由于不计杆重，杆AB 在A 、C 两处受绳索作用的拉力和，在B 点受到支座反力。
和相交于O 点，根据三力平衡汇交定理，可以判断必沿通过pB RpB Rp B T A N E N E N A N B N C N BN CN A N B N A N B N A T C T B N A T C TB NB、O两点的连线。
见图(d).第二章 力系的简化与平衡思考题：1. √;2. ×;3. ×;4. ×;5. √;6. ×;7. ×;8. ×;9. √.1． 平面力系由三个力和两个力偶组成，它们的大小和作用位置如图示，长度单位为cm ，求此力系向O 点简化的结果，并确定其合力位置。
工程力学(静力学与材料力学)课后习题答案
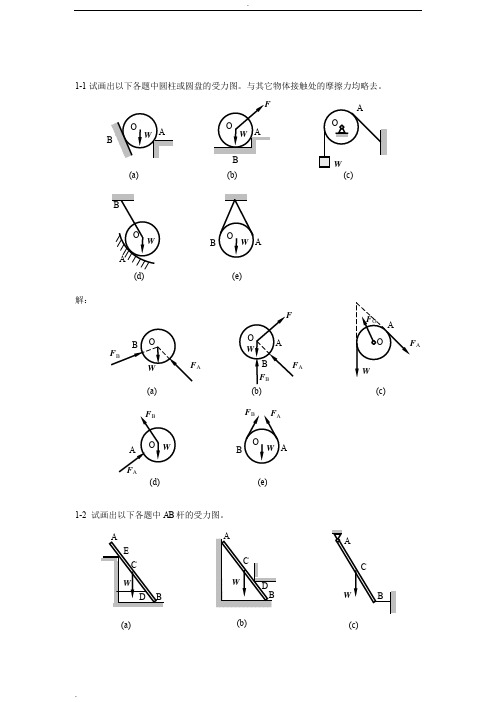
.1-1试画出以下各题中圆柱或圆盘的受力图。
与其它物体接触处的摩擦力均略去。
解：1-2 试画出以下各题中AB 杆的受力图。
(a) B(b)(c)(d)A(e)A(a)(b) A(c)A(d)A(e)(c)(a)(b)解：1-3 试画出以下各题中AB 梁的受力图。
(d)(e)BB(a)B(b)(c)F B(a)(c)F (b)(d)(e)解：1-4 试画出以下各题中指定物体的受力图。
(a) 拱ABCD ；(b) 半拱AB 部分；(c) 踏板AB ；(d) 杠杆AB ；(e) 方板ABCD ；(f) 节点B 。
解：(a)F (b)W(c)(d)D(e)F Bx(a)(b)(c)(d)D(e)W(f)(a)D(b)B(c)BF D1-5 试画出以下各题中指定物体的受力图。
(a) 结点A ，结点B ；(b) 圆柱A 和B 及整体；(c) 半拱AB ，半拱BC 及整体；(d) 杠杆AB ，切刀CEF 及整体；(e) 秤杆AB ，秤盘架BCD 及整体。
解：(a)(d)FC(e)WB(f)F FBC(c)(d)AT F BAF (b)(e)(b)(c)(d)(e)CAA C’CDDC ’B2-2 杆AC 、BC 在C 处铰接，另一端均与墙面铰接，如图所示，F 1和F 2作用在销钉C 上，F 1=445 N ，F 2=535 N ，不计杆重，试求两杆所受的力。
解：(1) 取节点C 为研究对象，画受力图，注意AC 、BC 都为二力杆，(2) 列平衡方程：12140 sin 600530 cos6005207 164 o y AC ox BC ACAC BC F F F F F F F F F N F N=⨯+-==⨯--=∴==∑∑ AC 与BC 两杆均受拉。
2-3 水平力F 作用在刚架的B 点，如图所示。
如不计刚架重量，试求支座A 和D 处的约束力。
解：(1) 取整体ABCD 为研究对象，受力分析如图，画封闭的力三角形：(2)F 1F FDF F AF D211 1.122D A D D A F F FF F BC AB AC F F F F F =====∴===2-4 在简支梁AB 的中点C 作用一个倾斜45o 的力F ，力的大小等于20KN ，如图所示。
工程力学第4次作业解答杆件的内力计算与内力图
6 ．剪力 F 、弯矩 M 与载荷集度 q 三者之间的微分关系是 dM ( x)= F ( x ) 、dx《工程力学》第 4 次作业解答（杆件的内力计算与内力图）2008-2009 学年第二学期一、填空题1．作用于直杆上的外力（合力）作用线与杆件的轴线重合时，杆只产生沿轴线方向的 伸长或缩短变形，这种变形形式称为轴向拉伸或压缩。
2．轴力的大小等于截面截面一侧所有轴向外力的代数和；轴力得正值时，轴力的方向 与截面外法线方向相同，杆件受拉伸。
3．杆件受到一对大小相等、转向相反、作用面与轴线垂直的外力偶作用时，杆件任意 两相邻横截面产生绕杆轴相对转动，这种变形称为扭转。
4．若传动轴所传递的功率为 P 千瓦，转速为 n 转/分，则外力偶矩的计算公式为M = 9549 ⨯ Pn。
5．截面上的扭矩等于该截面一侧（左或右）轴上所有外力偶矩的代数和；扭矩的正负， 按右手螺旋法则确定。
S S dF ( x )S dx= ±q ( x ) 。
7．梁上没有均布荷载作用的部分，剪力图为水平直线，弯矩图为斜直线。
8．梁上有均布荷载作用的部分，剪力图为斜直线，弯矩图为抛物线。
9．在集中力作用处，剪力图上有突变，弯矩图上在此处出现转折。
10．梁上集中力偶作用处，剪力图无变化，弯矩图上有突变。
二、问答题1．什么是弹性变形？什么是塑性变形？解答：在外力作用下，构件发生变形，当卸除外力后，构件能够恢复原来的大小和形状，则这种变形称为弹性变形。
如果外力卸除后不能恢复原来的形状和大小，则这种变形称为塑性变形。
2．如图所示，有一直杆，其两端在力 F 作用下处于平衡，如果对该杆应用静力学中“力的可传性原理”，可得另外两种受力情况，如图（b ）、（c ）所示。
试问：（1）对于图示的三种受力情况，直杆的变形是否相同？ （2）力的可传性原理是否适用于变形体？问答题 2 图问答题 3 图。
解答：（1）图示的三种情况，杆件的变形不相同。
《工程力学(工程静力学与材料力学)(第3版)》习题解答：第1章 静力学基本概念
(a) (b)习题1-1图FACBAxF Ay F 工程力学（工程静力学与材料力学）第1章 静力学基本概念1－1 图a 、b 所示，Ox1y1与Ox2y2分别为正交与斜交坐标系。
试将同一方F 分别对两坐标系进行分解和投影，并比较分力与力的投影。
知识点：力的分力与投影 难易程度：易 解答：（a ），图（c ）：11 sin cos j i F ααF F += 分力：11 cos i F αF x = ， 11 sin j F αF y =投影：αcos 1F F x = ，αsin 1F F y =讨论：ϕ= 90°时，投影与分力的模相等；分力是矢量，投影是代数量。
（b ），图（d ）： 分力：22)tan sin cos (i F ϕααF F x -= ，22sin sin j F ϕαF y =投影：αcos 2F F x = ，)cos(2αϕ-=F F y讨论：ϕ≠90°时，投影与分量的模不等。
1－2 试画出图a 、b 两情形下各物体的受力图，并进行比较。
1y F xx F 1y F α1x F yF（c ）x F 2y F 2y 2x 2x F 2y F F（d ）Ay F F B C A Ax F 'F C(a-2)C D C F D R (a-3)AxF F F A C BD Ay F (b-1)习题1－3图知识点：受力分析与受力图 难易程度：易 解答： 比较：图（a-1）与图（b-1）不同，因两者之FRD 值大小也不同。
1－3 试画出图示各物体的受力图。
F Ax F AyF D C B A B F 或(a-2) F B F A F D C A (a-1)BF AxF A AyF C(b-1) W F B DC F F (c-1) F F C B BF A 或(b-2)αD AF A BC B F(d-1)C F C A AF (e-1)Ax F A Ay F D F D CαF BF FC D B F A习题1－4图难易程度：易 解答：1－4 图a 所示为三角架结构。
工程力学(第3版)第6章
返回
图 6-1
返回
图 6-2
返回
图 6-3
返回
图 6-4
返回
图 6-5
返回
图 6-6
返回图Biblioteka 6-9返回• 下面以铆钉连接（图 6−3（a））为例进行分析。钢板受外力 F 作用 后又将力传递到铆钉上，而使铆钉的右上侧面和左下侧面受力（图 6−3（b））。这时，铆钉的上、下两半部分将沿着 m—n 截面发生 相对错动（图 6−3（c））。当外力足够大时，将会使铆钉剪断。由 铆钉受剪的实例分析可以看出剪切变形的受力特点是：作用在构件两 侧面上的外力的合力大小相等，方向相反，作用线平行且相距很近。 其变形特点是：介于两作用力之间的截面发生相对错动。这种变形称 为剪切变形。
下一页 返回
6.1 剪切与挤压概念
• 在承受剪切的构件中，发生相对错动的截面称为剪切面。剪切面上与 截面相切的内力称为剪力，用 F Q 表示（图 6−3（d）），其大小可 用截面法通过列平衡方程求出。
• 构件中只有一个剪切面的剪切称为单剪，如图 6−3 中的铆钉。构件 中有两个剪切面的剪切则称为双剪，拖车挂钩中螺栓所受的剪切是双 剪的实例，如图 6−4 所示。
上一页 下一页 返回
6.3 剪切胡克定律和切应力互等定理
• 由 ∑M =0得 • 得 τ ′ =τ （ 6 − 6 ） • 为了明确切应力的作用方向，对其作如下符号规定：使单元体产生顺
时针方向转动趋势的切应力为正，反之为负，则式（ 6 − 6 ）应改写 为τ = −τ ′ （ 6 − 7 ） • 式（ 6 − 7 ）表明，单元体互相垂直的两个平面上的切应力必定是同 时成对存在，且大小相等，方向都垂直指向或背离两个平面的交线。 这一关系称为切应力互等定理。
工程力学(静力学与材料力学)课后习题测验答案(单辉祖)
1-1试画出以下各题中圆柱或圆盘的受力图。
与其它物体接触处的摩擦力均略去。
解：1-2 试画出以下各题中AB 杆的受力图。
(a) B(b)(c)(d)A(e)A(a)(b) A(c)A(d)A(e)(c)(a)(b)解：1-3 试画出以下各题中AB 梁的受力图。
(d)(e)BB(a)B(b)(c)F B(a)(c)F (b)(d)(e)解：1-4 试画出以下各题中指定物体的受力图。
(a) 拱ABCD ；(b) 半拱AB 部分；(c) 踏板AB ；(d) 杠杆AB ；(e) 方板ABCD ；(f) 节点B 。
解：(a)F (b)W(c)(d)D(e)F Bx(a)(b)(c)(d)D(e)W(f)(a)D(b)B(c)BF D1-5 试画出以下各题中指定物体的受力图。
(a) 结点A ，结点B ；(b) 圆柱A 和B 及整体；(c) 半拱AB ，半拱BC 及整体；(d) 杠杆AB ，切刀CEF 及整体；(e) 秤杆AB ，秤盘架BCD 及整体。
解：(a)(d) FC(e)WB (f)F FBC(c)(d)AT F BAF (b)(e)(b)(c)(d)(e)CAA C’CDDB2-2 杆AC 、BC 在C 处铰接，另一端均与墙面铰接，如图所示，F 1和F 2作用在销钉C 上，F 1=445 N ，F 2=535 N ，不计杆重，试求两杆所受的力。
解：(1) 取节点C 为研究对象，画受力图，注意AC 、BC 都为二力杆，(2) 列平衡方程：12140 sin 600530 cos6005207 164 o y AC o x BC AC AC BC F F F F F F F F F N F N=⨯+-==⨯--=∴==∑∑ AC 与BC 两杆均受拉。
2-3 水平力F 作用在刚架的B 点，如图所示。
如不计刚架重量，试求支座A 和D 处的约束力。
解：(1) 取整体ABCD 为研究对象，受力分析如图，画封闭的力三角形：(2)F 1F FDF F AF D211 1.1222D A D D A F F FF F BC AB AC F F F F F =====∴===2-4 在简支梁AB 的中点C 作用一个倾斜45o 的力F ，力的大小等于20KN ，如图所示。
工程力学课后习题答案（静力学和材料力学）
1 一 3 试画出图示各构件的受力图。
F
D
习题 1－3 图
C
F
D
C
A
B
FA
FB
习题 1－3a 解 1 图
F Ax
A
B
FAy
FB
习题 1－3a 解 2 图
C
BF
B
D
FB
FD
C
A
FA 习题 1－3b 解 2 图
W
FAx
FAy
习题 1－3c 解图
F
A
A
F
α
B C
FA
D
FAFD 习题 1－3d 解 2 图
FB2 x
B
FDy
C FB2 y
F Dx D
W
习题 1－4b 解 2 图
F'B1
B
F'B2x
F'B2 y F1
A B
F'B2x
习题 1－4c 解 1 图
F1 F'B2 y
FDx D FDy
F'B2x B
C
F'B2 y
W
F'B2 B
习题 1－4c 解 2 图
习题 1－4b 解 3 图
FA
A
B
F B1
习题 1－4d 解 1 图
可推出图（b）中 FAB = 10FDB = 100F = 80 kN。
FED αD
FDB FD′ B
FCB
α
B
F 习题 1－12 解 1 图
F AB 习题 1－12 解 2 图
1—13 杆 AB 及其两端滚子的整体重心在 G 点，滚子搁置在倾斜的光滑刚性平面上，如
工程力学课后习题答案
工程力学练习册学校学院专业学号教师姓名第一章静力学基础1-1 画出下列各图中物体A，构件AB，BC或ABC的受力图，未标重力的物体的重量不计，所有接触处均为光滑接触。
（a）（b）（c）（d）（e）（f）（g）1-2 试画出图示各题中AC杆（带销钉）和BC杆的受力图（a）（b）（c）（a）1-3 画出图中指定物体的受力图。
所有摩擦均不计，各物自重除图中已画出的外均不计。
（a）（b）（c）（d）（e）（f）（g）第二章 平面力系2-1 电动机重P=5000N ，放在水平梁AC 的中央，如图所示。
梁的A 端以铰链固定，另一端以撑杆BC 支持，撑杆与水平梁的夹角为30 0。
如忽略撑杆与梁的重量，求绞支座A 、B 处的约束反力。
题2-1图解得: N P F F B A 5000===2-2 物体重P=20kN ，用绳子挂在支架的滑轮B 上，绳子的另一端接在绞车D 上，如图所示。
转动绞车，物体便能升起。
设滑轮的大小及轴承的摩擦略去不计，杆重不计，A 、B 、C 三处均为铰链连接。
当物体处于平衡状态时，求拉杆AB 和支杆BC 所受的力。
题2-2图解得: P F PF AB BC 732.2732.3=-=2-3 如图所示，输电线ACB 架在两电线杆之间，形成一下垂线，下垂距离CD =f =1m ，两电线杆间距离AB =40m 。
电线ACB 段重P=400N ，可近视认为沿AB 直线均匀分布，求电线的中点和两端的拉力。
题2-3图以AC 段电线为研究对象，三力汇交2-4 图示为一拔桩装置。
在木桩的点A 上系一绳，将绳的另一端固定在点C ，在绳的点B 系另一绳BE ，将它的另一端固定在点E 。
然后在绳的点D 用力向下拉，并使绳BD 段水平，AB 段铅直；DE 段与水平线、CB 段与铅直线成等角α=0.1rad （弧度）（当α很小时，tanα≈α）。
如向下的拉力F=800N ，求绳AB 作用于桩上的拉力。
题2-4图 作BD 两节点的受力图 联合解得：kN F F F A80100tan 2=≈=α 2-5 在四连杆机构ABCD 的铰链B 和C 上分别作用有力F 1和F 2，，机构在图示位置平衡。
工程力学课后习题答案第六章 杆类构件的内力分析
第六章 杆类构件的内力分析6.1。
（a ）（b ）题6.1图解：（a ）应用截面法：对题的图取截面2-2以下部分为研究对象，受力图如图一所示：BM图一图二由平衡条件得：0,AM=∑6320N F ⨯-⨯=解得： N F =9KN CD 杆的变形属于拉伸变形。
应用截面法，取题所示截面1-1以右及2-2以下部分作为研究对象，其受力图如图二所示，由平衡条件有：0,OM=∑6210N F M ⨯-⨯-=（1）0,yF=∑60N S F F --=（2）将N F =9KN 代入（1）-（2）式，得： M =3 kN·m S F =3 KN AB 杆属于弯曲变形。
（b ）应用截面法 ，取1-1以上部分作为研究对象，受力图如图三所示，由平衡条件有：0,Fx =∑20NF-=图三MNF =2KN0,DM=∑210M -⨯= M =2KNAB 杆属于弯曲变形 6.2题6.2图解：首先根据刚体系的平衡条件，求出AB 杆的内力。
刚体1的受力图如图一所示D2m图一图二平衡条件为：0,CM=∑104840D N F F ⨯-⨯-⨯=（1） 刚体2受力图如图二所示，平衡条件为：0,EM=∑240N D F F ⨯-⨯= （2）解以上两式有AB 杆内的轴力为：N F =5KN6.3（a ）（c ）题6.3图解：（a ） 如图所示，解除约束，代之以约束反力，做受力图，如图1a 所示。
利用静力平衡条件，确定约束反力的大小和方向，并标示在图1a 中，作杆左端面的外法线n ，将受力图中各力标以正负号，轴力图是平行于杆轴线的直线，轴力图线在有轴向力作用处要发生突变，突变量等于该处总用力的数值，对于正的外力，轴力图向上突变，对于负的外力，轴力图向下突变，轴力图如2a 所示，截面1和截面2上的轴力分别为1N F =-2KN 2N F =-8KN ，n （b 2 （面N F题6.4图解（a ）如图所示，分别沿1-1，2-2截面将杆截开，受力图如1a 所示，用右手螺旋法则，并用平衡条件可分别求得：1T =16 kN·m 2T =-20 kN·m ，根据杆各段扭矩值做出扭矩图如2a 所示。
工程力学课后习题答案（静力学和材料力学）
1 一 3 试画出图示各构件的受力图。
F
D
习题 1－3 图
C
F
D
C
A
B
FA
FB
习题 1－3a 解 1 图
F Ax
A
B
FAy
FB
习题 1－3a 解 2 图
C
BF
B
D
FB
FD
C
A
FA 习题 1－3b 解 2 图
W
FAx
FAy
习题 1－3c 解图
F
A
A
F
α
B C
FA
D
FAFD 习题 1－3d 解 2 图
E F
D C
FH
H
习题 1－6 解 2 图
A
D
F
FH ′ H
C
H
FH 习题 1－6 解 3 图
1—7 试画出图示连续梁中的 AC 和 CD 梁的受力图。
习题 1－7 图
FAx A FAy
C
F FC' x Cx
B
FB
FC' y
F1
C
FCy
习题 1－7 解图
F2
D
FDx
FDy
1—8 图示为一液压冷铆机，活塞同铆枪为一整体。工作时油缸内油压力推动活塞下降， 铆枪冲压铆钉将钢板铆接。活塞与油缸间为光滑接触。试分别画出：
(1) 油缸的受力图； (2) 活塞铆枪的受力图； (3) 铆钳的受力图。
习题 1－8 图
p
q FQ
p q'
FQ'
(b)
(c)
习题 1－8 解图
1—9 安置塔器的竖起过程如图所示，下端搁在基础上，C 处系以钢绳，并用绞盘拉住； 上端在 B 处系以钢缆，通过定滑轮 D 连接到卷扬机 E 上。设塔器的重量为 FW，试画出塔器 的受力图。
工程力学(静力学和材料力学)课后习题答案
工程力学（静力学与材料力学）习题详细解答(第1章)(a) (b) 习题1－1图第1章 静力学基础1一1 图a 和b 所示分别为正交坐标系11y Ox 与斜交坐标系22y Ox 。
试将同一个力F 分别在两中坐标系中分解和投影，比较两种情形下所得的分力与投影。
解：图（a ）：11 sin cos j i F ααF F +=分力：11 cos i F αF x = ， 11 sin j F αF y = 投影：αcos 1F F x = ， αsin 1F F y =讨论：ϕ= 90°时，投影与分力的模相等；分力是矢量，投影是代数量。
图（b ）： 分力：22)tan sin cos (i F ϕααF F x −= ， 22sin sin j F ϕαF y =投影：αcos 2F F x = ， )cos(2αϕ−=F F y讨论：ϕ≠90°时，投影与分量的模不等。
1一2 试画出图a 和b 两种情形下各构件的受力图，并加以比较。
比较：解a 图与解b 图，两种情形下受力不同，二者的F R D 值大小也不同。
DR习题1－2b 解图DR习题1－2a 解2图C习题1－2a 解1图(a) (b)习题1－2图1一3 试画出图示各构件的受力图。
习题1－3图B F 习题1－3a 解2图 B习题1－3a 解1图习题1－3b 解1图F Ay Ax 习题1－3c 解图 A习题1－3b 解2图习题1－3d 解1图习题1－3e 解1图习题1－3e 解2图1－4 图a 所示为三角架结构。
荷载F 1作用在B 铰上。
AB 杆不计自重，BD 杆自重为W ，作用在杆的中点。
试画出图b 、c 、d 所示的隔离体的受力图，并加以讨论。
习题1－4图1习题1－3f 解1图F习题1－3e 解3图'A习题1－3f 解2图1O 习题1－3f 解3图F F'F 1习题1－4d 解2图F y B 21习题1－4c 解1图 AA B 1B FDx y2B 习题1－4b 解2图 1习题1－4b 解3图 F y B 2习题1－4c 解2图 F A B1B FAxF'习题1－5b 解3图E D(a-3)E B F习题1－5b 解2图习题1－5b 解1图'AxFF B习题1－5c 解图1一5 试画出图示结构中各杆的受力图。
材料力学课后答案d
-3-
工程力学习题解答
A． M 1 > M 2 > M 3 > M 4 C． M1 > M 2 = M 3 > M 4 E． FS1 = FS2 = FS3 = FS4
F
B． M1 = M 2 > M 3 > M 4 D． M 1 > M 2 > M 3 = M 4 F． FS1 > FS2 > FS3 > FS4
A
B
C
D
分析：这是对称结构承受对称荷载的情况，支反力偶矩必定对称，扭矩图必定反对称。
-2-
第 6 章 杆件的内力
因此只需根据支反力偶矩进一步判断扭矩正负即可。
6-2(4) 在梁的集中力作用处，其左、右两侧无限接近的横截面上的弯矩是 A 的。
A．相同
B．数值相等，符号相反
C．不相同
D．符号一致，数值不相等
−
1 4
q0 L
−
q0
⎜⎛ ⎝
x
−
L 2
⎟⎞ ⎠
−
FS
=
0
，
FS
=
1 4
q0 L
−
q0 x
。
∑m = 0 ，
M
+
q0 L 4
⎜⎛ x ⎝
−
L 2
⋅
2 ⎟⎞ 3⎠
+
q0
⎜⎛ ⎝
x
−
L 2
⎟⎞ ⋅ ⎠
1 ⎜⎛ x 2⎝
−
L 2
⎟⎞ ⎠
=
0，
M = − q0 (12x2 − 6Lx + L2 ) 。 24
《工程力学(工程静力学与材料力学)(第3版)》习题解答：第6章 杆件的内力分析
（↑）
弯距图如图示，其中 |
M
|max
ql
2
。
6－13 试作图示刚架的弯矩图，并确定 | M |max 。
习题 6-13 图
1
1
2
1 2
A
B1
Fx 0 ， FAx ql
MA 0
ql
l 2
ql 2
FRB
l
0
— 58 —
FRB
3 2
ql
Fy
0 ， FAy
3 2
ql 2
（↑）
弯距图如图示，其中 | M |max ql 2 。
D
B
C
1
1
1.5
M (ql2)
A
M (ql2)
D
BC
10.75
D
B
C
1
25
2
32
知识点：梁的剪力图与弯矩图 难度：一般 解答：
Fy 0 ， FRA ql （↑）
M A 0 ， M A ql 2
MD
0，
ql 2
ql l
ql
l 2
MD
0
MD
3 2
ql 2
| FQ |max ql
|
M
| max
M (x) 1 q x 0 2 4ql x l 2
2ql x 3l 4ql x 5l
(5l x 6l)
M (x) 1 q x 0 2 4ql x l 2
即
2ql x 3l 4ql x 5l
(0 x 6l)
2．弯矩图如图（a）； 3．载荷图如图（b）； 4．梁的支承为 B、D 处简支（图 b）。
Fx 0 ， px FNx 0
工程力学(静力学与材料力学)课后习题答案(单辉祖)
1-1试画出以下各题中圆柱或圆盘的受力图。
与其它物体接触处的摩擦力均略去。
解：1-2 试画出以下各题中AB 杆的受力图。
(a) B(b)(c)(d)A(e)A(a)(b) A(c)A(d)A(e)(c)(a)(b)解：1-3 试画出以下各题中AB 梁的受力图。
(d)(e)BB(a)B(b)(c)F B(a)(c)F (b)(d)(e)解：1-4 试画出以下各题中指定物体的受力图。
(a) 拱ABCD ；(b) 半拱AB 部分；(c) 踏板AB ；(d) 杠杆AB ；(e) 方板ABCD ；(f) 节点B 。
解：(a)F (b)W(c)(d)D(e)F Bx(a)(b)(c)(d)D(e)W(f)(a)D(b)B(c)BF D1-5 试画出以下各题中指定物体的受力图。
(a) 结点A ，结点B ；(b) 圆柱A 和B 及整体；(c) 半拱AB ，半拱BC 及整体；(d) 杠杆AB ，切刀CEF 及整体；(e) 秤杆AB ，秤盘架BCD 及整体。
解：(a)(d) FC(e)WB (f)F FBC(c)(d)AT F BAF (b)(e)(b)(c)(d)(e)CAA C’CDDB2-2 杆AC 、BC 在C 处铰接，另一端均与墙面铰接，如图所示，F 1和F 2作用在销钉C 上，F 1=445 N ，F 2=535 N ，不计杆重，试求两杆所受的力。
解：(1) 取节点C 为研究对象，画受力图，注意AC 、BC 都为二力杆，(2) 列平衡方程：12140 sin 600530 cos6005207 164 o y AC o x BC AC AC BC F F F F F F F F F N F N=⨯+-==⨯--=∴==∑∑ AC 与BC 两杆均受拉。
2-3 水平力F 作用在刚架的B 点，如图所示。
如不计刚架重量，试求支座A 和D 处的约束力。
解：(1) 取整体ABCD 为研究对象，受力分析如图，画封闭的力三角形：(2)F 1F FDF F AF D211 1.122D A D D A F F FF F BC AB AC F F F F F =====∴===2-4 在简支梁AB 的中点C 作用一个倾斜45o 的力F ，力的大小等于20KN ，如图所示。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
矩为零，试：
1．在 Ox 坐标中写出弯矩的表达式；
2．画出梁的弯矩图；
3．确定梁上的载荷；
4．分析梁的支承状况。
0.5
A B
0.5
C
E
D
习题 6-18 图
M (ql2)
AB
3.5 (a)
q
C 2ql
(b)
E D
— 62 —
知识点：载荷、剪力、弯矩之间的微分关系的应用
难度：很难
解答：
由 FQ 图知，全梁有向下均布 q；B、D 处有相等的向上集中力 4ql；C 处有向下的集中力 2ql；结 合 M，知 A、E 为自由端，由 FQ 线性分布知，M 为二次抛物线，B、C、D 处 FQ 变号，M 在 B、 C、D 处取极值。
习题 6-8 图
— 54 —
FQ
ql
ql
FQ
0.5
D
EC
B
A
B
C
0.5
0.5
A
B
C
0.5
M (ql2)
1
知识点：梁的剪力图与弯矩图 难度：一般 解答：
Fy 0 ，FRC = 0
3
l
MC 0 ， ql 2 l ql 2 M C 0
M C ql 2
MB
0
，
MB
1 2
ql 2
Fy 0 ， FQB ql
习题 6-10 图
1
C 2
D
B
M (FPl)
A
知识点：刚架的弯矩图 难度：一般 解答：
M A 0 ， FRB 2l FP l FP l 0
FRB FP （↑）
— 56 —
Fy 0 ， FAy FP （↓） Fx 0 ， FAx FP （←） 弯距图如图示，其中 | M |max 2FPl ，位于刚节点 C 截面。
Fx 0 ， px FNx 0
习题 6-14 和 6-15 图
FNx px dFNx p
∴ dx
M px h 0
MC 0 ，
2
M 1 phx 2
dM 1 ph dx 2
方法 2． Fx 0 ， FNx dFNx pdx FNx 0
p M
C
FNx
x
(a)
FNx
p
（↑）
弯距图如图示，其中 |
M
|max
ql
2
。
6－13 试作图示刚架的弯矩图，并确定 | M |max 。
习题 6-13 图
1
1
2
1 2
A
B1
Fx 0 ， FAx ql
MA 0
ql
l 2
ql 2
FRB
l
0
— 58 —
FRB
3 2
ql
Fy
0 ， FAy
3 2
ql 2
（↑）
弯距图如图示，其中 | M |max ql 2 。
dFQ
（C） dx
q(x) dM
， dx
FQ ；
习题 6-1 图
（D）
dFQ dx
q(x)
，
dM dx
FQ 。
知识点：载荷、剪力、弯矩之间的微分关系及其与坐标的关系
难度：一般
解答：
正确答案是 B 。
6－2 对于图示承受均布载荷 q 的简支梁，其弯矩图凸凹性与哪些因素相关？试判断下列四 种答案中哪几种是正确的。 知识点：弯矩图的凸凹形状与载荷和坐标系的关系 难度：一般 解答：
MA
0 ， FRB
1 2
ql
（↑）
Fy
0，
FRA
1 2
ql
（↓）
Fy
0，
1 ql 2
ql
FQB
0
FQB
1 2
ql
MD
0，
1 2
ql l 2
q
l l 24
MD
0
MD
1 8
ql 2
ME
1 8
ql 2
|
FQ
|max
1 2
ql
|
M
| max
1 8
ql
2
6－10 试作图示刚架的弯矩图，并确定 | M |max 。
| FQ |max ql
| M |max ql 2
6－9 应用平衡微分方程，试画出图示梁的剪力图和弯矩图，并确定 | FQ |max 。
习题 6-9 图
ql
ql
FQ
0.5
D
EC
B
B
C
0.5
0.5
0.125
A
DB
M (ql2)
EC
0.125
知识点：梁的剪力图与弯矩图
— 55 —
难度：一般 解答：
1．画出轴的受力简图； 2．画出轴的全部内力图。
FQ
习题 6-19 图
6－19 图示传动轴传递功率 P = 7.5kW，轴的转速 n = 200r/min。齿轮 A 上的啮合力 FR 与水 平切线夹角 20°，皮带轮 B 上作用皮带拉力 FS1 和 FS2，二者均沿着水平方向，且 FS1 = 2FS2。 试：（分轮 B 重 FQ = 0 和 FQ = 1800N 两种情况）
FRC = 1 kN（↑）
FRB = 0.3 kN（↑）
q 0.3 (0.5) 0.2
4
kN/m（↓）
由 MA = MB = 0，可知 A、B 简支，由此得梁上载荷及梁的支承如图（a）或（b）所示。
q 0.2kN/m
A C
B
1kN
(a)
0.2kN/m
A
C
B
0.3kN
(b)
6－18 静定梁承受平面载荷，但无集中力偶作用，其剪力图如图所示。若已知截面 E 上的弯
ql
2
。
6－12 试作图示刚架的弯矩图，并确定 | M |max 。
— 57 —
习题 6-12 图
1 12 2
1
M (ql2)
A
B
知识点：刚架的弯矩图 难度：一般 解答：
Fx 0 ， FAx ql （←）
MA 0
ql
2
ql
l 2
FRB
l
0
FRB
1 2
ql
（↓）
Fy
0 ， FAy
1 2
ql
知识点：刚架的弯矩图 难度：一般 解答：
6－14 梁的上表面承受均匀分布的切向力作用，其集度为 p 。梁的尺寸如图所示。若已知 p 、
h、l，试导出轴力 FNx、弯矩 M 与均匀分布切向力 p 之间的平衡微分方程。
知识点：力的简化，载荷、剪力、弯矩之间的微分关系 难度：很难 解答：
1．以自由端为 x 坐标原点，受力图（a）
正确答案是 B、C、D 。
习题 6-2 图
— 50 —
6－3 已知梁的剪力图以及 a、e 截面上的弯矩 Ma 和 Me，如图所示。为确定 b、d 二截面上 的弯矩 Mb、Md，现有下列四种答案，试分析哪一种是正确的。
（A） M b M a Aab (FQ ) ， M d M e Aed (FQ ) ；
|M
|max
p 2
hl
（固定端）
FN
O M
lx
pl
lx
1 phl
2
6－16 静定梁承受平面载荷，但无集中力偶作用，其剪力图如图所示。若已知 A 端弯矩 M(A) 0 ，试确定梁上的载荷及梁的弯矩图，并指出梁在何处有约束，且为何种约束。
习题 6-16 图
7.5
4
m
A
3
BC
M kN m 40
3
(c)
MB 0
1 FRA 2l q 3l 2 ql l 0
5
FRA 4 ql （↑）
Fy
0，
FRB
3 4
ql
（↑）
MB
0
，MB
q 2
l2
MD
0，
M
D
25 32
ql 2
|
FQ
| max
5 4
ql
|
M
| max
25 32
ql 2
6－8 应用平衡微分方程，试画出图示梁的剪力图和弯矩图，并确定 | FQ |max 。
D
B
C
1
1
1.5
M (ql2)
A
M (ql2)
D
BC
10.75
D
B
C
1
25
2
32
知识点：梁的剪力图与弯矩图 难度：一般 解答：
Fy 0 ， FRA ql （↑）
M A 0 ， M A ql 2
MD
0，
ql 2
ql l
ql
l 2
MD
0
MD
3 2
ql 2
| FQ |max ql
|
M
| max
6－11 试作图示刚架的弯矩图，并确定 | M |max 。
习题 6-11 图
1
12
2C
B
M (ql2)
1
A
知识点：刚架的弯矩图 难度：一般 解答：
Fy 0 ， FAy ql （↑）
1
M A 0 ， FRB 2 ql （→）
Fx
0，
FAx
1 2
ql
（←）
弯距图如图示，其中 |
M
|max
6－17 已知静定梁的剪力图和弯矩图，如图所示，试确定梁上的载荷及梁的支承。
习题 6-17 图
知识点：载荷、剪力、弯矩之间的微分关系的应用 难度：很难