污染气象学 大气扩散参数
污染气象学课件-扩散理论

一 湍流擴散方程
dq dt
(qu)
x
(qv) y
(dq dt
x
(Kx
q) x
y
(Ky
q) y
z
(Kz
q) z
二 方程的簡化與求解
1 無風暫態點源
假定大氣的靜止的,湍流擴散係數為常數, 各向同性,則
q(x,
y,
z,
t)
8(
Q Kt )3/ 2
exp[
1 4Kt
(r2 )]
湍能擴散項
Si Ri chemis
源幹 化 排濕 學 放沉 反 項降 應
分子擴散項 忽略不計
拉格朗日方法
考慮一微粒 t位於 x ,隨後,其軌跡由X (x,t,t)描述
設粒子於t時間在一體積元的機率為
(x1, x2, x3,t)dx1dx2dx3 (x,t)d x
(x,t)為時間t,粒子位置的概率密度函數,並有
中性大氣:參量 非中性大氣: 和u* 。
u* HT
1 基本數學處理
用量綱分析的方法可得到:
垂直風速
dZ dt
bu*
(
Z L
)
(1)
式中b和 為待定的普適常數和普適函數,中性時, 1
進一步假設相應的水準位移的增長率等於在 Z 高度處的
平均風速,表示為
水準風速
d X u(cZ ) dt
(2)
2 中性層結的平均位移
2 y
y2 (T )
2v2
T 0
t
0 RL ( )d dt
定常均勻的湍流場中,粒子的湍流擴散範圍取 決於湍流脈動速度方差和拉格朗日相關性。
2.泰勒公式的另一種形式(自學)
y2(T) 2v2
大气污染物扩散模式

y z const (实际中成立) dc( x,0,0, H ) 0 d z
2q z πuH 2e y
由此求得
cmax
z |x x
cmax
H 2
第三节 污染物浓度的估算
计算或实测 u 平均风速 多年的风速资料 H 有效烟囱高度 y 、 z 扩散参数
q 源强
kW
Holland公式比较保守,特别在烟囱高、热释放率比较强的情况下。 在实际计算中,不稳定条件(A、B稳定度),ΔH 需增加10%~20%; 稳定条件(D、E、F稳定度), ΔH 需减少10%~20%。
(2)Briggs公式:适用不稳定及中性大气条件
不稳定或中性大气下,布里格斯公式用来确定不同的热释放 率和下风向距离条件下的烟气抬升高度:
萨顿实用模式
高斯模式(应用最为广泛)
第二节 高斯扩散模式
一、 高斯模式的有关假定 坐标系
右手坐标系(食指 —x 轴;中指 —y轴;拇指 —z轴), 原点:为无界点源或地面源的排放点,或者高架源排放 点在地面上的投影点;x为主风向;y为横风向;z为垂直 向
高斯模式的四点假设
a.污染物浓度在y、z风向上分布为正态分布 b.全部高度风速均匀稳定 c.源强是连续均匀稳定的 d.扩散中污染物是守恒的(不考虑转化)
地面最大浓度模式:
考虑地面轴线浓度模式
H2 c( x,0,0, H ) exp( 2 ) 2 z πu y z q
z 增大,第一项减小,第二 上式,x增大,则 y 、 项增大,必然在某x 处有最大值
高架连续点源扩散模式
地面最大浓度模式(续):
设
y z const (实际中成立) dc( x,0,0, H ) 0 d z
污染气象1.2影响污染物扩散的主要因子
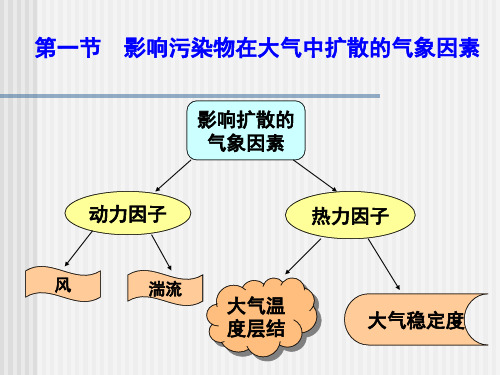
第一节 影响污染物在大气中扩散的气象因素
(三)大气稳定度
大气稳定度是大气中的某一气团在垂直方向上的稳 定程度,是对污染源排入其中的污染物扩散能力的 一种量度。
d
d
不稳定
稳定
第一节 影响污染物在大气中扩散的气象因素
2.大气稳定度与烟流扩散的关系
波浪型:大 气不稳定
锥型:大气 中性或稳定
扇型:大气 逆温稳定
屋脊型:排出口上方不 稳定;排出口下方稳定
熏烟型:排出口上方稳 定;排出口下方不稳定
第一节 影响污染物在大气中扩散的气象因素
(四)大气稳定度的分类
湍流
大气运动的重要形 式,使空气发生强 烈的铅直和水平扩 散,其强度和尺度
远大于分子扩散
蒸发,气温,光波、声 波和无线电波的传播有 重要的影响
风向的摆动
风速的脉动
第一节 影响污染物在大气中扩散的气象因素
湍流分类
机械力 机械湍流
热力 热力湍流
湍流运动最重要的结果:使大气中热量、水分、尘埃 等物理属性及混合物得以传递。
第一节 影响污染物在大气中扩散的气象因素
第一节 影响污染物在大气中扩散的气象因素
第一节 影响污染物在大气中扩散的气象因素
下垫面摩擦力
风速随高度变化的曲线
风速廓线
第一节 影响污染物在大气中扩散的气象因素
常用的两个风速廓线模式:
1.对数率
高度为Z处的风 速(m/s)
摩擦速度
ū u* ln Z
Z0
度最大的是_
pm2.5扩散系数

pm2.5扩散系数
PM2.5是指悬浮在空气中的颗粒物,其直径小于等于2.5微米。
PM2.5扩散系数是指PM2.5颗粒物在空气中的扩散系数,即在一定的时间内PM2.5颗粒物的扩散距离与空气流速的比值。
PM2.5扩散系数的大小与多种因素有关,包括气温、湿度、风速、PM2.5颗粒物的大小和密度等。
通常情况下,PM2.5扩散系数较大时,PM2.5颗粒物在空气中的扩散距离也较大,对空气质量的影响也较大。
在监测和控制PM2.5污染时,PM2.5扩散系数是一个重要的参数,可以帮助我们了解PM2.5颗粒物在空气中的扩散情况,为制定有效的治理措施提供依据。
在环境科学领域中,PM2.5扩散系数是常用的指标之一,用于评估PM2.5污染对人体健康的风险。
通常情况下,PM2.5扩散系数越大,PM2.5污染对人体健康的风险也越大。
举个例子,当PM2.5扩散系数较大时,PM2.5颗粒物可以在空气中扩散到较远的距离,可能会对周围多个社区造成影响。
因此,在监测和控制PM2.5污染时,要加强对PM2.5扩散系数的监测和评估,以便及时采取有效的治理措施。
此外,PM2.5扩散系数还与气象条件有关,如气温、湿度、风速等。
当气象条件发生变化时,PM2.5扩散系数也可能发生变化。
因此,在监测和控制PM2.5污染时,要注意对气象条件的监测和评估,以便及时采取应对措施。
大气污染扩散计算方法

二、有限长线源扩散模式
线源扩 散模型
(4)计祘源强 Ql 90 / 150 0.6( g / sm)
(5)计算浓度
A( y ) 2
p2
1 2
p1
exp(0.5 p )dp
2
0.918
1 2
0.918
exp(0.5 p 2 )dp
0.918
1 2
0
exp(0.5 p 2 )dp 2 * 0.3159
C
0.22x(1+0.0004x)-1/2
0.20x
D
0.16x(1+0.0004x)-1/2
0.14x(1+0.0003x)-1/2
E-F 0.11x(1+0.0004x)-1/2
0.08x(1+0.0015x)-1/2
六、实例计算
某火力发电厂的烟囱高度为50m,烟囱口直径1.5m,烟气出口速度 为:5m/s,烟气出口温度600K,SO2的排放率为270g/s,地面10m高的 风速为4.0m/s,太阳高度角>60度,气温为37C, 试计算下风侧地面x 轴线500m处SO2的浓度为多少?最大浓度?最大浓度位于何处?
……………………..(A)
三、高架点源高斯扩散模型
点源扩 散模型
地面浓度模式:取z=0代入上式,得
y2 H2 c( x, y ,0, H ) exp( 2 ) exp( 2 ) 2 y 2 z πu y z q
…………..(B)
地面轴线浓度模式:再取y=0代入上式
H2 c( x,0,0, H ) exp( 2 ) 2 z πu y z q
m
u1 —Z1 高度处的平均风速(m/s) Z1—风速仪的高度; ;m—指数;
第10章 大气扩散与污染控制(2)

2.15 y H tg15o 2.15 y H 8
例题 参照【例4-6】
烟囱高度的设计
烟囱高度的计算
(1)达到大气污染物稀释扩散的作用; (2)尽量节省投资(造价正比于H2 ); (3)地面浓度不超过《环境空气质量标准》。
z 2q z Cmax ( ) 2 y 在0.5~1.0之间取 πuH e y 2 q z Hs H πeu (C0 Cb ) y
烟温宜在100℃以上。
公式中与气象有关的参数取值方法: ū的取值:①取多年平均值;②取某一保证率的值:如已知ū >3m/s的频率为80%,取3m/s可保证有80%不超标,而 地面平均最大浓度可能比规定标准更低。 z 值在 0.5~1.0 间,即:当 Hs>100m 时, z y y 0 . 5 ;当 Hs<100m 时,
o
o
D-H
D-H D
二次反射 无反射 一次反射
2D-H
o 地面和逆温层底对烟云多次反射
封闭型扩散模式
简化计算:
例:位于北纬40°,东经117 °的某化工厂烟囱高50m, H2S排放量9kg/h ,排放筒直径0.5m,烟气出口温度50℃。 出口气速12m/s。距地面10m处风速为4m/s,早春2月 上午8时,天气晴朗,环境气温15℃,距地面500m处出 现逆温,试问在下风向5000m、8000m处H2S浓度有多 大? 第一步:确定大气稳定度——查太阳倾角-计算太阳高度角 -确定辐射等级-查出大气稳定度 第二步:确定H——计算QV、QH-计算50m处风速-计算 ΔH。 第三步:确定XD——计算σz,按远郊区查表4-8,反算XD。 第四步:按4-9计算5000m处H2S浓度。 第五步:按4-9计算XD 处H2S浓度;按4-36计算2XD 处 H2S浓度。然后内插,确定 5000m处H2S 浓度。
大气污染扩散计算方法
=5*1.5/5.09*(1.5+2.7*1.5*(600-310)/600)=5.1(m) H=50+5.1=55.1(m)
六、实例计算
(4)计算σy , σz. 查表得:
点源扩 散模型
σy = 0.32x ( 1+0.0004x )-1/2 = 0.32 * 500 ( 1+ 0.0004 * 500) -1/2 =146.1(m) σz = 0.24x(1+0.0001x) -1/2 = 0.24* 500(1+0.0001*500) -1/2 =117.1(m) (5)计算浓度q(e≈2.71828)
C
0.22x(1+0.0004x)-1/2
0.20x
D
0.16x(1+0.0004x)-1/2
0.14x(1+0.0003x)-1/2
E-F 0.11x(1+0.0004x)-1/2
0.08x(1+0.0015x)-1/2
六、实例计算
某火力发电厂的烟囱高度为50m,烟囱口直径1.5m,烟气出口速度 为:5m/s,烟气出口温度600K,SO2的排放率为270g/s,地面10m高的 风速为4.0m/s,太阳高度角>60度,气温为37C, 试计算下风侧地面x 轴线500m处SO2的浓度为多少?最大浓度?最大浓度位于何处?
H 2
…………..(E)
五、参数的求解
点源扩 散模型
Holland公式:适用于中性大气条件(稳定时减小,不稳时增 加10%~20%)
vs D Ts Ta 1 H (1.5 2.7 D) (1.5vs D 9.6 10 3 QH ) Ts u u
大气扩散课件课件
五、高斯模式使用条件的讨论(第一单元)
5.地形
不规则的地形不能应用高斯扩散模式。 高斯模式适合的地形必须是平坦,并且尺度范围 较小(<25km)。
6其他
模式中的有效源高He 扩散参数σy、σz,我们将在下面两节分别加以讨
论。
第四节烟流抬升高度
q 源强->计算或实测 u 平均风速->多年的风速资料 H 有效烟囱高度 y 、 z 扩散参数
2.源强Q
无论高架源还是地面源 连续排放稳定的点源, 源强Q为定值(g/s) mg/s 。
五、高斯模式使用条件的讨论(第一单元)
3.平均风速
讨论题: 1)当风速=0的时候,高斯公式会怎么样? 2)假定(2)中风速是个常量 ? 实际上成立吗?
高斯公式要求≥1m/s, 当<1m/s时就不用高斯模式而用其它模式处理
0
0 cdy
z2cdz
2 z
0
0 cdz
由假定4->源强积分式
(单位时间物料守恒) q
ucdydz
未知数:浓度c,待定函数A(x),待定系数a,b(
1 2
2
)
积分,可以解出四个未知数:得到高斯模式
c(x, y, z) q exp[( y 2 z 2 )]
烟气抬升高度的计算
抬升高度计算式(续)
(2)Briggs公式:适用不稳定及中性大气条件
当QH 21000kW时
x 10Hs
H=0.362QH1/3 x2/3 u1
x 10Hs
H=1.55QH1/3 H s2/3 u1
当QH 21000kW时
x 3x*
大气中污染物的扩散
地面最大浓度估算
由 和 H
| z xxcmax
H 2Biblioteka z由 z ~ x 曲线(图4-5)反查出 xcmax
由 y ~ x 曲线(图4-4)查 y
由式(4-10)求出Cmax
扩散参数的确定-中国国家标准规定的方法
扩散参数的选取
扩散参数的表达式为(取样时间0.5h,按表2-16查
算)
y
1xa1 , z
exp(
y2
2
2 y
) exp[
(H
vt x
2
2 z
/
u)2
]
vt
d
2 p
p
g
18
地面反射系数
污染物浓度的估算
q 源强 计算或实测
u 平均风速 多年的风速资料
H 有效烟囱高度
y 、 z 扩散参数
1.烟气抬升高度的计算
有效源高 H Hs H
Hs ――烟囱几何高度
H ――抬升高度
烟气抬升
初始动量: 速度、内径
x 3x *
H =0.332QH3/5 Hs2/5
x*=0.33QH
3/5
H
3/5 s
u
6
/
5
烟气抬升高度的计算
抬升高度计算式 (续)
(3)我国“制订地方大气污染物排放标准的技术方 法”(GB/T13201-91)中的公式
(1)当 Q H 2100kW 和 (Ts Ta ) 35K 时
H
H = 2 (1 .5vs D 0 .0 1Q H ) u
(4)当10m 高 处 的 年 平 均 风 速 小 于 或 等 于1.5m /s时
H
=
5
.5
大气扩散参数表格
大气扩散参数表格篇一:点源大气扩散模式计算参数点源大气扩散模式计算的参数选取邓新民【摘要】就实际环评工作中点源大气扩散模式计算参数选取的有关问题提出了一些新的看法。
关键词点源,扩散模式,参数中图法分类 X823PARAMETER SELECTION IN THE ATMOSPHERE DIFFUSION MODEL OF POINT SOURCEDeng Xinmin(Department of Meteorology,CIM)ABSTRACT Based on the actual environmental assessment,several methods on how to select parameters in the atmosphere diffusion model of point source are presented.Key Words Point source,Diffusion model,Parameters1 引言建设项目环境影响评价是我国环境保护的一项基本制度,大气环境影响评价是建设项目环境影响评价的重要内容,而大气环境影响预测与评价则是大气环境影响评价的重要内容或核心问题。
所谓大气环境影响预测与评价,就是计算或估计建设项目所排放的大气污染物在评价区域内对大气环境质量的影响。
在绝大多数情况下,影响预测采用模式计算的方法,通常用《环境影响评价技术导则大气环境》(HJ/T 2.2-93)(下称导则)推荐的模式或相关模式[1]。
环评实践表明,一般地讲,模式的选用通常是正确的,也符合建设项目实际。
因此,模式的参数选取是否恰当,就成为影响评价是否正确、是否符合实际的关键因素。
在我们看来,参数选取至少应满足以下条件:其一,满足计算公式本身所要求的条件;其二,参数的选取和计算结果要有典型性和代表性;其三,要符合实际情况。
但在实际的环评工作中,参数的选取或未引起足够注意,或存在这样那样问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4 J.S.Hay & F.Pasquill(1959)
出发点:统计理论,泰勒公式
方法:利用相关函数和湍流能谱关系,由湍 流观测资料做谱分析,计算扩散参数。
总结:模型合理可取,反映湍流场本质,而 且准确度较高,其探讨有一定理论意义, 但应用尚不普遍,观测要求高,计算工作 量大。
➢工业区和城市中心区,C提至B级,D、 E、 F向不稳定方向提一级
➢丘陵山区的农村或城市,同工业区
2 不同稳定度分类方法
(1)风向脉动标准差(EPA,1990)
• 以风速做细致调整,观测数据在粗糙度z0=15cm, 10m高度处测量得到。采样时间为15min。
• 如果风向发生转折,为了尽量减小风向转折的影 响,应该将长时间段分成小段进行计算,例如将
由 和 H
z
x xm
H 2
由 z ~ x 曲线(图
z
反查出 xcmax
由
y
~
x
曲线(图
y
由式(3.10 求出 Cmax
三 扩散曲线法的完善
1.国家标准中的修改应用(GB/T13201-91)
➢修正太阳高度角的计算方法 ➢适应我国大量地面观测无云高观测 的情况
中国国家标准规定的方法
➢平原地区和城市远郊区,D、E、F向不稳 定方向提半级
f为普适函数,扩散参数,函数形式随源高和
稳定度变化
(2) 特点
✓方法原理与湍流统计理论基础一致 ✓舍弃分离的稳定度级别,采用连续性稳定
度,接近实际 ✓考虑源高影响,认为f是稳定度状况函数 ✓使用方便,可用于多种情况
(3) 扩散函数f 的确定
由泰勒公式积分可得
1
y vT
2 tL T
T
tL
1
60min的时间划分为15min一段,最终小时量值:
60
2 15
2 15
2 15
2 15
4
(2)与温度递减率有关方法
①以温度递减率,即以两层(10m、60m) 的垂直温度梯度来表征水平和垂直向的湍 流状况。国际原子能机构(1980)推荐
以温度递减率来表征大气稳定度的方法对于 稳定大气的情形比较可靠,不稳定或者高 架源的情形适宜用水平风向脉动标准差方 法。
3 不同源高和不同下垫面的应用
• P-G扩散曲线实验依据:平坦理想条件,大 量低矮源扩散试验。
• 不同源高 • 不同下垫面-Briggs,1974内插完善
4 风向脉动和扩散函数法
• 扩散曲线法试验基础存在较大的经验 性,方案结果有许多不确定性
• 仅以宏观气象状况为判据,在稳定度 级别和湍流特性之间缺少清晰关系
• P-G-T方法 • 国家标准
二 稳定度扩散分级与扩散曲线法
由大量扩散试验(含气象观测和示踪物浓 度观测)资料分析及理论分析得出扩散参 数随下风方距离x的变化曲线
——P-G法,或者P-G-T法
1. P-G曲线法
方法要点
大气分成A-F共六个稳定度等级
(云、日照、风速……)
x ~ y曲线(六条)(对应A、B……F稳定度级)
• P-G曲线的应用
1 萨顿模式
2 y
y2 (T )
2v2
T 0
t
0 RL ( )d dt
具体步骤:
1 找出泰勒公式中的拉格朗日相关系数的具体 形式,即寻找它与某些可测气象参量的关系, 代入泰勒公式求扩散参数。
2 将扩散参数代入基本高斯扩散,得到萨顿扩 散公式。
3 基于简单物理考虑,认为拉格朗日相关系数与湍 流特征量,宏观黏滞度,时间间隔相关,并通过 量纲分析得到所有量的组合。
• 目前重要发展由风向脉动与扩散函数 确定扩散参数的方法
(1)方法原理
按照湍流扩散理论,在均匀定常条件下,粒 子位移的总体平均由泰勒公式表示。
2 y,z
2(v, w)2
T 0
t
0 RL ( )d dt
由泰勒公式可得
y,z
v,w T
T fy,z (tL )
tL 为拉格朗日时间尺度
tL 0 R( )d
指数取值,见书P140
2 直接测量湍流特征量的方法
H.E.Cramer(1957)提出
y Axp z Exg
脉动风方位 角标准差
脉动风高度 角标准差
A 和 E 由双向风标测量,反映大气湍流扩散
能力。
p,g与稳定度、下风向距离及地表粗糙度相关
3 BNL模式(M.E.Smith,1951)
• 特征量:水平风向摆动角的范围 • 高架源(108m高塔施放油雾)扩散试验
②以温度递减率和风速相结合(同时考 虑支配湍流活动的机械和热力因子)
③ 分别以温度梯度和 A表征湍流的水平 和垂直运动
④EPA(1990)推荐在缺乏云量和云高资
料时,采用表3.18替换原P-G-T方法
(3)边界层湍流参量法
Ri
g
z
u
2
z
L u*2Cp T gHT
注意:
• 除了使用公认的已有统一规范的方案,例 如P-G-T方案,国家标准给出的修改方案, 采用其他任何方案都应当验证其可行性, 提供充分的实验依据和例证,必要时还应 做专门的论证
§4.3 大气扩散参数
• 早期大气扩散参数处理 • 稳定度扩散级别与扩散曲线法 • 扩散曲线讨论 • 风向脉动与扩散函数法 • 扩散参数的研究现状
一 早期的扩散参数模式
格雷厄姆·萨顿,英国气象学家。1903年2月4日生于克温 坎。毕业于威尔士大学、阿伯里斯威恩大学和牛津大学。 1926—1928年在威尔士大学、阿伯里斯威恩大学任讲师, 1928—1941年任助理教授。第二次世界大战期间从事国防 科研工作。1942—1943年任英国国防部防化实验所所长。 1943—1945年任坦克实验所所长。1945—1947年任英国雷 达研究发展中心主任。1950—1955年任英国大气污染研究 委员会主席。1951年任英国陆军部科学顾问。1952—1953 年任英国皇家军事科学院教务长。1953年任皇家气象学会 主席。1953—1956年任世界气象组织常务理事。1960— 1966年任英国大地测量及地球物理学全国委员会主席。 1965—1971年任英国自然环境研究委员会主席。在自然环 境和气象研究方面取得了许多成果。曾获世界气象组织颁 发的奖金。著作:①《大气湍流》(Atmos-pheric turbulence,1948);②《微气象学》(Micrometeorology,1953)
以y向为例:
RL ( )
f
N
(v2 )
N u*z0
RL
(
)
(
N
N
v2
)n
n为由风速梯度观测确定的实验常数,n 2m
m为风速廓线幂指数。
1 m
2 y
2N n (1 n)(2
n)v2
• (v2
•T )2n
1 2
C
2 y
x2n
2 z
(1
2N n n)(2
n)w2
• (w2
•T )2n
1 2
Cz2 x2n
exp
T tL
2
f
y
T tL
f
y
x utL
Pasquill (1976)给出试验资料所得的f(x)数据
两者中间范围一致,近范围,理论值稍高,远 距离相反。
• 由试验资料分析求取扩散函数的方 法-自学,下堂课讨论
(4)几种扩散函数表达式
5 扩散参数的现状和发展
自学完成
• 大气稀释因子、烟流有效源高、虚拟 点源、
– 根据常规资料确定稳定度级别
Pasquill(1963)
Turner(1961)引入太阳高度角判定日射强 弱的定量办法,确定稳定度级别。
太阳高度角 云量
日射等级
风速
稳定度
• P-G曲线的应用(10分钟平均) – 利用扩散曲线确定 y和 z
水平扩散参数
垂直扩散参数
• P-G曲线的应用
–地面最大浓度估算
C
2 y
(1
4N n n)(2
n)u 2
• (v2 u2
Hale Waihona Puke )1nCz2(1
4N n n)(2
n)u 2
• ( w2 u2
)1n
萨顿参数
最早,但有局限性
补充内容:近地层指数律风廓线
中性层结:对数律 非中性层结:通量-廓线关系,指数律,综合
乘幂律
指数律:简单实用,但中性及近中性层结, 对数律更合适
