复旦大学金融学单独考试硕士研究生招生考试783高等数学单考试大纲 Fudan University.pdf
2021年硕士研究生入学考试自命题科目参考书目
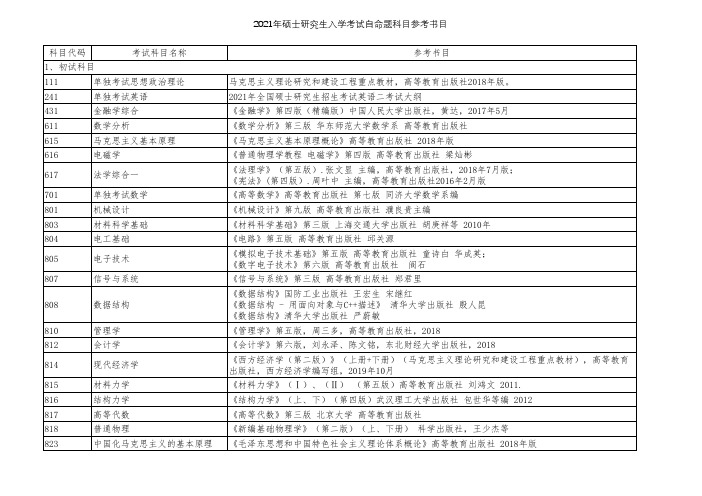
111单独考试思想政治理论马克思主义理论研究和建设工程重点教材,高等教育出版社2018年版。
241单独考试英语2021年全国硕士研究生招生考试英语二考试大纲431金融学综合《金融学》第四版(精编版)中国人民大学出版社,黄达,2017年5月611数学分析《数学分析》第三版 华东师范大学数学系 高等教育出版社615马克思主义基本原理《马克思主义基本原理概论》高等教育出版社 2018年版616电磁学《普通物理学教程 电磁学》第四版 高等教育出版社 梁灿彬617法学综合一《法理学》(第五版).张文显 主编,高等教育出版社,2018年7月版;《宪法》(第四版).周叶中 主编,高等教育出版社2016年2月版701单独考试数学《高等数学》高等教育出版社 第七版 同济大学数学系编801机械设计《机械设计》第九版 高等教育出版社 濮良贵主编803材料科学基础《材料科学基础》第三版 上海交通大学出版社 胡庚祥等 2010年804电工基础《电路》第五版 高等教育出版社 邱关源805电子技术《模拟电子技术基础》第五版 高等教育出版社 童诗白 华成英;《数字电子技术》第六版 高等教育出版社 阎石807信号与系统《信号与系统》第三版 高等教育出版社 郑君里808数据结构《数据结构》国防工业出版社 王宏生 宋继红《数据结构 - 用面向对象与C++描述》 清华大学出版社 殷人昆《数据结构》清华大学出版社 严蔚敏810管理学《管理学》第五版,周三多,高等教育出版社,2018812会计学《会计学》第六版,刘永泽、陈文铭,东北财经大学出版社,2018814现代经济学《西方经济学(第二版)》(上册+下册)(马克思主义理论研究和建设工程重点教材),高等教育出版社,西方经济学编写组,2019年10月815材料力学《材料力学》(Ⅰ)、(Ⅱ) (第五版)高等教育出版社 刘鸿文 2011. 816结构力学《结构力学》(上、下)(第四版)武汉理工大学出版社 包世华等编 2012 817高等代数《高等代数》第三版 北京大学 高等教育出版社818普通物理《新编基础物理学》(第二版)(上、下册) 科学出版社,王少杰等823中国化马克思主义的基本原理《毛泽东思想和中国特色社会主义理论体系概论》高等教育出版社 2018年版1、初试科目827自动控制原理《自动控制原理》第五版 国防工业出版社 胡寿松833环境工程学《环境工程学》第三版 高等教育出版社 蒋展鹏836电工电子技术《电工学》(上下册)第七版 高等教育出版社 秦曾煌846工程力学《工程力学》李福宝,周丽楠,李勤.化学工业出版社,2019.847法学综合二《民法》(第七版),魏振瀛主编,北京大学出版社,高等教育出版社,2017年8月版;《民事诉讼法》(第五版)江伟主编,高等教育出版社,2016年7月出版849数据库原理及应用《数据库系统概论》第五版 高等教育出版社 王珊 萨师煊 2014851化工原理《化工原理》(上下册)天津大学出版社 夏清 贾绍义主编 2012年第二版《化工原理》(上下册)化学工业出版社 谭天恩、窦梅等编著 2013年第四版853微电子制造原理《硅集成电路工艺基础》(第二版)关旭东 北京大学出版社 2014年04月F401通信原理《通信原理》国防工业出版社 樊昌信F402金属材料及热处理《金属学与热处理》第二版 机械工业出版社 崔忠圻 覃耀春等 2017年F403经济学综合《国际贸易实务》机械工业出版社 张孟才 2012年版(2013年10月重印)《金融市场学》清华大学出版社,张薇薇,2017年7月《产业经济学》第四版高等教育出版社苏东水 2015年9月F404流体力学《流体力学》李福宝,李勤.冶金工业出版社,2009.F405传感器与检测技术《传感器与检测技术》机械工业出版社 高成等编,2015F406材料物理化学《物理化学》第四版 上海科学技术出版社 任素贞等 2013年F407企业管理学《企业管理概论》第六版,尤建新,高等教育出版社,2018F500政治理论教育部推荐高校马克思主义理论课最新教材(2018版),包括马克思主义基本原理概论,毛泽东思想和中国特色社会主义理论体系概论,当代世界经济与政治。
复旦大学2022年硕士研究生招生考试自命题科目考试大纲

掌握流行病学的基本原理及研究方法,掌握流行病学研究方法的设计、实施和资料分析方法,熟悉流行病学研究中常见偏倚的来源、识别及控制方法。主要内容包括为:流行病学的定义和用途;人群疾病及健康状况的常用测量指标、疾病流行强度及疾病和健康状况“三间”分布的描述;现况研究的类型、设计、实施与评价;筛检试验的原则及评价;病例对照研究的原理、设计、实施和资料分析及相关指标、优点及局限性;队列研究的原理、设计、实施和资料分析及相关指标、优点及局限性;流行病学实验设计的基本特征、类型、设计与实施、资料分析及评价指标、优点及局限性;流行病学研究中的常见偏倚(选择性偏倚、信息偏倚及混杂偏倚)及控制方法;流行病学研究中的病因及其推断原则;疾病预防及控制策略、公共卫生监测;传染病传染过程、流行过程、预防策略与措施、免疫规划及效果评价。
二、试卷结构
卫生统计学(75分)。 包括:名词解释(15分)、单选题(30分)、问答题(30分)。
流行病学(75分)。 包括:名词解释(15分)、单选题(30分)、问答题(30分)。
预防医学(100分)。 包括(60分)。
社会医学(50分)。 包括:单选题(20分)、问答题(30分)。
2018年
第7版
夏昭林
预防医学导论
复旦大学出版社
2014年
第1版
复旦大学2022年硕士研究生招生考试自命题科目考试大纲
科目代码
353
科目名称
卫生综合
一、主要考试内容范围
一、卫生统计学(75分)
掌握卫生统计学基本理论、原理和统计方法;掌握卫生统计基本概念、统计描述、常见概率分布、抽样分布理论、参数估计和假设检验、连续型变量常用统计分析方法、离散型变量常用统计分析方法、直线回归和相关分析以及生存分析等内容;熟悉研究设计(实验设计、调查设计)的基本概念和类型。
复旦大学2019年全国硕士研究生招生考试881电子线路与集成电路设计考试大纲

试卷满分 150 分。
模拟电子线路部分总分值为 50 分,题型为简答题和计算题。 数字电路部分总分值为 50 分,题型为填空题和电路分析设计题。 集成电路设计部分总分值为 50 分,题型为简述题和分析计算题。
三、参考书目
作者 书名
出版社
出 版 时 版 备注
间
次
Rabaey 数字集成电路— 电子工业出版社 2004.10
(1)集成电路的分类及相应的设计方法; (2)各类集成电路的设计流程,及设计流程中所涉及的专用术语。 2、数字集成电路设计 (1)CMOS 集成电路制造工艺; (2)MOS 器件的电流方程和大信号等效模型,器件的 SPICE 模型参数; (3)基本数字电路模块的电路与版图分析与设计,如反相器、各种 MOS 组合逻辑电路、时序逻辑电路、存储器与阵列结构、运算单元等; (4)数字集成电路设计的导线模型与互联参数; (5)先进集成电路工艺下数字集成电路面临的设计问题,数字 IC 的实现 策略。 3、模拟集成电路设计 (1)MOS 器件物理,包括器件电流方程、二级效应对电流方程的修正、 寄生电容和电阻、小信号等效模型; (2)基本模拟集成电路模块的分析与设计。如单级放大器、差分放大器、 电流镜电路、放大器的频率响应、噪声分析、放大器反馈电路的分析方法、运算 放大器分析及频率补偿; (3)先进集成电路工艺下模拟集成电路面临的设计问题,模拟 IC 的鲁棒 设计方法及 IC 实现步骤。
等
电路、系统与设
计
拉 扎 维 模 拟 CMOS 集 成 西安交通大学出 2002.12
等
电路设计
版社
史密斯 专用集成电路 电子工业出版社 2004.1
第 1-8 、 12 章
第 1-10 章
2024年全国硕士研究生数学(三)考试大纲

2024年全国硕士研究生数学(三)考试大纲
2024年全国硕士研究生数学(三)考试大纲主要包括以下几个部分:
一、考试性质
数学(三)是2024年全国硕士研究生招生考试中的一门公共基础科目,用于检验考生的数学知识和思维能力。
二、考试目标
数学(三)的考试目标是检验考生是否具备以下能力:
1. 掌握高等数学的基本概念、基本理论和基本方法,包括微积分、线性代数、概率论与数理统计等方面的知识。
2. 具备一定的数学思维和解决实际问题的能力,包括分析和推理、计算和数据处理等方面的能力。
3. 了解数学在各领域的应用,包括经济、管理、工程等领域。
三、考试内容和要求
数学(三)的考试内容包括高等数学、线性代数和概率论与数理统计。
具体要求如下:
1. 高等数学:要求考生掌握微积分、级数、多元函数微分学、重积分等基本概念和理论,理解其在实际问题中的应用。
2. 线性代数:要求考生掌握矩阵论、向量空间与线性变换等基本概念和理论,理解其在解决实际问题中的应用。
3. 概率论与数理统计:要求考生掌握随机事件与概率、多维随机变量及其分布、大数定律与中心极限定理等基本概念和理论,理解其在数据处理和决策分析中的应用。
四、考试形式和试卷结构
1. 考试形式:数学(三)为闭卷考试,考试时间为180分钟,满分150分。
2. 试卷结构:试卷包括选择题和解答题两部分,其中选择题为四选一形式,共40分;解答题包括计算题、证明题和分析题等,共110分。
五、参考书目
数学(三)的参考书目包括《高等数学》(同济大学出版社)、《线性代数》(高等教育出版社)、《概率论与数理统计》(浙江大学出版社)等教材。
招收单独考试硕士生考试说明及考试大纲数学

招收单独考试硕士生考试说明及考试大纲数学考试科目:高等数学、线性代数、概率论与数理统计第一部分:考试内容及要求高等数学一、函数、极限、连续考试内容函数的概念及表示法函数的有界性、单调性、周期性和复合函数、反函数、分段函数和隐函数基本初等函数的性质及其图形初等函数简单应用问题的函数关系的建立数列极限与函数极限的定义及其性质函数的左极限与右极限无穷小和无穷大的概念及其关系无穷小的性质及无穷小的比较极限的四则运算极限存在的两个准则:单调有界准则和夹逼准则两个重要极限 :lim x→0sin xx=1,limx→∞(1+1x)x=e函数连续的概念函数间断点的类型初等函数的连续性闭区间上连续函数的性质考试要求1.理解函数的概念,掌握函数的表示法,并会建立简单应用问题中的函数关系式。
2.了解函数的有界性、单调性、周期性和3.理解复合函数及分段函数的概念,了解反函数及隐函数的概念。
4.掌握等函数的性质及其图形,了解初等函数的概念。
5.理解极限的概念,理解函数左极限与右极限的概念,以及函数极限存在与左、右极限之间的关系。
6.掌握极限的性质及四则运算法则。
7.掌握极限存在的两个准则,并会利用它们求极限,掌握利用两个重要极限求极限的方法。
8.理解无穷小、无穷大的概念,掌握无穷小的比较方法,会用等价无穷小求极限。
9.理解函数连续性的概念(含左连续与右连续),会判别函数间断点的类型。
10.了解连续函数的性质和初等函数的连续性,理解闭区间上连续函数的性质(有界性、最大值和最小值定理、介值定理)及其简单应用。
二、一元函数微分学考试内容导数和微分的概念导数的几何意义和物理意义函数的可导性与连续性之间的关系平面曲线的切线和法线基本初等函数的导数导数和微分的四则运算复合函数、反函数、隐函数以及参数方程所确定的函数的微分法高阶导数一阶微分形式的不变性。
微分中值定理洛必达LHospital法则函数单调性的判别函数的极值函数图形的凹凸性、拐点及渐近线函数图形的描绘函数最大值和最小值弧微分曲率的概念曲率半径。
复旦大学
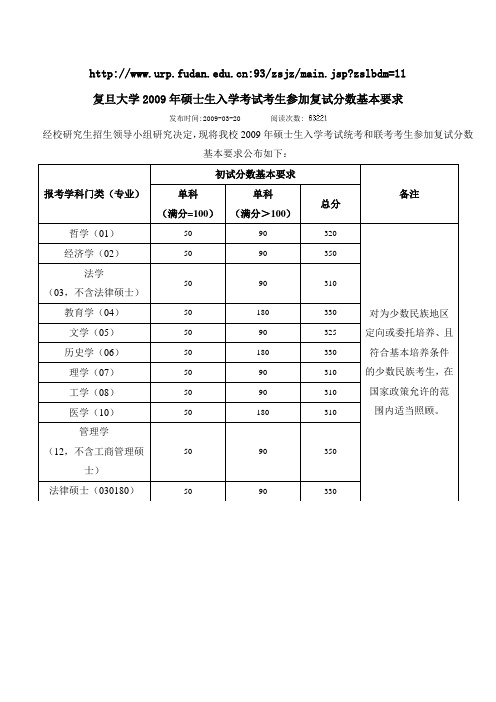
:93/zsjz/main.jsp?zslbdm=11复旦大学2009年硕士生入学考试考生参加复试分数基本要求发布时间:2009-03-20 阅读次数:经校研究生招生领导小组研究决定,现将我校2009年硕士生入学考试统考和联考考生参加复试分数基本要求公布如下:注:1.表中括号内01~12为学科门类代码,030180、120280为专业代码;2.复试通知将于3月底4月初由各院系寄发,具体复试时间、地点详见复试通知。
各学科专业一般按1:1.2的比例(个别学科专业可视生源情况作适当调整)复试。
复试的方式、科目及复试成绩权重可在我校研究生招生网上查询或向报考院系咨询;3.单独考试考生复试基本分数线根据教育部相关政策另行确定,考生可向研究生院招生办公室和相关院系查询。
2009年全日制专业学位硕士研究生招生信息汇总表发布时间:2009-03-20 阅读次数:注关于考生转报全日制专业学位硕士生的补充说明发布时间:2009-03-23 阅读次数:为保证2009年度科学学位和全日制专业学位硕士生复试工作的顺利进行,现将转报全日制专业学位硕士生的有关事项补充说明如下:1.是否转报专业学位依据考生个人意愿决定,若要转报专业学位则仅限报一个专业学位类型(含领域)。
2.我校科学学位硕士生的复试一般将在4月15日前结束,全日制专业学位硕士生的复试一般将在4月15日至20日进行。
申请转报全日制专业学位硕士生的考生,若已通过科学学位硕士生的复试且列入拟录取名单者,其转报志愿视为自动放弃。
复旦大学二〇〇九年招收单独考试硕士研究生简章单独考试是经教育部批准的部分高等学校为符合特定报名条件的在职人员单独组织的考试。
2009年,我校招收单独考试硕士研究生的专业有:(1)新闻学(由上海市有关新闻媒体单位推荐报考)(2)金融学(在上海和深圳面向社会招生)(3)外交学(面向上海市外办系统招生)(4)旅游管理(面向旅游及相关系统招生)一、报考条件符合各专业招生地域、行业(或系统)的人员满足下列条件者可报考:①大学本科毕业、一般取得学士学位后在报考专业或相近专业连续工作满4年(2005年9月1日前参加工作);②思想政治表现好,遵纪守法,业务优秀,为所在单位委托培养;③身体健康,年龄不限。
专业硕士《金融学综合》考研复旦大学历年考研真题库
专业硕士《金融学综合》考研复旦大学历年考研真题库复旦大学431金融学综合[专业硕士]考研真题一、名词解释(5分×5)1有效汇率2利率期限结构3流动性陷阱4大宗交易机制5正反馈投资策略二、选择题(4分×5)1套汇是什么样的行为?()A.保值B.投机C.盈利D.保值和投机2简单的戈登模型计算股价(考点)3以下理论中不属于商业银行管理理论的是()。
A.周期性收入理论B.真实贷款理论C.资产可转换理论D.资产管理理论4以下不属于金融抑制内容范围的是()。
A.名义利率限制B.金融产品单调C.金融监管D.金融贷款额度管理5依据蒙代尔-弗莱明模型,在固定汇率制度下,有()。
A.财政政策无效B.货币政策无效C.财政政策有效D.货币政策有效三、计算题(20分×2)1已知,A公司借美元借款的利率是LIBOR+1.0%,借欧元借款的固定利率是5.0%;B公司借美元借款的利率是LIBOR+0.5%,借欧元的固定利率是6.5%。
请帮金融机构给A、B两公司安排一套金融互换。
2A公司拟收购B公司,两家公司在收购前的相关财务资料见下表:A公司并购B公司前相关财务资料假如B公司目前的每股净收益为2元,将每年永续增长4%。
(1)B公司的价值为多少?(2)如果A公司为B公司每股发行在外的股票支付14元,则这一收购的NPV为多少?(3)如果A公司按每股净收益为换股率换取B公司发行在外的全部股票,那么,这一收购的NPV为多少?(4)如果这一方式可取,则应该选择现金收购还是换股收购?四、简答题(10分×2)1如果中央银行要降低货币乘数,应该怎么操作?2试论述正反馈机制在股市泡沫形成中的作用?五、论述题(20分+25分)1现金股利的信号传递效应,并联合我国的股市谈谈现金股利的信号传递效应的有效性。
2外汇储备需求决定因素与我国的外汇储备是否过度问题。
复旦大学金融专硕考研难度深度分析
复旦大学金融硕士难度考研分析目录1、复旦大学介绍 (2)2、复旦招收金融硕士的5个学院介绍 (2)(1)经济学院 (2)(2)管理学院 (2)(3)数学科学学院 (2)(4)泛海国际金融学院 (3)(5)大数据学院 (3)3、复旦大学2019年各学院招生人数 (4)4、历年分数线及报录比 (4)(一)历年分数线 (4)(二)近三年报录比 (5)5、初试考试科目 (5)6、初试参考书目 (5)7、专业课复习 (6)8、学费 (6)9、复试情况 (6)(一)复试流程 (7)(二)复试特点 (7)10、复旦金融硕士毕业就业去向 (7)11、复旦金融硕士辅导班哪个好? (7)本文重点讲解复旦大学金融硕士参考书、复旦大学金融硕士分数线、复旦大学金融硕士招生学院、复旦大学金融硕士学科特点、复旦大学金融硕士考试科目、复旦大学金融硕士就业、复旦大学金融硕士复试、复旦大学金融硕士资料、复旦大学金融硕士辅导班等内容,下面由老师给您详细介绍。
1、复旦大学介绍复旦大学(FudanUniversity),简称“复旦”,位于中国上海,由中华人民共和国教育部直属,中央直管副部级建制,国家双一流(A类)、985工程、211工程建设高校,入选珠峰计划、111计划、2011计划、卓越医生教育培养计划、国家建设高水平大学公派研究生项目,九校联盟(C9)、中国大学校长联谊会、东亚研究型大学协会、环太平洋大学协会的重要成员,是一所世界知名、国内顶尖的全国重点大学。
2、复旦招收金融硕士的5个学院介绍(1)经济学院复旦大学经济学院现设有:经济学系、世界经济系、国际金融系、公共经济学系、风险管理与保险系、世界经济研究所、中国社会主义市场经济研究中心和金融研究院等八个建制单位,1个“985工程”创新基地,28个研究机构。
经济学院拥有强大的老中青结合的教学和科研力量,既有在国内外享有盛誉的老一辈经济学家,又有近年来在国内理论界崭露头角的中青年经济学者,学术梯队完整,教研经验丰富,其整体实力在国内经济学界处于领先地位。
金融学考研考数学几考什么内容
金融学考研考数学几考什么内容数学对于很多考研的同学来说是个难题,那么哪些专业需要考数学呢?下面是由编辑为大家整理的“金融学考研考数学几考什么内容”,仅供参考,欢迎大家阅读本文。
金融学考研考数学几金融学硕士考试科目:101思想政治,201英语一,301数学三,经济学专业课。
考研数学三考试内容:一、微积分函数、极限、连续考试要求1.理解函数的概念,掌握函数的表示法,会建立应用问题的函数关系。
2.了解函数的有界性、单调性、周期性和奇偶性。
3.理解复合函数及分段函数的概念,了解反函数及隐函数的概念。
4.掌握基本初等函数的性质及其图形,了解初等函数的概念。
5.了解数列极限和函数极限(包括左极限与右极限)的概念。
6.了解极限的性质与极限存在的两个准则,掌握极限的四则运算法则,掌握利用两个重要极限求极限的方法。
7.理解无穷小的概念和基本性质,掌握无穷小量的比较方法,了解无穷大量的概念及其与无穷小量的关系。
8.理解函数连续性的概念(含左连续与右连续),会判别函数间断点的类型。
9.了解连续函数的性质和初等函数的连续性,理解闭区间上连续函数的性质(有界性、最大值和最小值定理,介值定理),并会应用这些性质。
二、一元函数微分学考试要求1.理解导数的概念及可导性与连续性之间的关系,了解导数的几何意义与经济意义(含边际与弹性的概念),会求平面曲线的切线方程和法线方程。
2.掌握基本初等函数的导数公式。
导数的四则运算法则及复合函数的求导法则,会求分段函数的导数会求反函数与隐函数的导数。
3.了解高阶导数的概念,会求简单函数的高阶导数。
4.了解微分的概念,导数与微分之间的关系以及一阶微分形式的不变性,会求函数的微分。
5.理解罗尔(Rolle)定理、拉格朗日( Lagrange)中值定理、了解泰勒定理、柯西(Cauchy)中值定理,掌握这四个定理的简单应用。
6.会用洛必达法则求极限。
7.掌握函数单调性的判别方法,了解函数极值的概念,掌握函数极值、最大值和最小值的求法及其应用。
复旦大学金融硕士考研经验——人如果没有梦想,那就和咸鱼没有区别
复旦大学金融硕士考研经验——人如果没有梦想,那就和咸鱼没有区别一、自我介绍2017年跨专业报考复旦大学管理学院的金融专硕,暑假开始备考,总分390+。
基本素质:在具体说备考信息之前,先说一下其他我认为需要了解的东西。
第一个是如何查信息。
考研的时候会加一些群,然后群里经常会有一些不明来源又说的好像确有其事的消息,比如经常会遇到有人说,啊,去年有3000多人报名,按以前的上升趋势来看,今年会有多少多少人,说的你各种慌;然后你考完了,加了个分数统计群,因为复旦没有出排名,又会有人在成绩统计群里说,400分一下的都不用指望了,赶紧该干嘛干嘛去。
都说整个考研的过程是一项大工程,你一直只努力学习是不行的,信息获取同样的重要,但是我觉得需要强调的是获取一手信息的搜索能力和理性思考的原则。
考研帮以及一些论坛上面会有别人整理过的信息,但是我还是觉得官方信息最可靠。
各种考研的信息都可以在复旦大学研究生招生网(/)上面查到,比如复旦今年某个专业总共招多少人,保研了多少人,还有多少名额给考研的人,成绩出来之后就可以根据经院的留给考研的名额乘以1.2大概地推算出今年的分数线是多少,还有去年的各种信息,比如每个院分数线是多少,校线是多少,哪些院接受校内调剂,还有往年的各种信息等,更加具体的信息一般在每个院的官方网站上都可以找到,等你把这些信息都查明白之后,你就会对群里的某些小道消息呵呵哒。
得到信息之后就是理性解读信息的能力了,比如报考人数每年都在创新高,那又怎样呢,真正和你在同一战线算得上对手的人数才重要,而且很多时候其实自己去努力了,尽全力了就不会后悔了,管它多少人报了这个专业呢。
所以总体上来说就是不要慌,根据官方的准确消息去理性地思考和勇敢地付出努力,心态要好。
第二,时间安排。
我觉得每个人都有自己的学习习惯和风格,照搬别人的时间安排和计划并没有太大的意义,有些人复习半年,有些人复习一年,还有二战三战,每个人的基础也都不一样,所以我觉得没有太大必要去做这种对比。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
考试要求 1、理解原函数与不定积分的概念,掌握不定积分的基本性质和基本积分公 式,掌握不定积分的换元积分法与分部积分法. 2、了解定积分的概念和基本性质,了解定积分中值定理,理解积分上限的 函数并会求它的导数,掌握牛顿-莱布尼茨公式以及定积分的换元积分法和分部 积分法. 3、会利用定积分计算平面图形的面积、旋转体的体积和函数的平均值,会 利用定积分求解简单的经济应用问题. 4、了解反常积分的概念,会计算反常积分. (四)多元函数微积分学 考试内容 多元函数的概念,二元函数的几何意义,二元函数的极限与连续的概念,有 界闭区域上二元连续函数的性质,多元函数偏导数的概念与计算,多元复合函数 的求导法与隐函数求导法,二阶偏导数,全微分,多元函数的极值和条件极值、 最大值和最小值,二重积分的概念、基本性质和计算,无界区域上简单的反常二 重积分. 考试要求 1、了解多元函数的概念,了解二元函数的几何意义. 2、了解二元函数的极限与连续的概念,了解有界闭区域上二元连续函数的 性质. 3、了解多元函数偏导数与全微分的概念,会求多元复合函数一阶、二阶偏 导数,会求全微分,会求多元隐函数的偏导数. 4、了解多元函数极值和条件极值的概念,掌握多元函数极值存在的必要条 件,了解二元函数极值存在的充分条件,会求二元函数的极值,会用拉格朗日乘 数法求条件极值,会求简单多元函数的最大值和最小值,并会解决简单的应用问 题. 5、了解二重积分的概念与基本性质,掌握二重积分的计算方法(直角坐标、 极坐标),了解无界区域上较简单的反常二重积分并会计算. (五)无穷级数
1
考试内容 导数和微分的概念,导数的几何意义和经济意义,函数的可导性与连续性之 间的关系,平面曲线的切线与法线,导数和微分的四则运算,基本初等函数的导 数,复合函数、反函数和隐函数的微分法,高阶导数,一阶微分形式的不变性, 微分中值定理,洛必达(L'Hospital)法则,函数单调性的判别,函数的极值, 函数图形的凹凸性、拐点及渐近线,函数图形的描绘,函数的最大值与最小值. 考试要求 1、理解导数的概念及可导性与连续性之间的关系,了解导数的几何意义与 经济意义(含边际与弹性的概念),会求平面曲线的切线方程和法线方程. 2、掌握基本初等函数的导数公式、导数的四则运算法则及复合函数的求导 法则,会求分段函数的导数,会求反函数与隐函数的导数. 3、了解高阶导数的概念,会求简单函数的高阶导数. 4、了解微分的概念、导数与微分之间的关系以及一阶微分形式的不变性, 会求函数的微分. 5、理解罗尔(Rolle)定理、拉格朗日( Lagrange)中值定理,了解泰勒 (Taylor)定理、柯西(Cauchy)中值定理,掌握这四个定理的简单应用. 6、会用洛必达法则求极限. 7、掌握函数单调性的判别方法,了解函数极值的概念,掌握函数极值、最 大值和最小值的求法及其应用. 8、会用导数判断函数图形的凹凸性(注:在区间 (a,b) 内,设函数 f (x) 具有
无穷大量的概念及其关系,无穷小量的性质及无穷小量的比较,极限的四则运算
极限存在的两个准则:单调有界准则和夹逼准则,两个重要极限:
lim sin x = 1 x→0 x
lim
x→∞
1
+
1 x
x
= e
函数连续的概念,函数间断点的类型,初等函数的连续性,闭区间上连续函
数的性质
考试要求
1、理解函数的概念,掌握函数的表示法,会建立应用问题的函数关系.
二阶导数.当 f ′′(x) > 0 时, f (x) 的图形是凹的;当 f ′′(x) < 0 时, f (x) 的图形是 凸的),会求函数图形的拐点和渐近线.
9、会描述简单函数的图形. (三)一元函数积分学 考试内容 原函数和不定积分的概念,不定积分的基本性质,基本积分公式,定积分的 概念和基本性质,定积分中值定理,积分上限的函数及其导数,牛顿-莱布尼茨 (Newton- Leibniz)公式,不定积分和定积分的换元积分法与分部积分法,反 常(广义)积分,定积分的应用.
3
考试内容 常数项级数的收敛与发散的概念,收敛级数的和的概念,级数的基本性质与 收敛的必要条件,几何级数与 p 级数及其收敛性,正项级数收敛性的判别法,任 意项级数的绝对收敛与条件收敛,交错级数与莱布尼茨定理,幂级数及其收敛半 径、收敛区间(指开区间)和收敛域,幂级数的和函数,幂级数在其收敛区间内 的基本性质,简单幂级数的和函数的求法,初等函数的幂级数展开式. 考试要求 1、了解级数的收敛与发散、收敛级数的和的概念. 2、了解级数的基本性质及级数收敛的必要条件,掌握几何级数及 p 级数的 收敛与发散的条件,掌握正项级数收敛性的比较判别法和比值判别法. 3、了解任意项级数绝对收敛与条件收敛的概念以及绝对收敛与收敛的关系, 了解交错级数的莱布尼茨判别法. 4、会求幂级数的收敛半径、收敛区间及收敛域. 5、了解幂级数在其收敛区间内的基本性质(和函数的连续性、逐项求导和 逐项积分),会求简单幂级数在其收敛区间内的和函数. 6、了解 ex , sin x , cos x , ln(1+ x) 及 (1+ x)α 的麦克劳林(Maclaurin)展 开式. (六)常微分方程与差分方程 考试内容 常微分方程的基本概念,变量可分离的微分方程,齐次微分方程,一阶线性 微分方程,线性微分方程解的性质及解的结构定理,二阶常系数齐次线性微分方 程及简单的非齐次线性微分方程,差分与差分方程的概念,差分方程的通解与特 解,一阶常系数线性差分方程,微分方程的简单应用. 考试要求 1、了解微分方程及其阶、解、通解、初始条件和特解等概念. 2、掌握变量可分离的微分方程、齐次微分方程和一阶线性微分方程的求解 方法. 3、会解二阶常系数齐次线性微分方程.
F= (x) P{X ≤ x} ( −∞ < x < +∞ )
的概念及性质,会计算与随机变量相联系的事件的概率. 2、理解离散型随机变量及其概率分布的概念,掌握 0-1 分布、二项分布 B(n, p) 、几何分布、超几何分布、泊松(Poisson)分布 P(λ) 及其应用.
型的标准形和规范形,用正交变换和配方法化二次型为标准形,二次型及其矩阵 的正定性.
考试要求 1、了解二次型的概念,会用矩阵形式表示二次型,了解合同变换与合同矩 阵的概念. 2、了解二次型的秩的概念,了解二次型的标准形、规范形等概念,了解惯 性定理,会用正交变换和配方法化二次型为标准形. 3、理解正定二次型、正定矩阵的概念,并掌握其判别法. 三、概率论与数理统计 (一)随机事件和概率 考试内容 随机事件与样本空间,事件的关系与运算,完备事件组,概率的概念,概率 的基本性质,古典型概率,几何型概率,条件概率,概率的基本公式,事件的独 立性,独立重复试验. 考试要求 1、了解样本空间(基本事件空间)的概念,理解随机事件的概念,掌握事 件的关系及运算. 2、理解概率、条件概率的概念,掌握概率的基本性质,会计算古典型概率 和几何型概率,掌握概率的加法公式、减法公式、乘法公式、全概率公式以及贝
6
似对角矩阵. 考试要求 1、理解矩阵的特征值、特征向量的概念,掌握矩阵特征值的性质,掌握求
矩阵特征值和特征向量的方法. 2、理解矩阵相似的概念,掌握相似矩阵的性质,了解矩阵可相似对角化的
充分必要条件,掌握将矩阵化为相似对角矩阵的方法. 3、掌握实对称矩阵的特征值和特征向量的性质. (六)二次型 考试内容 二次型及其矩阵表示,合同变换与合同矩阵,二次型的秩,惯性定理,二次
7、理解无穷小量的概念和基本性质,掌握无穷小量的比较方法,了解无穷
大量的概念及其与无穷小量的关系.
8、理解函数连续性的概念(含左连续与右连续),会判别函数间断点的类型.
9、了解连续函数的性质和初等函数的连续性,理解闭区间上连续函数的性
质(有界性、最大值和最小值定理、介值定理),并会应用这些性质.
பைடு நூலகம்
(二)一元函数微分学
2、了解函数的有界性、单调性、周期性和奇偶性.
3、理解复合函数及分段函数的概念,了解反函数及隐函数的概念.
4、掌握基本初等函数的性质及其图形,了解初等函数的概念.
5、了解数列极限和函数极限(包括左极限与右极限)的概念.
6、了解极限的性质与极限存在的两个准则,掌握极限的四则运算法则,掌
握利用两个重要极限求极限的方法.
4
4、了解线性微分方程解的性质及解的结构定理,会解自由项为多项式、指 数函数、正弦函数、余弦函数的二阶常系数非齐次线性微分方程.
5、了解差分与差分方程及其通解与特解等概念. 6、了解一阶常系数线性差分方程的求解方法. 7、会用微分方程求解简单的经济应用问题. 二、线性代数 (一)行列式 考试内容 行列式的概念和基本性质,行列式按行(列)展开定理. 考试要求 1、了解行列式的概念,掌握行列式的性质. 2、会应用行列式的性质和行列式按行(列)展开定理计算行列式. (二)矩阵 考试内容 矩阵的概念,矩阵的线性运算,矩阵的乘法,方阵的幂,方阵乘积的行列式, 矩阵的转置,逆矩阵的概念和性质,矩阵可逆的充分必要条件,伴随矩阵,矩阵 的初等变换,初等矩阵,矩阵的秩,矩阵的等价,分块矩阵及其运算. 考试要求 1、理解矩阵的概念,了解单位矩阵、数量矩阵、对角矩阵、三角矩阵的定 义及性质,了解对称矩阵、反对称矩阵及正交矩阵等的定义和性质. 2、掌握矩阵的线性运算、乘法、转置以及它们的运算规律,了解方阵的幂 与方阵乘积的行列式的性质. 3、理解逆矩阵的概念,掌握逆矩阵的性质以及矩阵可逆的充分必要条件, 理解伴随矩阵的概念,会用伴随矩阵求逆矩阵. 4、了解矩阵的初等变换和初等矩阵及矩阵等价的概念,理解矩阵的秩的概 念,掌握用初等变换求矩阵的逆矩阵和秩的方法. 5、了解分块矩阵的概念,掌握分块矩阵的运算法则. (三)向量 考试内容
5
向量的概念,向量的线性组合与线性表示,向量组的线性相关与线性无关 向量组的极大线性无关组,等价向量组,向量组的秩,向量组的秩与矩阵的秩之 间的关系,向量的内积,线性无关向量组的正交规范化方法.
考试要求 1、了解向量的概念,掌握向量的加法和数乘运算法则. 2、理解向量的线性组合与线性表示、向量组线性相关、线性无关等概念, 掌握向量组线性相关、线性无关的有关性质及判别法. 3、理解向量组的极大线性无关组的概念,会求向量组的极大线性无关组及 秩. 4、理解向量组等价的概念,理解矩阵的秩与其行(列)向量组的秩之间的 关系. 5、了解内积的概念.掌握线性无关向量组正交规范化的施密特(Schmidt) 方法. (四)线性方程组 考试内容 线性方程组的克拉默(Cramer)法则,线性方程组有解和无解的判定,齐次 线性方程组的基础解系和通解,非齐次线性方程组的解与相应的齐次线性方程组 (导出组)的解之间的关系,非齐次线性方程组的通解. 考试要求 1、会用克拉默法则解线性方程组. 2、掌握非齐次线性方程组有解和无解的判定方法. 3、理解齐次线性方程组的基础解系的概念,掌握齐次线性方程组的基础解 系和通解的求法. 4、理解非齐次线性方程组解的结构及通解的概念. 5、掌握用初等行变换求解线性方程组的方法. (五)矩阵的特征值和特征向量 考试内容 矩阵的特征值和特征向量的概念、性质,相似矩阵的概念及性质,矩阵可相 似对角化的充分必要条件及相似对角矩阵,实对称矩阵的特征值和特征向量及相
