四年级上册数学思维拓展题:和差积商变化规律
(完整版)和差积商的变化规律
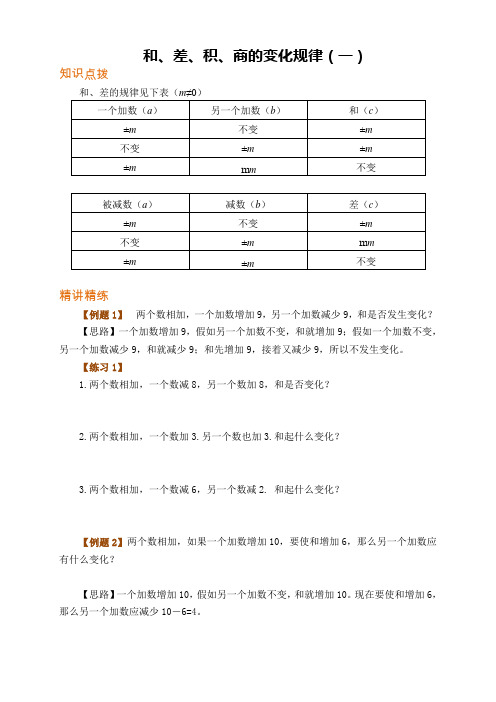
和、差、积、商的变化规律(一)知识点拨和、差的规律见下表(m≠0)精讲精练【例题1】两个数相加,一个加数增加9,另一个加数减少9,和是否发生变化?【思路】一个加数增加9,假如另一个加数不变,和就增加9;假如一个加数不变,另一个加数减少9,和就减少9;和先增加9,接着又减少9,所以不发生变化。
【练习1】1.两个数相加,一个数减8,另一个数加8,和是否变化?2.两个数相加,一个数加3.另一个数也加3.和起什么变化?3.两个数相加,一个数减6,另一个数减2. 和起什么变化?【例题2】两个数相加,如果一个加数增加10,要使和增加6,那么另一个加数应有什么变化?【思路】一个加数增加10,假如另一个加数不变,和就增加10。
现在要使和增加6,那么另一个加数应减少10-6=4。
【练习2】1.两个数相加,如果一个加数增加8,要使和增加15,另一个加数应有什么变化?2.两个数相加,如果一个加数增加8,要使和减少15,另一个加数应有什么变化?3.两个数相加,如果一个加数减少8,要使和减少8,另一个加数应有什么变化?【例题3】两数相减,如果被减数增加8,减数也增加8,差是否起变化?【思路】被减数增加8,假如减数不变,差就增加8;假如被减数不变,减数增加8,差就减少8。
两个数的差先增加8,接着又减少8,所以不起什么变化。
【练习3】1.两数相减,被减数减少6,减数也减少6,差是否起变化?2.两数相减,被减数增加12.减数减少12.差起什么变化?3.两数相减,被减数减少10,减数增加10,差起什么变化?【例题4】两数相乘,如果一个因数扩大8倍,另一个因数缩小2倍,积将有什么变化?【思路】如果一个因数扩大8倍,另一个因数不变,积将扩大8倍;如果一个因数不变,另一个因数缩小2倍,积将缩小2倍。
积先扩大8倍又缩小2倍,因此,积扩大了8÷2=4倍。
【练习4】1.两数相乘,如果一个因数缩小4倍,另一个因数扩大4倍,和是否起变化?2.两数相乘,如果一个因数扩大3倍,另一个因数缩小12倍,积将有什么变化?3.两数相乘,如果一个因数扩大3倍,另一个因数扩大6倍,积将有什么变化?【例题5】两数相除,如果被除数扩大4倍,除数缩小2倍,商将怎样变化?【思路】如果被除数扩大4倍,除数不变,商就扩大4倍;如果被除数不变,除数缩小2倍,商就扩大2倍。
四年级奥数和差积商的变化规律
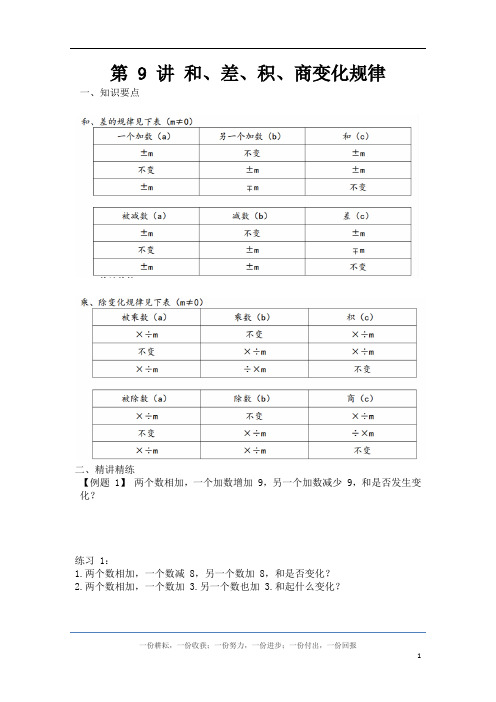
第 9 讲和、差、积、商变化规律一、知识要点二、精讲精练【例题 1】两个数相加,一个加数增加 9,另一个加数减少 9,和是否发生变化?练习 1:1.两个数相加,一个数减 8,另一个数加 8,和是否变化?2.两个数相加,一个数加3.另一个数也加 3.和起什么变化?【例题 2】两个数相加,如果一个加数增加 10,要使和增加 6,那么另一个加数应有什么变化?练习 2:1.两个数相加,如果一个加数增加 8,要使和增加 15,另一个加数应有什么变化?2.两个数相加,如果一个加数增加 8,要使和减少 15,另一个加数应有什么变化?【例题 3】两数相减,如果被减数增加 8,减数也增加 8,差是否起变化?练习 3:1.两数相减,被减数减少 6,减数也减少 6,差是否起变化?2.两数相减,被减数增加 12.减数减少 12.差起什么变化?【例题 4】两数相乘,如果一个因数扩大 8 倍,另一个因数缩小 2 倍,积将有什么变化?练习 4:1.两数相乘,如果一个因数缩小 4 倍,另一个因数扩大 4 倍,和是否起变化?2.两数相乘,如果一个因数扩大 3 倍,另一个因数缩小 12 倍,积将有什么变化?【例题 5】两数相除,如果被除数扩大 4 倍,除数缩小 2 倍,商将怎样变化?练习 5:1.两数相除,被除数扩大 30 倍,除数缩小 5 倍,商将怎样变化?2.两数相除,被除数缩小 12 倍,除数缩小 2 倍,商将怎样变化?【例题 6】两数相减,被减数减少 8,要使差减少 12.减数应有什么变化?练习6:1.两数相减,如果被减数增加 6,要使差增加 15,减数应有什么变化?2.两数相减,如果被减数增加 20,要使差减少 12.减数应有什么变化?【例题7】两个数相除,商是 8,余数是 20,如果被除数和除数同时扩大 10 倍,商是多少?余数是多少?练习7:1.两数相除,商是 6,余数是 30,如果被除数和除数同时扩大 10 倍,商是多少?余数是多少?2.两个数相除,商是 9,余数是 3。
和差积商的变化规律ppt课件

• ④如果除数缩小几倍,被除数不变,那么它们的 商反而扩大相同的倍数。
• 例 56÷4=14
•
56÷(4÷2)=28
• 它们的商14反而扩大2倍,变为28.
商 的变化规律
• ⑤如果被除数和除数都同时扩大相同的倍数,那 么它们的商不变。
• 例 150÷30=5
•
(150×2)÷(30×2)=5
• ⑥如果被除数和除数都同时缩小相同的倍数,那 么它们的商不变。
• 例 48÷4=12
•
(48×2)÷4=24
• ②如果被除数缩小几倍,除数不变,那么 它们的商也缩小相同的倍数。
• 例 48÷4=12
•
(48÷2)÷4=6
商的变化规律
• ③如果除数扩大几倍,被除数不变,那么它们的 商反而缩小相同的倍数。
• 例 56÷4=14
•
56÷(4×2)=7
• 它们的商14反而缩小2倍,变为7.
此课件下载可自行编辑修改,此课件供参考! 部分内容来源于网络,如有侵权请与我联系删除!感谢你的观看!
• 例 50×4=200
•
(50×2)×(4÷2)=200
• ④如果一个因数扩大a倍,另一个因数扩大b倍, 那么它们的积就扩大a×b倍。
• 例 50×2=100
• (50×4)×(2×5)=2000
• 它们的积扩大4×5=20倍。
商的变化规律
• ①如果被除数扩大几倍,除数不变,那么 它们的商也扩大相同的倍数。
Байду номын сангаас
• 例 150 ÷30=5
•
(150÷2)÷(30 ÷ 2)=5
• 被除数150和除数30都缩小2倍,它们的商不变, 仍是5.
四年级。积和商的变化规律

四年级。
积和商的变化规律第1讲:计算与规律本讲的研究目标是掌握乘法和除法的变化规律,以及快速确定积和商的位数。
一、积的变化规律1.两个数相乘,如果一个因数扩大或缩小若干倍(除非为0),那么积也会扩大或缩小相同的倍数。
2.两个数相乘,如果一个因数乘(或除以)一个数(除非为0),而另一个因数同时乘(或除以)相同的数,它们的积不变。
判断题:1.两个非零因数相乘,一个因数乘2,另一个因数除以2,积不变。
(错误)2.如果让“480×52”的第一因数除以5,第二个因数不变,则积不变。
(正确)3.两个非零数相乘,把这两个数同时扩大到它们原来的10倍,积不变。
(正确)4.在一个乘法算式中,要使积不变,一个乘数扩大10倍,另一个乘数扩大到原来的100倍。
(正确)5.几个数相乘,改变它们原来的运算顺序,它们的积不变。
(正确)6.两个非零数相乘,一个乘数扩大10倍,另一个乘数缩小5倍,积扩大到原来的50倍。
7.两个非零数相乘,一个乘数扩大3倍,另一个乘数缩小12倍,积缩小到原来的1/4.二、商的变化规律1.如果没有余数,则在除法算式中,被除数不变,除数乘以(或除以)几(除非为0),商反而要除以(或乘以)相同的数。
除数不变,被除数乘以(或除以)几(除非为0),商也要乘以(或除以)相同的数。
2.如果有余数,则在有余数的除法中,被除数和除数都缩小(或都扩大)相同的倍数(除非为0),商不变,但余数也随着缩小(或扩大)相同的倍数。
举例:已知A÷B=30,如果A除以6,B不变,则商是5.判断题:1.320÷40的结果与算式(320×5)÷(40×2)的结果相等。
(正确)2.如果a÷b=8······5,如果a和b都乘100,那么商是800,余数是500.(错误)1.两个数相乘,一个因数扩大3倍,另一个因数扩大4倍,那么积会扩大12倍。
(尖子生培优)积的变化规律的实际应用-四年级数学思维拓展

专题 积的变化规律的实际应用一个因数不变,另一个因数乘或除以几(0除外),积也乘或除以几,这就是积的变化规律。
运用积的变化规律可以使计算简便,也可以解决生活中的实际问题。
1.因为能力巩固提升乘100,积是( );两个因数同时乘10,积是( )。
综合拔高拓展18.有一块长方形的草坪,宽6米,面积是120平方米。
将这块长方形草坪的宽增加到18米,长不变。
扩大后的草坪的面积是多少平方米?19.王伯伯有一个宽25米,面积是1250平方米的长方形蔬菜大棚。
(1)明年他想把大棚的长扩大到原来的2倍,宽不变,扩建后的大棚面积是多少平方米?(2)12月份王伯伯收了2400千克西红柿,他将这些西红柿每15千克装成一箱,整箱批发给商场,可以装多少箱?20.慢城农场有50行果树,每行棵数相等。
如果再栽同样的5行,就比原来多出了120棵。
慢城农场原来有果树多少棵?21.一个长方形公园占地12公顷,将这个长方形公园的长扩大到原来的3倍,宽不变,扩建后公园的面积是多少?22.一块长方形草坪,宽6米,面积是72平方米,现在长方形草坪的长不变,宽增加到30米,增加后的草坪面积是多少平方米?(要求应用积的变化规律解决问题)23.一个长方形污水处理池的面积是3200平方米,将这个污水处理池的长扩大为原来的3倍,宽扩大为原来的2倍。
扩建后污水处理池的面积是多少平方米?24.下面这块长方形绿地的宽要增加到32米,长不变。
扩大后的绿地面积是多少?25.一块长方形草坪的面积约为480平方米,现在对这块草坪进行扩建。
(1)方案一:只把长扩大为原来的3倍,宽不变,扩建后的草坪面积是多少平方米?(2)方案二:把长和宽都扩大为原来的3倍,扩建后的草坪面积是多少平方米?26.学校长方形运动场的面积是1250平方米,长是50米,如果把长增加到原来的3倍,宽不变,那么运动场的面积是多少平方米?比原来增加了多少平方米?27.已知两个因数的积是73.6,其中一个因数扩大到原来的6倍,另一个因数缩小到原来的,最后的积是多少?28.两个因数相乘的积是4.25,其中一个因数扩大到原数的100倍,另一个因数缩小为原数的,积是多少?29.一块宽是9米的草坪占地面积是360平方米。
和、差、积、商变化规律

(a≥b且a≥m,b>m)。
例如:
500-200=300→(500+100)-(200+100)=300,
500-200=300→(500-100)-(200-100)=300
积的变化规律:
积的变化规律
字母表示及举例
如果一个因数扩大到原来的几倍或缩小到原来的几分之一,另一个因数不变,那么它们的积也相应地扩大到
或(a÷n)÷b=c÷n
(a、c都是n的倍数)。
例如:
40÷5=8→ (40×5)÷5=8×5
或(40÷4)÷5=8÷4
如果被除数不变,除数扩大到原来的几倍或缩小到原来的几分之一,那么它们的商反而缩小到原来的几分之一或扩大到原来的几倍
用字母表示:
a÷b=c→ a÷(b×n)=c÷n
(a是b×n的倍数)
或a÷(b÷n)=c×n
(b是n的倍数)
例如:
120÷20=6→120÷(20×3)=6÷3
或120÷(20÷2)=6×2
商不变的性质:
在除法里,被除数和除数同时乘或除以相同的数(0除外),商不变。这个性质
通常被称为“商不变的性质”。
用字母表示:如果a÷b=c→ (a×n)÷(b×n)=c(n≠0),
减少)同一个数
字母表示:
a-b=c →(a+m)-b=c+m,
(a-m)-b=c-m(a≥m)。
例如:
100-60=40→(100+50) -60=40+50,
100-60=40→(100-10)-60=40-10
如果被减数不变,减数增加(或减
少)一个数,那么它们的差反而减
少(或增加)同一个数
小学奥数经典专题点拨 对称变换+和差积商的变化规律
和差积商的变化规律【和的变化规律】(1)如果一个加数增加(或减少)一个数,另一个加数不变,那么它们的和也增加(或减少)同一个数。
用字母表达就是如果a+b=c,那么(a+d)+b=c+d;(a-d)+b=c-d。
(2)如果一个加数增加一个数,另一个加数减少同一个数,那么它们的和不变。
用字母表达就是如果a+b=c,那么(a+d)+(b-d)=c。
【差的变化规律】(1)如果被减数增加(或减少)一个数,减数不变,那么,它们的差也增加(或减少)同一个数。
用字母表达,就是如果a-b=c,那么(a+d)-b=c+d,(a-d)-b=c-d。
(a>d+b)(2)如果减数增加(或减少)一个数,被减数不变,那么它们的差反而减少(或增加)同一个数。
用字母表达,就是如果a-b=c,那么a-(b+d)=c-d(a>b+d),a-(b-d)=c+d。
(3)如果被减数和减数都增加(或都减少)同一个数,那么,它们的差不变。
用字母表达,就是如果a-b=c,那么(a+d)-(b+d)=c,(a-d)-(b-d)=c。
【积的变化规律】(1)如果一个因数扩大(或缩小)若干倍,另一个因数不变,那么,它们的积也扩大(或缩小)同样的倍数。
用字母表达,就是如果a×b=c,那么(a×n)×b=c×n,(a÷n)×b=c÷n。
(2)如果一个因数扩大若干倍,另一个因数缩小同样的倍数,那么它们的积不变。
用字母表达,就是如果a×b=c,那么(a×n)×(b÷n)=c,或(a÷n)×(b×n)=c。
【商或余数的变化规律】(1)如果被除数扩大(或缩小)若干倍,除数不变,那么它们的商也扩大(或缩小)同样的倍数。
用字母表达,就是如果a÷b=q,那么(a×n)÷b=q×n,(a÷n)÷b=q÷n。
第四讲 “和差积商”的变化规律
第四讲“和差积商”的变化规律【专题导引】这一讲主要是培养学生的探索能力、合作交流能力,发展学生的推理能力。
本节课的教学重点是引导学生自己发现规律、概括规律、进而运用规律。
知识要点如下:【典型例题】【例1】两个数相加,一个加数增加8,另一个加数减少8,和是否发生变化?【思路导航】一个加数增加8,假如另一个加数不变,和就增加8;假如一个加数不变,另一个加数减少8,和就减少8;和先增加8,接着又减少8,所以不发生变化。
【试一试】1.两个数相加,一个数减6,另一个数减2.和起什么变化?2.两个数相加,如果一个加数减少8,要使和减少8,另一个加数应有什么变化?3.两个数相加,如果一个加数增加8,要使和增加15,另一个加数应有什么变化?【例2】两数相减,被减数减少8,要使差减少12.减数应有什么变化?【思路导航】被减数减少8,假如减数不变,差也减少8;现在要使差减少12.减数应增加12-8=4。
【试一试】1.两数相减,被减数增加12.减数增加12.差起什么变化?2.两数相减,被减数减少10,减数增加10,差起什么变化?3.两数相减,减数减少9,要使差增加16,被减数应有什么变化?【例3】两数相乘,如果一个因数乘3,另一个因数除以12,积将有什么变化?【思路导航】如果一个因数扩大3倍,另一个因数不变,积将扩大3倍;如果一个因数不变,另一个因数缩小12倍,积将缩小12倍。
积扩大3倍又缩小12倍,因此,积缩小了12÷3=4倍。
[试一试]1.两数相乘,如果一个因数缩小5倍,另一个因数扩大5倍,积是否起变化?2.两数相乘,积是36,如果一个因数扩大2倍,另一个因数缩小3倍,那么积是多少?3.两数相乘,如果一个因数扩大3倍,另一个因数缩小12倍,积将有什么变化?【例4】两数相除,商是6,余数是30,如果被除数和除数同时扩大10倍,商是多少?余数是多少?【思路导航】根据商不变的规律,被除数和除数同时扩大10倍,商不变,余数也扩大10倍,所以商是6,余数是30×10=300。
小学数学四则运算的变化规则(和差积商变化规律)
四则运算的变化规则一、加法的变化规则(1)加法公式:加数+ 加数= 和加数= 和—另一个加数(2)加法的变化规则有:(一)如果一个加数增加几,另一个加数不变,那么和也增加几。
例如:13+5=18(13+2)+5=18+2题型1小丽在做一道加法题,一个加数十位上的4看作了7,个位上的5看作了2,算得的和是87。
正确的和是多少?一个加数十位4——7,个位5——2 增加 72-45=27另一个加数不变正确的和增加27即正确的和+27=87 => 正确的和=87-27=60(二)如果一个加数减少几,另一个加数不变,那么和也减少几。
例如:28+16=44(28-12)+16=44-12题型1小强在计算加法时,把一个加数十位上的7错写成1,把个位上的8错写成0,所得的和是285。
正确的和是多少?一个加数十位7——1,个位8——0 减少 78-10=68另一个加数不变正确的和减少68即正确的和-68=285 => 正确的和=285+68=353题型2两个数相加,一个加数减少29,另一个加数不变,和将有什么变化?一个加数减少29另一个加数不变和减少29题型3两个数相加,和是100,一个加数减少48,另一个加数不变,现在和是多少?一个加数减少48另一个加数不变和减少48即现在的和=100-48=52(三)如果一个加数增加几,另一个加数减少同样的几,那么和不变。
例如:112+23=135(112+3)+(23-3)=135题型1:两个加数的和是378,其中一个加数增加245,另一个加数减少245,现在这两个加数的和是(378 )。
题型2:一个加数增加6,要使和保持不变,另一个加数应(减少6 )。
(四)如果一个加数增加几,另一个加数增加另一个几,那么和增加了(几+另一个几)。
例如:35+48=83(35+12)+(48+5)=83+(12+5)题型1:小明在计算加法时,把一个加数十位上的0错写成8,把另一个加数个位上的6错写成9,所得的和是532。
2019年四年级寒假数学思维训练(第7讲)和差及积商变化的规律
2019年四年级寒假数学思维训练姓名:第7讲和差及积商变化的规律在加减乘除四则运算中,有它的变化规律,其关键是要抓住四种运算的基本数量关系式。
在乘法运算中,一个乘数不变,另一个乘数乘或除以一个数,积也跟着乘或除以相同的数。
在除法运算中,被除数不变,除数乘或除以一个非0数,商反而除以或乘相同的数;除数不变,被除数乘或除以一个非0数,商跟着乘或除以相同的数。
典例1:(1)两个数相加,一个加数增加8,另一个加数减少8,和是否发生变化?(2)两个数相加,如果一个加数增加20,要使和增加25,那么另一个加数应有什么变化?(3)两个数相减,如果被减数增加10,减数也增加10,差是否有变化?典例2:(1)两数相乘,如果一个乘数乘4,另一个乘数除以2,积有什么变化?(2)两数相除,如果被除数乘8,除数除以2,商怎样变化?典例3:两个数相除,商是6,余数是10,如果被除数和除数同时乘10,商是多少?余数是多少?典例4:两数相乘,积是60,如果一个乘数乘3,另一个乘数除以2,那么积是多少?典例5:小亮在计算两个数相加时,把一个加数个位上的6错误地写成9,把另一个加数十位上的5错误地写成7,所得的和是1998,原来两个数相加的正确答案是多少?典例6:小明在做计算题时,由于粗心大意把被减数个位上的2错写成8,十位上的6错写成0,这样算的差是365,正确的差是多少?练习1、两个数相加,一个数减6,另一个数加6,和是否变化?2、两个数相加,如果一个加数增加18,要使和减少25,另一个加数应有什么变化?3、两个数相减,被减数减少18,减数增加18,差有什么变化?4、两个数相乘,如果一个乘数乘3,另一个乘数除以6,积有什么变化?5、两个数相除,被除数除以10,除数除以2,商怎样变化?6、两个数相除,除数乘6,要使商乘18,被除数应怎样变化?7、两个数相减,如果被减数增加18,要使差减少12,减数应有什么变化?8、两个数相减,减数减少6,要使差增加16,被减数应有什么变化?9、两个数相除,商是9,余数是3,如果被除数和除数同时乘100,商是多少?余数是多少?10、两个数相乘,积是60,如果一个乘数乘3,另一个乘数除以4,那么积是多少?11、小月在计算加法时,把一个加数十位上的1错写成8,把另一个加数个位错写成9.所得的和是132,正确的和是多少?12、小雷在计算加法时,把一个加数个位上的5错写成3,把另一个加数十位上的3错写成8,所得的和是750,正确的和是多少?13、小红在做题时,把被减数十位上的0错写成8,把减数个位上的8错写成3,这样算得的差是986,正确的差是多少?思考题:小刘在计算乘法时,把一个乘数的个位上数字8错当做3,得345,实际应该为420,这两个乘数应该为多少?。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
四年级上册数学思维拓展题:和差积商变化规律
和的变化规律:
如果一个加数增加(或减少)一个数(不为0),另一个加数不变,则它们的和也增加(或减少)同一个数。
如果一个加数增加一个数(不为0),另一个加数减少同一个数,和不变。
差的变化规律:
如果一个被减数增加(或减少)一个数(不为0),减数不变,则差增加(或减少)同一个数。
如果一个被减数和减数同时增加(或减少)一个数(不为0),差不变。
如果被减数不变,一个减数增加(或减少)一个数(不为0),差也减少(或增加)同一个数。
积的变化规律:
1.一个因数扩大(或缩小)若干倍,另一个因数不变,积也扩大(或缩小)相同的倍数。
2.一个因数扩大(或缩小)若干倍,而另一个因数缩小(或扩大)相同的倍数,它们的积不变。
3.一个因数乘以(或除以)a,另一个因数乘以(或除以)b,积就乘以(或除以)ab的积。
商的变化规律:
1.被除数扩大(或缩小)若干倍,除数不变,商也扩大(或缩小)同样的倍数。
2.被除数不变,除数扩大(或缩小)若干倍,商反而缩小(或扩大)相同的倍数。
3.被除数乘以a,除数除以b,商就乘以ab的积。
4.被除数除以a,除数乘以b,商就除以ab的积。
参考答案:
1、两个数相加,如果一个加数减少9,要使和增加9,另一个加数应该有什么变化?
解题思路:一个加数减少9,假设另一个加数不变,和就减少了9;题目要求和增加9,所以另一个加数应该增加9+9=18。
2、两个数相减,如果被减数减少10,减数也减少10,差是否有变化?解题思路:
被减数减少10,假设减数不变,差就减少10;假设被减数不变,减数减少10,和就增加10;差先减少10,再增加10,所以无变化。
3、被减数、减数、差相加得2076,差是减数的一半。
如果被减数不变,差增加42,减数应该变成多少?
解题思路:
减数与差的和即是被减数,2076里有2个被减数,被减数等于2076÷2=1038。
差是减数的一半,也就是说减数是差的2倍,差应该为1038÷(2+1)=346,减数为346×2=692。
被减数不变,差增加42,减数应减少42,所以减数应该变为692-42=650。
4、两数相乘,一个乘数扩大3倍,要使积扩大9倍,另一个乘数应该怎么变化?
解题思路:
一个乘数扩大3倍,假设另一个乘数不变,积就扩大3倍;要使积扩大9倍,另一个乘数应扩大9÷3=3倍。
5、两数相乘,积是100。
如果一个因数扩大6倍,另一个因数也扩大6倍,那么积是多少?
解题思路:
已知积是100,一个因数扩大6倍,假设另一个因数不变,积扩大6倍也就是100×6=600;另一个因数也扩大6倍,所以积再扩大6倍,也就是600×6=3600。
所以积是3600。
6、两个数相除,被除数扩大3倍,除数扩大15倍,商如何变化?解题思路:
被除数扩大3倍,假设除数不变,那么商扩大3倍;因为除数扩大15倍,所以商在扩大3倍之后缩小15倍,即商缩小至原来的3÷15=1/5。
7、两个数相除,商是5,余数是15。
如果被除数和除数同时扩大20倍,商是多少?余数是多少?
解题思路:
假设算式是95÷16=5……15,被除数扩大20倍是95×20=1900;除数扩大20倍是16×20=320,1900÷320=5……300。
被除数和除数同时扩大20倍,商没有变化,余数扩大20倍,所以商是5,余数是300。
