郑州市2011年高中毕业班第一次高质量预测(数学理)考试卷及问题详解
2011年高考数学试卷(含答案)
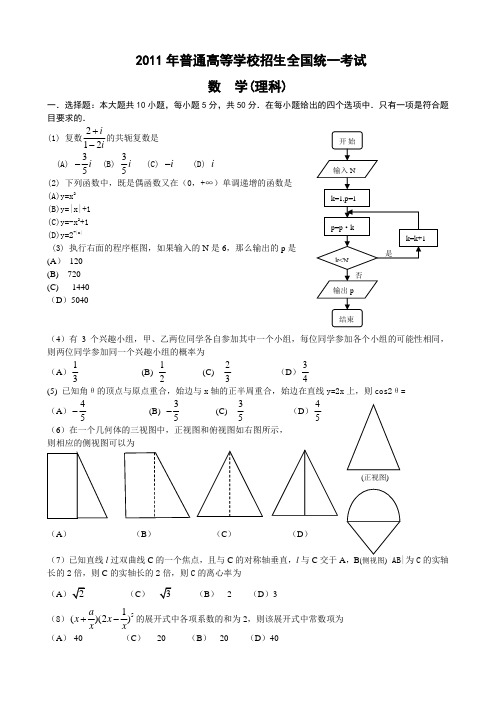
2011年普通高等学校招生全国统一考试数 学(理科)一.选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中.只有一项是符合题目要求的. (1) 复数212i i+-的共轭复数是(A) 35i -(B)35i (C) i - (D) i(2) 下列函数中,既是偶函数又在(0,+∞)单调递增的函数是(A)y=x 2(B)y=|x|+1 (C)y=-x 2+1 (D)y=2-|x|(3) 执行右面的程序框图,如果输入的N 是6,那么输出的p 是 (A ) 120 (B) 720 (C) 1440 (D )5040(4)有3个兴趣小组,甲、乙两位同学各自参加其中一个小组,每位同学参加各个小组的可能性相同,则两位同学参加同一个兴趣小组的概率为 (A )13(B)12(C)23(D )34(5) 已知角θ的顶点与原点重合,始边与x 轴的正半周重合,始边在直线y=2x 上,则cos2θ= (A )45-(B) 35-(C)35(D )45(6)在一个几何体的三视图中,正视图和俯视图如右图所示, 则相应的侧视图可以为(A ) (B ) (C ) (D )(7)已知直线l 过双曲线C 的一个焦点,且与C 的对称轴垂直,l 与C 交于为C 的实轴长的2倍,则C 的实轴长的2倍,则C 的离心率为 (A )(C )(B ) 2 (D )3(8)51()(2)a x x x x+-的展开式中各项系数的和为2,则该展开式中常数项为(A )-40 (C ) -20 (B ) 20 (D )40(9)由曲线y =y=x-2及y 轴所围成的图形的面积为(A )310(B )4 (C )163(D )6(10)已知a与b 均为单位向量,其夹角为θ,有下列四个命题 12:||10,3p a b πθ⎡⎫+>⇔∈⎪⎢⎣⎭ 22:||1,3p a b πθπ⎛⎤+>⇔∈ ⎥⎝⎦3:||10,3p a b πθ⎡⎫->⇔∈⎪⎢⎣⎭4:||1,3p a b πθπ⎛⎤->⇔∈ ⎥⎝⎦其中的真命题是(A )14,p p (B )13,p p (C )23,p p (D )24,p p (11)设函数()sin()cos()f x x x ωϕωϕ=+++(0,||)2πωϕ><的最小正周期为π,且()()f x f x -=,则(A )()f x 在(0,)2π单调递减 (B )()f x 在3(,)44ππ单调递减 (C )()f x 在(0,)2π单调递增 (D )()f x 在3(,)44ππ单调递增(12)函数11y x=-的图象与函数2sin (24)y x x π=-≤≤的图象所有交点的横坐标之和等于(A) 2 (B)4 (C)6 (D)8第Ⅱ卷包括必考题和选考题两部分.第(13)题~第(21)题为必考题,每个试题考生都必须作答,第(22)题~第(24)题为选考题,考生根据要求作答。
2011年新课标高考数学试题及答案(理科)

2011年新课标高考数学试题及答案(理科)Part IV Translation & WritingTranslationA. Translate the following sentences from Chinese intoEnglish.1) 约翰同时干许多事情。
我觉得他应当休息一下。
(work on, all at once, take a break)John works on many things all at once. I think he should takea break2) 杨教授说的话有着神奇的力量。
许多同学接受他的忠告,开始专注学业了。
(what, magical, advice, focus on)What Prof. Yang said has magical power. On his advice, many students began to focus on their schoolwork.3) 由于星期天晚上汤姆没有提示他将做何种选择,我无法弄清楚他会如何完成这项任务。
(clue, option, fgure out, accomplish) As Tom gave no clue Sunday night about which option he would choose, I can’t figure out how he will accomplish the task4) 我的父亲是极负责任的人。
虽然他总是很忙,但他设法每天都给家庭留出一些时间。
(responsibility, on the go, set aside) My father is a man of great responsibility. Though he is on the go all the time, he manages to set aside some time for the family every day.5) 这个项目的成功与否取决于我们如何确定轻重缓急。
2011年河南省中招数学试卷与答案

2011 年河南省初中学业水平暨高级中等学校招生考试试卷与答数学注意事项:1. 本试卷共 8 页,三大题,满分 120 分,考试时间 100 分钟请用蓝、黑色钢笔或圆珠笔直接答在试卷上 .2. 答卷前将密封线内的项目填写清楚 .参考公式:二次函数y ax 2 bx c( a 0) 图象的顶点坐标为 ( b , 4ac b 2) . 2a4a一、选择题(每小题3 分,共 18 分) 下列各小题均有四个答案,其中只有一个是正确的,将正确答案的代号字母填入题后括号内 .1. - 5 的绝对值 【 】 ( A ) 5 ( B )- 5 ( C ) 1( D )1 5 52. 如图,直线 a , b 被 c 所截, a ∥ b ,若∠ 1=35°,则∠ 2 的大小为 【 】( A ) 35° ( B )145° ( C ) 55° ( D ) 125°3. 下列各式计算正确的是 【】 ( A )( 1)0 (1 ) 13 (B ) 2 352( C )2a 24a 2 6a 4 ( D )(a 2 ) 3a 6 4.不等式 x+2> 0,x - 1≤2 的解集在数轴上表示正确的是【】5. 某农科所对甲、乙两种小麦各选用10 块面积相同的试验田进行种植试验,它们的平均亩产量分别是x甲=610千克, x乙=608千克,亩产量的方差分别是S2甲=29.6 ,S2乙 =2. 7.则关于两种小麦推广种植的合理决策是 【 】( A )甲的平均亩产量较高,应推广甲( B )甲、乙的平均亩产量相差不多,均可推广( C )甲的平均亩产量较高,且亩产量比较稳定,应推广甲( D )甲、乙的平均亩产量相差不多,但乙的亩产量比较稳定,应推广乙6. 如图,将一朵小花放置在平面直角坐标系中第三象限内的甲位置,先将它绕原点 O 旋转 180°到乙位置, 再将它向下平移 2 个单位长到丙位置, 则小花顶点 A 在丙位置中的对 应点 A ′的坐标为 【 】 来[源 学§科§网 Z §X §X §K]( A )( 3, 1) ( B )( 1, 3) ( C )( 3,- 1) (D )( 1, 1)二、填空题 (每小题 3 分,共 27 分) 7. 27 的立方根是 。
2011年高考新课标全国卷理科数学试题(附答案)

2011年普通高等学校招生全国统一考试(新课标全国卷)理科数学第Ⅰ卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的. (1)复数212ii +=- (A )35i - (B )35i (C )i - (D )i (2)下列函数中,既是偶函数又在(0,)+∞单调递增的函数是(A )3y x = (B )||1y x =+ (C )21y x =-+ (D )||2x y -= (3)执行右面的程序框图,如果输入的N 是6,那么输出的p 是(A )120 (B ) 720 (C ) 1440 (D ) 5040 (4)有3个兴趣小组,甲、乙两位同学各自参加其中一个小组,每位同学参加各个小组的可能性相同,则这两位同学参加同一个兴趣小组的概率为 (A )13 (B ) 12 (C )23 (D )34(5)已知角θ的顶点与原点重合,始边与x 轴的正半轴重合,终边在直线2y x =上,则cos 2θ= (A ) 45-(B )35- (C ) 35 (D )45(6)在一个几何体的三视图中,正视图与俯视图如右图所示,则相应的侧视图可以为俯视图正视图DCB A(7)已知直线l 过双曲线C 的一个焦点,且与C 的对称轴垂直,l 与C 交于A ,B 两点,||AB 为C 的实轴长的2倍,C 的离心率为(A (B (C ) 2 (D ) 3(8)51()(2)ax x x x+-的展开式中各项系数的和为2,则该展开式中常数项为(A )—40 (B )—20 (C )20 (D )40(9)曲线y =,直线2y x =-及y 轴所围成的图形的面积为(A )103 (B )4 (C ) 163(D ) 6 (10)已知a ,b 均为单位向量,其夹角为θ,有下列四个命题1:||1p +>a b ⇔2[0,)3πθ∈ 2:p ||+a b 1>⇔θ∈2(,]3ππ 3:||1p ->a b ⇔θ∈[0,)3π 4:||1p ->a b ⇔θ∈(,]3ππ其中真命题是(A ) 14,p p (B ) 13,p p (C ) 23,p p (D ) 24,p p (11)设函数()sin()cos()f x x x ωϕωϕ=+++(0,||)2πωϕ><的最小正周期为π,且()()f x f x -=则 (A )()y f x =在(0,)2π单调递减 (B )()y f x =在3(,)44ππ单调递减 (C )()y f x =在(0,)2π单调递增 (D )()y f x =在3(,)44ππ单调递增 (12)函数11y x=-的图象与函数2sin (24)y x x π=-剟的图象所有交点的橫坐标之和等于(A )2 (B )4 (C )6 (D )8第Ⅱ卷本卷包括必考题和选考题两部分.第13题-第21题为必考题,每个试题考生都必须做答.第22题-第24题为选考题,考生根据要求做答. 二、填空题:本大题共4小题,每小题5分.(13)若变量x ,y 满足约束条件32969x y x y ≤+≤⎧⎨≤-≤⎩,则2z x y =+的最小值是_________.(14)在平面直角坐标系xOy 中,椭圆C 的中心为原点,焦点12,F F 在x 轴上,离心率为.过点1F 的直线l 交C 于A ,B 两点,且2ABF ∆的周长为16,那么C 的方程为_________.(15)已知矩形ABCD 的顶点都在半径为4的球O 的球面上,且AB =6,BC =锥O ABCD -的体积为_____________.(16)ABC ∆中,60,B AC =︒=,则AB +2BC 的最大值为_________. 三、解答题:解答应写文字说明,证明过程或演算步骤. (17)(本小题满分12分)已知等比数列{}n a 的各项均为正数,且212326231,9a a a a a +==. (I )求数列{}n a 的通项公式.(II )设31323log log log n n b a a a =+++ ,求数列1{}nb 的前n 项和.(18)(本小题满分12分)如图,四棱锥P ABCD -中,底面ABCD 为平行四边形,60DAB ∠=︒,2AB AD =,PD ⊥底面ABCD(I )证明:PA BD ⊥;(II )若PD AD =,求二面角A PB C --的余弦值.(19)(本小题满分12分)某种产品的质量以其质量指标值衡量,质量指标越大表明质量越好,且质量指标值大于或等于102的产品为优质品.现用两种新配方(分别称为A 配方和B 配方)做试验,各生产了100件这种产品,并测量了每产品的质量指标值,得到时下面试验结果:A 配方的频数分布表B 配方的频数分布表(II )已知用B 配方生产的一种产品利润y (单位:元)与其质量指标值t 的关系式为2,942,941024,102t y t t -<⎧⎪=≤<⎨⎪≥⎩从用B 配方生产的产品中任取一件,其利润记为X (单位:元).求X 的分布列及数学期望.(以试验结果中质量指标值落入各组的频率作为一件产品的质量指标值落入相应组的概率).(20)(本小题满分12分)在平面直角坐标系xOy 中, 已知点(0,1)A -,B 点在直线3y =-上,M 点满足//MB OA ,MA AB MB BA =,M 点的轨迹为曲线C .(I )求C 的方程;(II )P 为C 上动点,l 为C 在点P 处的切线,求O 点到l 距离的最小值.(21)(本小题满分12分)已知函数ln ()1a x bf x x x=++,曲线()y f x =在点(1,(1))f 处的切线方程为 230x y +-=.(I )求,a b 的值;(II )如果当0x >,且1x ≠时,ln ()1x kf x x x>+-,求k 的取值范围.请考生在第(22)、(23)、(24)三题中任选一题做答,如果多做,则按所做的第一题记分.做答时用2B 铅笔在答题卡上把所选题目对应题号下方的方框涂黑. (22)(本小题满分10分)选修4-1:几何证明选讲如图,D ,E 分别为ABC ∆的边AB ,AC 上的点,且不与ABC ∆的顶点重合.已知AE 的长为m ,AC 的长为n ,AD ,AB 的长是关于x 的方程2140x x mn -+=的两个根.(I )证明:,,,C B D E 四点共圆;(II )若90A ∠=︒,且4,6,m n ==求,,,C B D E 所在圆的半径.(23)(本小题满分10分)选修4-4:坐标系与参数方程在直角坐标系xOy 中,曲线1C 的参数方程为2cos (22sin x y ααα=⎧⎨=+⎩为参数),M 为1C 上的动点,P 点满足2OP OM =,点P 的轨迹为曲线2C .(I )求2C 的方程;(II )在以O 为极点,x 轴的正半轴为极轴的极坐标系中,射线3πθ=与1C 的异于极点的交点为A ,与2C 的异于极点的交点为B ,求||AB .(24)(本小题满分10分)选修4-5:不等式选讲设函数()||3f x x a x =-+,其中0a >.(I )当1a =时,求不等式()32f x x ≥+的解集. (II )若不等式()0f x ≤的解集为{x|1}x ≤-,求a 的值.2011年普通高等学校招生全国统一考试(新课标全国卷)理科数学答案(1)C 【解析】212i i+-=(2)(12),5i i i ++=共轭复数为C . (2)B 【解析】3y x =为奇函数,21y x =-+在(0,)+∞上为减函数,||2x y -=在(0,)+∞上为减函数,故选B .(3)B 【解析】框图表示1n n a n a -=⋅,且11a =所求6a =720,选B .(4)A 【解析】每个同学参加的情形都有3种,故两个同学参加一组的情形有9种,而参加同一组的情形只有3种,所求的概率为P =3193=,选A . (5)B 【解析】由题知tan 2θ=,222222cos sin 1tan 3cos2cos sin 1tan 5θθθθθθθ--===-++,选B .(6)D 【解析】条件对应的几何体是由底面棱长为r 的正四棱锥沿底面对角线截出的部分与底面为半径为r 的圆锥沿对称轴截出的部分构成的。
河南省郑州市高中毕业年级第一次质量预测--数学(理科) 含参考答案

高中毕业年级第一次质量预测数学(理科) 参考答案一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.B2.D3.A4.C5.B6.B7.A8.C9.D 10.C 11.A 12.B.二、填空题:本大题共4题,每小题5分,共20,把答案填在答题卷的横线上13. 2-- 14. 13;- 16.4033. 三、解答题(本大题共6分,解答应写出文字说明、证明过程或演算步骤)17.(本小题满分12分)解: 2分所以3a =sin A ,sin 3b B =……6分(Ⅱ)8分 由余弦定理得2222cos c a b ab C =+-,即2224()3a b ab a b ab =+-=+-,又a b ab +=,所以2()340ab ab --=,解得4ab =或1ab =-(舍去).……10分所以11sin 422ABC S ab C ∆==⨯=12分 18. 解:(Ⅰ)证明:在BCA ∆中,由于∴222AB AC BC +=,故AB AC ⊥.……………2分 又SAB ABCD ⊥平面平面,SAB ABCD AB =平面平面,AC ABCD ⊂平面,SAB AC ∴⊥平面,……………4分 又AC SAC ⊂平面,故平面SAC ⊥平面SAB ……………6分(2)如图建立A xyz -空间直角坐标系,()0,0,0A ,()2,0,0,B0)(143)(24CS BC =-=-,,,,,, ()0,4,0,AC ……………8分 设平面SBC 的法向量()111,,n x y z =,00n BC n CS ⎧⋅=⎪⇒⎨⋅=⎪⎩令1111,2,3y x z ===则, n ⎛∴= ⎝⎭.…10分 设平面SCA 的法向量()222,,m x y z =,200m AC m CS ⎧⋅=⎪⇒⎨⋅=⎪⎪⎩⎩2x = (3,0,1∴=-m 219cos ,n mn m n m ⋅==⋅∴二面角--B SC A 的余弦值为……………12分 19. 解:(Ⅰ)由频率分布直方图可知,在抽取的100人中,“围棋迷”有25人,…1分 从而列联表如下:……………3分因为,所以没有理由认为“围棋迷”与性别有关. ……………6分(Ⅱ)由频率分布直方图知抽到“围棋迷”的频率为0. 25,将频率视为概率,即从观众中抽取一名“围棋迷”的概率为.由题意,从而的分布列为……………10分. ……………12分22⨯113,3X B ⎛⎫ ⎪⎝⎭X ()13==3=44E X np ⨯20.(Ⅰ)设动点),(y x N ,),,(00y x A 因为x AB ⊥轴于B ,所以)0,(0x B ,……1分 设圆M 的方程为222:,+=M x y r由题意得2r ==,所以圆M 的程为22:4M x y +=.……………3分由题意, 2AB NB =,所以00(0,)2(,)y x x y -=--,所以,即00,2,=⎧⎨=⎩x x y y 将(,2)A x y 代入圆22:4M x y +=,得动点N 的轨迹方程2214x y += ,……………5分 (Ⅱ)由题意设直线0,++=y m 设直线l 与椭圆交于221,4+=x y 1122(,),(,)P x y Q x y,联立方程22,44,⎧=-⎪⎨+=⎪⎩y m x y得2213440x m ++-=, 222192413(44)16(13)0m m m ∆=-⨯-=-+>,解得213m <,1,213x -±==, 又因为点O 到直线l 的距离2md =,122213PQ x x =-= (10)分1122OPQ m S ∆=⋅⋅=≤. OPQ ∆面积的最大值为1.……………12分21. (Ⅰ)令()()(1)ln(1)F x f x x mx x x =-=-+-,(0,1)x ∈,2分时,由于(0,1)x ∈,有 于是'()F x 在(0,1)x ∈上单调递增,从而'()'(0)0F x F >=,因此()F x 在(0,1)x ∈上单调递增,即()0F x >;……………3分 ②当0m ≥时,由于(0,1)x ∈,有 于是'()F x 在(0,1)x ∈上单调递减,从而'()'(0)0F x F <=, 因此()F x 在(0,1)x ∈上单调递减,即()(0)0F x F <=不符;……………4分,当0(0,]x x ∈时, ,于是'()F x 在0(0,]x x ∈上单调递减, 从而'()'(0)0F x F <=,因此()F x 在0(0,]x x ∈上单调递减, 即()(0)0F x F <=而且仅有(0)0F =不符. 综上可知,所求实数m 的取值范围是……………6分(Ⅱ)对要证明的不等式等价变形如下:对于任意的正整数n ,不等式251(1)n e n ++<恒成立,等价变形211(1)ln(1)0n ++-<相当于(28分 上单调递减,即()(0)0F x F <=;……………10分 211(1)ln(1)05n n n++-<成立; 令得证. ……………12分 22. (本小题满分10分)选修4—4,坐标系与参数方程解:(Ⅰ)消去参数ϕ可得1C 曲线2C 的圆心的直角坐标为)3,0(,∴2C 的直角坐标方程为1)3(22=-+y x .………………4分)2(设),sin ,cos 2(ϕϕM 则222)3(sin )cos 2(||-+=ϕϕMC 9sin 6sin cos 422+-+=ϕϕϕ 13sin 6sin 32+--=ϕϕ16)1(sin 32++-=ϕ.1sin 1≤≤-ϕ,∴,2||min 2=MC ,4||max 2=MC .根据题意可得,112||min =-=MN ,,514||max =+=MN即||MN 的取值范围是[]1,5..………………10分23. (本小题满分10分)选修4-5:不等式选讲解:(Ⅰ)因为,b a b a b x a x +=--≥-++, 所以()f x a b ≥+,当且仅当0))((<-+b x a x 时,等号成立,又0,0a b >>, 所以||a b a b +=+,所以()f x 的最小值为a b +,所以4a b +=..………………5分 (Ⅱ)由(1)知4,4a b b a +==-,分。
郑州市2011年高中毕业年级第一次质量预测数学(文科)试题(含答案)(word典藏版)

郑州市2011年高中毕业年级第一次质量预测数学试题(文科)第Ⅰ卷 (选择题 共60分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的) 1.下列四个命题中的真命题为A .Z x ∈∃0,3410<<xB .Z x ∈∃0,0150=+xC .R x ∈∀,012=-xD .R x ∈∀,022>++x x2.若向量、满足1||||==,且23)(=⋅+,则向量、的夹角为 A .030B .045C .060D .0903.若复数i R a iia ,(213∈-+为虚数单位)是纯虚数,则实数a 的值为 A .2-B .4C .6-D .64.已知集合}3,2{=A ,}06|{=-=mx x B ,若A B ⊆,则实数=mA .3B .2C .2或3D .0或2或35.设a 、b 是实数,且3=+b a ,则ba22+的最小值是A .6B .24C .62D .86.直线1+=kx y 与曲线b ax x y ++=3相切于点)3,1(A ,则=-b aA .4-B .1-C .3D .2-7.设α、β是两个不同的平面,a 、b 是两条不同的直线,给出下列四个命题,其中真命题是A .若α//a ,α//b ,则b a //B .若α//a ,β//b ,b a //,则βα//C .若α⊥a ,β⊥b ,b a ⊥,则βα⊥D .若a 、b 在平面α内的射影互相垂直,则b a ⊥ 8.已知等差数列}{n a 的前n 项和为n S ,且3184=S S ,则=168S S正视图 侧视图俯视图A .81 B .31 C .91 D .103 9.右图是一个空间几何体的三视图,如果直角三角形的直角 边长均为1,那么这个几何体的体积为A .1B .21 C .31 D .61 10.将函数)46sin(π+=x y 的图象上各点的横坐标伸长到原来的3倍,再向右平移8π个单位,得到的函数的一个对称中 心是A .)0,2(πB .)0,4(πC .)0,9(πD .)0,16(π11.已知双曲线的方程为)0,0(12222>>=-b a by a x ,双曲线一个焦点到一条渐近线的距离为c 35(c 为半焦距),则双曲线的离心率为 A .25 B .23 C .553 D .32 12.设a ,b ,c 分别是函数x x f x2log )21()(-=,x g 2)(=x x h x 21log 21()(-=的零点,则a ,b ,c 的大小关系是A .a c b <<B .c b a <<C .c a b <<D .a b c <<第Ⅱ卷(非选择题 共90分)二、填空题(本大题共4小题每小题5分,共20分.)13.阅读右图所示的程序框图,若运行该程序后输出的y 实数x 值为 . 14.已知)2,0(πα∈,53sin =α,计算αα2tan 2cos 1+的值为 .。
2011全国卷1理科数学试题及解析
2011年普通高等学校招生全国统一考试理科数学(全国卷Ⅰ)一、选择题:本大题共12小题,每小题5分,共60分、 1、复数212ii+-的共轭复数就是( ) A 、35i - B 、35i C 、i - D 、i 2、下列函数中,既就是偶函数又在+∞(0,)单调递增的函数就是( ) A 、3y x = B 、1y x =+ C 、21y x =-+ D 、2xy -=3、执行右面的程序框图,如果输入的N 就是6, 那么输出的p 就是( ) A 、120 B 、720 C 、1440 D 、50404、有3个兴趣小组,甲、乙两位同学各自参加其中一个小组,每位同学参加各个小组的可能性相同,则这两位同学参加同一个兴趣小组的概率为( ) A 、13 B 、12 C 、23 D 、345、已知角θ的顶点与原点重合,始边与x 轴的正半轴重合, 终边在直线2y x =上,则cos2θ=( ) A 、45-B 、35-C 、35D 、456、在一个几何体的三视图中,正视图与俯视图如右图所示, 则相应的俯视图可以为( )7、设直线L 过双曲线C 的一个焦点,且与C 的一条对称轴垂直,L 与C 交于 A ,B 两点,AB 为C 的实轴长的2倍,则C 的离心率为( )A B C 、2 D 、38、512a x x x x ⎛⎫⎛⎫+- ⎪⎪⎝⎭⎝⎭的展开式中各项系数的与为2,则该展开式中常数项为( )A 、-40B 、-20C 、20D 、409、由曲线y =,直线2y x =-及y 轴所围成的图形的面积为( )A 、103 B 、4 C 、163D 、6 10、已知a 与b 均为单位向量,其夹角为θ,有下列四个命题12:10,3P a b πθ⎡⎫+>⇔∈⎪⎢⎣⎭ 22:1,3P a b πθπ⎛⎤+>⇔∈⎥⎝⎦3:10,3P a b πθ⎡⎫->⇔∈⎪⎢⎣⎭ 4:1,3P a b πθπ⎛⎤->⇔∈ ⎥⎝⎦其中的真命题就是( )A 、14,P PB 、13,P PC 、23,P PD 、24,P P 11、设函数()sin()cos()(0,)2f x x x πωϕωϕωϕ=+++><的最小正周期为π,且()()f x f x -=,则( )A 、()f x 在0,2π⎛⎫ ⎪⎝⎭单调递减 B 、()f x 在3,44ππ⎛⎫⎪⎝⎭单调递减 C 、()f x 在0,2π⎛⎫ ⎪⎝⎭单调递增 D 、()f x 在3,44ππ⎛⎫⎪⎝⎭单调递增 12、函数11y x =-的图像与函数2sin (24)y x x π=-≤≤的图像所有交点的横坐标之与等于( ) A 、2 B 、 4 C 、6 D 、8二、填空题:本大题共4小题,每小题5分、13、若变量,x y 满足约束条件329,69,x y x y ≤+≤⎧⎨≤-≤⎩则2z x y =+的最小值为 、14、在平面直角坐标系xOy 中,椭圆C 的中心为原点,焦点12,F F 在x 轴上,离心率为2、过1F 的直线L 交C 于,A B 两点,且2ABF 的周长为16,那么C 的方程为 、15、已知矩形ABCD 的顶点都在半径为4的球O 的球面上,且6,AB BC ==,则棱锥O ABCD -的体积为 、16、在ABC 中,60,B AC ==则2AB BC +的最大值为 、三、解答题:解答应写出文字说明,证明过程或演算步骤、 17、(本小题满分12分)等比数列{}n a 的各项均为正数,且212326231,9.a a a a a +==(Ⅰ)求数列{}n a 的通项公式;(Ⅱ)设 31323log log ......log ,n n b a a a =+++求数列1n b ⎧⎫⎨⎬⎩⎭的前n 项与、18、(本小题满分12分)如图,四棱锥P-ABCD 中,底面ABCD 为平行四边形,∠DAB=60°,AB=2AD ,PD ⊥底面ABCD 、(Ⅰ)证明:P A ⊥BD ;(Ⅱ)若PD =AD ,求二面角A-PB-C 的余弦值、某种产品的质量以其质量指标值衡量,质量指标值越大表明质量越好,且质量指标值大于或等于102的产品为优质品,现用两种新配方(分别称为A配方与B配方)做试验,各生产了100件这种产品,并测量了每件产品的质量指标值,得到下面试验结果:(Ⅰ)分别估计用A配方,B配方生产的产品的优质品率;(Ⅱ)已知用B配方生成的一件产品的利润y(单位:元)与其质量指标值t的关系式为2,942,941024,102ty tt-<⎧⎪=≤<⎨⎪≥⎩, 从用B配方生产的产品中任取一件,其利润记为X(单位:元),求X的分布列及数学期望、(以试验结果中质量指标值落入各组的频率作为一件产品的质量指标值落入相应组的概率)在平面直角坐标系xOy 中,已知点A(0,-1),B 点在直线y = -3上,M 点满足//MB OA , MA AB MB BA ⋅=⋅,M 点的轨迹为曲线C 、 (Ⅰ)求C 的方程;(Ⅱ)P 为C 上的动点,l 为C 在P 点处得切线,求O 点到l 距离的最小值、21、(本小题满分12分)已知函数ln ()1a x bf x x x=++,曲线()y f x =在点(1,(1))f 处的切线方程为230x y +-=、 (Ⅰ)求a 、b 的值;(Ⅱ)如果当0x >,且1x ≠时,ln ()1x kf x x x>+-,求k 的取值范围、请考生在第22、23、24题中任选一题做答,如果多做,则按所做的第一题记分、做答时请写清题号、 22、(本小题满分10分)选修4-1:几何证明选讲如图,D ,E 分别为ABC ∆的边AB ,AC 上的点,且不与ABC ∆的顶点重合、已知AE 的长为n ,AD ,AB 的长就是关于x 的方程2140x x mn -+=的两个根、(Ⅰ)证明:C ,B ,D ,E 四点共圆;(Ⅱ)若90A ∠=︒,且4,6m n ==,求C ,B ,D ,E 所在圆的半径、23、(本小题满分10分)选修4-4:坐标系与参数方程在直角坐标系xOy 中,曲线C 1的参数方程为2cos 22sin x y αα=⎧⎨=+⎩(α为参数)M 就是C 1上的动点,P 点满足2OP OM =,P 点的轨迹为曲线C 2 (Ⅰ)求C 2的方程(Ⅱ)在以O 为极点,x 轴的正半轴为极轴的极坐标系中,射线3πθ=与C 1的异于极点的交点为A ,与C 2的异于极点的交点为B ,求AB 、24、(本小题满分10分)选修4-5:不等式选讲设函数()3f x x a x =-+,其中0a >、 (Ⅰ)当1a =时,求不等式()32f x x ≥+的解集; (Ⅱ)若不等式()0f x ≤的解集为{}|1x x ≤- ,求a 的值、2011年普通高等学校招生全国统一考试理科数学试卷参考答案一、选择题(1)C (2)B (3)B (4)A (5)B (6)D (7)B (8)D (9)C (10)A (11)A (12)D 二、填空题(13)-6 (14)221168x y +=(15)三、解答题 (17)解:(Ⅰ)设数列{a n }的公比为q,由23269a a a =得32349a a =所以219q =。
河南省郑州市2011年高中毕业班第一次质量预测英语
河南省郑州市2011年高中毕业年级第一次质量预测英语试题本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
考试时间120分钟,满分150分(听力算作参考分)。
考生应该首先阅读答题卷上的文字信息,然后在答题卷上作答,在试题卷上作答无效。
第Ⅰ卷选择题(共115分)第一部分:听力(共两阳,满分30分)第一节(共5小题;每小题l.5分,满分7.5分)听下面五段对话。
每段对话后有一小题,从题中所给的A、B、C三个选项中选出最佳选项,并在答题卡上将该项涂黑。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1.What color does the man prefer?A.Brown. B.Black. C.Blue.2.Who will leave Shanghai soon?A.Mary. B.David. C.Susan.3.Why did the woman thank the man?A.He lent her some money.B.He gave her five pounds.C.He returned her lost money.4.Where does the conversation most probably take place?A.At a dinner table. B.In a hotel. C.In the street.5.What does the man say about Kate?A.Many people have always liked Kate.B.Kate wasn’t expecting so many people at her party.C.A group of friends arranged a surprising party for Kate.第二节(共15小题;每小题1.5分,满分22.5分)听下面5段对话或独白。
2011年河南省五市高中毕业班第一次联考高三理科数学试题
2011年河南省五市高中毕业班第一次联考高三理科数学试题本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
考生作答时,将答案答在答题卡上,在本试卷上答题无效。
注意事项:1.答题前,考生务必将自己的姓名、准考证号等考生信息填写在答题卡上,并用2B 铅笔将准考证号在相应位置填涂。
2.选择题答案使用2B 铅笔填涂,如需改动,用橡皮擦干净后,再选涂其他答案标号;非选择题答案使用0.5毫米的黑色墨水签字笔书写,字体工整、笔迹清楚。
3.请按照题号在各题的答题区域(黑色线框)内作答,超出答题区域书写的答案无效。
4.保持卡面清洁,不折叠,不破损。
参考公式:球的表面积 S =4πR 2第Ⅰ卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的. 1.已知集合M ={-1,0,1},N =x ∈M},则M ∩N =(A ){1} (B ){0,1} (C ){-1,0,1} (D )φ2.复数Z =1i i -的模是(A(B )2 (C )2i (D )1+i 3.给出两个命题p :|x |=x 的充要条件是x 为正实数;q :命题“∃x 0∈R ,20x -x 0>0”的否定是“∀∈R ,2x -x ≤0”.则下列命题是假命题的是(A )p 且q (B )p 或q (C )⌝p 且q (D )⌝p 或q 4.程序框图如下:如果上述程序运行的结果为S =132,那么判断框中应填入(A )k ≤11? (B )k ≥11? (C )k ≤10? (D )k ≥10?5.曲线y =sinx 与直线y =2πx 所围成的平面图形的面积是(A )42π+ (B )44π- (C )42π- (D )22π-6.若对任意m ∈R ,直线x +y +m =0都不是曲线f (x )=133x -ax 的切线,则实数a 的取值范围是(A )a ≥1 (B )a>1 (C )a ≤1 (D )a<17.为了考察两个变量x 和y 之间的线性相关性,甲、乙两同学各自独立地做100次和150次试验,并且利用线性回归方法,求得回归直线分别为t 1和t 2,已知两个人在试验中发现对变量x 的观测值的平均值都是s ,对变量y 的观测值的平均值都是t ,那么下列说法正确的是(A )t 1和t 2有交点(s ,t ) (B )t 1和t 2相交,但交点不是(s ,t ) (C )t 1和t 2必定重合 (D )t 1和t 2必定不重合8.已知函数f (x )=2sin (2x -4π)·sin (2x +4π)(x ∈R ),下面结论错误的是(A )函数f (x )的最小正周期为2π (B )函数f (x )在区间[0,2π]上是增函数(C )函数f (x )的图像关于直线x =0对称 (D )函数f (x )是奇函数9.若一个正三棱柱存在外接球与内切球,则它的外接球与内切球表面积之比为 (A )2 :1 (B )3 :1 (C )4 :1 (D )5 :110.设函数f (x )=1xxa a +(a>0,且a ≠1),[m]表示不超过实数m 的最大整数,则实数[f (x )-12]+[f (-x )-12]的值域是(A ) [-1,1] (B )[0,1] (C ){-1,0} (D ){-1,1}11.直线L 经过双曲线2221x a b 2y -=(a>0,b>0)右焦点F 与其一条渐近线垂直且垂足为A ,与另一条渐近线交于B 点,AF =12FB ,则双曲线的离心率为 (A) (B) (C(D )212.设f (x )是定义在R 上的偶函数,对于任意的x ∈R ,都有f (x -2)=f (2+x ),且当x ∈[-2,0]时,f (x )=12x()-1,若在区间(-2,6]内关于x 的方程f (x )-log (2)a x +=0恰有3个不同的实数解,则a 的取值范围是(A )(1,2) (B )(2,+∞) (C )(1) (D ),2)第Ⅱ卷二、填空题:本大题共4小题,每小题5分,共20分.13.△ABC 的三个内角A 、B 、C 所对边长分别为a 、b 、c ,设向量m =(a +b ,sinC ),n +c ,sinB -sinA ),若m ∥n ,则角B 的大小为_____________.14.已知抛物线2y =2px (p>0)的焦点为F ,过F 作倾斜角为45°的直线与抛物线交于A 、B 两点,若线段AB的长为16,则p 的值等于__________.15.如右图所示,一个空间几何体的主视图和左视图都是边长为1的正方形,俯视图是一个直径为1的圆, 用一 段铁丝从几何体的A 处缠绕几何体两周到达B 处,则 铁丝的最短长度为________________.16.在区间[0,1]上随机取两个数m ,n ,则关于函数f (x )=343mx -nx +1在[1,+∞)上为增函数的概率为______.三、解答题:本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤. 17.(本小题满分12分) 设数列{n a }的前n 项和为nS ,已知1a =1,1n S +=4na +1.(Ⅰ)设nb =1n a +-2na ,证明数列{nb }是等比数列;(Ⅱ)求数列{na }的通项公式和前n 项和.18.(本小题满分12分)如图,已知四棱锥的P -ABCD ,PA ⊥底面 ABCD ,AB ∥CD ,AB ⊥AD 且AP =AB =3,AD ,∠ABC =60°.(Ⅰ)点F 为线段PB 上一点,PF :FB =2,求证:CF ∥面ADP ;(Ⅱ)求二面角F -AC -B 的余弦值. 19.(本小题满分12分)为了了解大学生在购买饮料时看营养说明是否与性别有关,对某班50人进行问卷调查得到2×2列联表。
2011年高考数学及参考答案(河南卷)
2011理科数学第I 卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
(1)复数212ii+-的共轭复数是 (A )35i - (B )35i (C )i - (D )i(2)下列函数中,既是偶函数又在+∞(0,)单调递增的函数是 (A )3y x = (B) 1y x =+ (C )21y x =-+ (D) 2xy -=(3)执行右面的程序框图,如果输入的N 是6,那么输出的p 是(A )120 (B )720 (C )1440 (D )5040(4)有3个兴趣小组,甲、乙两位同学各自参加其中一个小组,每位同学参加各个小组的可能性相同,则这两位同学参加同一个兴趣小组的概率为(A )13 (B )12 (C )23 (D )34(5)已知角θ的顶点与原点重合,始边与x 轴的正半轴重合,终边在直线2y x =上,则cos2θ=(A )45- (B )35- (C )35 (D )45(6)在一个几何体的三视图中,正视图和俯视图如右图所示,则相应的俯视图可以为(7)设直线L 过双曲线C 的一个焦点,且与C 的一条对称轴垂直,L 与C 交于A ,B 两点,AB 为C 的实轴长的2倍,则C 的离心率为(A 2 (B 3 (C )2 (D )3(8)512a x x x x ⎛⎫⎛⎫+- ⎪⎪⎝⎭⎝⎭的展开式中各项系数的和为2,则该展开式中常数项为(A )-40 (B )-20 (C )20 (D )40 (9)由曲线y x =2y x =-及y 轴所围成的图形的面积为(A )103 (B )4 (C )163(D )6 (10)已知a 与b 均为单位向量,其夹角为θ,有下列四个命题12:10,3P a b πθ⎡⎫+>⇔∈⎪⎢⎣⎭ 22:1,3P a b πθπ⎛⎤+>⇔∈⎥⎝⎦3:10,3P a b πθ⎡⎫->⇔∈⎪⎢⎣⎭ 4:1,3P a b πθπ⎛⎤->⇔∈ ⎥⎝⎦其中的真命题是(A )14,P P (B )13,P P (C )23,P P (D )24,P P (11)设函数()sin()cos()(0,)2f x x x πωϕωϕωϕ=+++><的最小正周期为π,且()()f x f x -=,则(A )()f x 在0,2π⎛⎫ ⎪⎝⎭单调递减 (B )()f x 在3,44ππ⎛⎫⎪⎝⎭单调递减 (C )()f x 在0,2π⎛⎫⎪⎝⎭单调递增(D )()f x 在3,44ππ⎛⎫⎪⎝⎭单调递增 (12)函数11y x =-的图像与函数2sin (24)y x x π=-≤≤的图像所有交点的横坐标之和等于(A )2 (B) 4 (C) 6 (D)8第Ⅱ卷本卷包括必考题和选考题两部分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
22.(本小题满分10分)选修4-1:几何证明选讲
如图,AB是⊙O的直径,C、F为⊙O上的点,
CA是∠BAF的角平分线,过点C作CD⊥AF交
AF的延长线于D点,CM⊥AB,垂足为点M.
(Ⅰ)求证:DC是⊙O的切线;
(Ⅱ)求证:AM·MB=DF·DA.
气象观测仪器的垂直弹射高度:在C处进行该仪
器的垂直弹射,观测点A、B两地相距100米,
∠BAC=60°,在A地听到弹射声音的时间比B
地晚 秒.A地测得该仪器在C处时的俯角为
15°,A地测得最高点H时的仰角为30°,求该
仪器的垂直弹射高度CH.
(声音的传播速度为340米/秒)
19.(本小题满分12分)
23.(本小题满分10分)选修4-5:不等式选讲
设函数f(x)=|x-1|+|x-a|.(a<0)
(Ⅰ)若a=-1,解不等式f(x)≥6;
(Ⅱ)如果 ∈R,f( )<2,求a的取值围.
理科数学 参考答案
一、选择题DCDCA ACDBA BB
二、填空题
13. ;14. ;15. ;16. .
三、解答题
17.解:⑴分层抽样中,每个个体被抽到的概率均为 ,…………2分
故甲同学被抽到的概率 .………………………………………3分
⑵由题意
.
…………………………4分
故估计该中学达到优秀线的人数
(人). 6分
⑶
频率分布直方图.………………3分
该学校本次考试数学平均分
估计该学校本次考试的数学平均分为90分.………12分
所以 面 .……………4分
⑵解:由⑴得 两两互相垂直,
故可以以 点为坐标原点,建立如图空间直角坐标系 ,则
.
……………………………………6分
,
.
即异面直线 与 所成的角的余弦值为 .……………………8分
⑶解:若 为线段 上的一点,且 (点 与点 重合时不合题意),
则 .………………………………9分
设平面 和平面 的法向量分别为 ,
A.3 B.2 C.2或3 D.0或2或3
4.若 的展开式中的第5项为常数,则n=
A.8 B.10 C.12 D.15
5.已知a∈R,则“a>2”是“ >2a”成立的
A.充分不必要条件B.必要不充分条件
C.充要条件D.既不充分也不必要条件
6.直线y=kx+1与曲线y= +ax+b相切于点A(1,3),则a-b=
由题意,直线 的斜率不可能为 ,故可设 ,
由 消 得: .
所以
…………………………………………………………7分
,……9分
由 ,解得 ,即 .……10分
因为 是 的中点,
所以 , .
故直线 的斜率 .……12分
21.⑴解:由题意,函数 的定义域为 ,
由函数 是增函数知 对 恒成立,……3分
令 ,则 ,
市2011年高中毕业年级第一次质量预测
理科数学
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。第Ⅰ卷1至2页,第Ⅱ卷3至4页,考试时间120分钟,满分150分。考生应首先阅读答题卷上的文字信息,然后在答题卷上作答,在试题卷上作答无效。
第Ⅰ卷
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
A. B. C. D.
9.右图是一个空间几何体的三视图,如果直角三角形的直
角边长均为1,那么这个几何体的外接球的表面积为
A.πB.3π
C.4πD.12π
10.将函数y=sin(6x+ )的图象上各点的横坐标伸长
到原来的3倍,再向右平移 个单位,得到的函数的
一个对称中心是
A.( ,0)B.( ,0)
C.( ,0)D.( ,0)
11.已知双曲线的方程为 (a>b>0),它的一个顶点到一条渐近线的距离为 c(c为双曲线的半焦距长),则双曲线的离心率为
A. 或 B. C. D.
12.若定义在R上的偶函数f(x)满足f(x+2)=f(x),且当x∈[0,1]时,f(x)=x,则函数y=f(x)- |x|的零点个数是
A.多于4个B.4个C.3个D.2个
三、解答题(共70分)
17.(本小题满分12分)
某中学共有1000名学生参加了该地区高三第一次质量检测的数学考试,数学成绩如下表所示:
数学成绩分组
[0,30)
[30,60)
[60,90)
[90,120)
[120,150]
人数
60
90
300
x
160
(Ⅰ)为了了解同学们前段复习的得失,以便
制定下阶段的复习计划,学校将采用分
第Ⅱ卷
本卷包括必考题和选考题两部分,第(13)题~第(21)题为必考题,每个试题考生都必须做答,第(22)题~第(23)题为选考题,考试根据要求做答.
二、填空题:本大题共4小题,每小题5分,共20分.
13.阅读右图所示的程序框图,若运行该程序后
输出的y值为 ,则输入的实数x值为
_________________。
注意到 ,所以 ,
即 ,所以 为所求.………6分
⑵证明:由⑴知, 是增函数,
所以 ,即 ,对 恒成立.…………8分
注意到 ,所以 .…………10分
即 成立.………………………………12分
22. ⑴证明:连接 ,
,
又 .
.
,即 是⊙O的切线.…………5分
⑵证明:因为CA是∠BAF的角平分线,
,所以 .
层抽样的方法抽取100名同学进行问卷
调查,甲同学在本次测试中数学成绩为
95分,求他被抽中的概率;
(Ⅱ)已知本次数学成绩的优秀线为110分,
试根据所提供数据估计该中学达到优
秀线的人数;
(Ⅲ)作出频率分布直方图,并估计该学校本
次考试的数学平均分.
18.(本小题满分12分)
某气象仪器研究所按以下方案测试一种“弹射型”
1.若复数 (a∈R,i为虚数单位)是纯虚数,则实数a的值为
A.-2 B.4 C.-6 D.6
2.若向量a、b满足|a|=|b|=1,且(a+3b)·(a+5b)=20,则向量a、b的夹角为
A.30°B.45°C.60°D.90°
3.已知集合A={2,3},B={x|mx-6=0},若B A,则实数m=
18.解:由题意,设 ,则 ,
在△ ,由余弦定理: ,3分
即 ,解之得 .…………5分
在△ 中, ,
由正弦定理: .………………………………8分
所以 ………11分
答:该仪器的垂直弹射高度 米.…………………………12分
19.⑴证明:因为面 面 , 交线 ,
(Ⅰ)求轨迹E的方程;
(Ⅱ)过点P(1,0)的直线l交轨迹E于两个不同的点A、B,△AOB(O是坐标原点)的面积S∈( , ),若弦AB的中点为R,求直线OR斜率的取值围.
21.(本小题满分12分)
已知函数f(x)= -lnx(p>0)是增函数.
(Ⅰ)数p的取值围;
(Ⅱ)设数列{ }的通项公式为 = ,前n项和为 ,求证: ≥2ln(n+1).
由⑴知 ,又 ,
所以AM·MB=DF·DA.……………………10分
23.解:(Ⅰ)当 时, ,
解之得 .
所以原不等式的解集为 .……………………5分
(Ⅱ) , 函数 的最小值小于2,
因为 ,故 的最小值为 .由
解得 为所求.…………………………………………10分
A.-4 B.-1 C.3 D.-2
7.设α、β是两个不同的平面,a、b是两条不同的直线,给出下列四个命题,其中真命题是
A.若a∥ ,b∥ ,则a∥b
B.若a∥ ,b∥ ,a∥b,则 ∥
C.若a⊥ ,b⊥ ,a⊥b,则 ⊥
D.若a、b在平面 的射影互相垂直,则a⊥b
8.已知等差数列{ }的前n项和为 ,且 = ,则 =
由 得,
即
所以 为平面 的一个法向量,
同理可求得 为平面 的一个法向量.…………11分
当 ,即 时平面 平面 ,
故存在这样的点 ,此时 .………………………………12分
20.⑴解:由题意 ,
所以轨迹 是以 为焦点,长轴长为 的椭圆 ,…………2分
即轨迹 的方程为 .………………………………4分
⑵解:记 ,
如图,正方形ADEF和等腰梯形ABCD垂直,
已知BC=2AD=4,∠ABC=60°,BF⊥AC.
(Ⅰ)求证:AC⊥面ABF;
(Ⅱ)求异面直线BE与AC所成的角的余弦
值;
(Ⅲ)在线段BE上是否存在一点P,使得平
面PAC⊥平面BCEF?若存在,求出
的值,若不存在,请说明理由.
20.(本小题满分12分)
已知圆C: ,点A( ,0),Q是圆上一动点,AQ的垂直平分线交CQ于点M,设点M的轨迹为E.
14.已知tanα=2,计算 +tan2 的值
为_____________________.
15.若不等式组 表示的平面区域
为M,不等式y≥ 所表示的平面区域为N,
现随机向区域M抛一粒豆子,则豆子落
在区域N的概率为_______________.
16.已知抛物线 =4x,焦点为F,△ABC三个顶点均在抛物线上,若 + + = ,则|FA|+|FB|+|FC|=______________.
