光连续通过多个球面折射成像的研究
光在球面上的折射

主光轴:球面顶点 C 与 球心 O 连线为主光轴.
近轴光线:在主光轴附近与
主光轴的夹角很小的光线,称
为近轴光线,或傍轴光线.
2
如图,在 AS1O 中,根
据正弦定理应有
S1O sin i
S1 A sin
同样,在 OAS 2中,根据
正弦定理应有
S2 A sin
S2O sin r
以上两式相乘,考虑到折射定律,可得
b.推导公式时使用符号法则,应用公式时必须遵守 符号法则.
5
(2)同时适用于凸、凹球面折射,光线左、右入 射均可.
(3)l1、l
、R
2
均可正可负,由符号法则决定,n1 为入
射光束所在空间折射率,n 2 为折射光束所在空间折射
率.
三、高斯公式
第二主焦点:平行于主轴的入射光线折射后和主轴
相交的位置称为球面的第二主焦点,用 F2表示;第二 主焦点到顶点 C 的距离为第二主焦距,用 f2表示.
则,单心性被破坏,出现像差,不能成像,此时光束
也称为像散光束.
1
实像:自物点发出的单心光束经光学系统后仍保持
为单心光束,且光束的心有实际光线通过,那么这个 心叫实像.
虚像:自物点发出的单心光束经光学系统后仍保持 为单心光束,其光线反向延长线的交点与该单心光束 的心重合,那么这个顶点叫虚像.
二、球面折射公式
例1如图表示一根折射率为 1.50 的玻璃棒,其一端被磨成半径 为20.0mm 的半球面.若将它先 后放在折射率为1.00 的空气中和 折射率为1.33的水中,求在这两 种情况下在棒轴上距离顶点80.0mm 处的物点的像距和 像的横 向放大率.
10
解:(1)空气中的情形.这时 n1 1.00 ,l1 80.0mm ,
光的反射与成像

光的反射与成像光的反射与成像是光学中的重要概念,它涉及到光的传播规律以及光线在不同介质中的行为。
通过对光的反射与成像的研究,我们可以深入了解光的本质以及它在现实生活中的应用。
本文将从光的传播规律、光的反射及成像原理等几个方面进行探讨。
一、光的传播规律光的传播遵循直线传播的规律,即光线在均匀介质中沿直线传播。
这一规律可由光的粒子性质解释,光通过介质之间的传播路径是最短路径,因此光线呈直线传播。
二、光的反射光线遇到介质的界面时,部分光线会从一种介质射向另一种介质,这一现象称为光的反射。
光的反射满足入射角等于反射角的规律,即入射角(θ1)等于反射角(θ2)。
光的反射有以下几个特点:1. 入射光线、反射光线和法线在同一平面上。
2. 入射角和反射角的大小相等。
3. 反射光线的方向与入射光线的方向相反。
三、光的成像光的成像是指光线经过反射或折射后,聚焦在特定位置形成图像的现象。
光的成像原理主要包括平面镜和球面镜成像原理。
1. 平面镜成像原理平面镜是一种以平面为反射界面的镜子,它的成像特点如下:a. 想象入射光线和反射光线以及法线的关系。
b. 入射光线、反射光线和法线在同一平面上。
c. 入射光线与反射光线的角度相等。
2. 球面镜成像原理球面镜是一种以球面为反射界面的镜子,根据球面镜的形状和位置不同,成像特点有所不同:a. 凸面镜成像特点:- 入射光线平行于主轴,反射后经过焦点。
- 入射光线经过顶点,反射后平行于主轴。
- 入射光线经过焦点,反射后成为平行光线。
b. 凹面镜成像特点:- 入射光线平行于主轴,反射后经过焦点。
- 入射光线经过焦点,反射后成为平行光线。
- 入射光线经过顶点,反射后平行于主轴。
四、光的反射与成像的应用光的反射与成像原理在日常生活中有着广泛的应用:1. 镜子:镜子是利用光的反射成像原理制成的光学仪器,广泛应用于人们的生活和工作中,如化妆镜、反光镜等。
2. 光学仪器:光的反射与成像原理也应用于光学仪器的制作中,如望远镜、显微镜等。
光在球面上的反射与折射

光在球⾯上的反射与折射光在球⾯上的反射与折射1.4.1、球⾯镜成像(1)球⾯镜的焦距球⾯镜的反射仍遵从反射定律,法线是球⾯的半径。
⼀束近主轴的平⾏光线,经凹镜反射后将会聚于主轴上⼀点F (图1-4-1),这F 点称为凹镜的焦点。
⼀束近主轴的平⾏光线经凸⾯镜反射后将发散,反向延长可会聚于主轴上⼀点F (图1-4-2),这F 点称为凸镜的虚焦点。
焦点F 到镜⾯顶点O 之间的距离叫做球⾯镜的焦距f 。
可以证明,球⾯镜焦距f 等于球⾯半径R 的⼀半,即2R f =(2)球⾯镜成像公式f u 111=+υ上式是球⾯镜成像公式。
它适⽤于凹⾯镜成像和凸⾯镜成像,各量符号遵循“实取正,虚取负”的原则。
凸⾯镜的焦点是虚的,因此焦距为负值。
在成像中,像长和物长h 之⽐为成像放⼤率,⽤m 表⽰,u h h m υ='=由成像公式和放⼤率关系式可以讨论球⾯镜成像情况,对于凹镜,如表Ⅰ所列;对于凸镜,如表Ⅱ所列。
1.4.2、球⾯折射成像(1)球⾯折射成像公式r n n v n u n 1221-=+ 这是球⾯折射的成像公式,式中u 、υ的符号同样遵循“实正虚负”的法则,对于R ;则当球⼼C 在出射光的⼀个侧,(凸⾯朝向⼊射光)时为正,当球⼼C 在⼊射光的⼀侧(凹⾯朝向⼊射光)时为负。
若引⼊焦点和焦距概念,则当⼊射光为平⾏于主轴的平⾏光(u=∝)时,出射光(或其反向延长线)的交点即为第⼆焦点,(也称像⽅焦点),此时像距即是第⼆焦距2f,有1222n n R n f -=。
当出射光为平⾏光时,⼊射光(或其延长线)的交点即第⼀焦点(即物⽅焦点),这时物距即为第⼀焦距1f,有1211nn R n f -=,将1f 、2f 代⼊成像公式改写成图1-4-1 图1-4-2 图1-4-6A121=+u fu f反射定律可以看成折射定律在12n n -=时的物倒,因此,球⾯镜的反射成像公式可以从球⾯镜折射成像公式中得到,由于反射光的⾏进⽅向逆转,像距υ和球⾯半径R 的正负规定应与折射时相反,在上述公式中令12n n -=,υυ-→,R R -→,即可得到球⾯镜反射成像公式R u 211=+υ,对于凹⾯镜0>R ,221R f f ==,对于凸⾯镜0f f ==,厚透镜成像。
理解几何光学中的球面折射与成像

理解几何光学中的球面折射与成像光学是物理学的一个重要分支,研究光的传播、反射、折射和成像等现象。
在光学中,球面折射与成像是一个重要的概念,它涉及到光线在球面上的传播和折射,以及由此产生的成像效果。
理解球面折射与成像对于我们认识光学现象和应用光学原理具有重要意义。
首先,我们来了解一下球面折射的基本原理。
当光线从一种介质射向另一种介质时,由于介质的折射率不同,光线会发生折射。
而当光线射入球面时,由于球面的曲率,光线会发生弯曲。
这种现象就是球面折射。
球面折射的基本原理可以用斯涅尔定律来描述,即光线在折射时入射角和折射角之间的关系满足sinθ1/sinθ2=n2/n1,其中θ1为入射角,θ2为折射角,n1和n2分别为两种介质的折射率。
在理解了球面折射的基本原理后,我们可以进一步探讨球面折射对成像的影响。
当光线通过球面折射后,会发生折射点的偏移和成像的变化。
具体来说,对于一束平行光线射入球面,经过折射后,光线会集中到球面的一个焦点上。
这个焦点就是球面的主焦点,它是球面折射后光线汇聚的位置。
而对于一个物体,当光线经过球面折射后,会在另一侧的球面上形成一个像。
这个像的位置和形状取决于物体的位置和球面的曲率。
当物体位于球面的主焦点上时,成像会出现在无限远处,形成一个实像。
当物体位于主焦点和球面之间时,成像会出现在球面的另一侧,形成一个放大的虚像。
当物体位于主焦点和球面之外时,成像会出现在球面的同一侧,形成一个缩小的虚像。
除了主焦点外,球面还具有次焦点和次主焦点。
次焦点是光线平行射入球面后汇聚的位置,次主焦点是光线从球面射出后汇聚的位置。
次焦点和次主焦点的位置和主焦点相对应。
当光线从球面射出时,会经过次焦点或次主焦点,然后发散出去。
这种现象在实际应用中有着重要的意义,比如在望远镜和显微镜中,通过调节物镜和目镜之间的距离,可以使光线从球面射出,从而实现放大或缩小的效果。
理解球面折射与成像对于我们认识光学现象和应用光学原理具有重要意义。
光在球面上的反射和折射
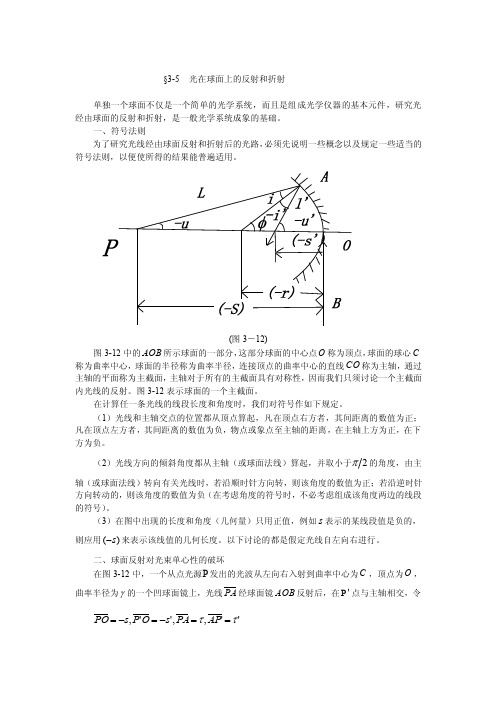
§3-5 光在球面上的反射和折射单独一个球面不仅是一个简单的光学系统,而且是组成光学仪器的基本元件,研究光经由球面的反射和折射,是一般光学系统成象的基础。
一、符号法则为了研究光线经由球面反射和折射后的光路,必须先说明一些概念以及规定一些适当的符号法则,以便使所得的结果能普遍适用。
(图3-12)图3-12中的AOB 所示球面的一部分,这部分球面的中心点O 称为顶点,球面的球心C 称为曲率中心,球面的半径称为曲率半径,连接顶点的曲率中心的直线CO 称为主轴,通过主轴的平面称为主截面,主轴对于所有的主截面具有对称性,因而我们只须讨论一个主截面内光线的反射。
图3-12表示球面的一个主截面。
在计算任一条光线的线段长度和角度时,我们对符号作如下规定。
(1)光线和主轴交点的位置都从顶点算起,凡在顶点右方者,其间距离的数值为正;凡在顶点左方者,其间距离的数值为负,物点或象点至主轴的距离,在主轴上方为正,在下方为负。
(2)光线方向的倾斜角度都从主轴(或球面法线)算起,并取小于2π的角度,由主轴(或球面法线)转向有关光线时,若沿顺时针方向转,则该角度的数值为正;若沿逆时针方向转动的,则该角度的数值为负(在考虑角度的符号时,不必考虑组成该角度两边的线段的符号)。
(3)在图中出现的长度和角度(几何量)只用正值,例如s 表示的某线段值是负的,则应用()s -来表示该线值的几何长度。
以下讨论的都是假定光线自左向右进行。
二、球面反射对光束单心性的破坏在图3-12中,一个从点光源P 发出的光波从左向右入射到曲率中心为C ,顶点为O ,曲率半径为γ的一个凹球面镜上,光线PA 经球面镜AOB 反射后,在'P 点与主轴相交,令 '',,'',ττ==-=-=AP PA s O P s PO半径AC 与主轴的夹角为ϕ,则光线'PAP 的光程为 (')'P A P n n ττ=+ 在PAC ∆和'ACP ∆中应用余弦定理,并注意c o s c o s ()()()'()(')',P C sr r s C P r s s r ϕπϕ=--=---=-=---=- 从而可得()()()()[]2122cos 2ϕs r r s r r l --+-+-=(3-10)以及()()()()[]2122'cos '2'ϕr s r r s r l ----+-= (3-11)因此,光线'PAP 的光程可写成12221222(')()()2()()cos ()(')2()(')cos PAP n r r s r r s n r s r r s r ϕϕ⎡⎤=-+-+--⎣⎦⎡⎤+-+----⎣⎦(3-12)由于当A 点在镜面上移动时,半径r 是常数,而ϕ才是位置的变量,根据费马原理,物象间的光程应取稳定值,为此,把(3-12)式对ϕ求导,并令其等于零,即()()[]()[]0sin '21sin 21''=-+--=ϕϕϕr s r ln s r r l n d PAP d 由此可得 0''=---l rs l s r 或者⎪⎭⎫⎝⎛+=+l s l s r l l ''111'(3-13) 如果发光点P 至O 点的距离s 为已知,从此式即可算出任一反射线和主轴的交点'P 到 O 点的距离's 的值,显然's 的值将随着所取入射线的倾斜角u ,亦即角ϕ的变化而变化,这就是说,从物点发散的单心光束经球面反射后,将不再保持单心(即使平等光束入射时也不例外),关于这一点可说明如下:PC A 1A 2OP 2P'P 3 (图3-13)图3-13中,相应于1PA 及2PA 两入射光线的反射线分别交主轴于1P 和2P 两点,且相交于'P 点,把该图绕主轴PO 转过一个小角度,使三角形12PA A 展成一单心的空间光束,此时'P 点描出一条很短的弧线,它垂直于图面即反射光束的子午象线,而图面中的12PP 则为弧矢象线。
几何光学基本定律球面反射和折射成像

P
P
CF
凹面镜: 物距:P>R 像距:R/2(f)<p’<R 倒立缩小实像
P CPF
凹面镜: 物距:f<P<R 像距:p’>R 倒立放大实像
几何光学基本定律球面反射和折射成像
C F P P
凹面镜: 物距:0<P<f: 像距:p’<0 正立放大虚像
P
P F C
凸面镜: 物距:任意值 像距:-f<p’<0 正立缩小虚像
n21
sin i sinr
v1 v2
绝对折射率:一种介质相对于真空的折射率 n c v 。
设
c n1 v1
c n2 v2
n 21
v1 v2
n2 n1
n1sinin2sinr 几何光学基本定律球面反射和折射成像
几种介质的折射率:
介质 金刚石 玻璃 水晶 岩盐
冰
折射率 2.42
1.50 ~ 1.75 1.54 ~ 1.56
发散光入射凸面镜: 总是成虚像 P
几何光学基本定律球面反射和折射成像
R
P
C
符号法则:
物点 P 在镜前时,物距为正;物点 P 在镜后 时,物距为负。
像点在镜前时,像距为正;像点在镜后时, 像距为负。
凹面镜的曲率半径 R 取正,凸面镜的曲率半 径 R 取负。
实正虚负!
几何光学基本定律球面反射和折射成像
i i
几何光学基本定律球面反射和折射成像
11-1-3 光的折射
折射定律: ⑴ 折射光线总是位于入射面内, 并且与入射光线分居在法线的两 侧;
i i v1 n1
n2
r v2
球面镜成像实验
球面镜成像实验
球面镜成像实验是通过利用球面镜的成像特性来观察物体的成像过程。
实验装置包括一个球面镜和一个物体。
首先要确定球面镜的焦距和曲率半径,可以使用方法如下:
1. 将一个远距离的物体放在球面镜的前方,向球面镜的光线发射入射线,使其在球面镜上折射。
根据光线的折射规律,可以确定球面镜的曲率半径。
2. 将一个距离球面镜较近的物体放在球面镜的前方,让光线经过球面镜后在球面镜的另一侧集中成一点。
通过调整物体的位置,可以确定出球面镜的焦点位置,从而确定焦距。
在实验过程中,可以使用以下步骤观察球面镜成像:
1. 将物体放在球面镜的前方,调整物体的位置和球面镜的位置,使得球面镜与物体之间的距离合适。
2. 观察球面镜的反射光线,通过调整物体的位置和焦距,可以观察到球面镜的实像和虚像。
3. 调整物体的位置和焦距,观察实像和虚像的大小、位置和方向的变化。
通过这个实验,可以观察到球面镜成像的特点,进一步了解球面镜的工作原理和成像规律。
光的反射与折射成像
光的反射与折射成像光是一种电磁波,它在空气和真空中的传播速度为每秒约299,792.458千米。
光在传播过程中会发生反射和折射现象,这些现象在我们的日常生活中随处可见。
本文将探讨光的反射与折射现象对成像的影响。
一、光的反射成像光的反射是指光线从一种介质射入另一种介质时,在两种介质的交界面上发生改变方向的现象。
根据光的反射定律,入射角等于反射角。
利用这个定律,我们可以解释为什么我们能够看到镜子或者其他光滑表面的反射图像。
当平行的光线照射到光滑平面上时,它们会按照相同的角度反射。
这意味着光线在反射后仍然保持它们的相互位置关系,因此我们能够看到一个与实际物体相同但位于镜面后方的图像。
二、平面镜成像平面镜是一种常见的用于反射成像的光学设备。
平面镜的反射成像规律符合光的反射定律,入射角等于反射角。
因此,对于一束平行光线来说,它们会被平面镜反射后汇聚到一个点上,这个点被称为焦点。
这个焦点与入射光线的垂直平分线相交,形成了虚像。
平面镜成像的特点是图像位置与实物位置关于镜面对称,图像大小与实物大小相等。
例如,如果我们将一根直的铅笔放在一个镜面前,我们会看到铅笔在镜面后形成的反射图像与铅笔在镜面前的位置相对称,且大小相等。
三、球面镜成像球面镜是一种曲面镜,通常由玻璃或者塑料制成,其中一侧为球形。
根据球面镜的形状,我们将球面镜分为凸面镜和凹面镜。
3.1 凸面镜成像当平行光线射入凸面镜时,它们会被逐渐汇聚到一个点上,这个点被称为凸透镜的焦点。
这是因为凸面镜会使平行光线向凸透镜的焦点方向汇聚。
这个焦点与入射光线的垂直平分线相交,形成了实像。
实像的位置取决于物体离凸面镜的距离,距离越远,实像越小。
凸面镜的成像特点是图像位置与实物位置关于焦点对称,图像大小与实物大小有关。
如果物体位于焦点以外,那么图像将位于焦点的一侧,并放大。
如果物体位于焦点内部,图像将位于焦点的另一侧,并缩小。
3.2 凹面镜成像当平行光线射入凹面镜时,它们会被逐渐分散。
球面镜成像规律的实验验证与应用
球面镜成像规律的实验验证与应用球面镜是光学领域中重要的器件之一,它广泛应用于望远镜、显微镜、摄影镜头等光学仪器中。
球面镜的成像规律是光学研究的基础之一,通过实验验证这一规律的正确性,可以加深我们对光学原理的理解,并进一步应用于实际问题的解决。
本文将从实验验证球面镜成像规律的方法入手,探讨其在实践中的应用。
一、实验验证球面镜成像规律的方法实验验证球面镜成像规律的方法有多种,下面将介绍其中两种常用的方法:几何法和光线追迹法。
1. 几何法几何法是一种通过几何关系推导出球面镜成像规律的方法。
实验中,我们可以利用成像物体与球面镜之间的几何关系,如焦距公式、放大率公式等进行推导。
这种方法相对简单,适用于初学者。
实验中,我们可以通过调整物体位置和镜片位置,观察成像物体的位置和倍率的变化,验证球面镜成像规律的正确性。
2. 光线追迹法光线追迹法是一种通过追踪光线路径来验证球面镜成像规律的方法。
实验中,我们可以利用透明物体在球面镜中的折射原理,根据入射光线和反射光线的路径关系,确定成像物体的位置和形状。
通过观察光线的传播路径和成像效果,验证球面镜成像规律的正确性。
二、球面镜成像规律的应用球面镜成像规律的应用广泛,以下列举几个常见的应用场景:1. 望远镜望远镜是利用球面镜成像原理实现远处物体清晰观察的光学仪器。
通过球面镜的集光和放大作用,望远镜可以将远处的物体成像,并通过目镜放大显示。
球面镜成像规律在望远镜设计中起到了关键作用,通过调整镜片的位置和焦距等参数,可以获得更清晰和放大倍率更大的成像效果。
2. 摄影镜头摄影镜头是利用球面镜成像原理实现物体成像的光学器件。
通过调整球面镜的位置和焦距,摄影镜头可以实现对物体的调焦和成像。
球面镜成像规律在摄影镜头设计中起到了决定性作用,通过合理地选择球面镜的曲率半径和折射率,可以获得高质量和高清晰度的图像。
3. 显微镜显微镜是利用球面镜成像原理观察微小物体的光学仪器。
通过球面镜的放大和透视作用,显微镜可以将微小物体放大并显示出来。
光的反射定律与成像规律
光的反射定律与成像规律光是一种电磁波,当它遇到物体界面时,会发生反射和折射。
反射是当光线遇到一个物体界面时,一部分光线被物体界面上的分子重新发射出来,按照相同的角度返回进入空气中。
而折射则是光线从一种介质进入到另一种介质时,由于介质间的光速不同,光线会改变传播方向。
这其中涉及到两个重要的规律,即光的反射定律和成像规律。
一、光的反射定律光的反射定律是描述入射光线、法线和反射光线之间的关系的规律。
根据光的反射定律,入射光线和反射光线的夹角等于入射光线和法线的夹角。
这可以用一个简单的公式来表示:θi =θr其中,θi代表入射角,θr代表反射角。
光的反射定律可以应用于许多实际问题中,比如镜面反射。
在平面镜上,当光线照射到镜子上时,根据光的反射定律,入射光线和反射光线的角度是相等的。
这也是我们在镜子中看到自己的原理。
二、成像规律成像规律是研究光在反射或折射过程中形成像的规律。
根据成像规律,物体上的每个点都可以看作是由从该点发出的光线经过反射或折射后形成的。
成像规律可以分为平面镜成像和球面镜成像两种情况。
1. 平面镜成像平面镜成像是指当光线照射到平面镜上时,反射光线的特性。
根据成像规律,平面镜上的任意一点,其形成像必然在镜面的对称位置上,且与物体的位置相反。
也就是说,光线从物体经过平面镜反射后,形成的像与物体位置关于镜面对称。
2. 球面镜成像球面镜成像是指光线经过球面镜折射或反射后的图像形成。
球面镜分为凸透镜和凹透镜两种情况。
对于凸透镜,根据成像规律可以得出以下结论:当物体远离凸透镜时,形成的像在透镜的焦点处,图像为倒立、缩小的实像;当物体靠近凸透镜时,形成的像在透镜的另一侧,图像为倒立、放大的虚像。
对于凹透镜,同样根据成像规律可以得出以下结论:无论物体的位置如何,凹透镜所成的像都是倒立、缩小的虚像。
三、光的反射定律与成像规律的应用光的反射定律和成像规律在日常生活和科学研究中有着广泛的应用。
在光学仪器设计中,如望远镜、显微镜、相机等,光的反射定律和成像规律被用于确定透镜的焦距、镜片的曲率和位置,以实现物体清晰成像。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
光连续通过多个球面折射成像的研究
【摘要】分别利用薄透镜成像法、球面折射逐次成像法和厚透镜成像法计算光连续通过两个透镜组成的四个折射球面的成像位置,并用实验方法测量其成像位置,对三种理论计算值与实验测量值进行比较和分析,发现三种理论计算的结果与实验测量的结果有一定的差距,且理论值均比实验值小,但用球面折射逐次成像法和厚透镜成像理论计算所得结果更准确。
【关键词】球面;薄透镜;厚透镜;折射成像
透镜特有的成像性质具有良好的应用前景。
在日常的生产、生活中透镜无处不在,它发挥着无可替代的作用,日常生活中的眼镜、照相机和投影仪,医学上应用广泛的显微镜、内窥镜,天文观察所用的各类望远镜等都运用到了透镜的成像性质。
因此前人对球面折射、薄透镜、厚透镜折射成像都分别单独进行了比较深入的研究,但没有在同一条件下利用薄透镜成像理论、球面折射逐次成像法和厚透镜成像理论计算像距,同时又用实验的方法进行测量像距,并分析比较它们理论计算的结果与实验值的差值。
这里,我们通过研究光连续通过两个透镜组成贩四个球面的理论计算结果与实验测量结果,这对透镜成像公式的使用具有十分重要的指导意义。
1.折射成像原理
1.1 球面折射成像的物像公式
1.2 薄透镜折射成像的物像公式
因为薄透镜厚度可忽略,则两顶点可看作重合于点O,所以研究薄透镜成像时,测量距离都从透镜中心O点量起。
1.3 厚透镜成像的物像公式
图3表示置于空气中的厚度为d的厚透镜,P和P’分别为物点和像点,F和F’分别为物方焦点和像方焦点,在近轴条件下,厚透镜的物像关系可以由曲率半径为和的两个折射球面逐次成像求得[1]。
2.实验测量透镜的焦距、折射率和球面曲率半径
为了对光线通过由两个透镜组成的四个球面的成像位置,我们先对这两个透镜的折射率、焦距和这两个透镜对应的四个球面的曲率半径进行测定。
实验测定透镜折射率的方法有很多种,这里我们采用阿贝折射仪测定这两个透镜的折射率[2],经测量,这两个透镜的折射率均为 1.51。
测定透镜的焦距的方法也有很多种,我们采用二次成像法[2]对这两个透镜的折射率进行测定,所
得的结果是透镜Ⅰ的,透镜Ⅱ的。
同时,我们采用成像法[3]对这两个透镜对应的四个球面的曲率半径进行测量,所得结果如表1所示。
对于由两个透镜结成的四个球面的成像问题,其成像原理图如图4所示。
分别选取5个物距进行理论计算和实验测量。
理论计算分别采用薄透镜成像法、厚透镜成像法和单球面折射的逐个球面成像法的原理进行计算,再用实验的方法进行实验测量成像的位置,所得结果如表2所示。
表中的第1列()为物到第1个球面的顶点的距离,第2列()为透镜右球面顶点到透镜左球面顶点的距离,第3列()、4列()、5列()、6列()分别为用实验的方法进行实验测量、薄透镜成像法、厚透镜成像法和单球面折射的逐个球面成像法的原理进行计算得到的像距透镜右球面顶点的距离,第7列()、第8列()、第9列()分别是上述三种理论计算的结果与实验测量的结果的差值。
从表2可见,用薄透镜成像法、球面折射逐次成像法和厚透镜成像原法计算得到的理论值均比实验值小,而且它们的理论值和实验值的差值还比较大。
出现这样的差别可能是因为在实验测量过中存在一定的误差。
但三种理论值相差不大,说明在近轴条件下,三种方法都可以用来计算球面的成像问题。
但用球面折射逐次成像法计算和用厚透镜成像法计算所得的结果会比用薄透镜成像法计算所得的结果更准确一些。
因为用球面折射逐次成像法和用厚透镜成像法得到的结果与实验值比较接近,而用薄透镜成像法得到结果与实验值相差更大。
这是因为在用球面折射逐次成像法和用厚透镜成像法计算过程中考虑了透镜的厚度,把厚度加入到计算过程中,这就使得它们计算过程更严密,所以它们的计算值与实验值比较接近。
而用薄透镜成像法计算时忽略了透镜的厚度,薄透镜物像公式的推导过程取了近似值,导致了它的计算值与实验值相差较大。
所以在各种条件相同的情况下,对于由透镜组成的多球面折射系统,利用球面折射逐次成像法和用厚透镜成像法计算更准确,与实验值更接近。
参考文献:
[1]姚启钧.光学教程[M].北京:高等教育出版社,2002:131-133.136-138.146-147.
[2]杨述武,赵立竹,沈国土.普通物理实验光学部分[M].北京:高等教育出版社,2007:21.38-40.
[3]宋晓欣.测量薄透镜折射及曲率半径的一种方法[J].物理实验,1989:11(2).57-59.
资助。
