光在球面上地反射与折射球面镜成像球面镜地焦距
光学球面镜成像规律解析

光学球面镜成像规律解析光学球面镜是一种由球形曲面构成的光学元件,通过其特殊的形状和材质,可以对光线进行折射、反射,并实现物体成像的功能。
球面镜在光学系统中有着广泛的应用,例如在显微镜、望远镜和眼镜等光学仪器中都有其身影。
本文将探讨光学球面镜的成像规律,从理论和实践两个方面进行分析。
一、理论解析1. 凸球面镜的成像规律:凸球面镜是一种中心凸起的球形镜面。
当平行光线垂直射入凸球面镜时,根据光线的折射规律可以得出以下结论:a) 光线经球面镜折射后会汇聚于球面镜的焦点。
该焦点称为凸球面镜的主焦点(F)。
b) 物体距离凸球面镜的距离和其像距离具有一定的关系,称为球面镜公式:1/f = 1/v + 1/u其中,f为球面镜的焦距,v为像的距离,u为物的距离。
根据该公式,当物距u为正时,像距v为正,成像为实像。
当物距u为负时,像距v为负,成像为虚像。
2. 凹球面镜的成像规律:凹球面镜是一种中心凹陷的球形镜面。
与凸球面镜相比,凹球面镜的成像规律略有不同:a) 光线经凹球面镜折射后会发散,无法汇聚于焦点。
因此,凹球面镜没有实焦点。
b) 性质类似于凸球面镜,物的距离与像的距离之间仍然满足球面镜公式。
但凹球面镜的成像为虚像。
二、实践案例为了更好地理解光学球面镜成像规律,我们可以通过一些实践案例进行演示和验证。
1. 凸球面镜成像实验:准备一个凸球面镜和一根细直尺。
将直尺直立放置,并在直尺顶端放置一小物体作为物。
将凸球面镜放在直尺上方,调整距离,观察其成像情况。
根据凸球面镜的成像规律,应该能够观察到物体在凸球面镜后方产生实像。
可以移动观察者的位置,观察实像的大小、位置和倒立程度的变化。
2. 凹球面镜成像实验:同样准备一个凹球面镜和一根细直尺,按照上述方法进行实验。
根据凹球面镜的成像规律,我们预期应该能够观察到物体在凹球面镜后方产生虚像。
通过上述实验,我们能够亲身体验到光学球面镜的成像效果,进一步加深对其成像规律的理解。
综上所述,光学球面镜的成像规律可以通过理论分析和实践案例来解析。
光在球面上的反射和折射
和
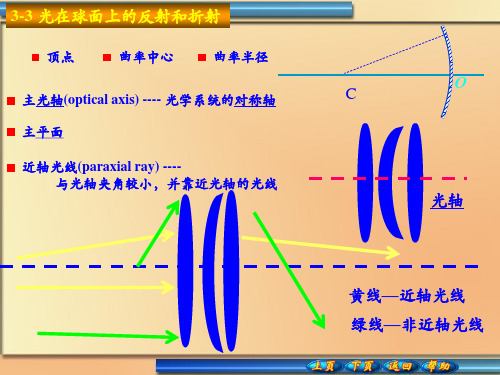
f ' n' r n'n
Gauss成像公式: f ' f 1 s' s
P
F
O
P’ F’
n n’
-f -x
f’ x’
-s
s’
分别以F和F’为基准点,量度物点P和像点P’ 的位置,物距和
和像距分别用 x 和 x’ 表示:
-s = -x-f s’ = x’+f’
xx' ff '
Newton成像公式
凹面镜 r 0, f f 0;
凸面镜 r 0, f f 0.
球面反射物像公式: 1 1 1 s s f
Mirror
例3.3
3 单个球面的折射成像
A. Abbe不变式 B. 焦距(focal lengh) C. Gauss成像公式和 Newton成像公式
4球面折射对光束单心性的破坏
f
'
(nL
1)
1 r1
1 r2
C2
O
证明: I1面: s1, s1’, r1 I2面: s2, s2’, r2
-r2
nL
I1 I2
r1 C1
薄透镜
3-3 光在球面上的反射和折射
顶点
曲率中心
曲率半径
主光轴(optical axis) ---- 光学系统的对称轴
C
主平面
近轴光线(paraxial ray) ---与光轴夹角较小,并靠近光轴的光线
o
光轴
黄线—近轴光线 绿线—非近轴光线
1. 符号规则(sign convention) 几何光学常用的符号规则: 笛卡尔坐标规则。
u
S
•
C
1. 4. 光在球面上的反射与折射
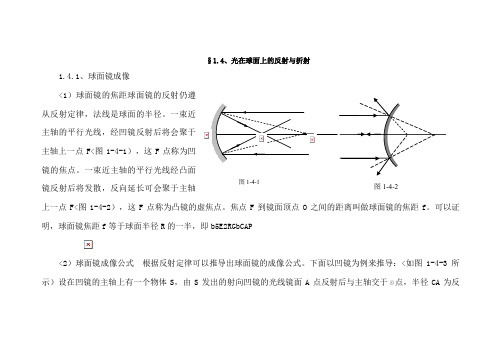
§1.4、光在球面上的反射与折射1.4.1、球面镜成像<1)球面镜的焦距球面镜的反射仍遵从反射定律,法线是球面的半径。
一束近主轴的平行光线,经凹镜反射后将会聚于主轴上一点F<图1-4-1),这F 点称为凹镜的焦点。
一束近主轴的平行光线经凸面镜反射后将发散,反向延长可会聚于主轴上一点F<图1-4-2),这F 点称为凸镜的虚焦点。
焦点F 到镜面顶点O 之间的距离叫做球面镜的焦距f 。
可以证明,球面镜焦距f 等于球面半径R 的一半,即b5E2RGbCAP<2)球面镜成像公式 根据反射定律可以推导出球面镜的成像公式。
下面以凹镜为例来推导:<如图1-4-3所示)设在凹镜的主轴上有一个物体S ,由S 发出的射向凹镜的光线镜面A 点反射后与主轴交于点,半径CA为反图1-4-1图1-4-2射的法线,即S的像。
根据反射定律,,则CA为角A的平分线,根据角平分线的性质有p1EanqFDPw①由为SA为近轴光线,所以,,①式可改写为②②式中OS叫物距u,叫像距v,设凹镜焦距为f,则代入①式化简这个公式同样适用于凸镜。
使用球面镜的成像公式时要注意:凹镜焦距f取正,凸镜焦距f取负;实物u取正,虚物u取负;实像v为正,虚像v为负。
DXDiTa9E3d上式是球面镜成像公式。
它适用于凹面镜成像和凸面镜成像,各量符号遵循“实取正,虚取负”的原则。
凸面镜的焦点是虚的,因此焦距为负值。
在成像中,像长和物长h之比为成像放大率,用m表示,RTCrpUDGiT由成像公式和放大率关系式可以讨论球面镜成像情况,对于凹镜,如表Ⅰ所列;对于凸镜,如表Ⅱ所列。
表Ⅰ 凹镜成像情况~2f表Ⅱ 凸镜成像情况~~2f同侧~<3)球面镜多次成像 球面镜多次成像原则:只要多次运用球面镜成像公式即可,但有时前一个球面镜反射的光线尚未成像便又遇上了后一个球面镜,此时就要引进虚像的概念。
5PCzVD7HxA 如图1-4-4所示,半径为R 的凸镜和凹镜主轴相互重合放置,两镜顶点O1 、 O2 相距2.6R ,现于主轴上距凹镜顶点O1为0.6R 处放一点光源S 。
球面反射境

放大率 折射球面
反射球面 高斯 牛顿
b=y’/y
=dl’/dl
nl’/n’l nl’2/n’l2
n’ —>-n
-l’/l -x’/f’=-f/x -(l’/l)2 -x’/x
g=u’/u
l/l’
l/l’ x/f’= f/x’
例题-共轴球面光学系统
例题1 一个玻璃球直径为40mm,折射率为1.5,一 束平行光入射到玻璃球上,其汇聚点在什么 位置?如果在玻璃球前25mm处放置一个高 为1mm的物体,试求解像的位置和大小.
例题-球面镜成像
例题1 一球面反射境,半径r=12cm,当物相距 球面镜顶点物距分别为-18cm,-2cm和 12cm时,求像的位置和垂轴放大率。
折射球面 n’/l’ –n/l =(n’-n)/r
球面镜 1/l’ +/l =2/r A (2) 高斯公式
1 1 1 或 f ' f 1
l' l f '
l' l
(3) 牛顿公式
A
xx' f '2 或 xx' ff '
A’
C F(F’) O
-l’ -l
A’
C F(F’) O
-x’
-x
-f ’
3 放大率公式—球面反射镜成像关系
1 焦距—球面反射镜成像关系
(1) 光焦度
折射球面
球面镜 (2) 像方焦距
折射球面
球面镜 (3) 物方焦距
折射球面
球面镜
j=(n’-n)/r
j=-2n/r
f’=n’j
f’=r/2
f=-n/j
f=r/2
C F(F’) O
-f=-f ’
光学基础知识镜面反射和球面反射的成像原理

光学基础知识镜面反射和球面反射的成像原理光学基础知识:镜面反射和球面反射的成像原理光学是研究光的传播、反射、折射和干涉等现象的科学。
在光学中,镜面反射和球面反射是两个重要的概念。
本文将详细介绍镜面反射和球面反射的成像原理,以及其在实际应用中的重要性。
一、镜面反射的成像原理镜面反射是指光线在平滑的镜面上的反射现象。
根据光的传播规律,入射光线与法线的夹角等于反射光线与法线的夹角,且位于同一个平面上。
这一定律被称为反射定律。
当平行光射向一个平滑的镜面时,根据反射定律,光线会经过反射后汇聚于焦点。
这一特性使得平面镜可以作为反射光线的凸面镜。
我们可以用镜像法则来确定成像位置和形状。
成像原理可以通过以下步骤简单总结:1. 对于平行光,光线射向镜面后发生反射。
2. 入射光线与镜面的法线以相等的角度形成反射光线。
3. 反射光线会汇聚到某一焦点处,形成实像。
4. 实像的位置取决于入射光线的角度和镜面的曲率。
二、球面反射的成像原理球面反射是指光线在球面上的反射现象。
和镜面反射相比,球面反射具有一定的特殊性。
在球面反射中,焦点并不是固定不变的,而是根据入射光线的角度和球面的曲率而变化。
球面反射的成像原理如下:1. 入射光线射向球面后发生反射。
2. 入射光线与球面的切线以相等的角度形成反射光线。
3. 反射光线会在球面上发生折射,并聚焦于某一点成为实像。
4. 实像的位置取决于入射光线的角度、球面的曲率和球心位置。
三、镜面反射和球面反射的应用镜面反射和球面反射的成像原理在现实生活中得到广泛应用。
1. 镜面反射应用:a. 平面镜:平面镜常见于家庭中的化妆镜、衣柜镜等。
平面镜的成像原理使得我们能够清晰地看到自己的影像。
b. 曲面镜:曲面镜可以分为凸面镜和凹面镜。
凸面镜通过收敛光线形成实像,常用于放大镜、汽车后视镜等。
凹面镜则通过发散光线形成虚像,常用于化妆镜和安全后视镜。
2. 球面反射应用:a. 球面反射镜:球面反射镜广泛应用于天文望远镜、摄影镜头等光学设备中。
球面镜成像规律的数学推导

球面镜成像规律的数学推导在光学中,球面镜是一种常见的光学器件,用于将光线经过反射或折射后进行聚焦或发散。
球面镜成像规律描述了入射光线与球面镜之间的数学关系,帮助我们理解球面镜的成像特性。
本文将对球面镜成像规律进行数学推导。
首先,我们先介绍球面镜的基本概念。
球面镜由一段曲线形成,在球体的内表面上涂上一层光学材料,通常是玻璃或塑料。
根据球面镜的曲率半径,我们可以将其分为凸面镜和凹面镜。
凸面镜的曲率半径为正,而凹面镜的曲率半径为负。
接下来,我们假设一个凸面镜,其曲率半径为R。
现在我们来推导球面镜成像规律。
球面镜成像规律一:物距、像距和焦距之间的关系根据球面镜的成像规律,我们可以得到以下公式:1/f = 1/v + 1/u其中,f表示球面镜的焦距,v表示像距,u表示物距。
球面镜成像规律二:放大率的计算在球面镜成像中,放大率(M)定义为像的高度(h′)与物的高度(h)之间的比值:M = h′/h根据球面镜成像规律,我们可以得到以下公式:M = -v/u其中,正负号表示像的位置相对于物的位置。
球面镜成像规律三:虚像与实像根据球面镜成像规律,当物距u在球面镜前方时(负值),像的位置v可能为正实像或者为负虚像。
当物距u在球面镜后方时(正值),像的位置v可能为负实像或者为正虚像。
通过上述的数学推导,我们可以得到球面镜成像规律的数学表达式。
这些规律为我们研究球面镜的成像提供了坚实的理论基础。
同时,球面镜成像规律也帮助我们更好地理解和应用球面镜在实际中的应用。
总结本文通过数学推导介绍了球面镜成像规律,并详细解释了物距、像距、焦距以及放大率等概念之间的关系。
球面镜成像规律为我们理解球面镜成像特性提供了重要的理论基础。
理解和掌握球面镜成像规律的数学推导对于光学领域的学习和应用具有重要意义。
球面反射和球面折射成像
球面反射成像
一、凹面镜的反射成像
1
2
3
4
5
f
c
F
成像公式
焦距公式
横向放大率
物点在焦点之内,凹面镜成虚像
y
f
l
l’
y’
c
2
1
F
物点在焦点之外,凹面镜成实像
f
c
l
y
l’
y’
1
1
2
2
F
二、凸面镜的反射成像
f
1
2
3
F
y
1
2
1
2
y’
fቤተ መጻሕፍቲ ባይዱ
l
l’
所以成的是缩小正立的虚像,位于镜前右方10 cm处。
解 按题意,l=-30cm,r =30cm,y=10mm
由成像公式可得 cm
二、球面折射成像公式
物方焦距
-
像方焦距
Q
Q´
O
n
n´
r
C
l´
P´
P
y´
y
三、横向放大率
Q
Q´
O
n
n´
r
C
l´
P´
P
y´
y
定义
|β|>1 放大 |β|<1 缩小
β > 0 像正立 β < 0 像倒立
F
F'
四、近轴光线的作图法
共轴球面系统成像(逐次成像)
01
共轴球面系统所成的最终像,可由第一球面所成之像作为第二球面之物、第二球面所成之像作为第三球面之物逐次计算而得。 光学系统的横向放大率为每次球面成像的横向放大率的乘积。
光在球面上的反射折射
1 2 3 4 5
物理学教程 (第二版)
凹面镜的焦点
F
f r 2
曲率半径
主 光 轴
f
* 第十三章 几何光学
13 – 3 光在球面上的反射、折射成像 利用作图法 确定像的位置和 大小 成像公式 A 2 1 2 1
物理学教程 (第二版)
2 . 凸面镜的反射成像
1
虚焦点
1 2 3 4 5
O
F
h0
1 2 2
O
f
p0
p
h1
f
F
f 0
凸面镜焦距
* 第十三章 几何光学
p0 0, p 0
凸面镜成像
13 – 3 光在球面上的反射、折射成像 二 . 球面上的折射成像 1. 成像公式(近轴光线)
物理学教程 (第二版)
O
物理学教程 (第二版)
h0 F
h1
p
1 1 1 p p f
凹面镜 f 0 (A) p 0, p 0 B
p
f
p
h0
1 F
O
h1
1 2
2
(B)
p 0, p 0
* 第十三章 几何光学
p
f
13 – 3 光在球面上的反射、折射成像 成像公式
物理学教程 (ቤተ መጻሕፍቲ ባይዱ二版)
n n n n p p r
M
f f 1 p p
Q
i
o
i
c
光学教程___第3章_几何光学的基本原理
i2 ic的光线折射出光纤;i2 ic 的光线在两层介质间多次全
反射从一端传到另一端.
内窥镜、光导通讯……
为了使更大范围内的光束能在纤维中传播,应选择n1和n2的差
值较大的材料去制造光学纤维。
/ 77
20
四.棱镜
主截面:垂直于两界面的截面. 偏向角:出射线与入射线间的夹角.
=(i1-i2 )+(i1 -i2 )= i1 +i1 -A
由P点所发出的单心光束经球面反射后,单心性被破坏
/ 77
26
三、近轴光线条件下球面反射的物像公式
当φ很小时,cosφ 1
l r2 r s2 2 rr s r r s2 s
l' r2 s' r 2 2 r s' r r s' r 2 s'
由:
A
d l
n 2rs rsin 0 P
l
l
-u
i
-i′ l '
-u`
C
P` -s` O
化简有:r l
s
s r l'
0
-r -s
即:1 l'
1 l
1 r
s l'
s l
对一定的球面和发光点P(S一定),不同的入射点对应有不同的S‘。
即:同一个物点所发出的不同光线经球面反射后不再交于一点。
第三章 几何光学的基 本原理
/ 77
1
干涉和衍射现象揭示了光的波动性,所有 光学现象都能够用波动概念解释。但是在波面 线度远大于波长时,研究光的反射,折射成象 等问题,如果不用波长、位相等波动概念而代 之以光线和波面等概念,即用几何的方法来研 究,将更为方便。
球面镜成像与公式推导
球面镜成像与公式推导球面镜是一种光学器件,具有球面形状的反射面。
它广泛应用于望远镜、显微镜、摄影镜头等领域。
本文将介绍球面镜的成像原理以及相关公式的推导。
一、球面镜成像原理球面镜的成像原理是基于反射光的规律,即光线入射到球面镜上的反射角等于入射角。
通过对球面镜成像的研究,我们可以得到以下几个关键概念:1. 光心(O):球面镜的中心点,与球心重合。
2. 焦点(F):与光心相对应,在凹面镜中,焦点位于镜面一侧;在凸面镜中,焦点位于镜面背后。
3. 焦距(f):焦点到球面镜的距离。
根据球面镜的形状,可以将球面镜分为凹面镜和凸面镜。
凹面镜成像:当平行光线入射到凹面镜上时,根据反射规律,光线会被球面镜反射后汇聚于焦点F处。
这是凹面镜的主焦点成像。
主焦点与光心之间的距离即为凹面镜的焦距f。
凸面镜成像:对于凸面镜而言,当平行光线入射到凸面镜上时,经过反射后看似来自焦点F处发出。
这时,焦点F称为虚焦点。
凸面镜的焦距f也是焦点F到光心O的距离。
二、球面镜成像公式的推导为了准确定量化球面镜成像的特征,我们需要推导出球面镜的成像公式。
以凹面镜为例进行推导。
1. 设入射光线的高度为h_i,入射角为θ_i。
2. 根据几何关系,设成像光线的高度为h_o,出射角为θ_o,焦距为f。
根据反射定律,有sinθ_o/sinθ_i = n,其中n为介质的折射率。
根据三角形的相似关系,得到:h_o/(R-h_o) = h_i/(R-f)其中R为球面镜的曲率半径。
通过以上关系,可以推导出凹面镜的成像公式:1/f = (n-1)*(1/R - 1/h_i)在推导凸面镜的成像公式时,同样可以通过类似的步骤得到:1/f = (n-1)*(1/R + 1/h_i)三、球面镜成像公式的应用推导出球面镜的成像公式后,我们可以通过这些公式来计算球面镜成像的特征。
以凹面镜为例,当知道入射光线的高度和入射角时,可以通过公式计算出成像位置和成像高度。
反之,当知道成像位置和成像高度时,也可以借助公式计算出入射光线的高度和入射角。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
文档§1.4、光在球面上的反射与折射1.4.1、球面镜成像(1)球面镜的焦距球面镜的反射仍遵从反射定律,法线是球面的半径。
一束近主轴的平行光线,经凹镜反射后将会聚于主轴上一点F (图1-4-1),这F 点称为凹镜的焦点。
一束近主轴的平行光线经凸面镜反射后将发散,反向延长可会聚于主轴上一点F (图1-4-2),这F 点称为凸镜的虚焦点。
焦点F 到镜面顶点O 之间的距离叫做球面镜的焦距f 。
可以证明,球面镜焦距f 等于球面半径R 的一半,即2Rf =(2)球面镜成像公式 根据反射定律可以推导出球面镜的成像公式。
下面以凹镜为例来推导:(如图1-4-3所示)设在凹镜的主轴上有一个物体S ,由S 发出的射向凹镜的光线镜面A 点反射后与主轴交于S '点,半径CA 为反射的法线,S '即S 的像。
根据反射定律,AC S SAC '∠=∠,则CA 为S SA '角A 的平分线,根据角平分线的性质有O图1-4-1图1-4-2文档S C CSS A AS '=' ①由为SA 为近轴光线,所以O S S A '=',SO AS=,①式可改写为S C CSS O OS '=' ②②式中OS 叫物距u ,S O '叫像距v ,设凹镜焦距为f ,则f u OC OS CS2-=-=υ-='-='f S O OC S C 2代入①式υυ--=f fu u22化简f u 111=+υ 这个公式同样适用于凸镜。
使用球面镜的成像公式时要注意:凹镜焦距f 取正,凸镜焦距f 取负;实物u 取正,虚物u 取负;实像v 为正,虚像v 为负。
f u 111=+υ文档上式是球面镜成像公式。
它适用于凹面镜成像和凸面镜成像,各量符号遵循“实取正,虚取负”的原则。
凸面镜的焦点是虚的,因此焦距为负值。
在成像中,像长 和物长h 之比为成像放大率,用m 表示,u h h m υ='=由成像公式和放大率关系式可以讨论球面镜成像情况,对于凹镜,如表Ⅰ所列;对于凸镜,如表Ⅱ所列。
表Ⅰ 凹镜成像情况表Ⅱ 凸镜成像情况文档(3)球面镜多次成像 球面镜多次成像原则:只要多次运用球面镜成像公式即可,但有时前一个球面镜反射的光线尚未成像便又遇上了后一个球面镜,此时就要引进虚像的概念。
如图1-4-4所示,半径为R 的凸镜和凹镜主轴相互重合放置,两镜顶点O 1 、 O 2 相距2.6R ,现于主轴上距凹镜顶点O 1为0.6R 处放一点光源S 。
设点光源的像只能直接射到凹镜上,问S 经凹镜和凸镜各反射一次后所成的像在何处?O 图1-4-4文档S 在凹镜中成像,Ru 6.01=,R f 211=111111f u =+υR R 216.011=+υ可解得 R 31=υ R O O 6.221=,根据题意:所以凹镜反射的光线尚未成像便已又被凸镜反射,此时可将凹镜原来要成像1S 作为凸镜的虚物来处理, R R R u 4.0)36.2(2-=-=,22R f -= 222111f u =+υR R 214.012-=+-υ可解得 R 22=υ文档说明凸镜所成的像2S 和S 在同一位置上。
1.4.2、球面折射成像 (1)球面折射成像公式 (a )单介质球面折射成像如图1-4-5所示,如果球面左、右方的折射率分别为1和n ,S '为S 的像。
因为i 、r 均很小,行以n rir i ==sin sin ① 因为 αθ+=i ,βθ-=r 代入①式可有)(βθαθ-=+n r ②对近轴光线来说,α、θ、β同样很小,所以有u x =α,R x =θ,υβx =代入②式可得R n n u 11-=+υ图1-4-5文档当∞→u 时的v 是焦距f ,所以n n Rf ⋅-=1(b )双介质球面折射成像如图1-4-6所示,球形折射面两侧的介质折射率分别n 1和n 2,C 是球心,O 是顶点,球面曲率半径为R ,S 是物点,S '是像点,对于近轴光线2211i n i n = βα+=1i , θβ-=2i ,u A 0=α,R A 0=β,v A 0=θ联立上式解得r n n vn u n 1221-=+ 这是球面折射的成像公式,式中u 、υ的符号同样遵循“实正虚负”的法则,对于R ;则当球心C 在出射光的一个侧,(凸面朝向入射光)时为正,当球心C 在入射光的一侧(凹面朝向入射光)时为负。
若引入焦点和焦距概念,则当入射光为平行于主轴的平行光(u=∝)时,出射光(或其反向延长线)的交点即为第二焦点,(也称像方焦点),此时像距图1-4-6文档即是第二焦距2f ,有1222n n Rn f -=。
当出射光为平行光时,入射光(或其延长线)的交点即第一焦点(即物方焦点),这时物距即为第一焦距1f ,有1211nn Rn f -=,将1f 、2f 代入成像公式改写成121=+u fu f反射定律可以看成折射定律在12n n -=时的物倒,因此,球面镜的反射成像公式可以从球面镜折射成像公式中得到,由于反射光的行进方向逆转,像距υ和球面半径R 的正负规定应与折射时相反,在上述公式中令12n n -=,υυ-→,R R -→,即可得到球面镜反射成像公式R u 211=+υ,对于凹面镜0>R ,221R f f ==,对于凸面镜0<R ,221R f f ==,厚透镜成像。
(C )厚透镜折射成像设构成厚透镜材料的折射率为n ,物方介质的折射率为1n ,像方介质的折射率为2n ,前后两边球面的曲率半径依次为1r 和2r ,透镜的厚度为t o o =',当物点在主轴上的P 点时,物距OP u =,现在来计算像点P '的像距。
P O S '=',首先考虑第一个球面AOB 对入射光的折射,这时假定第二个球面AOB 不存在,并认为球AOB 右边,都为折射率等于n 的介质充满,在这种情况下,P 点的像将成在P ''处,其像距P O ''='υ,然后再考虑光线在第二个球面的折射,对于这个球面来说,P ''便是虚物。
A文档因此对于球面AOB ,物像公式为1112r n n u n vn -=+ 对于球面AOB ,物像公式为222r n n t u n v n -=-+这样就可以用二个球面的成像法来求得透镜成像的像距u 。
(2)光焦度折射成像右端仅与介质的折射率及球面的曲率半径有关,因而对于一定的介质及一定形状的表面来说是一个不变量,我们定义此量为光焦度,用φ表示:rn n -'=Φ它表征单折射球面对入射平行光束的屈折本领。
φ的数值越大,平行光束折得越厉害;φ>0时,屈折是会聚性的;φ<0时,屈折是发散性的。
φ=0时,对应于∞=r ,即为平面折射。
这时,沿轴平行光束经折射后仍是沿轴平行光束,不出现屈折现象。
光焦度的单位是[米-1],或称[屈光度],将其数值乘以100,就是通常所说的眼镜片的“度数”。
图1-4-8文档(3)镀银透镜与面镜的等效有一薄平凸透镜,凸面曲率半径R =30cm ,已知在近轴光线时:若将此透镜的平面镀银,其作用等于一个焦距是30cm 的凹面镜;若将此透镜的凸面镀银,其作用也等同于一个凹面镜,其其等效焦距。
当透镜的平面镀银时,其作用等同于焦距是30cm 的凹面镜,即这时透镜等效面曲率半径为60cm 的球面反射镜。
由凹面镜的成像性质,当物点置于等效曲率中心 时任一近轴光线经凸面折射,再经平面反射后将沿原路返回,再经凸面折射后,光线过 点,物像重合。
如图1-4-8所示。
i n i '=,i u i '+=,i u n '+=1。
依题意,60h u =,30h i =,故5.1=n 。
凸面镀银,光路如图1-4-9所示。
关键寻找等效曲率中心,通过凸面上任一点A 作一垂直于球面指向曲率中心C 的光线。
此光线经平面折射后交至光轴于B C ,令r OC B =则i n i'=,Rh i =,r h i '=',得cm nR r 20==。
由光的可逆性原理知,B C 是等效凹面镜的曲率中心,f =10cm 。
例1、如图1-4-10所示,一个双凸薄透镜的两个球面的曲率半径均为r ,透镜的折射率为n ,考察由透镜后表面反射所形成的实像。
试问物放于何处,可使反射像与物位于同一竖直平面内(不考虑多重反射)。
解: 从物点发出的光经透镜前表面(即左表面)反射后形成虚像,不合题意,无须考虑。
图1-4-9图1-4-10文档从物点发出的光经透镜前表面折射后,再经透镜后表面反射折回,又经前表面折射共三次成像,最后是实像,符合题意。
利用球面折射成像公式和球面反射成像公式,结合物与像共面的要求。
就可求解。
球面反射的成像公式为:f v u 111=+,其中反射面的焦距为2Rf =(R 为球面半径),对凹面镜,f 取正值,对凸面镜,f 取负值。
球面折射的成像公式为:R n n v n u n 1)(2121-=+。
当入射光从顶点射向球心时,R 取正值,当入射光从球心射向顶点时,R 取负值。
如图1-4-11甲所示,当物点Q 发出的光经透镜前表面折射后成像于Q ',设物距为u ,像距为v ,根据球面折射成像公式:R n n vn u n 1)(2121-=+ 这里空气的折射率11=n ,透镜介质的折射率n n =2,入射光从顶点射向球心,R=r 取正值,所以有r n v n u 11-=+ (1)图1-4-11甲文档这是第一次成像。
对凸透镜的后表面来说,物点Q 经透镜前表面折射所成的风点Q '是它的物点,其物距v u -=1(是虚物),经透镜后表面反射后成像于1Q ',像距为1v -(如图1-4-11乙所示),由球面反射成像公式r f v u 2111211==+ 将前面数据代入得r v v 2111=+-(2)这是第二次成像。
由透镜后表面反射成的像点1Q '又作为透镜前 表面折射成像的物点2Q ,其物距12v u -=(是虚物),再经过透镜前表面折射成像于2Q ',像距为2v ,图1-4-11乙图1-4-11丙文档(见图1-4-11丙所示),再由球面折射成像公式Rn n v n u n 1)(2121-=+ 这时人射光一侧折射率,折射光一侧折射率(是空气),入射光由球心射向顶点,故R 值取负值。
所以可写出rn v u n --=+1)1(122 代入前面得到的关系可得rn v u n 1121-=+-(3) 这是第三次成像,由(1)、(2)两式可解得rn v n u 1311-=+ (4) 再把(4)式和(3)式相加,可得rn v u )12(2112-=+ (5) 为使物点Q 与像点2Q '在同一竖直平面内,这就要求 12v u -=文档代入(5)是可解得物距为12-=n r u说明 由本题可见,观察反射像,调整物距,使反射像与物同在同一竖直平面内,测出物距P ,根据上式就可利用已知的透镜折射率n 求出透镜球面的半径r ,或反过来由已咋的球面半径r 求出透镜的折射率n 。
