统计学计算题复习(学生版)
统计学期末复习资料_计算题

五、计算题(要求写出公式、列出计算步骤) 1. 某产品资料如下:要求按以下三种方法计算产品的平均收购价格:(1) 不加权的平均数;(2)加权算术平均数;(3)调和平均数 解:不加权05.139.005.12.1=++=x (元/斤)加权02.140003000200040009.0300005.120002.1=++⨯+⨯+⨯==∑∑fxf x (元/斤)加权调和02.19.0360005.131502.1240036000315024001=++++==∑∑m xm x (元/斤)2. 某公司所属三个企业生产同种产品,2004年实际产量、计划完成情况及产品优质品率资料如下:要求计算:(1)该公司产量计划完成百分比; (2)该公司的实际优质品率。
解:1)以实际产值为m,完成计划百分比为x,该公司产量计划完成百分比:%95.9320.5325008.02501.11502.1100250150100==++++==∑∑x m m x2)以实际优质品率为x,以实际产量为f,该公司的实际优质品率:%8.9650048425015010098.025096.015095.0100==++⨯+⨯+⨯==∑∑fxfx3. 某企业有50名工人,其月产值(万元)如下:要求:(1)根据上述资料将50名工人按产值分7组编制组距为10万元的等组距数列;(2)按上述分组编制向上累计的累计频数和累计频率数列;(3)并以第三组为例说明累计频数和累计频率的含义。
解:(1)根据上述资料将50名工人按产值分7组编制组距为10万元的等组距数列;(2)按上述分组编制向上累计的累计频数和累计频率数列;(3)并以第三组为例说明累计频数和累计频率的含义。
第三组数据说明在50名工人中,月产值在105以下的有30人,占总数的60%4. 南宁化工厂2008年现有生产工人600人。
现用不重复抽样抽出40人调查其年产值(万元)如下:(1)将40个工人按产值分组,编制组距为10万元的等组距数列,并列出向上累计频数和累计频率。
统计初步复习-学生版

统计初步复习知识精要一、统计的意义 1. 数据整理与表示条形图、折线图和扇形图是常用的统计图: *条形图有利于比较数据的差异;*折线图可以直观地反映出数据变化的趋势;*扇形图凸显了由数据所体现出来的部分与整体的关系。
2.统计的意义统计学是研究如何收集、处理、分析数据从而得出结论或找出规律的科学。
调查时,调查对象的全体叫做总体,其中每一个调查对象叫做个体。
从总体中取出的一部分个体叫做总体的一个样本,样本中个体的数量叫做样本容量。
收集数据的方法一般有两种,即普查和抽样调查。
普查是收集数据的基本方法,需要对总体中的每个个体都进行调查,所费的人力物力和时间较多,优点是数据准确度较高,调查的结论较可靠。
抽样调查是从总体中抽取样本进行调查,并以此来估计整体的情况。
比普查省时省力,但要按一定的统计方法收集数据。
抽样调查是收集数据最常用的方法。
样本的选择要具有代表性,每个个体应有均等的机会被选中。
具有代表性的样本叫做随机样本。
二、基本的统计量 1.平均数与加权平均数一般地,如果一组数据:12,...,,n x x x 它们的平均数记做x ,这时:()121...n x x x x n =+++或12''...'nx x x x a n+++=+加权平均数1122112212.........k kk k kf x f x f x x m x m x m x f f f +++==+++++2.中位数、众数和截尾平均数将n 个数由小到大排列后,居中的一个数据(n 为奇数时),或居中的两个数据(n 为偶数时)的平均数,称为这组数据的中位数.众数:出现次数最多的数据称为众数.截尾平均数:去掉最高分和最低分计算的平均分. *比较平均数、中位数和众数的异同: ①同:都反映一组数据的平均水平②异:平均数比较敏感,能反映所有数据的情况,缺点是易受极端值的影响;中位数和众数不受极端值的影响,运算简单,但不能反映所有数据的情况。
统计学考试计算题答案统计学试题及答案

统计学考试计算题答案统计学试题及答案一、填空题(每空1分,共10分)1.从标志与统计指标的对应关系来看,标志通常与( )相同。
2.某连续变量数列,其首组为开口组,上限为80,又知其邻组的组中值为95,则首组的组中值为( )。
3.国民收入中消费额和积累额的比例为1:0.4,这是( )相对指标。
4.在+A的公式中,A称为( )。
5.峰度是指次数分布曲线项峰的( ),是次数分布的一个重要特征。
6.用水平法求平均发展速度本质上是求( )平均数。
7.按习惯做法,采用加权调和平均形式编制的物量指标指数,其计算公式实际上是( )综合指数公式的变形。
8.对一个确定的总体,抽选的样本可能个数与( )和( )有关。
9.用来反映回归直线代表性大小和因变量估计值准确程度的指标称( )。
二、是非题(每小题1分,共10分)1.统计史上,将国势学派和图表学派统称为社会经济统计学派。
2.统计总体与总体单位在任何条件下都存在变换关系统计学原理试题及答案统计学原理试题及答案。
3.学生按身高分组,适宜采用等距分组。
4.根据组距数列计算求得的算术平均数是一个近似值。
5.基尼系数的基本公式可转化为2(S1+S2+S3)。
6.对连续时点数列求序时平均数,应采用加权算术平均方法。
7.分段平均法的数学依据是Σ(Y-YC)2=最小值。
8.平均数、指数都有静态与动态之分。
9.在不重复抽样下,从总体N中抽取容量为n的样本,则所有可能的样本个数为Nn个10.根据每对____和y的等级计算结果ΣD2=0,说明____与y之间存在完全正相关。
三、单项选择题(每小题2分,共10分)1.在综合统计指标分析^p 的基础上,对社会总体的数量特征作出归纳、推断和预测的方法是A.大量观察法B.统计分组法C.综合指标法D.模型推断法2.对同一总体选择两个或两个以上的标志分别进行简单分组,形成A.复合分组B.层叠分组C.平行分组体系D.复合分组体系3.交替标志方差的最大值为A.1B.0.5C.0.25D.04.如果采用三项移动平均修匀时间数列,那么所得修匀数列比原数列首尾各少A.一项数值B.二项数值C.三项数值D.四项数值5.可变权数是指在一个指数数列中,各个指数的A.同度量因素是变动的B.基期是变动的C.指数化因数是变动的D.时期是变动的四、多项选择题(每小题2分,共10分)1.反映以经济指标为中心的三位一体的指标总体系包括A.社会统计指标体系B.专题统计指标体系C.基层统计指标体系D.经济统计指标体系E.科技统计指标体系2.典型调查A.是一次性调查B.是专门组织的调查C.是一种深入细致的调查D.调查单位是有意识地选取的E.可用采访法取得资料3.下列指标中属于总量指标的有A.月末商品库存额B.劳动生产率C.历年产值增加额D.年末固定资金额E.某市人口净增加数4.重复抽样的特点是A.各次抽选互不影响B.各次抽选相互影响C.每次抽选时,总体单位数逐渐减少D.每次抽选时,总体单位数始终不变E.各单位被抽中的机会在各次抽选中相等5.下列关系中,相关系数小于0的现象有A.产品产量与耗电量的关系B.单位成本与产品产量的关系C.商品价格与销售量的关系D.纳税额与收入的关系E.商品流通费用率与商品销售额的关系五、计算题(每小题10分,共60分)要求:(1)写出必要的计算公式和计算过程,否则,酌情扣分。
《统计学》科目考试题库大全及答案(学生备考)

《统计学》科目考试题库大全及答案(学生备考)一、单选题1.间隔不相等的间断时点数列计算平均发展水平,应采取()A、以每次变动持续的时间长度对各时点水平加权平均B、用各间隔长度对各间隔的平均水平加权平均C、对各时点水平简单算术平均D、以数列的总速度按几何平均法计算【试题答案】:B2.划分全面调查和非全面调查的标志是()A、调查结果是否全面资料B、调查对象包括范围不同C、调查登记时间是否连续D、调查组织方式是否不同【试题答案】:B3.时间数列中,每个指标值可以相加的是()A、相对数时间数列B、时期数列C、平均数时间数列D、时点数列【试题答案】:B4.加权算术平均数的大小()A、只受各组标志值的影响B、只受各组次数的影响C、与各组标志值和次数无关D、受各组标志值和次数共同影响【试题答案】:D5.假如组距数列各组的标志值不变,而每组的次数都增加20%,则加权算术平均数()A、增加B、减少C、没有变化D、无法判断【试题答案】:C6.中位数是变量数列中()的变量值。
A、中间位置B、次数最高C、变量值最大D、最终位置【试题答案】:A7.从统计指标的作用和表现形式来看可以分为()A、数量指标和质量指标B、考核指标和非考核指标C、总量指标、相对指标和平均指标D、综合指标和样本指标【试题答案】:C8.构成统计总体的基础和前提是()A、综合性B、同质性C、大量性D、变异性【试题答案】:B9.当样本统计量的观察值未落入原假设的拒绝域时,表示()。
A、可以放心地接受原假设B、没有充足的理由否定与原假设C、没有充足的理由否定备择假设D、备择假设是错误的【试题答案】:B10.当所有观测值都落在回归直线上,则这两个变量之间的相关系数为()A、1B、-1C、+1或-1D、大于-1,小于+1【试题答案】:C11.下列变量中属于连续变量的是()A、职工人数B、设备台数C、学生体重D、工业企业数【试题答案】:C12.下列属于时点数列的是()。
统计学期末复习计算题

统计学期末复习计算题第四章统计特征值1.某车间工人日生产零件分组资料如下:要求(1)计算零件的众数、中位数和均值;(2)说明该数列的分布特征。
解:()()()())(71.6571.5601050804080408060111个=+=?-+--+=?-+--+=+--i f f f ff f L Mo)(6556010806022006021个=+=?-+=?-+=-i f S NL M mm e)(5.6420012900个===∑∑fxf x因为o e <M <M x ,所以,该数据分布属于左偏分布。
2.某公司所属三个企业生产同种产品,2002年实际产量、计划完成情况及产品优质品率资料如下:试计算(1)该公司产量计划完成百分比;(2)该公司实际的优质品率。
解:(1)产量计划完成百分比:%95.9320.5325008.02501.11502.1100250150100==++++==∑∑xm m x(2)实际优质品率:%8.9650048425015010098.025096.015095.0100==++?+?+?==∑∑fxf x3.某企业2003年一、二季度生产某产品产量资料如下:要求(1)计算平均等级指标说明二季度比一季度产品质量的变化情况;(2)由于质量变化而给该企业带来的收益(或损失)。
解:(1)平均等级:)(22.15010075050310027501111级=++?+?+?==∑∑fxfx)(5.1100300600100330026001222级=++?+?+?==∑∑fxf x二季度比一季度平均等级下降0.28级。
(2)由于质量下降而带来的损失:)(33.1683501007505080010012507501800111元=++?+?+?==∑∑fpf p)(153510030060010080030012506001800222元=++?+?+?==∑∑fpfp()())(148330100033.16831535212元-=?-=?-∑fp p由于产品质量下降而损失148330元。
统计计算练习题

统计计算练习题在统计学中,计算是不可或缺的一部分,它可以帮助我们分析和理解数据。
下面是一些统计计算的练习题,通过解答这些问题,可以增进对统计学的理解,并提升计算能力。
1. 均值计算一家超市有10种商品的价格如下:5元,6元,7元,8元,10元,12元,15元,18元,20元,21元。
计算这些商品的价格均值。
解答:将所有商品的价格相加,得到5+6+7+8+10+12+15+18+20+21=122,然后将总和除以商品的数量10,即122/10=12.2,所以这些商品的价格均值为12.2元。
2. 中位数计算某班级10位学生的考试成绩如下:80,85,88,90,92,95,97,98,99,100。
计算这些分数的中位数。
解答:首先将分数从小到大排列:80,85,88,90,92,95,97,98,99,100。
由于班级人数为10,是一个偶数,所以中位数是第5位和第6位分数的平均值。
即 (92+95)/2 = 93.5,所以这些分数的中位数为93.5。
3. 众数计算一组数据中出现次数最多的数称为众数。
某个班级10个学生的考试成绩如下:85,90,75,90,88,90,92,90,75,90。
计算这些分数的众数。
解答:将分数按照出现的次数从多到少排列:90,90,90,90,90,85,88,92,75,75。
由于90出现的次数最多,所以90是这些分数的众数。
4. 方差计算方差是度量数据集中值与其平均值偏离程度的一种统计量。
某支股票过去5天的收盘价分别为10元,12元,15元,11元,13元。
计算这些收盘价的方差。
解答:首先计算这些收盘价的平均值:(10+12+15+11+13)/5 = 12.2。
然后计算每个收盘价与平均值的差值,分别为-2.2,-0.2,2.8,-1.2,0.8。
将差值的平方相加并除以数据的数量5,即((-2.2)^2+(-0.2)^2+(2.8)^2+(-1.2)^2+(0.8)^2)/5 = 3.12,所以这些收盘价的方差为3.12。
《统计学》计算题
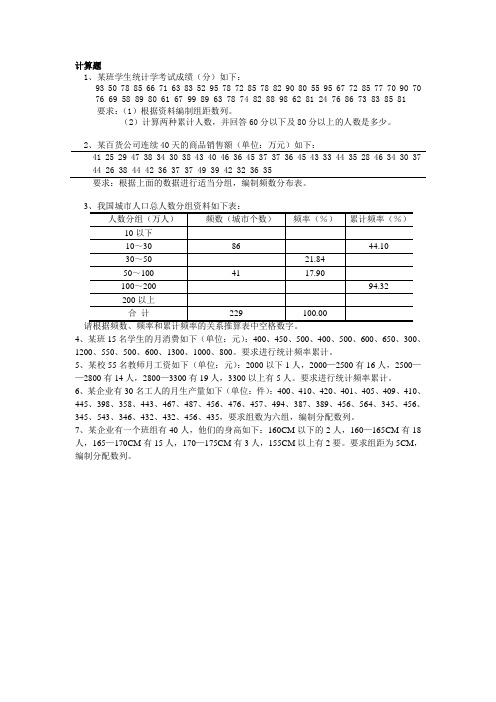
计算题1、某班学生统计学考试成绩(分)如下:93 50 78 85 66 71 63 83 52 95 78 72 85 78 82 90 80 55 95 67 72 85 77 70 90 7076 69 58 89 80 61 67 99 89 63 78 74 82 88 98 62 81 24 76 86 73 83 85 81要求:(1)根据资料编制组距数列。
(2)计算两种累计人数,并回答60分以下及80分以上的人数是多少。
2、某百货公司连续40天的商品销售额(单位:万元)如下:41 25 29 47 38 34 30 38 43 40 46 36 45 37 37 36 45 43 33 44 35 28 46 34 30 3744 26 38 44 42 36 37 37 49 39 42 32 36 35要求:根据上面的数据进行适当分组,编制频数分布表。
4、某班15名学生的月消费如下(单位:元):400、450、500、400、500、600、650、300、1200、550、500、600、1300、1000、800。
要求进行统计频率累计。
5、某校55名教师月工资如下(单位:元):2000以下1人,2000—2500有16人,2500——2800有14人,2800—3300有19人,3300以上有5人。
要求进行统计频率累计。
6、某企业有30名工人的月生产量如下(单位:件):400、410、420、401、405、409、410、445、398、358、443、467、487、456、476、457、494、387、389、456、564、345、456、345、543、346、432、432、456、435,要求组数为六组,编制分配数列。
7、某企业有一个班组有40人,他们的身高如下:160CM以下的2人,160—165CM有18人,165—170CM有15人,170—175CM有3人,155CM以上有2要。
统计学发给学生复习题(含答案)

1.只能归于某一类别的非数字型数据,称为()。
A.顺序数据 B.分类数据 C.数值型数据 D.比例数据2.人们对某件事情的“满意度”是()。
A.分类数据 B.顺序数据 C.数值型数据 D.相对数据3.下列数据中层次最高、也最精确的数据是()。
A.分类数据 B.顺序数据 C.数值型数据 D.调查数据4.一个学生的统计课考试成绩是90分,则“成绩”是()。
A.分类变量 B.顺序变量 C.数值型变量 D.品质变量5.变量值可以做无限分割的变量,称为()。
A.离散型变量 B.连续型变量 C.随机变量 D.平均变量1.B 2.B 3.C 4.C 5.B6.普查之所以要规定统一的标准调查时间,是为了( )A.避免调查数据的重复或遗漏B.使数据更全面C.使数据更及时D.使数据更大7.通过观察与实验取得统计数据时,常常采用( )A.访问调查B.观察法C.电脑辅助调查D.问卷调查8.确定调查对象是为了解决( )A.为什么要调查B.调查范围C.调查什么D.调查时间9.问卷调查中,提问项目的设计,应注意( )A一项提问可包含几项内容B.注意敏感性问题提问C.用词要确切、通俗D.时间10.我们国家和地方政府部门统计数据主要来源于( )A.普查B.抽样调查C.统计报表D.典型调查6.A7.B8.B9.C 10.C11.________ =频数÷组距,它能准确反映频数分布的实际情况。
A.组中值B.组数C.频数密度D.频率密度12.对连续型变量分组,相邻组的组限必须()。
A.重叠B.间断C.相等D.相离13.将某地区100个工厂按产值多少分组而编制的频数分布中,频数是()。
A.各组的产值数B.各组的工人数 C.各组的工厂数 D.各组职工人数14.某管理局对其所属企业的生产计划完成百分比采用如下分组,指出哪项是正确的。
()A.80%~90% 90%~99% 100%~109% 110%以上B.80%以下 90%~100% 89%~100% 100%~110%C.90%以下 90%~100% 100%~110 110%以上D.90% 90%~105% 100%~110 115%以上15.频数分布中,靠近中间的变量值分布的频数少,靠近两端的变量值分布频数多,这种分布的类型是()。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
统计学计算题复习(学生版)统计学复习提纲一、期末考卷题型1. 单项选择题;2. 多项选择题;3. 简答题4. 计算题二、知识点复习1. 统计学分类、指标、变量、参数、统计量等概念,以及各种统计图形;2.统计数据的相关内容,以及测量数据分布的测度的描述;平均数、中位数和众数的计算公式。
3. 调查的各种方式; 4. 组距数列的相关概念。
5. 置信区间的相关概念,以及单个总体均值、比例、方差的区间估计;6. 估计单个总体均值、比例时的样本容量的计算公式;7. 单个总体均值、比例、方差的假设检验;8. 相关系数和回归系数的相关知识;9. 一元、二元回归模型的EXCEL操作结果的解释以及模型的建立和检验;10. 时间序列的各种分类;平均速度等指标、移动平均法的概念等;平均发展水平的计算和季节指数的计算; 11.统计指数的相关概念,制作综合指数要点和原则,综合指数、平均指数的计算。
1统计学计算题复习一.平均数、中位数和众数的计算和三者之间的关系1.算术平均数。
也叫均值,是全部数据的算术平均,是集中趋势的最主要测度值。
主要适用于定距数据和定比数据,但不适用于定类数据和定序数据。
2.众数。
众数是一组数据中出现次数最多的变量值,用Mo表示。
主要用于测度定类数据的集中趋势。
组距式数列确定众数,是先根据出现次数确定众数所在组,然后利用下列公式计算众数的近似值:M?L?0f?f?1?i (f?f?1)?(f?f?1) 3.中位数。
中位数是一组数据按从小到大排序后,处于中间位置上的变量值,用Me表示。
主要用于测度定序数据的集中趋势。
分组数据计算中位数时,先根据公式N确定中位数所在的组,然后用下列公式计算2N?Sm?1中位数的近似值: M?L?2?i efm4.众数、中位数和算术平均数的关系 x?Me?Mo,数据是对称分布; x<Me<Mo,数据是左偏分布; x>Me>Mo,数据是右偏分布。
例题1:某地区有下列资料:人均月收入400以下400~500 500~600 600~700 700~800 800~900 900以上合计要求计算算术平均数、众数、中位数。
2户数 50 100 450 xx年收入情况,抽取一个80户组成的简单随机样本,得出每户农民年平均收入为3210元,标准差为xx年平均收入和全村年总收入的置信度为95%的置信区间。
例题2:有一大批糖果,现从中随机地取16袋, 称得重量(克)如下: 506508499503504510497512 ,设袋装糖果的重量服从正态分布, 试求总体514505493496506502509496均值? 的置信水平为的置信区间.例题3:为调查某市郊区72000户农民家庭中拥有彩电的成数,随机抽取了其中的400户,结果有92户有彩电,试求总体成数和拥有彩电户数的置信度为95%的置信区间。
三.估计单个总体均值、比例时的样本容量的计算确定样本容量首先必须满足抽样推断需要达到的置信度和精确度,可以根据估计总体均值确定样本容量、和根据估计总体比率确定样本容量。
2Z22(1)估计总体均值时,样本容量的确定:n??X222(2)估计总体比率时,样本容量的确定:n?2Z??p(1?p)?p(3)有限总体问题 A. 估计总体均值时,样本容量的确定:n?2Z2N22?XN?Z222B. 估计总体比率时,样本容量的确定:n?42Z??p(1?p)N2?pN?Z??p(1?p)222例题1:检验某食品厂本月生产的10000袋产品的重量,根据上月资料,这种产品每袋重量的标准差为25克。
要求在%的概率保证程度下,平均每袋重量的误差范围不超过5克,应抽查多少袋产品?例题2:一个市场分析人员想知道:为了确定某小区内看过某种报纸广告的家庭占多大成数,想要从该区抽选多少家庭作样本。
这个居民区共有1000户,分析人员希望以95%的置信度对这个成数作出估计,并使估计值处在真正成数附近范围之内。
在一个先前抽取的样本中,有25%的家庭看过这种广告。
试问应抽取多大的样本?例题3:回顾本章开头的引例(已知X=4小时,n=100,?=小时)如果已知居民每天观看该电视台节目时间的总体方差为1小时。
试求:(1)该地区内居民每天观看该电视台节目的平均时间的置信区间(置信度是95%); (2)如果要求估计的误差不超过27分钟,这时置信度是多少?四.单个总体均值、比例、方差的假设检验类型条件检验统计量 (1) H0,H1 拒绝域 H0:0 H1:0 H0:0 H1:0 H0:0 H1:0 H0:0 H1:0 z?Z?/2 z?Z? I 正态总体 ?2已知 Z?x??0?n (2)(3)z??Z? (1) 正态总体II (n?30) t?t?/2?n?1? t?t??n?1? t??t??n?1? t?x??0Sn (2)(3) ?2未知H0:0 H1:0 H0:0 H1:0 5方差分析表方差来源组内平方和自度均方和 F 值 F?SA(m?1)=? SE(n?m) 临界值 SA SE ST m?1 SA?SA m?1组间总和 n?m n?1 SE?SE n?m Fa例题1:(第五章习题)某牌号彩电规定无故障时间为10 000小时,厂家采取改进措施,现在从新批量彩电中抽取100台,测得平均无故障时间为10 150小时,标准差为500小时,能否据此判断该彩电无故障时间有显著增加(?=)?例题2:加油站经理希望了解驾车人士在该加油站的加油习惯。
在一周内,他随机地抽取100名驾车人士调查,得到如下结果:平均加油量等于加仑,样本标准差是加仑,有19人购买无铅汽油。
试问以的显著性水平,是否有证据说明平均加油量并非12加仑?例题3:某电器零件的平均电阻一直保持在Ω,改变加工工艺后,测得100个零件的平均电阻为Ω,如改变工艺前后电阻的标准差保持在Ω,问新工艺对此零件的电阻有无显著影响(α=)?6例题4:从某种试验物中取出24个样品,测量其发热量,计算得x=11958,样本标准差s=323,问以5%的显著水平是否可认为发热量的期望值是12100(假定发热量是服从正态分布的)?例题5. 有一批产品,取50个样品,其中含有4个次品。
在这样情况下,判断假设H0:p≤是否成立(α=)?五.一元、二元回归模型EXCEL解释以及模型的建立和检验例题1:例题2:P2787六.平均发展水平的计算和季节指数的计算1、水平指标和速度指标水平指标动态指标序时平均数序时平均数环比增长量定基增长量平均增长量计算公式 a??ai/n 1 1a1?a2an?1?an 2a?2 n?1a?a4a1?a2?f1?3?f2 a?(22 a?an n?1?fn?1)?2 (f1?f2fn?1) c?a/b △?at?at?1 △?an?a0 △?(an?a0)/n 2?(at?a0)△? n(n?1)说明适用于时期总量指标和按日连续登记的时点指标数列。
适用于不连续登记、间隔相等的时点指标数列。
适用于不连续登记间隔不相等的时点指标数列。
分子 a和分母b 按各自数列的指标形式参照(1)、(2)、(3)求序时平均数。
水平法适用于多期增长量平稳变化的数列。
累计法适用于各期增长变化较大的数列。
8速度指标环比发展速度定期发展速度平均发展速度平均增长速度年份aa1a2 ,,?,na0a1an?1 aa1a2 ,,?,na0a0a0 n nx?xi i?1 x?x2?x3xn??aia0 ? 等于环比发展速度的连乘积。
几何平均法适用于水平指标的平均发展速度计算。
累计法可查《平均发展速度查对表》。
平均发展速度-100% xx年末居民存款余额如下表:存款余额 7 034 9 110 11 545 14 746 21 519 29 662 试计算该地区“十五”期间居民年平均存款余额。
例题2、某工厂xx年第一季度人事变动资料登记如下:日期人数资料 1月1日 258 1月25日 264 2月4日275 3月6日 270 3月23日 273 直到3月底均为273人,试根据以上资料计算该厂第一季度平均人数。
例题3、某酿酒厂成品库xx年各月库存量资料如下:月份库存量 1月1日 326 2月1日 330 4月1日 335 6月1日 408 9月1日 414 12月1日 412 另:xx年初的库存量为400箱。
试计算该成品库xx年的平均库存量。
92、季节变动的测定按月平均法季度年份第一年第二年第三年三年合计同季平均数季节指数% 季度 (1)同季平均数 (2)趋势增量 (3) =(1)-(2) (4)季节指数% 一二三四全年12个季度合计 12个季度平均 100% 长期趋势剔除法一二三四平均 12个季度平均——总平均(无趋势) 100% 例题4 (习题7)某商店xx年各月销售量资料如下,用按月平均法计算季节比率。
月份 2001 2002 2003 2004 2005 1 80 150 240 280 345 2 60 90 150 140 210 3 20 40 60 80 90 4 10 25 40 30 45 5 6 10 20 12 10 6 4 8 11 9 9 7 8 12 32 37 18 8 12 20 40 48 32 9 20 35 70 83 65 10 50 85 150 140 180 11 210 340 420 470 450 12 250 350 480 510 530七.综合指数、平均指数的计算1、指数化因素×同度量因素总量指标 = 综合指数= 指数化因素×同度量因素总量指标所要研究其变动程度的引入一个同一时期的经济量,两个时期的某一经济变量起到媒介或权数的作用用102、数量指标的综合指数以基期价格计算的报告期销售额 ?q1?P0?q1P0销售量指数?? 基期实际销售额 ?q0?P0?q0P0 报告期和基期的销售基期价格作为同度量因素量,为指数化因素该指数说明多种商品销售量的综合变动程度。
分子、分母之差: ?q1P??q0P0??(q10 说明产量变动带来的销售额的增量。
q0)P03、质量指标的综合指数报告期实际销售额价格 ?P?q1?Pq111??指数 ?P0?q1?P0q1报告期销售量以报告期销售量报告期和基期的价格计算的基期销售额该指数说明多种商品价格的综合变动程度。
q??P0q1??(P1?P0)?q1分子、分母之差: ?P11说明价格变动带来的销售额的增量。
编制综合指数的一般方法原则:同度量因素与指数化因素相乘后必须是有实际经济意义的总量指标;数量指标指数以质量指标为同度量因素;质量指标指数以数量指标为同度量因素;比较:用哪种公式好?销售量 Kq?指数Kq?q1?q0p0q0?qP?10?q0p0?q0P0?q1p1?qP?11q?q0P1?0?q1p 1q1价格指数P1q1P1q1KPP0P0q1P1q1P1KPP1P0q0P0Pq10P0q011 P0q0例题1:给出某市场上四种蔬菜的销售资料如下表:品种白菜黄瓜萝卜西红柿合计销售量 ( 公斤 ) 基期 550 224 308 168 1250 计算期 560 250 3xx年单位成本 1100 1000 3000 —— xx年产量 138 90 60 ——单位成本 1050 1000 3100 ——产量 100 90 70 ——计算:三种产品产量总指数以及于产量变动使总成本变动的绝对额;单位成本总指数以及于单位成本变动使总成本变动的绝对额。
