晶格振动部分习题参考解答
固体物理基础(邵起越)2012晶格振动作业答案

3. 下图为一晶体的晶格振动谱,此晶体为简单晶格还是复式晶格?并简单解释原因。
答:复式晶格;因为存在两支光学支,原胞应包含两个原子。
4. 根据你的理解,什么是声子?声子可以有多少种?你如
何理解声子的产生、消灭?
答:格波能量等价于一谐振子能量,是量子化的,即吸收或释放能量有一个最小单位ħ 。
声子即为格波能量的量子。
一种振动模式(或格波)对应一种声子。
N个原子组成的三维晶体对应3N种集体振动模式,即具有3N种声子。
固体内原子相互作用,从而形成不同的集体振动模式。
外界与晶格振动的相互作用,不是对某个原子的相互作用,实际上是对一种或多种振动模式的作用。
外界作用使某种振动模式的能量增加,对应声子数增加,产生声子;外界作用使某种振动模式的能量减少,对应声子数减少,声子消灭。
声子的产生和消灭就是对应振动模式能量的增加和减少。
晶格振动与晶体的热学性质-习题

第三章 晶格振动与晶体的热学性质1。
什么是简谐近似?解:当原子在平衡位置附近作微小振动时,原子间的相互作用可以视为与位移成正比的虎克力,由此得出原子在其平衡位置附近做简谐振动。
这个近似即称为简谐近似。
2.试定性给出一维单原子链中振动格波的相速度和群速度对波矢的关系曲线,并简要说明其意义.解:由一维单原子链的色散关系2sin2qamβω= ,可求得一维单原子链中振动格波的相速度为22sinqa qamaqv p βω== (1)2cos qam a dq d v g βω==. 由(1)式及结合上图3。
1中可以看出,由于原子的不连续性,相速度不再是常数。
但当0→q 时,mav p β=为一常数。
这是因为当波长很长时,一个波长范围含有若干个原子,相邻原子的位相差很小,原子的不连续效应很小,格波接近与连续媒质中的弹性波。
由(2)式及结合上图3。
1中可以看出,格波的群速度也不等于相速度.但当0→q ,mav v p g β==,体现出弹性波的特征,当q 处于第一布区边界上,即aq π=时,0=g v ,而mav p βπ2=,这表明波矢位于第一布里渊区边界上的格波不能在晶体中传播,实际上它是一种驻波。
3。
周期性边界条件的物理含义是什么?引入这个条件后导致什么结果?如果晶体是无限大,q 的取值将会怎样?解:由于实际晶体的大小总是有限的,总存在边界,而显然边界上原子所处的环境与体内原子的不同,从而造成边界处原子的振动状态应该和内部原子有所差别。
考虑到边界对内部原子振动状态的影响,波恩和卡门引入了周期性边界条件.其具体含义是设想在一长为Na 的有限晶体边界之外,仍然有无穷多个相同的晶体,并且各块晶体内相对应的原子的运动情况一样,即第j 个原子和第j tN +个原子的运动情况一样,其中t =1,2,3…。
引入这个条件后,导致描写晶格振动状态的波矢q 只能取一些分立的不同值。
如果晶体是无限大,波矢q 的取值将趋于连续。
(整理)固体物理课后习题与答案

第一章 金属自由电子气体模型习题及答案1. 你是如何理解绝对零度时和常温下电子的平均动能十分相近这一点的?[解答] 自由电子论只考虑电子的动能。
在绝对零度时,金属中的自由(价)电子,分布在费米能级及其以下的能级上,即分布在一个费米球内。
在常温下,费米球内部离费米面远的状态全被电子占据,这些电子从格波获取的能量不足以使其跃迁到费米面附近或以外的空状态上,能够发生能态跃迁的仅是费米面附近的少数电子,而绝大多数电子的能态不会改变。
也就是说,常温下电子的平均动能与绝对零度时的平均动能十分相近。
2. 晶体膨胀时,费米能级如何变化?[解答] 费米能级3/222)3(2πn mE o F= , 其中n 单位体积内的价电子数目。
晶体膨胀时,体积变大,电子数目不变,n 变小,费密能级降低。
3. 为什么温度升高,费米能反而降低?[解答] 当K T 0≠时,有一半量子态被电子所占据的能级即是费米能级。
除了晶体膨胀引起费米能级降低外,温度升高,费米面附近的电子从格波获取的能量就越大,跃迁到费米面以外的电子就越多,原来有一半量子态被电子所占据的能级上的电子就少于一半,有一半量子态被电子所占据的能级必定降低,也就是说,温度生高,费米能反而降低。
4. 为什么价电子的浓度越大,价电子的平均动能就越大?[解答] 由于绝对零度时和常温下电子的平均动能十分相近,我们讨论绝对零度时电子的平均动能与电子的浓度的关系。
价电子的浓度越大,价电子的平均动能就越大,这是金属中的价电子遵从费米—狄拉克统计分布的必然结果。
在绝对零度时,电子不可能都处于最低能级上,而是在费米球中均匀分布。
由式3/120)3(πn k F =可知,价电子的浓度越大费米球的半径就越大,高能量的电子就越多,价电子的平均动能就越大。
这一点从3/2220)3(2πn m E F=和3/222)3(10353πn mE E oF ==式看得更清楚。
电子的平均动能E 正比于费米能o F E ,而费米能又正比于电子浓度32l n。
晶格能精编练习含答案

晶格能精编练习含答案晶格能一.选择题(每题2分共60分)1.下列各组元素性质的递变情况错误的是A. Na、Mg、Al原子最外层电子数依次增多B. P、S、Cl元素最高正价依次升高C. N、O、F第一电离能依次增大D. Na、K、Rb电负性逐渐减小2.泽维尔研究发现,当用激光脉冲照射NaI,使Na+和I-两核间距为1.0~1.5 nm时,呈离子键;当两核靠近约距0.28 nm时,呈共价键。
根据泽维尔的研究成果能得出的结论是() A.NaI晶体是离子晶体和分子晶体的混合物B.离子晶体可能含有共价键C.NaI晶体中既有离子键,又有共价键D.共价键和离子键没有明显的界线3.下列关于晶体的说法中,不正确的是( )①晶胞是晶体结构的基本单元②分子晶体若是密堆积方式,其配位数都是12③含有离子的晶体一定是离子晶体④共价键的强弱决定分子晶体熔沸点的高低⑤MgO远比NaCl的晶格能大⑥含有共价键的晶体一定是原子晶体⑦分子晶体的熔点一定比金属晶体低⑧NaCl晶体中,阴、阳离子的配位数都为6.A.①③④⑦B.②④⑥⑧C.③⑤⑦⑧D.③④⑥⑦4.氧化钙在2973 K时熔化,而氯化钠在1074 K时熔化,两者的离子间距离和晶体结构类似,有关它们熔点差别较大的原因叙述不正确的是()A.氧化钙晶体中阴、阳离子所带的电荷数多B.氧化钙的晶格能比氯化钠的晶格能大C.氧化钙晶体的结构类型与氯化钠晶体的结构类型不同D.在氧化钙与氯化钠的离子间距离类似的情况下,晶格能主要由阴、阳离子所带电荷的多少决定5.下列叙述错误的是A.由于ZnS的晶格能大于PbS的晶格能,所以岩浆冷却时ZnS 先析出B.金属晶体中,六方最密堆积的空间利用率大于面心立方最密堆积C.干冰晶体中,每个CO2分子周围距离相等且最近的CO2分子共有12个D.AgCl沉淀不溶于硝酸,但能溶于氨水6.离子晶体熔点的高低决定于阴、阳离子之间距离、晶格能的大小,据所学知识判断KCl、NaCl、CaO、BaO四种晶体熔点的高低顺序是()A.KCl>NaCl>BaO>CaO B.NaCl>KCl>CaO>BaOC.CaO>BaO>KCl>NaCl D.CaO>BaO>NaCl>KCl7.现有如下各种说法:①在水中H、O原子间均以化学键相结合。
固体物理 课后习题解答(黄昆版)第三章

(2)计算与该频率相当的电磁波的波长,并与 Nacl 红外吸收频率的测量 值 61 μ 进行比较。
w
波矢取值 因此
3.6 计算一维单原子链的频率分布函数 ρ (ω )
解:设单原子链长度 L=Na
q=
w
. e h c 3 . w
-6-
m o c
α e2
r +
β
rn
其中
2π 2π Na q= ×h Na Na ,状态密度 2π 每个波矢的宽度
解
•
w
M M
将
us −1
d 2us = C (Vs −1 − us ) + 10C (Vs − us ) , dt 2 d 2Vs = 10C ( us − Vs ) + C ( us +1 − Vs ) , dt 2
w
a/2
o
vs −1
. e h c 3 . w
c 10c
m o c
o
•
o
•
us
vs
解:如上图所示,质量为 M 的原子位于 2n-1, 2n+1, 2n+3 ……
质量为 m 的原子位于 2n, 2n+2, 2n+4 …… 牛顿运动方程:
m μ 2 n = − β (2 μ 2 n − μ 2 n +1 − μ 2 n −1 ) M μ 2 n +1 = − β (2 μ 2 n +1 − μ 2 n + 2 − μ 2 n )
所以可以得到
w
μl +1,m = μ (0) exp{i[(l + 1)k x a + mk y a − ωt ]} μl −1,m = μ (0) exp{i[(l − 1)k x a + mk y a − ωt ]} μl ,m+1 = μ (0) exp[i (lk x a + (m + 1)k y a − ωt )] μl ,m−1 = μ (0) exp[i (lk x a + (m − 1)k y a − ωt )]
固体物理习题解答参考答案晶体结构

r
( )
。由 R 所定义的也是一个点阵常数为
r
r r r ( i 2 的 SC 点阵,但相对于上面一个 SC 点阵位移了一个矢量 + j + k ) ,
这个点正好位于体心位置。 上面两个 SC 点阵穿套起来正好是一个 bcc 点阵,故 ni 或全为奇数,或全为偶数所定义的是一个 bcc 点阵。 (2)若
体心立方晶格原胞基矢 a1 = (−i + j + k ) a2 = (i − j + k ) a3 = (i + j − k ) 体心立方晶格原胞体积 倒格子基矢:
r
a 2
r
r
r r
ห้องสมุดไป่ตู้
a r 2
r
r r
a r 2
r
r
同理: 可见由 为基矢构成的格子为面心立方格子。
面心立方格子原胞基矢: 面心立方格子原胞体积: 倒格子基矢: 同理 可见由 为基矢构成的格子为体心立方格子。
(2) 体心立方(书P3,图1-3)
r 取 原 子 球 相 切 时 的 半 径 ( 体 对 角 线 的 1/4 ) , r= 3a / 4 ,n=2, V = a 3 所 以
ρ=
n 4π r 3 3 = 3π / 8 V
(3) 面心立方(书P4,图1-7)
r 取 原 子 球 相 切 时 的 半 径 ( 面 对 角 线 的 1/4 ) r= 2a / 4 ,n=4, V = a 3 , 所 以
则由 ε = AxT ε Ax 得
固体物理第3章 晶格振动 参考答案 2011
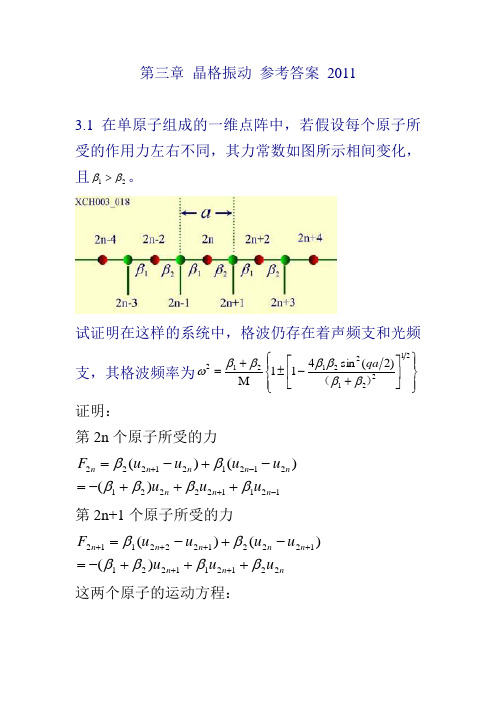
第三章 晶格振动 参考答案 20113.1 在单原子组成的一维点阵中,若假设每个原子所受的作用力左右不同,其力常数如图所示相间变化,且21ββ>。
试证明在这样的系统中,格波仍存在着声频支和光频支,其格波频率为⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎦⎤⎢⎣⎡+-±+=21221221212)2(sin 411M )(ββββββωqa 证明:第2n 个原子所受的力121122221212121222)()()(-+-++++-=-+-=n n n n n n n n u u u u u u u F ββββββ第2n+1个原子所受的力nn n n n n n n u u u u u u u F 22121122112221222112)()()(ββββββ+++-=-+-=++++++这两个原子的运动方程:n n n n n n n n u u u um u u u um 221211221121211222212)()(ββββββββ+++-=+++-=+++-+方程的解⎥⎦⎤⎢⎣⎡+-+⎥⎦⎤⎢⎣⎡-==q a n t i n q a n t i n Beu Aeu 2)12(122)2(2ωω代入到运动方程,可以得到B A e e B m A B e e A m q a i q a i q ai q a i )()(21222122122212ββββωββββω+-⎪⎪⎭⎫ ⎝⎛+=-+-⎪⎪⎭⎫ ⎝⎛+=--- 经整理,有0)(0)(22122212221221=-+-⎪⎪⎭⎫ ⎝⎛+=⎪⎪⎭⎫ ⎝⎛+--+--B m A e e B e e A m q a i q a i q ai q a i ωββββββωββ 若A ,B 有非零解,系数行列式满足,.,22122212221221=-+++-+--ωββββββωββm eeeem q a i q ai q a i q a i根据上式,有⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎦⎤⎢⎣⎡+-±+=21221221212)2(sin 411M )(ββββββωqa3.2具有两维正方点阵的某简单晶格,设原子质量为M ,晶格常量为a ,最近邻原子间相互作用的恢复力常数为β,假定原子垂直于点阵平面作横振动,试证明此二维系统的格波色散关系为)(a q a q y x cos cos 22M 2--=βω。
(整理)第三章晶格振动与晶体热学性质习题解答

第三章晶格振动与晶体热学性质习题解答1. 相距为不是晶格常数倍数的两个同种原子, 其最大振幅是否相同?[解答]以同种原子构成的一维双原子分子链为例, 相距为不是晶格常数倍数的两个同种原子, 设一个原子的振幅A, 另一个原子振幅B, 由本教科书的(3.16)可得两原子振幅之比(1)其中m原子的质量. 由本教科书的(3.20)和(3.21)两式可得声学波和光学波的频率分别为, (2). (3)将(2)(3)两式分别代入(1)式, 得声学波和光学波的振幅之比分别为, (4). (5)由于=,则由(4)(5)两式可得, . 即对于同种原子构成的一维双原子分子链, 相距为不是晶格常数倍数的两个原子, 不论是声学波还是光学波, 其最大振幅是相同的.2. 引入玻恩卡门条件的理由是什么?[解答](1)(1)方便于求解原子运动方程.由本教科书的(3.4)式可知, 除了原子链两端的两个原子外, 其它任一个原子的运动都与相邻的两个原子的运动相关. 即除了原子链两端的两个原子外, 其它原子的运动方程构成了个联立方程组. 但原子链两端的两个原子只有一个相邻原子, 其运动方程仅与一个相邻原子的运动相关, 运动方程与其它原子的运动方程迥然不同. 与其它原子的运动方程不同的这两个方程, 给整个联立方程组的求解带来了很大的困难.(2)(2)与实验结果吻合得较好.对于原子的自由运动, 边界上的原子与其它原子一样, 无时无刻不在运动. 对于有N个原子构成的的原子链, 硬性假定的边界条件是不符合事实的. 其实不论什么边界条件都与事实不符. 但为了求解近似解, 必须选取一个边界条件. 晶格振动谱的实验测定是对晶格振动理论的最有力验证(参见本教科书§3.2与§3.4). 玻恩卡门条件是晶格振动理论的前提条件. 实验测得的振动谱与理论相符的事实说明, 玻恩卡门周期性边界条件是目前较好的一个边界条件.3.什么叫简正振动模式?简正振动数目、格波数目或格波振动模式数目是否是一回事?[解答]为了使问题既简化又能抓住主要矛盾,在分析讨论晶格振动时,将原子间互作用力的泰勒级数中的非线形项忽略掉的近似称为简谐近似. 在简谐近似下, 由N 个原子构成的晶体的晶格振动, 可等效成3N个独立的谐振子的振动. 每个谐振子的振动模式称为简正振动模式, 它对应着所有的原子都以该模式的频率做振动, 它是晶格振动模式中最简单最基本的振动方式. 原子的振动, 或者说格波振动通常是这3N个简正振动模式的线形迭加.简正振动数目、格波数目或格波振动模式数目是一回事, 这个数目等于晶体中所有原子的自由度数之和, 即等于3N.4.长光学支格波与长声学支格波本质上有何差别?[解答]长光学支格波的特征是每个原胞内的不同原子做相对振动, 振动频率较高, 它包含了晶格振动频率最高的振动模式. 长声学支格波的特征是原胞内的不同原子没有相对位移, 原胞做整体运动, 振动频率较低, 它包含了晶格振动频率最低的振动模式, 波速是一常数. 任何晶体都存在声学支格波, 但简单晶格(非复式格子)晶体不存在光学支格波.5. 晶体中声子数目是否守恒?[解答]频率为的格波的(平均) 声子数为,即每一个格波的声子数都与温度有关, 因此, 晶体中声子数目不守恒, 它是温度的变量.按照德拜模型, 晶体中的声子数目N’为.作变量代换,.其中是德拜温度. 高温时,,即高温时, 晶体中的声子数目与温度成正比.低温时, ,,即低温时, 晶体中的声子数目与T 3成正比.6.温度一定,一个光学波的声子数目多呢, 还是声学波的声子数目多?[解答]频率为的格波的(平均) 声子数为.因为光学波的频率比声学波的频率高, ()大于(), 所以在温度一定情况下, 一个光学波的声子数目少于一个声学波的声子数目.7.对同一个振动模式, 温度高时的声子数目多呢, 还是温度低时的声子数目多?[解答]设温度T H>T L, 由于()小于(), 所以温度高时的声子数目多于温度低时的声子数目.8.高温时, 频率为的格波的声子数目与温度有何关系?[解答]温度很高时, , 频率为的格波的(平均) 声子数为.可见高温时, 格波的声子数目与温度近似成正比.9. 从图3.6所示实验曲线, 你能否判断哪一支格波的模式密度大? 是光学纵波呢, 还是声学纵波?[解答]从图3.6所示实验曲线可以看出, 在波矢空间内, 光学纵波振动谱线平缓, 声学纵波振动谱线较陡. 单位频率区间内光学纵波对应的波矢空间大, 声学纵波对应的波矢空间小. 格波数目与波矢空间成正比, 所以单位频率区间内光学纵波的格波数目大. 而模式密度是单位频率区间内的格波数目, 因此光学纵波的模式密度大于声学纵波的模式密度.10.喇曼散射方法中,光子会不会产生倒逆散射?[解答]晶格振动谱的测定中, 光波的波长与格波的波长越接近, 光波与声波的相互作用才越显著. 喇曼散射中所用的红外光,对晶格振动谱来说, 该波长属于长波长范围. 因此, 喇曼散射是光子与长光学波声子的相互作用. 长光学波声子的波矢很小, 相应的动量不大. 而能产生倒逆散射的条件是光的入射波矢与散射波矢要大, 散射角也要大. 与大要求波长小, 散射角大要求大(参见下图), . 但对喇曼散射来说, 这两点都不满足. 即喇曼散射中,光子不会产生倒逆散射.11.长声学格波能否导致离子晶体的宏观极化?[解答]长光学格波所以能导致离子晶体的宏观极化, 其根源是长光学格波使得原胞内不同的原子(正负离子)产生了相对位移. 长声学格波的特点是, 原胞内所有的原子没有相对位移. 因此, 长声学格波不能导致离子晶体的宏观极化.12.金刚石中的长光学纵波频率与同波矢的长光学格横波频率是否相等? 对KCl晶体, 结论又是什么?[解答]长光学纵波引起离子晶体中正负离子的相对位移, 离子的相对位移产生出宏观极化电场, 电场的方向是阻滞离子的位移, 使得有效恢复力系数变大, 对应的格波的频率变高. 长光学格横波不引起离子的位移, 不产生极化电场, 格波的频率不变. 金刚石不是离子晶体, 其长光学纵波频率与同波矢的长光学格横波频率相等. 而KCl晶体是离子晶体, 它的长光学纵波频率与同波矢的长光学格横波频率不相等, 长光学纵波频率大于同波矢的长光学格横波频率.13.何谓极化声子? 何谓电磁声子?[解答]长光学纵波引起离子晶体中正负离子的相对位移, 离子的相对位移产生出宏观极化电场, 称长光学纵波声子为极化声子.由本教科书的(3.103)式可知, 长光学横波与电磁场相耦合, 使得它具有电磁性质, 人们称长光学横波声子为电磁声子.14.你认为简单晶格存在强烈的红外吸收吗?[解答]实验已经证实, 离子晶体能强烈吸收远红外光波. 这种现象产生的根源是离子晶体中的长光学横波能与远红外电磁场发生强烈耦合. 简单晶格中不存在光学波, 所以简单晶格不会吸收远红外光波.15.对于光学横波, 对应什么物理图象?[解答]格波的频率与成正比. 说明该光学横波对应的恢复力系数.时, 恢复力消失, 发生了位移的离子再也回不到原来的平衡位置, 而到达另一平衡位置, 即离子晶体结构发生了改变(称为相变). 在这一新的结构中, 正负离子存在固定的位移偶极矩, 即产生了自发极化, 产生了一个稳定的极化电场.16. 爱因斯坦模型在低温下与实验存在偏差的根源是什么?[解答]按照爱因斯坦温度的定义, 爱因斯坦模型的格波的频率大约为, 属于光学支频率. 但光学格波在低温时对热容的贡献非常小, 低温下对热容贡献大的主要是长声学格波. 也就是说爱因斯坦没考虑声学波对热容的贡献是爱因斯坦模型在低温下与实验存在偏差的根源.17.在甚低温下, 不考虑光学波对热容的贡献合理吗?[解答]参考本教科书(3.119)式, 可得到光学波对热容贡献的表达式.在甚低温下, 对于光学波, , 上式简化为.以上两式中是光学波的模式密度, 在简谐近似下, 它与温度无关. 在甚低温下, , 即光学波对热容的贡献可以忽略. 也就是说, 在甚低温下, 不考虑光学波对热容的贡献是合理的.从声子能量来说, 光学波声子的能量很大(大于短声学波声子的能量), 它对应振幅很大的格波的振动, 这种振动只有温度很高时才能得到激发. 因此, 在甚低温下, 晶体中不存在光学波.18.在甚低温下, 德拜模型为什么与实验相符?[解答]在甚低温下, 不仅光学波得不到激发, 而且声子能量较大的短声学格波也未被激发, 得到激发的只是声子能量较小的长声学格波. 长声学格波即弹性波. 德拜模型只考虑弹性波对热容的贡献. 因此, 在甚低温下, 德拜模型与事实相符, 自然与实验相符.19.在绝对零度时还有格波存在吗? 若存在, 格波间还有能量交换吗?[解答]频率为的格波的振动能为,其中是由个声子携带的热振动能, ()是零点振动能, 声子数.绝对零度时, =0. 频率为的格波的振动能只剩下零点振动能.格波间交换能量是靠声子的碰撞实现的. 绝对零度时, 声子消失, 格波间不再交换能量.20.温度很低时, 声子的自由程很大, 当时, , 问时, 对于无限长的晶体, 是否成为热超导材料?[解答]对于电绝缘体, 热传导的载流子是声子. 当时, 声子数n. 因此,时, 不论晶体是长还是短, 都自动成为热绝缘材料.21.石英晶体的热膨胀系数很小, 问它的格林爱森常数有何特点?[解答]由本教科书(3.158)式可知, 热膨胀系数与格林爱森常数成正比. 石英晶体的热膨胀系数很小, 它的格林爱森常数也很小. 格林爱森常数大小可作为晶格非简谐效应大小的尺度. 石英晶体的格林爱森常数很小, 说明它的非简谐效应很小.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
晶格振动部分习题参考解答晶格振动部分习题参考解答9.设有一双子链最近邻原子间的力常数为和10,两种原子质量相等,且最近邻距离为a/2,求在q=0,q=aπ处的(q).并定性画出色散曲线。
m m 10 m m ____________________________________________________→←→←22aa 解:已知 21)cos 2(1212221212qa mmA ββββββω++-+=(1) 21)cos 2(12122212120a mmββββββω++-+= (2) 由题意 2=101=10代入(1)式得21)cos 20100(111222qa m m A ββββω++-= =21)cos 20101(11qa mm +-ββ=[]21)cos 20101(11qa m+-β当q=0时 0)1111(02=-==mq Aβω 当q=aπ时 mmaq A ββωπ2)911(2=-== 把2=101=10代入(2)式得 []21)cos 20101(1120qa m++βω=当q=0时m q βω2202== 时aq π±= maq βωπ2020== 10.设三维晶格的光学格波在q=0的长波极限附近有i ω(q)=0-Aq 2(A0),求证光学波频率分布函数(格波密度函数)为:g()=∑-=)1(31s i 24πV2321)(0Ai ωω- i ω≤0g()=0 i ω>0证:由格波密度函数的定义已知,对一支格波在d i ω区间格波数为g (i ω)d i ω=q d d Viτπωωω+3)2(由题意可知在长波极限下等频率面为球面则g(i ω)d i ω=dq q V234)2(ππ 当i ω0ω≤时因为 q 2=Aq i )(0ωω- Aq q i )(0ωω-=dq=-[]2121)(2)(0q A q d i i ωωω-所以g(i ω)=2121)(214)2(003i i A A V ωωωωππ--?-??= -2321204)(AV i πωω- 由模式密度的物理意义,取其绝对值而当i ω>0ω时因为i ω=0ω-Aq 2 所以Aq 2=0ω-i ω 又因为 A >0 q 2>0 (因为q 本身为实数)所以上式右边必满足0ω>i ω 即不存在i ω>0ω的格波则则 g(i ω)=0 又因为三维晶体中共要有3(S -1)支光学格波所以光学波频率分布函数为: g 21203314)()(AV i S i πωωω-=∑-= i ω≤0ωg(ω)=0 ω> 0ω 11.求一维单原子链的格波密度函数;若用德拜模型,计算系统的零点能。
解: (1)设一维单原子链长L =Na ,a 为原子间距,N 为原子数,在aπ-π≤区域内q 只能取N 个值,dq 间距内的格波数为 f(q)dq=dq L dq Na dq aN πππ222==色散关系为2sin4qam βω=(1) )cos 1(22qa m-=βω=22m ω(1-cosqa) (2)其中m =21)4(mβ由于对应于q, 取相同的值,(色散关系的对称性〕,则d 区间的格波数为g()d=2dqd Nad dq Na ωπωπ=2 (3) 由色散关系(2)可得: 2d=22a m ωsinqa dqqa a qa a dq d m m 222cos 14sin 4-==ωωωωω=222ωω-m a 代入(3)可得: g()=222ωωπ-mN(4)(2)在德拜模型下,色散关系为线性=p qp dqd υω=代入(3)式得; g()=ppLNaπυπυ=(5)则零点能为: E 零=ωωπυωωωωωd L d g p D D221)(0ηη?==pDL πυω42η (6)又因为N L d Ld g pDpDD===πυωωπυωωωω0)(得:πωυN LD p = (7) 代入(6)式得:E 零=aN Q K NN D B d 444ρυπωηη==12试用平均声子数n =(1)1--KTeωη证明:对单式格子,波长足够长的格波平均能量为KT ;当T <3)DQ T 。
解:单式格子仅有声学格波,而对声学波波长入足够长,则很低对满足Tk B ωη<<1的格波把TB K weη泰勒展开,只取到一次项TB K weη-1≈(1+T k w B η)-1=Tk wB η,平均声子数n =(1)1--KTeωη,=所以而属于该格波的声子能量为Tk n B ≈当T <<θD 时,可使用德拜模型,格波密度函数为教材(3-72)g(w)=23223ωυπρV只有≤ηTk B 的格波才能激发,已激发的格波数可表示为:ωωd g A TB K )(0η==332)(2ηT k VB ρυπ 由上已知,此时格波平均能量为K B T 则晶格热容可表示为T k Tk V TC B B V )(232ηρυπ==333242T vk B ηρυπ把(3-75)式ρυπω31)6(2VN D =及 D B D Q K =ωη代入整理为: C v =12NK B 3)(DQ T 所以晶格比热正比于(3)DQ T 得证 13.对于金刚石、Zns 、单晶硅、金属Cu 、一维三原子晶格,分别写出(1) 初基元胞内原子数;(2). 初基元胞内自由度数(3).格波支数;(4). 声学波支数 (5).光学波支数金刚石Zns Si Cu 一维三原子晶格初基元胞内原子数2 2 2 13 初基元胞内自由度数6 6 6 3 3 格波支数6 6 6 3 3 声学波支数3 3 3 3 1 光学波支数3 3 3 0 214.证明在极低温度下,一维单式晶格的热容正比于T . ωη证:在极低温度下,可用德拜模型,q 点密度为π2Lg ρυω= d区间格波数为 g()d=2ωπυωππρd L d dq L wq dw =12=?所以格波密度函数g()=ρπυL只有ηTk B ≤的格波才能被激发,已激发的格波数为; A =ηηT k Ld g B T K B ?ρπυωω=)(/0由第12题已证,在极低温度下,一维单式格子主要是长声波激发对满足kTωη<<1的格波能量为K B T 。
则晶格热容为T LK T K T LK TC BB B V ρρυππυηη22==即热容正比于T 。
15.NaCl 和KCl 具有相同的晶体结构。
其德拜温度分别为320K 和230K 。
KCl 在5K 时的定容热容量为3.8×10-2J .mol -1.K -1,试计算NaCl 在5K 和KCl 在2K 时的定容热容量。
解:设NaCl 和KCl 晶体所包含的初基元胞数相等,均为N ,T <<="" ,kcl="" =230k="" =320k="">C V =qNk(2403)1()-?x x De dxe x Q T TDQTQ D>>1. 积分上限近似可取为∞、则有154)1(2240π=-?∞x x e dx e x 34)(512DB v Q TNK C π=对KCl : T =5K 时 C v =3.8X10-2 当T =2K 时 23311024.012588.325-===v v C C (J.mol -1.K -1) 对NaCl :T=5K 时 3310311311)320()230(8.3)()(2=?=-X D D v v Q Q C C =1.41X10-2(J.mol -1.K -1)16. 在一维无限长的简单晶格中,设原子的质量均为M ,若在简谐近似下考虑原子间的长程作用力,第n 个原子与第n+m 和第n -m 个原子间的恢复力系数为m , 试求格波的色散关系。
解:设第n 个原子对平衡位置的位移为u n , 第n+m 和第n -m 个原子对平衡位置的位移为u n +m 和u n -m (m=1,2,3……), 则第n+m 和第n -m 个原子对第n 个原子的作用力为 f n,m = m (u n +m -u n )+m (u n -m -u n )=m (u n +m +u n -m -2u n )第n 个原子受的总力为 F n =∑∞=1,m mn f=∑∞=1m m (u n +m +u n -m -2u n )因此,第n 个原子的运动方程为M 22dt u d n =∑∞=1m m (u n +m +u n -m -2u n )将格波的试解 u n = A )(t qna i e ω-代入运动方程,得-M2 =∑∞=-+1)2(m iqma iqma me e β=∑∞=-1]1)[cos(2m mqma β= -4)2/(sin 12qma m m∑∞=β所以 2= M4)2/(sin 12qma m m∑∞=β17. 求半无限单原子链晶格振动的色散曲线。
提示:仍作近邻近似和简谐近似。
设原子编号为:0,1,2,3,4,······(表面原子为n=0) 原子间的力常数均为β,原子的振幅均为A 。
解:设原子编号为:0,1,2,3,4,······(表面原子为n=0)第0个原子的运动方程:22dt U d m =-β(U 0-U 1)(1)第1个原子的运动方程:212dt U d m =-β(U 1-U 2)-β(U 1-U 0)(2)第n 个原子的运动方程:22dt U d m n=β(U n+1+U n-1-2U n )(3)设试探解 U 0=A 0t i e ω n=0 (4)U n =A 0t i qna e ω+- n >1 q=q s +iq ’ (5)把试探解(5)代入(3)得色散关系:m ω2=2β[1-ch(qa)] (6)(chx=2x e x e -+ e i π=e -i π=1)另外,q=q s +iq ’’ 当q ’’=aπ时,代入上色散关系,得m ωs 2=2β[1+ch(q s a)] (7)出现ω≥ωm(体内截止频率)――――相当于在禁带中出现表面能级。
