3.2三维晶格振动

−
π π <q≤ 2 2
u2n = u2(n+ N )
晶格振动的波矢数目 =晶体的原胞数 ， 晶体的原胞数N， 晶体的原胞数 格波振动频率数目=晶体的自由度数， 晶体的自由度数 晶体的自由度数， 格波的支数 =原胞内原子的自由度数。 原胞内原子的自由度数 原胞内原子的自由度数。
ω
ωm
一维单原子链，设晶体有N个原胞。
色散关系 波矢q范围 波矢 范围 B--K条件 条件 波矢q取值 波矢 取值
u2n+1 = B e
'
u2n = Ae i[qna+qb−ωt ]
i (qna−ωt )
= Be
i (qna−ωt )
12 (β1 + β2 ) 16mMβ1β2 2 qa 2 sin ( ) ω2 = (m + M) ± (m + M) − 2mM 2 (β1 + β2 )2
3
(2π)3 每个波矢代表点占有的体积为： 每个波矢代表点占有的体积为： Vc l q′ = q + K h u α ( q ′ ) = A α s e − i (ω t − R l .( q + K h ) ) s l − i (ω t − R l .q ) = Aαs e = uα ( q ) s
(2)运动方程和解 运动方程和解
l m s uα = ⋅ ⋅ ⋅ (α=1,2,3；s=1,2,3,···,n) ； s [ (α=3,s=n)共有 个方程 共有3n个方程 共有 个方程]
..
在简谐近似下，上式的右端是位移的线性代数式。 上式的右端是位移的线性代数式。
′ 试探解： 试探解：uα l = A α s e i [(R l + r s ). q − ω t ] = A α s e i (R l . q − ω t )
的取值限制在一个倒格子原胞范围内，此区间称为简 将 q 的取值限制在一个倒格子原胞范围内，此区间称为简 约布里渊区。 约布里渊区。
波矢可取的数目： 波矢可取的数目： 3支声学波 支声学波 每个 q
∗
ω A (q )
Vc ⋅ = 3 ( 2 π)
N ( 2 π) 3
∗
= N
(3n-3)支光学波 ω O (q ) 支光学波
− i ( ω t − R l ⋅q )
a2 Rl a1
Rl + N1 a1
e
( =e
− i ω t − R l ⋅q − N 3 a 3 ⋅q
)
N 1 a 1 ⋅ q = 2πµ1 N 2 a 2 ⋅ q = 2πµ 2
N 3 a 3 ⋅ q = 2πµ 3
a1 ⋅q =
µ1
N
2π
a2 ⋅q =
µ2
1
N2
2π
为整数) (µ1、µ2、µ3为整数)
a3 ⋅q =
µ3
N3
2π
具有倒格矢的量纲，得出: 波矢 q 具有倒格矢的量纲，得出
b1 b2 b3 q = µ1 + µ2 + µ3 N1 N2 N3
( b 1、 2、 3 为倒格基矢 ) b b
b1 b 2 b 3 、 、 N1 N 2 N 3
三维格波的波矢不是连续的而是分立的， 三维格波的波矢不是连续的而是分立的，其中 为波矢的基矢，波矢的点阵亦具有周期性。 为波矢的基矢，波矢的点阵亦具有周期性。 每个波矢代表点占有的体积为： 每个波矢代表点占有的体积为：
原胞内原子的自由度数=1 原胞内原子的自由度数 原子的自由度数 晶体的自由度数 晶体的自由度数=N 的自由度数 1支格波 支格波 频率数为N 频率数为
维双原子链，设晶体有N个原胞。
原胞内原子的自由度数=2 原胞内原子的自由度数 原子的自由度数 晶体的自由度数 晶体的自由度数=2N 的自由度数 2支格波 支格波 频率数为2N 频率数为
Rl + N2 a2
a2 Rl a1
Rl + N1 a1
uα
e − i ( ω t − R l ⋅q ) = e − i (ω t − R l ⋅q − N 1 a 1 ⋅q )
l = Aα e s
− i ω t − R
(
l
.q
)
Rl + N2 a2
e − i ( ω t − R l ⋅q ) = e − i (ω t − R l ⋅q − N 2 a 2 ⋅q )
− π a
o
π a
q
§3.2 三维晶格的振动
3.2.1 色散关系 1.模型
设三维无限大的晶体,每个原胞中有 个原子 设三维无限大的晶体 每个原胞中有n个原子，各原子的质 每个原胞中有 个原子， 原胞中这n个原子 个原子平衡时的相对 量分别为 m1 , m2 , m3 ,⋅ ⋅ ⋅, mn ; 原胞中这 个原子平衡时的相对 位矢分别为 r 1 , r 2 , r 3 ,⋅ ⋅ ⋅, r n 。
∗ b1 b2 b3 (2π)3 (2π)3 ⋅ × = = = N 2 N3 N N N1 Vc
b2 N2
b1 N1
正格子原胞体积
晶体体积
(二维图示 二维图示) 二维图示
波矢密度： 波矢密度： 波矢空间中单位体积的波矢数目。
1 ( 2 π) V c
3
=
V c ( 2 π)
s
− m sω 2 Asα = ⋅ ⋅ ⋅
可得到3n 个线性齐次方程。 可得到 线性齐次方程。
Asα有非零解,必须其系数行列式为零 有非零解 必须其系数行列式为零 个实根中， 个当波矢q 在3n个实根中，其中有 个当波矢 → 0时, 个实根中 其中有3个当波矢 时
3n个ω的实根 个
ωAi = vAi (q)q,(i = 1,2,3) 这3支格波称为声学支格波。
几支声学波?几支光学波 例2：金刚石结构有几支格波 几支声学波 几支光学波 设晶 ：金刚石结构有几支格波?几支声学波 几支光学波?设晶 体有N个原胞，晶格振动模式数为多少 体有 个原胞，晶格振动模式数为多少? 个原胞 答: 晶格振动的波矢数目 =晶体的原胞数 ， 晶体的原胞数N， 格波振动频率数目=晶体的自由度数 格波振动频率数目=晶体的自由度数mNn， ， 晶体中格波的支数=原胞内原子的自由度数 。 晶体中格波的支数=原胞内原子的自由度数mn。 金刚石结构为复式格子, 每个原胞有 个原子。 个原子。 金刚石结构为复式格子 每个原胞有2个原子
其余的(3n-3)支格波的频率比声学支格波的最高频率还要 高称之为光学支格波。
3.2.2 波矢q的取值和范围
设晶体有N个原胞 原胞的基矢为 设晶体有 个原胞,原胞的基矢为： a 1 , a 2 , a 3 ; 个原胞 原胞的基矢为： 沿基矢方向各有N 个原胞, 沿基矢方向各有 1、N2、N3个原胞 N = N 1 N 2 N 3
第二节 三维晶格的振动
本节主要内容: 本节主要内容: 3.2.1 色散关系 波矢q的取值和范围 3.2.2 波矢 的取值和范围
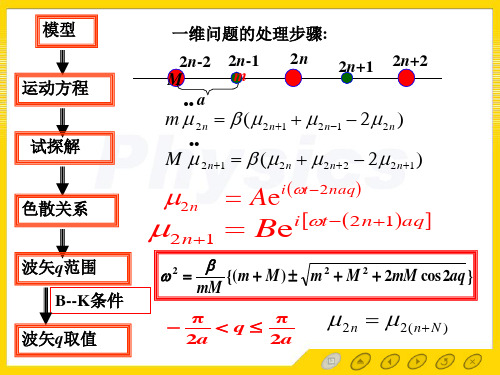
模型 运动方程 试探解
一维问题的处理步骤: 一维问题的处理步骤 2n-2 M a 2n-1 m 2 n 2n+1 2n+2
ɺɺ Mu2n = β1(u2n+1 − u2n ) − β2 (u2n −u2n−1 ) ɺɺ Mu2n+1 = β2 (u2n+2 − u2n+1 ) − β1(u2n+1−u2n )
表示平衡时顶点位矢为 的原胞内第 个原子的位矢； 平衡 个原子的位矢 Rl + r s 表示平衡时顶点位矢为 R l 的原胞内第s个原子的位矢； uα l 表示顶点位矢为 R l 的原胞内 s rs 个原子离开平衡位置在α 第s个原子离开平衡位置在α方向的位移。 个原子离开平衡位置在 方向的位移。 Rl
Rl + N1 a1 = (l1 + N1)a1 + l2 a2 + l3 a3
Rl + N2 a2 = l1 a1 + (l2 + N2 )a2 + l3 a3
根据玻恩---卡门周期性条件： 根据玻恩 卡门周期性条件： 卡门周期性条件
l l l l + N1 , l2l3 uα l = uα 1, 2, 3 = uα 1 s s s l l l l , l + N 2, l 3 uα l = uα 1, 2, 3 = uα 1 2 s s s l ,l l + N3 l l l uα l = uα 1, 2, 3 = uα 1 2 , 3 s s s
晶格振动频率数目: 晶格振动频率数目 N × 3 + N × (3n − 3) = 3nN 设晶体有N个原胞 每个原胞有 个原子, 是晶体的维数 设晶体有 个原胞,每个原胞有 个原子 m是晶体的维数。 个原胞 每个原胞有n个原子 是晶体的维数。 晶格振动的波矢数目= 晶体的原胞数N， 晶格振动的波矢数目 晶体的原胞数 ， 格波振动频率数目= 晶体的自由度数mNn（m由维度决定） 格波振动频率数目= 晶体的自由度数 由维度决定） （ 由维度决定 晶体中格波的支数= 原胞内原子的自由度数mn。 晶体中格波的支数= 原胞内原子的自由度数 。 m支声学波，m(n-1)支光学波。 支声学波， 支光学波。 支声学波 支光学波
m = 3, n = 2,
支格波， 支声学波 支声学波， 支光学波 支光学波。 有6支格波，3支声学波，3支光学波。 支格波 振动模式数为6N。 振动模式数为 。
金刚石的振动谱