信号与系统第7章(陈后金)1
合集下载
信号与系统 陈后金

*连续时间周期信号定义: t ∈ R ,存在非零T,使得
成立,则f(t) 为周期信号. *离散时间周期信号定义: k∈I , 存在非零N,使得
f [k + N ] = f [k ]
成立,则f[k] 为周期信号. 满足上述条件的最小的正 ,正N称为信号的基本周期. 最小的正T, 最小的正 *不满足周期信号定义的信号称为非周期信号. *周期信号每一周期内信号完全一样故只需研究信号 周期信号每一周期内信号完全一样故只需研究信号 在一个周期内的状况. 在一个周期内的状况.
[例2] 试判断下列系统是否为时不变系统
(1)y(t)=sin[f(t)] (2)y(t)=costf(t) (3)y(t)=4f 2(t) +3f(t) (4)y(t)=2tf(t)
时不变系统 时变系统 时不变系统 时变系统
分析: 判断系统是否为时不变系统,只需判断当输入激励f(t) 变为f(t-t0)时,相应的输出响应y(t)是否变为 y(t-t0). 注意:时不变特性只考虑系统的零状态响应 零状态响应,因此在判 零状态响应 断系统的时不变特性时,不涉及系统的初始状态 不涉及系统的初始状态. 不涉及系统的初始状态
系统的分类
系统是指由相互作用和依赖的若干事物组 成的,具有特定功能的整体.
输入信号 输出信号
信息源
传感 器
发送 设备
信道
接收 设备
传感 器
有用信息
电视广播通信系统框图
输入f(t)
防混迭 滤波器
A/D
数字处 理系统
D/A
平滑滤 波器
输出信号处理系统一系统的描述1. 数学模型
di (t ) L + Ri (t ) = f (t ) dt
信号与系统第7章(陈后金)1

Re z
-1
z平面
例:求以下序列的z变换及收敛域。
(1) x[k ] a u[k ]
k
(2)
1 0 k N - 1 x[k ] 0 其它
Im z
解:
(1)
X ( z) a z
k k 0
-k
1 -1 1 - az
|a|
Re z
ROC : z a
(2)
X ( z ) z -k
四、单边z变换的主要性质
3. 指数加权特性
z a x[ k ] X ( ) a
k Z
ROC a Rx
例:求aksin(0k) u[k] 的z变换及收敛域
解:
sin( 0 k )u[k ]
z
sin 0 z -1 1 - 2 z cos 0 z
-1 -2
z 1
对上式应用初值定理,即得
a x[1] limz{X ( z) - x[0]} lim a -1 z z 1 - az 当|a|<1时,(z-1)X(z)的收敛域包含单位圆,由终 值定理,有 z -1 0 x[] lim z -1) X (z) lim ( -1 z 1 1 - az z1
例:求以下单边周期序列的单边z变换。
k
n 0, 1, 2, 1, k 2n, (1) x[ k ] 0, k 2n 1, n 0, 1, 2,
(2) y[k ] (-1)i x[k - i]
i 0
一般情况:周期为N的单边周期序列xN[k]u[k]可以表示为第一 个周期序列x1[k]及其位移x1[k-lN]的线性组合,即
证:Z{x1[k ] x2 [k ]} Z{ x1[n]x2 [k - n]}
信号与系统-陈后金-北京交通大学-全

*周期信号每一周期内信号完全一样故只需研究信号 在一个周期内的状况。
4 能量信号与功率信号
•能量信号: 0<E<,P=0。 •功率信号: E,0<P<。
归一化能量E与归一化功率P的计算
连续信号 离散信号
EБайду номын сангаас lim
T/2 f (t ) T
N
T/2
2
dt
1 T/2 2 P lim f (t ) dt T T T/2
f1[k ] f 2 [k ] y1[k ] y2 [k ]
其中,为任意常数 • 非线性系统:不具有线性特性的系统。
• 线性系统的数学模型是线性微分方程式或线性差分 方程式。
•含有初始状态线性系统的定义
连续时间系统 若 则
f1 (t ) y1 (t ) T x1 (0)
(2) y(t ) 2 y(0) 6 f (t )
2
线性系统
非线性系统
非线性系统 线性系统
分析 注意
(3) y(t ) 4 y(0) f (t ) 3 f (t )
df (t ) (4) y (t ) 4 y (0) 3 f (t ) 2 dt
[解] :分析 任意线性系统的输出响应都可分解为零输入响应与 零状态响应两部分之和,即。 y (t ) y x (t ) y f (t ) 因此,判断一个系统是否为线性系统,应从三个方面 来判断:
5. 稳定系统与不稳定系统
•稳定系统:指有界输入产生有界输出的系统
•不稳定系统:系统输入有界而输出无界
[例1] 判断下列输出响应所对应的系统是否为 线性系统?(其中y(0)为系统的初始状态,f(t)为 系统的输入激励,y(t)为系统的输出响应)。
陈后金《信号与系统》(第2版)课后习题(连续时间信号与系统的复频域分析)

4 / 42
圣才电子书 十万种考研考证电子书、题库视频学习平台
7-5 试求图 7-2 示信号的单边 Laplace 变换。
(a)
(b)
图 7-2
解:(1) 可用阶跃信号和斜波信号的线性组合表示,即
利用阶跃信号和斜波信号的 Laplace 变换及时秱特性,可得
(2)
7-6 试利用 Laplace 变换的性质求下列函数的 Laplace 变换。
解:周期为 T 的单边周期信号 可以表示为第一个周期信号
及其时秱
的线性组合,即
(a)
(b)
(c)
(d)
图 7-1
若计算出 的 Laplace 变换 ,利用 Laplace 变换的时秱特性和线性特性,即
可求得单边周期信号的 Laplace 变换为
(1)
(2)设 因为
所以
3 / 42
圣才电子书
至
经过什么运算才得到的,则将 迚行相应的运算即可求出
,故由 Laplace
(4)由 Laplace 变换的指数加权特性,可得
(5)由 Laplace 变换的微分特性,可得
6 / 42
圣才电子书 十万种考研考证电子书、题库视频学习平台
(6)由 Laplace 变换的线性加权特性,可得
(7) 可得
的微分,由第(3)小题的结果及 Laplace 变换的微分特性,
7-9 试求下列 的初值
和终值
解:根据初值定理和终值定理即可求出信号 的初值
和终值
。但应用初
值定理时, 应为真分式,若 丌是真分式,则应将其表示为多项式不真分式乊和,
对真分式部分应用初值定理。在应用终值定理时也要注意,只有 的极点在 左半平面或
陈后金《信号与系统》(第2版)章节题库(连续时间信号与系统的复频域分析)

(5)
由微分性质
得:
。
(6)
(7) (8)
12.已知 F(s)和收敛域,求 f(t)。
17 / 76
圣才电子书 十万种考研考证电子书、题库视频学习平台
解:(1) 由于 <-3,f(t)是反因果信号,所以 (2) 由于 <-1,f(t)是反因果信号,所以 (3)
(1)f(-t)u(-t)↔F(-s);(2)f(t)u(-t)↔—F(s);
(3)f(-t)u(t)↔F(-s)。
证明:用定义式来证明
,则
(1)
令-t=λ,则
(2)
(3)
7.已知
求下列信号的拉氏变换:
(1)
解:从收敛域知 f(t)是因果信号,利用拉氏变换的性质求解。
(1) (2)
(3)
12 / 76
的单边拉普拉斯
2.因果信号 f(t)的拉普拉斯变换为 度为________。
【答案】2
2 / 76
则 f(t)在 t=0 的冲激强
圣才电子书
【解析】用长除法得
十万种考研考证电子书、题库视频学习平台
则
由于 F(s)含常数项 2,其逆变换正好对应 F(t),故 f(t)在 t=0 的冲激强度为 2。
圣才电子书 十万种考研考证电子书、题库视频学习平台
(4)
8.已知 f(t)的波形如图 7-3 所示,求下列信号的拉氏变换。
解:(1)
图 7-3
(2) (3) (4) (5) (6)
9.用拉氏变换性质求以下各题(f(t)是因果信号)。
13 / 76
圣才电子书 十万种考研考证电子书、题库视频学习平台
解:(1) (2) (3) (4)
信号与系统第七章课后答案
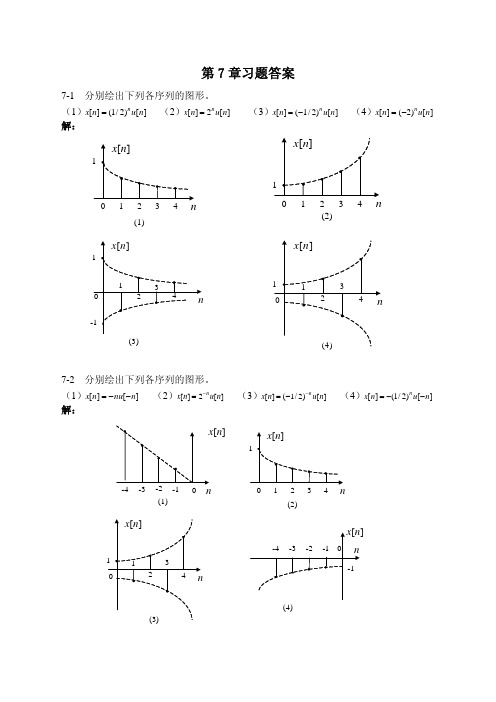
第 7 章习题答案
7-1 分别绘出下列各序列的图形。 (2)x[n] 2n u[n] (3)x[n] (1/ 2)n u[n] (4)x[n] (2) n u[ n] (1)x[n] (1/ 2)n u[n] 解:
x[ n ]
1
x[n]
1
0 1 2 (1) 3 4
n
0
1
2 3 (2)
x[n]
1
x[n]
-4
-3
-2 (1)
-1
0
n
0
1
2 (2)
3
4
n
x[n]
-4 1 0 1 2 3 4 -3 -2 -1 0
x[n] n
-1
n
(4)
(3)
7-3
分别绘出下列各序列的图形。 (2) x[n] cos
n 10 5
n (1) x[n] sin 5
1 z2 X (z) ( 1 1 2 z 1 )( 1 2 z 1 ) ( z 1 2 )( z 2 ) X (z) z 1 4 z ( z 1 2 )( z 2 ) 3( z 1 2 ) 3( z 2 )
X (z)
z 4z 3( z 1 2 ) 3 ( z 2 )
N
)
由于 x[n] 、 h[n] 均为因果序列,因此 y[n] 亦为因果序列,根据移位性质可求得
y [ n ] Z 1 [Y ( z )]
1 1 (1 a n 1 ) u [ n ] (1 a n 1 N ) u [ n N ] 1 a 1 a
7-24 计算下列序列的傅里叶变换。
(2)
7-1 分别绘出下列各序列的图形。 (2)x[n] 2n u[n] (3)x[n] (1/ 2)n u[n] (4)x[n] (2) n u[ n] (1)x[n] (1/ 2)n u[n] 解:
x[ n ]
1
x[n]
1
0 1 2 (1) 3 4
n
0
1
2 3 (2)
x[n]
1
x[n]
-4
-3
-2 (1)
-1
0
n
0
1
2 (2)
3
4
n
x[n]
-4 1 0 1 2 3 4 -3 -2 -1 0
x[n] n
-1
n
(4)
(3)
7-3
分别绘出下列各序列的图形。 (2) x[n] cos
n 10 5
n (1) x[n] sin 5
1 z2 X (z) ( 1 1 2 z 1 )( 1 2 z 1 ) ( z 1 2 )( z 2 ) X (z) z 1 4 z ( z 1 2 )( z 2 ) 3( z 1 2 ) 3( z 2 )
X (z)
z 4z 3( z 1 2 ) 3 ( z 2 )
N
)
由于 x[n] 、 h[n] 均为因果序列,因此 y[n] 亦为因果序列,根据移位性质可求得
y [ n ] Z 1 [Y ( z )]
1 1 (1 a n 1 ) u [ n ] (1 a n 1 N ) u [ n N ] 1 a 1 a
7-24 计算下列序列的傅里叶变换。
(2)
信号与系统陈后金ppt

信号的时域分析
• 连续时间信号的时域描述 • 连续时间信号的基本运算 • 离散时间信号时域描述 • 离散时间信号的基本运算 • 确定信号的时域分解
连续时间信号的时域描述
• 典型普通信号
• 正弦信号 • 实指数信号 • 虚指数信号 • 复指数信号 • 抽样函数
• 奇异信号
• 单位阶跃信号 • 冲激信号 • 斜坡信号 • 冲激偶信号
服务特 权
共享文档下载特权
VIP用户有效期内可使用共享文档下载特权下载任意下载券标价的文档(不含付费文档和VIP专享文档),每下载一篇共享文
档消耗一个共享文档下载特权。
年VIP
月VIP
连续包月VIP
享受100次共享文档下载特权,一次 发放,全年内有效
赠每的送次VI的发P类共放型的享决特文定权档。有下效载期特为权1自个V月IP,生发效放起数每量月由发您放购一买次,赠 V不 我I送 清 的P生每 零 设效月 。 置起1自 随5每动 时次月续 取共发费 消享放, 。文一前档次往下,我载持的特续账权有号,效-自
-
t0 -
(2)冲激信号具有强度,其强度就是冲激信号对时间的 定积分值。在图中用括号注明,以区分信号的幅值。
(3)冲激信号的物理意义: 表征作用时间极短,作用值很大的物理现象的数学模型
(4)冲激信号的作用:
A. 表示其他任意信号; B. 表示信号间断点的导数。
4) 冲激信号的极限模型
f (t) 1 2
二、奇异信号
1 单位阶跃信号
定义:
u(t
)
1 0
t >0 t<0
1 u(t - t0 ) 0
t >t0 t <t0
u (t ) 1
0
• 连续时间信号的时域描述 • 连续时间信号的基本运算 • 离散时间信号时域描述 • 离散时间信号的基本运算 • 确定信号的时域分解
连续时间信号的时域描述
• 典型普通信号
• 正弦信号 • 实指数信号 • 虚指数信号 • 复指数信号 • 抽样函数
• 奇异信号
• 单位阶跃信号 • 冲激信号 • 斜坡信号 • 冲激偶信号
服务特 权
共享文档下载特权
VIP用户有效期内可使用共享文档下载特权下载任意下载券标价的文档(不含付费文档和VIP专享文档),每下载一篇共享文
档消耗一个共享文档下载特权。
年VIP
月VIP
连续包月VIP
享受100次共享文档下载特权,一次 发放,全年内有效
赠每的送次VI的发P类共放型的享决特文定权档。有下效载期特为权1自个V月IP,生发效放起数每量月由发您放购一买次,赠 V不 我I送 清 的P生每 零 设效月 。 置起1自 随5每动 时次月续 取共发费 消享放, 。文一前档次往下,我载持的特续账权有号,效-自
-
t0 -
(2)冲激信号具有强度,其强度就是冲激信号对时间的 定积分值。在图中用括号注明,以区分信号的幅值。
(3)冲激信号的物理意义: 表征作用时间极短,作用值很大的物理现象的数学模型
(4)冲激信号的作用:
A. 表示其他任意信号; B. 表示信号间断点的导数。
4) 冲激信号的极限模型
f (t) 1 2
二、奇异信号
1 单位阶跃信号
定义:
u(t
)
1 0
t >0 t<0
1 u(t - t0 ) 0
t >t0 t <t0
u (t ) 1
0
北京交通大学陈后金教授信号处理课件

第8章 数字滤波器的实现
第9章 数字语音信号
主要参考书
[1] 陈后金等译:数字信号处理及MATLAB仿真, 机械工业出版社, 2015
[2] S.K. Mitra. 数字信号处理(第4版) 清华大学出版社, 2012
[3] A.V.Oppenheim. 离散时间信号处理(第3版)英文版 ,电子工业出版社, 2011 [4] 胡广书.数字信号处理.清华大学出版社(第3版), 2012. [5]P.P. Vaidyanathan, Multirate systems and filter banks, Prentice Hall, Englewood Cliffs NJ,1993. [6] N.J.Fliege, Multirate digital signal processing. John Wiley &Sons, NY,1994. [7] I.Daubechies, 小波十讲(修订版) ,国防工业出版社, 2011 [8] S. Mallat 信号处理的小波导引:稀疏方法(第3版)英文影印版, 2012
第4章 IIR数字滤波器的设计
第5章 FIR数字滤波器的设计
第6章 随机信号功率谱估计
第7章 数字系统的结构 第8章 多速率信号处理基础Fra bibliotek主要教材
第1章 概述 第2章 离散时间信号 第3章 频域概念 第4章 抽样与重建 第5章 FIR滤波器设计与分析 第6章 IIR滤波器设计与分析 第7章 抽样速率转换
近代数字信号处理
(Advanced Digital Signal Processing)
信号与图像处理研究室 电子信息工程学院
主要教材
主教材: 普通高等教育“十一五”国家级规划教材
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
对上式应用初值定理,即得
a x[1] limz{X ( z) - x[0]} lim a -1 z z 1 - az 当|a|<1时,(z-1)X(z)的收敛域包含单位圆,由终 值定理,有 z -1 0 x[] lim z -1) X (z) lim ( -1 z 1 1 - az z1
n 0
k
x[k ] X ( z ), z Rx
z
利用z变换的卷积特性,以及 1 z u[k ] , z 1 -1 1- z 可得
X ( z) Z{ x[n]} Z{x[k ]} Z{u[k ]} 1 - z -1 n 0 z max(1, Rx )
k
四、单边z变换的主要性质
为什么进行信号与系统的复频域分析? 如何进行信号的复频域分析?
如何从复频域分析系统的响应?
系统函数的地位和作用是什么?
离散时间信号的复频域分析
由离散时间Fourier变换到z变换
单边z变换及其收敛域 常用单边序列的z变换 单边z变换的性质 单边z反变换
一、由离散时间Fourier变换到z变换
例:求以下单边周期序列的单边z变换。
k
n 0, 1, 2, 1, k 2n, (1) x[ k ] 0, k 2n 1, n 0, 1, 2,
(2) y[k ] (-1)i x[k - i]
i 0
一般情况:周期为N的单边周期序列xN[k]u[k]可以表示为第一 个周期序列x1[k]及其位移x1[k-lN]的线性组合,即
1 1 - 2z -1
一、由离散时间Fourier变换到z变换
推广到一般情况
DTFT{x[k ]r }
-k k -
x[k ]r -k e- jk
z=rej
k -
x[k ]z -k X (z)
定义 z反变换
X ( z)
k -
x[k ]z -k
双边z变换
四、单边z变换的主要性质
3. 指数加权特性
z a x[ k ] X ( ) a
k Z
ROC a Rx
例:求aksin(0k) u[k] 的z变换及收敛域
解:
sin( 0 k )u[k ]
z
sin 0 z -1 1 - 2 z cos 0 z
-1 -2
z 1
解:
1 u[k ] , -1 1- z
Z
z 1
利用因果序列的位移特性和线性特性,可得
-N 1 z-N 1- z X ( z) -1 -1 1- z 1- z 1 - z -1
由于RN[k]为有限长序列,故其收敛域为
|z|>0
ROC扩大
线性加权后序列z变换的ROC可能比原序列z变换的ROC大
az -1 ,za -1 2 (1 - az )
利用z变换的线性特性,可得
1 ,za (k 1)a u[k ] -1 2 (1 - az )
k Z
四、单边z变换的主要性质
5. 序列卷积
x1[k ] x2 [k ] X1 ( z) X 2 ( z) ROC 包含Rx1∩Rx2
k 0
N -1
1- z -N 1 - z -1
ROC: z 0
有限长序列z变换的收敛域为|z|>0
三、常用单边序列的z变换
1) Z{[k]}1, z 0
1 2) Z{a u[k ]} 1 - a z -1
k
za
1 3) Z{u[k ]} 1 - z -1
z 1
四、单边z变换的主要性质
x[k ] X ( z ), z Rx
z
x1[k ] X1 ( z), z Rx1
z
x2 [k ] X 2 ( z), z Rx 2
z
1.线性特性
ax [k ] bx2[k ] aX1( z) bX2 ( z) 1
z
z max(Rx1 , Rx 2 )
i 0 k n
0
n
k
z X (z)
-n
|z|> Rx
四、单边z变换的主要性质
2. 位移特性
证明
x[k ]
Z x[k - n]u[k ] z -n [ X ( z )
k - n
x[k ]z -k ]
x[k - 2]
-1
X (z )
z
k
0
x[k - 1]
0
k
0
Re z
-1
z平面
例:求以下序列的z变换及收敛域。
(1) x[k ] a u[k ]
k
(2)
1 0 k N - 1 x[k ] 0 其它
Im z
解:
(1)
X ( z) a z
k k 0
-k
1 -1 1 - az
|a|
Re z
ROC : z a
(2)
X ( z ) z -k
x[k ] z X ( z)
二、单边z变换及其收敛域
单边z变换 收敛域(ROC)
X ( z ) x上式级数收敛的所有z的范围称为X(z)的收敛域 一般右边序列的收敛域为z平面中的一圆外区域
z Rx
Im z
ROC
Im z
|z|=1 单位圆
Re z 1
R
x
利用[k]的z变换及因果序列的位移特性,可得
(2) 将y[k]改写为 y[k ]
1 X ( z) 1 z z 1 - z -2 k
-2 -4
i 0
z 1
(-1)i x[k - i] (-1) k u[k ] * x[k ]
z 1
1 由(1)题的结果及卷积特性,可得 Y ( z) (1 z -1 )(1 - z -2 )
证:Z{x1[k ] x2 [k ]} Z{ x1[n]x2 [k - n]}
x1[n]Z{x2 [k - n]}
n
X 2 ( z ) x1[n]z
n
n
-n
X1 ( z ) X 2 ( z )
例:求 Z{
x[n]}
n 0
k
解:
设
x[n] x[k ]* u[k ]
xN [k ]u[k ] x1[k - lN ]
l 0
若计算出x1[k]的z变换X1(z),利用因果序列的位移特性
和线性特性,则可求得其单边周期序列的z变换为
Z xN [k ]u[k ] X 1 ( z ) z
l 0
- Nl
X1 ( z) 1- z -N
z 1
四、单边z变换的主要性质
4. z域微分特性
dX ( z ) kx[k ] - z dz
ROC Rx
例:求x[k]=(k+1)aku[k]的z变换及收敛域
1 a u[k ] , -1 1 - az
k Z
解:
z a
利用z域微分特性,可得
1 d 1 - az -1 k Z{ka u[k ]} - z dz
利用z变换的指数加权特性,可得
a k sin( 0 k )u[k ]
sin 0 ( z / a ) -1 1 - 2( z / a ) -1 cos 0 ( z / a ) -2
a sin 0 z -1 za 2 -1 -2 a - 2a z cos 0 z
1 x[k ] X ( z ) z k -1dz 2 πj c
C为X(z) 的收敛域(ROC )中的一闭合曲线
一、由离散时间Fourier变换到z变换
1 k -1 x[k ] c X ( z ) z dz 2 πj
物理意义: 离散信号可分解为不同频率复指数zk的线性组合
符号表示 正变换:X(z)=Z{x[k]} 或 反变换: x[k] =Z-1{X(z)}
四、单边z变换的主要性质
2. 位移特性
因果序列的位移 x[k - n] u[k - n] z-nX(z) 非因果序列的位移
n -1
|z|> Rx |z|> Rx |z|> Rx
Z x[k n]u[k ] z n [ X ( z ) - x[k ]z -k ]
x[k - n]u[k ] z -n [ X ( z) x[k ]z -k ] Z
例:求以下周期序列的单边z变换。
k
n 0, 1, 2, 1, k 2n, (1) x[ k ] 0, k 2n 1, n 0, 1, 2,
(2) y[k ] (-1)i x[k - i]
i 0
解: x[k]可表示为 x[k ] [k ] [k - 2] [k - 4] (1)
k - n
k 0 -1
四、单边z变换的主要性质
2. 位移特性
证明
x[k ]
Zx[k - n]u[k - n] z -n X ( z)
x[k - n]
z X (z )
0 k
Z{x[k - n]u[k - n]} x[k - n]z -k k - n i x[i]z -(i n )
例:求sin(0k)u[k] 和cos(0k)u[k] 的z变换及 收敛域
解:利用
Z {e
j 0 k
u[k ]}
1 1- e
j 0
z
-1
|z|>1
将上式改写,可得
a x[1] limz{X ( z) - x[0]} lim a -1 z z 1 - az 当|a|<1时,(z-1)X(z)的收敛域包含单位圆,由终 值定理,有 z -1 0 x[] lim z -1) X (z) lim ( -1 z 1 1 - az z1
n 0
k
x[k ] X ( z ), z Rx
z
利用z变换的卷积特性,以及 1 z u[k ] , z 1 -1 1- z 可得
X ( z) Z{ x[n]} Z{x[k ]} Z{u[k ]} 1 - z -1 n 0 z max(1, Rx )
k
四、单边z变换的主要性质
为什么进行信号与系统的复频域分析? 如何进行信号的复频域分析?
如何从复频域分析系统的响应?
系统函数的地位和作用是什么?
离散时间信号的复频域分析
由离散时间Fourier变换到z变换
单边z变换及其收敛域 常用单边序列的z变换 单边z变换的性质 单边z反变换
一、由离散时间Fourier变换到z变换
例:求以下单边周期序列的单边z变换。
k
n 0, 1, 2, 1, k 2n, (1) x[ k ] 0, k 2n 1, n 0, 1, 2,
(2) y[k ] (-1)i x[k - i]
i 0
一般情况:周期为N的单边周期序列xN[k]u[k]可以表示为第一 个周期序列x1[k]及其位移x1[k-lN]的线性组合,即
1 1 - 2z -1
一、由离散时间Fourier变换到z变换
推广到一般情况
DTFT{x[k ]r }
-k k -
x[k ]r -k e- jk
z=rej
k -
x[k ]z -k X (z)
定义 z反变换
X ( z)
k -
x[k ]z -k
双边z变换
四、单边z变换的主要性质
3. 指数加权特性
z a x[ k ] X ( ) a
k Z
ROC a Rx
例:求aksin(0k) u[k] 的z变换及收敛域
解:
sin( 0 k )u[k ]
z
sin 0 z -1 1 - 2 z cos 0 z
-1 -2
z 1
解:
1 u[k ] , -1 1- z
Z
z 1
利用因果序列的位移特性和线性特性,可得
-N 1 z-N 1- z X ( z) -1 -1 1- z 1- z 1 - z -1
由于RN[k]为有限长序列,故其收敛域为
|z|>0
ROC扩大
线性加权后序列z变换的ROC可能比原序列z变换的ROC大
az -1 ,za -1 2 (1 - az )
利用z变换的线性特性,可得
1 ,za (k 1)a u[k ] -1 2 (1 - az )
k Z
四、单边z变换的主要性质
5. 序列卷积
x1[k ] x2 [k ] X1 ( z) X 2 ( z) ROC 包含Rx1∩Rx2
k 0
N -1
1- z -N 1 - z -1
ROC: z 0
有限长序列z变换的收敛域为|z|>0
三、常用单边序列的z变换
1) Z{[k]}1, z 0
1 2) Z{a u[k ]} 1 - a z -1
k
za
1 3) Z{u[k ]} 1 - z -1
z 1
四、单边z变换的主要性质
x[k ] X ( z ), z Rx
z
x1[k ] X1 ( z), z Rx1
z
x2 [k ] X 2 ( z), z Rx 2
z
1.线性特性
ax [k ] bx2[k ] aX1( z) bX2 ( z) 1
z
z max(Rx1 , Rx 2 )
i 0 k n
0
n
k
z X (z)
-n
|z|> Rx
四、单边z变换的主要性质
2. 位移特性
证明
x[k ]
Z x[k - n]u[k ] z -n [ X ( z )
k - n
x[k ]z -k ]
x[k - 2]
-1
X (z )
z
k
0
x[k - 1]
0
k
0
Re z
-1
z平面
例:求以下序列的z变换及收敛域。
(1) x[k ] a u[k ]
k
(2)
1 0 k N - 1 x[k ] 0 其它
Im z
解:
(1)
X ( z) a z
k k 0
-k
1 -1 1 - az
|a|
Re z
ROC : z a
(2)
X ( z ) z -k
x[k ] z X ( z)
二、单边z变换及其收敛域
单边z变换 收敛域(ROC)
X ( z ) x上式级数收敛的所有z的范围称为X(z)的收敛域 一般右边序列的收敛域为z平面中的一圆外区域
z Rx
Im z
ROC
Im z
|z|=1 单位圆
Re z 1
R
x
利用[k]的z变换及因果序列的位移特性,可得
(2) 将y[k]改写为 y[k ]
1 X ( z) 1 z z 1 - z -2 k
-2 -4
i 0
z 1
(-1)i x[k - i] (-1) k u[k ] * x[k ]
z 1
1 由(1)题的结果及卷积特性,可得 Y ( z) (1 z -1 )(1 - z -2 )
证:Z{x1[k ] x2 [k ]} Z{ x1[n]x2 [k - n]}
x1[n]Z{x2 [k - n]}
n
X 2 ( z ) x1[n]z
n
n
-n
X1 ( z ) X 2 ( z )
例:求 Z{
x[n]}
n 0
k
解:
设
x[n] x[k ]* u[k ]
xN [k ]u[k ] x1[k - lN ]
l 0
若计算出x1[k]的z变换X1(z),利用因果序列的位移特性
和线性特性,则可求得其单边周期序列的z变换为
Z xN [k ]u[k ] X 1 ( z ) z
l 0
- Nl
X1 ( z) 1- z -N
z 1
四、单边z变换的主要性质
4. z域微分特性
dX ( z ) kx[k ] - z dz
ROC Rx
例:求x[k]=(k+1)aku[k]的z变换及收敛域
1 a u[k ] , -1 1 - az
k Z
解:
z a
利用z域微分特性,可得
1 d 1 - az -1 k Z{ka u[k ]} - z dz
利用z变换的指数加权特性,可得
a k sin( 0 k )u[k ]
sin 0 ( z / a ) -1 1 - 2( z / a ) -1 cos 0 ( z / a ) -2
a sin 0 z -1 za 2 -1 -2 a - 2a z cos 0 z
1 x[k ] X ( z ) z k -1dz 2 πj c
C为X(z) 的收敛域(ROC )中的一闭合曲线
一、由离散时间Fourier变换到z变换
1 k -1 x[k ] c X ( z ) z dz 2 πj
物理意义: 离散信号可分解为不同频率复指数zk的线性组合
符号表示 正变换:X(z)=Z{x[k]} 或 反变换: x[k] =Z-1{X(z)}
四、单边z变换的主要性质
2. 位移特性
因果序列的位移 x[k - n] u[k - n] z-nX(z) 非因果序列的位移
n -1
|z|> Rx |z|> Rx |z|> Rx
Z x[k n]u[k ] z n [ X ( z ) - x[k ]z -k ]
x[k - n]u[k ] z -n [ X ( z) x[k ]z -k ] Z
例:求以下周期序列的单边z变换。
k
n 0, 1, 2, 1, k 2n, (1) x[ k ] 0, k 2n 1, n 0, 1, 2,
(2) y[k ] (-1)i x[k - i]
i 0
解: x[k]可表示为 x[k ] [k ] [k - 2] [k - 4] (1)
k - n
k 0 -1
四、单边z变换的主要性质
2. 位移特性
证明
x[k ]
Zx[k - n]u[k - n] z -n X ( z)
x[k - n]
z X (z )
0 k
Z{x[k - n]u[k - n]} x[k - n]z -k k - n i x[i]z -(i n )
例:求sin(0k)u[k] 和cos(0k)u[k] 的z变换及 收敛域
解:利用
Z {e
j 0 k
u[k ]}
1 1- e
j 0
z
-1
|z|>1
将上式改写,可得
