2021年盈亏问题的经典例题
盈亏问题公式及例题
盈亏问题公式及例题
盈亏问题是指在经营或交易过程中，根据成本和收入的差额判断是否盈利或亏损的问题。
以下是盈亏问题的公式和例题：
1. 盈利公式：盈利 = 收入 - 成本
例题：某商店有一件商品的成本为100元，售价为150元，
计算该商品的盈利金额。
解答：盈利 = 收入 - 成本 = 150元 - 100元 = 50元。
该商品
的盈利金额为50元。
2. 盈利率公式：盈利率 = (盈利金额 / 成本) * 100%
例题：某公司某产品的成本为80元，售价为100元，求该
产品的盈利率。
解答：盈利金额 = 收入 - 成本 = 100元 - 80元 = 20元。
盈利
率 = (20元 / 80元) * 100% = 25%。
该产品的盈利率为25%。
3. 亏损公式：亏损 = 成本 - 收入
例题：某人以120元的价格购买了一件商品，但在出售时只
能以100元的价格出售，计算该人的亏损金额。
解答：亏损 = 成本 - 收入 = 120元 - 100元 = 20元。
该人的
亏损金额为20元。
4. 亏损率公式：亏损率 = (亏损金额 / 成本) * 100%
例题：某商店某商品的成本为200元，售价为150元，计算
该商品的亏损率。
解答：亏损金额 = 成本 - 收入 = 200元 - 150元 = 50元。
亏
损率 = (50元 /200元) * 100% = 25%。
该商品的亏损率为25%。
这些例题只是盈亏问题的常见形式，实际应用中可能会涉及更复杂的情况，但是根据以上公式可以解决大部分盈亏问题。
盈亏问题举例(二)
盈亏问题举例(二)例1 小明去买练习本,他付给营业员的钱买4本多1元,买6本又差2元.小明付给营业员多少钱?每本练习本多少元?分析与解答:由题意可知，小明带的钱与每本书的单价是不变的。
比较两个购买方案可知：第二方案比第一方案多买两本书，多花３元钱；也就是买两本书要花３元钱，由此可求每本书的单价。
(1)第一方案：小明带的钱买４本，盈１元；第二方案：小明带的钱买６本，亏２元．（2）“方案差”：6-4=2（本）——第二方案比第一方案多买了2本。
（3）“盈亏差”（盈亏相加）：2+1=3（元）——第二方案比第一方案多花了3元。
（4）每本单价：（2+1）÷（4-2）=3÷2=1.5（元）（5）小明带的钱：1.5×4+1=7（元）——根据第一方案也可以这样：1.5×6-2=7（元）——根据第二方案（6）检验：1.5×6-7=2（元），正确。
答语（略）例２六年级（１）班第小队的同学去栽树，如果每人栽８棵则少２７棵；如果每人栽６棵则少５棵．六（１）班第一小队有多少个同学？他们要栽多少棵树？分析与解答：由题意可知，六（１）班第一小队的人数与栽树的总棵数是不变的。
（1）第一方案中，每人栽８棵，亏２７棵；第二方案中，每人栽６棵，亏５棵。
（2）“方案差”：8-6=2（棵）——第二方案比第一方案每人少栽2棵树。
（3）“盈亏差”（亏亏相减）：27-5=22（棵）——第二方案比第一方案少亏22棵。
也就是说，如果每人少栽2棵树，那么总棵数就会少22棵，由此可求六（1）班第一小队的人数。
（4）（27-5）÷（8-6）=22÷2=11（人）（5）栽树总棵数：11×8-27=88-27=61（棵）——由第一方案求得。
盈亏问题应用题50道
盈亏问题应用题50道一、一盈一亏类型1. 小明去买糖果，如果每个糖果3元，他买了一些后还剩10元；如果每个糖果5元，他买同样多的糖果就差20元。
问小明打算买多少个糖果？2. 学校组织学生去春游，坐大巴车，如果每辆大巴坐40人，就会有10个人没座位；如果每辆大巴坐45人，就会空出20个座位。
有多少辆大巴车呢？3. 小红去买笔记本，每本笔记本2元的时候，她买完后还能剩下8元；当每本笔记本3元时，她就少了12元。
小红打算买几本笔记本？4. 工人搬砖，如果每人搬5块砖，最后还剩15块砖；要是每人搬8块砖，就差18块砖。
有几个工人在搬砖？5. 小朋友分苹果，每人分3个苹果，多出来12个；每人分5个苹果，少10个。
有多少个小朋友？6. 服装店卖衣服，每件衣服卖80元时，盈利150元；每件衣服卖100元时，亏损50元。
一共进了多少件衣服？7. 一群人去住旅店，如果每个房间住3人，多出来5人；如果每个房间住4人，少3人。
旅店有几个房间？8. 植树小组种树，如果每人种4棵树，还剩16棵树没种；如果每人种6棵树，就差8棵树。
植树小组有多少人？9. 老师给学生分练习本，每人分7本，多20本；每人分10本，少10本。
这个班有多少学生？10. 食堂买大米，如果每袋大米100元，买完后还剩300元；如果每袋大米120元，就差100元。
要买多少袋大米？二、双盈类型11. 小朋友分糖果，每人分5颗，多15颗；每人分7颗，多3颗。
有多少个小朋友？12. 学校给老师发办公用品，每人发3个笔记本多20个笔记本；每人发5个笔记本多8个笔记本。
有多少位老师？13. 工人加工零件，每天加工8个，多24个零件；每天加工10个，多8个零件。
加工了多少天？14. 同学们去划船，如果每条船坐4人，多12人；如果每条船坐6人，多4人。
有几条船？15. 果农摘苹果，每个筐装10个苹果，多30个苹果；每个筐装12个苹果，多10个苹果。
有几个筐？16. 书法班发毛笔，每人发2支，多18支；每人发4支，多6支。
第十二讲 盈亏问题
注意本题的分配对象是时间 条件转化：“每分钟走40米，则要迟到2分钟”转化为“每分钟走40米，则少80米。”“每分钟 走50米，则早到4分钟”转化为“每分钟走50米，则可多出200米。” 一盈一亏问题用公式：(盈＋亏)÷两次分配差=参与分配对象总数
笔记：一盈一亏问题用公式： (盈＋亏)÷两次分配差=参与分配对象总数 注意将条件转换成盈或亏。
【随堂练习3】某校有若干个学生寄宿学校,若每一间宿舍住6人，则多 出34人;若每间宿舍住7人,则多出4间宿舍。问宿舍有多少间?寄宿学生 有多少人?
条件转化：“每间宿舍住7人,则多出4间宿舍”转化为“每间宿舍住7 人,则少（4×7＝28）人。” 一盈一亏问题用公式：(盈＋亏)÷两次分配差=参与分配对象总数
典型例题3
三(1)班学生去公园划船，如果每条船坐4人，则少1条船;如果每条船坐6 人,则多出4条船。公园里有多少条船?三(1)班学生有多少人?
【思路指示】为了帮助理解，我们可以将题目中的条件进行转化。将条 件“如果每条船坐4人，则少1条船"转化为“如果每条船坐4人，则多出 4人”;再将条件“如果每条船坐6人，则多出4多船”转化为“如果每条 船坐6人，则差6×4=24(人)”，这样两种分配方法就相差了 24+4=28(人),这是因为每条船多坐了6-4=2(人)。根据这一关系，可知船 有28÷2= 14(条)，学生有4×(14+1)= 60(人)。列式如下: 船的条数:(6×4+4×1)÷(6-4)=14(条) 学生人数:4×(14+1)=60(人) 答:公园有14条船,三(1)班学生有60人。 【思路指示】为了帮助理解，我们可以将题目中的条件进行转化。
2021年人教版五年级数学思维训练第八讲盈亏问题
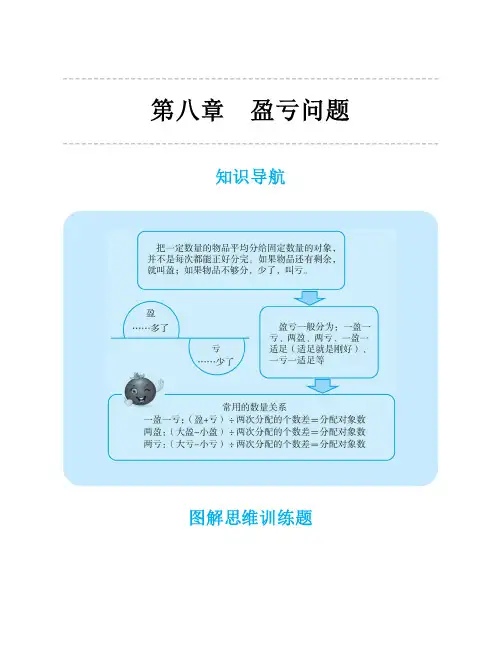
第八章 盈亏问题知识导航图解思维训练题例1 东榆小学有一组同学去栽树，如果每人栽8棵则剩12棵；如果每人栽10棵则差12棵。
问：这组同学有多少个？他们要栽多少棵树？图解思路这是一道“一盈一亏”的题，从题中可知，这组同学的人数与要栽的棵数是不变的。
比较两次植树方案，发现每人栽10棵树比栽8棵树要多需12+12=24（棵）树，怎么多出24棵树呢？就是因为每人多栽了10-8=2（棵）。
每人多栽2棵，就多栽了24棵，说明一共有24÷2=12（人），有12×8+12=108（棵）树。
规范解答总人数：(12+12)÷(10-8)=24÷2=12（人）总棵数：12×10-12=108（棵）答：这个小组有12人，要栽108棵树。
例2 幼儿园老师给小朋友分草莓，如果每人分9粒则差6粒；如果其中8人每人分6粒，其余每人发12粒，就刚好分完。
那么小朋友有多少个？草莓有多少粒？图解思路从条件“其中8人每人分6粒，其余每人发12粒，就刚好分完”可推出：如果每人都发12粒草莓，则差(12-6)×8=48（粒）。
实际上这是一道“两亏”问题，解决“两亏”问题一般用到的数量关系：（大亏-小亏）÷两次分配的个数差＝分配对象数。
规范解答(12-6)×8=48（粒）小朋友人数：(48-6)÷(12-9)=42÷3=14（人）草莓总数：14×9-6=120（粒）答：小朋友有14人，草莓有120粒。
例3 林老师开学买进篮球与足球若干个，如果少买8个篮球，多买4个足球，则篮球与足球同样多；如果在原来的基础上再买20个篮球，则篮球是足球的3倍。
林老师买来篮球和足球各多少个？图解思路第一个假设：少买8个篮球，多买4个足球，篮球与足球同样多。
由此可推出篮球比足球多12个。
第二个假设：再买20个篮球，则篮球是足球的3倍。
篮球已经比足球多12个，再买20个，这时篮球比足球多20+12=32（个）。
盈亏问题的经典例题
盈亏问题经典例题一、基础盈亏问题1. 幼儿园老师给小朋友分糖果，每人分5 颗，则多10 颗；每人分7 颗，则少8 颗。
问有多少个小朋友？多少颗糖果？-解析：根据盈亏问题公式，（盈+亏）÷两次分配之差=份数。
这里小朋友的人数为（10 + 8）÷（7 - 5）=9（个）。
糖果数为9×5 + 10 = 55（颗）。
2. 把一些书分给学生，如果每人分3 本，则余8 本；如果每人分5 本，则缺2 本。
问有多少学生？多少本书？-解析：（8 + 2）÷（5 - 3）=5（个）学生，书有5×3 + 8 = 23（本）。
3. 学校分配宿舍，每个房间住3 人，则多出20 人；每个房间住5 人，恰好住满。
问有多少间宿舍？有多少人？-解析：20÷（5 - 3）=10（间）宿舍，人数为10×5 = 50（人）。
二、复杂盈亏问题1. 少先队员去植树，如果每人挖5 个树坑，还有3 个树坑没人挖；如果其中两人各挖4 个树坑，其余每人挖 6 个树坑，就恰好挖完所有的树坑。
问共有多少少先队员？一共要挖多少个树坑？-解析：设少先队员有x 人。
5x + 3 = 2×4 + (x - 2)×6，解得x = 7。
树坑数为5×7 + 3 = 38（个）。
2. 用绳子测量井深，把绳子三折来量，井外余2 米；把绳子四折来量，还差1 米到井口。
求井深和绳长。
-解析：设井深为x 米。
3(x + 2) = 4(x - 1)，解得x = 10。
绳长为3×(10 +3. 一些苹果分给若干人，每人5 个余10 个苹果；如果人数增加到3 倍还少5 人，那么每人分 2 个苹果还缺8 个。
问有多少苹果？多少人？-解析：设原来有x 人。
5x + 10 = (3x - 5)×2 - 8，解得x = 28。
苹果数为5×28 + 10 = 150（个）。
盈亏问题经典例题
一、选择题1.小明去商店买铅笔，如果买5支则多出3元，如果买7支则还差1元。
每支铅笔的价格是多少元？A.1元B. 1.5元C. 2元D. 2.5元（答案）2.幼儿园老师给小朋友分糖果，如果每人分3颗则多出8颗，如果每人分5颗则还差14颗。
请问有多少位小朋友？A.8位B. 9位C. 10位D. 11位（答案）3.某校安排学生宿舍，如果每间住6人则多出34人，如果每间住8人则还有一间宿舍不空也不满。
问该校有多少间宿舍？可安排多少位学生？对于不空也不满的宿舍，住了多少人？（设宿舍间数为x）A.宿舍19间，学生150人，不空也不满的宿舍住了6人B.宿舍19间，学生150人，不空也不满的宿舍住了7人（答案）C.宿舍20间，学生150人，不空也不满的宿舍住了6人D.宿舍20间，学生154人，不空也不满的宿舍住了7人4.学校给参加夏令营的同学租了几辆大轿车，若每辆车乘28人则有13名同学上不了车，若每辆车乘32人则还有3个空座。
那么有多少名同学？A.121名B. 125名C. 129名D. 133名（答案）5.小红把自己的一些连环画借给她的几个同学。
若每人借5本，则差17本；若每人借3本，则差3本。
问小红的同学有几人？她一共有多少本连环画？A.同学7人，连环画32本B.同学7人，连环画38本（答案）C.同学8人，连环画32本D.同学8人，连环画38本6.将一些练习本分给若干名同学。
如果每人分4本，则多9本；如果每人分5本，则有一个同学无练习本。
问一共有多少个同学？有多少本练习本？A.同学6人，练习本21本B.同学7人，练习本37本（答案）C.同学8人，练习本29本D.同学9人，练习本36本7.猴王带领一群猴子去摘桃。
下午收工后，猴王开始分配。
若大猴分5个，小猴分3个，猴王可留10个。
若大、小猴都分4个，猴王能留下20个。
在这群猴子中，大猴（不包括猴王）比小猴多几只？A.3只B. 4只C. 5只D. 6只（答案）8.某校安排学生宿舍，如果每间4人，则有6人没有床位；如果每间6人，则空出2间宿舍。
盈亏问题双盈练习题和双亏练习题
盈亏问题双盈练习题和双亏练习题盈亏问题——双盈练习题和双亏练习题一、双盈练习题练习题1：某商店购进一批商品，每个单位的进价为30元，他预计每个单位的售价为40元。
该商店计划出售200个单位的商品，但实际上只卖出了150个单位。
请计算该商店的盈亏情况。
解答：预计总收入 = 预计售价 ×卖出单位数= 40元 × 150个= 6000元总成本 = 进价 ×卖出单位数 + 进价 × (预计卖出单位数 - 卖出单位数)= 30元 × 150个 + 30元 × (200个 - 150个)= 4500元 + 1500元= 6000元盈亏情况 = 总收入 - 总成本= 6000元 - 6000元= 0元练习题2：某人购进了1000股某公司的股票，每股成本为20元。
他预计将在未来的一个月内以25元/股的价格卖出这些股票。
然而，由于市场突然下跌，他最终只能以15元/股的价格卖出全部股票。
请计算该人的盈亏情况。
解答：总收入 = 售价 ×卖出股票数= 15元/股 × 1000股= 15000元总成本 = 成本 ×卖出股票数= 20元/股 × 1000股= 20000元盈亏情况 = 总收入 - 总成本= 15000元 - 20000元= -5000元该人的盈亏情况为亏损5000元。
二、双亏练习题练习题1：一家公司制作某种商品，每个单位的成本为10元，他们预计能以15元/单位的价格卖出这些商品。
但是，由于突然出现了新的竞争对手，他们只能以8元/单位的价格出售这些商品。
最终，他们卖出了2000个单位。
请计算该公司的盈亏情况。
解答：总收入 = 售价 ×卖出单位数= 8元/单位 × 2000个单位= 16000元总成本 = 成本 ×卖出单位数= 10元/单位 × 2000个单位= 20000元盈亏情况 = 总收入 - 总成本= 16000元 - 20000元= -4000元该公司的盈亏情况为亏损4000元。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
盈亏问题
欧阳光明（2021.03.07）
课时一
一．理解盈亏问题的三种基本类型
1“盈亏”型
例如：学而思学校四年级基础班的同学分糖果，如果每人分4粒就多9粒，如果每人分5粒则少6粒，问：有多少位同学分多少粒糖果？
【分析】由题目条件知道，同学的人数与糖果的粒数不变，比较两种分配方案，第一种没人分4粒就多9粒，，第二种每人分5粒则少6粒，两种不同方案一多一少差9+6=15（粒），相差原理在于两种方案分配数不同，两次分配数之差为5-4=1（粒）。
有盈亏问题公式得：人数：15115
⨯+=（粒）。
÷=（位），糖果的粒数为：415969
2“盈盈”型
例如：老猴子给小猴子分桃，每只小猴10个桃，就多出9个桃，每只小猴分11个桃则多出2个桃，那么一共有多少只小猴子？老猴子一共有多少个桃子？
分析：老猴子的第一种方案盈9个桃子，第二种方案盈2个，所以盈亏综合是9-2=7（个），两次分配之差是11-10-1（个）有盈亏问题公式得，有小猴子：717
÷=（只），老猴子有710979
⨯+=（个）桃子。
3.“亏亏”型
例如：学校新近一批书，将它们分给几位老师，如果每人发9本，还差9本，每人发10本，还差16本，那么一共有好多位老师，好多本书
分析：第一种方案亏9本书，第二种方案亏16本书，所以盈亏综合是16-9=7（个），两次分配之差是10-9-1（个）有盈亏问题公式得，人数：717
÷=（位），书有7×10-9=54本书。
根据以上具体题目的分析，可以得出盈亏问题的基本关系式：
(盈+亏)÷两次分得之差=人数或单位数
（盈-盈）÷两次分得之差=人数或单位数
（亏-亏）÷两次分得之差=人数或单位数
二、练习
1、“盈亏”型
（1）某校安排学生宿舍，如果每间住5人则有14人没有床位；如果每间住7人，则多出4个床位，问宿舍几间?住宿生几人?
2“盈盈”型
（1）明明过生日，同学们去给他买蛋糕，如果每人出8元，就多出了8元；每人出7元，就多出了4元．那么有多少个同学去买蛋糕？这个蛋糕的价钱是多少？
3.“亏亏”型
（1）学校新买来一批书，将它们分给几位老师，如果每人发10本，还差9本，每人发9本，还差2本，请问有多少老师？多少本书？课时二
一．复习盈亏问题的三种基本类型
（1）“盈亏”型
（2）“盈盈”型
（3）“亏亏”型
根据以上具体题目的分析，可以得出盈亏问题的基本关系式：
(盈+亏)÷两次分得之差=人数或单位数
（盈-盈）÷两次分得之差=人数或单位数
（亏-亏）÷两次分得之差=人数或单位数
二、练习
（1）秋天到了，小白兔收获了一筐萝卜，它按照计划吃的天数算了一下，如果每天吃4个，要多出48个萝卜；如果每天吃6个，则又少8个萝卜．那么小白兔买回的萝卜有多少个？计划吃多少天？（2）王老师去琴行买儿童小提琴，若买7把，则所带的钱差110元；若买5把，则所带的钱还多30元，问儿童小提琴多少钱一把？王老师一共带了多少钱？
（3）老猴子给小猴子分桃，每只小猴分8个桃，就多出9个桃，每只小猴分9个桃则多出2个桃，那么一共有多少只小猴子？老猴子一共有多少个桃子？
（4）有一批练习本发给学生，如果每人5本，则多70本，如果每人7本，则多10本，那么这个班有多少学生，多少练习本呢？（5）幼儿园给获奖的小朋友发糖，如果每人发6块就少12块，如果每人发9块就少24块，总共有多少块糖呢？
（6）学校同学去植树，如果每人种3棵，还有12棵没有种；如果每人种4棵，还有5棵没有种。
问有多少位同学参加种树？一共要
种多少棵树？
课时三
一、条件转化型的盈亏问题
这种类型的题目不能直接计算，要将其中的一个条件转化，使之成为普通盈亏问题。
例1猫妈妈给小猫分鱼，每只小猫分10条鱼，就多出8条鱼，每只小猫分11条鱼则正好分完，那么一共有多少只小猫？猫妈妈一共有多少条鱼？
例2阳光小学学生乘汽车到香山春游．如果每车坐65人，则有5人不能乘上车；如果每车多坐5人，恰多余了一辆车，问一共有几辆汽车，有多少学生？
二、练习
1、学校三年级基础班的一部分同学分小玩具，如果每人分4个就少9个，如果每人分3个正好分完，问：有多少位同学分多少个小玩具？
2、校买来一批小足球分给各班：如果每班分4个，就差66个，如果每班分2个，则正好分完，小学一共有多少个班？买来多少个足球？
3、幸福小学少先队的同学到会议室开会，若每条长椅上坐3人则多出7人，若每条长椅上多坐4人则多出3条长椅．问：到会议室开会的少先队员有多少人？
4、智康小合唱队的同学到会议室开会，若每条长椅上坐3人则多出9人，若每条长椅上坐4人则多出3人.问：合唱队有多少人？
课时四
巩固练习条件转化型的盈亏问题
1、老师给学生分糖果，如果每人分4粒就多9粒，如果每人分5粒正好分完，问：有多少位学生？共多少粒糖果？
2、小学学生乘车去春游，如果每辆车坐60人，则有15人上不了车；如果每辆车多坐5人，恰好多出一辆车.问一共有几辆车，多少个学生？
3、队员去植树，如果每人挖5个树坑，还有3个树坑没人挖；如果其中两人各挖4个树坑，其余每人挖6个树坑，就恰好挖完所有的树坑。
请问，共有多少名少先队员？共挖了多少树坑？
4、四年级学生出去划船。
老师算了一下，如果每船坐6人，那么还剩下22人没船坐。
安排时发现有3条船坏了，于是改为每船坐8人，结果还剩下6人没地方坐，请问：一共有多少学生？
5、为新生分配宿舍．每个房间住3人，则多出22人；每个房间多住5人，则空1个房间．问宿舍有多少间？新生有多少人？
6、妈妈带着一笔钱去买肉，若买10千克牛肉则还差6元，若买12千克猪肉则还剩4元．已知每千克牛肉比猪肉贵3元，问：小明妈妈带了多少钱？
7、从家去学校，如果每分走80米，结果比上课提前6分到校，如果每分走50米，则要迟到3分，那么东东家到学校的路程是______米．。