2009理论力学随堂测验参考答案
北京理工大学 理论力学真题2009年
2009 北京理工理论力学试题
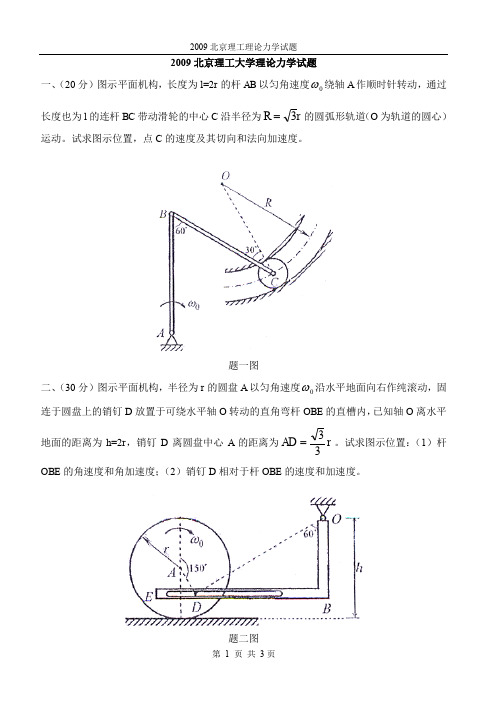
2009 北京理工大学理论力学试题 一、 (20 分)图示平面机构,长度为 l=2r 的杆 AB 以匀角速度 0 绕轴 A 作顺时针转动,通过 长度也为 l 的连杆 BC 带动滑轮的中心 C 沿半径为 R (O 为轨道的圆心) 3r 的圆弧形轨道
运动。试求图示位置,点 C 的速度及其切向和法向加速度。
题三图 四、 (20 分) 图示平面结构由直杆 O1A、 AB、 O 2B 、 CD 在接触处相互铰接而成, 已知 O1A= O2B =AB=2l,C、D、E 分别为杆 O1A、AB、O2B 的中点,系统所受到的主动载荷如图所示,且 M=2Fl,若不计各构件自重和接触处摩擦,试求杆 CD 的内力。
题四图 五、 (25 分)图示系统处于同一铅垂平面内,可沿光滑水平滑道滑动的质量为 m1=2m 的直杆 GH,通过光滑圆柱铰链 A 连接一质量为 m,长度为 l 2 3r 的均质细长直杆 AB,一刚度
第 2 页 共 3页
2009 北京理工理论力学试题
系数为 k
3mg ,原长为 l 0 2r 的弹簧,其两端分别与杆 AB 的中点 C 和杆 GH 上的点 4l
D 相连, 且 AD=r, 系统于图示直立位置处于平衡状态。 因受到微小扰动, 杆 AB 向右侧倒下, 试求杆 AB 发生 60° 转角的瞬时:杆 GH 的位移和杆 AB 的角速度。
理论力学习题及解答1
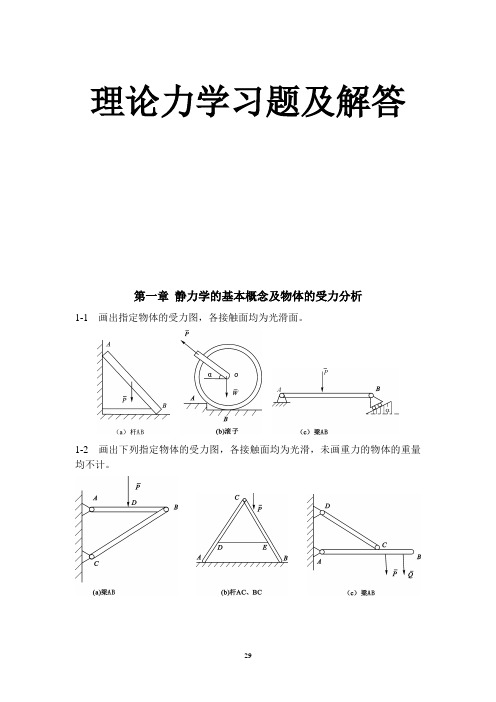
理论力学习题及解答第一章静力学的基本概念及物体的受力分析1-1 画出指定物体的受力图,各接触面均为光滑面。
1-2 画出下列指定物体的受力图,各接触面均为光滑,未画重力的物体的重量均不计。
1-3 画出下列各物体以及整体受力图,除注明者外,各物体自重不计,所有接触处均为光滑。
(a) (b)(c) (d)(e) (f)第二章平面一般力系2-1 物体重P=20kN,用绳子挂在支架的滑轮B上,绳子的另一端接在铰车D 上,如图所示。
转动铰车,物体便能升起,设滑轮的大小及滑轮转轴处的摩擦忽略不计,A、B、C三处均为铰链连接。
当物体处于平衡状态时,试求拉杆AB和支杆CB所受的力。
2-2 用一组绳悬挂重P=1kN的物体,求各绳的拉力。
2-3 某桥墩顶部受到两边桥梁传来的铅直力P1=1940kN,P2=800kN及制动力T=193kN,桥墩自重W=5280kN,风力Q=140kN。
各力作用线位置如图所示,求将这些力向基底截面中心O简化的结果,如能简化为一合力,试求出合力作用线的位置。
2-4 水平梁的支承和载荷如图所示,试求出图中A、B处的约束反力。
2-5 在图示结构计算简图中,已知q=15kN/m,求A、B、C处的约束力。
2-6 图示平面结构,自重不计,由AB、BD、DFE三杆铰接组成,已知:P=50kN,M=40kN·m,q=20kN/m,L=2m,试求固定端A的反力。
图2-6 图2-72-7 求图示多跨静定梁的支座反力。
2-8 图示结构中各杆自重不计,D、E处为铰链,B、C为链杆约束,A为固定端,已知:q G=1kN/m,q=1kN/m,M=2kN·m,L1=3m,L2=2m,试求A、B、C 处约束反力。
图2-8 图2-92-9 支架由两杆AO、CE和滑轮等组成,O、B处为铰链,A、E是固定铰支座,尺寸如图,已知:r=20cm,在滑轮上吊有重Q=1000N的物体,杆及轮重均不计,试求支座A和E以及AO杆上的O处约束反力。
09年三峡大学理论力学参考答案(A卷).

三峡大学2009年研究生入学考试试题参考答案(A 卷考试科目: 理论力学(二一、(15分如图1 所示的三铰拱桥,由左、右两拱铰接而成。
设各拱自重不计,在拱AC 上作用有载荷P 。
试分别画出拱AC 和CB 的受力图。
图1解:由于拱BC 自重不计,且只在B 、C 两处受到铰链约束,因此拱BC 为二力构件。
由于拱AC 在P 、CS '和A N 三个力作用下平衡,根据三力平衡汇交定理,确定铰链A 处约束反力A N 的方向。
拱AC 和CB 的受力,如图1a 所示。
BC'A图1a二、(25分如图2所示,压路机的辗子重kN P 20=,半径cm r 60=。
若将此辗子拉过高cm h 8=的障碍物,在其中心O 作用一水平拉力F ,求此拉力的大小和辗子对障碍物的压力。
P图2a 图2b 图2c解:选辗子为研究对象。
辗子在重力P 、地面只承力A N 、水平拉力F 和障碍物的支反力B N 的作用下处于平衡,如图2b 所示。
这些力汇交于点O ,是一个平面汇交力系。
当辗子刚离开地面时,0=A N ,拉力F 有最大值,这就是辗子越过障碍物的力学条件。
根据平面汇交力系平衡的几何条件,P 、B N 和F 三个力应组成一个封闭的力三角形。
应用三角公式,求得:αPtg F = (1αcos PN B =(2 由图中的几何关系,求得:577.0(22=---=hr h r r tg α (3代入(1、(2式:kNN kN F B 1.235.11==由作用力和反作用力关系知,辗子对障碍物的压力也等于23.1kN 。
三、(30分梯子AB 靠在墙上,与水平面成θ角。
梯子长l AB =,重量可以略去,如图3所示。
已知梯子与地面、墙面间的静摩擦系数分别为1f 、2f 。
重量为P 的人沿梯子登,他在梯上的位置C 点不能过高,即距离s AC =如超过一定限度,则梯子即将滑到。
试求s 的范围。
Ax图3a 图3b解:设人沿梯子登已到极限位置,当max s s =时,梯子处于从静止转入滑倒的临界状态。
理论力学(静力学) 随堂练习

7.(单选题) 如图所示的三铰刚架,支座A、B处的约束力一定通过 ( )。
(A)C点
(B)D点
(C)E点
(D)F点
参考答案:C
8.(单选题) 下列各式中,表示正确的是( )。
(A) (B)
(C) (D)
参考答案:D
9.(单选题) 图示用羊角锤拔钉子,下面四图所示的作用力中,( )是最省力的。
(C)必为一合力偶 (D)为一合力偶或平衡
参考答案:D
5.(单选题) 在刚体上作用3个大小相等的力,其力三角形如图所示,则该力系的简化结果( )。
(A)必为一个力
(B)必为一个力和一个力偶
(C)必为一个力偶
(D)可能平衡或简化为一力偶
参考答案:D
6.(单选题) 平面任意力系简化时若取不同的简化中心,则( )
参考答案:B
3.(单选题) 如图所示,在刚体上的四个点上各作用一个大小相等的力,则该力系的简化结果为 ( )。
(A)一个力
(B)一个力和一个力偶
(C)一个力偶
(D)平衡
参考答案:C
4.(单选题) 某平面力系,其简化结果与简化中心无关,则该力系的简化结果( )。
(A)必为一合力 (B)必平衡
(A)静止 (B)临界平衡
(C)滑动 (D)无法判断
参考答案:A
6.(单选题) 如图所示若尖劈两侧与槽之间的摩擦角均为,则欲使尖劈被打入后不致自动滑出,角应为( )。
(A) (B)
(C) (D)
参考答案Байду номын сангаасC
.(单选题) 圆轮绕固定轴O转动,某瞬时轮缘上一点的速度和加速度如下图所示,则不可能产生的运动情况为( )。
理论力学习题册答案

理论力学习题册答案第一章静力学公理与受力分析(1)一.是非题1、加减平衡力系公理不但适用于刚体,还适用于变形体。
()2、作用于刚体上三个力的作用线汇交于一点,该刚体必处于平衡状态。
()3、刚体是真实物体的一种抽象化的力学模型,在自然界中并不存在。
()4、凡是受两个力作用的刚体都是二力构件。
()5、力是滑移矢量,力沿其作用线滑移不会改变对物体的作用效果。
()二.选择题1、在下述公理、法则、原理中,只适于刚体的有()①二力平衡公理②力的平行四边形法则③加减平衡力系公理④力的可传性原理⑤作用与反作用公理三.画出下列图中指定物体受力图。
未画重力的物体不计自重,所有接触处均为光滑接触。
多杆件的整体受力图可在原图上画。
)a (球A )b (杆AB)c (杆AB 、CD 、整体)d (杆AB 、CD 、整体)e(杆AC、CB、整体)f(杆AC、CD、整体四.画出下列图中指定物体受力图。
未画重力的物体不计自重,所有接触处均为光滑接触。
多杆件的整体受力图可在原图上画。
)a(球A、球B、整体)b(杆BC、杆AC、整体第一章静力学公理与受力分析(2)一.画出下列图中指定物体受力图。
未画重力的物体不计自重,所有接触处均为光滑接触。
多杆件的整体受力图可在原图上画。
WADBCEOriginal FigureADBCEWWF AxF Ay F BFBD of the entire frame ) a(杆AB、BC、整体)b(杆AB、BC、轮E、整体)c(杆AB、CD、整体)d(杆BC带铰、杆AC、整体)e(杆CE、AH、整体)f(杆AD、杆DB、整体)g(杆AB带轮及较A、整体)h(杆AB、AC、AD、整体第二章平面汇交和力偶系一.是非题1、因为构成力偶的两个力满足F= - F’,所以力偶的合力等于零。
()2、用解析法求平面汇交力系的合力时,若选用不同的直角坐标系,则所求得的合力不同。
()3、力偶矩就是力偶。
()二.电动机重P=500N,放在水平梁AC的中央,如图所示。
理论力学习题及答案(全)

第一章静力学基础一、是非题1.力有两种作用效果,即力可以使物体的运动状态发生变化,也可以使物体发生变形。
()2.在理论力学中只研究力的外效应。
()3.两端用光滑铰链连接的构件是二力构件。
()4.作用在一个刚体上的任意两个力成平衡的必要与充分条件是:两个力的作用线相同,大小相等,方向相反。
()5.作用于刚体的力可沿其作用线移动而不改变其对刚体的运动效应。
()6.三力平衡定理指出:三力汇交于一点,则这三个力必然互相平衡。
()7.平面汇交力系平衡时,力多边形各力应首尾相接,但在作图时力的顺序可以不同。
()8.约束力的方向总是与约束所能阻止的被约束物体的运动方向一致的。
()二、选择题1.若作用在A点的两个大小不等的力F1和F2,沿同一直线但方向相反。
则其合力可以表示为。
①F1-F2;②F2-F1;③F1+F2;2.作用在一个刚体上的两个力F A、F B,满足F A=-F B的条件,则该二力可能是。
①作用力和反作用力或一对平衡的力;②一对平衡的力或一个力偶。
③一对平衡的力或一个力和一个力偶;④作用力和反作用力或一个力偶。
3.三力平衡定理是。
①共面不平行的三个力互相平衡必汇交于一点;②共面三力若平衡,必汇交于一点;③三力汇交于一点,则这三个力必互相平衡。
4.已知F1、F2、F3、F4为作用于刚体上的平面共点力系,其力矢关系如图所示为平行四边形,由此。
①力系可合成为一个力偶;②力系可合成为一个力;③力系简化为一个力和一个力偶;④力系的合力为零,力系平衡。
5.在下述原理、法则、定理中,只适用于刚体的有。
①二力平衡原理;②力的平行四边形法则;③加减平衡力系原理;④力的可传性原理;⑤作用与反作用定理。
三、填空题1.二力平衡和作用反作用定律中的两个力,都是等值、反向、共线的,所不同的是。
2.已知力F沿直线AB作用,其中一个分力的作用与AB成30°角,若欲使另一个分力的大小在所有分力中为最小,则此二分力间的夹角为度。
理论力学B答案(08-09)
理论力学B(2008-2009)一、填空题(每空3分,共48分。
请将计算结果或分析结果填入下面的各空格中,方向”表示矢量的方向与水平线的夹角为300。
)1.已知作用于点O 的力F 在水平轴x上的投影为N 233,如将该力沿左下图所示的轴x 和轴y 方向分解,该力F 沿轴x 方向的分力大小为N 3,则该力F 的大小为 3N ;方向与轴x 正向的夹角为 30o;沿轴y 方向的分力大小为 N 3 。
2. 一矩形钢板放在水平地面上,其边长a =4m ,b =3m 如右上图所示。
如按图示方向加一对力 (F ,F ’) ,转动钢板所需最小力为F =F ’=250N 。
欲使转动钢板所用的力最小,则所加力的方向为 与对角线垂直 ,最小力的大小是 150 N 。
3.左下图所示物块A 重100kN ,物块B 重25kN ,物块A 与地面的摩擦系数为0.2,滑轮处摩擦不计。
则地面对物块A 的法向约束力为 80kN ;物块A 与地面间的摩擦力为 15kN 。
4.右上图所示正立方体,各边长为2a ,一力大小等于F ,作用线如图所示。
则该力对轴x 、y 、z的矩分别为=)(F M x v aF 32 、=)(F M y v aF 34− 、=)(F M z v aF 34。
5.右图所示边长为l 的等边三角形板在其自身平面内运动,已知A 点相对B 点的加速度AB a 的大小为a ,方向平行于CB ,则此瞬时三角形板的角速度大小=ωl a2;角加速度大小=αla 23 。
34 ABxCAB6.行星齿轮机构如右图所示,已知系杆OA 长为l ,质量为m ,行星齿轮可视为匀质轮,质量为2m ,半径为r ,系杆绕轴O 转动的角速度为ω 。
则该系统动量主矢的大小为ωml 25;对轴Ο 的动量矩的大小为 ωωmrl ml −237;动能为2235ωml ;系杆OA 与行星齿轮A 的虚角位移的关系为=AOA δϕδϕl r。
二、计算题(15分)图示机构的自重不计。
理论力学课后题参考答案
1.1 沿水平方向前进的枪弹,通过某一距离s 的时间为t 1,而通过下一等距离s 的时间为2t .试证明枪弹的减速度(假定是常数)为由题可知示意图如题1.1.1图: {{SSt t 题1.1.1图设开始计时的时刻速度为0v ,由题可知枪弹作匀减速运动设减速度大小为a .则有:()()⎪⎪⎩⎪⎪⎨⎧+-+=-=221210211021221t t a t t v s at t v s 由以上两式得 11021at t s v +=再由此式得 ()()2121122t t t t t t s a +-=1.26一弹性绳上端固定,下端悬有m 及m '两质点。
设a 为绳的固有长度,b 为加m 后的伸长,c 为加m '后的伸长。
今将m '任其脱离而下坠,试证质点m 在任一瞬时离上端O 的距离为解 以绳顶端为坐标原点.建立如题1.26.1图所示坐标系.题1.26.1图设绳的弹性系数为k ,则有 kb mg = ① 当 m '脱离下坠前,m 与m '系统平衡.当m '脱离下坠前,m 在拉力T 作用下上升,之后作简运.运动微分方程为 ()ym a y k mg &&=-- ② 联立①② 得 b b a g y b g y +=+&& ③ 0=+y bg y &&齐次方程通解 t b g A t b g A Y sin cos 211+= 非齐次方程③的特解 b a Y +=0 所以③的通解b a t bg A t b g A Y +++=sin cos 211代入初始条件:0=t 时,,c b a y ++=得0,21==A c A ;故有 b a t b g c y ++=cos 即为m 在任一时刻离上端O 的距离.'1.39 一质点受一与距离23次方成反比的引力作用在一直线上运动。
试证此质点自无穷远到达a 时的速率和自a 静止出发到达4a 时的速率相同。
武汉大学2008-2009学年《理论力学》期末考试试卷及参考答案详解
解:(1)分别选择整体和ABC 为研究对象 (2分)(2)分别进行受力分析(两图每图各3分)(3) 分别列平衡方程整体:0=∑xF,0=Ex F0)(=∑F D M,023=⨯+⨯aqa a F Ey23qaF Ey -= (4分) ABC 杆:∑=0)(F C M ,0245sin 0=⨯+⨯-aqa a F BD qa F BD 22=分)四、均质杆AD 重P ,与长为2l 的铅直杆BE 的中心D 铰接,如图所示。
柔绳的下端吊有重为G 的物体M 。
假设杆BE 、滑轮和柔绳的重量都忽略不计,连线AB 以及柔绳的CH 段都处于水平位置,求固定铰链支座A 的约束反力。
(15分)解:(1)分别选整体和杆AD 为研究对象(2分)(2)分别画出它们的受力图(5分) (3)分别列平衡方程 整体: 由()0BM=∑F ,有o o 2cos30(2)cos300Ay HC F l G r F l r P l -⨯-⨯--+⨯= (3分)杆AD :由()0DM=∑F ,有o o o 2sin302cos30cos300Ax Ay F l F l P l -⨯-⨯+⨯= (3分) 其中HC F G =。
联立求解,可得2Ax F G =,2Ay P F =(2分)五、如图所示,曲柄OA 长20cm ,绕轴O 以匀角速度010/rad s ω=转动。
此曲柄借助F Bx DxBDq连杆AB 带动滑块B 沿铅垂方向运动,连杆长100cm 。
求当曲柄与连杆相互垂直并与水平线各成o45α=与o45β=时,连杆的角速度、角加速度和滑块B 的加速度。
(15分)解:(1)由A v 和B v 的速度方向可知P 点为杆AB 的速度瞬心。
故连杆的角速度为0o 20102(/)tan45100A ABOA v rad s PA AB ωω⋅⨯==== (4分) (2)由nn B A BABA τ=++a a a a 作B 点的加速度合成图。
理论力学复习题答案.doc
一、选择题1、A (4分)2、D (4分)3、B (4分)4、A (4分)二、填空题1、ωml 21,ω231ml 2、2243ωmR , ω223mR 3、 2/15三、判断题1、( × )2、( √ )3、( √ )四、计算题解:分别取CD 和整体为研究对象,列CD 杆平衡方程:02sin ,0=⨯-+⨯⇒=∑a F M a F M B C β (3分) )(5sin 2↑=-=KN aMF F B β(向上) (1分)列整体平衡方程:23sin 43,00sin ,00cos ,02=--++⇒=∑=+⨯-+⇒=∑=+⇒=∑qa Fa a F M M M F a q F F F F F F B A A NB AY Y AX X βββ (7分)将ο30,4,/1,.20,10=====βm a m KN q m KN M KN F 代入方程,联立求解,可得)(35←-=KN F AX (水平向右) , )(4↑=KN F AY (铅直向上), m KN M A .24= (逆时针) (4分)五、计算题解:动点:套筒A动系:固连在O 2B 上 (1分) 作速度平行四边形 (4分)r e a V V V += (2分)s cm V a /40=s rad A O /41=ω (3分)s cm V r /320= (2分)2/340s cm a C = (3分)六、计算题解: AB 作平面运动,以A 为基点,分析B 点的速度。
由图中几何关系得:(4分)(4分)(2分)B A BA =+r r rv v v cot30103cm/s B A v v ==o 20cm/s sin 30A BA vv ==o 1rad sBAAB v lω==方向如图所示。
七、计算题解:用动能定理求运动以杆为研究对象。
由于杆由水平位置静止开始运动,故开始的动能为零,即:01=T (1分)杆作定轴转动,转动到任一位置时的动能为222222181)32(1212121ωωml l l m ml J T O =⎥⎦⎤⎢⎣⎡-+==(1分) 在此过程中所有的力所作的功为ϕsin 6112mgl mgh W ==∑ (1分) 由2112T T W -=∑得22110sin 186ml mgl ωϕ-=23sin g l ωϕ=ω= (2分)将前式两边对时间求导,得:d 3d 2cos d d g t l tωϕωϕ= 3cos 2gl αϕ= (1分)A现求约束反力:质心加速度有切向和法向分量:tcos 4C g a OC αϕ=⋅=n2sin 2C g a OC ωϕ=⋅= (2分) 将其向直角坐标轴上投影得:t n3sin cos sin cos 4Cx C C ga a a ϕϕϕϕ=--=-t n23cos sin (13sin )4Cy C C g a a a ϕϕϕ=-+=-- (2分)由质心运动定理可得;,Cx x Cy y ma F ma F =∑=∑3sin cos 4Ox mgF ϕϕ-= 23(13sin )4Oy mg F mg ϕ--=- (3分)解得:3sin 28Ox mg F ϕ=-2(19sin )4Oy mgF ϕ=+ (2分)一、选择题(每题 4 分,共 16 分)1、A (4分)2、A (4分)3、C (4分)4、C (4分)二、填空题(每空 4 分,共 20 分)1、杆的动量为ωml 21,杆对O 轴的动量矩为ω231ml , 2、 此瞬时小环M 的牵连加速度a e 为 2ωR ,小环M 科氏加速度a C 为 r V ω2 3、夹角θ应该满足的条件是 f φθ2≤三、判断题(每空 3 分,共 9 分)1、( × )2、( √ )3、( √ )四、计算题(共 15 分)解:)(↑=-⨯+⨯=kN 35)22(1M aqa a F a F B ;(5分) )(kN 40←==qa F Cx ,)(↑=-=-=kN 53540B Cy F F F ;(5分))(kN 80←=Ax F ,)(kN5↑=Ay F ,m kN 240⋅=A M (逆时针)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
理论力学随堂测验(开卷,满分100分)
2008-2009学年第2学期 授课教师 宋梅
专业年级 学号 姓名 分数
一、 判断(每题2分,共60分)(正确的在括号内标T ,不正确的标F )
1. 两个质点沿同一圆周运动,则加速度较大的质点,其切向加速度分量一定较大。
( F )
2. 质点沿其轨迹运动时,若其速度始终垂直于加速度,则有v =常量。
( T )
3. 若刚体运动时,其上两点的轨迹相同,则该刚体一定作平动。
( F )
4. 如果刚体上各点的轨迹都是圆,该刚体不一定作定轴运动。
( T )
5. 凡是平动刚体,其上各点的法向加速度始终为零。
( F )
6. 如果角加速度与角速度的方向相同,则越转越快,属加速转动。
( T )
7. 刚体作平面平行运动时,其上任意一个垂直于固定平面的直线皆作平动。
( T )
8. 作平面平行运动的刚体,某瞬时若角速度和角加速度同时为零,则此时刚体上各点的
速度和加速度均相等。
( T )
9. 质点运动的速度越大,说明它所受的力也越大。
( F )
10. 质点的运动方向,就是质点所受合力的方向。
( F )
11. 质点在常力作用下,只有给定初始条件,才能确定质点运动的轨迹。
( T )
12. 甲站在地面上以某初速度抛一个球给在另一个位置固定站立的乙。
在球的初速度大小
不变的条件下,可供甲选择的抛出角度是无限多的。
( F )
13. 两个质点质量相同,初始速度的大小和方向也完全相同,以后任何瞬时的速度大小都
相同。
则任何瞬时,这两个质点的切向加速度大小必相同。
( T )
14. 质点系的质心位置保持不变的条件是作用于质点系的所有外力的主矢恒为零及质心
的初速度为零。
( T )
15. 若系统的动量守恒,则其对任意点的动量矩一定守恒;若系统对某点的动量矩守恒,
则其动量一定守恒。
( F )
16. 平面平行运动刚体,若所受外力对质心的主矩等于零,则刚体只能作平动。
( T )
17. 刚体平面平行运动的动能等于任取基点的平动动能加上绕基点转动动能之和。
( F )
18. 动能定理既适用于保守系,也适用于非保守系,而机械能守恒只适用于保守系。
(T )
19. 两个物体在完全弹性碰撞时,无机械能损失,若已知碰撞前两物体速度的大小,方向,
则可用动能定理完全确定碰撞后的速度。
( F )
20. 由于碰撞过程非常短促,物体在碰撞开始和结束时位置基本上没有改变,因此在碰撞
过程中,物体的位移可以忽略不计,即可以认为物体在碰撞开始时与碰撞结束时处于同一位置。
(T )
21. 刚体运动时的动能T 可以表示为J ⋅ω21。
( F )
22. 质点在某段时间里,若所受冲量等于零,则所受力做功之和等于零。
(T )
23. 若刚体有(质量)对称面,则所有与此面垂直的轴都是垂足处的惯性主轴。
( T )
24. 若不计空气阻力,在同一地点,静止下落的石块与以一定初始速度水平抛出的石块相
比,落到同一水平面的时间相同。
( T )
25. 质点系的动量越大,则动能也越大。
( F)
26. 质量越大,惯性也越大,故惯性力也越大。
( F)
27. 质点在有心力作用下将始终作平面运动。
( T)
28. 保守力沿闭合回路一周所作功一定为零。
( T )
29. 恢复系数e 衡量的是碰撞后变形恢复的程度,它等于恢复阶段冲量与变形阶段冲量的
大小之比。
( T )
30. 一个力不可能分解为一个力偶,一个力偶也不可能合成为一个力。
( T )
二、 填空(每空2分,共20分)
1. 半径为r 的刚性车轮在平直地面上以匀角速ω 纯滚动,请给出以下各量的大小:轮心的速度为 r ω ,加速度为 0 ;轮缘最低点的速度为 0 ,加速度为 2r ω ;轮缘最高点的速度为 2r ω ,加速度为 2r ω 。
2. 两个质量相同,大小一样的小球A,B ,其中A 为弹性球,B 为非弹性球,它们从同一
高度无初速下落与水平地面碰撞时,若地面对A 球的反冲量大小为A I ,对B 球的反冲
量为B I ,则A I 和B I 大小关系为 A B I I > 。
3. 一均质杆在光滑的水平面上绕其质心作匀角速度为ω的转动,假如突然将杆的一个端
点固定到水平面上,且使杆可绕该端点继续转动,则此时杆的转动角速度将 减小 。
4. 对于质量为1
kg ,半径为r 的均质实心球沿平直轨道纯滚动,假如已知其球心速度为
ˆˆ32v i j =++ ,则球的动量P 和动能T 的大小分别是 4 和 11.2 。
三、 计算(20分)
一货车连同所运货物的初始质量为0M ,在雨中沿光滑轨道按惯性行驶,初速
为0v ,已知单位时间竖直落入车中的雨水质量为α,而单位时间从槽底排水口
排出的雨水质量为β,求货车速度随时间的变化规律。
解:选前进的方向为正方向,由题意知,0m M t t αβ=+-,0F =
落入:|dm
dt α=入,r v v =-入;排出:
|dm dt β=-出,0r v =出 代入变质量物体运动微分方程:r dv dm m v F dt dt -= 有:0()()()00dv M t t v dt αβαβ+-----⨯= ,即0()dv M t t v dt αβα+-=- ,
考虑初始条件分别对速度和时间积分,有000v t v dv dt v M t t ααβ=-+-⎰
⎰, 积分得: 000
ln ln M t t v
v M αβααβ+-⇒=--,即000()M v v M t t ααβαβ-=+-。
