语音信号处理_线性预测分析
第三章语音信号的数字分析
Pe
(e)
=
1 ∆
, − ∆ ≤ e(n) ≤ ∆
2
2
0 , 其它
在上述假设的统计模型下,量化噪声的均值和方差分别为:
∫ me
=
∆ 2
e( 1
)de
=
0
−∆2 ∆
∫ σ
2 e
=
∆ 2
−∆2
e2
(1 ∆
)de
=
∆2 12
信噪比:
∑∑ SNR
=
σ x2 σ e2
=
E[x 2 (n)] E[e 2 (n)]
(输入间距) (输出间距)
∆:量化阶距(间距)
例:3bit 均匀量化器
xˆ (输出)
7∆/2
011
5∆/2
010
3∆/2
001
∆/2 000
-4∆ -3∆ -2∆ -∆
∆ 2∆ 3∆ 4∆
100 101 110 111
-∆/2 -3∆/ 2 -5∆/ 2 -7∆/ 2
x (输入)
峰— 峰值范围 (a) “上升中点”型量化器
-120 0
(b)
0.1
0.2
0.3
0.4
0.5
归一化频率
图. 矩形窗(a)和哈明窗(b)的幅频特性
•哈明窗的带宽大约是同样宽度矩形窗带宽的两倍, •哈明窗通带外的衰减也比矩形窗大一倍多 •这两种窗的衰减基本上与窗的持续时间无关 •矩形窗的谱平滑较好,但波形细节丢失,而哈明窗则反之
2、窗口的长度
•无论窗口形状如何,窗口长度N将起决定性的作用
时域波形展开:
语音信号具有很强的“ 时变特性”,在有些段 落中它具有很强的周期 性,有些段落中又具有 噪声特性,而且周期性 语音和噪声语音的特征 也在不断变化之中,只 有在较短的时间间隔( 20~200ms)语音信号 的特征才基本保持不变
语音信号处理-语音信号的线性分析

2015.10.141.介绍语音是人类相互交流和通信最方便快捷的手段。
如何高效地实现语音传输、存储或通过语音实现人机交互,是语音信号处理领域中的重要研究课题。
语音信号处理涉及数字信号处理、语言学、语音学、生理学、心理学、计算机科学以及模式识别、人工智能等诸多学科领域,是目前信息科学技术学科中发展最为迅速的一个领域。
在语音处理技术中,线性预测是第一个真正得到实际应用的技术,可以用于估计基本的语音参数,如基因周期、共振峰频率、频谱特征及声道面积函数等。
线性预测的基本原理是把待分析的信号用一个模型表示出来,信号是这个模型的输出,构成这个模型的参数是这个信号的重要特征,称为线性预测系数。
一个语音取样的现在值可以用若干个语音取样的过去值的加权线性组合来逼近。
加权系数称为预测系数。
如果利用过去p个样点值来进行预测,称为p 阶线性预测。
线性预测编码就是利用过去的样值对新鲜值进行预测,然后将样值的实际值与其预测值相减得到一个误差信号,显然误差信号的动态范围小于原始语音信号的动态范围,对误差信号进行量化编码,可大大减少量化所需的比特数,使编码速率降低。
通常情况下,随着线性预测阶数p的增大,预测误差也将会越来越小,但是p也不是一直增加的,随着线性预测阶数p的增大,信号中的可预测部分也将越来越少,预测误差的变化趋于平稳,误差减小不再明显。
此时,伴随着预测阶数p的增大,整个系统的计算量将会越来越大。
为此,对于不同的信号,我们需要确定一个最优的预测阶数p,进而进行预测分析。
在对原始语音信号进行处理之前我们要对信号进行预处理,语音信号的预处理也叫作前端处理,是指在特征提取之前,先对原始语音进行处理,使处理后的信号更能满足实际的需要,对提高处理精确度有重要的意义。
一般预处理的步骤包括采样、预加重、加窗分帧和去噪等,本文采取分帧去除直流分量后再剔除噪声帧来进行预处理,本文求阈值的方法就是求出语音信号中的高斯白噪声,然后设置阈值,将没帧信号和阈值进行比较,如果比阈值小的就是噪声帧,直接去除。
语音信号处理(电气与电子工程学院)

四、实验条件
计算机、高分辨麦克、matlab 及相关软件。 五、实验步骤
可以使用已有工作空间文件也可以自己录制一段语音(录制方法见附加内容)
1、听一下 we_be10k(可用 sound) 2、使用函数 specgram_ex3p19.显示语谱图和语音波形。对比调用参数窗长 20ms (200 点)、帧间隔 1ms(10 点)和参数窗长 5ms(50 点)、帧间隔 1ms(10 点); 再对比窗长>20ms 或小于 5ms,以及帧间隔>1ms 时的语谱图说明宽带语谱图、窄 带语谱图与时频分辨率的关系及如何得到时频折中。
1-3
在自相关法中
1-1,1-3 变为
P
∑αk rn [i − k ] = rn [i − 0],i = 1, 2,3,...p
k =1
1-4
P
En = Rn [0] − ∑αk Rn [k ]
k =1
1-5
由 1-4 可列出方程组 1-6
⎛ ⎜ ⎜
Rn Rn
[0] [1]
Rn [1] Rn [0]
图2
图3
7
采用 MATLAB 中的录音函数 wavrecord()进行语音信号的录制。同样,选 择三种频率不同的采样率对同一语音信号进行采样,试听回放效果,进行比较。
二、实验涉及的 MATLAB 子函数 Wavrecord 功能:录制语音 调用格式: filename=wavrecord(N, fs, ‘dtype’);录制一段 N/fs 秒长度的语音信号,采样率为 fs Hz,缺省值为 11025Hz,dtype 是录制声音的数据类型。具体可通过 help wavrecord 命令查阅。 y=wavrecord(N, fs, ch);与上面语句不同的是最后一个参数,ch 是指录音的声 道,ch 为 1 是单声道,ch 为 2 是双声道。 Wavread 功能:把数据文件的声音数据赋给变量 x。 【x,fs,bits】=wavread(’filename’);把数据文件的声音数据赋给变量 x,同 时把 x 的采样频率 fs 和数据的位数 bits 放进 MATLAB 的工作空间。 Sound 功能:将变量 x 的数据转换成 MATLAB 的数据文件保存。 调用格式: Sound(x,fs,bits); Save 功能:将变量 x 的数据转换成 MATLAB 的数据文件保存。 调用格式: Save‘filename’x;将数据转换成文件名与‘filename’相同,扩展名为.mat 的数据并保存,以便用 MATLAB 的各种工具进行处理。
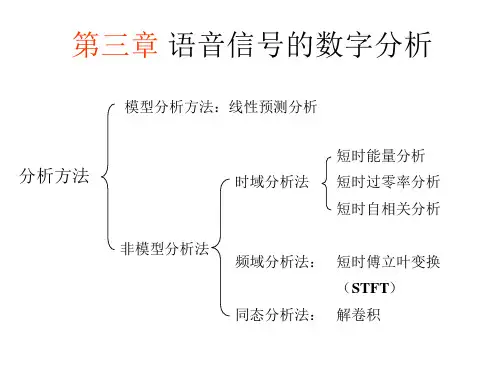
4第三章 语音信号分析---频域、倒谱、线性预测 语音信号处理 课件

D*1[ ] :
X
(e
jw
)
exp[Xˆ
(e
jw
)]
逆特征系统
x(n) IDTFT[ X (e jw )]
33
☆复倒谱的离散傅立叶变换定义
xˆ(n) IDFT [ln DFT (x(n))] IDFT [ Xˆ (k)]
N 1
X (k) DFT(x(n)) x(n)WNnk n0
x(n)
fˆl fˆk fˆl1
如果采样频率为8kHz,在0.1~4kHz范围内需要 安排16个临界带。将每个临界带内中的|Xn(k)|2取 和即可得到相应的临界带特征矢量。记为: G=[g1,g2,….gL]。
18/160
第1临界带
第2临界带
fˆ1 118 .6Hz fˆ2 188 .7Hz
fˆ3 297.2Hz
越逼X n近(e j于w)
。
但窗长X (Ne j太w) 大,窗选信号不满足语音的短时平稳
特性,
不能正X n确(e反jw映) 短时语音的频谱了。
为此,必须要合理选择窗长N。
4
3.短时功率谱和短时谱的关系
Sn (e
jw )
X n (e
jw )
X
* n
(e
jw )
|
X n (e
jw )
|2
4.短时功率谱和短时自相关函数的关系
D*1[D*[x(n)]] x(n)
(1)Z[x(n)] X (z), (2) ln X (z), (3)Z 1[ln X (z)] (4)Z{Z 1[ln X (z)]} ln X (z), (5) exp{ln X (z)} X (z) (6)Z 1[ X (z)] x(n)
第2章语音信号的线性预测分析

残差信号
s } n }
图2 - 1线性预测合成滤波器
、 ( : ) 一 卜 1 a , z -
( 2 . 1 )
第z 章 语音信号的线性预测分析
第2 章 语音信号的线性预测分析
和波形内插编码器一样,大多数低速率的语音编码算法都基于线性预测分 析。语音信号模型是一个线性合成模型,语音信号的每个取样值能够用过去若 千个取样值的线性组合 ( 预测值) 来逼近。
本章主 要介绍了 线性预测分 析( L P A -L i n e a r P r e d i c t i v e A n a l y s i s ) 滤波器,因为 用来合成 语音, 通常被称为 线性预测 合
成 滤 波 器 , 其 系 数 扣 I L 1 , 2 , , 即 为 L P 系 数 . 如 果 阶 数 P 足 够 大 , 线 性 预 测 合 成
l J
理
‘ 乃
L P 系数的求解方法及其线谱频率参数表示,最后讨论了带宽扩展的概念。
线性预测分析的基本原理
语音信号的产生过程可以 看成是声门 激励信号激励声道模型的过程, 该过程
在线性预测分析中可以 等效为线性预测残差信号激励时变线性滤波器的过程,
如图2 - 1 所示,
语音信号线性预测分析

《视频语音处理技术》语音信号线性预测分析学院名称:计算机与信息工程学院专业名称:计算机科学与技术年级班级:姓名:学号:计算机与信息技术学院综合性、设计性实验报告一、实验目的:综合采用各种线性预测分析的方法,能够达到预测更为准确。
要求掌握各种下列语音信号线性预测分析技术,提高学生数字语音信号处理的能力。
利用MATLAB 编程环境和强大的处理功能,实现语音信号线性预测。
主要训练如下的项目从而获得线性预测的综合能力:1、LPC 方程的自相关解法。
2、LPC 参数到LSP 参数的转换。
3、LSP 参数到LPC 参数的转换。
4、LPC 参数到ISP 参数的转换。
二、实验仪器或设备:w indowsXP 下的Matlab 编程环境 三、总体设计(设计原理、设计方案及流程等)线性预测编码原理:利用过去的样值对新样值进行预测,然后将样值的实际值与其预测值相减得到一个误差信号,显然误差信号的动态范围远小于原始语音信号的动态范围,对误差信号进行量化编码,可大大减少量化所需的比特数,使编码速率降低。
1.LPC 方程的自相关解法利用对称托普利兹(Toeplitz)矩阵的性质,自相关法求解可用Levinson-Durbin (莱文逊-杜宾)递推算法求解。
该方法是目前广泛采用的一种方法。
利用Levinson-Durbin 算法递推时,从最低阶预测器开始,由低阶到高阶进行逐阶递推计算。
自相关法递推过程如下:pi E j i r ai r k i i j i ji ≤≤⎥⎦⎤⎢⎣⎡-=-∑= 1 )(-)( )1(1-11)-(,()() 0 0r E =)1(2)1(--=i i i E k E联立左面5式可对i=1、2…、p 进行递推求解,其最终解为 对于p 阶预测器,在上述求解预测器系数的过程中,阶数低于p 的各阶预测器系数也同时得到。
2、LPC 参数到LSP 参数的转换。
将P(z)和Q(z)中与LSP 系数无关的两个实根取得到如下两个新的多项式从LPC 系数到LSP 系数的转换过程,其实就是求解使以上两式等于零时的 的值。
语音信号线性预测分析仿真课程设计报告书
专业课设2013年1月语音信号线性预测分析仿真院(系、部): 信 息 工 程 学 院 姓 名: 熊 洁班 级: 通 092 学 号: 090935 指导教师签名: 王 嵩摘要作为最有效的语音分析技术之一,线性预测是一种基于全极点模型假定和均方预测误差最小准则下的波形逼近技术,通过对音频信号的时域和频域分析对声道参数进行估值,以少量低信息率的时变参数精确地描述语音波形与其频谱的性质,能够在尽量保持原音质的基础上合成出高质量的语音。
本文重点研究了线性预测(LPC)的原理、Levinson-Durbin算法,基于MATLAB进行语音线性预测仿真,并对参数的选取做了比较分析。
关键词语音信号 LPC Levinson-Durbin算法MATLAB仿真AbstractAs one of the most effective speech analysis technique, linear prediction is a kind of based on the pole model assumption and minimum mean square error criterion of wave approximation technique, based on the audio signal of time domain and frequency domain analysis of track parameters valuations, with a few low information rate of time-varying parameters accurately describe the nature of the speech waveform and spectrum, to be able to try to keep the original sound quality on the basis of the synthesis of high quality speech.This paper mainly studies the linear prediction (LPC), Levinson - from the principle of the algorithm, based on MATLAB speech linear prediction simulation, and the selection of parameters to do a comparative analysis.Keywords voice signal LPC Levinson - Durbin algorithmMATLAB simulation目录第1章绪论11.1 语音信号LPC分析技术的基本概念1第2章线性预测编码的基本原理22.1 语音信号的产生22.2线性预测的概念与原理22.2.1线性预测分析的概念22.2.2LPC和语音信号模型的关系42.3解线性预测参数方程组的算法52.3.1Levinson-Durbin自相关解法52.3.2利用格型法求解线性预测系数6第3章simulink仿真的分析合成系统10 3.1仿真容103.2仿真系统模型103.3 仿真工作过程113.3.1语音信号采样113.3.2预加重113.3.3叠接窗分析133.3.4汉明窗143.3.5自相关算法143.3.6数字滤波器163.4仿真结果分析18参考文献18第1章绪论1.1 语音信号LPC分析技术的基本概念语音是人们交流思想和进行社会活动的最基本手段, 我们要对语音信号进行测定并将其转变为另一种形式, 以提高我们的通信能力。
语音信号处理__第三章_语音信号线性预测分析
i 1
• 预测误差为: p (n) s (n) ai s (n i ) Ge(n)
i 1
• 线性预测分析要解决的问题是:给定语音序列(显然,鉴于
语音信号的时变特性,LPC分析必须按帧进行),使预测误 差在某个准则下最小,求预测系数的最佳估值ai,这个准则 通常采用最小均方误差准则。
H ( z) G 1 bl z l 1 ai z i
i 1 l 1 p q
预测增益
• 根据H(z)的形式不同,有3种不同的信号模型: • 1)如上式, H(z)同时含有零点和极点,称为自回归-滑动平均 模型,是一种一般的模型。 • 2)当上式中的分子多项式为常数,即bl=0,H(z)为全极点模
线性预测分析就是为线性系统H(z)建立一个模型,并按照某种 准则,利用已知的s(n)进行模型参数估计。估计出来的参数即可 确定H(z),然后根据模型 S z E z V z 则可得到E(z)。这样, 我们就完全确定了语音的激励模型和声道模型。
模型的系统函数H(z)可以写成有理分式的形式:
i 1
• 即语音样点间有相关性,可以用过去的样点值预测未来样点 值。对于浊音,激励e(n)是以基音周期重复的单位冲激,对 于清音,e(n)是稳衡白噪声。
• 在模型参数估计程中,把如下系统称为线性预测器:
ˆ s (n) ai s (n i )
i 1 p
• 式中ai称为线性预测系数。从而,p阶线性预测器的系统函 数具有如下形式: p
• 再考虑公式(3-77)和(3-78) ,可得
n 0, 0 i n 0, i
i 1 p
• 可见,最小预测误差由一个固定分量和一个依赖于预测器
语音信号处理-第04章 语音信号线性预测(LPC)分析方法
定义相关矩阵
∑ φn (i, k ) = sn (m − i)sn (m − k ) m
对于平稳时间序列ai不随时间变化。
§4.3.1正则方程的自相关法
设:Sn(m)在 0≤m≤N−1 外取零值,信号范围为[0,N-1], 则线性预测的残差能量为
语音信号处理
Speech Signal Processing
长春工业大学图像工程研究所 史东承教授
dcshi@ 2010.8
• 从变换域考虑,同样根据V(Z) 和S(Z)可确 定E(Z)。
• 当 gQ ≠ 0 和 aP ≠ 0 时称为ARMA(Q,P)自回 归滑动模型。
∑ ∑ ∑ 2
=
e
n
⎡⎣s(n) − s(n)⎤⎦2 =
n
( ) ⎡
⎢s ⎣
n
−
p i=1
ai
z−i
⎤2 ⎥ ⎦
∑ ∑ ∑ ∑∑ ∑ =
⎧ ⎨
⎩
n
s2
(
n)⎫⎬
⎭
−
p
2
k =1
ak
⎧ ⎨ ⎩
n
s(n− k)s(n)⎫⎬+ p
⎭ n=1
l
⎧
i=1
ak
ai
⎨ ⎩
n
s(n−k) s(n−i)⎫⎬
⎭
σ ∑s ∑ ∑ 所以
v (n) = ∑ gisw (n − i) i=0
此时:
∑∑ ∑ ( ) ( ) <
F(Z),G(Z)
>=
M i=0
M j=0
f
⎧N +M −1
语音编码的基本方法
语音编码的基本方法语音编码是将语音信号转换为数字信号的过程,以便能够利用数字信号处理技术进行存储、传输、分析和合成。
语音编码的目标是尽可能减小存储和传输所需的比特率,同时尽量保持原始语音信号的质量。
下面将介绍语音编码的基本方法。
1.线性预测编码(LPC)线性预测编码(Linear Predictive Coding,LPC)是一种基于声道模型的语音编码方法。
该方法假设语音信号可以由线性滤波器和一个激励源合成。
LPC编码先通过线性预测分析,估计出语音信号的线性滤波器参数,然后将这些参数进行编码传输。
2.矢量量化矢量量化是一种有损数据压缩技术,也是常用的语音编码方法。
它将一组相关的样本(向量)映射到一组有限的离散码字中。
在语音编码中,矢量量化可以应用于线性预测编码的残差信号,以及其他一些语音特征参数的编码。
3.短时傅里叶变换编码(STFT)短时傅里叶变换编码(Short-Time Fourier Transform,STFT)是一种频域分析方法,常用于语音信号的编码。
STFT将语音信号分段进行傅里叶变换,将时域信号转换为频域信号,然后对频域信号进行编码传输。
4.频率对齐线性预测编码(FSLP)频率对齐线性预测编码(Frequency-Selective Linear Prediction,FSLP)是一种新型的语音编码方法。
它通过对语音信号进行预处理,将频率对齐后的语音信号分帧,然后利用线性预测分析得到每一帧的滤波器系数,并对这些系数进行编码传输。
5.自适应编码自适应编码是一种根据传输条件自动调整编码参数的方法。
最常见的自适应编码方法是可変速率编码(Variable Bit Rate,VBR)和可变码率编码(Adaptive Bit Rate,ABR)。
这些编码方法根据语音信号的特性和传输条件,动态调整编码参数,以尽可能减小比特率,并保持较高的语音质量。
除了上述几种基本方法,还有很多其他的语音编码技术,如无失真编码、人工神经网络编码等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
音语音信号处理第九讲:语音信号的线性预测分析应冬文中国科学院声学研究所提纲☐简介(为何建模)⏹Linear Prediction Coefficient 缩写为LPC☐原理(如何建模)⏹信号模型⏹LPC误差滤波⏹LPC语音建模☐在语音上的应用(具体于语音, 如何建模)☐经典解法(求解模型参数)☐频域特性(物理意义)建音域段语音信号采样点(LPC建模的动机:语音时域波形的相关性 一段语音信号采样点x t 样点,构造散点图(x t , x t+p )语音信号波形采样值存在强烈的相关性线性预测理论的发展史☐N.Wiener C.E.Shannon Gunnar Fant1919-2009器官发音的机理官音中☐语音是由声道中的激励信号产生,它受声道、鼻腔和咽喉的形状而形成的共振峰调节。
☐三种激励信号⏹声带周期性开合而产生的声门波,声门波的开合周期决定了语音信号的基音频率。
⏹肺部收缩而产生的空气流。
肺部收缩而产生的空气流⏹上述二者的组合。
声道鼻腔和咽喉中的声☐声道、鼻腔和咽喉中的声波共振由共振峰描述。
音成语音生成过程激励源滤波器卷积语音声波基本用途与思想基想☐LPC基本思想:⏹利用信号间相关性,用过去值预测现在或未来的值,即用过去若干个取样值的线性组合逼近一个取样值。
⏹在某种测度准则下,通过使实际的取样值与预测值之间的差别达最小,确定唯一的一组预测系数。
☐语音领域的用途⏹参数估计:基音周期、共振峰频率、谱特征、声道截面积函数等⏹特点:LPC能精确估计语音参数,用少量参数有效表示语音,计算LPC参数较简单。
⏹语音编码、语音增强、语音合成、声源定位、解混响、语音识音别等。
☐本次课的内容⏹如何建模、求解模型参数、模型的物理意义。
如何建模求解模型参数模型的物理意义☐简介(Linear Prediction Coefficient LPC)提纲(Linear Prediction Coefficient, LPC)☐原理(如何建模)⏹信号模型⏹LPC 误差滤波⏹LPC 语音建模☐在音(何建模)在语音上的应用(如何建模)☐经典解法(求解模型参数)☐频域特性(物理意义)☐简介(Linear Prediction Coefficient LPC)提纲(Linear Prediction Coefficient, LPC)☐原理(如何建模)⏹信号模型⏹LPC 误差滤波⏹LPC 语音建模☐在音(何建模)在语音上的应用(如何建模)☐经典解法(求解模型参数)☐频域特性(物理意义)信号模型(1)☐☐信号模型(2)☐☐三种信号模型(按滤波器的有理分式)信号模型(3)种信号模型(按滤波器的有理分式)⏹ARMA 模型:传递函数含有极点和零点(零极点模型)(自回归−滑动平均模型)过程序列ARMA 模型产生的序列称为ARMA 过程序列。
⏹AR 模型:传递函数的分子多项式为常数(全极点模型)。
(自回归模型)输出只取决于过去的信号值。
AR 模型产生的序列称为AR 过程序列。
⏹MA 模型:传递函数的分母多项式为常数(全零点模型)(滑动平均模型)输出只由模型的输入来决定。
MA 模型产生的序列称为MA 过程序列。
☐ARMA 模型是AR 模型和MA 模型的混合结构。
信号模型(4)☐LPC ☐LPC ☐求解☐推导正交方程的另一种形式☐☐最佳预测时,误差的最小方均值,即正向预测误差功率2min 1[()][()(()())][()()][()()]pp i i pi E E e n E e n x n a x n i E e n x n a E e n x n i ===--=--∑因1i =∑[()()]0;1,2,,p E e n x n j j p -==⎧⎪⎨=-- 即1[()()][()()][()()]pp i i E E e n x n E x n x n a E x n i x n ===--∑(00)(0p -1()()()i i e n x n a x n i =⎪⎩∑☐上式成立条件,最佳预测系数时。
☐合并标准方程式和上式,最后得到:1(0,0)(0,)p i i E c a c i ==∑解出1;0(,0)(,)0;1,2,,p p i i E j c j a c j i j p==⎧-=⎨=⎩∑ ——称为标准方程。
可解出p +1个未知数a 1,a 2,…,a p ,E p 。
正向预测误差功率☐结论☐☐(Linear Prediction Coefficient LPC)提纲简介(Linear Prediction Coefficient, LPC)☐原理⏹信号模型⏹LPC 误差滤波⏹LPC 语音建模☐在音的在语音上的应用☐经典解法☐频域特性语音信号的☐☐音求解滤波器参数和增益常数的过程称为语音信号的LPC 分析☐语音信号的LPC分析。
⏹基本问题是从语音信号序列确定一组LPC 系数。
⏹预测系数的估计须在一短段(帧)语音信号的范围内进行。
☐激励源问题用模型合成语音时产生的序列与和被分析序列⏹清音:用模型合成语音时,产生的序列与和被分析序列有相同的谱包络特性⏹)的谱是一组幅度相同的浊音:激励源u (n )的谱是组幅度相同的谐波线谱,与模型化中的信号源假设有所不同。
⏹但激励源u (n ) 的大部分时间的值非常小(零值),由于均方预测误差最小准则使预测误差e (n )逼近于u (n ),与u (n )能量很小这一事实并不矛盾。
因此,为简便起见,认为模型适于清音、浊音。
语音信号的LPC分析音☐使用全极点模型进行语音信号LPC分析的主要缺点:⏹理论上,语音是极零点模型(特别是清音和鼻音),应用模型;应该用ARMA⏹模型中,对于浊音时,激励源不满足白噪声的假设条件。
☐全极点模型求解方便,在相当广泛的条件适于工程,在数字语音信号处理的众多领域得到了非常成功的应用。
☐(Linear Prediction Coefficient LPC)提纲简介(Linear Prediction Coefficient, LPC)☐原理⏹信号模型⏹LPC 误差滤波⏹LPC 语音建模☐在音的在语音上的应用☐经典解法☐频域特性☐LPC LPC 分析的解法求信号模型参数可以通过C 完成⏹LPC 系数以及预测误差功率可从下式标准方程解出:j =⎧⏹1;(,0)(,)0;1,2,,pp i i E c j a c j i j p=-=⎨=⎩∑ 解线性方程组的方法有多种⏹以系数矩阵的特殊性质可简化解法标准方程=--☐的系数矩阵中,的值取决于求数学期望的方法。
⏹c j,i 的定义不同,导致不同的LPC 解法。
(,)[()()]c j i E x n i x n j (j,)的定不同,导不同的解☐经典解法:自相关法、协方差法。
自自相关法☐☐利用Toeplitz Yule–Walker Levinson–杜宾法快速求解对称p 矩阵,方程可用Durbin (杜宾法)递推算法高效地求解。
⏹算法的计算复杂度为O (p 2)(一般解法复杂度为O (p 3))Y l W lk 为☐设已知p -1阶Yule–Walker 方程的解为:1,11,21,11[1,,,,],Tp p p p p a a a E -------- 则有:11,11(0)(1)(2)(1)(1)(0)(1)(2)0p p r r r r p E a r r r r p ---⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥--⎢⎥⎢⎥⎢⎥1,211(2)(1)(0)(3)0p a r r r r p -⎢⎥-⎢⎥⎢⎥=-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥----☐由方程的系数矩阵的对称特点知,将p 阶和p -1 阶两方程中1,(1)(2)(3)(0)0p p a r p r p r p r --⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦后面两个列矢量倒置,再代入到原方程中,等式保持不变。
杜宾法快速求解(2)杜宾法☐Levinson–Durbin的递推公式r ⎡11,1121(0)(1)(2)(1)(1)(0)(1)(2)0p p r r r p E a r r r r p ---⎡⎤⎤⎡⎤⎢⎥⎢⎥⎢⎥--⎢⎥⎢⎥⎢⎥-- 1,211(2)(1)(0)(3)01)(2)(3)(0)0p a r r r r p a r r p r r -⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥----1,()))()p p p p --⎣⎦⎣⎦⎣⎦11110(0)(1)(2)()111r r r r p a a r r r r ⎡⎤⎡⎡⎤⎢⎥⎢⎥--- 10p p E k q -⎧⎫-⎤⎡⎤⎪⎪⎢⎥⎢⎥1,1,11,21,2()(0)()()(2)(1)(0)(2)p p p p p p p p a a r r r r p k ------⎢⎥⎢⎥⎢⎥--⎢⎥--⎢⎥⎢⎥⎢⎥⎢⎥0⎪⎪⎢⎥⎢⎥⎪⎪⎢⎥⎢⎥⎪⎪=⎢⎥⎢⎥⎨⎬⎢⎥⎢⎥⎪⎪ 1,11,1(1)(2)(3)(1)()(1)(2)(0)01p p p a a r p r p r p r r p r p r p r ---⎢⎥⎢⎥-----⎢⎥⎢⎥--⎢⎥⎣⎦⎣⎦ 10p p q k E -⎢⎥⎢⎥⎪⎪⎢⎥⎢⎥⎪⎪-⎢⎥⎢⎥⎪⎪⎣⎦⎣⎦⎩⎭杜宾法((1)结论从式☐(Linear Prediction Coefficient LPC)提纲简介(Linear Prediction Coefficient, LPC)☐原理⏹信号模型⏹LPC 误差滤波⏹LPC 语音建模☐在音的在语音上的应用☐经典解法☐频域特性最小预测误差的频域解释最小预测误差的频域解释因最小预测误差的频域解释定义:预测误差信号LPC ☐LPC ☐逼近语音信号谱即:型谱则以任意小的误差逼近语音信号谱,即:22j j lim (e)(e)p H X ωω→∞=☐p →∞,表明成立式:22j j (e )(e )H X ωω=812☐因相位的因素,但不一定成立式j j (e (e H X ≠ωω131620()()信号功率谱元音☐在信号谱的谷底处,LPC谱和信号谱匹配较差;☐浊音语音谱,在谐波成分处匹配效果要远比谐波之间好得多。
的准则原因:源于方均误差最小的准则,谱值大时误差要小。
LPC谱与实际谱的比较参☐p 从、、LPC谱参数选择阶数p 的选择:谱估计精度计算量存储量综合考虑,与LPC 求解方法无关。
一般原则:先保证足够的极点模拟声道响应的谐振结构。
通常,每kHz 两个极点(或共轭极点)表征声道响应,需3~4个极点逼近可能的零点、声门激励和辐射效应。
10 kHz 取样时,要求12~24阶数。
若谱估计关注声道谐振特性,取p =12~14N ☐帧长N 的选择N 小,则求解LPC 参数的计算量小一般,帧长N 取2~3个基音周期才是合理的☐语音信号谱的高频分量小,常采用预加重提高之。
