模型解题法经典例题
初中几何43模型解题 模型【07】 图形变化类(附解析)

模型【07】图形变化类【模型分析】解决图形规律题的步骤:(1)标序数——按图号标序;(2)找规律——观察图形,随着序号增加,后一个图形与前一个图形相比,找出图形变化规律,注意变量与不变量,将每个图中所求量的个数表示成与序数有关的式子;(3)验证——代入序号验证所归纳的式子是否正确;【经典例题】例1.(2021·重庆渝北区·八年级期末)如图是一组有规律的图案,第①个图案中有4个三角形,第②个图案中有7个三角形,第③个图案中有10个三角形……,依此规律,第⑧个图案中有()个三角形.A.19B.21C.22D.25【分析】由题意可知:第①个图案有3+1=4个三角形,第②个图案有3×2+1=7个三角形,第③个图案有3×3+1=10个三角形,…依此规律,第n个图案有(3n+1)个三角形,代入n=8即可求得答案.【解析】∵第①个图案有3+1=4个三角形,第②个图案有3×2+1=7个三角形,第③个图案有3×3+1=10个三角形,…∴第n个图案有(3n+1)个三角形.当n=8时,3×8+1=25,选D.【小结】考查图形的变化规律,解题的关键是找出图形之间的变化规律,利用规律解决问题.例2.(2021·北京东城区·八年级期末)如图,30MON ∠=︒,点1234,,,A A A A ,…在射线ON 上,点123,,B B B ,…在射线OM 上,且112223334,,A B A A B A A B A △△△,…均为等边三角形,以此类推,若11OA =,则202120212022A B A △的边长为_______.【分析】根据30MON ∠=︒,11OA =,112A B A △是等边三角形,得11260∠=︒B A A ,进而得1130∠=︒OB A ,1111A O B A ==,可得22OA =,以此类推即可求解.【解析】∵30MON ∠=︒,11OA =,112A B A △是等边三角形,∴11260∠=︒B A A ∴1130∠=︒OB A ∴1111A OB A ==∴22OA =同理:223A B A △,334A B A △,…均为等边三角形,2222B A OA ==,233342B A OA ===…则202120212022A B A △的边长为20202.【小结】本题考查了规律型-图形的变化类,解决本题的关键是观察图形的变化寻找规律.例3.(2021·安徽芜湖市·七年级期末)如图,同一行的两个图形中小正方形的个数相等,但它们的排列方式不一样,根据不同的排列方式可以得到一列等式.(12)223+⨯=⨯(123)234++⨯=⨯(1234)245+++⨯=⨯(1)第n 个图形中对应的等量关系是()21231n +++⋯++⨯=⎡⎤⎣⎦______.(2)根据(1)的结论,求24650+++⋅⋅⋅+的值.【分析】(1)根据前三幅图可知右边的式子等于左边括号内最大的数与比它大1数的积;(2)先逆用乘法分配律变形,然后根据(1)中结论计算即可;【解析】(1)∵(12)223+⨯=⨯,(123)234++⨯=⨯,(1234)245+++⨯=⨯,…,∴[]123(1)2(1)(2)n n n +++++⨯=++ (2)246501(5)2322+++⋅⋅⋅+=+++⋅⋅⋅+⨯2526650=⨯=【小结】本题考查了规律型—图形类规律与探究,要求学生通过观察,分析、归纳发现其中的规律,并应用发现的规律解决问题.也考查了有理数的混合运算.【巩固提升】1.(2020·浙江台州市·七年级期末)如图,用大小相等的黑色三角形按一定规律拼成如图的图案,其中第①个图案中有1个黑色三角形,第②个图案中有3个黑色三角形,第③个图案中有6个黑色三角形…,依照此规律,第⑩个图案中黑色三角形的个数为()A .50B .55C .58D .61【分析】根据前3个图案中黑色三角形的个数找出规律,利用规律解题即可.【解析】第①个图案中有1个黑色三角形,第②个图案中有3个黑色三角形,312=+,第③个图案中有6个黑色三角形,6123=++,……第⑩个图案中黑色三角形的个数为1234567891055+++++++++=,选B【小结】本题注意考查图形类规律探索,找到规律是解题的关键.2.(2021·北京房山区·八年级期末)如图甲,直角三角形ABC 的三边a ,b ,c ,满足222+=a b c 的关系.利用这个关系,探究下面的问题:如图乙,OAB 是腰长为1的等腰直角三角形,90OAB ∠=︒,延长OA 至1B ,使1AB OA =,以1OB 为底,在OAB 外侧作等腰直角三角形11OA B ,再延长1OA 至2B ,使121A B OA =,以2OB 为底,在11OA B 外侧作等腰直角三角形22OA B ,……,按此规律作等腰直角三角形n n OA B (1n ≥,n 为正整数),则22A B 的长及20212021OA B 的面积分别是()A .2,20202B .4,20212C .20202D .2,20192【分析】根据题意结合等腰直角三角形的性质,即可判断出22A B 的长,再进一步推出一般规律,利用规律求解20212021OA B 的面积即可.【解析】由题意可得:11OA AB AB ===,12OB =,∵11OA B 为等腰直角三角形,且“直角三角形ABC 三边a ,b ,c ,满足222+=a b c 关系”,∴根据题意可得:111OA A B ==,∴212OB OA ==,∴22222OA A B ===, ,∴总结出n n OA =,∵111122△OAB S =⨯⨯=,11112△OA B S =,2212222△OA B S =⨯⨯=,∴归纳得出一般规律:1122n n n n n OA B S -=⨯⨯= ,∴2021202120202OA B S = ,选A【小结】本题考查等腰直角三角形的性质,图形变化类的规律探究问题,立即题意并灵活运用等腰直角三角形的性质归纳一般规律是解题关键.3.(2021·山东青岛市·七年级期末)下列图形均是用长度相同的火柴棒按一定的规律搭成,搭第1个图形需要4根火柴棒,搭第2个图形需要10根火柴棒,…,依此规律,搭第10个图形需要________根火柴棒.【分析】由题意,分别求出前面几个的火柴棒数量,然后得到数量的规律,再求出第10个图形的数量即可.【解析】根据题意可知:第1个图案需4根火柴,()4113=⨯+,第2个图案需10根火柴,()10223=⨯+,第3个图案需21根火柴,()18333=⨯+,……,第n 个图案需()3n n +根火柴,则第10个图案需:()10103130⨯+=(根).【小结】此题考查了平面图形,图形变化规律,主要培养学生的观察能力和空间想象能力.4.(2021·全国七年级)如图,△ABC 是边长为1的等边三角形,取BC 边中点E ,作ED ∥AB ,EF ∥AC ,得到四边形EDAF ,它的周长记作C 1;取BE 中点E 1,作E 1D 1∥FB ,E 1F 1∥EF ,得到四边形E 1D 1FF 1,它的周长记作C 2.照此规律作下去,则C 2020=__.【分析】先计算出C 1、C 2的长,进而得到规律,最后求出C 2020的长即可.【解析】∵E 是BC 的中点,ED ∥AB ,∴DE 是△ABC 的中位线,∴DE =12AB =12,AD =12AC =12,∵EF ∥AC ,∴四边形EDAF 是菱形,∴C 1=4×12,同理C 2=4×12×12=4×212,…C n =4×12n ,∴20202020201811422C =⨯=.【小结】本题考查了中位线的性质,菱形的判定与性质,根据题意得到规律是解题关键.5.(2021·山东青岛市·七年级期末)(问题提出)以长方形ABCD 的4个顶点和它内部的n 个点,共(4)n +个点作为顶点,可把原长方形分割成多少个互不重叠的小三角形?(问题探究)为了解决上面的问题,我们将采取一般问题特殊化的策略,先从简单的情形入手:(探究一)以长方形ABCD 的4个顶点和它内部的1个点P (如图①),共5个点为顶点显然,此时可把长方形ABCD 分割成________个互不重叠的小三角形.(探究二)以长方形ABCD 的4个顶点和它内部的2个点P 、Q ,共6个点为顶点,可把长方形ABCD 分割成多少个互不重叠的小三角形?在探究一的基础上,我们可看作在图①长方形ABCD 的内部,再添加1个点Q ,那么点Q 的位置会有两种情况:一种情况是,点Q 在图①分割成的小三角形的某条公共边上不妨设点Q 在PB 上(如图②);另一种情况是,点Q 在图①分割成的某个小三角形内部.不妨设点Q 在PAB △的内部(如图③).显然,不管哪种情况,都可把长方形ABCD 分割成________个互不重叠的小三角形.(探究三)长方形ABCD 的4个顶点和它内部的3个点P 、Q 、R ,共7个点为顶点,可把长方形ABCD 分割成________个互不重叠的小三角形请在图④中画出一种分割示意图.(问题解决)以长方形ABCD 的4个顶点和它内部的n 个点,共(4)n +个点作为顶点,可把原长方形分割成________个互不重叠的小三角形.(实际应用)以梯形的4个顶点和它内部的2021个点作为顶点,可把梯形分割成________个互不重叠的小三角形.(拓展延伸)以五边形的5个顶点和它内部的m 个点,共(5)m +个点作为顶点,可把原五边形分割成________个互不重叠的小三角形.【分析】探究一:根据图形可回答;探究二:根据图形可回答;探究三:根据图形可回答;n ,进而解决问题;问题解决:由探究活动可得规律为2(1)实际应用:把2021代入所得规律,求值即可;拓展延伸:由四边形的规律可得五边形的规律.【解析】探究一:以长方形ABCD的4个顶点和它内部的1个点P,共5个点为顶点显然,此时可把长方形ABCD 分割成4个互不重叠的小三角形.故答案为:4;探究二:如图,不管哪种情况,都可把长方形ABCD分割成6个互不重叠的小三角形.故答案为;6;探究三:长方形ABCD的4个顶点和它内部的3个点P、Q、R,共7个点为顶点,可把长方形ABCD分割成8个互不重叠的小三角形问题解决:以长方形ABCD 的4个顶点和它内部的1个点,共5个点作为顶点,可把原长方形分割成互不重叠的小三角形个数为:4=2(1+1).以长方形ABCD 的4个顶点和它内部的2个点,共6个点作为顶点,可把原长方形分割成互不重叠的小三角形个数为:6=2(2+1).以长方形ABCD 的4个顶点和它内部的3个点,共7个点作为顶点,可把原长方形分割成互不重叠的小三角形个数为:8=2(3+1).所以,以长方形ABCD 的4个顶点和它内部的n 个点,共(4)n +个点作为顶点,可把原长方形分割成互不重叠的小三角形个数为:2(n +1).实际应用:当n =2021时,以梯形的4个顶点和它内部的2021个点作为顶点,可把梯形分割成互不重叠的小三角形2(2021+1)=4044个.拓展延伸:根据前面的解决问题可知:以五边形的5个顶点和它内部的m 个点,共(5)m +个点作为顶点,可把原五边形分割成互不重叠的小三角形个数为(2m +3)个.故答案为:(2m +3)【小结】本题考查了应用与设计作图,图形的变化规律的问题,读懂题目信息,根据前四个探究得到每多一个点,则三角形的个数增加2是解题的关键.6.(2021·青岛实验学校九年级期末)在平面直角坐标系中,点A 从原点O 出发,沿x 轴正方向按半圆形弧线不断向前运动,其移动路线如图所示,其中半圆的半径为1个单位长度,这时点1234,,,A A A A 的坐标分别为()()()()12340,0,1,12,03,1A A A A -,按照这个规律解决下列问题:()1写出点5678,,,,A A A A 的坐标;()2点2018A 的位置在_____________(填“x 轴上方”“x 轴下方”或“x 轴上”);()3试写出点n A 的坐标(n 是正整数).【分析】()1可根据点在图形中的位置及前4点坐标直接求解;()2根据图形可知点的位置每4个数一个循环,20184504...2÷=,进而判断2018A 与2A 的纵坐标相同在x 轴上方,即可求解;()3根据点的坐标规律可分4种情况分别写出坐标即可求解.【解析】(1)由数轴可得:()54,0A ,()65,1A ,()76,0A ,()87,1A -;(2)根据图形可知点的位置每4个数一个循环,20184504...2÷=,2018A ∴与2A 的纵坐标相同,在x 轴上方,故答案为:x 轴上方;(3)根据图形可知点的位置每4个数一个循环,每个点的横坐标为序数减1,纵坐标为0、1、0、-1循环,∴点n A 的坐标(n 是正整数)为A (n -1,0)或()1,1A n -或()1,0A n -或()1,1A n --.【小结】本题主要考查找点的坐标规律,点的坐标的确定,方法,根据已知点的坐标及图形总结点坐标的变化规律,并运用规律解决问题是解题的关键.。
8字型和燕尾模型 模型分析 经典例题

OD CBAODCBA模型20 “8”字型模型问题【模型分析】模型1 角的“8”字模型如图所示,AB 、CD 相交于点O 连接AD 、BC结论:∠A +∠D =∠B +∠C模型2 边的“8”字模型如图所示,AC 、BD 相交于点O ,连接AD 、BC 结论:AC +BD >AD +BC【经典例题】例1.(2020·全国九年级模型练习)如图,求∠A +∠B +∠C +∠D +∠E +∠F +∠G +∠H +∠I =__【分析】根据多边形的内角和,可得答案 【解析】连EF ,GI ,如图,∵6边形ABCDEFK 的内角和=(6-2)×180°=720° ∵∠A +∠B +∠C +∠D +∠E +∠F =720°-(∠1+∠2) 即∠A +∠B +∠C +∠D +∠E +∠F +(∠1+∠2)=720°∵∠1+∠2=∠3+∠4,∠5+∠6+∠H =180°∴∠A +∠B +∠C +∠D +∠E +∠F ∠H +(∠3+∠4)=900°∵∠A +∠B +∠C +∠D +∠E +∠F (∠3+∠4)+∠5+∠6+∠H =720°+180° ∵∠A +∠B +∠C +∠D +∠E +∠F +∠G +∠H +∠I =900°【小结】本题考查了n 边形的内角和定理:n 边形的内角和为(n -2)×180°(n ≥3的整数)例2.(2020·浙江金华市·八年级期末)如图,BP 平分ABC ∠,交CD 于点F ,DP 平分ADC ∠交AB 于点E ,AB 与CD 相交于点G ,42A ∠=︒(1)若60ADC ∠=︒,求AEP ∠的度数 (2)若38C ∠=︒,求P ∠的度数 【分析】(1)根据角平分线的定义可得∠ADP =12ADC ∠ ,然后利用三角形外角的性质即可得解 (2)根据角平分线的定义可得∠ADP =∠PDF ,∠CBP =∠PBA ,再根据三角形的内角和定理可得∠A +∠ADP =∠P +∠ABP ,∠C +∠CBP =∠P +∠PDF ,所以∠A +∠C =2∠P ,即可得解 【解析】(1)∵DP 平分∠ADC ,∵∠ADP =∠PDF =12ADC ∠ ∵60ADC ∠=︒,∵30ADP ∠=︒,∵304272AEP ADP A ∠=∠+∠=︒+︒=︒ (2)∵BP 平分∠ABC ,DP 平分∠ADC ,∵∠ADP =∠PDF ,∠CBP =∠PBA ∵∠A +∠ADP =∠P +∠ABP ,∠C +∠CBP =∠P +∠PDF ,∵∠A +∠C =2∠P ∵∠A =42°,∠C =38°,∵∠P =12(38°+42°)=40° 【小结】本题考查了三角形的内角和定理及三角形外角的性质,角平分线的定义,熟记定理并理解“8字形”的等式是解题的关键.【巩固提升】1.(2020·湖北恩施土家族苗族自治州·八年级期中)如图,将矩形纸片ABCD 沿EF 折叠,点C 落在边AB 上的点H 处,点D 落在点G 处,若111GEF ∠=︒,AHG ∠度数为( )A .42°B .69°C .44°D .32°【分析】根据翻折的性质,及矩形的性质,求出AEG ∠,再利用“8”字模型求解即可 【解析】由图形翻折的性质可知,111GEF DEF ∠=∠=︒180111AEF ∴∠=︒-︒=69︒,1116942AEG GEF AEF ∠=∠-∠=︒-︒=︒ 90A G ∠=∠=︒,利用“8”字模型 42AHG AEG ∴∠=∠=︒,选A【小结】本题考查了矩形翻折问题,能够根据图形翻折的性质推理出AEG ∠是解决问题的关键,熟练运用“8”字模型是求最终结果的关键2.(2020·九年级练习)如图,∠A +∠B +∠C +∠D +∠E +∠F +∠G +∠H +∠I +∠K 度数为__【分析】连KF ,GI ,根据n 边形的内角和定理得到7边形ABCDEFK 的内角和=(7-2)×180°=900°,则∠A +∠B +∠C +∠D +∠E +∠F +∠K +(∠1+∠2)=900°,由三角形内角和定理可得到∠1+∠2=∠3+∠4,∠5+∠6+∠H =180°,则∠A +∠B +∠C +∠D +∠E +∠F +∠K +(∠3+∠4)+∠5+∠6+∠H =900°+180°,即可得到∠A +∠B +∠C +∠D +∠E +∠F +∠G +∠H +∠I +∠K 的度数 【解析】连KF ,GI ,如图,∵7边形ABCDEFK的内角和=(7-2)×180°=900°∵∠A+∠B+∠C+∠D+∠E+∠F+∠K=900°-(∠1+∠2)即∠A+∠B+∠C+∠D+∠E+∠F+∠K+(∠1+∠2)=900°∵∠1+∠2=∠3+∠4,∠5+∠6+∠H=180°∵∠A+∠B+∠C+∠D+∠E+∠F+∠K+(∠3+∠4)=900°∵∠A+∠B+∠C+∠D+∠E+∠F+∠K+(∠3+∠4)+∠5+∠6+∠H=900°+180°∵∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠I+∠K=1080°故∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠I+∠K的度数为1080【小结】本题考查了n边形的内角和定理:n边形的内角和为(n-2)×180°(n≥3的整数)3.(2020·全国九年级模型练习)阅读材料:如图1,AB、CD交于点O,我们把∵AOD和∵BOC叫做对顶三角形结论:若∵AOD和∵BOC是对顶三角形,则∠A+∠D=∠B+∠C结论应用举例:如图2:求五角星的五个内角之和,即∠A+∠B+∠ACE+∠ADB+∠E的度数解:连接CD,由对顶三角形的性质得:∠B+∠E=∠1+∠2在∵ACD中,∵∠A+∠ACD+∠ADC=180°即∠A+∠3+∠1+∠2+∠4=180°∵∠A+∠ACE+∠B+∠E+ADB=180°,即五角星的五个内角之和为180°解决问题:(1)如图①,∠A+∠B+∠C+∠D+∠E+∠F=;(2)如图②,∠A+∠B+∠C+∠D+∠E+∠F+∠G=;(3)如图③,∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H=;(4)如图④,∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠M+∠N=;请你从图③或图④中任选一个,写出你的计算过程.【分析】(1)连接CD,由对顶角三角形可得∠A+∠B=∠BDC+∠ACD,再由四边形的内角和定理得出结论;(2)连接ED,由对顶角三角形可得∠A+∠B=∠BED+∠ADE,再由五边形的内角和定理得出结论;(3)连接B H、DE,由对顶角三角形可知∠EB H+∠B H D=∠H DE+∠BED,再根据五边形的内角和定理得出结论;(4)连接ND、NE,由对顶角三角形可知∠1+∠2=∠N GH+∠E HG,再由六边形的内角和定理得出结论.【解析】(1)连接CD,由对顶角三角形可得∠A+∠B=∠BDC+∠ACD,则∠A+∠B+∠C+∠D+∠E+∠F=360°;(2)连接ED,由对顶角三角形可得∠A+∠B=∠BED+∠ADE,则∠A+∠B+∠C+∠D+∠E+∠F+∠G=540°;(3)连接B H、DE,∵由对顶角三角形可知∠EB H+∠B H D=∠H DE+∠BED,∵∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H=五边形CDEF G的内角和+∵AB H的内角和=540°+180°=720°;(4)连接ND、NE,∵由对顶角三角形可知∠1+∠2=∠N GH+∠E HG,∵∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠M+∠N=六边形BCF GH M的内角和+∵AND的内角和+∵NDE的内角和=(6-2)×180°+360°=1080°.【小结】本题考查的是三角形内角和定理,根据题意作出辅助线,利用∵AOD和∵BOC叫做对顶三角形的性质及多边形的内角和定理解答是解答此题的关键.4.(2020·全国九年级模型练习)如图,求∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠K度数.【分析】如图所示,由三角形外角的性质可知:∠A+∠B=∠IJ L,∠C+∠D=∠ML J,∠H+∠K=∠GIJ,∠E+∠F=∠G ML,然后由多边形的内角和公式可求得答案.【解析】如图所示:由三角形外角性质:∠A+∠B=∠IJ L,∠C+∠D=∠ML J,∠H+∠K=∠GIJ,∠E+∠F=∠G ML∵∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠K=∠IJ L+∠ML J+∠G ML+∠G+∠GIJ=(5-2)×180°=3×180°=540°.【小结】本题主要考查的是三角形外角的性质和多边形的内角和公式的应用,利用三角形外角和的性质将所求各角的和转化为五边形的内角和是解题的关键5.(2020·全国九年级练习)如图,求∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H六个角的和【分析】根据三角形内角和外角的性质可得:∠G+∠D=∠3,∠F+∠C=∠4,∠E+∠H =∠2,再根据三角形内角和定理可得答案【解析】∵∠G+∠D=∠3,∠F+∠C=∠4,∠E+∠H=∠2∵∠G+∠D+∠F+∠C+∠E+∠H=∠3+∠4+∠2∵∠B+∠2+∠1=180°,∠3+∠5+∠A=180°∵∠A+∠B+∠2+∠4+∠3=360°∵∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H=360°【小结】此题主要考查了三角形内角与外角的性质,关键是掌握三角形的一个外角等于和它不相邻的两个内角的和6.(2019·全国九年级模型练习)如图,在直角ABC ∆中,BD 是ABC ∠的平分线,3BAO OAD ∠=∠,AO 的延长线与BDC ∠的平分线交于点F ,求F ∠的度数.【分析】设OAD x ∠=︒,则3BAO x ∠=︒,452ABO x ∠=︒-︒,22.5ODF x ∠=︒+︒ 根据三角形ABO 与三角形DFO 的内角和相等即可建立方程,整理方程即可得出答案 【解析】设OAD x ∠=︒,则3BAO x ∠=︒ 在直角ABC ∆中,904ABC x ∠=︒-︒ ∵BD 是ABC ∠的平分线 ∵452ABO x ∠=︒-︒在直角DBC ∆中,22.5ODF x ∠=︒+︒∵180OAB OBA AOB ODF F FOD ∠+∠+∠=∠+∠+∠=︒ 又∵AOB FOD ∠=∠∵OAB OBA ODF F ∠+∠=∠+∠ 即345222.5x x x F ︒+︒-︒=︒+︒+∠ ∵22.5F ∠=︒【小结】本题考查了对顶角相等、三角形内角和定理及其推论等知识.根据对顶三角形构建方程是解题的关键模型21 燕尾角模型问题【模型分析】如图所示,有结论:∠D =∠A +∠B +∠C 。
(完整版)初中常用数学模型
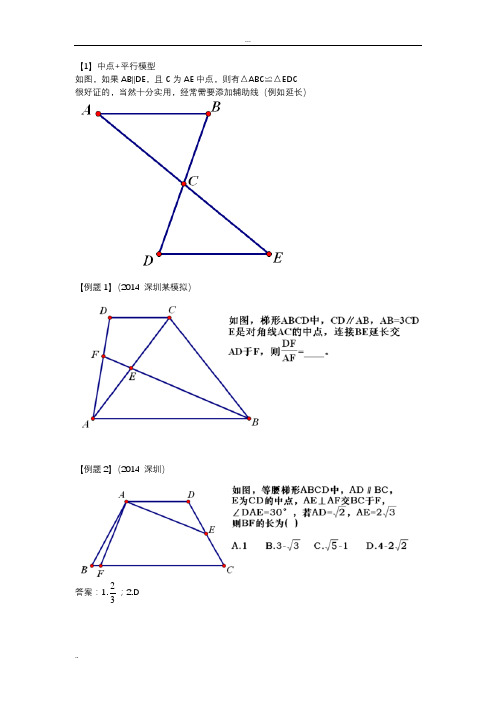
如图,如果AB ‖DE ,且C 为AE 中点,则有△ABC ≌△EDC 很好证的,当然十分实用,经常需要添加辅助线(例如延长)【例题1】(2014 深圳某模拟)【例题2】(2014 深圳)答案:1.32;2.D如图,若∠B=∠C=∠DEF=α(0<α≤90)则一定有△BDE与△CEF相似。
十分好证(外角和什么一大堆),并且也很实用。
经常在矩形里出题。
【例题1】(2009 太原)【例题2】(2006 河南)【例题3】(原创)答案:1. 2或3-24或25 2.(5453-,) 【3】巧造旋转模型在某些几何题中,往往有一些奇怪的结论,此时可以通过几何三大变换之一【旋转】求解。
巧造旋转往往要有一定的等量关系和特殊角度,如下题:通过观察可得∠ABC=∠C=45°,AB=AC 。
我们可以将△ACD 绕A 顺时针旋转90°得到△ABE ,使得AC 与AB 重合。
那么就有EB ⊥BC ,而在RT △AED 中,DE ²=2AD ²(等腰直角三角形) 所以BE ²+BD ²=DE ²,即BD ²+CD ²=2AD ²是不是赶脚很难想到?要学会判断,这种感觉是要练出来的! 【例题1】(2014 武汉)【例题2】【例题3】(2014 菏泽改编)答案:1.41 2.9 3.(1.)2,(2.)直角三角形,旋转后证全等,证明略【4】等腰模型这是一个很基础的模型——什么样的结构会生成等腰三角形首先:平行+角平分线,如图,若AD‖BE,BC平分∠ABE,则AB=AC,很好证的,导角即可。
其次:垂直+角平分这个不难理解,因为等腰三角形三线合一。
这种模型很常用,常常需要做辅助线(延长之类)【例题1】(原创)AB‖CD【例题2】(原创)【例题3】(改编)1.112.33.延长CD交AB于M,利用中位线,证明略【5】倍长中线法常考,选填大证明都可能会用。
高中物理模型法解题——板块模型

高中物理模型法解题———板块模型【模型概述】板块模型是多个物体的多个过程问题,是一个最经典、最基本的模型之一。
木板和物块组成的相互作用的系统称为板块模型,该模型涉及到静摩擦力、滑动摩擦力的转化、方向判断等静力学知识,还涉及到牛顿运动定律、运动学规律、动能定理和能量的转化和守恒等方面的知识。
板块类问题的一般解题方法(1)受力分析.(2)物体相对运动过程的分析.(3)参考系的选择(通常选取地面).(4)做v-t图像(5)摩擦力做功与动能之间的关系.(6)能量守恒定律的运用.一、含作用力的板块模型问题:【例题1】如图所示,木板静止于水平地面上,在其最右端放一可视为质点的木块.已知木块的质量m=1kg,木板的质量M=4kg,长L=2.5m,上表面光滑,下表面与地面之间的动摩擦因数μ=0.2.现用水平恒力F=20N拉木板,g取10m/s2,求:(1)木板的加速度;(2)要使木块能滑离木板,水平恒力F作用的最短时间;(3)如果其他条件不变,假设木板的上表面也粗糙,其上表面与木块之间的动摩擦因数为0.3,欲使木板能从木块的下方抽出,需对木板施加的最小水平拉力是多大?(设最大静摩擦力等于滑动摩擦力)(4)若木板的长度、木块质量、木板的上表面与木块之间的动摩擦因数、木块与地面间的动摩擦因数都不变,只将水平恒力增加为30N,则木块滑离木板需要多长时间?【解题思路】(1)根据牛顿第二定律求出木板的加速度.(2)让木板先做匀加速直线运动,然后做匀减速直线运动,根据牛顿第二定律,结合位移之和等于板长求出恒力F作用的最短时间.(3)根据牛顿第二定律求出木块的最大加速度,隔离对木板分析求出木板的加速度,抓住木板的加速度大于木块的加速度,求出施加的最小水平拉力.(4)应用运动学公式,根据相对加速度求所需时间.【答案】(1)木板的加速度2.5m/s2;(2)要使木块能滑离木板,水平恒力F作用的最短时间1s;(3)对木板施加的最小水平拉力是25N;(4)木块滑离木板需要2s【解析】解:(1)木板受到的摩擦力F f=μ(M+m)g=10N木板的加速度=2.5m/s2(2)设拉力F作用t时间后撤去,木板的加速度为木板先做匀加速运动,后做匀减速运动,且a=﹣a′有at2=L解得:t=1s,即F作用的最短时间是1s.(3)设木块的最大加速度为a木块,木板的最大加速度为a木板,则对木板:F1﹣μ1mg﹣μ(M+m)g=Ma木板木板能从木块的下方抽出的条件:a木板>a木块解得:F>25N(4)木块的加速度木板的加速度=4.25m/s2木块滑离木板时,两者的位移关系为x木板﹣x木块=L即带入数据解得:t=2s【变式练习】如图所示,质量M=1kg的木块A静止在水平地面上,在木块的左端放置一个质量m=1kg的铁块B(大小可忽略),铁块与木块间的动摩擦因数μ1=0.3,木块长L=1m,用F=5N的水平恒力作用在铁块上,g取10m/s2.(1)若水平地面光滑,计算说明两木块间是否会发生相对滑动.(2)若木块与水平地面间的动摩擦因数μ2=0.1,求铁块运动到木块右端的时间.【解题思路】(1)假设不发生相对滑动,通过整体隔离法求出A、B之间的摩擦力,与最大静摩擦力比较,判断是否发生相对滑动.(2)根据牛顿第二定律分别求出A、B的加速度,结合位移之差等于木块的长度求出运动的时间.【答案】(1)A、B之间不发生相对滑动;(2)铁块运动到木块右端的时间为.【解析】(1)A、B之间的最大静摩擦力为:f m>μmg=0.3×10N=3N.假设A、B之间不发生相对滑动,则对AB整体分析得:F=(M+m)a对A,f AB=Ma代入数据解得:f AB=2.5N.因为f AB<f m,故A、B之间不发生相对滑动.(2)对B,根据牛顿第二定律得:F﹣μ1mg=ma B,对A,根据牛顿第二定律得:μ1mg﹣μ2(m+M)g=Ma A根据题意有:x B﹣x A=L,,联立解得:.二、不含作用力的板块模型问题:【例题2】一长木板在水平地面上运动,在t =0时刻将一相对于地面静止的物块轻放到木板上,以后木板运动的速度—时间图像如图所示。
平行线之猪脚模型(M模型)-【压轴必刷】中考数学压轴大题之经典模型(解析版)
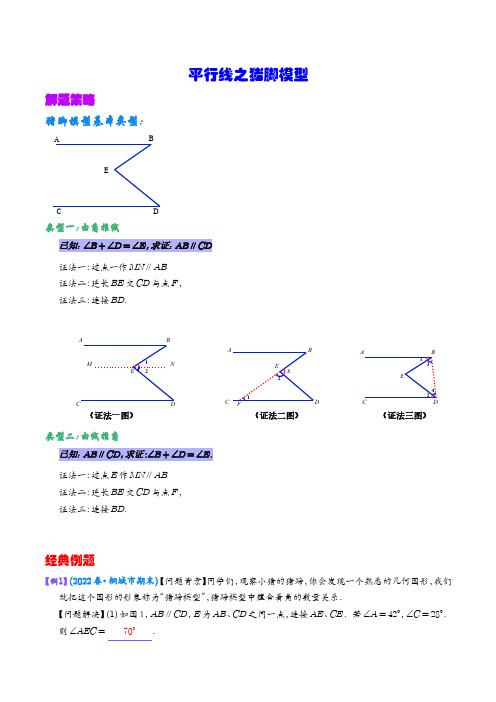
平行线之猪脚模型解题策略猪脚模型基本类型:A BC DE类型一:由角推线已知:∠B +∠D =∠E ,求证:AB ∥CD证法一:过点一作MN ∥AB 证法二:延长BE 交CD 与点F ,证法三:连接BD .A BC D E MN AB C D EF A B C DE 121231234(证法一图)(证法二图)(证法三图)类型二:由线推角已知:AB ∥CD ,求证:∠B +∠D =∠E .证法一:过点E 作MN ∥AB证法二:延长BE 交CD 与点F ,证法三:连接BD .经典例题【例1】(2022春•桐城市期末)【问题背景】同学们,观察小猪的猪蹄,你会发现一个熟悉的几何图形,我们就把这个图形的形象称为“猪蹄模型”,猪蹄模型中蕴含着角的数量关系.【问题解决】(1)如图1,AB ∥CD ,E 为AB 、CD 之间一点,连接AE 、CE .若∠A =42°,∠C =28°.则∠AEC = 70° .【问题探究】(2)如图2,AB∥CD,线段AD与线段BC交于点E,∠A=36°,∠C=54°,EF平分∠BED,求∠BEF的度数.【问题拓展】(3)如图3.AB∥CD,线段AD与线段BC相交于点G,∠BCD=56°,∠GDE=20°,过点D作DF∥CB交直线AB于点F,AE平分∠BAD,DG平分∠CDF,求∠AED的度数.【分析】(1)延长CE交AB于点F,利用平行线的性质可得∠AFC=28°,然后再利用三角形的外角可得∠AEC=∠A+∠C,进行计算即可解答;(2)利用猪蹄模型可得:∠AEC=∠A+∠C=90°,再利用对顶角相等可得∠BED=90°,然后利用角平分线的定义进行计算即可解答;(3)利用平行线的性质可求出∠CDF的度数,从而利用角平分线的定义求出∠CDG的度数,进而利用平行线的性质可求出∠BAD的度数,然后根据角平分线的定义求出∠BAE的度数,再利用平角定义求出∠EDH的度数,最后根据猪蹄模型可得∠AED=∠BAE+∠EDH,进行计算即可解答.【解答】解:(1)延长CE交AB于点F,∵AB∥CD,∴∠AFC=∠C=28°,∵∠AEC是△AEF的一个外角,∴∠AEC=∠A+∠AFC=∠A+∠C=70°,故答案为:70°;(2)利用(1)的结论可得:∠AEC=∠A+∠C=36°+54°=90°,∴∠AEC=∠BED=90°,∵EF平分∠BED,∠BED=45°,∴∠BEF=12∴∠BEF的度数为45°;(3)∵BC∥DF,∴∠CDF=180°-∠BCD=124°,∵DG平分∠CDF,∴∠CDG=1∠CDF=62°,2∵AB∥CD,∴∠BAG=∠CDG=62°,∵AE平分∠BAD,∠BAD=31°,∴∠BAE=12∵∠GDE=20°,∴∠EDH=180°-∠CDG-∠GDE=98°,利用(1)的结论可得:∠AED=∠BAE+∠EDH=31°+98°=129°,∴∠AED的度数为129°.【例2】(2022春•南京期中)已知直线AB∥CD,点E,F分别在AB,CD上,O是平面内一点(不在直线AB、CD、EF上),OG平分∠EOF,射线OH∥AB,交EF于点H.(1)如图①,若∠AEO=45°,∠CFO=75°,则∠HOG= 15° ,(2)如图②,若∠AEO=150°,∠HOG=20°,则∠CFO= 110° ;(3)直接写出点O在不同位置时∠AEO、∠CFO和∠HOG三个角之间满足的数量关系.【分析】(1)由AB∥CD,OH∥AB可得AB∥OH∥CD,利用平行线的性质可得∠AEO=∠EOH,∠CFO=∠FOH,由∠EOF=∠EOH+∠FOH,等量代换可得∠AEO+∠CFO=∠EOF,根据已知条件和角平分线的定义求出∠EOG=60°,即可得到∠HOG的度数;(2)同(1)类似,利用平行线的性质和角平分线的定义计算可以得出∠CFO的度数;(3)由(1)和(2)的计算方法可以得出结论.【解答】解:(1)∵AB∥CD,OH∥AB,∴AB∥OH∥CD,∴∠AEO=∠EOH,∠CFO=∠FOH,∴∠AEO+∠CFO=∠EOH+∠FOH,即∠AEO+∠CFO=∠EOF,∵∠AEO=45°,∠CFO=75°,∴∠EOF=120°,∵OG平分∠EOF,∴∠EOG=60°,∴∠HOG=∠EOG-∠EOH=15°,故答案为:15°;(2)∵AB∥CD,OH∥AB,∴AB∥OH∥CD,∴∠AEO+∠EOH=180°,∠CFO+∠FOH=180°,∴∠AEO+∠CFO+∠EOH+∠FOH=360°,即∠AEO+∠CFO+∠EOF=360°,∵AB∥OH,∴∠AEO+∠EOH=180°,∵∠AEO=150°,∴∠EOH=30°,∵∠HOG=20°,∴∠EOG=∠EOH+∠HOG=30°+20°=50°,∵OG平分∠EOF,∴∠EOF=2∠EOG=100°,∵∠AEO+∠CFO+∠EOF=360°,∠AEO=150°,∴∠CFO=360°-150°-100°=110°,故答案为:110°;(3)①若点O在直线AB与CD之间,则有|∠AEO-∠CFO|=2∠HOG;②若点O在直线AB与CD之外,且在直线EF的左侧,则有∠AEO+∠CFO=2∠HOG;若点O在直线AB与CD之外,且在直线EF的右侧,则有360°-∠AEO-∠CFO=2∠HOG.【例3】(2022春•上城区校级期中)如图,一副三角板,其中∠EDF=∠ACB=90°,∠E=45°,∠A=30°.(1)若这副三角板如图摆放,EF∥CD,求∠ABF的度数.(2)将一副三角板如图1所示摆放,直线GH∥MN,保持三角板ABC不动,现将三角板DEF绕点D以每秒2°的速度顺时针旋转,如图2,设旋转时间为t秒,且0≤t≤180,若边BC与三角板的一条直角边(边DE,DF)平行时,求所有满足条件的t的值.(3)将一副三角板如图3所示摆放,直线GH∥MN,现将三角板ABC绕点A以每秒1°的速度顺时针旋转,同时三角板DEF绕点D以每秒2°的速度顺时针旋转.设旋转时何为t秒,如图4,∠BAH= t°,∠FDM=2t°,且0≤t≤150,若边BC与三角板的一条直角边(边DE,DF)平行时,请直接写出满足条件的t的值.【分析】(1)由题意得,∠EBF=90°,∠E=45°,∠ABC=60°,利用平行线的性质可得∠CDE=∠E=45°,即可求得答案;(2)①当DE∥BC时,延长AC交MN于点P,分两种情况:当DE在MN上方时或当DE在MN下方时,分别运用平行线的性质即可;②当BC∥DF时,延长BC交MN于点T,分两种情况:当DF在MN上方时或当DF在MN下方时,分别运用平行线的性质即可;(3)当DE∥BC时,延长AC交MN于点P,分两种情况讨论:①DE在MN上方时,②DE在MN下方时,∠FDP=2t°-180°,列式求解即可;(2)当BC∥DF时,延长AC交MN于点I,①DF在MN上方时,∠FDN=180°-2t°,②DF在MN下方时,∠FDN=180°-2t°,列式求解即可.【解答】解:(1)如图,由题意得,∠EBF=90°,∠E=45°,∠ABC=60°,∵EF∥CD,∴∠CDE=∠E=45°,∴∠ABE=∠ABC-∠CDE=60°-45°=15°,∴∠ABF=∠EBF-∠ABE=90°-15°=75°;(2)如图,①当DE∥BC时,延长AC交MN于点P,当DE在MN上方时,∵DE∥BC,DE⊥DF,AC⊥BC,∴AP∥DF,∴∠FDM=∠MPA,∵MN∥GH,∴∠MPA=∠HAC,∴∠FDM=∠HAC,即2t°=30°,∴t=15;当DE在MN下方时,∠F′DP=2t°-180°,∵DE′∥BC,DE′⊥DF′,AC⊥BC,∴AP∥DF′,∴∠F′DP=∠MPA,∵MN∥GH,∴∠MPA=∠HAC,∴∠F′DP=∠HAC,即2t°-180°=30°,∴t=105;②当BC∥DF时,当DF在MN上方时,BC∥DF,如图,延长BC交MN于点T,根据题意得:∠FDN=180°-2t°,∵DF∥BC,∴∠FDN=∠BTN,∵GH∥MN,∴∠BTN=∠ABC=60°,∴∠FDN=60°,即180°-2t°=60°,∴t=60;当DF在MN下方时,如图,延长BC交MN于点T,根据题意可知:∠FDN=2t°-180°,∵DF∥BC,∴∠FDN=∠BTM,∵GH∥MN,∴∠BTN=∠ABC=60°,∴∠BTM=180°-∠BTN=120°,∴∠NDF=120°,即2t°-180°=120°,∴t=150,综上所述:所有满足条件的t的值为15或60或105或150;(3)由题意得,∠HAC=∠BAH+∠BAC=t°+30°,∠FDM=2t°,①如图,当DE∥BC时,延长AC交MN于点P,当DE在MN上方时,∵DE∥BC,DE⊥DF,AC⊥BC,∴AP∥DF,∴∠FDM=∠MPA,∵MN∥GH,∴∠MPA=∠HAC,∴∠FDM=∠HAC,即2t°=t°+30°,∴t=30,当DE′在MN下方时,∠F′DP=2t°-180°,∵DE′∥BC,DE′⊥DF′,AC⊥BC,∴AP∥DF′,∴∠F′DP=∠MPA,∵MN∥GH,∴∠MPA=∠HAC,∴∠F′DP=∠HAC,即2t°-180°=t°+30°,∴t=210(不符合题意,舍去),②当BC∥DF时,延长AC交MN于点I,当DF在MN上方时,BC∥DF,如图,根据题意得:∠FDN=180°-2t°,∵DF∥BC,AC⊥BC,∴CI⊥DF,∴∠FDN+∠MIC=90°,即180°-2t°+t°+30°=90°,∴t=120,∴2t=240°>180°,此时DF应该在MN下方,不符合题意,舍去;当DF在MN下方时,如图,根据题意可知:∠FDN=2t°-180°,∵DF∥BC,∴∠MIC=∠NDF,∴∠NDF=∠AQI=t+30°-90°=t-60°,即2t°-180°=t°-60°,∴t=120,综上所述:所有满足条件的t的值为30或120.【例4】(2021春•梅江区期末)如图(1),AB∥CD,点E在AB、CD之间,连接EA、EC;如图(2),AB∥CD.点M、N分别在AB、CD上,连接MN.(1)在图(1)中,若∠A=30°,∠C=50°,则∠AEC= 80° ;若∠A=25°,∠C=40°,则∠AEC= 65° .(2)图(1)的条件下,猜想∠EAB、∠ECD、∠AEC的关系,并说明你的结论.(3)如图(2),点E是四边形ACDB内(不含边界和MN)任意一点,请说明∠EMB、∠END、∠MEN的关系.【分析】(1)过点E作EF∥AB,如图1,根据平行线的性质,两直线平行,内错角相等可得∠AEG=∠A,∠CEG=∠C,由∠AEC=∠AEG+∠CEG,可得∠AEC=∠A+∠C,代入计算即可得出答案;(2)过点E作EF∥AB,如图1,根据平行线的性质可得,∠AEG=∠EAB,∠CEG=∠ECD.由∠AEC=∠AEG+∠CEG,即可得出答案;(3)根据题意画图,如图2,过点E作EF∥AB,根据平行线的性质,两直线平行,同旁内角互补可得,∠EMB+∠MEF=180°,∠NEF+∠END=180°,由∠EMB+∠MEF+∠NEF+∠END=360°,根据∠MEN=∠MEF+∠NEF,即可得出答案.【解答】解:(1)过点E作EF∥AB,如图1,∵AB∥CD,∴GF∥CD,∴∠AEG=∠A,∠CEG=∠C,∴∠AEC=∠AEG+∠CEG,∴∠AEC=∠A+∠C,若∠A=30°,∠C=50°,则∠AEC=30°+50°=80°,若∠A=25°,∠C=40°,则∠AEC=25°+40°=65°;故答案为:80°,65°;(2)∠AEC=∠EAB+∠ECD.理由如下:过点E作EF∥AB,如图1,∵AB∥CD,∴GF∥CD,∴∠AEG=∠EAB,∠CEG=∠ECD.∵∠AEC=∠AEG+∠CEG,∴∠AEC=∠EAB+∠ECD;(3)∠ENB+∠NEN+∠END=360°.理由如下:根据题意画图,如图2,过点E作EF∥AB,∴∠EMB+∠MEF=180°,∵AB∥CD,∴GF∥CD,∴∠NEF+∠END=180°,∴∠EMB+∠MEF+∠NEF+∠END=360°,∵∠MEN=∠MEF+∠NEF,∴∠ENB+∠NEN+∠END=360°.培优训练一、选择题1.(2022•黔东南州)一块直角三角板按如图所示方式放置在一张长方形纸条上,若∠1=28°,则∠2的度数为()A.28°B.56°C.36°D.62°【分析】过直角的顶点E作MN∥AB,利用平行线的性质解答即可.【解答】解:如下图所示,过直角的顶点E作MN∥AB,交AD于点M,交BC于点N,则∠2=∠3.∵四边形ABCD是矩形,∴AB∥CD,∵AB∥MN,∴MN∥CD,∴∠4=∠1=28°,∵∠3+∠4=90°,∴∠3=90°-∠4=62°.∴∠2=∠3=62°.故选:D.2.(2022•临清市二模)如图,若AB∥CD,CD∥EF,那么∠BCE=()A.180°-∠2+∠1B.180°-∠1-∠2C.∠2=2∠1D.∠1+∠2【分析】先利用平行线的性质说明∠3、∠1、∠4、∠2间关系,再利用角的和差关系求出∠BCA【解答】解:∵AB∥CD,CD∥EF,∴∠1=∠3,∠2+∠4=180°.∴∠BCE=∠3+∠4=∠1+180°-∠2.故选:A.3.(2021春•硚口区月考)如图,AB与HN交于点E,点G在直线CD上,GF交AB于点M,∠FMA=∠FGC,∠FEN=2∠NEB,∠FGH=2∠HGC,下列四个结论:①AB∥CD;②∠EHG=2∠EFM;③∠EHG+∠EFM=90°;④3∠EHG-∠EFM=180°.其中正确的结论是()A.①②③B.②④C.①②④D.①④【分析】过点F作FP∥AB,HQ∥AB,设∠NEB=x,∠HGC=y,利用猪脚模型、锯齿模型表示出∠EHG、∠EFM,即可分析出答案.【解答】解:∵∠FMA=∠FGC∴AB∥CD∴①正确;过点F作FP∥AB,HQ∥AB,∵AB∥CD,∴FP∥AB∥HQ∥CD,设∠NEB=x,∠HGC=y,则∠FEN=2x,∠FGH=2y∴∠EHG=∠EHQ+∠GHQ=∠AEH+∠HGC=∠NEB+∠HGC=x+y,∠EFM=∠BEF-∠FME=∠BEF-∠AMG=∠BEF-(180°-∠FGC)=x+2x-(180°-y-y) =3x+3y-180°,∴2∠EFM=6x+6y-360°,∴∠EHG≠2∠EFM∴②错误;∴∠EHG+∠EFM=x+y+3x+3y-180°=4x+4y-180°≠90°,∴③错误;∴3∠EHG-∠EFM=3(x+y)-(3x+3y-180°)=180°,∴④正确.综上所述,正确答案为①④.故选:D.4.(2018春•南昌期中)如图,AB∥CD,∠1=30°,∠2=90°,则∠3的度数是()A.30°B.45°C.50°D.60°【分析】作辅助线,过点O做OP∥AB∥CD,再结合两直线平行内错角相等的性质,即可得出∠3的度数.【解答】解:过点O做OP∥AB∥CD,∴∠A=∠AOP=30°,∠D=∠POC,∵∠2=90°,即∠AOC=90°,∴∠POC=60°,∴∠3=60°.故选:D.5.(2018春•沂源县期末)如图,AB∥CD,∠ABF=23∠ABE,∠CDF=23∠CDE,则∠E:∠F=()A.2:1B.3:1C.3:2D.4:3【分析】本题主要利用两直线平行,内错角相等作答.【解答】解:过点E、F分别作AB的平行线EG、FH,由平行线的传递性可得AB∥EG∥FH∥CD,∵AB∥FH,∴∠ABF=∠BFH,∵FH∥CD,∴∠CDF=∠DFH,∴∠BFD=∠DFH+∠BFH=∠CDF+∠ABF;同理可得∠BED=∠DEG+∠BEG=∠ABE+∠CDE;∵∠ABF=23∠ABE,∠CDF=23∠CDE,∴∠BFD=∠DFH+∠BFH=∠CDF+∠ABF=23(∠ABE+∠CDE)=23∠BED,∴∠BED:∠BFD=3:2.故选:C.6.(2022春•诸暨市期末)从汽车灯的点O处发出的一束光线经灯的反光罩反射后沿CO方向平行射出,已知入射光线OA的反射光线为AB,∠OAB=∠COA=72°.在如图中所示的截面内,若入射光线OD经反光罩反射后沿DE射出,且∠ODE=27°.则∠AOD的度数是 45°或99° .【分析】分两种情况:如果∠AOD是锐角,∠AOD=∠COA-∠COD;如果∠AOD是钝角,∠AOD=∠COA+∠COD,由平行线的性质求出∠COA,∠COD,从而求出∠AOD的度数.【解答】解:∵DE∥CF,∴∠COD=∠ODE.(两直线平行,内错角相等)∵∠ODE=22°,∴∠COD=22°.在图1的情况下,∠AOD=∠COA-∠COD=72°-27°=45°.在图2的情况下,∠AOD=∠COA+∠COD=72°+27°=99°.∴∠AOD的度数为45°或99°.故答案为:45°或99°.7.(2022春•潜山市月考)如图,AB∥CD,点E,F分别是AB,CD上的点,点M位于AB与CD之间且在EF的右侧.(1)若∠M=90°,则∠AEM+∠CFM= 270° ;(2)若∠M=n°,∠BEM与∠DFM的角平分线交于点N,则∠N的度数为 1n° .(用含n的2式子表示)【分析】(1)过点M 作MP ∥AB ,则AB ∥CD ∥MP ,根据两直线平行,内错角相等可得答案;(2)过点N 作NQ ∥AB ,则AB ∥CD ∥NQ ,根据两直线平行内错角相等和角平分线的定义可得答案.【解答】解:(1)过点M 作MP ∥AB ,∵AB ∥CD ,∴AB ∥CD ∥MP ,∴∠1=∠MEB ,∠2=∠MFD ,∵∠M =∠1+∠2=90°,∴∠MEB +∠MFD =90°,∵∠AEM +∠MEB +∠CFM +∠MFD =180°+180°=360°,∴∠AEM +∠CFM =360°-90°=270°.故答案为:270°;(2)过点N 作NQ ∥AB ,∵AB ∥CD ,∴AB ∥CD ∥NQ ,∴∠3=∠NEB ,∠4=∠NFD ,∴∠NEB +∠NFD =∠3+∠4=∠ENF ,∵∠BEM 与∠DFM 的角平分找交于点N ,∵∠NEB =12∠MEB ,∠DFN =12∠MFD ,∴∠3+∠4=∠BEN +∠DFN =12(∠MEB +∠MFD ),由(1)得,∠MEB +∠MFD =∠EMF ,∴∠ENF =12∠EMF =12n °.故答案为:12n °.8.(2019•大丰区一模)如图,已知:AB ∥CD ,∠1=50°,∠2=113°,则∠3= 63 度.【分析】如图,作EF ∥AB .证明基本结论;∠AEC =∠1+∠3即可解决问题.【解答】解:如图,作EF ∥AB .∵AB ∥CD ,AB ∥EF ,∴EF ∥CD ,∴∠1=∠AEF,∠3=∠CEF,∴∠AEC=∠1+∠3,∴113°=50°+∠3,∴∠3=63°.故答案为63;9.(2019秋•福田区校级期末)如图,AB∥CD,∠BED=110°,BF平分∠ABE,DF平分∠CDE,则∠BFD= 125° .【分析】首先过点E作EM∥AB,过点F作FN∥AB,由AB∥CD,即可得EM∥AB∥CD∥FN,然后根据两直线平行,同旁内角互补,由∠BED=110°,即可求得∠ABE+∠CDE=250°,又由BF平分∠ABE,DF平分∠CDE,根据角平分线的定义,即可求得∠ABF+∠CDF的度数,又由两直线平行,内错角相等,即可求得∠BFD的度数.【解答】解:过点E作EM∥AB,过点F作FN∥AB,∵AB∥CD,∴EM∥AB∥CD∥FN,∴∠ABE+∠BEM=180°,∠CDE+∠DEM=180°,∴∠ABE+∠BED+∠CDE=360°,∵∠BED=110°,∴∠ABE+∠CDE=250°,∵BF平分∠ABE,DF平分∠CDE,∴∠ABF=12∠ABE,∠CDF=12∠CDE,∴∠ABF+∠CDF=12(∠ABE+∠CDE)=125°,∵∠DFN=∠CDF,∠BFN=∠ABF,∴∠BFD=∠BFN+∠DFN=∠ABF+∠CDF=125°.故答案为125°10.(2022春•交城县期中)如图,已知AB∥CD,AE和CF分别平分∠BAF和∠DCE,若∠AEC=57°,∠AFC=63°,则∠BAF的度数为 46° .【分析】延长AE 交CD 于点H ,延长AF 交CD 于点G ,设∠BAE =x ,∠FCG =y ,根据角平分线的定义可得∠BAF =2x ,∠ECG =2y ,然后利用平行线的性质可得∠AGC =2x ,∠AHC =x ,,再利用三角形的外角性质可得∠AEC =x +2y ,∠AFC =2x +y ,最后列出关于x ,y 的方程组,进行计算即可解答.【解答】解:延长AE 交CD 于点H ,延长AF 交CD 于点G ,设∠BAE =x ,∠FCG =y ,∵AE 和CF 分别平分∠BAF 和∠DCE ,∴∠BAF =2∠BAE =2x ,∠ECG =2∠FCG =2y ,∵AB ∥CD ,∴∠BAF =∠AGC =2x ,∠BAH =∠AHC =x ,∵∠AEC 是△EHC 的一个外角,∴∠AEC =∠AHC +∠ECG =x +2y ,∵∠AFC 是△GCF 的一个外角,∴∠AFC =∠AGC +∠FCG =2x +y ,∵∠AEC =57°,∠AFC =63°,∴x +2y =57o2x +y =63o ,解得:x =23o y =17o ,∴∠BAF =46°,故答案为:46°.11.(2022春•濠江区期末)已知直线AB ∥CD ,直线EF 分别截AB 、CD 于点G 、H ,点M 在直线AB 、CD 之间,连接MG ,MH .(1)如图1,求证:∠M =∠AGM +∠MHC ;(2)如图2,若HM 平分∠GHC ,在HM 上取点Q ,使得∠HGQ =∠AGM ,求证:∠M +∠GQH =180°;(3)如图3,若GH 平分∠MGB ,N 在为HD 上一点,连接GN ,且∠GNH =∠M ,∠HGN =2∠MHC ,求∠MHG 的度数.【分析】(1)过点M作MN∥AB,利用平行线的猪脚模型,即可解答;(2)根据角平分线的定义可得∠MHG=∠CHM,再利用(1)的结论可得∠GMH=∠AGM+∠MHC,从而可得∠GMH=∠HGQ+∠MHG,然后利用三角形内角和定理进行计算即可解答;(3)设∠AGM=2α,∠CHM=β,从而可得∠HGN=2β,再利用(1)的结论可得∠GMH=2α+β,从而可得∠GNH=2α+β,然后利用角平分线的定义可得∠MGH=90°-α,再利用三角形的外角可得∠CHG= 3β+2α,最后利用平行线的性质可得∠AGH+∠CHG=180°,从而可得α+β=30°,再利用角的和差关系进行计算即可解答.【解答】(1)证明:过点M作MN∥AB,∴∠AGM=∠GMN,∵AB∥CD,∴MN∥CD,∴∠NMH=∠CHM,∵∠GMH=∠GMN+∠NMH,∴∠GMH=∠AGM+∠MHC;(2)证明:∵HM平分∠GHC,∴∠MHG=∠CHM,由(1)得:∠GMH=∠AGM+∠MHC,∵∠HGQ=∠AGM,∴∠GMH=∠HGQ+∠MHG,∵∠GQH+∠HGQ+∠MHG=180°,∴∠GMH+∠GQH=180°;(3)解:设∠AGM=2α,∠CHM=β,由(1)可得:∠GMH=∠AGM+∠MHC,∴∠GMH=2α+β,∵∠GNH=∠M,∴∠GNH=2α+β,∵∠HGN=2∠MHC,∴∠HGN=2β,∵GH平分∠MGB,∴∠MGH=12∠BGM=12(180°-∠AGM)=90°-α,∵∠CHG是△GHN的一个外角,∴∠CHG=∠HGN+∠GNH=2β+2α+β=3β+2α,∵AB∥CD,∴∠AGH+∠CHG=180°,∴∠AGM+∠MGH+∠CHG=180°,∴2α+90°-α+3β+2α=180°,∴α+β=30°,∴∠MHG=∠CHG-∠CHM=3β+2α-β=2β+2α=60°,∴∠MHG的度数为60°.12.(2022春•沂源县期末)在综合与实践课上,同学们以“一个含30°的直角三角尺和两条平行线”为背景开展数学活动如图,已知两直线a,b且a∥b和直角三角形ABC,∠BCA=90°,∠BAC=30°,∠ABC=60°.操作发现:(1)在图1中,∠1=46°,求∠2的度数.(2)某同学把直线a向上平移,并把∠2的位置改变,如图2,发现∠2-∠1=120°,说明理由.【分析】(1)根据直角三角形的性质求出∠3,根据平行线的性质解答;(2)过点B作BD∥a,根据平行线的性质得到∠ABD=180°-∠2,∠DBC=∠1,结合图形计算,证明结论.【解答】解:(1)∵∠BCA=90°,∴∠3=90°-∠1=44°,∵a∥b,∴∠2=∠3=44°.(2)理由如下:过点B作BD∥a,则∠ABD=180°-∠2,∵a∥b,BD∥a,∴BD∥b,∴∠DBC=∠1,∵∠ABC=60°∴180°-∠2+∠1=60°,∴∠2-∠1=120°.13.(2022春•无棣县期末)如图1,已知∠BAE=∠AEC-∠ECD,点E在直线AB,CD之间.(1)求证:AB∥CD;(2)若AH平分∠BAE,FG∥CE.①如图2,若∠AEC=84°,FH平分∠DFG,求∠AHF的度数;②如图3,若FH平分∠CFG,试判断∠AHF与∠AEC的数量关系并说明理由.【分析】(1)过E作EN∥AB,可得∠BAE=∠AEN,∠BAE=∠AEC-∠ECD,证得∠ECD=∠CEN,故EF∥CD∥AB;(2)①HF平分∠DFG,设∠GFH=∠DFH=x,根据平行线的性质可以得到∠AHF的度数;②设∠GFD=2x,∠BAH=∠EAH=y,根据角平分线的性质以及平行线的性质即可得到∠AHF与∠AEC的数量关系.【解答】解:(1)如图1,过点E作直线EN∥AB,∴∠BAE=∠AEN,∵∠BAE=∠AEC-∠ECD,∴∠BAE+∠ECD=∠AEC,∵∠AEN+∠CEN=∠AEC,∴∠ECD=∠CEN,∴EN∥CD,∴CD∥AB;(2)∵AH平分∠BAE,∴∠BAH=∠EAH,①∵HF平分∠DFG,设∠GFH=∠DFH=x,又CE∥FG,∴∠ECD=∠GFD=2x,又∠AEC=∠BAE+∠ECD,∠AEC=84°,∴∠BAH=∠EAH=42°-x,如图2,过点H作HM∥AB,∴∠BAH=∠AHM,∵HM∥AB,∴HM∥CD,∴∠DFH=∠MHF,∴∠AHF=∠BAH+∠DFH=42°-x+x=42°;②设∠GFD=2x,∠BAH=∠EAH=y,∵HF平分∠CFG,∴∠GFH=∠CFH=90°-x,由(1)知∠AEC=∠BAE+∠ECD=2x+2y,如图3,过点H作HK∥AB,∴∠BAH=∠AHK,∵HK∥AB,∴HK∥CD,∴∠KHF+∠CFH=180°,∴∠AHF-y+∠CFH=180°,即∠AHF-y+90°-x=180°,∠AHF=90°+(x+y),∴∠AHF=90°+1∠AEC.214.(2022春•墨玉县期末)问题情景:(1)如图①,已知AB∥DE.试∠B、∠E、∠BCE有什么关系?小明添加了一条辅助线.解决了这道题.得到的结果是∠B+∠E=∠BCE.请你帮他完善证明过程:如图②,过点C作CF∥AB∴ ∠B = ∠1 ( 两直线平行,内错角相等 )∵AB∥DE,AB∥CF∴ DE ∥ CF .∴∠E= ∠2 ( 两直线平行,内错角相等 )∴∠B+∠E=∠1+∠2即∠B+∠E=∠BCE.(2)在图①中.若BC⊥CE,且∠B=52°,请你计算∠E的度数等于 38° .(3)问题迁移:如图③.AD∥BC.当点P在射线AM上运动时,∠ADP=∠α,∠BCP=∠β请你猜想∠α、∠β与∠CPD之间有怎样的数量关系?并说明理由.【分析】(1)根据两直线平行,内错角相等即可求解;(2)由(1)可知∠B+∠E=90°,即可求解;(3)由三角形外角性质可得∠CPD+∠CDP=∠OCP,从而可得∠CPD+∠α+∠ADO=∠β+∠BCO,由AD∥BC可得∠ADO=∠BCO,即可得出∠CPD+∠α=∠β.【解答】解:(1)过点C作CF∥AB,∴∠B=∠1(两直线平行,内错角相等),∵AB∥DE,AB∥CF,∴DE∥CF,∴∠E=∠2(两直线平行,内错角相等),∴∠B+∠E=∠1+∠2,即∠B+∠E=∠BCE,故答案为:∠B=∠1;两直线平行,内错角相等;DE;CF;∠2;两直线平行,内错角相等;(2)由(1)可知∠B+∠E=∠BCE,∵∠BCE=90°,∠B=52°,∴∠E=∠BCE-∠B=38°,故答案为:38°;(3)∠CPD+∠α=∠β,理由如下:∵∠CPD+∠CDP=∠OCP,∴∠CPD+∠α+∠ADO=∠β+∠BCO,∵AD∥BC,∴∠ADO=∠BCO,∴∠CPD+∠α=∠β.15.(2022春•抚远市期末)如图,已知AD∥BC,AB∥CD,点E在线段BC的延长线上,AE平分∠BAD,连接DE,∠ADC=2∠CDE,∠AED=60°.(1)求证∠ABC=∠ADC;(2)求∠CDE的度数.【分析】(1)根据平行线的性质即可得到答案.(2)根据∠ADE=3∠CDE,设∠CDE=x,∠ADE=3x,∠ADC=2x,根据平行线的性质得出方程90°-x+60°+3x=180°,求出x即可.【解答】(1)证明:∵AB∥CD,∴∠ABC=∠DCE,∵AD∥BC,∴∠ADC=∠DCE,∴∠ABC=∠ADC.(2)解:设∠CDE=x,则∠ADC=2x,∵AB∥CD,∴∠BAD=180°-2x,∵AE平分∠BAD,∴∠EAD=12∠BAD=90°-x,∵AD∥BC,∴∠BEA=∠EAD=90°-x,∴∠BED+∠ADE=180°,∴90°-x+60°+3x=180°,∴x=15°,∴∠CDE=15°.16.(2022春•来宾期末)如图,直线PQ∥MN,直角三角尺ABC的∠BAC=30°,∠ACB=90°.(1)若把三角尺按图甲方式放置,则∠MAC+∠PBC= 90 °;(2)若把三角尺按图乙方式放置,点D,E,F是三角尺的边与平行线的交点,若∠AEN=∠A,求∠BDF的值;(3)如图丙,三角尺的直角顶点C始终在两条平行线之间,点G在线段CD上,连接EG,适当转动三角尺,使得CE恰好平分∠MEG,求∠GEN∠BDF的值.【分析】(1)延长BC交MN于点D,根据平行线的性质可得∠PBC=∠ADC,再利用三角形的外角可得∠ACB=∠ADC+∠MAC,然后利用等量代换即可解答;(2)根据已知可得∠AEN=∠A=30°,再利用对顶角相等可得∠CEM=30°,然后利用(1)的结论可得:∠PDC=60°,最后利用对顶角相等即可解答;(3)利用角平分线的定义设∠CEM=∠CEG=x,从而利用平角定义可得∠GEN=180°-2x,再利用(1)的结论可得:∠PDC=90°-x,然后利用对顶角相等可得∠BDF=90°-x,进行计算即可解答.【解答】解:(1)延长BC交MN于点D,∵PQ∥MN,∴∠PBC=∠ADC,∵∠ACB是△ACD的一个外角,∴∠ACB=∠ADC+∠MAC,∴∠ACB=∠PBC+∠MAC=90°,故答案为:90;(2)∵∠AEN=∠A,∠BAC=30°,∴∠AEN=∠A=30°,∴∠CEM=∠AEN=30°,∠ACB=∠PDC+∠MEC,∴∠PDC=∠ACB-∠MEC=60°,∴∠BDF=∠PDC=60°,∴∠BDF的度数为60°;(3)∵CE平分∠MEG,∴∠CEM=∠CEG,设∠CEM=∠CEG=x,∴∠GEN=180°-∠CEM-∠CEG=180°-2x,利用(1)的结论可得:∠ACB =∠PDC +∠MEC ,∴∠PDC =∠ACB -∠MEC =90°-x ,∴∠BDF =∠PDC =90°-x ,∴∠GEN ∠BDF =180O -2x 90o -x=2,∴∠GEN ∠BDF的值为2.17.(2022春•咸安区期末)(1)如图1,已知AB ∥CD ,∠AEP =40°,∠PFD =110°,求∠EPF 的度数.(2)如图2,AB ∥CD ,点P 在AB 的上方,问∠PEA ,∠PFC ,∠EPF 之间有何数量关系?并说明理由;(3)如图3,在(2)的条件下,已知∠EPF =60°,∠PEA 的平分线和∠PFC 的平分线交于点G ,求∠G 的度数.【分析】(1)延长EP 交CD 于点G ,利用平行线的性质可得∠PGF =40°,再利用平角定义可得∠PFG =70°,然后利用三角形的外角进行计算即可解答;(2)设AB 与PF 交于点M ,先利用三角形的外角可得∠PMA =∠PEA +∠EPF ,再利用平行线的性质可得∠PMA =∠PFC ,然后利用等量代换可得∠PFC =∠PEA +∠EPF ,即可解答;(3)利用(2)的结论可得∠EPF =∠PFC -∠PEA =60°,再利用角平分线的性质可得∠GEA =12∠AEP ,∠GFC =12∠PFC ,然后利用(2)的结论可得∠G =∠GFC -∠GEA =12(∠PFC -∠AEP ),进行计算即可解答.【解答】解:(1)延长EP 交CD 于点G ,∵AB ∥CD ,∴∠AEG =∠PGF =40°,∵∠PFD =110°,∴∠PFG =180°-∠PFD =70°,∵∠EPF 是△PFG 的一个外角,∴∠EPF =∠PGF +∠PFG =110°,∴∠EPF 的度数为110°;(2)∠PFC =∠PEA +∠EPF ,理由:如图:设AB 与PF 交于点M ,∵∠PMA 是△PME 的一个外角,∴∠PMA =∠PEA +∠EPF ,∵AB ∥CD ,∴∠PMA =∠PFC ,∴∠PFC =∠PEA +∠EPF ;(3)由(2)可得:∠PFC =∠PEA +∠EPF ,∴∠EPF =∠PFC -∠PEA =60°,∵EG 平分∠AEP ,FG 平分∠PFC ,∴∠GEA =12∠AEP ,∠GFC =12∠PFC ,由(2)得:∠GFC =∠G +∠GEA ,∴∠G =∠GFC -∠GEA=12∠PFC -12∠AEP =12(∠PFC -∠AEP )=12×60°=30°,∴∠G 的度数为30°.18.(2022春•上虞区期末)如图1,已知点E ,F 分别是直线AB ,CD 上的点,点M 在AB 与CD 之间,且AB ∥CD .(1)若∠EMF =80°,则∠AEM +∠CFM = 80° .(2)如图2,在图1的基础上,作射线EN ,FN 交于点N ,使∠AEN =13∠AEM ,∠CFN =13∠CFM ,设∠EMF =α,猜想∠ENF 的度数(用α表示),并说明理由.(3)如图3,在图1的基础上,分别作射线EP ,FP 交于点P ,作射线EQ ,FQ 交于点Q ,若∠AEP =1m ∠AEM ,∠CFP =1m ∠CFM ,∠BEQ =1n ∠BEM ,∠DFQ =1n∠DFM ,请直接写出∠P 与∠Q 间的数量关系.【分析】(1)过点M 作MP ∥AB ,利用平行线的性质,把∠AEM +∠CFM 转化为∠EMF ,从而求得度数.(2)过点M 作MP ∥AB ,过点N 作NQ ∥AB ,利用平行线的性质,把∠EMF 转化为∠AEM +∠CFM ,把∠ENF 转化为∠AEN +∠CFN ,得出∠ENF =13∠EMF ,从而用α表示出∠ENF 的度数.(3)利用(2)的结论,同时利用两直线平行,同旁内角互补得出∠BEM +∠DFM +∠M =360°,进而找到∠P 与∠Q 间的数量关系.【解答】解:(1)过点M 作MG ∥AB ,∵AB ∥CD ,∴AB ∥CD ∥MG ,∴∠AEM =∠EMG ,∠GMF =∠CFM ,∴∠AEM +∠CFM =∠EMG +∠GMF =∠EMF =80°.故答案为:80°.(2)∠ENF =13α.理由如下:过点M 作MG ∥AB ,由(1)知,∠EMF =∠AEM +∠CFM ,过点N 作NH ∥AB ,∵AB ∥CD ,∴AB ∥CD ∥NH ,∴∠AEN =∠ENH ,∠HNF =∠CFN ,∴∠ENF =∠ENH +∠HNF =∠AEN +∠CFN ,∵∠AEN =13∠AEM ,∠CFN =13∠CFM ,∴∠ENF =13∠AEM +13∠CFM =13(∠AEM +∠CFM )=13∠EMF ,∵∠EMF =α,∴∠ENF=13α.(3)n∠Q+m∠P=360°.理由如下:由(2)的结论可知,∠P=1m∠M,∠Q=∠BEQ+∠DFQ,∠BEM+∠DFM+∠M=360°,∵∠BEQ=1n ∠BEM,∠DFQ=1n∠DFM,∴∠Q=1n ∠BEM+1n∠DFM,=1n(∠BEM+∠DFM)=1n(360°-∠M),∴∠M=360°-n∠Q,∵∠M=m∠P,∴360°-n∠Q=m∠P,即n∠Q+m∠P=360°.19.(2022春•西岗区期末)如图1,AB∥CD,点P,Q分别在AB,CD上,点E在AB,CD之间.连接PE,QE,PE⊥QE.(1)直接写出∠BPE与∠DQE的数量关系为 ∠BPE+∠DQE=90° ;(2)如图2,∠APE的平分线PG和∠CQE的平分线QH的反向延长线相交于点G,求∠G的度数;(3)如图3,M为线段PE上一点,连接QM,∠BPE和∠MQD的平分线相交于点N,直接写出∠PNQ和∠MQE的数量关系为 2∠PNQ-∠MQE=90° .【分析】(1)延长PE交CD于点F,根据垂直定义可得∠PEQ=90°,根据平行线的性质可得∠BPE=∠PFC,然后再利用三角形的外角可得∠DQE+∠PFC=90°,即可解答;(2)过点G作GF∥CD,从而可得∠HQC=∠HGF,再利用平行线的性质可得∠PGF=180°-∠APG,利用(1)的结论可得∠APE+∠CQE=270°,然后利用角平分线的定义可得∠APG+∠CQH=135°,最后根据∠HGP=∠PGF-∠HGF=180°-∠APG-∠HQC,进行计算即可解答;(3)根据角平分线的定义可得∠BPE=2∠BPN,∠MQN=∠DQN,再利用猪脚模型可得∠BPE+∠DQE=90°,∠BPN+∠DQN=∠PNQ,再利用角的和差关系进行计算即可解答.【解答】解:(1)延长PE交CD于点F,∵PE ⊥QE ,∴∠PEQ =90°,∵AB ∥CD ,∴∠BPE =∠PFC ,∵∠PEQ 是△QEF 的一个外角,∴∠PEQ =∠DQE +∠PFC =90°,∴∠BPE +∠DQE =90°,故答案为:∠BPE +∠DQE =90°,(2)过点G 作GF ∥CD ,∴∠HQC =∠HGF ,∵AB ∥CD ,∴AB ∥FG ,∴∠PGF =180°-∠APG ,由(1)得:∠BPE +∠DQE =90°,∴∠APE +∠CQE =360°-(∠BPE +∠DQE )=270°,∵PG 平分∠APE ,QH 平分∠CQE ,∴∠APG =12∠APE ,∠CQH =12∠CQE ,∴∠APG +∠CQH =12(∠APE +∠CQE )=135°,∵∠HGP =∠PGF -∠HGF=180°-∠APG -∠HQC=45°,∴∠HGP 的度数为45°;(3)2∠PNQ -∠MQE =90°,理由:∵PN 平分∠BPE ,QN 平分∠MQD ,∴∠BPE =2∠BPN ,∠MQN =∠DQN ,由(1)可得:∠BPE +∠DQE =90°,∴2∠BPN +∠DQN +∠EQN =90°,由(1)可得:∠BPN +∠DQN =∠PNQ ,∴∠PNQ +∠BPN +∠MQN -∠MQE =90°,∴∠PNQ +∠BPN +∠DQN -∠MQE =90°,∴∠PNQ+∠PNQ-∠MQE=90°,∴2∠PNQ-∠MQE=90°,故答案为:2∠PNQ-∠MQE=90°.20.(2022春•宜春期末)问题:已知线段AB∥CD,在AB、CD间取一点P(点P不在直线AC上),连接PA、PC,试探索∠APC与∠A、∠C之间的关系.(1)端点A、C同向:如图1,点P在直线AC右侧时,∠APC-(∠A+∠C)= 0 度;如图2,点P在直线AC左侧时,∠APC+(∠A+∠C)= 360 度;(2)端点A、C反向:如图3,点P在直线AC右侧时,∠APC与∠A-∠C有怎样的等量关系?写出结论并证明;如图4,点P在直线AC左侧时,∠APC-(∠A-∠C)= 180 度.【分析】(1)过点P作PE∥AB,分别利用猪脚模型,铅笔模型即可解答;(2)过点P作PE∥CD,利用平行线的性质,以及角的和差关系进行计算即可解答.【解答】解:(1)如图:过点P作PE∥AB,∴∠A=∠APE,∵AB∥CD,∴PE∥CD,∴∠C=∠EPC,∵∠APC=∠APE+∠EPC,∴∠APC=∠A+∠C,∴∠APC-(∠A+∠C)=0度,故答案为:0;如图:过点P作PE∥AB,∴∠A+∠APE=180°,∵AB∥CD,∴PE∥CD,∴∠C+∠EPC=180°,∴∠A+∠APE+∠C+∠EPC=360°,∴∠APC+∠A+∠C=360°,∴∠APC+(∠A+∠C)=360度,故答案为:360;(2)∠APC+∠A-∠C=180°,证明:过点P作PE∥CD,∴∠C=∠EPC,∵AB∥CD,∴PE∥AB,∴∠A+∠APE=180°,∴∠A+∠APC-∠EPC=180°,∴∠A+∠APC-∠C=180°,∴∠APC+∠A-∠C=180°;如图:过点P作PE∥AB,∴∠A=∠APE,∵AB∥CD,∴PE∥CD,∴∠C+∠EPC=180°,∴∠C+∠APC-∠APE=180°,∴∠C+∠APC-∠A=180°,∴∠APC-(∠A-∠C)=180°,故答案为:180.。
专题 一元二次方程的解法压轴题四种模型全攻略(老师版)

专题02一元二次方程的解法压轴题四种模型全攻略【类型一解一元二次方程——直接开平方法】例题:(2022·上海·八年级期末)解方程:(1)x (x +5)=x -4(2)4(x ﹣1)2=9.(3)()21160x +-=;(4)100(x -1)2=121.【答案】(1)122x x ==-;(2)x =52或x =﹣12;(3)13x =,25x =-;(4)x 1=2110,x 2=-110【解析】【分析】把原方程整理后化成一元二次方程的一般形式,然后选取适当的方法即可求解.【详解】解:(1)254x x x +=-,2440x x ++=,2(2)0x +=,122x x ==-.(2)4(x ﹣1)2=9,则(x ﹣1)2=94,故x ﹣1=±32,解得:x =52或x =﹣12.(3)()21160x +-=移项得:()2116x +=,开平方得:14x +=±,解得:13x =,25x =-;(4)解∶(x -1)2=121100,x -1=±1110,即x 1=2110,x 2=-110.【点睛】本题考查一元二次方程的解法,熟练掌握直接开平方法、因式分解法、配方法、公式法是关键.【变式训练1】(2022·全国·九年级单元测试)解方程(x -3)2=4,最合适的方法是()A .直接开平方法B .配方法C .公式法D .因式分解法【答案】A【解析】【分析】观察方程特点确定出适当的解法即可.【详解】解:方程(x -3)2=4,最合适的方法是直接开平方法;故答案为:A【点睛】本题考查了一元二次方程的解法.解一元二次方程常用的方法有直接开平方法,配方法,公式法,因式分解法,要根据方程的特点灵活选用合适的方法.【变式训练2】(2021·广东·梅州市学艺中学八年级期末)一元二次方程(x -1)2=4的根是______________.【答案】123,1x x ==-【解析】【分析】根据直接开平方法解一元二次方程即可.【详解】解:()214x -=12x -=±123,1x x ∴==-故答案为:123,1x x ==-.【点睛】本题考查了直接开平方法解一元二次方程,掌握解一元二次方程的方法是解题的关键.【变式训练3】(2022·广东·模拟预测)方程23(21)0x --=的解是_______.【答案】12x x ==【解析】【分析】先移项化为()2213x -=,再利用直接开平方的方法解方程即可.【详解】解:23(21)0x --=即()2213x -=21x \-=21x -=12x x \==故答案为:1211,22x x ==【点睛】本题考查的是一元二次方程的解法,掌握“直接开平方法解一元二次方程”是解本题的关键.【类型二解一元二次方程——配方法】例题:(2022·河南安阳·九年级期末)解下列方程:(1)2220x x --=;(2)23620x x -+=【答案】(1)11x =21x =(2)1211x x =+=【解析】【分析】(1)先移项,然后配方,再开平方,求出方程的解即可;(2)先移项,然后分解因式,最后求出方程的解即可.(1)解:2220x x --=,移项得:222x x -=,配方得:22121x x -+=+,即()213x -=,开平方得:1-=x ,∴11x =21x =.(2)23620x x -+=,22203x x -+=,222113x x -+=-,()2113x -=,1x -=,解得1211x x =+=【点睛】本题主要考查了配方法和因式分解法解一元二次方程,熟练进行配方和因式分解,是解题的关键.【变式训练1】(2022·云南·红河县教育科学研究室九年级期末)用配方法解一元二次方程2620x x ++=,变形后的结果正确的是()A .2(3)2x +=-B .2(3)2x +=C .2(3)7x -=D .2(3)7x +=【答案】D【解析】【分析】先将二次项配成完全平方式,再将常数项移项,即得答案.【详解】解:∵2620x x ++=,∴269920x x ++-+=,即()237x +=,故选:D .【点睛】本题考查了配方法解一元二次方程,熟练掌握配方法是解题关键.【变式训练2】(2022·辽宁大连·模拟预测)解方程:2480x x +-=.【答案】12x =,22x =--【解析】【分析】利用配方法解一元二次方程.【详解】解:x 2+4x =8,x 2+4x +4=8+4,2(2)12x +=,2x =±-,12x =,22x =-.【点睛】本题考查利用配方法解一元二次方程,解决问题的关键是降次.【变式训练3】(2022·上海·八年级开学考试)用配方法解方程x 2﹣4x ﹣2=0.【答案】x 1=2,x 2=2【解析】【分析】根据配方法即可求解.【详解】解:x 2﹣4x ﹣2=0,x 2﹣4x =2,x 2﹣4x +4=2+4,(x ﹣2)2=6,x ﹣2=,解得x 1=2x 2=2【点睛】本题考查了配方法解一元二次方程.配方法的一般步骤:(1)把常数项移到等号的右边;(2)把二次项的系数化为1;(3)等式两边同时加上一次项系数一半的平方.选择用配方法解一元二次方程时,最好使方程的二次项的系数为1,一次项的系数是2的倍数.【类型三根据判别式判断一元二次方程解得情况】例题:(2022·山东青岛·二模)关于x 的一元二次方程2(1)0x m x m -++=有两个相等的实数根,则m 值为__________.【答案】1【解析】【分析】由题意知,()21410m m =-+-⨯⨯=⎡⎤⎣⎦,计算求解即可.【详解】解:由题意知,()()2214110m m m =-+-⨯⨯=-=⎡⎤⎣⎦,解得1m =,故答案为:1.【点睛】本题考查了一元二次方程的根的个数与判别式的关系.解题的关键在于明确当0=时,一元二次方程有两个相等的实数根.【变式训练1】(2022·上海·八年级期末)下列一元二次方程没有实数根的是()A .x 2-2=0B .x 2-2x =0C .x 2+x +1=0D .(x -1)(x -3)=0【答案】C【解析】【分析】分别计算四个方程的根的判别式Δ=b 2﹣4ac ,然后根据△的意义分别判断方程根的情况.【详解】解:A 、Δ=02﹣4×1×(﹣2)=8>0,方程有两个不相等的实数根,所以A 选项不符合题意;B 、Δ=(﹣2)2﹣4×1×0=4>0,方程有两个不相等的实数根,所以,B 选项不符合题意;C 、Δ=12﹣4×1×1=﹣4<0,方程有没有的实数根,所以C 选项符合题意;D 、由原方程得到:x 2﹣4x +3=0,则Δ=(﹣4)2﹣4×1×3=4>0,方程有两个不相等的实数根,所以D 选项不符合题意;故选:C .【点睛】本题考查了一元二次方程ax 2+bx +c =0(a ≠0)的根的判别式Δ=b 2﹣4ac :当Δ>0,方程有两个不相等的实数根;当Δ=0,方程有两个相等的实数根;当Δ<0,方程没有实数根.【变式训练2】(2022·四川成都·九年级期末)已知方程2240x x -+=,则该方程的根的情况为()A .方程没有实数根B .方程有两个相等的实数根C .方程有两个不相等的实数根D .方程的根无法判定【答案】A【解析】【分析】求出一元二次方程根的判别式的值,判断即可.【详解】解:方程x 2-2x +4=0,∵a =1,b =-2,c =4,∴Δ=b 2-4ac =(-2)2-4×1×4=4-16=-12<0,则方程没有实数根.故选:A .【点睛】此题考查了根的判别式,根的判别式大于0,一元二次方程有两个不相等的实数根;根的判别式等于0,一元二次方程有两个相等的实数根;根的判别式小于0,一元二次方程没有实数根.【变式训练3】(2022·河北·一模)新定义运算:2a b a ab b =-+※,例如22122113=-⨯+=※,则方程25x =※的根的情况为()A .没有实数根B .有一个实数根C .有两个相等的实数根D .有两个不相等的实数根【答案】D【解析】【分析】根据新定义,列出方程2225x x -+=,再利用一元二次方程根的判别式,即可求解.【详解】解:根据题意得:2225x x -+=整理得:2230x x --=,∴()()22430∆=--⨯->,∴方程25x =※有两个不相等的实数根.故选:D【点睛】本题主要考查了一元二次方程根的判别式,熟练掌握一元二次方程()200++=≠ax bx c a ,当240b ac ∆=->时,方程有两个不相等的实数根;当240b ac ∆=-=时,方程有两个相等的实数根;当240b ac ∆=-<时,方程没有实数根是解题的关键.【类型四解一元二次方程——公式法】例题:(2022·云南文山·九年级期末)按要求解方程.(1)2x 2-5x +1=0(公式法)(2)23410x x -+=.(公式法)【答案】(1)x 1=54+,x 2=5174(2)11x =,213x =【解析】【分析】(1)根据公式法,可得方程的解;(2)先计算根的判别式,再利用公式法解方程即可.(1)解:∵a =2,b =-5,c =1,∴Δ=b 2﹣4ac =(-5)2-4×2×1=17,∴x =42b a-=∴x 1x 2(2)解:23410x x -+=则3,4,1,a b c ==-=()22=444314,b ac \-=--创=V 42,6x ±\=解得:1211,.3x x ==【点睛】本题考查的是一元二次方程的解法,掌握“利用配方法与公式法解一元二次方程”是解本题的关键.【变式训练1】(2022·重庆·西南大学附中八年级期中)计算解方程:22630x x -+-=【答案】x 1=32x 2【解析】【分析】利用公式法解方程即可.解:22630x x -+-=,Δ=()()26423120-⨯-⨯-=>,∴462324b x a --±==-,解得:x 1x 2【点睛】本题考查了公式法解一元二次方程,这种方法简便易用,是解一元二次方程最常用的方法.【变式训练2】(2022·重庆市育才中学八年级期中)解方程:(1)2260x x --=;(2)23620x x -+=【答案】(1)11x =-21x =+(2)12x x ==【解析】【分析】(1)利用公式法解一元二次方程即可得;(2)利用公式法解一元二次方程即可得.(1)2260x x --=,∴1a =,2b =-,6c =-,()24441628b ac ∆=-=-⨯⨯-=,2122b x a -±∴===11x ∴=21x =+,(2)解:方程23620x x -+=中的362a b c ==-=,,,()22b 4ac 6432120=-=--⨯⨯=>,则(6)23x --=⨯故12x x ==.【点睛】本题考查了解一元二次方程,熟练掌握解方程的方法是解题关键.【变式训练3】(2022·山东烟台·八年级期中)已知关于x 的方程21(1)230mm x x +--+=是一元二次方程.(1)求m 的值;(2)解这个一元二次方程.【答案】(1)-1(2)112x -=,212x -=【解析】【分析】(1)根据一元二次方程的定义求解即可,一元二次方程定义,只含有一个未知数,并且未知数项的最高次数是2的整式方程叫做一元二次方程;(2)根据公式法解一元二次方程即可.(1)关于x 的方程21(1)230m m x x +--+=是一元二次方程,212,10m m ∴+=-≠解得1m =-(2)方程为22230x x --+=,即22230x x +-=,∴2,2,3a b c ===-,2224328∴∆=+⨯⨯=解得112x -=,212x -=【点睛】本题考查了一元二次方程的定义,解一元二次方程,正确的计算是解题的关键.【类型五解一元二次方程——因式分解法】例题:(2022·四川成都·九年级期末)解下列一元二次方程.(1)x 2﹣4x =5;(2)2(x +1)2=x (x +1).【答案】(1)125,1x x ==-(2)121,2x x =-=-【解析】【分析】(1)通过移项,分解因式,化为一元一次方程,即可求解;(2)通过移项,分解因式,化为一元一次方程,即可求解.(1)解:x 2﹣4x =5,移项得:x 2﹣4x -5=0,分解因式得:(x -5)(x +1)=0,∴x -5=0或x +1=0,解得:125,1x x ==-;(2)解:2(x +1)2=x (x +1),移项得:2(x +1)2-x (x +1)=0,分解因式得:(x +1)(2x +2-x )=0,∴x +1=0或2x +2-x =0,解得:121,2x x =-=-.【点睛】本题主要考查解一元二次方程,掌握因式分解法解方程,是解题的关键.【变式训练1】(2022·江苏·苏州草桥中学八年级期中)解方程:(1)290x -=;(2)2230x x --=.【答案】(1)3x =或3x =-;(2)32x =或1x =-【解析】【分析】(1)运用公式法解一元二次方程即可;(2)运用十字相乘法解一元二次方程.(1)∵290x -=∴()()330x x +-=解得:3x =或3x =-;(2)∵2230x x --=∴()()2310x x -+=,解得:32x =或1x =-.【点睛】本题主要考查了解一元二次方程,掌握运用公式法、十字相乘法解一元二次方程是解答本题的关键.【变式训练2】(2022·黑龙江·哈尔滨市第六十九中学校八年级期中)解下列方程:(1)2325x x-=(2)24(3)(3)0x x x -+-=【答案】(1)113x =-,22x =(2)13x =,2125x =【解析】【分析】(1)利用因式分解法解方程;(2)利用因式分解法解方程.(1)解:2325x x-=23520x x --=()()3x 1x 20+-=∴113x =-,22x =(2)24(3)(3)0x x x -+-=[](3)4(3)0x x x --+=()(3)5120x x --=∴13x =,2125x =【点睛】本题考查了解一元二次方程−因式分解法,因式分解是解本题的关键.【变式训练3】(2022·黑龙江·哈尔滨市第十七中学校八年级期中)解方程:(1)2230x x --=(2)()()325320x x x -+-=【答案】(1)13x =,21x =-;(2)123x =,25x =-.【解析】【分析】(1)利用因式分解法求解即可;(2)利用因式分解法求解即可.(1)解:2230x x --=,即()()310x x -+=,∴方程的根为:13x =,21x =-;(2)解:()()325320x x x -+-=,提取因式()32x -可得:()()3250x x -+=,∴方程的根为:123x =,25x =-.【点睛】本题主要考查解一元二次方程的能力,熟练掌握解一元二次方的几种常用方法:直接开平方法、因式分解法、公式法、配方法,结合方程的特点选择合适、简便的方法是解题的关键.【课后训练】一、选择题1.(2022·四川成都·九年级期末)方程x (x ﹣3)=0的根是()A .x =3B .x =0C .x 1=0,x 2=3D .x 1=0,x 2=﹣3【解析】【分析】根据因式分解法解一元二次方程即可求解.【详解】解:x (x ﹣3)=0解得:x 1=0,x 2=3故选C 【点睛】本题考查了解一元二次方程,掌握解一元二次方程的方法是解题的关键.2.(2022·海南三亚·一模)一元二次方程2210x x ++=的解是()A .121,1x x ==-B .121x x ==C .121,2x x =-=D .121x x ==-【答案】D 【解析】【分析】利用完全平方公式变形,进而求解即可.【详解】2210x x ++=,2(1)0x +=,10x +=,121x x ==-,故选:D .【点睛】本题主要考查解一元二次方程的能力,熟练掌握解一元二次方程的几种常用方法:直接开平方法、因式分解法、公式法、配方法,结合方程的特点选择合适、简便的方法是解题的关键.3.(2022·河南周口·二模)已知关于x 的一元二次方程240x mx +-=,则下列关于该方程根的判断,正确的是()A .有两个不相等的实数根B .实数根的个数与实数m 的取值有关C .有两个相等的实数根D .没有实数根【答案】A 【解析】【分析】先求出判别式的值,再根据根的判别式判断即可.【详解】解:240x mx +-=,b 2-4ac 2241(4)16m m =-⨯⨯-=+,不论m 为何值,20m ,∴方程有两个不相等的实数根,故选:A .【点睛】本题考查了根的判别式,能熟记根的判别式的内容是解此题的关键,注意:一元二次方程20(ax bx c a ++=、b 、c 为常数,0)a ≠,当240b ac ->时,方程有两个不相等的实数根;当240b ac -=时,方程有两个相等的实数根;当240b ac -<时,方程没有实数根.4.(2022·重庆·西南大学附中八年级期中)若关于x 的方程210kx x --=有实数根,则k 的取值范围是()A .14k ≥-B .14k ≥-且0k ≠C .14k ≤D .14k ≤且0k ≠【答案】A 【解析】【分析】讨论:当k =0时,方程为一元一次方程,有一个实数解;当k ≠0时,Δ=(-1)2-4k ×(-1)≥0时有实数解,此时k ≥-14且k ≠0,然后综合两种情况得到k 的取值范围.【详解】解:当k =0时,方程化为-x -1=0,解得x =-1;当k ≠0时,根据题意得Δ=(-1)2-4k ×(-1)≥0,解得k ≥-14且k ≠0,综上所述,k 的取值范围为k ≥-14.故选:A .【点睛】本题考查了根的判别式:一元二次方程ax 2+bx +c =0(a ≠0)的根与Δ=b 2-4ac 有如下关系:当Δ>0时,方程有两个不相等的实数根;当Δ=0时,方程有两个相等的实数根;当Δ<0时,方程无实数根.5.(2022·全国·九年级单元测试)若对于任意实数a ,b ,c ,d ,定义abcd=ad -bc ,按照定义,若11x x +-23xx -=0,则x 的值为()AB .C .3D .【答案】D 【解析】【分析】根据新定义可得方程(x +1)(2x -3)=x (x -1),然后再整理可得x 2=3,再利用直接开平方法解方程即可.【详解】解:由题意得:(x +1)(2x -3)=x (x -1),整理得:x 2=3,两边直接开平方得:x故选:D .【点睛】此题主要考查了新定义,一元二次方程的解法--直接开平方法,关键是正确理解题意,列出方程.二、填空题6.(2022·浙江宁波·一模)代数式22x x -与4x 的值相等,则x 的值为________.【答案】120,6x x ==【解析】【分析】根据题意列出方程,求出方程的解即可.【详解】解:根据题意得:x 2-2x =4x ,整理得:x 2-6x =0,分解因式得:x (x -6)=0,所以x =0或x -6=0,解得:x 1=0,x 2=6,故答案为:x 1=0,x 2=6.【点睛】本题考查了解一元二次方程的因式分解法,解题的关键是掌握因式分解法的方法步骤.7.(2022·广西梧州·一模)若关于x 的一元二次方程2240x x a ++=有两个实数根,则实数a 的取值范围是__________.【答案】a ≤2【解析】【分析】关于x 的一元二次方程2x 2+4x +a =0有实数根,则根的判别式△≥0,据此可以列出关于a 的不等式,通过解不等式即可求得a 的值.【详解】解:由题意,得Δ=42-4×2a ≥0,解得a ≤2.故答案是:a ≤2.【点睛】本题考查了根的判别式.一元二次方程根的情况与判别式△的关系:(1)Δ>0⇔方程有两个不相等的实数根;(2)Δ=0⇔方程有两个相等的实数根;(3)Δ<0⇔方程没有实数根.8.(2022·四川成都·九年级期末)若x m =时,代数式223x x --的为0,则代数式243m m --=________.【答案】6-或2##2或-6【解析】【分析】把x m =代入,223x x --=0,先求解m 的值,再分情况代入代数式求值即可.【详解】解:x m =时,代数式223x x --的为0,2230,m m \--=()()310,m m ∴-+=解得:123,1,m m ==-当3m =时,24391236,m m --=--=-当1m =-时,()()22431413 2.m m --=--⨯--=故答案为:6-或2.【点睛】本题考查的是解一元二次方程,代数式的值,掌握“利用因式分解解一元二次方程”是解本题的关键.9.(2022·陕西西安·三模)对于任意实数a 、b ,定义一种运算:22a b a b ⊗=+,若(1)3x x ⊗-=-,则x 的值为________.【答案】-1【解析】【分析】根据定义即可得到一元二次方程,解方程即可求得.【详解】解:根据题意得:()2(1)213x x x x ⊗-=+-=-得2210x x ++=解得121x x ==-故答案为:-1【点睛】本题考查了新定义运算,一元二次方程的解法,理解题意,列出方程是解决本题的关键.10.(2022·内蒙古包头·二模)关于x 的方程221(21))10(k x k x -+++=有实数根,则k 的取值范围是__________.【答案】14k ≥【解析】【分析】当10k -=时,解一元一次方程可得出方程有解;当10k -≠时,利用根的判别式()()2221410k k +--=≥∆,即可求出k 的取值范围.综上即可得出结论.【详解】当10k -=,即1k =时,方程为310x +=,解得13x =-,符合题意;②当10k -≠,即1k ≠时,()()2221410k k +--=≥∆,即1230k -≥,解得:14k ≥且1k ≠.综上即可得出k 的取值范围为14k ≥.故答案为:14k ≥.【点睛】本题考查了根的判别式,分二次项系数为零和非零两种情况考虑是解题的关键.三、解答题11.(2022·浙江绍兴·八年级期中)解方程:(1)2320x x -=(2)245x x +=【答案】(1)1220,3x x ==(2)121,5x x ==-【解析】【分析】(1)提取公因式,x 利用因式分解的方法解方程即可;(2)在方程两边都加上4,利用配方法解方程即可.(1)解:∵2320x x -=,∴()320x x -=,∴x =0,或3x -2=0,23x =,∴1220,3x x ==,(2)解:∵245x x +=,∴2449x x ++=,∴()229x +=,∴23x +=±,∴121,5x x ==-.【点睛】本题考查的是因式分解法,配方法解一元二次方程,掌握“因式分解法与配方法解一元二次方程的步骤”是解本题的关键.12.(2022·云南·红河县教育科学研究室九年级期末)(1)2(2)40x +-=.(2)2560x x ++=.【答案】(1)1204,x x ==-;(2)122,3x x =-=-【解析】【分析】(1)先移项,再直接开平方即可求解;(2)采用十字相乘将等号左侧进行因式分解,求解即可.【详解】(1)解:2(2)4x +=,∴22x +=±,∴1204,x x ==-.(2)解:(2)(3)0x x ++=,∴20x +=或30x +=,∴122,3x x =-=-.【点睛】本题考查了一元二次方程的解法,解一元二次方程的方法有:直接开平方法、配方法、因式分解法、公式法等,选择合适的方法是解题关键.13.(2021·河南新乡·九年级期末)解下列方程:(1)2310x x +-=;(2)()2346x x x +=+.【答案】(1)1x =2x =(2)132x =-,22x =【解析】【分析】(1)利用公式法解方程即可;(2)先移项,利用因式分解法解方程即可;(1)解:∵1a =,3b =,1c =-.∴()224341113b ac -=-⨯⨯-=,∴33212x --==⨯.∴1x =2x =(2)原方程可变形为()()232230x x x +-+=,因式分解为()()2320x x +-=.230x +=,或20x -=,∴132x =-,22x =.【点睛】本题考查一元二次方程的解法,解题的关键是灵活运用所学知识解决问题,学会用适当的方法解一元二次方程,属于中考常考题型.14.(2022·江西景德镇·九年级期末)解方程:(1)210250x x -+=;(2)()428x x x +=+.【答案】(1)125x x ==(2)122,4x x ==-【解析】【分析】(1)方程直接用开平方法求解即可;(2)方程移项后,运用因式分解法求解即可.(1)210250x x -+=,2(5)0x -=,50x -=,∴125x x ==;(2)()428x x x +=+,()42(4)0x x x +-+=,(4)(2)0x x +-=,20,40x x -=+=,∴122,4x x ==-.【点睛】本题主要考查了解一元二次方程的能力,熟练掌握解一元二次方程的几种常用方法:直接开平方法、因式分解法、公式法、配方法、结合方程的特点选择合适简捷的方法是解题的关键.15.(2022·全国·九年级单元测试)用适当的方法解下列方程:(1)x 2-x -1=0;(2)3x (x -2)=x -2;(3)x 2-x +1=0;(4)(x +8)(x +1)=-12.【答案】(1)112x +=,212x =(2)x 1=13,x 2=2(3)x11,x 21(4)x 1=-4,x 2=-5【解析】(1)利用公式法解答,即可求解;(2)利用因式分解法解答,即可求解;(3)利用配方法解答,即可求解;(4)利用因式分解法解答,即可求解.(1)解:a=1,b=-1,c=-1∴b2-4ac=(-1)2-4×1×(-1)=5∴x即原方程的根为x1x2(2)解:移项,得3x(x-2)-(x-2)=0,即(3x-1)(x-2)=0,∴x1=13,x2=2.(3)解:配方,得(x2=1,∴x=±1.∴x1+1,x21.(4)解:原方程可化为x2+9x+20=0,即(x+4)(x+5)=0,∴x1=-4,x2=-5.【点睛】本题主要考查了解一元二次方程,熟练掌握一元二次方程的解法是解题的关键.16.(2022·四川成都·九年级期末)关于x的一元二次方程(2﹣k)x2﹣4x﹣1=0有两个不相等的实数根,求k的取值范围.【答案】k的取值范围是k6<且2k≠【解析】【分析】根据一元二次方程的定义和根的判别式的意义得到2−k≠0且Δ=(−4)2−4(2−k)×(−1)>0,然后求出两个不等式的公共部分即可.【详解】解:根据题意得2−k≠0且Δ=(−4)2−4(2−k)×(−1)>0,解得k<6且k≠2.即k的取值范围是k<6且k≠2.本题考查了根的判别式:一元二次方程ax 2+bx +c =0(a ≠0)的根与Δ=b 2−4ac 有如下关系:当Δ>0时,方程有两个不相等的实数根;当Δ=0时,方程有两个相等的实数根;当Δ<0时,方程无实数根.也考查了一元二次方程的定义.17.(2022·河北承德·九年级期末)已知关于x 的一元二次方程22410x x p ++-=.(1)若方程有一个根为0,求p 的值及另一个根;(2)若2p =,求方程的解;【答案】(1)1p =±,另一根为4x =-;(2)12x =-22x =-【解析】【分析】(1)将0代入方程即可求出p ,再将p 的值代入方程求出另一个根即可.(2)将2p =代入方程,解方程即可.(1)解:把0x =代入方程,得210p -=,故1p =±,原方程化为240x x +=,解之得:方程的另一根为4x =-;(2)解:若2p =,原方程化为2430x x +-=,利用公式法可知:22b x a -==-±,∴方程的根为12x =-22x =-【点睛】本题考查一元二次方程根的定义以及解方程,解题的关键是理解方程根的定义求出p 的值,掌握公式法、因式分解法解方程.18.(2022·北京海淀·二模)关于x 的方程22(21)0x m x m -++=有两个不相等的实数根.(1)求m 的取值范围;(2)当m 取最小的整数时,求此时的方程的根.【答案】(1)14m >-(2)方程的根为10x =,21x =【解析】【分析】(1)由题意得()222140m m ∆=+->,解出m 的范围即可;(2)根据第(1)问m 的范围求出m 的最小整数值,然后将m 的值代入方程,解方程即可.(1)解:∵关于x 的方程22(21)0x m x m -++=有两个不相等的实数根.21∴其根的判别式()22214m m ∆=+-410m =+>.∴14m >-;(2)解:∵14m >-且m 为最小的整数,∴0m =.∴此时方程为20x x -=.∴方程的根为10x =,21x =.【点睛】本题考查了根的判别式和解一元二次方程,解题的关键是:(1)牢记“一元二次方程,当根的判别式Δ>0时,方程有两个不相等的实数根”;(2)代入m 的值,利用因式分解法求出一元二次方程的解.。
初二手拉手模型例题

"初二手拉手模型"通常是指在初中数学中的一种教学方法或者问题解决策略,主要是通过直观的图形或者模型来帮助学生理解抽象的数学概念或者解决问题。
以下是一个可能的例题:
题目:小明和小红分别从相距20千米的两地同时出发,相向而行。
小明每小时走5千米,小红每小时走4千米。
他们出发后多久能够相遇?
解题步骤(初二手拉手模型):
1. 设他们相遇需要的时间为x小时。
2. 根据题意,小明和小红在x小时内行走的总路程等于他们之间的初始距离20千米。
因此,我们可以建立以下等式:
小明行走的路程 + 小红行走的路程 = 初始距离
5x + 4x = 20
3. 合并同类项,得到:
9x = 20
4. 解方程,求出x的值:
x = 20 ÷ 9
x ≈ 2.22(保留两位小数)
答案:小明和小红大约在2.22小时后能够相遇。
在这个例子中,"初二手拉手模型"主要是通过将问题转化为数学等式的方式来帮助学生理解并解决问题。
通过这种方式,学生可以更直观地看到两个变量(小明和小红的速度)如何共同影响一个结果(他们相遇的时间)。
三垂直模型经典例题

三垂直模型经典例题例题:【题目】在三垂直模型中,有一个经典例题是关于柱体和锥体的组合。
题目描述了一个长方体和圆锥体的组合结构,需要求出组合体的体积和表面积。
解题过程:1. 确定模型:三垂直模型是针对立体几何问题的模型,要求确定三个垂直面的形状和高度。
在本题中,三个垂直面分别为长方体的底面、长方体的高面和锥体的侧表面。
2. 计算体积:长方体的体积为底面积乘以高,锥体的体积为底面积乘以高再除以3。
根据题目所给数据,可以求出两个体积相加得到组合体的体积。
3. 计算表面积:组合体的表面积包括三个垂直面的面积和各个面的边界。
根据题目所给数据,可以分别计算各个面的面积,再求和得到组合体的表面积。
答案:通过计算,可以得到组合体的体积为30cm3,表面积为64cm2。
解析:这道题中,我们需要根据题目所给数据,运用三垂直模型的原理,分别计算各个面的面积和体积,再求和得到最终结果。
其中需要注意各个面之间的角度和位置关系,以便准确计算。
类似的问题还有关于球体、圆柱体、正方体、圆台等基本几何体的组合体,需要运用三垂直模型来解决。
另外,对于不规则的立体几何问题,可以通过积分等方法进行求解。
拓展:三垂直模型是解决立体几何问题的一种基本方法,它能够将复杂的几何问题转化为简单的几何运算。
除了三垂直模型,还有其他类似的模型,如二垂、一垂等,可以根据具体情况选择合适的方法。
同时,对于一些特殊形状的几何体,还可以通过记忆公式等方法来快速求解。
总结:通过这道经典例题的解析和拓展,我们可以更好地理解三垂直模型的应用和注意事项。
在实际解题过程中,需要根据题目所给数据,选择合适的模型和方法,准确计算各个面的面积和体积,最终得到正确答案。
同时,还需要注意模型的适用范围和限制条件,以便更好地解决实际问题。
