最佳适应算法流程图
最佳适应算法
0K 操作系统[100K]
分 配 前 存 储 器 示 意 图
100K 作业A[40K] 140K 45K
185K 195K 225K 245K
作业C[10K] 30K 作业D[20K] 作业E[20K]
分 配 前 存 储 器 示 意 图
已分配表 序号 首址 大小 状态 1 100K 40K 已分配 2 160K 10K 已分配 3 185K 10K 已分配 4 225K 20K 已分配 5 245K 20K 已分配 6 回收作业B前 序号 首址 大小 状态 1 100K 40K 已分配 2 160K 10K 空白 3 185K 10K 已分配 4 225K 20K 已分配 5 245K 20K 已分配 6 回收作业B后
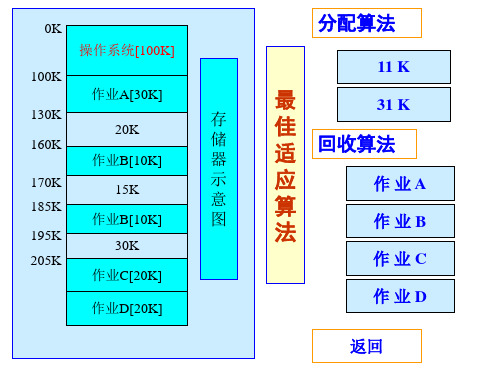
0K 操作系统[100K] 100K 作业A[30K] 130K 20K 160K 作业B[10K] 170K 185K 195K 205K 15K 作业B[10K] 30K 作业C[20K] 作业D[20K]
分配算法
11 K 存 储 器 示 意 图
最 31 K 佳 适 回收算法 应 作业A 算 作业B 法
225K 20K 245K 20K
225K 20K 245K 20K
回收作业E前
回收作业E后
首次适应算法已分配区变化示意图
未分配表 序号 1 2 3 4 5 6 首址 140K 170K 195K 大小 20K 15K 30K 状态 未分配 未分配 未分配 序号 1 2 3 4 5 6 首址 170K 140K 245K 195K 大小 状态 15K 未分配 20K 未分配 20K 未分配 30K 未分配
已分配表 序号 首址 大小 状态 1 100K 40K 已分配 2 160K 10K 已分配 3 185K 10K 已分配 4 225K 20K 已分配 5 245K 20K 已分配 6 分配前 序号 首址 大小 状态 1 100K 40K 已分配 2 160K 10K 已分配 3 185K 10K 已分配 4 225K 20K 已分配 5 245K 20K 已分配 6 170K 11K 已分配 分配后
操作系统实验_最佳适应算法最坏适应算法

学号专业计算机科学与技术姓名实验日期2017/11/23教师签字成绩实验报告【实验名称】基于顺序搜索的动态分区分配算法(二)【实验目的】理解在连续分区动态的存储管理方式下,如何实现贮存空间的分配与回收。
采用可变式分区管理,使用最佳适应算法实现主存空间的分配与回收。
采用可变式分区管理,使用最坏适应算法实现主存空间的分配与回收。
【实验原理】C++语言程序设计数据结构最佳适应算法最坏适应算法数据结构和符号说明1、boolROM[N];//定义主存信息,如果内存被占用,则标记为1,否则标记为0,设置内存单元为10242、pcbnum[20];//定义作业数组,最大支持20个作业3、typedefstructPcb//定义作业结构体,包括名称,开始时间,大小,是否执行状态{charname[10];intstart;intsize;intstate=0;}pcb;主要函数:voidfind_free_rom();//寻找空闲区voidsort1();//对空闲区进行排序从小到大voidsort1();//对空闲区进行排序从大到小voidshow();//显示函数voidinsert_pcb1(pcb&a);//最佳适应算法voidinsert_pcb2(pcb&a);//最坏适应算法voidinit();//初始化函数算法流程图:最佳适应算法:最坏适应算法:#include<stdio.h>#include<string.h>#defineN1024boolROM[N];intp=0;intcount=0;intfree_rom_counter=0;//空闲区数目typedefstructPcb//进程结构体{charname[10];intstart;intsize;//大小intstate=0;//状态}pcb;pcbnum[20];//进程数组typedefstructFree_rom//空闲区结构体{intnum;intstart;intend;intspace;//空闲区大小}Free_room;Free_romfree_rom[100];//空闲区数组voidshow()//显示空闲区信息{printf("****************************************************************\n\n" );printf("空闲区名\t开始地址\t\t大小\t\t结束地址\t\t\n");for(inti=1;i<=free_rom_counter;i++)printf("%d\t\t%d\t\t\t%d\t\t%d\t\t\n",free_rom[i].num,free_rom[i].start,free_ rom[i].space,free_rom[i].end);printf("\n");printf("****************************************************************\n\n" );}voidfind_free_rom()//寻找空闲区,更新空闲区数组{free_rom_counter=0;inti,j,p;for(i=0;i<N;i++)if(ROM[i]==0){p=i;for(j=i;j<N;j++){if(ROM[j]==0){i=j;continue;}if(ROM[j]==1)//找到就更新信息{free_rom_counter++;free_rom[free_rom_counter].num=free_rom_counter;free_rom[free_rom_counter].start=p;free_rom[free_rom_counter].end=j-1;free_rom[free_rom_counter].space=j-p;i=j+1;break;}}if(j==N&&ROM[j-1]==0)//对最后一个内存进行特殊处理{free_rom_counter++;free_rom[free_rom_counter].num=free_rom_counter;free_rom[free_rom_counter].start=p;free_rom[free_rom_counter].end=j-1;free_rom[free_rom_counter].space=j-p;}}}voidsort1()//最佳适应算法对空闲区从小到大排序{find_free_rom();Free_roma;for(inti=1;i<free_rom_counter;i++)for(intj=1;j<free_rom_counter;j++)if(free_rom[j].space>free_rom[j+1].space){a=free_rom[j];free_rom[j]=free_rom[j+1];free_rom[j+1]=a;}}voidsort2()//最坏适应算法对空闲区从大到小排序{find_free_rom();Free_roma;for(inti=1;i<free_rom_counter;i++)for(intj=1;j<free_rom_counter;j++)if(free_rom[j].space<free_rom[j+1].space){a=free_rom[j];free_rom[j]=free_rom[j+1];free_rom[j+1]=a;}}voidinit()//初始化{for(inti=0;i<N;i++)ROM[i]=0;}voidinput(pcb&a)//输入{charname[10];printf("输入进程名\n");scanf("%s",&);printf("输入进程大小\n");scanf("%d",&a.size);}voidinsert_pcb1(pcb&a)//最佳适应算法插入进程{find_free_rom();sort1();inti,j,k;for(i=1;i<=free_rom_counter;i++)//判断插入if(a.size<=free_rom[i].space){for(j=free_rom[i].start;j<free_rom[i].start+a.size;j++) ROM[j]=1;a.state=1;a.start=free_rom[i].start;num[count++]=a;break;}if(i==free_rom_counter+1)//插入失败printf("可用空间不足!\n");}voidinsert_pcb2(pcb&a)//最坏适应算法插入{find_free_rom();sort2();inti,j,k;for(i=1;i<=free_rom_counter;i++)if(a.size<=free_rom[i].space){for(j=free_rom[i].start;j<free_rom[i].start+a.size;j++)//寻找ROM[j]=1;a.state=1;a.start=free_rom[i].start;num[count++]=a;break;}if(i==free_rom_counter+1)//插入失败printf("可用空间不足!\n");}voidDelete(pcb&a)//内存中释放进程{inti;for(i=a.start;i<a.start+a.size;i++)ROM[i]=0;//更新内存信息,更新进程状态数组a.state=0;printf("删除成功\n");find_free_rom();}intmain()//主函数{init();find_free_rom();intchoose1;intchoose;charname[10];printf("1、最佳适应算法\n");//主界面printf("2、最坏首次适应算法\n");scanf("%d",&choose1);pcba;do{printf("\n\n1、插入进程\n");printf("2、删除进程\n");printf("3、显示进程信息\n");printf("4、显示空余内存信息\n");scanf("%d",&choose);if(choose==1)//选择{input(a);if(choose1==1)insert_pcb1(a);elseinsert_pcb2(a);}elseif(choose==2){printf("输入删除进程的名字\n");scanf("%s",&name);for(inti=0;i<count;i++)if(!strcmp(num[i].name,name))Delete(num[i]);}elseif(choose==3){printf("****************************************************************\n\n" );printf("进程名\t\t开始地址\t\t大小\t\t结束地址\t\t\n");//输出内存信息for(inti=0;i<count;i++)if(num[i].state!=0)printf("%s\t\t%d\t\t\t%d\t\t%d\t\t\n",num[i].name,num[i].start,num[i].size,nu m[i].size+num[i].start-1);printf("\n****************************************************************\n\ n");}elseif(choose=4){find_free_rom();show();}elsebreak;}while(1);return0;}截图:构造如下空闲区:此时插入一个进程G,大小为80H,应插入到第二块空闲区再插入一个大小为30的进程H,应插入到第三块中再插入一个小进程,大小为5,插入到第二块空闲区,查看进程信息和空闲区信息:最佳适应算法成立。
动态分区分配算法描述

动态分区分配算法描述一、引入动态分区分配算法:在动态分区分配方式中,当很多个空闲分区都能满足需求时,应该选择哪个分区进行分配?二、首次适应算法(First Fit)算法思想:每次都从低地址开始查找,找到第一个能满足大小的空闲分区。
如何实现:空闲分区以地址递增的次序排列。
每次分配内存时顺序查找空闲分区链(或空闲分区表),找到大小能满足要求的第一个空闲分区。
三、最佳适应算法(Best Fit)算法思想:由于动态分区分配是一种连续分配方式,为各进程分配的空间必须是连续的一整片区域。
因此为了保证当“大进程”到来时能有连续的大片空间,可以尽可能多地留下大片的空闲区,即优先使用更小的空闲区。
如何实现:空闲分区按容量递增次序链接。
每次分配内存时顺序查找空闲分区链(或空闲分区表),找到大小能满足要求的第一个空闲分区。
缺点:每次都选最小的分区进行分配,会留下越来越多的、很小的、难以利用的内存块。
因此这种方法会产生很多的外部碎片。
四、最坏适应算法(Worst Fit)又称最大适应算法(Largest Fit)算法思想:为了解决最佳适应算法的问题——即留下太多难以利用的小碎片,可以在每次分配时优先使用最大的连续空闲区,这样分配后剩余的空闲区就不会太小,更方便使用。
如何实现:空闲分区按容量递减次序链接。
每次分配内存时顺序查找空闲分区链(或空闲分区表),找到大小能满足要求的第一个空闲分区。
重新排序:空闲分区按容量递减次序链接缺点:每次都选最大的分区进行分配,虽然可以让分配后留下的空闲区更大,更可用,但是这种方式会导致较大的连续空闲区被迅速用完。
如果之后有“大进程”到达,就没有内存分区可用了。
五、邻近适应算法(Next Fit)算法思想:首次适应算法每次都从链头开始查找的。
这可能会导致低地址部分出现很多小的空闲分区,而每次分配查找时,都要经过这些分区,因此也增加了查找的开销。
如果每次都从上次查找结束的位置开始检索,就能解决上述问题。
第十一讲存储器管理之连续分配方式

第十一讲存储器管理之连续分配方式所谓连续分配方式:是指为一个用户程序分配一个连续的内存空间。
又可把连续分配方式分为:单一连续分配,固定分区分配,动态分区分配,动态重定位分区分配,四种方式。
1 单一连续分配(单独分区分配)最简单的一种存储管理方式,但只能用于单用户、单任务的OS中。
概念:单一连续分配就是整个主存区域的用户空间均归一个用户作业使用。
存储管理方法:将内存分为系统区(内存低端,分配给OS用)和用户区(内存高端,分配给用户用)。
其中用户区是指除了系统区外的内存空间,提供给用户程序使用。
采用静态分配方式,即作业一旦进入内存,就要等待它运行结束后才能释放内存。
主要特点:管理简单,只需小量的软件和硬件支持,便于用户了解和使用。
但因内存中只装入一道作业运行,内存空间浪费大,各类资源的利用率也不高。
例子:一个容量为256KB的内存,操作系统占用32KB,剩下224KB全部分配给用户作业,如果一个作业仅需64KB,那么就有160KB的存储空间被浪费。
2 固定分区分配分区分配方式是满足多道程序设计需要的一种最简单的存储管理方法。
2.1 思想:将内存分成若干个分区(大小相等/不相等),除OS占一区外,其余的每一个分区容纳一个用户程序。
这样来实现多道并发。
2.2 分区划分方法:分区大小相等,分区大小不等。
但事先必须确定,在运行时不能改变。
即分区大小及边界在运行时不能改变。
2.3 内存分配:首先:要先建立一张分区说明表或使用表,以记录分区号、分区大小、分区的起始地址及状态(已分配或未分配)。
其次:当某个用户程序要装入内存时,由内存分配程序检索分区说明表,从表中找出一个满足要求的尚未分配的分区分配该程序,同时修改说明表中相应分区的状态;若找不到大小足够的分区,则拒绝为该程序分配内存。
第三:当程序执行完毕,释放占用的分区,管理程序将修改说明表中相应分区的状态为未分配,实现内存资源的回收。
2.4 特点主要特点:管理简单,但因作业的大小并不一定与某个分区大小相等,从而使一部分存储空间被浪费。
首次适应算法和最佳适应算法【讲解】

首次适应算法和最佳适应算法是动态存储分配解决方案研究的内容,所以本文对这两种算法的讨论是通过研究动态存储管理来进行的。
一、存储管理的基本问题:存储管理讨论的基本问题是:1)、系统如何应用户的“请求”执行内存分配动作?2)、系统如何对用户不再使用后“释放”的内存执行回收动作,以保证为新的“用户请求”提供内存分配?内存的分配可以以静态方式进行,内存空间被分割为固定大小的若干内存块,用户的请求到达只要找到一块空闲的内存块予以分配即可,很显然静态存储分配的好处主要是实现比较方便,效率高,程序执行中系统需要做的事情比较简单。
然而实际情况下提出“请求”的用户可能是进入系统的一个作业,也可能是程序执行过程中的一个动态变量。
“请求”需要获得的内存容量大小不一,这种做法造成了对程序大小的严格的限制,使某些问题不能够合理的解决,此外,也会造成内存空间的浪费。
动态存储管理就是确定如何满足一个个内存“请求”,如何更合理的使用有限的内存空间的一种内存分配解决方案,它以能够依据用户的请求依次进行内存空间的分配和回收,能够尽可能少的使用有限的空闲内存空间,最大限度的保证后续“请求”的可满足性为最终目的。
二、关于动态分配方案的分析:通常我们将已分配给用户是用的一段连续的内存空间称为“占用块”,将未分配给任何用户的一段连续的内存空间称为“可利用空间块”或者“空闲块”,我们在这里的描述将使用“占用块”和“空闲块”这两个概念。
整个内存区在没有任何用户进入和运行的情况下只有一个空闲块,即整个可供用户“请求”使用的用户内存区域。
随着不断的有用户请求进入系统,并依次获得系统为其分配的内存,使得整个内存区域逐渐被分割成两大部分:低地址区域包含若干占用块;高低址区域是空闲内存区域。
经过一段时间后,有的用户运行结束,它们所占用的内存区释放后转变为一个个空闲块,这就使整个内存区域呈现出占用块和空闲块交错相隔的状态。
而此时,如果再有新的用户“请求”到达,那么,系统如何为这个“请求”进行内存分配呢?在肯定动态存储管理的前提下,我们可以采取两种方案解决这个问题,一种解决方案是系统继续把高地址的空闲块分配给用户,而不理会低地址区域是否有结束执行的用户释放的内存块,直到剩余的高地址区域的空闲块不能满足新的用户“请求”,分配操作无法再进行下去时,才去回收结束执行的用户释放的内存块,并重新组织内存,进而完成内存分配。
内存管理中一些算法

内存管理中⼀些算法在内存管理中存在这两类算法:⼀类是内存分配算法,⼀类是页⾯置换算法内存分配算法:是指怎么从连续的逻辑地址空间上分配内存地址给进程。
常见内存分配算法及优缺点如下: (1)⾸次适应算法。
使⽤该算法进⾏内存分配时,从空闲分区链⾸开始查找,直⾄找到⼀个能满⾜其⼤⼩要求的空闲分区为⽌。
然后再按照作业的⼤⼩,从该分区中划出⼀块内存分配给请求者,余下的空闲分区仍留在空闲分区链中。
该算法倾向于使⽤内存中低地址部分的空闲分区,在⾼地址部分的空闲分区很少被利⽤,从⽽保留了⾼地址部分的⼤空闲区。
显然为以后到达的⼤作业分配⼤的内存空间创造了条件。
缺点在于低址部分不断被划分,留下许多难以利⽤、很⼩的空闲区,⽽每次查找⼜都从低址部分开始,这⽆疑会增加查找的开销。
(2)循环⾸次适应算法。
该算法是由⾸次适应算法演变⽽成的。
在为进程分配内存空间时,不再每次从链⾸开始查找,⽽是从上次找到的空闲分区开始查找,直⾄找到⼀个能满⾜要求的空闲分区,并从中划出⼀块来分给作业。
该算法能使空闲中的内存分区分布得更加均匀,但将会缺乏⼤的空闲分区。
(3)最佳适应算法。
该算法总是把既能满⾜要求,⼜是最⼩的空闲分区分配给作业。
为了加速查找,该算法要求将所有的空闲区按其⼤⼩排序后,以递增顺序形成⼀个空⽩链。
这样每次找到的第⼀个满⾜要求的空闲区,必然是最优的。
孤⽴地看,该算法似乎是最优的,但事实上并不⼀定。
因为每次分配后剩余的空间⼀定是最⼩的,在存储器中将留下许多难以利⽤的⼩空闲区。
同时每次分配后必须重新排序,这也带来了⼀定的开销。
(4)最差适应算法。
最差适应算法中,该算法按⼤⼩递减的顺序形成空闲区链,分配时直接从空闲区链的第⼀个空闲分区中分配(不能满⾜需要则不分配)。
很显然,如果第⼀个空闲分区不能满⾜,那么再没有空闲分区能满⾜需要。
这种分配⽅法初看起来不太合理,但它也有很强的直观吸引⼒:在⼤空闲区中放⼊程序后,剩下的空闲区常常也很⼤,于是还能装下⼀个较⼤的新程序。
操作系统 首次最佳适应算法

学号专业姓名实验日期教师签字成绩实验报告【实验名称】采用可变式分区管理,使用首次获最佳适应算法实现内存分配与回收【实验目的与原理】1、理解首次获最佳适应算法的内涵,并熟练掌握该算法。
2、学会可变式分区管理的原理是即在处理作业过程中建立分区,使分区大小正好适合作业的需要,并且分区个数是可以调整的。
3、当有一个新作业要求装入主存时,必须查空闲区说明表,从中找出一个足够大的空闲区没有时应将空闲区一分为二。
为了便于快速查找,要不断地对表格进行紧缩,即让“空表目”项留在表的后部。
4、当一个作业执行完成时,作业所占用的分区应归还给系统。
作业的释放区与空闲区的邻接分以下四种情况考虑:①释放区下邻(低地址邻接)空闲区;②释放区上邻(高地址邻接)空闲区③释放区上下都与空闲区邻接;④释放区与空闲区不邻接。
【实验内容】#include<stdio.h>#include<iostream>#include<string>using namespace std;const int MAXJOB=100;//定义表最大记录数typedef struct node{int front;int length;char data[20];}job;job frees[MAXJOB];//定义空闲区表int free_quantity;job occupys[MAXJOB];//定义已分配区表int occupy_quantity;//初始化函数void initial(){int i;for(i=0;i<MAXJOB;i++){frees[i].front=-1;frees[i].length=0;strcpy(frees[i].data,"free");occupys[i].front=-1;occupys[i].length=0;strcpy(occupys[i].data," ");}free_quantity=0;occupy_quantity=0;}//创建空闲分区表int creatfree(){FILE *fp;char fname[20];cout<<"请输入空闲区数据文件来源的文件名:"; cin>>fname;if((fp=fopen(fname,"r"))==NULL){cout<<"错误,文件打不开,请检查文件名"<<endl; }else{while(!feof(fp)){fscanf(fp,"%d\t%d\n",&frees[free_quanti ty].front,&frees[free_quantity].length);free_quantity++;}cout<<"空闲的分区表已建立!\n";return 1;}return 0;}void sort()//将free空间安首地址从小到大的顺序排列{int i,j,p;for(i=0;i<free_quantity-1;i++){p=i;for(j=i+1;j<free_quantity;j++){if(frees[j].front<frees[p].front){p=j;}}if(p!=i){frees[free_quantity]=frees[i];frees[i]=frees[p];frees[p]=frees[free_quantity];}}}//显示函数void show(){int i;cout<<endl<<"----------------------------------------------------------"<<endl;cout<<"当前空闲表:"<<endl;cout<<" 起始地址长度状态"<<endl;for(i=0;i<free_quantity;i++){cout.setf(2);cout.width(12);cout<<frees[i].front;cout.width(10);cout<<frees[i].length;cout.width(8);cout<<frees[i].data<<endl;}cout<<endl<<"----------------------------------------------------------"<<endl;cout<<"当前已分配表:"<<endl;cout<<" 起始地址长度占用作业名"<<endl;for(i=0;i<occupy_quantity;i++){cout.setf(2);cout.width(12);cout<<occupys[i].front;cout.width(10);cout<<occupys[i].length;cout.width(8);cout<<occupys[i].data<<endl;}cout<<endl<<"----------------------------------------------------------"<<endl;}//最先适应分配算法void assign(){char job_name[20];int job_length;int i,j,flag,t;cout<<"请输入新申请内存空间的作业名和空间大小:";cin>>job_name;cin>>job_length;flag=0;for(i=0;i<free_quantity;i++){if(frees[i].length>=job_length)//如果空闲空间I的长度〉作业长度{flag=1; //空闲标志位就置1 }}if(flag==0){cout<<endl<<"对不起,当前没有能满足你申请长度的空闲内存,请稍候再试!"<<endl;}else{t=0;i=0;while(t==0)//为空闲区间的时候{if(frees[i].length>=job_length){t=1;}i++;//如果空闲空间I的长度不大于作业长度,I加一,判断下一个空间}i--;occupys[occupy_quantity].front=frees[i] .front;strcpy(occupys[occupy_quantity].data,jo b_name);occupys[occupy_quantity].length=job_len gth;occupy_quantity++;if(frees[i].length>job_length)//如果空间的长度大于作业的长度,{frees[i].front+=job_length;frees[i].length-=job_length;}else{for(j=i;j<free_quantity-1;j++){frees[j]=frees[j+1];}free_quantity--;cout<<"内存空间成功:)"<<endl;}}}//撤消作业void cancel(){char job_name[20];int i,j,flag,p=0;int front;int length;cout<<"请输入要撤消的作业名:";cin>>job_name;flag=-1;for(i=0;i<occupy_quantity;i++){if(!strcmp(occupys[i].data,job_name))//当输入作业名匹配时{flag=i;front=occupys[i].front;length=occupys[i].length;}}if(flag==-1){cout<<"没有这个作业名"<<endl;}else{//加入空闲表for(i=0;i<free_quantity;i++){if((frees[i].front+frees[i].length)==fr ont)//上空{if(((i+1)<free_quantity)&&(frees[i+1].f ront==front+length))//下空{frees[i].length=frees[i].length+frees[i +1].length+length;for(j=i+1;j<free_quantity;j++){frees[j]=frees[j+1];}free_quantity--;p=1;}else{frees[i].length+=length;p=1;}}if(frees[i].front==(front+length))//下空上不空{frees[i].front=front;frees[i].length+=length;//第i 个空闲区间的长度=第i个空闲区间的长度+lengthp=1;}}if(p==0)//上下空闲区都不空{frees[free_quantity].front=front;frees[free_quantity].length=length;free_quantity++;}//删除分配表中的该作业for(i=flag;i<occupy_quantity;i++){occupys[i]=occupys[i+1];}occupy_quantity--;}}void main(){int flag=0;int t=1;int chioce=0;cout<<"*********** xxxxxxxxx***********\n"; initial();flag=creatfree();while(flag==1){sort();cout<<" 可变分区存储管理模拟系统"<<endl;cout<<" 1.申请空间 "<<endl;cout<<" 2.撤消作业 "<<endl;cout<<" 3.显示空闲表和分配表"<<endl;cout<<" 0.退出"<<endl;cout<<"请选择:";cin>>chioce;switch(chioce){case 1:assign();break;case 2:cancel();break;case 3:show();break;case 0:flag=0;break;default:cout<<"选择错误!"<<endl;}}}实验结果显示:【实验小结】本实验难度在两个方面,一是首次最佳适应算法assign(),这里我用的是结构体数组来存储空闲分区;二是对已分配分区的释放,这里同样采取结构体数组来存储已分配分区,用cancle()函数来实现。
存储管理首次、最佳、最坏适应算法

最佳适应算法最佳适应算法是从全部空闲区中找出能满足作业要求的、且大小最小的空闲分区的一种计算方法,这种方法能使碎片尽量小。
找到:满足要求的自由分区分配排序:从小到大含义最佳适应算法(Best Fit):它从全部空闲区中找出能满足作业要求的、且大小最小的空闲分区,这种方法能使碎片尽量小。
为适应此算法,空闲分区表(空闲区链)中的空闲分区要按从小到大进行排序,自表头开始查找到第一个满足要求的自由分区分配。
该算法保留大的空闲区,但造成许多小的空闲区。
应用问题Best fit算法等价于装箱问题,举例如下:装箱问题:有体积为V的箱子N个,体积为Vi的物品M个,求使得物品全部能够装入箱子,箱子数量的最小值。
假设 V=6 M=10,V1,V2,...,V10分别为:3 4 4 3 5 1 2 5 3 1。
计算过程如下:第一步按物品体积降序排序:5 5 4 4 3 3 3 2 1 1第二步:取未装箱的最大值5装入第一个箱子。
第三步:判断第一个箱子是否已满,不满且剩余空间为1,搜寻剩下体积小于等于1的物品填入箱子1,箱子1填满。
第四步:重复第二,第三步,直到所有物品装入箱子为止,得到箱子数量为6. 6即时本例N的最小值。
最坏适应算法特点:扫描整个空闲分区或链表优点:可使剩下的空闲分区不至于太小最坏适应算法(worst fit)最坏适应分配算法要扫描整个空闲分区或链表,总是挑选一个最大的空闲分区分割给作业使用。
该算法要求将所有的空闲分区按其容量从大到小的顺序形成一空闲分区链,查找时只要看第一个分区能否满足作业要求。
优点:可使剩下的空闲分区不至于太小,产生碎片的几率最小,对中、小作业有利,同时该算法查找效率很高。
缺点:会使存储器中缺乏大的空闲分区。
首次适应算法首次适应算法从空闲分区表的第一个表目起查找该表,把最先能够满足要求的空闲区分配给作业,这种方法目的在于减少查找时间。
为适应这种算法,空闲分区表(空闲区链)中的空闲分区要按地址由低到高进行排序。
